
图1 单体结构震害预测研究思路
Fig.1 Diagram of seismic damage prediction for a building
自 19世纪初,人们在建造房屋时便逐渐有了提高房屋抗震能力的意识和举措,随着社会经济的不断发展和建筑抗震设计规范的不断更新完善,新建建筑结构的抗震能力也在不断提升。同时,科学家们意识到在不断提高新建建筑抗震能力的同时,必须对现有结构抗震能力和潜在危害进行估计,进而对不满足抗震要求的建筑结构采取抗震加固、改建等措施,制定综合防御对策,提高房屋综合抗震能力,从而促使了震害预测理论研究工作的飞速发展[1]。对于党政机关、学校、医院等重要建筑物开展震害预测工作尤为必要[2]。
美国和日本是开展震害预测工作较为广泛且较早的国家。1964年日本在新泻地震发生后成立了地震部,并对制定震害预测方法的工作进行了布置,自1965年开始了震害预测的研究工作[3]。1969年,美国 Algermissen对各种烈度下的木结构房屋破坏率做了研究,自此开始了震害预测方法的研究工作;20世纪七八十年代开展了大量的震害预测工作,形成了 NOAA/USGS方法,编制了建筑物(ATC-13)[4]和生命线工程(ATC-25)[5]震害预测方法等;于 90年代初逐步形成了地震灾害损失预测工作的基本工作框架;1997年开发出以地震动参数作为输入的应用软件HAZUS97地震风险评估软件并得到广泛应用。其他国家在震害预测研究工作中也取得了一些重要成果,如D’Ayala[6]在葡萄牙里斯本市的震害预测研究工作中,建立了五类房屋的易损性曲线;Kustu等[7]以Monte Carlo法计算一个城市中的建筑物在未来地震中的损失等。Loureneo等[8]对葡萄牙 58座历史教堂开展了易损性研究,提出了一种简化的古建筑地震易损性指标;Safar等[9]利用弹塑性位移反应谱,提出了基于位移的易损性估计方法,同年,Pasticier等[10]利用SAP2000对古建筑进行IDA分析,并利用分析结果对其地震易损性进行了评估;Rota和Penna[11]利用TREMURI[12]程序对典型结构进行了Pushover和增量动力分析,得到了其易损性曲线;Karbassia等[13]等用离散单元建立结构模型,结合增量动力分析方法,进行非线性动力分析,对结构进行了基于性能的地震易损性分析。
我国的震害预测工作是在 1980年开始的,中国地震局工程力学研究所(当时为国家地震局工程力学研究所)等16个单位对豫北地震重点监视区进行了房屋的震害预测工作。我国在“七五”“八五”“九五”期间,开展了大量的震害预测和地震损失评估方面的工作,尹之潜等[1]国内专家在震害预测和损失评估方面做了大量的研究工作,并取得了显著的研究成果。张令心等[14]利用拉丁超立方采样技术和非线性地震反应时程分析,对多层砖砌体住宅进行计算分析,建立了多层砖砌体住宅结构的易损性曲线。钟德理、冯启民[15]基于多步简化的 Pushover(MSP)方法给出了各类结构单体和群体建筑物易损性指数与峰值加速度的关系曲线。刘晶波、于晓辉等[16―17]通过 Pushover分析建立性能水平与结构极限破坏状态的对应关系,结合弹塑性动力时程分析,进行结构地震易损性分析。赵桂峰等[18]引入基于性态抗震设防思想,将村镇建筑分为农村、乡镇、县城三个层次,分别进行了相应的易损性分析。孙柏涛等[19]首次提出分区分类的建筑物抗震能力分类评价方法及地震易损性研究,建立了不同区域各类建筑物地震易损性分析模型。
目前国内外单体建筑结构的震害预测方法大致分为:历史震害统计法、专家评估法、模糊类比法、半经验半理论法、结构理论计算方法和动态分析法 6种方法[20],分别从不同角度或根据不同理论对建筑结构的震害预测进行了尝试,有一定的适用性和优越性,同时也存在着以下几方面问题:1) 结构类型不同的建筑物所采用的单体震害预测方法不同,给震害预测工作带来了很多不便;2) 各种震害预测方法所用的震害资料具有一定的局限性,没有普遍适用性;3) 现有震害预测方法不能很好地适应城镇不断发展、防震减灾能力不断提升的需求[21]。
房屋各影响因素对结构震害的影响程度存在明显差异,且具有不确定性,理论上无法用一个确定性数值来描述。针对以上特点,本文提出了一种基于模糊层次分析模型(FAHP)的单体建筑结构震害预测方法。模糊层次分析法通过充分利用模糊数学中的新成果,将层次分析法(AHP)[22]扩展到模糊环境中,是一种综合考虑人为判断的模糊性的定性与定量相结合的系统分析方法。本文总结整理了影响建筑结构震害的主要因素,通过构造模糊互补判断矩阵,建立了适用于各类建筑结构的快速简便的单体震害预测方法。本方法已分别在2015年和2017年应用于 HAZ-China地震应急快速评估系统和大中城市地震灾害情景构建系统平台中。
某类结构的地震易损性矩阵代表了该类结构在不同地震烈度下平均意义上的抗震能力,事实上形成矩阵时抽样的各个样本有其独立的特性,抗震能力亦有差别。本文试图通过某城市或地区已知的某种结构类型在不同烈度下的易损性矩阵和该类结构影响抗震能力的影响因子推出其单体样本的抗震能力。
通常情况下研究某一城市或者区域房屋抗震能力时多采用以下方法:1) 对抽样样本逐栋调查结构的基础资料,采用某种单体预测的方法分析每一栋抽样结构在不同烈度下的震害指数,然后对抽样结构进行统计分析得到该类结构的易损性矩阵,该做法如果抽样的样本数量较大的时候能够较全面的反映该地区房屋结构的抗震能力,但是一座城市和区域有数十万或者百万栋房屋,即便抽样率达到5%~8%时其工作量也是相当大的,且未作抽样样本结构的抗震能力也没有得到体现;2) 根据大量的震害资料和已经做过的震害预测地区或城市的易损性矩阵,通过对比将要工作的目标地区结构类型、自然环境等得到该地区不同结构的易损性矩阵,但是这种方法也不能逐栋反映单体结构的抗震能力。
本文是基于某类结构已有震害矩阵情况下,将矩阵中不同烈度的平均震害指数作为该类结构震害指数的基准值,通过地震现场调查中的震害经验和震害预测分析提炼出各类建筑物抗震能力主要影响因素(如砌体结构抗震能力的主要影响因素是设防状况、建造年代、房屋用途、层数等),利用模糊层次分析法计算得到各类建筑结构不同影响因素对建筑物整体抗震能力的影响程度,即用权重值来表示;由于不同地区影响因素对抗震能力的影响程度有所差别,根据地震现场工作及震害预测工作经验,对不同地区震害影响因素的权重值进行修正;通过考虑各影响因素中不同影响因子对建筑结构的贡献程度,计算得到其震害影响因子值;采用综合加权法计算得到预模拟单体结构震害指数,根据震害指数与震害等级的对应关系,最终预测得出单体结构在不同地震烈度下的破坏等级。

图1 单体结构震害预测研究思路
Fig.1 Diagram of seismic damage prediction for a building
对于某个预模拟的单体建筑结构在某一地震烈度下的震害指数Di,首先计算该结构所在城市或地区同种结构类型在该烈度下的基准震害指数Dib,然后考虑该类结构主要抗震影响因素,分析不同影响因素对结构抗震能力的影响程度,通过模糊层次分析法计算得到各影响因素权重值mω,通过对不同影响因素中各震害影响因子进行修正,得到各影响因子的修正系数kjn,利用综合加权平均法计算得到预模拟单体结构的综合影响因子值,最终计算得到预测结构模拟震害指数Di。由上述分析得到单体结构的震害指数Di的计算公式为:
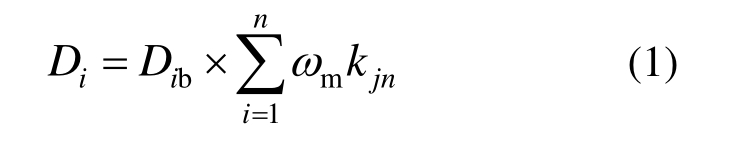
式中:Di为预测单体结构震害指数;Dib为结构基准震害指数;kjn为结构考虑第n个影响因素第j个影响因子修正系数;mω为结构各影响因素的权重。
1.2.1 基准震害指数
建筑结构的震害等级通常分为基本完好、轻微破坏、中等破坏、严重破坏和毁坏5个等级。为了定量地描述地震强度和破坏等级,20世纪70年代刘恢先、胡聿贤等[23]地震工程专家提出了震害指数的概念。结构震害指数是房屋破坏等级的量化描述,即对结构震害程度的定量描述,一般用0~1之间的数值来表示结构的震害程度,如0表示结构完好,1表示结构已经完全毁坏。表1为5个破坏等级所对应的震害指数情况[1]。
表1 震害指数与震害等级对应关系
Table 1 Corresponding relation between seismic damage index and damage degree
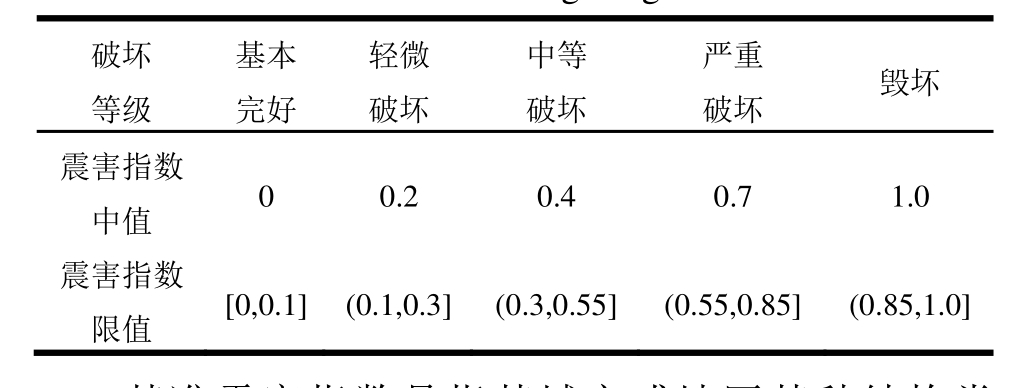
破坏等级基本完好轻微破坏中等破坏严重破坏 毁坏震害指数中值 0 0.2 0.4 0.7 1.0震害指数限值 [0,0.1] (0.1,0.3](0.3,0.55](0.55,0.85](0.85,1.0]
基准震害指数是指某城市或地区某种结构类型房屋在特定烈度下的平均震害程度,即震害指数的平均值或群体建筑结构的平均震害指数。本文将其作为评定某个单体结构破坏情况的基准震害指数。在不同地震烈度下,基准震害指数计算公式为:
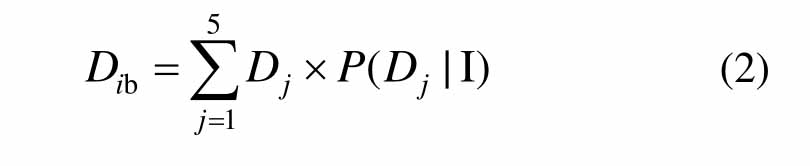
式中:Dib为某类结构在I烈度下的基准震害指数;Dj为结构发生j级破坏的震害指数中值;P(Dj|I)为某类结构在I烈度下发生j级破坏的概率值。
1.2.2 影响因素权重的确定
历次破坏性地震震害表明,结构类型不同的房屋,其主要震害影响因素是不同的,且同一影响因素对不同的结构类型而言其震害影响程度也是不同的。基于此,本文在对历史地震震害资料总结的基础上,对不同结构类型采用不同的影响因素。
1) 结构类型分类
一般情况房屋建筑主要有两种分类方法:按结构类型分类和按使用功能分类。国内外专家对于建筑结构类型的分类也不尽相同。如美国联邦紧急事务管理署(FEMA)编制形成的建筑物(ATC-13)将建筑物和构筑物划分为50多种类型;尹之潜在进行地震易损性分析研究中将我国建筑物分为20种类型,见参考文献[1]。
本文依据GB/T 19428—2013《地震灾害预测及其信息管理系统技术规范》,参考第六次人口普查数据、地震应急数据库数据等,将房屋建筑分成高层建筑、多层钢筋混凝土框架结构、多层砌体结构、砖木结构、土木结构及其他6种结构类型。
2) 影响因素的选择
建筑结构的震害形式多种多样,震害程度更是不尽相同。在同一地区遭受同样地震强度的建筑物,导致其不同程度破坏的主要原因是房屋自身的抗震能力存在很大的差别。对于同一种结构类型而言,影响其抗震性能的因素很多,如多层砌体结构的震害与诸多因素有关,在综合考虑结构构造特点、震害分析结果及结构力学模型的基础上,可概括为以下14条:设防标准、建造年代、承重墙厚、砂浆强度等级、层数、用途、屋盖类别、屋盖重量、楼板类别、砌筑方式、平立面规则程度、房屋现状、建筑物场址和场地土类别[24]。
针对以上影响因素,本文开展了详细的调研和分析。首先,统计整理了“七五”以来我国做过的近100余个城市和区域房屋震害预测研究成果及唐山大地震以来近百次破坏性地震震害资料分析结果。分别对设防标准、建造年代、层数、用途、屋盖类别、平立面规则程度等因素进行了定性和定量分析,且在以往研究成果的基础上得出,设防标准、建造年代、用途、层数、平立面规则程度是影响各类房屋抗震能力的几个主要影响因素[25]。本文在综合分析了上述六种结构类型建(构)造特点及震害特征后,针对每种结构类型自身的综合特性,同时考虑不同因素数据收集的难易程度,选取了各类建筑结构的主要震害影响因素,见表2。
表2 各类建筑结构主要震害影响因素
Table 2 Earthquake damage factors of all kinds of structures
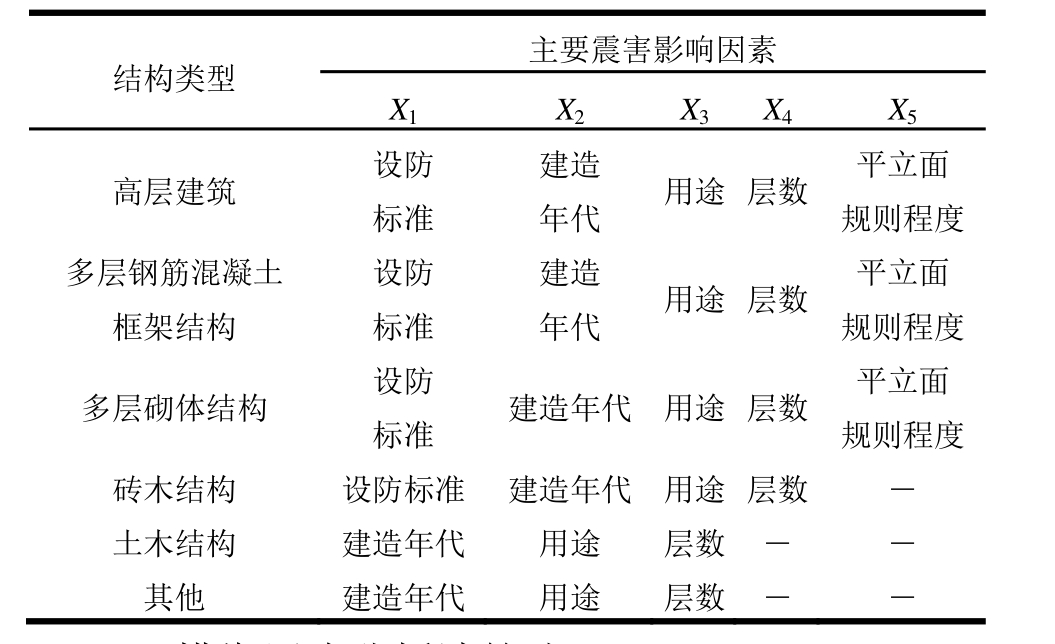
结构类型 主要震害影响因素X1X2X3X4X5高层建筑 设防标准 年代 用途 层数 平立面规则程度建造多层钢筋混凝土框架结构 年代 用途 层数 平立面规则程度多层砌体结构 设防设防标准建造标准 建造年代 用途 层数 平立面规则程度砖木结构 设防标准 建造年代 用途 层数 ―土木结构 建造年代 用途 层数 ― ―其他 建造年代 用途 层数 ― ―
3) 模糊层次分析法简述
层次分析法(AHP)是美国匹茨堡大学运筹学家Thomas Saaty在20世纪70年代提出的一种多因素分析、多指标分级的评价方法。模糊层次分析法是将模糊数学思想和方法同层次分析法相结合,建立模糊互补判断矩阵,通过数学变换将模糊互补判断矩阵转化为模糊一致性判断矩阵,并利用行和归一化方法计算其权重并对其进行一致性检验[26]。
模糊层次分析法中不同因素间两两进行比较判断时,根据一个因素对另一个因素的重要程度来表示,得到模糊判断矩阵,若该矩阵满足如下性质:

则该矩阵称之为模糊互补判断矩阵。同时,为了定量描述两两因素比较的重要程度,通常采用表3标度方式将其数量化[27]。
表3 模糊判断矩阵标度值及含义
Table 3 Scaling value and meaning of the fuzzy judgement matrix

标度值 含义 备注0.5 同等重要 两元素相比较,同等重要0.6 稍微重要 两元素相比较,一元素比另一元素稍微重要0.7 明显重要 两元素相比较,一元素比另一元素明显重要0.8 重要得多 两元素相比较,一元素比另一元素重要得多0.9 极端重要 两元素相比较,一元素比另一元素极端重要0.1,0.2,0.3,0.4 反比较若元素ai与元素aj相比较得到判断rij,则原素aj与元素ai相比较得到的判断为1r= -rjiij
由此构建评价指标的判断矩阵A。
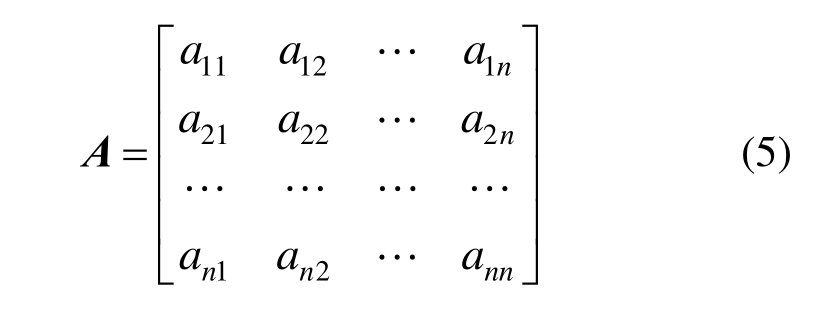
对模糊互补判断矩阵A按行求和,见式(4),并按照式(5)作如下数学变换,得到模糊一致性矩阵![]()
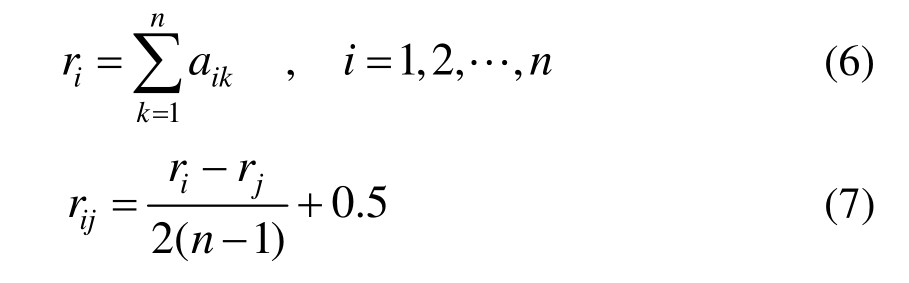
4) 权重取值的确定
徐泽水[26]推导给出了求解模糊互补判断矩阵权重的一种通用公式,该公式不仅充分包括了模糊互补判断矩阵的优良特性及其判断信息,而且计算量小,为实际应用带来很大的方便。具体求解公式如下:
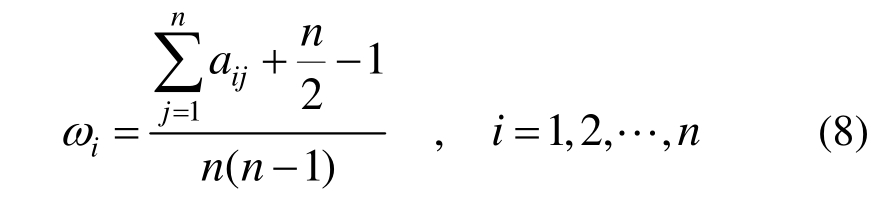
5) 一致性检验
上述公式计算得到的权重值是否合理还需进行一致性检验,本文根据模糊判断矩阵的相容性[28]来检验其一致性。
① 假设对于两个模糊矩阵A和B均为模糊判断矩阵,则:称为A和B的相容性指标。
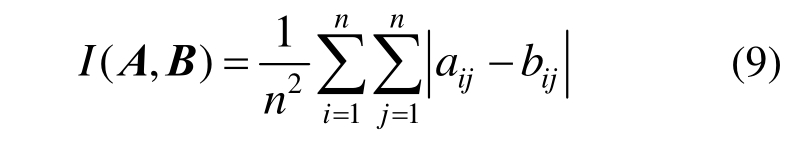
② 设![]() 是模糊判断矩阵A的权重向量
是模糊判断矩阵A的权重向量![]()
 则称n阶矩阵:
则称n阶矩阵:
为判断矩阵A的特征矩阵。
当相容性指标I(A,B)小于或等于决策者的态度T时,认为判断矩阵为满意一致性的。T越小说明决策者对模糊判断矩阵的一致性要求越高,一般可取T=0.1。
一般情况下,对于某一项决策需要多位专家参与。上述方法亦可推广到群体决策中。假设有m个专家给出模糊互补判断矩阵![]() 对矩阵
对矩阵![]() 分别求权重并进行一致性检验,理论证明,模糊互补判断矩阵在一致性检验通过的情况下,它们的综合判断矩阵也是满足一致性检验要求的[29],并将m个权重集的均值作为因素集的权重分配向量。
分别求权重并进行一致性检验,理论证明,模糊互补判断矩阵在一致性检验通过的情况下,它们的综合判断矩阵也是满足一致性检验要求的[29],并将m个权重集的均值作为因素集的权重分配向量。
6) 基于模糊层次分析法建立的各影响因素权重
① 构造模糊互补判断矩阵。
表4 高层建筑主要震害影响因素模糊判断矩阵
Table 4 Fuzzy judgement matrix of earthquake damage factors for high-rise buildings

影响因素X1X2X3X4X5X10.5 0.6 0.7 0.7 0.75X20.4 0.5 0.6 0.6 0.7X30.3 0.4 0.5 0.5 0.6X40.3 0.4 0.5 0.5 0.6X50.25 0.3 0.4 0.4 0.5
表5 多层钢筋混凝土框架结构主要震害影响因素模糊
判断矩阵
Table 5 Fuzzy judgement matrix of earthquake damage factors for multistory reinforced concrete frame structures

影响因素X1X2X3X4X5X10.5 0.6 0.7 0.7 0.75X20.4 0.5 0.6 0.6 0.7X30.3 0.4 0.5 0.5 0.6X40.3 0.4 0.5 0.5 0.6X50.25 0.3 0.4 0.4 0.5
针对给出的六种常见结构类型,采用模糊层次分析法,分别构建六种结构类型的模糊互补判断矩阵,具体见表 4~表 9。其中比较系数的选取,本文主要参考了尹之潜、孙柏涛等地震工程专家的文献[30―32],同时,参考了大量振动台试验和计算分析的结果,并以问卷打分的方式咨询了同行专家判断。
表6 多层砌体结构主要震害影响因素模糊判断矩阵
Table 6 Fuzzy judgement matrix of earthquake damage factors for multi-story masonry structures
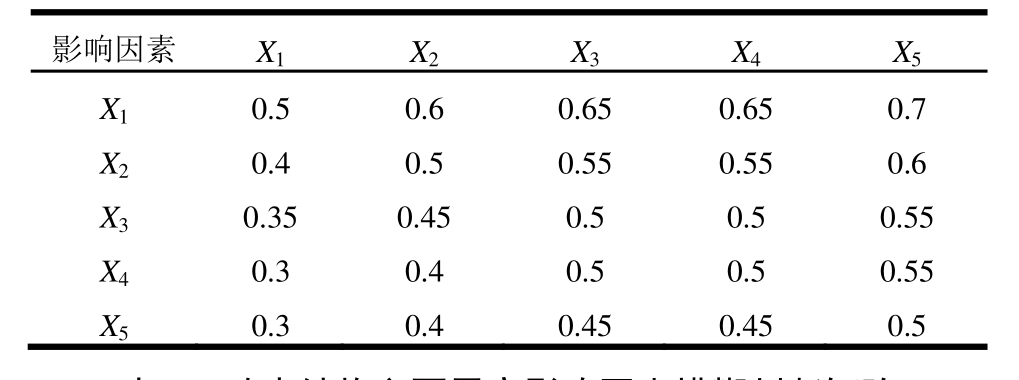
影响因素X1X2X3X4X5X10.5 0.6 0.65 0.65 0.7X20.4 0.5 0.55 0.55 0.6X30.35 0.45 0.5 0.5 0.55X40.3 0.4 0.5 0.5 0.55X50.3 0.4 0.45 0.45 0.5
表7 砖木结构主要震害影响因素模糊判断矩阵
Table 7 Fuzzy judgement matrix of earthquake damage factors for brick-wood structures
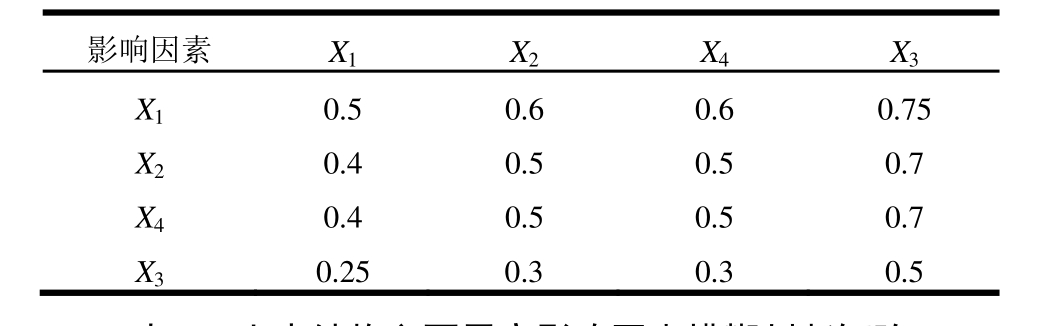
影响因素X1X2X4X3X10.5 0.6 0.6 0.75X20.4 0.5 0.5 0.7X40.4 0.5 0.5 0.7X30.25 0.3 0.3 0.5
表8 土木结构主要震害影响因素模糊判断矩阵
Table 8 Fuzzy judgement matrix of earthquake damage factors for earth structures
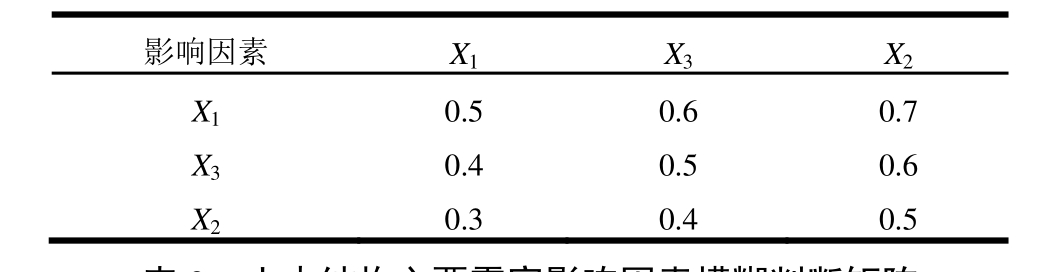
影响因素X1X3X2X10.5 0.6 0.7X30.4 0.5 0.6X20.3 0.4 0.5
表9 土木结构主要震害影响因素模糊判断矩阵
Table 9 Fuzzy judgement matrix of earthquake damage factors for other structures
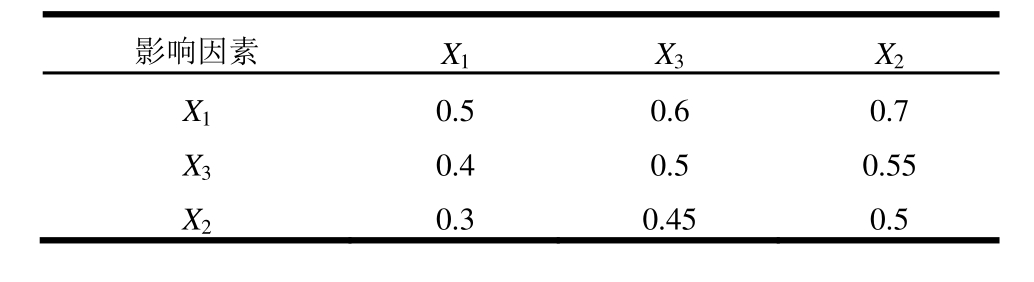
影响因素X1X3X2X10.5 0.6 0.7X30.4 0.5 0.55X20.3 0.45 0.5
② 各影响因素权重值的确定。
根据上述模糊层次分析计算方法,利用式(6),分别计算求得各影响因素的权重值,具体见表10。
表10 六种结构类型各影响因素权重
Table 10 Weight values of influence factors for the six types of structures
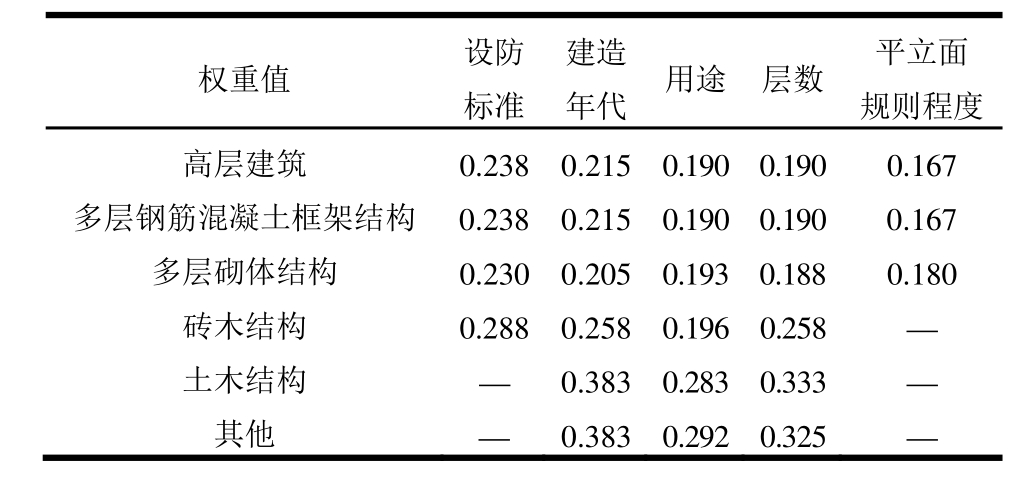
权重值 设防标准建造年代 用途 层数 平立面规则程度高层建筑 0.238 0.215 0.190 0.190 0.167多层钢筋混凝土框架结构 0.238 0.215 0.190 0.190 0.167多层砌体结构 0.230 0.205 0.193 0.188 0.180砖木结构 0.288 0.258 0.196 0.258 —土木结构 — 0.383 0.283 0.333 —其他 — 0.383 0.292 0.325 —
③ 一致性检验。
本文利用式(7)和式(8)对表10中各权重值的取值是否合理进行了检验。以高层建筑为例,给出了计算相容性指标的具体过程,根据高层建筑主要震害影响因素模糊判断矩阵A(表4),可计算得到其特征矩阵B,见表11。利用式(7),计算得到其相容性指标![]() 其他5种结构类型计算过程同高层建筑计算过程,检验结果见表12。
其他5种结构类型计算过程同高层建筑计算过程,检验结果见表12。
表11 高层建筑特征矩阵
Table 11 Characteristic Matrix for high-rise buildings
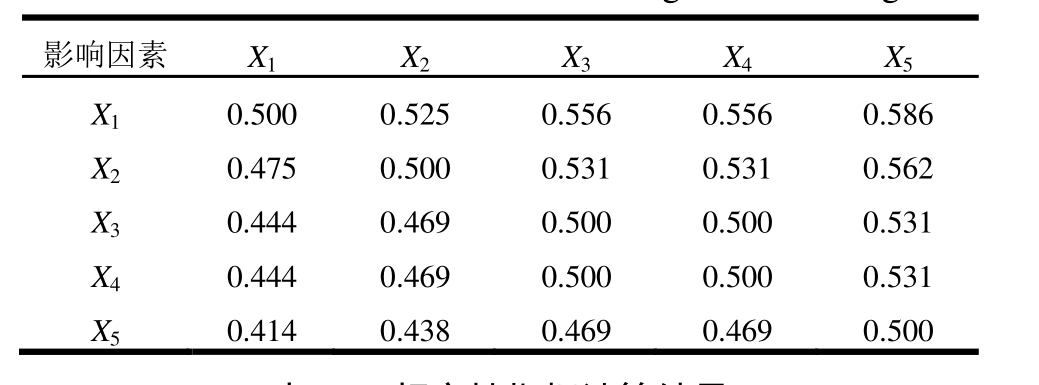
影响因素X1X2X3X4X5X10.500 0.525 0.556 0.556 0.586X20.475 0.500 0.531 0.531 0.562X30.444 0.469 0.500 0.500 0.531X40.444 0.469 0.500 0.500 0.531X50.414 0.438 0.469 0.469 0.500
表12 相容性指标计算结果
Table 12 Results of the compatibility index

结构类型 高层建筑 多层钢筋混凝土框架结构 多层砌体结构相容性指标 0.075 0.075 0.054结构类型 砖木结构 土木结构 其他相容性指标 0.071 0.055 0.048
经检验,计算得到六种结构类型的相容性指标都小于 0.1,因此认为六种结构类型的模糊判断矩阵都是满意一致的,且其权重的分配是合理的。
1.2.3 单体结构影响因子的修正
影响因子是表征某一影响因素在给定烈度下对房屋震害影响程度的物理量,有的因子对房屋抗震能力有提高的作用,如设防的建筑相对于未设防的建筑抗震能力强;有的因子削减结构的抗震能力,如不规则的建筑对结构抗震非常不利。因此,每个因子对房屋抗震能力的影响不能一概而论。针对表2中各类建筑结构的主要影响因素的选取,本文对近些年数次破坏性地震震害及历年的震害预测结果进行了统计分析,并对各种结构类型房屋的震害及震害预测数据进行了相关研究。
1) 设防标准
随着社会经济的迅猛发展及人们对抗震意识的不断提高,建筑结构的设防水准不断提高。但是在广大农村地区及部分经济发展水平较落后的地区,仍然存在大量的自建房未考虑设防情况或未严格按照规范要求进行抗震设防,加之老旧房屋仍广泛分布于我国大陆各个区域,目前仍有大量的建筑结构没有经过抗震设防。汶川地震、玉树地震等多次地震中,经过抗震设计或抗震加固同没有经过抗震设防的房屋建筑相比在地震中的破坏程度差异很大。
2) 建造年代
建造年代是影响房屋抗震能力的主要因素之一。主要体现在两个方面:一方面是房屋随着建造年代的增加,其老旧损坏程度增加,导致其整体抗震能力降低;另一方面,人类在建造房屋过程中不断发展和完善建筑抗震设计理念,新建结构抗御地震的能力在不断提高。因此,建造年代越久的房屋其抗震能力相对越差。
3) 建造层数
通过对历史典型地震震害和对不同层数建筑的计算分析得出,房屋建造的层数也是影响其抗震能力的一个重要因素,各版建筑抗震设计规范中对不同结构类型的层数和总高度都有严格的限制条件。而且结构类型不同的房屋其层数的影响程度有很大的差别,如砌体结构,由于其材料的脆性及构造措施等特点,层数对震害程度的影响比较明显。作者[25]曾将多层砌体结构 1979年~2001年的住宅类房屋和 1990年以后建造的钢筋混凝土房屋按层数统计了平均震害指数,展示了层数对震害程度的影响。
4) 房屋用途
为了确定某个结构破坏后对社会造成的影响,需要考虑结构的使用功能,即房屋的用途。使用功能不同,房屋整体设计、使用材料等大有不同。尹之潜等[32]将房屋建筑的使用功能分为居住房屋、办公用房屋、文化教育和医疗用房等6大类29个小类。本文通过考虑每种使用功能房屋的抗震能力差异,将其综合为三种用途:民用居住、公用办公和工业用生产。统计分析得出,住宅类易损性指数偏低,工业类易损性指数偏高。
5) 房屋平立面规则程度
一般来说,房屋的平面和立面布置是否规则,对房屋的抗震性能有很大影响。如结构布置不规则,结构质心同刚度中心不重合,则会产生扭转振动,加剧震害。如 1985年的墨西哥地震中,有些高层建筑由于结构不对称发生扭转,导致结构遭到严重破坏。
某一地区某一类建筑结构的震害矩阵能够综合反映该地区该类结构的总体抗震能力,其各烈度下的平均震害指数亦能表征该类结构在相应地震烈度下的抗震水平。基于此,本文以单个因子对平均震害指数的影响差异为出发点,考虑单个影响因子对已知震害矩阵的影响大小时,通过比较在单体样本数据库中去除及不去除该因子两种情况下震害矩阵各烈度下的平均震害指数的差别,进而得出这个因子对已知震害矩阵的贡献大小,即为影响因子的修正系数。具体计算步骤为[33]:
1) 建立不同地区各类建筑结构的震害数据库和震害预测数据库;
2) 选取数据库中不同结构类型房屋结构,分别计算其在某一地震烈度下的平均震害指数Di;
3) 在上述同样条件下,考虑某一影响因子对结构整体的贡献情况,即将包含这个因子的结构从样本数据中去掉,然后计算此时的平均震害指数Di[j];
4) 计算 2)和 3)两种情况下震害指数的相对变化,即为结构考虑第n个影响因素第j个影响因子修正系数kjn。
2008年5月12日汶川8.0级地震发生后,作者通过现场科学考察得到了大量的第一手震害资料。利用本方法对数十栋结构的破坏等级进行了验证,其结果吻合很好。本文选取都江堰市一栋5层多层砌体结构作为模拟结构,该结构为 1978年建造的设防学生公寓,平立面均匀布置。该栋房屋所处位置在汶川地震中实际地震烈度为Ⅸ度区,房屋鉴定结果为中等破坏[34]。

图2 都江堰多层砌体结构
Fig.2 The masonry structure in Dujiangyan City
利用考虑设防水准的建筑物群体震害预测方法[28],计算得到四川省砌体结构基准震害指数,见表13。利用式(9),分别计算得到各震害影响因子的修正系数,见表14。
表13 四川省砌体结构基准震害指数
Table 13 Standard seismic damage indexes of the multi-story masonry structures in Sichuan Province
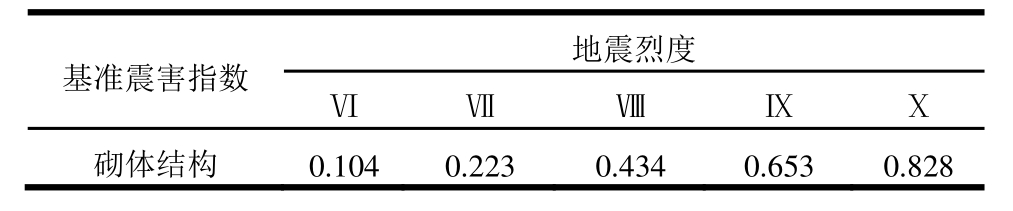
基准震害指数 地震烈度Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ砌体结构 0.104 0.223 0.434 0.653 0.828
表14 模拟结构各震害影响因子值
Table 14 Seismic damage impact factors of the predicted structure

震害影响因素建造年代建造层数房屋用途平立面规则程度设防标准震害影响因子值 0.95 0.92 0.83 0.65 0.65
最后,利用式(1)和表10,计算得到预模拟结构在不同地震烈度下震害指数,如表15所示。
该栋房屋所处位置在汶川地震中实际地震烈度为Ⅸ度区,从表 13可以看出,预模拟结构在地震烈度为Ⅸ度时震害指数为 0.519,对应表 1中中等偏重破坏震害等级。
同时,为了验证本文方法的可靠性和有效性,随机选取了曾做过震害预测工作城市的 30栋建筑物样本进行计算,本文仅列出其中的6栋样本,见表16。表中同时给出了利用尹之潜求解结构抗力方法[1]计算得到的单体震害预测结果。通过比较得出,两种方法计算得到的建筑物单体震害预测结果完全一致。
表15 模拟结构震害指数
Table 15 Seismic damage indexes of the predicted structure
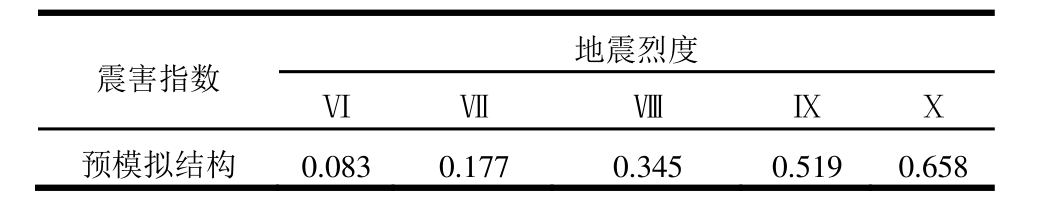
震害指数 地震烈度Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ预模拟结构 0.083 0.177 0.345 0.519 0.658
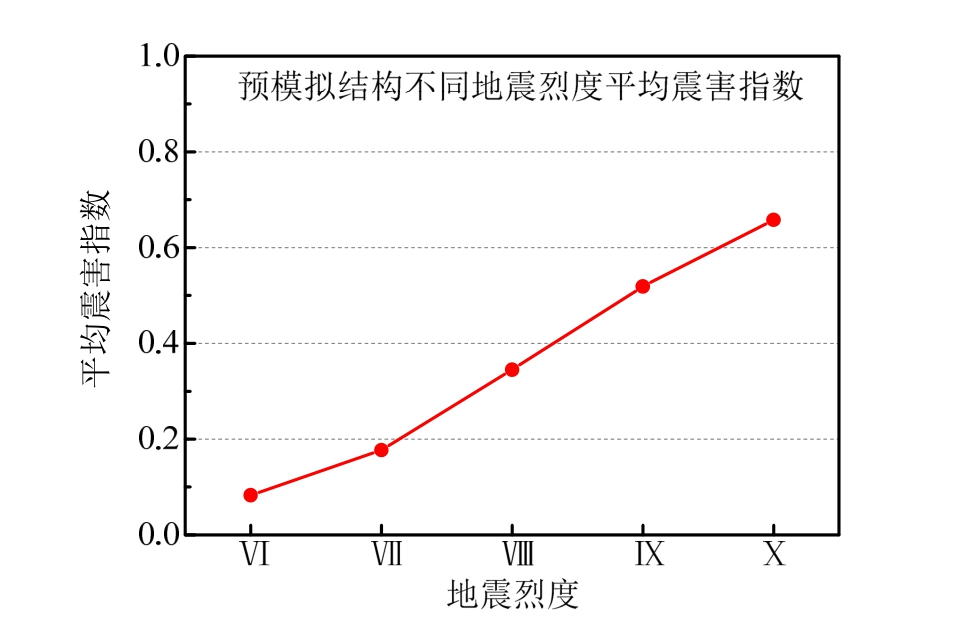
图3 预模拟结构不同地震烈度震害指数
Fig.3 Seismic damage indexes of the predicted structure under the different earthquake intensities
表16 两种方法计算结果比较
Table 16 Comparison of the two methods

编号 房屋名称 结构类型 烈度本文计算震害指数本文计算震害等级 尹之潜方法计算震害等级1 自贡市残疾人联合会住宅 砌体结构 8度 0.359 中等破坏 中等破坏2 自贡市自流井区五星街办事处珍珠山E23号房住宅 砌体结构 8度 0.736 严重破坏 严重破坏3 漳州市东铺头街道办事处县后居委会民房 砌体结构 8度 0.296 轻微破坏 轻微破坏4 厦门市佳丽花园公寓E楼 钢筋混凝土框架结构8度 0.085 基本完好 基本完好5 厦门市第五中学办公楼 钢筋混凝土框架结构8度 0.284 轻微破坏 轻微破坏6 天津市丸善食品有限公司办公楼 钢筋混凝土框架结构8度 0.236 轻微破坏 轻微破坏
本文通过研究一个城市或地区不同结构类型房屋建筑的地震易损性,提出了一种基于模糊层次分析的建筑物单体震害预测方法。通过计算不同结构类型各影响因素权重及各影响因素不同震害影响因子修正系数,采用综合加权法计算得到预模拟单体结构综合影响因子值,最终计算得到预测结构模拟震害指数,进而给出单体结构破坏等级。利用本文方法对汶川地震及曾做过震害预测城市的数十栋房屋进行了验算,计算结果与实际震害和震害预测报告中的结果完全一致。
该方法最大限度地开发和利用了已有群体震害结果及震害预测结果数据,同以往的单体震害预测方法相比,本文方法思路简明,易于实现,可大大减少现场调查及计算分析等工作量。但是预测结果准确性同选取的该地区结构的震害矩阵的合理性有关系,通常情况下采用该地区或相近地区实际震害矩阵或者模拟矩阵。
[1]尹之潜. 地震灾害及损失预测方法[M]. 北京: 地震出版社, 1996: 1―3, 28―31.Yin Zhiqian. Method of prediction for seismic disaster and loss [M]. Beijing: Seismological Press, 1996: 1―3,28―31. (in Chinese)
[2]韩博, 熊琛, 许镇, 等. 城市区域建筑物震害预测剪切层模型及其参数确定方法[J]. 工程力学, 2014, 31(增刊1): 73―85.Han Bo, Xiong Chen, Xu Zhen, et al. A multi-story concentrated-mass shear model for urban regional seismic damage prediction and associated parameter determination [J]. Engineering Mechanics, 2014,31(Supll 1): 73―85. (in Chinese)
[3]章在墉. 地震危险性分析及其应用[M]. 上海: 同济大学出版社, 1996 Zhang Zaiyong. Seismic hazard analysis and its applications [M]. Shanghai: Tongji University, 1996. (in Chinese)
[4]ATC-13, Earthquake damage evaluation data for California [S]. Advanced Technology Council, 1985.
[5]Risk Management Solutions, Inc. Earthquake loss estimation Method-HAZUS97 technical manual [M].Washington. D. C: National Institute of Building Sciences, 1997.
[6]D’Ayala D, Spence R, Oliveira C, et al. Earthquake loss estimation for europe’s historic town centres [J].Earthquake Spectra, 1997, 13(4): 773―793.
[7]Kustu O, Miller D D, Brokken S T. Development of damage functions for high-rise building components[EB]. 百度学术,http://xueshu.baidu.com/usercenter/paper/show?paperid=c2b9cf1af7aa6e8168cd686040dee1 a4&site=xueshu_se, 1982.
[8]Loureneo P B, Roque J A. Simplified indices for the seismic vulnerability of ancient masonry buildings [J].Construction and Building Materials, 2006, 20(4): 200―208.
[9]Safar M, Ghobarah A. Inelastic Response spectrum for simplified deformation based seismic vulnerability assessment [J]. Journal of Earthquake Engineering, 2008,12(2): 222―248.
[10] Pasticier L, Amadio C, Fragiacomo M. Nonlinear seismic analysis and vulnerability evaluation of a masonry building by means of the SAP2000 V. 10 cod [J].Earthquake Engineering and Structural Dynamics, 2010,37(3): 467―485.
[11] Rota M, Penna A, Magenes G. A methodology for deriving analytical fragility curves for masonry buildings based on stochastic nonlinear analyses [J]. Engineering Structures, 2010, 32(5): 1312―1323.
[12] Galasco A, Lagomarsino S, Penna A. TREMURI program: Seismic analyses of 3D masonry building [R].Italy, University of Genoa, 2009.
[13] Karbassi A, Nollet, Marie-José. Performance- based seismic vulnerability evaluation of masonry buildings using applied element method in a nonlinear dynamic-based analytical procedure [J]. Earthquake Spectra, 2013, 29(2): 399―426.
[14] 张令心, 江近仁, 刘洁平. 多层住宅砖房的地震易损性分析[J]. 地震工程与工程振动, 2002, 22(1): 49―55.Zhang Lingxin, Jiang Jinren, Liu Jieping. Seismic vulnerability analysis of multistory dwelling brick buildings [J]. Earthquake Engineering and Engineering Vibration, 2002, 22(1): 49―55. (in Chinese)
[15] 钟德理, 冯启民. 基于地震动参数的建筑物震害研究[J]. 地震工程与工程振动, 2004, 24(5): 46―51.Zhong Deli, Feng Qimin. Investigation on building destruction based on seismic coefficient [J]. Earthquake Engineering and Engineering Vibration, 2004, 24(5):46―51. (in Chinese)
[16] 刘晶波, 刘阳冰, 闫秋实, 等. 基于性能的方钢管混凝土框架结构地震易损性分析[J]. 土木工程学报, 2010,43(2): 39―47.Liu Jingbo, Liu Yangbing, Yan Qiushi, et al.Performance-based seismic fragility analysis of CFST frame structures [J]. China Civil Engineering Journal,2010, 43(2): 39―47. (in Chinese)
[17] 于晓辉, 吕大刚, 范峰. 基于易损性指数的钢筋混凝土框架结构地震损伤评估[J]. 工程力学, 2017, 34(1):69―75.Yu Xiaohui, Lü Dagang, Fan Feng. Seismic damage assessment of RC frame structures based on vulnerability index [J]. Engineering Mechanics, 2017, 34(1): 69―75.(in Chinese)
[18] 赵桂峰, 马玉红, 陈小飞. 村镇建筑基于性态标准的地震易损性分析[J]. 土木工程学报, 2014, 47(9): 1―8.Zhao Guifeng, Ma Yuhong, Chen Xiaofei. Vulnerability analysis of performance-based seismic design criteria for rural buildings [J]. China Civil Engineering Journal,2014, 47(9): 1―8. (in Chinese)
[19] 孙柏涛, 张桂欣. 中国大陆建筑物地震灾害风险分布研究[J]. 土木工程学报, 2017, 50(9): 1―7.Sun Baitao, Zhang Guixin. Study on seismic disaster risk distribution of buildings in mainland China [J]. China Civil Engineering Journal, 2017, 50(9): 1―7. (in Chinese)
[20] 程庆乐, 曾翔, 熊琛, 等. 区域建筑震害模拟方法分析对比[J]. 工程力学, 2017, 34(增1): 105―128.Cheng Qingle, Zeng Xiang, Xiong Chen, et al.Comparison of seismic damage simulation methods for different regional buildings [J]. Engineering Mechanics,2017, 34(Supll 1): 105―128. (in Chinese)
[21] Ngo T, Deb S K, Dutta A. Mitigation of seismic vulnerability of prototype low-rise masonry building using U-FREIs [J]. Journal of Performance of Constructed Facilities, 2018, 32(2): 04017136.
[22] 邓雪, 李家铭, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2014, 42(7): 93―100.Deng Xue, Li Jiaming, et al. Research on computation methods of AHP wight vector and its applications [J].Mathematics in Practice and Theory, 2014, 42(7): 93―100. (in Chinese)
[23] 胡聿贤. 地震工程学[M]. 北京: 地震出版社, 1988.Hu Yuxian. Earthquake engineering [M]. Beijing:Seismological Press, 1988. (in Chinese)
[24] 张桂欣, 孙柏涛. 多因素影响的建筑物群体震害预测方法研究[J]. 世界地震工程, 2010, 26(1): 26―30.Zhang Guixin, Sun Baitao. A method for earthquake damage prediction of building groups based on multiple factors [J]. World Earthquake Engineering, 2010, 26(1):26―30. (in Chinese)
[25] Sun Baitao, Zhang Guixin. Study on vulnerability matrices of masonry buildings of mainland China [J].Earthquake Engineering and Engineering Vibration,2018, 17(2): 251―259.
[26] 徐泽水. 模糊互补判断矩阵排序的一种算法[J]. 系统工程学报, 2001, 16(4): 311―314.Xu Zeshui. Algorithm for priority of fuzzy complementary judgement matrix [J]. Journal of Systems Engineering, 2001, 16(4): 311―314. (in Chinese)
[27] 姬东朝, 宋笔锋, 喻天翔. 基于模糊层次分析法的决策方法及其应用[J]. 火力与指挥控制, 2007, 32(11):38―41.Ji Dongchao, Song Bifeng, Yu Tianxiang. The method of decision-making based on FAHP and its application [J].Fire Control and Command Control, 2007, 32(11): 38―41. (in Chinese)
[28] 陈华友, 赵佳宝. 模糊判断矩阵的相容性研究[ J]. 运筹与管理, 2004, 13(1): 44―47.Chen Huayou, Zhao Jiabao. Research on compatibility of fuzzy judgement matrices [J]. Operations Research and Management Science, 2004, 13(1): 44―47. (in Chinese)
[29] 徐泽水. 模糊互补判断矩阵的相容性及一致性研究[J].解放军理工大学学报, 2002, 3(2): 94―97.Xu Zeshui. Research on compatibility and consistency of fuzzy complementary judgement matrices [J]. Journal of PLA University of Science and Technology, 2002, 3(2):94―97. (in Chinese)
[30] 孙柏涛, 张桂欣. 考虑设防水准的群体建筑物震害预测方法 [J]. 土木工程学报, 2013, 46(5): 117―121.Sun Baitao, Zhang Guixin. A method for earthquake damage prediction of building group considering seismic fortification level [J]. China Civil Engineering Journal,2013, 46(5): 117―121. (in Chinese)
[31] Sun Baitao, Zhang Guixin. The Wenchuan earthquake creation of a rich database of building performance [J].Science China Technological Sciences, 2010, 53(10):2668―2680.
[32] 尹之潜, 杨淑文. 地震损失分析与设防标准[M]. 北京:地震出版社, 2004: 74―80.Yin Zhiqian, Yang Shuwen. Seismic loss analysis and fortification criterion [M]. Beijing: Seismological Press,2004: 74―80. (in Chinese)
[33] 孙柏涛, 孙得璋. 建筑物单体震害预测新方法[J]. 北京工业大学学报, 2008, 34(7): 701―707.Sun Baitao, Sun Dezhang. New method of seismic damage prediction of single building [J]. Journal of Beijing University of Technology, 2008, 34(7): 701―707. (in Chinese)
[34] 孙柏涛. 汶川地震工程震害调查技术报告[R]. 哈尔滨: 中国地震局工程力学研究所, 2009.Sun Baitao. Technical report on seismic damage investigation of Wenchuan earthquake [R]. Harbin:Institute of Engineering Mechanics, China Earthquake Administration, 2009. (in Chinese)
SEISMIC DAMAGE PREDICTION FOR A SINGLE BUILDING BASED ON A FUZZY ANALYTICAL HIERARCHY APPROACH