表1 材料性能试验结果
Table 1 Experimental results of material properties
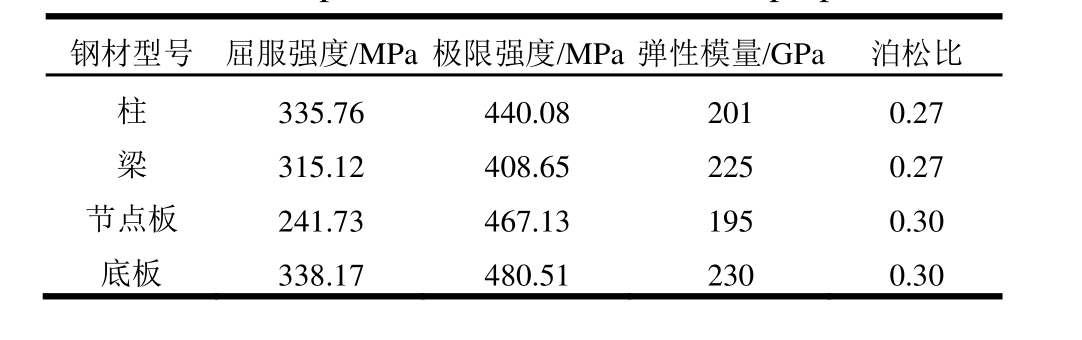
钢材型号 屈服强度/MPa 极限强度/MPa 弹性模量/GPa 泊松比柱 335.76 440.08 201 0.27梁 315.12 408.65 225 0.27节点板 241.73 467.13 195 0.30底板 338.17 480.51 230 0.30
冷弯薄壁型钢自重轻、节能、环保,轻质高强,材料性能得到充分发挥,制作安装方便,可以实现装配式施工,具有良好的抗震性能[1],当前已广泛应用到房屋建筑结构中[2]。为了探究冷弯薄壁C型钢结构的特性,国内外部分学者研究了冷弯薄壁C型钢结构的力学性能、抗震性能[3]。国外学者 Lim和Nethercot[4―6]对冷弯C型钢采用背靠背布置,并通过填板、螺栓相连接的屋脊和屋檐节点进行静力性能和抗震性能的研究。Shahbazian和Wang[7]对计算高温条件下冷弯薄壁C型钢柱屈曲承载力的直接强度法进行了研究。Dundu[8]对冷弯C型钢门式刚架提出了新的设计方法。Mohammed和Emad[9]对冷弯C型钢梁的转动性能进行了评价。国内学者黄川等[10]等建立了冷弯 C型钢梁柱连接节点的M-θ曲线,并对由自攻螺栓连接的该类型截面框架的受力状态进行研究。彭雄等[11]运用有限元对冷弯薄壁C型钢构件进行轴压和循环荷载作用下的力学分析。陈明等[12―15]运用试验和有限元模拟分析的方法对采用垫板连接的双肢冷弯薄壁C型钢节点和冷弯薄壁C型钢框架的抗震性能进行了研究,给出了该类结构的性能指标。
冷弯薄壁C型钢框架具有良好的抗震性能,但是抗侧移刚度较小,为了提高冷弯薄壁C型钢框架的抗侧移能力,在该框架内填钢板墙可提高该类框架的承载力和抗侧刚度。目前对这种内填钢板墙双肢C型钢框架(后简称钢板墙框架)的研究较少,本文对2榀三层单跨双肢冷弯薄壁C型钢框架进行拟静力试验,以是否采用内填钢板墙作为设计差异,对比试验现象与结果,验证内填钢板墙的优势,建立了内填钢板墙双肢C型钢框架有限元分析模型,并用试验结果进行过验证。考虑钢板墙高厚比、钢板墙高宽比、框架柱刚度系数等参数,分析各个参数下内填钢板墙框架的抗震性能,为内填钢板墙双肢C型钢框架提供参考。
2榀三层单跨双肢C型钢框架(KJ-1和KJ-2)柱、梁分别采用双肢 C220 mm×50 mm×20 mm×2.5 mm和双肢C140 mm×50 mm×20 mm×2.5 mm截面,中间节点板为8 mm厚热轧钢板,KJ-1为空框架,KJ-2为钢板墙框架,钢板墙采用非加肋薄钢板,全长、全高布置。试验框架按 1∶4的缩尺比例设计,如图1所示。
根据现行规范[16]的有关规定,对组成框架的梁、柱、节点板、底板进行材性测试,得到各材料的弹性模量、屈服强度、极限抗拉强度、泊松比等参数。材性测试所得材料物理力学指标如表1所示。
表1 材料性能试验结果
Table 1 Experimental results of material properties

钢材型号 屈服强度/MPa 极限强度/MPa 弹性模量/GPa 泊松比柱 335.76 440.08 201 0.27梁 315.12 408.65 225 0.27节点板 241.73 467.13 195 0.30底板 338.17 480.51 230 0.30


图1 框架尺寸 /mm
Fig.1 Dimensions of frame
1.3.1 加载装置
试验水平荷载施加采用如图2(a)所示的推拉千斤顶来施加,千斤顶两端采用铰接的方式与框架顶端和反力墙连接。在框架一层和二层梁中部两侧沿水平加载方向设置侧向限位装置,确保试件不会因为平面外刚度不足导致试验失败。按轴压比0.3对应施加竖向荷载 10 kN,采用如图 2(b)所示的定滑轮体系,可保证竖向荷载和柱顶的自由水平移动同步[17]。框架柱底板由4个地脚螺栓把框架固定在混凝土地梁上。
1.3.2 加载制度
试验采用荷载-位移混合加载方式[18],施加水平荷载前,先在柱顶上施加 10 kN的竖向荷载,同时缓慢加载完成。水平荷载的施加在框架的竖向荷载加载稳定后,开始对框架施加水平荷载。正式加载时先用10 kN加载步长力控制,每级循环1次,在框架屈服后用位移控制,位移加载步长是按框架屈服位移Δy来确定的,每级循环加载3次。当采集框架的荷载值降低到极限承载力的50%时停止试验。
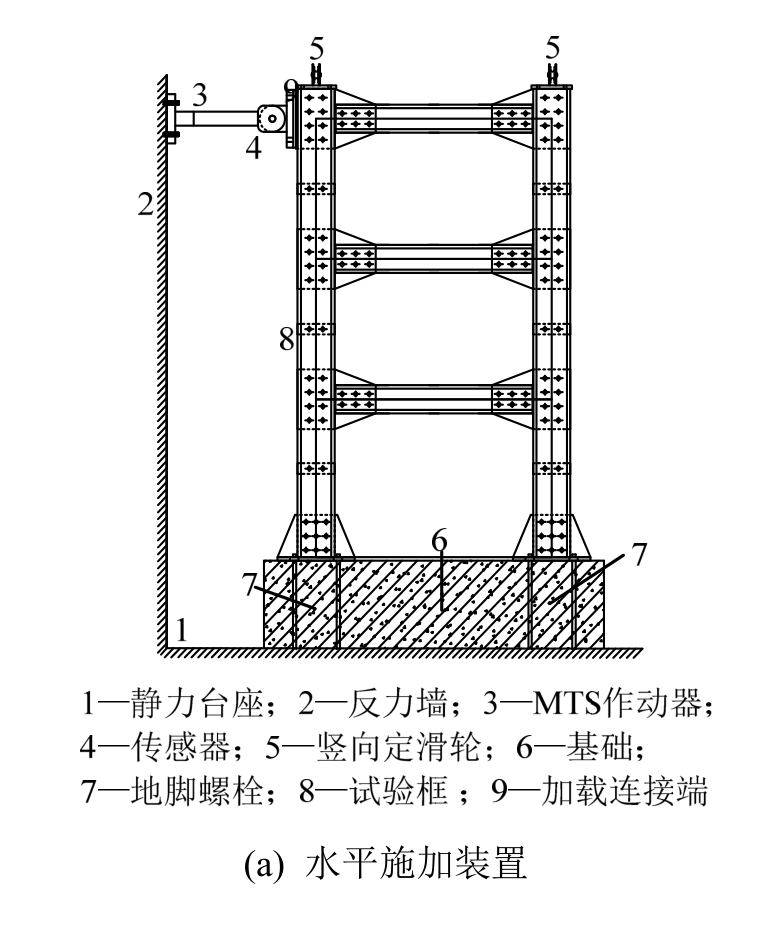
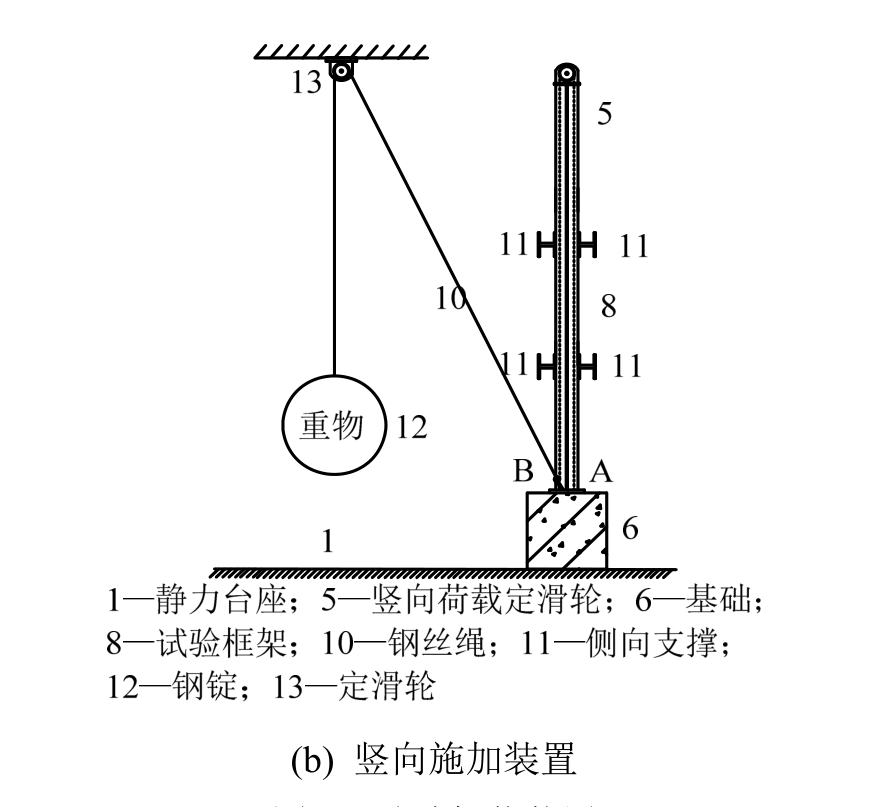
图2 试验加载装置
Fig.2 Loading rig used in the test
为了试验描述的方便,将框架的加载端定为左侧,非加载端定为右侧,将人与框架平行且左右对应站立时的前方称为前,后方称为后。
KJ-1加载初期框架没有明显的试验现象,加载的过程中伴有轻微声响。之后一层梁端腹板与翼缘交界处产生微小的局部变形如图3(a)所示,一层、二层梁左右端腹板均出现鼓曲。随着荷载的增加,一层梁左侧前后两肢下侧翼缘出现变形,同时,右侧柱脚前后两肢出现开裂如图3(b)。最后,框架柱左右柱脚严重变形。梁腹板发生鼓曲如图3(c),右侧后肢梁翼缘发生变形。框架破坏过程符合“强柱弱梁”、“强节点弱构件”的抗震设计要求。整体破坏如图3(d)所示。

图3 KJ-1破坏现象
Fig.3 Failure phenomena of KJ-1
KJ-2加载初期也没有明显的试验现象,只是在推拉转换的过程中伴有轻微的声响。之后框架左右柱脚微弱张开,各层钢板墙梁柱连接端附近出现微小的局部变形如图4(a)。随着荷载的增加,一层右侧梁端前后肢C型钢腹板张开,一层、二层梁与柱螺栓连接线上形成多条拉力带。最后,一层钢板墙出现一条宽而通长的连接左右柱的拉力带如图4(b)。二层钢板墙与梁、柱螺栓连接处屈曲变形严重,钢板上呈现两条拉力带。框架左右柱脚出现明显屈曲变形如图4(c),腹板局部屈曲严重。钢板墙框架破坏过程钢板墙形成了拉力带,有效地耗散能量。整体破坏如图4(d)所示。

图4 KJ-2破坏现象
Fig.4 Failure phenomena of KJ-2
2榀框架的水平荷载-位移滞回曲线如图5所示。KJ-1的滞回曲线为典型的“梭形”,屈服之前,框架变形较小,荷载-位移曲线斜率稳定不变;进入弹塑性阶段后,滞回环更加饱满;进入位移控制阶段,框架的承载力降低,变形增大,最后发生破坏。可以看出,KJ-1的变形能力和抗震性能良好。KJ-2在加载初期滞回环基本重合,框架处于弹性阶段时,框架的初始刚度大,滞回曲线呈现一条过原点的直线;框架处于弹塑性阶段时,刚度呈现出下降趋势,滞回环面积逐渐增大;进入位移控制加载阶段,钢板墙发生屈曲变形,刚度及承载力明显下降,滞回曲线出现捏拢现象,面积进一步增大,可以看出带钢板墙的框架与空框架相比,承载力、初始刚度有了明显的提升,同时耗能能力、延性也表现良好。
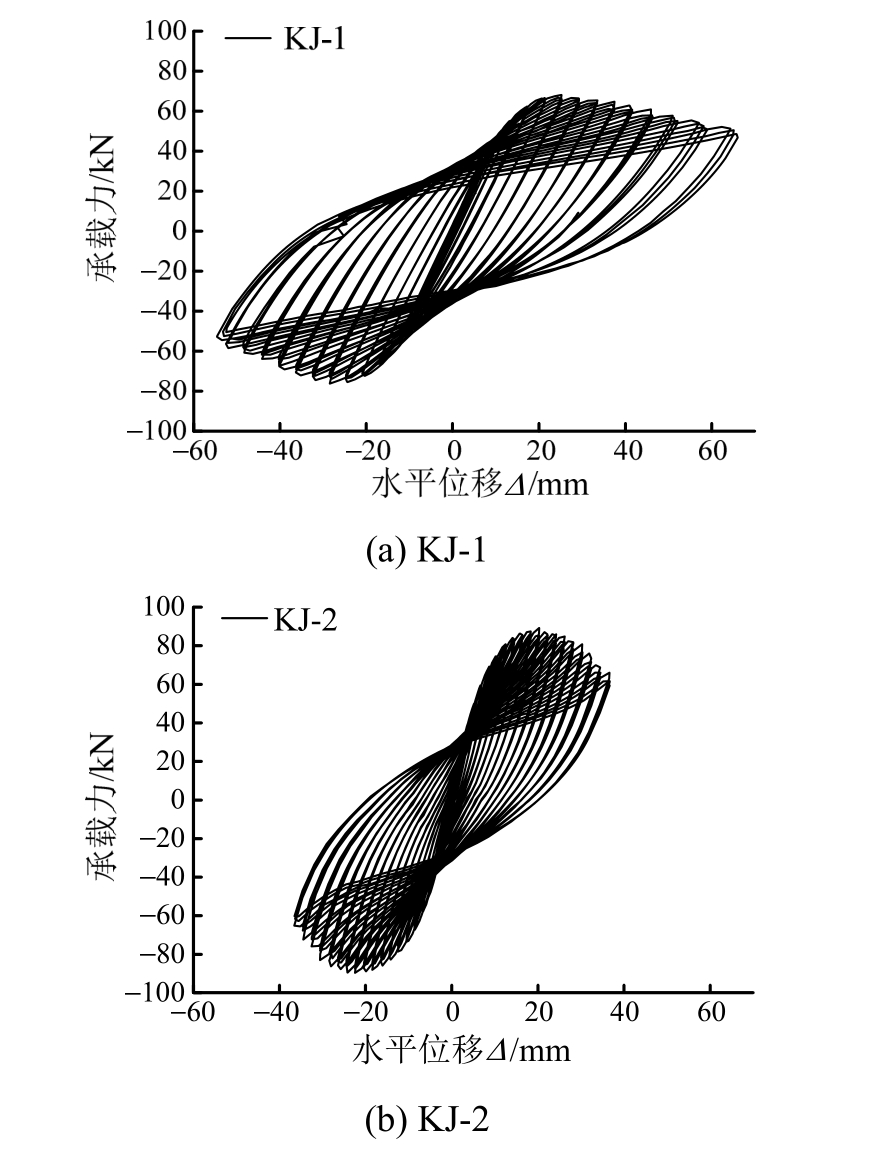
图5 钢板墙框架滞回曲线
Fig.5 Hysteretic curves of specimens
2榀框架在加载过程承载力水平位移骨架曲线如图6所示。2榀框架均呈现出良好的承载能力和延性,KJ-2的内填钢板既提高了框架的承载力,消耗了一定的能量,减少了框架的侧移。
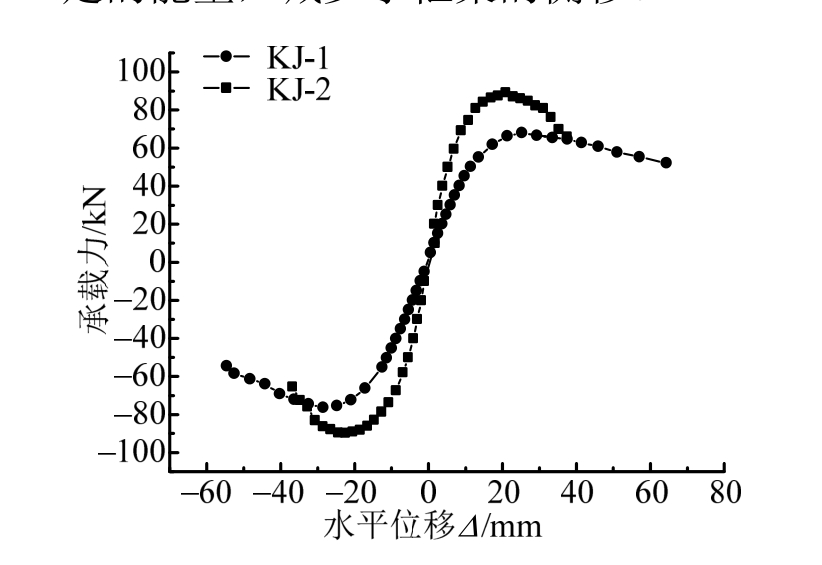
图6 框架骨架曲线
Fig.6 Skeleton curves of frames
承载力退化曲线如图7所示。2榀框架承载力退化稳定,退化系数均大于0.95,加载后期柱脚发生破坏承载力退化明显,内填钢板墙并未影响框架的持荷能力。

图7 承载力退化系数
Fig.7 Bearing capacity degradation coefficient of frames
框架刚度及其退化情况如图8所示。KJ-2在整个加载过程中刚度始终大于KJ-1,说明内填钢板可以有效的提高框架的刚度。KJ-1刚度退化平缓,在屈服之前刚度下降约25%,屈服后刚度下降约75%,说明双肢C型钢框架在屈服之前框架整体性能好,当发生屈服后框架的整体性降低,刚度退化明显。KJ-2在屈服之前,由于钢板不能完全参与受力,导致初始阶段刚度下降约75%,框架屈服后,钢板参与受力发挥作用,刚度退化变缓。
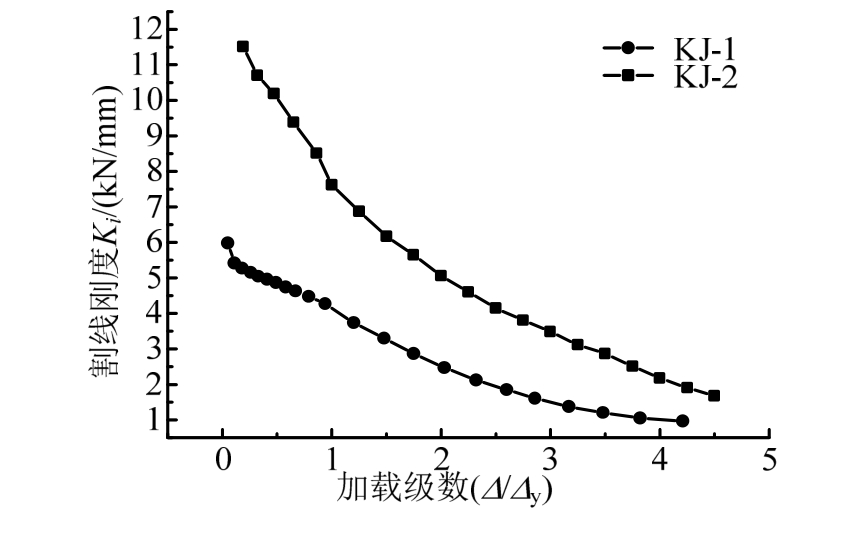
图8 钢板墙框架刚度退化曲线
Fig.8 Stiffness degradation curves
从表2耗能指标可以看出,框架在极限和破坏阶段塑性变形较大,耗能明显大于屈服阶段。内填钢板墙提高了框架的刚度,降低了框架的耗能能力,但钢板墙框架的耗能能力足以满足抗震的需求。
从表3框架延性系数μ可以看出,KJ-1在加载过程中的位移延性系数在 2.6~4.3,KJ-2的延性系数在3.5~7.2。KJ-2各层延性系数明显大于KJ-1。KJ-1的弹性阶段层间位移角为1/201,大于规范要求的1/250的限值,弹性阶段延性不符合要求;弹塑性阶段,框架的最大层间位移角为1/60,小于规范要求的1/50的限值,弹塑性阶段延性性能符合要求。KJ-2的弹性阶段层间位移角为1/308,小于规范要求的1/250的限值,弹性阶段延性性能符合要求;弹塑性阶段,框架的最大层间位移角为1/55,小于规范要求的1/50的限值,弹塑性阶段延性性能符合要求。可以看出,内填钢板墙可以有效的改善该类框架的延性性能,提高该类框架的抗震性能和整体稳定性,可以解决该类框架弹性阶段层间位移角太大的缺陷。
表2 钢板墙框架耗能能力指标
Table 2 Energy dissipation indices of specimens
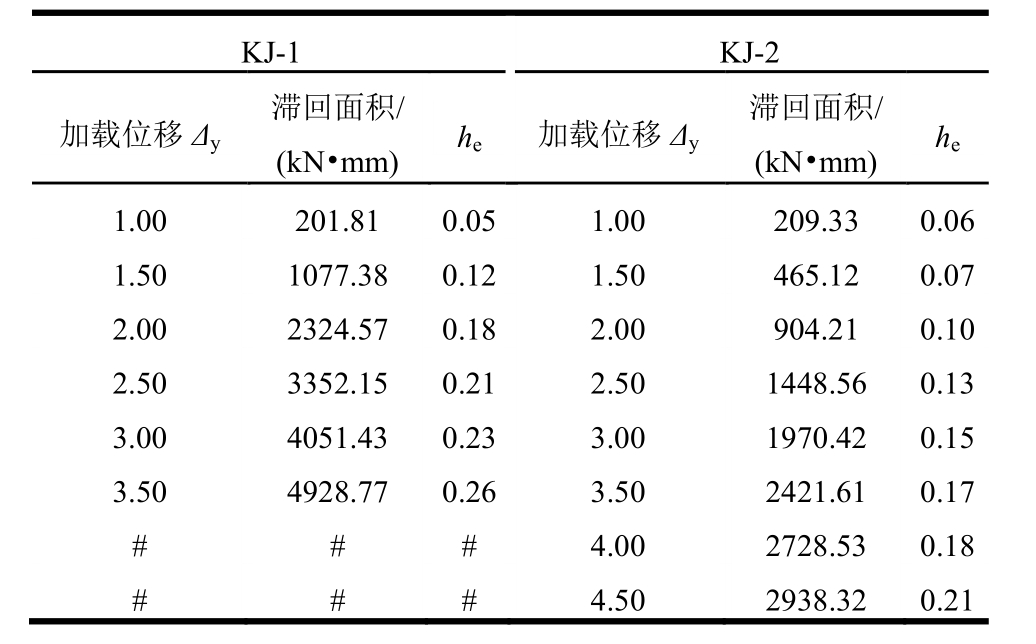





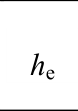

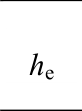







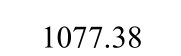
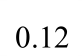
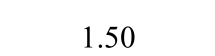


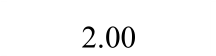
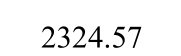
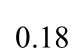



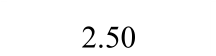
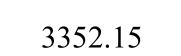


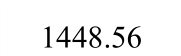
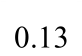
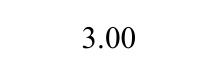
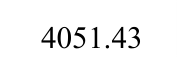


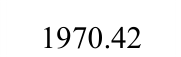
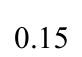
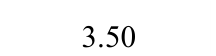
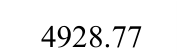










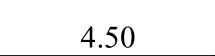
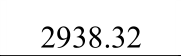

表3 框架延性系数
Table 3 Ductility coefficient of frames

KJ-1 KJ-2三层 二层 一层 三层 二层 一层拉 3.87 3.81 3.39 2.80 3.01 2.95屈服层间位移角 推 1/240 1/256 1/201 1/415 1/391 1/308拉 1/233 1/210 1/265 1/500 1/266 1/306极限位移/mm 推 7.62 11.32 11.32 5.51 8.02 8.32拉 9.34 9.72 9.72 5.66 8.26 8.66极限层间位移角 推 1/105 1/71 1/80 1/163 1/100 1/108拉 1/96 1/82 1/93 1/159 1/97 1/104破坏位移/mm 推 9.90 13.36 14.14 7.70 14.66 15.40拉 11.55 12.60 13.35 8.94 14.24 15.08破坏层间位移角 推 1/81 1/60 1/64 1/116 1/55 1/58拉 1/69 1/63 1/67 1/101 1/56 1/60延性系数μ推 4.84 4.89 4.81 4.81 5.39 5.67拉 4.27 4.51 5.15 3.04 3.69 3.78屈服位移/mm 推 3.76 3.13 4.47 2.17 2.05 2.92
有限元模型建立采用 ANSYS前处理器中PRPE7程序,在模型建立的过程中,梁、柱、节点板、钢板墙均采用四节点的有限应变壳SHELL181单元[19];用弹簧单元 COMBIN39将螺栓杆与节点板和C型钢的螺栓孔相连接,模拟摩擦型高强螺栓的剪切和扭转的效果,并以PSMESH命令生成预紧力单元作用于螺栓孔;高强摩擦型螺栓采用3D线性有限应变梁BEAM188单元,具有扭转变形效果。框架柱、梁和节点板本构关系简化为多线性随动强化刚度(MKIN),高强螺栓简化为双线性随动强化刚度(BKIN),应力-应变曲线如图9所示。
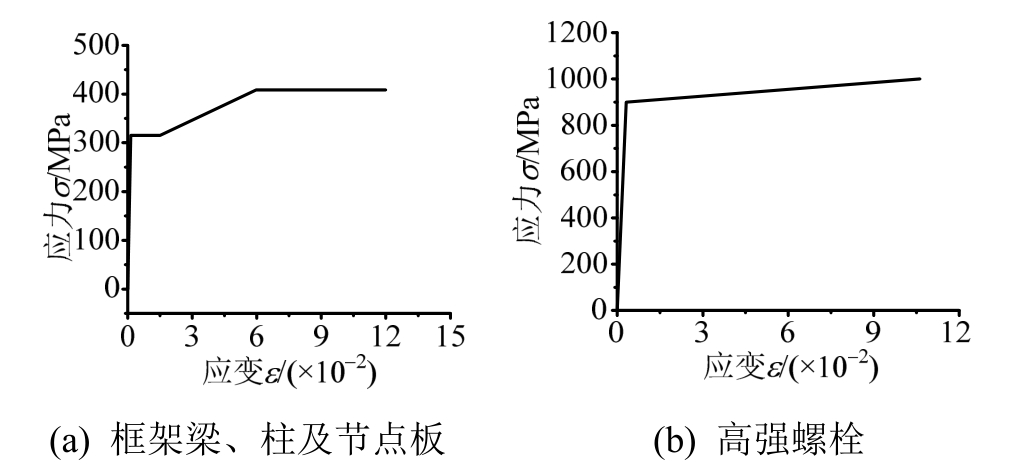
图9 各材料简化应力-应变曲线
Fig.9 Stress-strain curves of various materials
网格划分前,为了方便计算,首先对图元进行切分,使网格划分更整齐,然后对图元附着属性,最后划分网格。对框架柱底进行固接,参照试验加载的方式对柱端进行加载。有限元模型如图10所示。

图10 钢板墙框架有限元模型
Fig.10 Finite element model of frame filled with steel plate walls
从钢板墙框架滞回曲线(图 11)和应力云图(图12)可以看出:有限元分析的破坏形态及过程与试验相同,梁端先于柱脚屈服,钢板墙应力集中出现在墙板与框架梁、柱连接部位。分析数值结果整体上承载力偏高,位移偏小,滞回环偏饱满,这是由于有限元模型忽略了框架的初始变形,同时施加了平面外约束造成的。承载力的偏差在误差允许范围内,而位移值偏差较大,主要是因为有限元模拟采用BEAM188和COMBIN39单元无法精准实现框架螺栓的滑动,尤其是加载后期的螺栓滑移,而采用实体 SOLID单元会耗费较大的计算资源,考虑摩擦型高强螺栓在设计上是不允许螺栓滑移的,因此在分析时采用了BEAM单元进行模拟,能较为准确地反映框架受力过程。

图11 钢板墙框架滞回曲线
Fig.11 Hysteretic curves of frame filled with steel plate walls
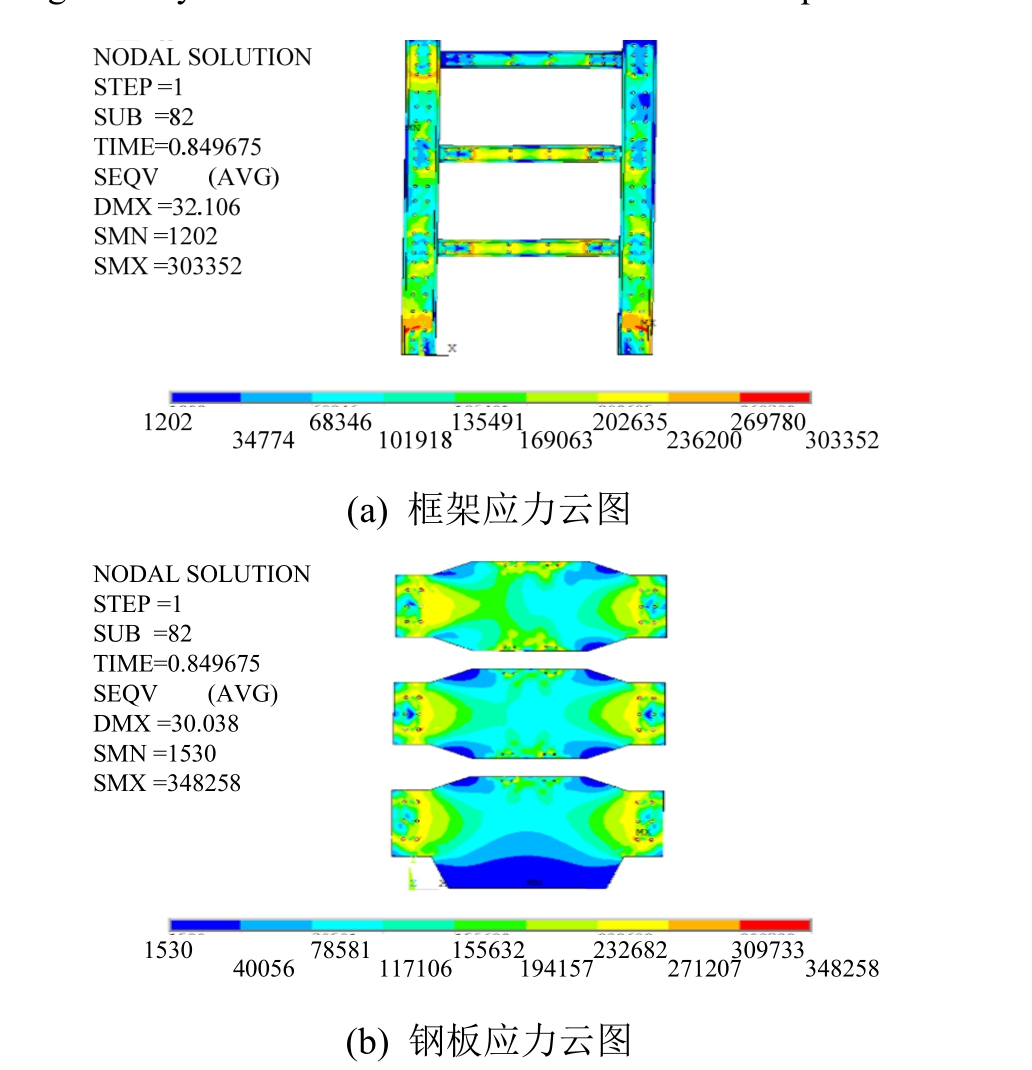
图12 钢板墙框架应力云图
Fig.12 Stress nephogram of frame filled with steel plate walls
以钢板墙的高厚比α和高宽比β、框架柱的刚度系数γ为分析参数,研究对钢板墙框架的抗震性能,建立7个有限元模型进行分析,具体参数见表4。
表4 有限元模拟框架构造参数
Table 4 Parameters of the finite element frame models

注:表中TH600和TH1000表示钢板墙高厚比α为600和1000;BH05和BH10表示钢板墙高宽比β为0.5和1.0;CS45和CS99表示框架柱的刚度系数γ为45.3和99.8。
框架编号 高厚比α高宽比β柱刚度系数γBASE 800 0.7 74.1 TH600 600 0.7 74.1 TH1000 1000 0.7 74.1 BH05 800 0.5 74.1 BH10 800 1.0 74.1 CS45 800 0.7 45.3 CS99 800 0.7 99.8
1) 钢板墙高厚比α公式为:
2) 钢板墙高宽比β公式为:
3) 框架柱刚度系数γ公式为:
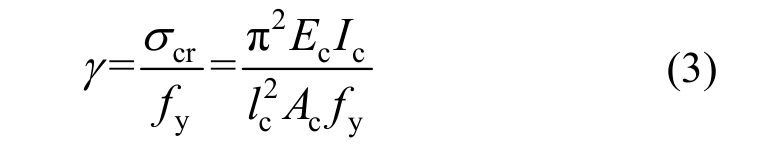
式中:H/mm、t/mm、B/mm分别为钢板的高度、厚度和宽度;Ec/MPa为柱 C型钢弹性模量;Ic/mm4为柱截面惯性矩;lc/mm为柱高度;Ac/mm2为柱截面面积。


图13 有限元模拟框架滞回曲线
Fig.13 Hysteresis curves of finite element models
图 13所示为各参数框架滞回曲线,滞回环形状饱满,类似于梭形,说明内填钢板墙框架的抗震性能好。开始加载时框架处于弹性阶段,滞回曲线基本呈现出一条过原点的直线。进入弹塑性工作阶段时,钢板墙部分区域发生屈曲,框架刚度开始出现下降趋势,滞回环所包络的面积逐步增大。进入破坏阶段后,钢板墙依靠所形成的拉力带支撑框架,受力简图类似于柔性支撑框架,滞回曲线饱满。
钢板墙高厚比α、高宽比β和框架柱的刚度系数γ不同时骨架曲线对比如图14所示。

图14 有限元模拟框架骨架曲线
Fig.14 Skeleton curves of finite element models
当钢板墙的高厚比α由600提高到800再提高1000时,屈服承载力分别降低了 2.67%、3.84%,极限承载力分别降低了12.03%、9.10%,初始刚度降低了10.23%、5.94%。随着钢板墙高厚比α的变大,其承载力、初始刚度也随之降低。
当钢板墙的高宽比β由0.5提高到0.7再提高到1.0时,屈服承载力分别降低2.61%、17.38%,极限承载力分别降低1.8%、17.82%,初始刚度降低了0.99%、16.52%。钢板墙的高宽比在小于1的范围变化对其承载力和刚度的影响不大,而接近正方形时拉力带的形成方向会发生变化,给框架柱带来不利,过早的屈服。
当框架柱的刚度系数γ由45.3提高到74.1再提高到99.8时,屈服荷载分别提高25.03%、12.87%,极限荷载分别提高20.00%、20.10%,初始刚度分别提高39.26%、33.3%。随着框架柱的刚度系数的增大,提高框架各阶段承载力提高,相应的位移减少,框架柱的刚度系数的变化对结构的承载力和位移有一定影响,但框架柱的刚度系数γ不必太大,会带来用钢量的大幅度提升,只需满足钢板墙形成有效的拉力带即可。
7榀有限元模拟框架的刚度退化如图15所示。有限元模拟刚度退化曲线的变化趋势相似,开始加载时,各榀框架初始刚度大,刚度退化明显。框架屈服后,钢板墙逐步参与受力充分发挥作用,刚度退化较屈服前明显变缓。框架破坏以后,刚度退化趋于稳定。TH600各个阶段的退化刚度大于TH1000,BH05各个阶段的退化刚度大于 BH10,CS99各个阶段的退化刚度大于CS45。数据分析得知,钢板墙高厚比、高宽比、框架柱的刚度系数等因素对这7榀框架的刚度退化影响较大。

图15 有限元模拟刚度退化曲线
Fig.15 Stiffness degradation curves of finite element models
延性是体现结构破坏所用时间和变形性能的指标。本文采用位移延性系数μ作为判断框架延性性能的依据,计算结果如表5所示。
各榀框架的延性系数μ>5,内填钢板墙框架延性良好。随着钢板墙高厚比α由600提高到800再提高到1000,延性系数分别提高了0.35%、3.67%。随着钢板墙高宽比β由0.5提高到0.8再提高到1.0时,延性系数分别提高了1.41%、1.76%。随着刚架柱的刚度系数γ由45.3提高到74.1再提高到99.8时,延性系数分别降低了11.4%、12.3%。说明增加钢板墙高厚比α、高宽比β对该类框架延性影响较小,增加框架柱的刚度系数γ对该类框架延性影响较大。
表5 有限元模拟框架延性系数
Table 5 Ductility coefficients of finite element models
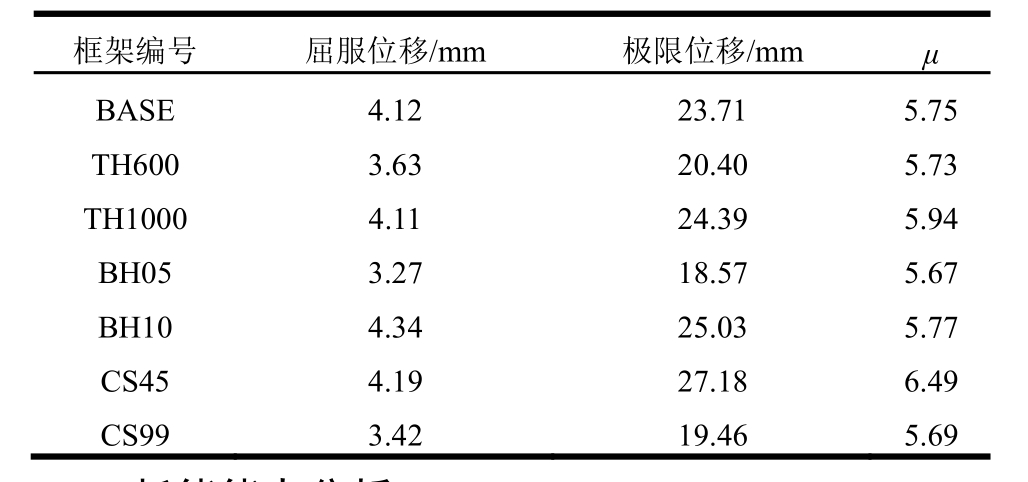
框架编号 屈服位移/mm 极限位移/mmμBASE 4.12 23.71 5.75 TH600 3.63 20.40 5.73 TH1000 4.11 24.39 5.94 BH05 3.27 18.57 5.67 BH10 4.34 25.03 5.77 CS45 4.19 27.18 6.49 CS99 3.42 19.46 5.69
框架耗能指标如表 6所示。该类框架的抗震耗散能力在弹塑性阶段开始显现,各个框架的等效粘滞系数he在0.32~0.41,呈现出良好的耗能能力。钢板墙高宽比由0.5增加到0.8时,框架的等效粘滞系数he增加了2.38%,由0.8增加到1.0时,框架的减少了4.87%,说明改变钢板墙的高宽比对该类框架的耗散能力影响较小。框架柱的刚度系数由45.3增加到74.1时,框架的等效粘滞系数he增加了10.81%,框架柱的刚度系数由74.1增加到99.8时,框架的等效粘滞系数he增加了2.44%,说明刚架柱的刚度系数γ对该类框架的耗散能力影响较大。
表6 有限元模拟耗能指标
Table 6 Energy dissipation indices of finite element models

框架编号 屈服阶段 极限阶段 破坏阶段EheEheEheBASE 1.52 0.24 2.38 0.37 2.55 0.41 TH600 1.52 0.24 2.31 0.37 2.55 0.40 TH1000 1.51 0.20 2.30 0.36 2.56 0.41 BH05 1.35 0.19 2.18 0.32 2.35 0.42 BH10 1.49 0.24 2.25 0.36 2.46 0.39 CS45 1.31 0.21 2.22 0.35 2.34 0.37 CS99 1.63 0.26 2.13 0.34 2.41 0.42
本文结合试验及ANSYS有限元模拟分析得出以下结论:
(1) 由于钢板可以起到应力重分布作用,使其比空框架在受力过程中应力分布更为合理。钢板墙可以提高框架的抗震性能。钢板墙框架加载过程中强度退化缓慢,刚度退化平稳。
(2) 钢板墙可以有效的提高框架各个阶段的刚度和承载力,在框架梁柱尺寸不变的基础上,刚度提高约80%,承载力提高约30%。
(3) 钢板与框架通过良好的配合,可以解决该类框架弹性阶段层间位移角太大的缺陷,有效地改善该类框架的延性性能,同时提高框架的抗震性能。形成有效的拉力带可以降低框架柱的用钢量,不需过大的柱刚度系数。
(4) 采用 SHELL181模拟该类 C型钢框架梁柱、钢板墙、节点板,采用BEAM188模拟螺栓连接,而非实体建模,这样的做法可以提高计算效率,较为准确地模拟框架的变形过程和应变发展,但承载力和位移数值具有一定的偏差。在后期的研究中需要继续探索模型求解中对材料损伤、初始缺陷等进行仔细研究,得到更为精确且高效的计算模型。
(5) 钢板墙高厚比α越大,钢板的变形越明显,钢板墙的高厚比α对框架的承载力及初始刚度影响较大,延性和耗能能力影响较小。高宽比β影响钢板墙内部拉力带的形成,当高宽比β太大时拉力带无法充分发展,影响框架承载力。
(6) 框架柱的刚度系数γ增大有利于提高各阶段承载力,具有良好延性和耗能能力。
[1]钟国辉. 冷弯薄壁型钢在房屋建筑中的研究与发展[J].建筑钢结构进展, 2002, 4(4): 31―38.Chung K F. Researching development on building construction using cold-formed steel sections [J].Progress in steel Building Structures, 2002, 4(4): 31―38.(in Chinese)
[2]周绪红, 管宇, 石宇. 多层冷弯薄壁型钢结构住宅抗震性能分析[J]. 建筑钢结构进展, 2017, 19(6): 10―15.Zhou Xuhong, Guan Yu, Shi Yu. Seismic performance analysis of multi-story cold-formed thin-walled steel structure residential buildings [J]. Progress in steel Building Structures, 2017, 19(6): 10―15. (in Chinese)
[3]陈明, 黄骥辉, 赵根田. 组合截面冷弯薄壁型钢结构研究进展[J]. 工程力学, 2016, 33(12): 1―11.Chen Ming, Huang Jihui, Zhao Gentian. Research progress of compound section cold-formed thin-wall steel structures [J]. Engineering Mechanics, 2016,33(12): 1―11. (in Chinese)
[4]Lim J B P, Nethercot D A. Stiffness prediction for bolted moment-connections between cold-formed steel members [J]. Journal of Construction Steel Research,2004, 60(1): 85―107.
[5]James B P Lim, David A. Nethercot. Finite element idealization of a cold-formed steel portal frame [J].Journal of Structural Engineering, 2004, 130(1): 8―94.[6]Lim J B P, Nethercot D A. Ultimate strength of bolted moment-connections between cold-formed steel members [J]. Thin-Walled Structures, 2003, 41(11):1019―1039.
[7]Ashkan Shahbazian, Yong Chang Wang. Direct strength method for calculating distortional buckling capacity of cold-formed thin-walled steel columns with uniform and non-uniform elevated temperatures [J]. Thin-Walled Structures, 2012, 53(4): 188―199.
[8]Dundu M. Design approach of cold-formed steel portal frames [J]. International Journal of Steel Structures,2011, 11(3): 259―273.
[9]Mohammed H. Serror, Emad M. Hassan, Sherif A.Mourad. Experimental study on the rotation capacity of cold-formed steel beams [J]. Journal of Constructional Steel Research, 2016, 121: 216―228.
[10] 黄川, 崔佳, 龙莉萍. 自攻螺钉连接冷弯薄壁 C 型钢梁柱节点试验及分析[J]. 重庆建筑大学学报, 2003,25(5): 37―41.Huang Chuan, Cui Jia, Long Liping. Experiment and analysis of cold-formed thin-walled C steel beam-tocolumn connections in self-drilling [J]. Journal of Chongqing Jianzhu University, 2003, 25(5): 37―41. (in Chinese)
[11] 彭雄, 杨娜, 孟庆桐. 冷弯薄壁型钢组合截面构件试验研究与数值分析[J]. 工程力学, 2012, 29(9): 272―293.Peng Xiong, Yang Na, Meng Qingtong. Experimental research and numerical analysis on the combination effect of cold-formed steel specimens [J]. Engineering Mechanics, 2012, 29(9): 272―293. (in Chinese)
[12] 陈明, 马晓飞, 赵根田. 冷弯型钢组合截面 T形节点抗震性能研究[J]. 工程力学, 2015, 32(1): 184―191.Chen Ming, Ma Xiaofei, Zhao Gentian. Seismic behavior of T-shaped joint using cold-formed compound section steel [J]. Engineering Mechanics, 2015, 32(1): 184―191.(in Chinese)
[13] 陈明, 李梦祺, 马晓飞, 等. 双肢冷弯C型钢斜节点抗震性能研究[J]. 工程力学, 2015, 32(3): 192―202.Chen Ming, Li Mengqi, Ma Xiaofei, et al. Aseismic behavior of oblique joint using cold-formed double C steel [J]. Engineering Mechanics, 2015, 32(3): 192―202.(in Chinese)
[14] 陈明, 李梦琪, 邓渤凡. 双肢冷弯薄壁型钢框架抗震性能分析[J]. 建筑钢结构进展, 2015, 17(2): 7―12.Chen Ming, Li Mengqi, Deng Bofan. A study on the seismic behavior of cold-formed thin-wall steel frames[J]. Progress in Steel Building Structures, 2015, 17(2):7―12. (in Chinese)
[15] 陈明, 马晓飞. 带垫板双肢冷弯 C型钢框架抗震性能研究[J]. 工程力学, 2017, 34(2): 111―119.Chen Ming, Ma Xiaofei. Seismic behavior of cold-formed double C steel frames with gusset plates [J].Engineering Mechanics, 2017, 34(2): 111―119.
[16] GB1T2975-1998, 钢及钢产品力学性能试验取样位置及试样制备[S]. 北京: 中国标准出版社, 1998.GB1T2975-1998, Steel and steel products mechanical properties test sampling position and sample preparation[S]. Beijing: China Standard Press, 1998. (in Chinese)
[17] 陈明, 陈亚栋, 刘海生. 一种结构框架试验竖向加载装置[P]. 中国: ZL2016201748279, 2016. 3. 8.Chen Ming, Chen Yadong, Liu Haisheng. The vertical loading device of frame test [P]. China:ZL2016201748279, 2016. 3. 8. (in Chinese)
[18] JGJ 101-96, 建筑抗震试验方法规程[S]. 北京: 中国建筑工业出版社, 1996.JGJ 101-96, Specification of testing methods for earthquake resistant building [S]. Beijing: China Architecture & Building Press, 1996. (in Chinese)
[19] 王新敏. ANSYS 工程结构数值分析[M]. 北京: 人民交通出版社, 2007.Wang Xinmin. ANSYS numerical analysis of engineering structures [M]. Beijing: China Communication Press,2007. (in Chinese)
SEISMIC BEHAVIOR OF COLD-FORMED DOUBLE C STEEL FRAME FILLED WITH STEEL PLATE WALLS