
图1 不锈钢材料的非线性特性
Fig.1 Nonlinear characteristic of stainless steel material
耐腐蚀、耐高温低温、具有良好抗冲击性能和加工性能的不锈钢材料[1]越来越多地应用在建筑的结构构件中。例如,不锈钢板作为围护结构应用于巴西贝洛奥里藏特的阿尔塔维拉塔[2]以及广州亚运城综合体育馆工程中[3];不锈钢材料还作为屋面结构应用于日本札幌体育馆、英国滑铁卢火车站及我国昆明绿博园人与自然馆[4];位于魁北克的加拿大国家档案保存中心和斯德哥尔摩的Berjinska植物园均采用了不锈钢作为承重结构[5]。目前,有关不锈钢轴心受压构件的研究相对全面[6―16],而压弯构件是建筑结构中更为常见的一种构件形式(如框架柱等),其稳定性能和承载能力对整个工程的安全性具有重要的影响。GB 50017―2017《钢结构设计标准》[17]主要针对碳素钢和低合金高强度钢,而不锈钢结构的材料性能与普通碳素钢有很大不同,具体表现在其应力-应变曲线有极强的非线性,没有明显的屈服点和屈服平台(如图1所示),且弹性模量随着应力的增加逐渐减小。CECS 410―2015《不锈钢结构技术规程》[18]于2015年12月正式施行,规范中关于压弯构件承载力的相关计算采用了GB 50018―2002《冷弯薄壁型钢结构技术规范》中的相关规定,但是对于热轧不锈钢焊接截面构件是否适用还需进一步研究。

图1 不锈钢材料的非线性特性
Fig.1 Nonlinear characteristic of stainless steel material
目前国内外仅有少量针对不锈钢压弯构件的研究,且国内多为有限元研究而缺少试验研究。员翔等[19]对奥氏体不锈钢冷弯方钢管进行了有限元研究,通过拟合得到了不锈钢方矩管偏心受压构件平面内稳定承载力的下限式及线性相关公式;Zheng等[20]进行了奥氏体不锈钢方管和焊接工字形压弯构件进行了试验研究,并将试验数据与现行的欧洲、美国和澳大利亚规范进行对比,提出了改进方法;Lui等[21]对20个双相型不锈钢方管进行了偏心加载试验,将试验值与美国和澳大利亚规范计算值进行对比,结果表明两个规范计算值均偏于保守;Huang Yuner和YoungBen[22]的双相型不锈钢方矩管偏心加载试验也证实规范的计算结果偏于保守,因此,在文献[23]中通过有限元分析并基于澳大利亚规范和直接强度法对计算方法进行了改进。
已有的研究中,对冷弯不锈钢构件的研究较多,对焊接截面构件的研究较少。因此,本文对奥氏体型和双相型不锈钢焊接箱形压弯构件进行了试验研究,并将试验结果与现行规范进行了对比。
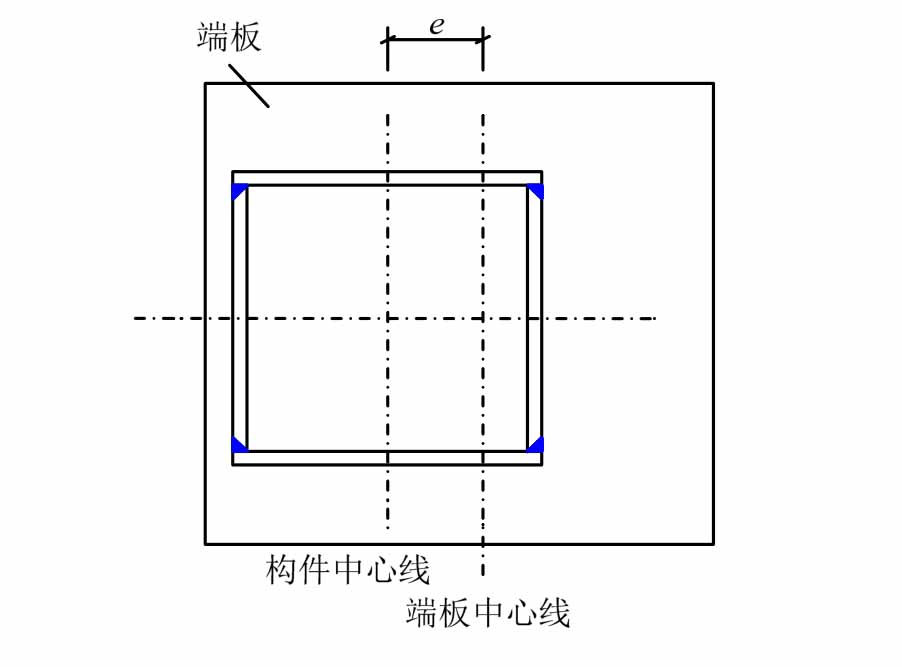
图2 构件和端板相对位置示意图
Fig.2 Illustration of counter-position of specimen and end-plate
表1 构件实测尺寸
Table 1 Measurements of specimens

试件编号B/mmt/mme/mmL/mmLt/mmλS304-2500 130.5 5.85 60.3 2497 2837 55.7 S304-3000-1 131.8 5.85 48.3 2993 3333 64.8 S304-3000-2 131.5 5.85 70.0 2992 3332 64.5 S304-4000-1 131.2 5.85 47.7 3994 4334 84.6 S304-4000-2 131.4 5.85 56.4 4012 4352 84.8 S2205-2500 131.7 5.87 58.0 2495 2835 55.1 S2205-3000-1 131.4 5.87 54.4 2999 3339 65.0 S2205-3000-2 131.0 5.87 70.6 2999 3339 65.3 S2205-4000-1 131.0 5.87 50.4 4017 4357 85.2 S2205-4000-2 131.5 5.87 58.6 4016 4356 84.8
试验设计了10根不锈钢焊接箱形试件,包括5根奥氏体型304和5根双相型2205不锈钢柱,两种牌号不锈钢构件的几何尺寸完全相同。为了实现偏心加载,在加工时先将构件偏心地焊接在两个端板上(见图2),再将整个构件置于千斤顶的加载中心。包括3种长细比和3种荷载偏心距,其实测尺寸如表 1所示,试件编号中的第一个字母“H”和“I”分别代表工字型绕弱轴失稳和绕强轴失稳的压弯构件;S表示箱形截面;304和2205分别代表奥氏体和双相型不锈钢;2500代表试件长度,单位为mm;最后的数字1或2表示两试件偏心距不同,其中B为翼缘宽度,t为板件厚度,e为荷载偏心距,L为构件几何长度,Lt为构件端部单刀铰支座的转动中心距离(Lt=L+340),λ为长细比(λ=Lt/i,i为回转半径)。构件的截面如图3所示。试件采用的不锈钢板由激光切割而成,激光切割是一种高能量切割,精度高,不存在切割断面的倾斜和残留熔渣等问题[24]。奥氏体型和双相型构件分别应用A102E和E2209焊条进行焊接,焊脚尺寸均为6 mm。加工完成后对构件进行调直以减少焊接残余应力产生初始弯曲的影响。试件两端约束为铰接。为了避免发生局部屈曲,试件宽厚比按照 CECS 410:2015[18]的规定设计,满足板件局部稳定性要求。
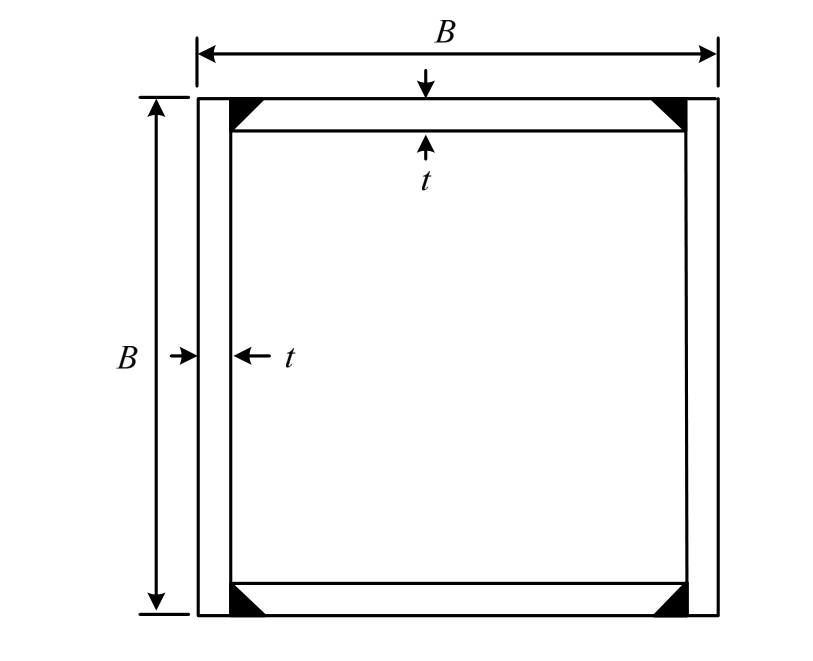
图3 箱形截面尺寸符号示意图
Fig.3 Symbolic illustration for box-section geometry
试件所采用不锈钢的材料力学性能通过拉伸试验确定,根据 GB/T 228.1—2010《金属材料 拉伸试验 第 1部分:室温试验方法》[25]中有关比例试样的规定在同一批次的不锈钢板上切取拉伸试验试样,每一批次包括3个相同的试样。拉伸试验采用 300 kN电液伺服万能试验机完成,选用标距为25 mm的引伸计测量试样的变形。拉伸试验得到的不锈钢力学性能指标如表2所示,其中,E0为初始弹性模量,f0.2为残余应变 0.2%时对应的应力值(即为不锈钢材料的名义屈服强度),fu为抗拉强度,A*为断后伸长率,根据试验曲线拟合得到应变硬化指数n。拉伸试验得到的应力-应变曲线如图4所示,其中在奥氏体型不锈钢材性试验时,由于引伸计在拉断前提前脱落,导致奥氏体型不锈钢应力-应变曲线后段缺失。
表2 不锈钢拉伸试验材料力学性能
Table 2 Material properties of tensile coupon tests

牌号t/mmE0/MPaf0.2/MPafu/MPaA*/(%)n奥氏体型 5.85 200 000 298.2 630.7 57.0 6.1双相型 5.87 205 000 568.0 740.9 36.4 6.9

图4 不锈钢材料实测应力-应变曲线
Fig.4 Measured stress-strain curves of stainless steel
在进行静力加载试验前,对所有试件的初始弯曲进行了测量,方法如下[26]:首先沿构件长度方向标记四分点,利用经纬仪镜筒中的竖向十字叉丝在地面上进行定位,每次测量都将试件摆放在定位点上。将游标卡尺置于四分点上,在镜筒中找到和竖向叉丝对应的游标卡尺刻度,即为每点截面中心偏离柱端部截面中心连线的距离(δ1、δ2及δ3),并取其中绝对值最大的值作为试件的几何初弯曲值δ0[27]。但在实际测量过程中很难直接量测四分点截面中心的偏离值,因此取柱中四条棱边在同一四分点截面位置处偏离值的平均值作为该截面中心线的偏离值。构件整体几何初弯曲如图5所示,现场测量情况如图6所示。测量结果见表3。

图5 构件整体几何初弯曲示意图
Fig.5 Illustration of measurement of global initial bending

图6 构件整体几何初弯曲现场测量照片
Fig.6 Photograph of measurement of global initial bending
表3 试件初弯曲测量结果Table 3 Measured initial bending

试件编号 初弯曲/mmδ0/Lt/(‰)δ1δ2δ3δ0S304-2500 1.890 -0.960 -1.295 1.890 0.67 S304-3000-1 -1.661 -2.468 -1.094 2.468 0.74 S304-3000-2-1.673 2.765 -0.468 2.765 0.83 S304-4000-1-0.745 -3.665 -2.400 3.665 0.85 S304-4000-2 -1.742 -2.490 -2.292 2.490 0.57 S2205-2500 4.634 3.932 4.326 4.634 1.63 S2205-3000-1 -1.156 -0.928 1.376 1.376 0.41 S2205-3000-2-0.459 -0.122 -0.346 0.459 0.14 S2205-4000-12.166 2.548 0.479 2.548 0.58 S2205-4000-2 3.193 3.565 2.428 3.565 0.82平均值 0.72
试验采用 500 t液压式长柱压力试验机进行竖向加载,构件端部各布置一个单刀铰和压力机相连以实现两端铰接的边界条件,试件上下端板与试验设备加载端通过焊接进行固定,试验装置的照片和示意图见图7。
为了减少焊接对应变数据的影响,在距试件两端 20 mm(图 7(b)中截面 2-2、3-3)的棱边处分别布置4个应变片用于反算荷载初偏心(图8(b)),在柱中截面(截面 1)布置了 8个应变片用于分析试件临界截面在失稳前后的应变分布(图 8(a))。整个构件共布置有7个位移计,如图7(b)所示,柱中截面的LVDT-6和LVDT-7通过拉丝固定,用来测量柱中截面失稳平面内的水平位移,LVDT-5和固定在柱中的玻璃片接触,用来测量柱中截面失稳平面外的水平位移;在柱底单刀铰发生转动的对称位置布置两个位移计LVDT-1和LVDT-2,通过两者读数之差和间距得到柱端转角;构件的轴向压缩变形通过LVDT-3和LVDT-4测量。

图7 试验装置
Fig.7 Test configuration

图8 应变片布置
Fig.8 Layout of strain gauges
首先进行预加载,以检查加载装置和数据采集系统处于正常工作状态,然后卸载至一个相对很小的荷载水平(约5 kN),以便消除试件端板与加载板之间可能存在的空隙。在加载初期,采用荷载控制,加载速度约 30 kN/min,当荷载达到峰值之后,采用柱中侧向水平位移控制加载,加载速度约10 mm/min,以便保证荷载-位移曲线具有平滑完整的下降段。
试验过程中,试件中间截面随着荷载的增加逐渐向偏心方向屈曲,上、下两端的单刀铰随试件的屈曲发生转动,当荷载下降至试件承载力约 60%时开始卸载,可以观察到试件的挠度逐渐减小直至弹性变形完全恢复。试验中所有试件均发生平面内的整体弯曲失稳,图9为典型失稳模态。图10为铰支座的转动情况,单刀铰在试验过程中能够灵活转动。

图9 典型失稳模态
Fig.9 Typical failure mode

图10 铰支座转动情况
Fig.10 Rotation of knife edge
图11给出了构件的荷载-柱中水平位移曲线。由于试件具有初始加载偏心,且加工过程中产生了初始弯曲,所有试件均发生极值点失稳。从图 11可以看出,在加载初期,奥氏体型不锈钢压弯构件的变形发展更快;构件长细比和偏心距对不锈钢压弯构件的承载力有很大影响,偏心距相同的试件,其长细比越大,构件承载力越小;长细比相同的试件,偏心距越大,构件承载力越小。

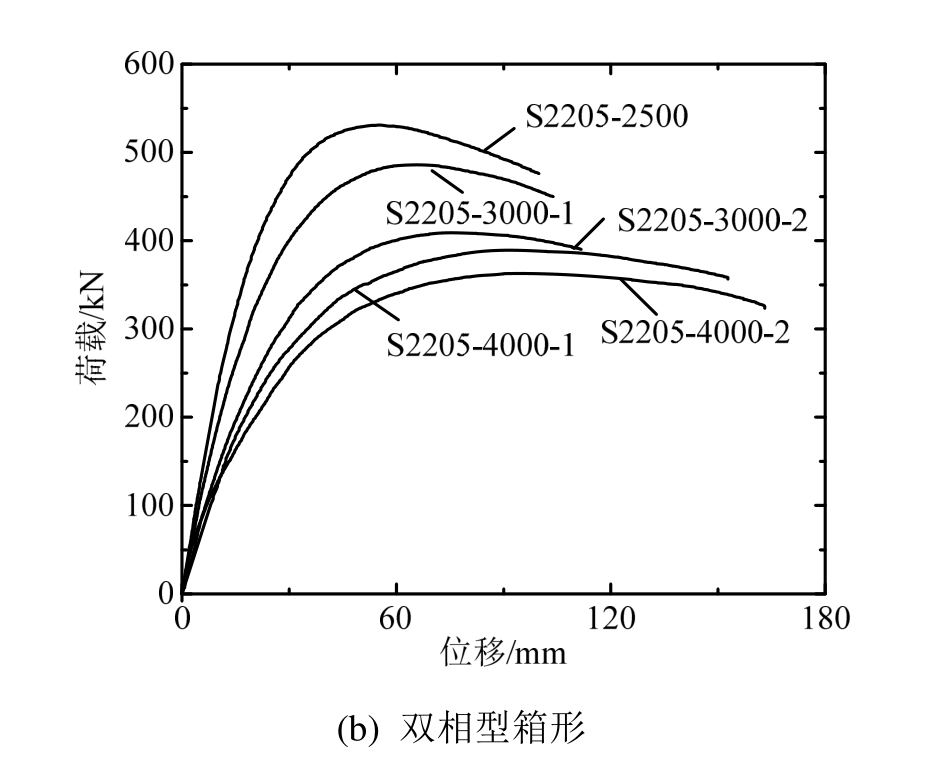
图11 试验荷载-位移曲线
Fig.11 Measured load-displacement curves

图12 试验荷载-应变曲线
Fig.12 Measured load-strain curves
每个试件中间截面均布置8个应变片,以构件S304-2500和S2205-2500为例,在图12中列出所有8个测点的荷载-应变曲线。其中,ε0.2表示材料屈服时对应的应变,应变片1-1、1-4和1-6呈现正(受拉)应变,而应变片1-2、1-3、1-5、1-7、1-8均呈负(受压)应变,且相同截面高度处的荷载-应变曲线重合。由于偏心受压的影响,受压侧的纵向应变均大于受拉侧的应变;随着荷载的增加,拉压应变呈非线性增长,达到承载力极限状态,截面出现塑性区并且不断扩展,钢材塑性发展良好。此外,构件失稳时,柱中位置有部分截面的最大应变超过屈服应变,部分截面应变尚未达到屈服应变。
根据CECS 410―2015,双轴对称截面的压弯构件平面内的稳定性可以按下式计算[18]:
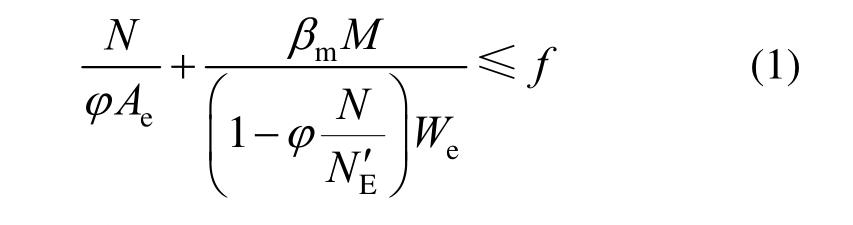
式中:M为计算弯矩,本试验试件的计算弯矩M为轴力N与试件荷载偏心距e的乘积;Ae为有效截面面积;βm为等效弯矩系数;NE′为欧拉临界力;We为对最大受压边缘的有效截面模量。本试验所有构件均发生平面内失稳,因此可以采用式(1)进行稳定性计算。
EN 1993-1-4针对不锈钢压弯构件的稳定性能有如下规定[28]:
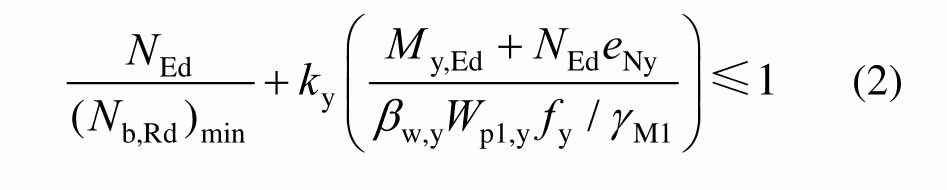
式中:NEd和My,Ed分别为轴力和最大弯矩设计值;(Nb,Rd)min为以下四种屈曲模态的轴力最小值:绕强轴屈曲、绕弱轴屈曲、扭转屈曲和扭转-弯曲屈曲;ky为相关系数;对于第 1、2类截面,βW,y=1.0;e为偏心距,分项系数γM1=1.1;Wpl,y为塑性模量。
按照EN 1993-1-4和CECS 410―2015中压弯构件整体稳定设计方法计算相应试验构件的承载力结果列于表4中,并将结果和试验承载力进行对比。计算过程中材料参数为试验实测值。
从表4可以看出,CECS 410―2015计算值对于双相型构件偏于安全,但对于奥氏体箱形压弯构件,试件S304-3000-2 和S304-4000-2试验值略低于规范计算值,其他试件试验值均高于规范计算值,中国规范CECS 410―2015总体偏于安全。欧洲规范EN 1993-1-4计算方法对于奥氏体型构件和双相型构件均偏于安全。
上述规范中提供的压弯构件设计公式形式相似,即分为轴心受压和受弯两部分,对两部分之和的数值进行限定。为了更为直观地比较试验结果与EN 1993-1-4和CECS 410―2015中压弯构件整体稳定设计方法,现将横坐标定义为受弯部分,纵坐标定义为受压部分,画出图13和图14的对比示意图。计算过程中采用实测的材料参数。图示结果与列表得到的分析结果一致。其中对CECS 410―2015中的设计公式进行了转化,转换形式如下:
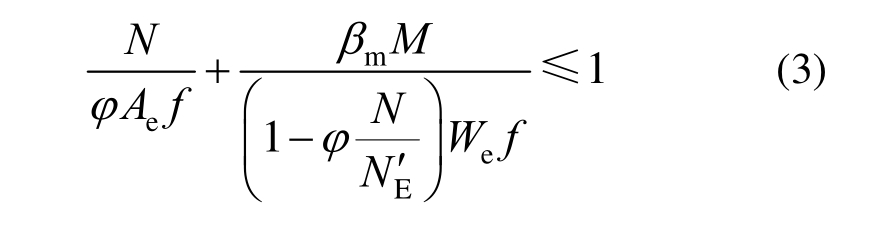
表4 试验承载力和规范承载力对比
Table 4 Comparison of ultimate load between test and specification
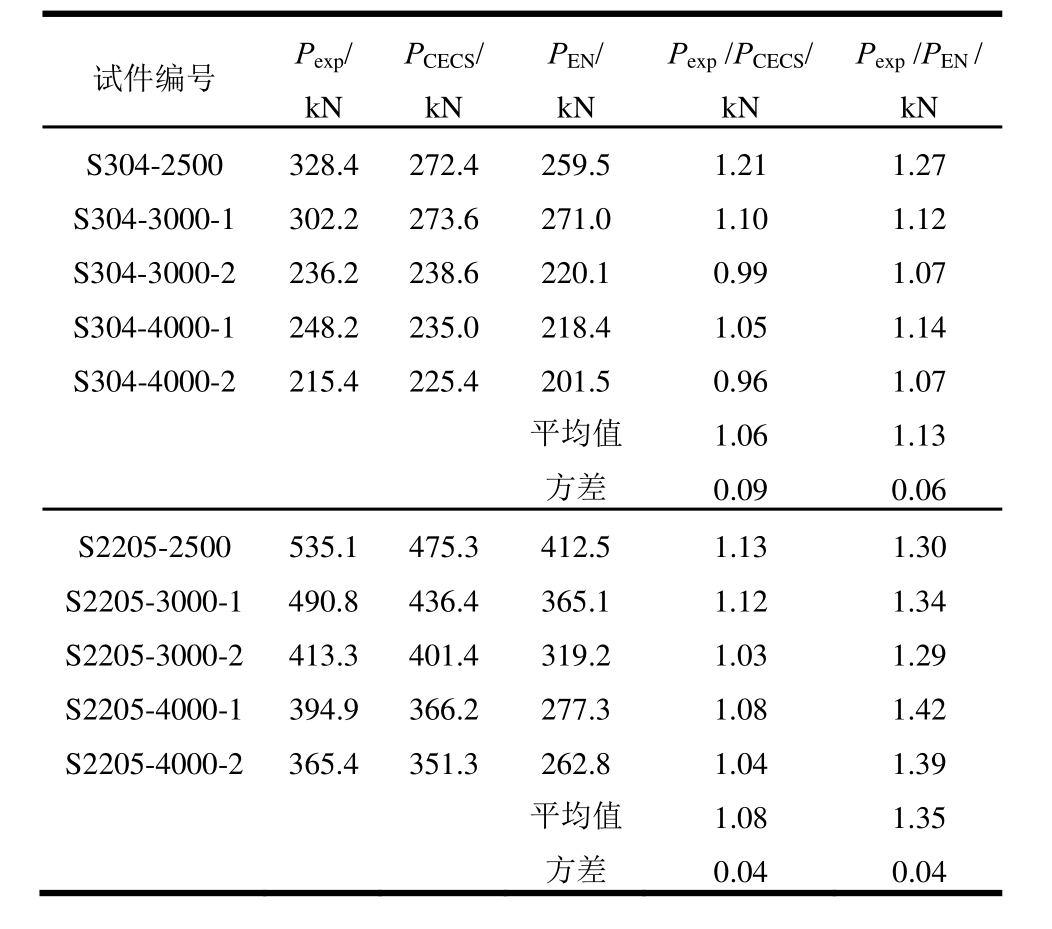
试件编号Pexp/kNPCECS/kNPEN/kNPexp/PCECS/kNPexp/PEN/kN S304-2500 328.4 272.4 259.5 1.21 1.27 S304-3000-1 302.2 273.6 271.0 1.10 1.12 S304-3000-2 236.2 238.6 220.1 0.99 1.07 S304-4000-1 248.2 235.0 218.4 1.05 1.14 S304-4000-2 215.4 225.4 201.5 0.96 1.07平均值 1.06 1.13方差 0.09 0.06 S2205-2500 535.1 475.3 412.5 1.13 1.30 S2205-3000-1 490.8 436.4 365.1 1.12 1.34 S2205-3000-2 413.3 401.4 319.2 1.03 1.29 S2205-4000-1 394.9 366.2 277.3 1.08 1.42 S2205-4000-2 365.4 351.3 262.8 1.04 1.39平均值 1.08 1.35方差 0.04 0.04
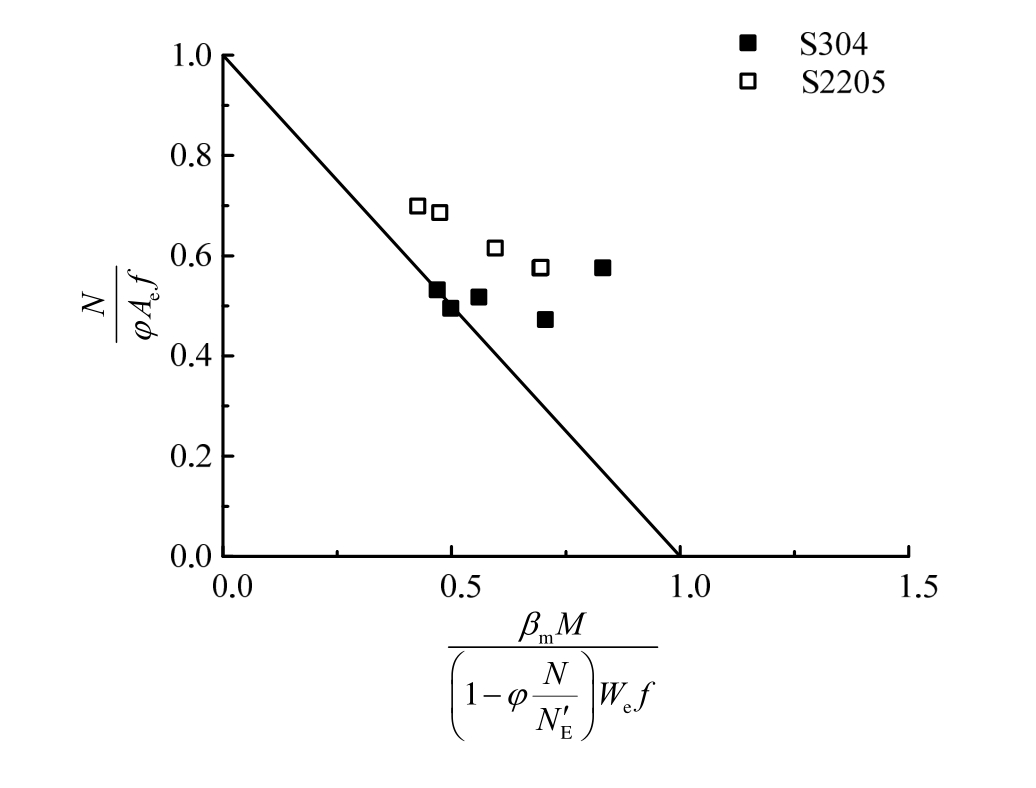
图13 试验值和CECS 410―2015计算值对比
Fig.13 Comparison of test results and predictions of CECS 410―2015

图14 试验值和EN 1993-1-4计算值对比
Fig.14 Comparison of test results and predictions of EN 1993-1-4
本文对 10根奥氏体型和双相型不锈钢焊接箱形柱进行了偏心受压试验,且在试验前对试件的材料性能及初始缺陷进行了量测。试验得到以下结论:
(1) 构件两端均为单刀铰,试验过程中刀铰转动灵活,所有构件均发生平面内的整体弯曲失稳,整体失稳前没有发现明显的局部板件屈曲。
(2) 所有试件均发生极值点失稳;偏心距和长细比为影响不锈钢压弯构件承载力的主要因素,偏心距和长细比越大,构件承载力越小。
(3) 从试验结果与 CECS 410―2015和 EN 1993-1-4计算值的对比情况可以看出,不锈钢箱形压弯构件试验结果均高于EN 1993-1-4计算值,规范偏于安全;CECS 410―2015的计算结果和试验结果相比,存在个别试件试验结果略低于规范计算值,但规范总体偏于安全,可以用于此类构件的设计。
(4) 本试验结果为建立不锈钢压弯构件数值模型和进一步的参数分析提供了依据。
[1]袁焕鑫. 焊接不锈钢轴心受压构件局部稳定和相关稳定性能研究[D]. 北京: 清华大学, 2014.Yuan Huanxin. Local and local-overall buckling behaviour of welded stainless steel members under axial compression [D]. Beijing: Tsinghua University, 2014. (in Chinese)
[2]Tarcísio Reis de Oliveira, Roberto Bamenga Guida, 张岩. 不锈钢在巴西建筑中的应用[J]. 建筑技艺,2011(6): 164―167.Tarcísio Reis de Oliveira, Roberto Bamenga Guida,Zhang Yan. Stainless steel application in architecture and construction in brazil [J]. Architecture Technique,2011(6): 164―167. (in Chinese)
[3]黄唯, 李宏, 李冰. 不锈钢板在广州亚运城综合体育馆围护系统中的运用[J]. 建筑技艺, 2011(11): 170―173.Huang Wei, Li Hong, Li Bing. Application of stainless steel sheet in envelope system of gymnasium for Guangzhou asian games [J]. Architecture Technique,2011(11): 170―173. (in Chinese)
[4]郑宝锋. 不锈钢冷弯薄壁型钢轴心受压和压弯构件理论分析与试验研究[D]. 南京: 东南大学, 2010.Zheng Baofeng. Theoretical and experimental investigations on cold-formed stainless steel columns and beam-columns [D]. Nanjing: Southeast University, 2010.(in Chinese)
[5]埃斯科·米耶蒂宁[芬兰]. 不锈钢与建筑[M]. 天津: 天津大学出版社, 2004: 9―10.Esko·Miettinen [Finland]. Stainless Steel in Architecture[M]. Tianjin: Tianjin University Press, 2004: 9―10. (in Chinese)
[6]杨璐, 徐东辰, 王元清, 等. 奥氏体型不锈钢焊接箱形截面轴压构件整体稳定性能试验研究[J]. 土木工程学报, 2014(8): 83―88.Yang Lu, Xu Dongchen, Wang Yuanqing, et al.Experimental study on the overall buckling behavior of austenitic stainless steel columns under axial compression [J]. China Civil Engineering Journal,2014(8): 83―88. (in Chinese)
[7]范圣刚, 孙文隽, 桂鹤阳, 等. 轴心受压H形截面不锈钢柱抗火性能分析[J]. 工程力学, 2016, 33(6): 154―162.Fan Shenggang, Sun Wenjun, Gui Heyang, et al. Fire resisttance pereormance analysis of H-section stainless steel column under axial compression [J]. Engineering Mechanics, 2016, 33(6): 154―162. (in Chinese)
[8]袁焕鑫, 王元清, 石永久, 等. 焊接箱形截面不锈钢柱相关稳定性能分析[J]. 工程力学, 2015(9): 84―91.Yuan Huanxin, Wang Yuanqing, Shi Yongjiu, et al.Behavior of interactive buckling in welded stainless steel box section columns [J]. Engineering Mechanics,2015(9): 84―91. (in Chinese)
[9]杨璐, 徐东辰, 尚帆, 等. 双相型不锈钢焊接箱形截面轴压构件整体稳定性能试验研究[J]. 东南大学学报:自然科学版, 2015, 45(2): 364―369.Yang Lu, Xu Dongchen, Shang Fan, et al. Experimental study on overall buckling behavior of duplex stainless steel welded box columns under axial compression[J].Journal of Southeast University (Natural Science Edition), 2015, 45(2): 364―369. (in Chinese)
[10] 杨璐, 尚帆, 赵梦晗, 等. 不锈钢工字形截面构件轴心受压整体稳定计算方法[J]. 湖南大学学报: 自然科学版, 2016, 43(3): 55―65.Yang Lu, Shang Fan, Zhao Menghan, et al. Calculation method of the overall stability for I-shaped stainless steel member under axial compression load [J]. Journal of Hunan University (Natural Science), 2016, 43(3): 55―65. (in Chinese)
[11] 尚帆, 杨璐, 赵梦晗, 等. 不锈钢工字形截面轴心受压构件整体稳定性能有限元研究[J]. 工程力学, 2016(3):112―119.Shang Fan, Yang Lu, Zhao Menghan, et al. FEA of the overall stability for i-section stainless steel member under axial compression[J]. Engineering Mechanics,2016(3): 112―119. (in Chinese)
[12] Yang L, Zhao M H, Xu D C, et al. Flexural buckling behavior of welded stainless steel box-section columns[J]. Thin-Walled Structures, 2016, 104: 185―197.
[13] Yang L, Zhao M, Chan T M, et al. Flexural buckling of welded austenitic and duplex stainless steel I-section columns [J]. Journal of Constructional Steel Research,2016, 122: 339―353.
[14] Yang L, Shi G, Zhao M H, et al. Research on interactive buckling behavior of welded steel box-section columns[J]. Thin-Walled Structures, 2017, 115: 34―47.
[15] Anbarasu M, Ashraf M. Behaviour and design of cold-formed lean duplex stainless steel lipped channel columns [J]. Thin-Walled Structures, 2016, 104: 106―115.
[16] Gardner L, Bu Y, Theofanous M. Laser-welded stainless steel I-sections: Residual stress measurements and column buckling tests [J]. Engineering Structures, 2016,127: 536―548.
[17] GB 50017—2017, 钢结构设计标准[S]. 北京: 中国建筑工业出版, 2017.GB 50017—2017, Standard for design of steel structures[S]. Beijing: China Architecture & Building Presss, 2017.(in Chinese)
[18] CECS 410―2015, 不锈钢结构技术规程[S]. 北京: 中国计划出版社, 2015.CECS410―2015, Technical specification for stainless steel structures [S]. Beijing: China Planning Press, 2015.(in Chinese)
[19] 员翔, 赵果, 段宝山, 等. 不锈钢方矩管压弯构件平面内稳定承载力理论研究[J]. 工业建筑, 2015, 43(3):150―155.Yuan Xiang, Zhao Guo, Duan Baoshan, et al. Theoretical research on in-plane stability capacity of rhs stainless Steel Beam-Columns [J]. Industrial Construction, 2015,43(3): 150―155. (in Chinese)
[20] Zheng B, Hua X, Shu G. Tests of cold-formed and welded stainless steel beam-columns [J]. Journal of Constructional Steel Research, 2015, 111: 1―10.
[21] Lui W M, Ashraf M, Young B. Tests of cold-formed duplex stainless steel SHS beam-columns J]. Engineering Structures, 2014, 74: 111―121.
[22] Huang Y, Young B. Experimental investigation of cold-formed lean duplex stainless steel beam-columns[J]. Thin-walled Structures, 2014, 76(3): 105―117.
[23] Huang Y, Young B. Design of cold-formed lean duplex stainless steel members in combined compression and bending [J]. Journal of Structural Engineering, 2015,141(5): 1―10.
[24] 桥本政哲[日]. 不锈钢及其应用[M]. 北京: 冶金工业出版社, 2011: 226―238.Hashimoto[Japan]. Stainless steel and application [M].Beijing: Metallurgical Industry Press, 2011: 226―238.(in Chinese)
[25] GB/T 228.1—2010, 金属材料 拉伸试验 第1部分: 室温试验方法[S]. 北京: 中国标准出版社, 2010.GB/T228.1—2010, Metallic materials-Tensile testing-Part1: Method of test at room temperature [S]. Beijing:Standards Press of China, 2010 (in Chinese)
[26] 袁焕鑫, 王元清, 石永久, 等. 不锈钢焊接箱形截面柱轴心受压相关稳定试验研究[J]. 土木工程学报, 2015,48(2): 63―72.Yuan Huanxin, Wang Yuanqing, Shi Yongjiu, et al.Interactive buckling tests on welded stainless steel axial compression members with box sections[J]. China Civil Engineering Journal, 2015, 48(2): 63―72. (in Chinese)
[27] 班慧勇, 施刚, 石永久, 等. Q460高强钢焊接箱形截面轴压构件整体稳定性能研究[J]. 建筑结构学报,2013, 34(1): 22―29.Ban Huiyong, Shi Gang, Shi Yongjiu, et al. Overall buckling behavior of Q460 high strength steel welded box section columns under axial compression[J]. Journal of Building Structures, 2013, 34(1): 22―29. (in Chinese)
[28] EC3. Design of steel structures-Part 1-4: General rules-supplementary rules for stainless steels [S]. EN 1993-1-4, 2006.
EXPERIMENTAL RESEARCH ON FLEXURAL BUCKLING OF STAINLESS STEEL WELDED BOX-SECTION BEAM-COLUMNS