
图1 某工程施工现场照片
Fig.1 Construction photo
在钢筋混凝土柱截面中部设置钢管混凝土而形成的一种组合构件,称为钢管混凝土组合柱;若钢管内外混凝土不同期浇筑,则称为钢管混凝土叠合柱。该类组合柱继承了钢管混凝土强度高、抗震性能好等优点,还能克服防腐、防火性能差的缺点[1-7];与型钢、钢管混凝土节点相比,解决任意角度梁相交节点构造简单、不外露,满足复杂建筑功能和美观要求[8-9](见图1),在深圳中海油大厦、长沙泊富国际广场等高层建筑中得到广泛应用。

图1 某工程施工现场照片
Fig.1 Construction photo
我国现行《钢管混凝土叠合柱结构技术规程》CECS 188:2005中第6.2.9条规定:压弯承载力按照现行《混凝土结构设计规范》中钢筋混凝土柱计算,不计入钢管作用,轴力取管外钢筋混凝土分担的部分轴力。这样处理会造成计算承载力保守、材料利用率低,大小偏压构件的纵筋配筋不合理等问题[10]。因此,急需完善压弯承载力计算理论。
目前,有关钢管混凝土组合柱压弯承载力计算方法的研究不够丰富。林拥军等[11]将钢管和腹部纵筋等效为钢腹板,根据截面极限平衡理论推导出压弯承载力计算公式,指出小偏心受压情况下需要考虑钢管对核心混凝土的约束影响。王犇[12]采用数值积分法计算钢管混凝土、外围钢筋混凝土部分承载力,再根据试验结果进行修正,该计算方法存在三次方程求解繁琐,不能反映出钢管直径与截面尺寸关系、偏心距等因素对钢管约束作用的影响等问题。为此,安钰丰[13]提出能够考虑多参数约束影响的计算公式,遗憾的是部分参数计算复杂,计算思路及表述方式与规范不协调,给工程师带来困惑。
本文通过偏心受压试验,考察偏心距、长细比和钢管直径对组合柱破坏机理和极限承载力的影响,采用截面极限平衡理论推导出既能保持现有规范形式,又能考虑钢管直径与截面高度比值、偏心距和长细比等因素的钢筋混凝土和钢管混凝土正截面压弯承载力计算公式,最后基于叠加理论提出钢管混凝土组合柱压弯承载力计算方法。
设计 16根钢管混凝土组合柱进行偏压试验,设计参数见表1。方形截面柱边长220 mm,高度有660 mm、1320 mm、1980 mm三种,试件截面配筋形式如图2所示。钢管采用Q235级无缝管,表面未设置抗剪件,钢管内外混凝土使用同一批次混凝土进行浇筑,混凝土由人工搅拌配制,实测立方体抗压强度见表1。D=114 mm、89 mm的钢管屈服强度为336.36 MPa和 378.66 MPa,d=6 mm、12 mm的HRB400钢筋屈服强度为547 MPa和407 MPa。

注:l为试件高度;h为试件截面高度,220 mm;e0为轴向力对截面重心的偏心距;D为钢管外径;t为钢管壁厚;fcu为混凝土立方体抗压强度。
试件编号l/he0/mmD/mmt/mmfcu/MPa 试件编号l/he0/mmD/mmt/mmfcu/MPa C-0 6 0 114.1 3.80 57.9 C-3-2 6 132 114.2 3.86 53.8 C-1-1 6 44 114.3 3.82 59.1 C-3-3 6 132 114.0 3.84 53.8 C-1-2 6 44 114.2 3.84 53.8 C-3-4 6 132 113.9 3.80 51.8 C-1-3 6 44 114.2 3.88 53.8 C-3-5 6 132 113.9 3.78 57.9 C-1-4 6 44 113.9 3.86 51.8 C-4 9 132 114.0 3.82 57.9 C-1-5 6 44 114.3 3.92 57.9 C-5 6 132 88.9 3.82 57.9 C-2 6 88 113.9 3.78 57.9 C-6 3 44 114.1 3.86 57.9 C-3-1 6 132 114.1 3.80 59.1 C-7 3 132 114.2 3.86 57.9
通过YE-10000F液压试验机施加竖向荷载,加载速率为1 mm/min,当荷载下降至预定值或变形剧增时,停止加载。试件上下端部采用专利(ZL 20162 0897811.0)“一种适用于混凝土柱构件偏压试验的加载装置”施加竖向荷载,如图3所示。图中数字编号顺序依次表示承载板(或厚钢板)、三棱柱铰、与压力机接触面板、短螺杆、角钢、长螺杆、矩形钢板和试件。应变片测点如图2中1-1截面所示,图中测点1~4为纵筋应变,测点5~8为箍筋应变,测点 9~12为钢管纵、横向应变。试件施加的竖向荷载与对应竖向位移由试验机自动采集。

图2 试件配筋形式
Fig.2 Construction form of specimens

图3 加载装置
Fig.3 Test set-up
钢管混凝土组合柱偏压破坏过程与钢筋混凝土柱相似,呈现出大、小偏心受压破坏两种形态。
1.2.1 大偏心受压破坏
当偏心距e0=132 mm(0.6h)时,试件呈现出大偏心受压破坏特征。以试件C-3-5为例,当荷载加载至峰值荷载40%左右时,加载点远侧混凝土出现弯曲裂缝;继续加载,弯曲裂缝增多,原有裂缝变宽,并向截面中部延伸。接近峰值荷载时,远侧主裂缝明显、纵筋屈服,钢管应变仍较小,随后加载点近侧混凝土出现纵向裂缝、压碎脱落,箍筋外露、纵筋压曲,试件破坏,如图4(a)所示。
1.2.2 小偏心受压破坏
当偏心距e0=44 mm(0.2h)时,试件呈现出小偏心受压破坏特征。以试件C-1-5为例,加载点远侧出现弯曲裂缝较晚,约为峰值荷载的90%。接近峰值荷载时,加载点近侧混凝土外鼓,瞬间压溃承载力急剧降低,伴有爆裂声,破坏突然无明显预兆。破坏时,加载点近侧混凝土受压剥落严重,箍筋外露、纵筋压曲,加载点远侧纵筋和钢管均未屈服,典型破坏形态见图4(b)。
1.2.3 界限破坏
试件 C-2(e0=0.4h=88 mm)破坏特征接近于界限破坏。开裂比大偏心受压破坏的要晚,开裂荷载约为峰值荷载的60%。破坏时,在加载点远侧受拉钢筋屈服的同时,加载点近侧受压区混凝土出现纵向裂缝并被压碎,之后箍筋外露、纵筋压曲。

图4 典型破坏形态
Fig.4 Typical failure pattern
选取不同偏心距e0=0h、0.2h、0.6h对应典型试件 C-0、C-1-5、C-3-5进行分析(其中e0=0.4h试件C-2部分测点失效,不作讨论),实测钢管、纵筋应变曲线如图5~图7所示,图中负号表示压应变。
1.3.1 钢管纵向应变曲线
由图5(a)可知,加载点远侧钢管在偏心距0.2h时受压,0.6h时受拉,可见改变偏心距直接影响钢管纵向受力状态。由图5(b)可知,加载初期,曲线基本重合,随后差异明显,小偏心受压时曲线上升迅速,轴压次之,大偏心受压上升缓慢,但无论何种情况,加载近侧钢管纵向始终受压。所有偏压试件达到峰值荷载时,钢管纵向应变均未屈服。
1.3.2 钢管横向应变曲线
由图6可知,无论是加载点远侧还是近侧,达到峰值荷载时,除轴压试件外,偏压试件的钢管横向应变变化甚小,未屈服,其中小偏心受压试件的相对大些,说明偏心距越小,钢管横向约束效果倾向于轴压试件,即约束作用不可忽略。试验还发现,箍筋应变变化规律与钢管横向应变的相似,两者数值相当,偏压试件均未达到屈服强度。

图5 荷载-钢管纵向应变曲线
Fig.5 Load-axial strain curves of steel tube

图6 荷载-钢管横向应变曲线
Fig.6 Load-transverse strain curves of steel tube
1.3.3 纵筋应变曲线
由图7可知,无论是加载点远侧还是近侧,纵筋应变变化规律与钢管基本相似,应变数值增加,原因是纵筋位于钢管外侧,离截面边缘越近,变形越大。在偏心距0.2h条件下,加载后期纵筋受力状态由压变为拉,这是在接近峰值荷载时,试件两侧混凝土压碎、开裂使得有效截面减小,加载点近侧混凝土压碎区域深度远超过远侧裂缝深度,导致截面中和轴向加载点远侧移动,使得加载点远离中和轴、相对偏心距增大,纵筋应变变化规律倾向于大偏心受力构件,纵筋受力出现受拉情形。

图7 荷载-纵筋应变曲线
Fig.7 Load- axial strain curves of longitudinal reinforcement
通过上述典型试件应变分析,可获得以下规律:① 加载点远近两侧钢筋和钢管的变形基本协调一致,未发生明显滑移现象,截面应变符合平截面假定;② 无论何种破坏形式,加载点近侧受压纵筋屈服总是先于受压区混凝土压碎;③ 峰值荷载过后,钢管截面逐渐屈服,避免试件承载力突然降低,变形能力增强;④ 钢管横向应变、箍筋应变的变化规律相似,随着偏心距减小而增大,虽然应变未屈服,但约束作用不可忽视。
图8为根据实测极限承载力绘制的N-M关系曲线(该曲线仅示意变化趋势,其中0.2h、0.6h取均值绘制)。结合试验现象和应变数据可知,偏心距0.6h和0.2h试件分别呈现出大、小偏心受压破坏特征,偏心距0.4h试件C-2接近界限破坏特征,即加载点远侧受拉纵筋屈服,同时受压侧混凝土边缘达到极限压应变,但试件C-2偏离N-M曲线较远,未达到理想极限承载力,原因在于浇筑不密实。

图8N-M关系
Fig.8 The relationship betweenNandM
钢管混凝土组合柱属于一种新型组合结构柱,偏压破坏机理与钢筋混凝土柱相似,因此参照组合结构叠加理论和混凝土结构截面极限平衡理论,建立钢管混凝土组合柱压弯承载力计算理论。
根据叠加理论,钢管混凝土组合柱正截面压弯承载力可视为由管外钢筋混凝土部分和钢管混凝土部分承担,即:

式中:Nr、Ns和Nu为管外钢筋混凝土、钢管混凝土和钢管混凝土组合柱承担的轴力;Mr、Ms和Mu为管外钢筋混凝土、钢管混凝土和钢管混凝土组合柱承担的弯矩。
影响组合柱截面应变变化的因素众多,例如偏心距、钢管截面尺寸及含钢率、纵筋分布及配筋率、混凝土强度等。本文选择影响比较直观的偏心距进行分析,当偏心距由小变大,构件通常会出现全截面受压、部分受压部分受拉的情形,即中和轴在截面外还是截面内的两种情况。
计算时作如下假设:① 截面应变分布符合平截面假定;② 不考虑钢管、钢筋与混凝土之间黏结滑移;③ 钢材应力应变曲线简化为理想弹塑性曲线;④ 不考虑混凝土抗拉强度;⑤ 混凝土极限压应变值随混凝土立方体抗压强度标准值而变化,满足下式:εcu=0.0033-(fcuk-50)×10-5≤0.0033。
2.1.1 管外钢筋混凝土的承载力
管外钢筋混凝土截面简化思想是将中空部分对称拆分成两块并移至截面边缘,近似简化成工字型截面,如图 9所示。图中:D、b为工字型截面腹板高度、宽度,b=bf-D;bf′和bf为受压、受拉翼缘宽度;hf′和hf为受压、受拉翼缘高度,hf=hf′=(h-D)/2。

图9 管外钢筋混凝土截面简化
Fig.9 Simplify process of reinforced concrete
图10所示为管外钢筋混凝土承担轴力Nr和弯矩Mr=Nre共同作用下的计算简图。只要知道中和轴位置,即截面受压区高度x,就能建立平衡方程。但是在截面配筋设计前,无法确定截面受压区高度。为此,本文提出一种以偏心距e0(e0=M/Nr)近似判断截面受压区高度范围的计算方法。

图10 管外钢筋混凝土计算模型
Fig.10 Calculated model of reinforced concrete
1) 当e0>h-hf+as时,即![]()

2) 当![]() 时,即
时,即![]()
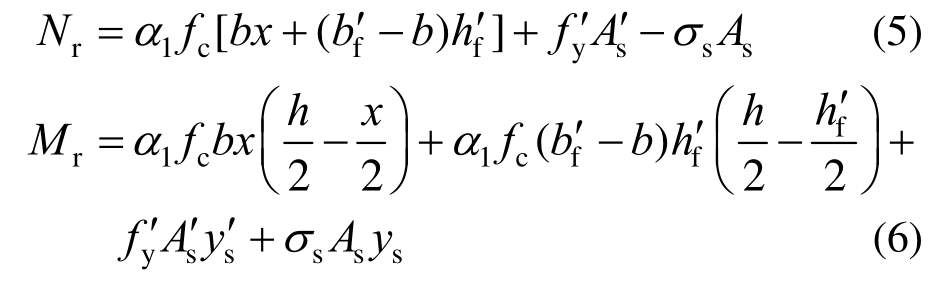
3) 当e0≤h′f-as时,即x>h-hf

式中:fc为混凝土轴心抗压强度;fy、fy′为纵筋屈服强度;σs为根据平截面假定所得受拉纵筋应力,σs=fy(β1-ξ)/(β1-ξb),其中ξ为相对受压区高度,界限相对受压区高度ξb和受压区等效矩形应力系数α1、β1按照现行混凝土规范GB 50010取值;![]() 和As为受压、受拉纵筋截面面积;sα′和sα为受压、受拉纵筋截面形心到截面最近边缘处的距离;
和As为受压、受拉纵筋截面面积;sα′和sα为受压、受拉纵筋截面形心到截面最近边缘处的距离;![]() 和ys为受压、受拉纵筋截面形心到截面形心的距离。
和ys为受压、受拉纵筋截面形心到截面形心的距离。
本文试验试件属于两端铰支、两端偏心距相等的标准偏压柱(M1=M2=M),长细比超过30。现行混凝土规范GB 50010规定:当长细比大于22时,应考虑二阶效应产生附加弯矩的不利影响,如果是压弯构件自身挠曲引起的二阶效应(P-δ效应),可采用柱截面偏心距增大系数(弯矩增大系数)的传统方法,即Mr=CmηnsM,其中Cm为截面偏心距调节系数,取值1;ηns为偏心距增大系数或弯矩增大系数。就钢管混凝土组合柱而言,偏心距增大系数不仅要体现出偏心距的影响,还需考虑偏心距改变对钢管内外混凝土相互作用的影响,因此,以钢管外径D为界限,提出以下计算公式:
1) 当e0≤D/2 时

2) 当e0>D/2 时

式中:ζc为截面曲率修正系数,ζc=0.5fcA/Nr,中和轴在截面内时可以近似取值1.0;ei为初始偏心距,ei=e0+ea,附加偏心距ea取偏心方向截面尺寸的1/30和20 mm中的较大值;l0为柱等效计算长度,l0=μkl,其中l为柱实际长度,μ、k均为1.0。
2.1.2 钢管混凝土的承载力
压弯荷载作用下钢管混凝土柱的屈服曲线方程如下:

式中:N0为钢管混凝土短柱轴压承载力;M0为纯弯作用下钢管混凝土短柱的抗弯承载力;θ为钢管混凝土套箍指标,θ=faAa/(fcAci),其中fa、Aa为钢管的屈服强度和截面面积,Aci为核心混凝土截面面积;套箍指标界限值[θ]=1/(α-1)2,其中α为与混凝土强度等级有关的系数,C50以下取值 2.0,C55~C80之间取值1.8;r为核心混凝土截面半径;Ns为压弯荷载作用下钢管混凝土柱承担的轴向承载力,按照我国现行《钢管混凝土结构技术规程》CECS 28:2012计算:
综合式(11)~式(14),可得压弯荷载作用下钢管混凝土柱承担的弯矩Ms

式中:φe、φl为钢管混凝土柱考虑偏心率、长细比影响的承载力折减系数。试验发现,当偏心距减小且钢管外径与组合柱截面高度比值D/h较小(在含钢量相近条件下)时,钢管核心混凝土受到钢管和管外钢筋混凝土的约束作用明显;反之偏心距增大,约束减弱,并且随着D/h增大,管外围保护层厚度变薄,协同工作性能变差,影响构件承载力。因此,以D/h和e0/h为判断依据,对现行规程CECS 28∶2012中规定调整如下:
1) 当D/h>0.5时,不考虑增强作用

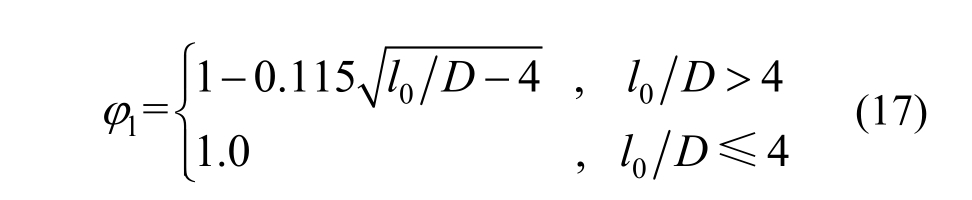
2) 当D/h≤0.5且e0≤h/2时,考虑增强作用

3) 当D/h≤0.5且e0>h/2时,不考虑增强作用,折减系数φe按照式(16)中e0>1.55r情形计算,折减系数φl按照式(17)计算。
当中和轴在截面外,受压区混凝土极限压应变将小于0.0033,上述方法并不严格成立。参照文献[13],针对x>h情形给出以下计算方法:
1) 根据式(1)和式(2)计算x=h时对应承载力Nu,h,求解此时所对应的偏心距e0=eh;
2) 根据式(20)计算偏心距e0=0时的轴压承载力Nu,0:
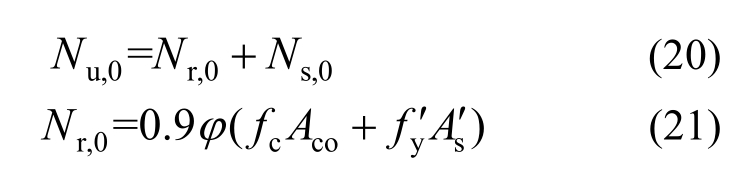
式中:Nr,0为管外钢筋混凝土轴压承载力;φ为稳定系数,按照现行混凝土规范GB50010确定:Aco为管外钢筋混凝土截面面积;Ns,0为钢管混凝土轴压承载力,计算同2.1.2节,即Ns,0=Ns。
3) 假设x>h(中和轴在截面外)时,任意偏心距e0=ex对应承载力Nu,x可由Nu,0与Nu,h之间插值确定。因此,钢管混凝土组合柱正截面承载力Nu,x计算公式如下:

为了检验上述压弯承载力计算方法的准确性,采用本文作者、林拥军[11]、王犇[12]、李鹏[14]完成的40组试验样本进行验证,计算值Nu,c与实测值Nu的对比如表2、图11所示。由表 2和图11可知:
1) 对于中和轴在截面内的情况Ⅰ,文献[11]中正截面压弯承载力计算结果偏低,可能与实测混凝土轴心抗压强度有关;文献[12]中虽然钢管内外混凝土强度等级不同,但仍可满足计算精度要求,其中少数样本离散较大的原因是由于不同厚度钢管屈服强度值相同所致。如不计入文献[11]中五组数据进行分析,计算结果与实测结果比值的范围0.890~1.148,均值0.979,变异系数0.071。
表2 极限承载力计算值与试验值比较
Table 2 Comparison between calculated values and test values

编号b(h)l/he0/mmD/mmt/mmfa/MPa 纵筋fy/MPafcu/MPaNu/kNNu,c/kNNu,c/Nu类型C-1-1 220 6 44 114.3 3.82 336.36 4Φ12 407 59.1 1275.0 1214.25 0.952 ⅠC-1-2 220 6 44 114.2 3.84 336.36 4Φ12 407 53.8 1253.5 1155.65 0.922 ⅠC-1-3 220 6 44 114.2 3.88 336.36 4Φ12 407 53.8 1261.0 1154.78 0.916 ⅠC-1-4 220 6 44 113.9 3.86 336.36 4Φ12 407 51.8 1192.0 1127.84 0.946 ⅠC-1-5 220 6 44 114.3 3.92 336.36 4Φ12 407 57.9 1333.5 1204.52 0.903 ⅠC-2 220 6 88 113.9 3.78 336.36 4Φ12 407 57.9 627.0 686.42 1.095 ⅠC-3-1 220 6 132 114.1 3.80 336.36 4Φ12 407 59.1 508.5 484.97 0.954 ⅠC-3-2 220 6 132 114.2 3.86 336.36 4Φ12 407 53.8 528.5 471.77 0.893 ⅠC-3-3 220 6 132 114.0 3.84 336.36 4Φ12 407 53.8 529.0 470.95 0.890 ⅠC-3-4 220 6 132 113.9 3.80 336.36 4Φ12 407 51.8 438.0 463.76 1.059 ⅠC-3-5 220 6 132 113.9 3.78 336.36 4Φ12 407 57.9 486.5 481.13 0.989 ⅠC-4 220 9 132 114.0 3.82 336.36 4Φ12 407 57.9 482.5 448.21 0.929 ⅠC-5 220 6 132 88.9 3.82 378.66 4Φ12 407 57.9 468.5 437.72 0.934 ⅠC-6 220 3 44 114.1 3.86 336.36 4Φ12 407 57.9 1380.0 1317.75 0.955 ⅠC-7 220 3 132 114.2 3.86 336.36 4Φ12 407 57.9 565.5 525.44 0.929 ⅠCSRC3 220 6.4 20 165 3.2 274 4Φ12 338.2 21 1870 1147.73 0.614 ⅠCSRC4 220 6.4 60 165 3.2 274 4Φ12 338.2 21 1085 777.59 0.717 ⅠCSRC5 220 6.4 90 165 3.2 274 4Φ12 338.2 16.7 750 515.86 0.688 ⅠCSRC6 220 6.4 110 165 3.2 274 4Φ12 338.2 17 600 462.07 0.770 ⅠCSRC7 220 6.4 140 165 3.2 274 4Φ12 338.2 17 500 437.85 0.876 Ⅰ
续表

注:C系列为本文试验样本;CSRC系列、Z系列、FZ系列依次为文献[11]、文献[12]和文献[14]中试验样本;fcu为混凝土立方体抗压强度,Z系列中46.8/40.7依次为钢管内、外混凝土立方体抗压强度,CSRC系列为混凝土轴心抗压强度;Nu、Nu,c为极限承载力的实测值和计算值。
编号b(h)l/he0/mmD/mmt/mmfa/MPa 纵筋fy/MPafcu/MPaNu/kNNu,c/kNNu,c/Nu类型Z-2 300 4.7 50 133 4.5 339 6Φ12 2902210 2198.66 0.995 ⅠZ-3 300 4.7 100 133 4.5 339 6Φ12 290 1427 1394.42 0.977 ⅠZ-4 300 4.7 130 133 4.5 339 6Φ12 290 1111 1146.14 1.032 ⅠZ-5 300 4.7 150 133 4.5 339 6Φ12 290 921 1015.80 1.103 ⅠZ-6 300 4.7 190 133 4.5 339 6Φ12 290 601 581.14 0.967 ⅠZ-7 300 4.7 220 133 4.5 339 6Φ12 290 501 491.27 0.981 ⅠZ-8 300 4.7 190 89 7.0 339 6Φ12 290 531 501.52 0.944 ⅠZ-9 300 4.7 190 102 6.0 339 6Φ12 290 573 522.18 0.911 ⅠZ-10 300 4.7 190 168 3.5 339 6Φ12 290 611 660.28 1.081 ⅠZ-11 300 4.7 190 133 4.5 339 6Φ16 275 671 702.02 1.046 ⅠZ-12 300 4.7 190 133 4.5 339 8Φ16 275 671 770.32 1.148 ⅠZ-13 300 4.7 190 133 4.5 339 10Φ16 275 791 828.58 1.048 ⅠFZ-1 300 3 29 102 14 280.6 12Φ10 368.6 68.2 4010 3931.4 0.980 Ⅰ46.8/40.7 FZ-2 300 3 27 127 10 280.6 12Φ10 368.6 68.2 4102 4034.8 0.984 ⅠFZ-3 300 3 28 159 9 280.6 12Φ10 368.6 68.2 4292 4176.2 0.973 ⅡFZ-4 300 3 31 203 7 280.6 12Φ10 368.6 68.2 4745 4097.6 0.864 ⅡFZ-5 300 3 35 195 3.5 280.6 12Φ10 368.6 68.2 3815 3541.0 0.928 ⅡFZ-6 300 3 34 202 16.5 280.6 12Φ10 368.6 68.2 4702 4858.2 1.033 ⅡFZ-7 300 3 35 203 7 280.6 12Φ10 368.6 68.2 4855 3995.3 0.823 ⅡFZ-8 300 3 75 203 7 280.6 12Φ10 368.6 68.2 2792 2499.89 0.895 Ⅰ
2) 对于中和轴在截面外的情况Ⅱ,计算结果与实测结果比值的范围0.823~1.033,均值0.924,变异系数 0.091。可见本文提出的钢管混凝土组合柱压弯承载力计算方法所得计算值与试验值吻合良好,计算合理可靠,可用于指导设计。

图11 计算结果与试验结果对比
Fig.11 Comparison of calculation and test results
(1) 钢管混凝土组合柱偏压破坏过程与钢筋混凝土柱相似,破坏形态有大、小偏心受压破坏两种,以加载点远侧受拉纵筋达到屈服强度,近侧混凝土受压边缘达到极限压应变为界限破坏准则。
(2) 压弯荷载作用下的钢管混凝土组合柱截面平均应变符合平截面假定,以混凝土受压达到极限压应变为破坏特征,钢管横向应变随着偏心距减小而增大,虽不能像轴心受压构件达到屈服,但约束作用对构件承载力提高的影响不可忽略。
(3) 基于叠加理论和截面极限平衡理论,提出了既能保持现有规范形式,又能考虑钢管直径与截面高度比值、偏心距、长细比等因素的钢管混凝土组合柱正截面压弯承载力计算方法,计算结果与试验结果吻合良好,表明该方法计算合理可靠,可用于指导设计。
[1]陈周熠, 赵国藩, 林立岩. 钢管混凝土增强高强混凝土柱的正截面强度计算[J]. 建筑结构, 2001, 31(7):11―13.Chen Zhouyi, Zhao Guofan, Lin Liyan. The method for calculating flexural strength of high strength concrete column reinforced with concrete filled steel tube [J].Building Structures, 2001, 31(7): 11―13. (in Chinese)
[2]蔡健, 谢晓锋, 杨春, 等. 核心高强钢管混凝土柱轴压性能的试验研究[J]. 华南理工大学学报: 自然科学版,2002, 30(6): 81―85.Cai Jian, Xie Xiaofeng, Yang Chun, et al. An experimental research on the composite column with core of high-strength concrete filled steel tube under axial compression loading [J]. Journal of South China University of Technology: Natural Science, 2002, 30(6):81―85. (in Chinese)
[3]聂建国, 柏宇, 李盛勇, 等. 钢管混凝土核心柱轴压组合性能分析[J]. 土木工程学报, 2005, 38(9): 9―13.Nie Jianguo, Bai Yu, Li Shengyong, et al. Analyses on composite column with inside concrete filled steel tube under axial compression [J]. China Civil Engineering Journal, 2005, 38(9): 9―13. (in Chinese)
[4]廖飞宇, 韩林海. 方形钢管混凝土叠合柱的力学性能研究[J]. 工程力学, 2010, 27(4): 153―162.Liao Yufei, Han Linhai. Performance of concrete-filled steel tube reinforced concrtet columns with square sections [J]. Engineering Mechanics, 2010, 27(4): 153―162. (in Chinese)
[5]钱稼茹, 江枣. 钢管混凝土组合柱轴心受压承载力计算方法[J]. 工程力学, 2011, 28(4): 49―57.Qian Jiaru, Jiang Zao. Calculation method for axial compressive strength of steel tube-reinforce concrete composite columns [J]. Engineering Mechanics, 2011,28(4): 49―57. (in Chinese)
[6]刘阳, 郭子雄, 贾磊鹏, 等. 核心钢管混凝土叠合短柱轴压性能及设计方法研究[J]. 建筑结构学报, 2015,36(12): 135―142.Liu Yang, Guo Zhixiong, Jia Leipng, et al. Experimental study on axial compression performance and design method of core steel tube reinforced concrete short columns [J]. Journal of Building Structures, 2015,36(12): 135―142. (in Chinese)
[7]杨勇, 张超瑞, 泮勇溥, 等. 内藏钢管超高强混凝土芯柱组合柱抗震性能试验研究[J]. 工程力学, 2017,34(8): 96―104.Yang Yong, Zhang Chaorui, Pan Yongfu, et al.Experimental study on seismic performance of composite columns with high strength concrete filled steel tube cores [J]. Engineering Mechanics, 2017, 34(8): 96―104.(in Chinese)
[8]Liao Feiyu, Han Linhai, Tao Zhong. Behaviour of composite joints with concrete encased CFST columns under cyclic loading: Experiments [J]. Engineering Structures, 2014, 59: 745―764.
[9]周颖, 于海燕, 钱江, 等. 钢管混凝土叠合柱节点环梁试验研究[J]. 建筑结构学报, 2015, 36(2): 69―78.Zhou Yin, Yu Haiyan, Qian Jiang, et al. Experimental study on ring beams of joints of concrete filled steel tubular laminated columns [J]. Journal of Building Structures, 2015, 36(2): 69―78. (in Chinese)
[10] 郭全全, 赵羽西, 李芊, 等. 钢管混凝土叠合柱偏心受压性能试验研究[J]. 建筑结构学报, 2013, 34(12):103―111.Guo Quanquan, Zhao Yuxi, Li Qian, et al. A Experimental study on eccentric compressive property of steel tube-reinforced concrete column [J]. Journal of Building Structures, 2013, 34(12): 103―111. (in Chinese)
[11] 林拥军, 冯远, 官庆, 等. 配有圆钢管的钢骨混凝土柱的设计方法[J]. 建筑结构, 2004, 34(1): 13―15.Lin Yongjun, Feng Yuan, Guan Qing, et al. Design method of SRC columns with circular steel tube [J].Building Structure, 2004, 34(1): 13―15. (in Chinese)
[12] 王犇. 钢管混凝土叠合柱偏心受压试验研究及承载力计算分析[D]. 太原: 太原理工大学, 2011.Wang Ben. Research on the eccentric compression test and load bearing capacity calculation of steel tube-reinforced concrete column [D]. Taiyuan: Taiyuan University of Technology, 2011. (in Chinese)
[13] 安钰丰. 方形钢管混凝土叠合压弯构件力学性能和设计方法研究[D]. 北京: 清华大学, 2015.An Yufeng. Performance and design method of square concrete-encased CFST members under combined compression and bending [D]. Beijing: Tsinghua University, 2015. (in Chinese)
[14] 李鹏. 钢管高强混凝土核心柱受压性能试验与理论研究[D]. 杭州:浙江大学, 2005.Li Peng. Experimental and theoretic study on compression characteristics of composite column with core of high-strength concrete filled steel tube [D].Hangzhou: Zhejiang University, 2005. (in Chinese)
STRENGTH CALCULATION AND ECCENTRIC COMPRESSIVE TEST OF STEEL TUBE-REINFORCED CONCRETE COMPOSITE COLUMNS