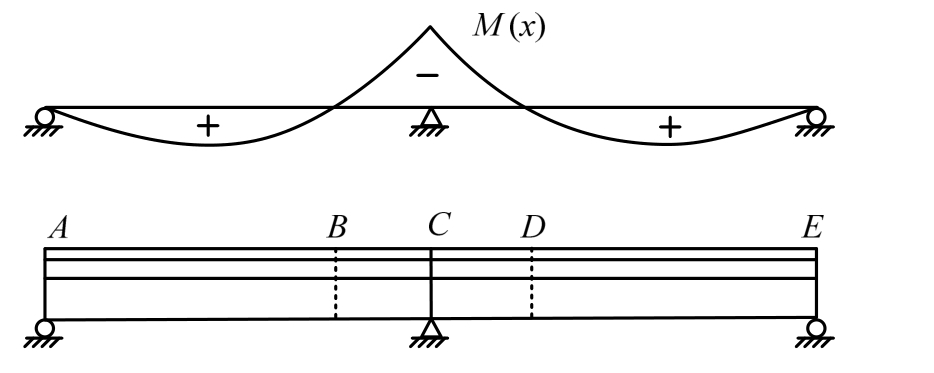
图1 连续梁负弯矩区示意
Fig.1 Sketch of negative moment region of continuous composite girder
钢-混凝土组合梁因相较于其他结构形式突出的技术、经济及力学性能优势,被认可为最有效的结构形式,广泛应用于桥梁、建筑工程中[1]。在各种结构体系中,多跨连续梁体系因均匀的内力分布,良好的使用性能和增强的跨越能力,在桥梁建设中应用最为普遍。多跨桥梁采用连续组合梁时可进一步减小变形,提高承载力及延性能力。但连续组合梁正、负弯矩区力学性能不同,不仅设计、分析较为复杂,而且在中支座的负弯矩区存在混凝土受拉、钢梁大部分截面受压的不利受力状态,易于发生钢梁下翼缘及腹板的局部失稳破坏[2-3]。
连续组合梁在中支座负弯矩区同时存在弯矩、剪力及弯剪相关作用。已有文献对负弯矩区组合梁的抗弯性能研究较多[4-5],而对抗剪及弯剪相关性能研究较少。White等[6]通过对大量试验数据的统计分析,对比了 12种常用的加劲工字钢梁抗剪承载力计算模型,研究表明Basler模型是综合精度及简化程度的最适用模型。薛建阳等[7]进行了3根负弯矩作用下的组合梁静载试验,研究了组合梁承载力及延性的主要影响因素,通过对钢梁的塑性分析,得出负弯矩组合梁的抗剪承载力提高并非由钢梁腹板的应变强化所致,而是由混凝土的翼板贡献产生。周安等[8]通过5根简支钢箱-预应力混凝土组合梁负弯矩下的试验研究,提出了考虑混凝土翼板贡献的变刚度挠度计算方法。Liang等[9]通过有限元分析研究了负弯矩区组合梁的极限承载力,分析了混凝土翼板的抗剪贡献,基于数值结果,拟合了负弯矩区组合梁的抗剪及弯剪相关承载力计算公式。唐亮等[10]采用有限元分析研究了负弯矩区组合梁的抗剪性能,分析了截面尺寸、材料强度及剪跨长度等参数的影响,研究表明负弯矩区组合梁竖向抗剪强度的提高仅来源于混凝土翼板的抗剪贡献,而与组合作用无关。
为设计较传统工字形钢板梁更能有效利用抗弯、抗剪强度的高性能钢桥,新型管翼缘截面梁近十几年来得到了不断的研发、应用[11-20]。管翼缘梁由圆形或矩形管翼缘、平腹板及加劲肋焊接而成。管翼缘梁桥力学性能优势显著,具有较大的局部屈曲承载力、扭转刚度及较小的腹板长细比[11]。Kim等[12-13]研究了内填混凝土圆管翼缘组合梁的抗弯性能,在有限元分析的基础上建立了侧向弯扭屈曲承载力计算公式,并通过试验研究验证了数值模型的适用性。Dong等[14]分析了双空管翼缘钢梁的抗弯性能,结果表明合适的横向加劲肋布置可降低截面扭转效应对侧向弯扭屈曲承载力影响。Hassanein等[15-16]研究了柔腹板矩形空管翼缘钢梁的抗弯、抗剪性能,提出了基于现行规范的改进抗弯及抗剪承载力计算方法。王春生等[17-18]进行了内填混凝土圆管、双管翼缘组合梁的抗弯、抗剪性能试验研究,在试验成果基础上提出了相应组合梁抗弯、抗剪承载力计算公式,并将研究成果应用于国内首座管翼缘组合梁桥的设计与建造[19]。
然而以往开展的管翼缘组合梁研究均针对正弯矩区的受力性能,而对于管翼缘组合梁负弯矩区的力学性能,迄今尚无研究涉及。本文对圆管翼缘新型组合梁开展负弯矩区力学性能试验研究,分析圆管翼缘组合梁的受力特性及破坏规律,建立负弯矩区圆管翼缘组合梁承载力计算方法,以供理论研究及工程实践参考应用。
试验采用跨中受集中力简支梁模型来模拟连续组合梁中墩位置的负弯矩区(图1中B-C-D区)。以钢板下翼缘宽度bb为变化参数,共设计制作了3组5根简支圆管翼缘组合梁:
第1组:bb=150 mm,共2根试验梁,编号为NCTFCGS-1-1、NCTFCGS-1-2。
第2组:bb=260 mm,共2根试验梁,编号为NCTFCGS-2-1、NCTFCGS-2-2。
第3组:bb=300 mm,共1根试验梁,编号为NCTFCGS-3-1。

图1 连续梁负弯矩区示意
Fig.1 Sketch of negative moment region of continuous composite girder
试验梁构造如图2所示。梁长L=1800 mm,计算跨径L0=1500 mm,剪跨长度Ls=750 mm,总梁高H=500 mm;混凝土翼板宽度bf=600 mm,厚度hf=80 mm;钢梁按密实截面设计,采用组件焊接而成,高度hs=420 mm;上翼缘圆钢管外径R=133 mm,壁厚tt=4 mm;腹板高度hw=271 mm,厚度tw=6 mm;下翼缘钢板厚度hb=16 mm。为防止腹板发生局部屈曲,在支撑及加载位置腹板双侧焊接12 mm厚加劲肋。混凝土翼板内按构造配置φ6光圆钢筋,纵筋分2层布置18根,箍筋按80 mm等间距布置22根。
试验梁翼板及钢管内填充C40混凝土。翼板及钢管内填混凝土实测轴心抗压强度fc分别为56.3 MPa、50.4 MPa,混凝土弹性模量Ec分别为37.1 GPa、36.2 GPa。钢板及钢筋实测抗拉屈服强度fy、fr分别为312 MPa、310 MPa,抗拉极限强度分别为 430 MPa、460 MPa,钢材弹性模量Es为210 GPa。
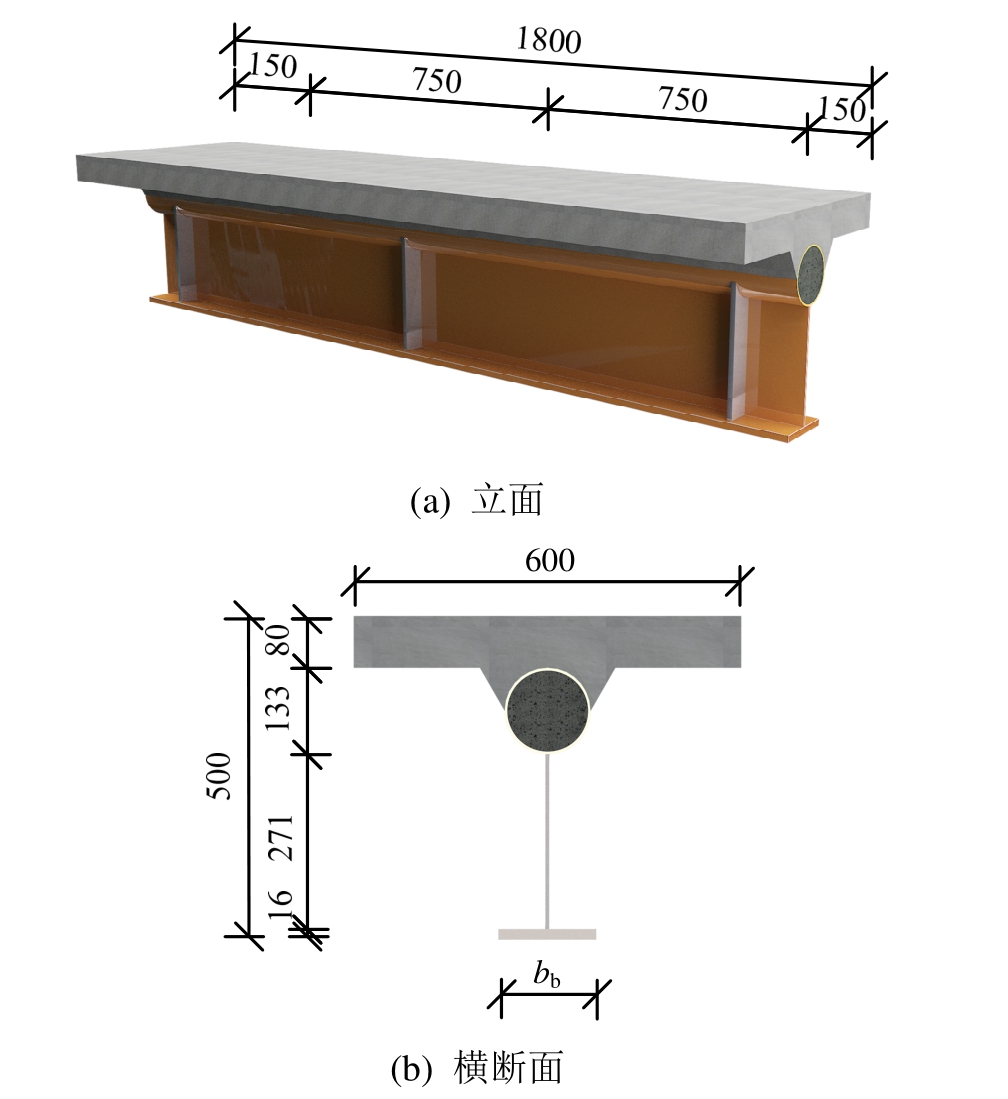
图2 试验梁构造图 /mm
Fig.2 Test girder structures
为模拟连续组合梁负弯矩区的受力性能,试验梁采用简支条件下的截面梁倒置方式,由液压千斤顶通过钢垫板进行跨中加载,荷载F由压力传感器量测,钢梁受压翼缘无侧向约束。试验加载装置见图3。
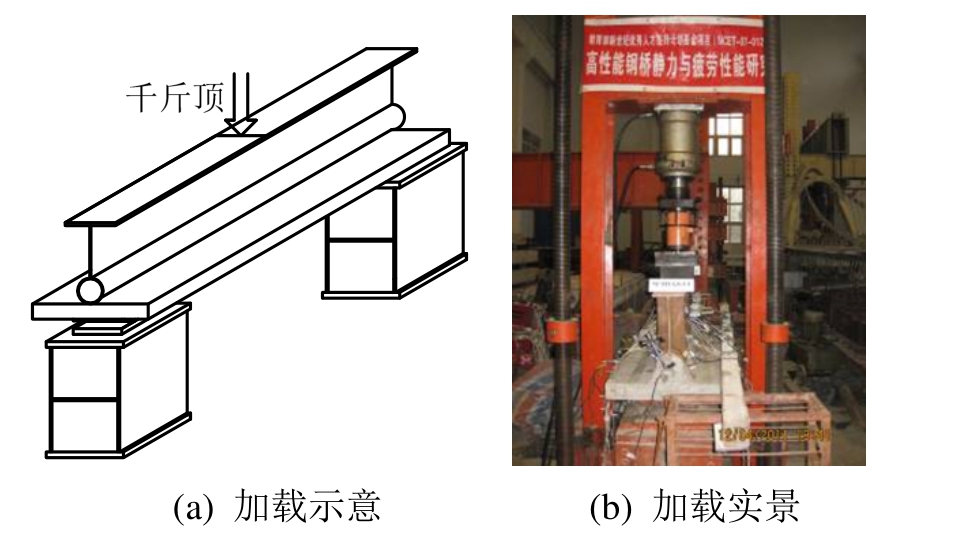
图3 加载装置
Fig.3 Loading device
在距试验梁两侧支撑点各1/2Ls和1/2hs位置处取测试断面,沿梁截面高度布置应变花测点,测试试验梁剪切应变;在跨中截面布置应变测点测试轴向应变,布置百分表测试跨中挠度;在腹板布置百分表测试腹板面外变形;在钢梁与混凝土翼板交界面布置滑移计测试二者相对滑移;采用TDS-602静态数据采集仪对试验全过程的应变和位移进行数据采集。试验中,使用裂缝放大器来测试混凝土翼板裂缝发展情况。试验梁测点布置见图4。
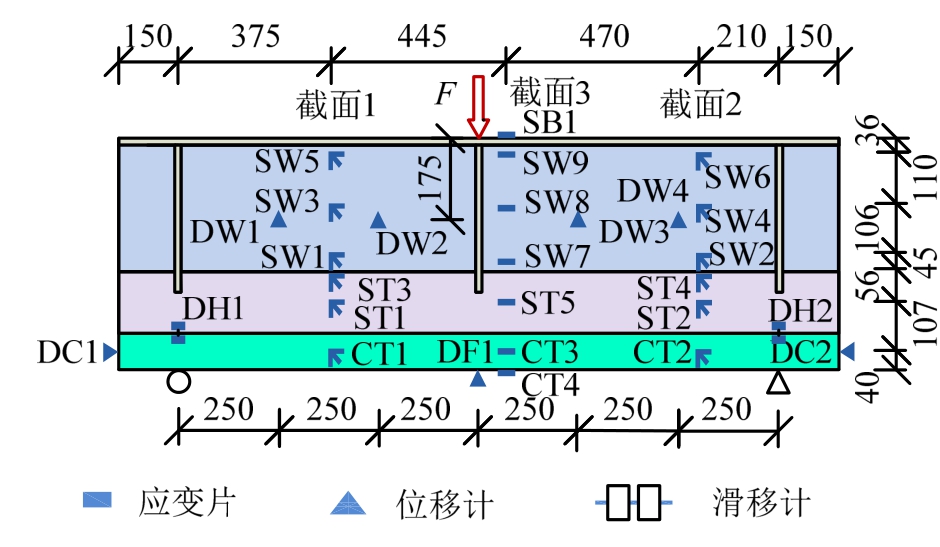
图4 测点布置 /mm
Fig.4 Arrangement of measurement points
试验结果表明,所有试验梁的破坏过程为首先混凝土翼板受拉开裂退出工作,之后混凝土翼板内纵向钢筋屈服,在腹板发生剪切屈服后,试验梁钢梁发生局部剪切屈曲破坏而达到极限承载力。试验梁最终破坏时伴随有4种典型破坏形态:局部剪切屈曲、下翼缘侧向屈曲、梁端腹板压屈和钢梁整体弯扭屈曲,如图5所示。

图5 破坏形态
Fig.5 Failure modes
当试验梁加载至 0.14Fu时(Fu为试验梁极限荷载),在跨中截面的混凝土翼板顶面中部首先出现第1条裂缝,并随荷载的增加很快贯通混凝土翼板顶面。随荷载的不断增大,在第1条裂缝两侧对称位置出现第2批裂缝,间距约为80 mm~160 mm。之后,裂缝数目不断增加,已有裂缝不断加宽。同批裂缝间距仍约为80 mm~160 mm。随着受拉钢筋的屈服,试验梁挠度增速略有加快,但仍基本随荷载增大均匀增大。当荷载增至0.65Fu时,钢梁腹板发生剪切屈服,此后,跨中挠度增速不断加快,腹板屈服区域侧向位移增速加快。挠度随荷载非线性增加的同时,已有裂缝宽度也随荷载非线性增大。当荷载增至0.82Fu时,钢梁受压翼缘发生屈服。荷载临近Fu时,试验梁跨中加载区腹板发生剪切屈曲,同时梁端腹板自由边出现受压屈曲,加载区下翼缘产生向梁内的凹曲,试验梁挠度、腹板及翼缘屈曲变形、裂缝宽度等均随荷载的增加而迅速增大。荷载达到Fu后,试验梁承载力开始下降,但挠度仍可继续增大,表现出较好的延性性能。
试验梁跨中截面荷载-挠度曲线如图6所示。随下翼缘宽度增加,试验梁抗弯刚度增大,极限抗弯承载力理应增大,但由图6可以看出,各试验梁荷载-挠度曲线发展规律较为一致,抗弯刚度及极限承载力相近,表明试验梁极限状态并非完全由抗弯性能控制,而是由试验梁抗弯、抗剪相关特性控制。根据荷载-挠度曲线,并结合试验梁破坏特性,负弯矩区圆管翼缘组合梁破坏过程可划分为5个阶段:① 从开始加载至混凝土翼板受拉开裂前,挠度随荷载的增大呈线性增长,组合梁整体工作性能良好,处于未开裂弹性阶段;② 当荷载大于开裂荷载后,受拉区混凝土开裂,荷载-挠度曲线斜率稍有下降,但因受拉混凝土裂缝宽度较小,故荷载-挠度曲线仍近似呈线性关系。随荷载的增加,受拉钢筋逐渐屈服,中性轴向钢梁侧移动,不断有新的裂缝出现,组合梁处于开裂后弹性阶段;③ 当荷载加至0.65Fu时,钢梁腹板发生剪切屈服。随屈服区域逐渐加大,截面刚度不断下降,内力重新分配。当荷载加至0.82Fu时,钢梁受压翼缘屈服,截面刚度进一步降低。此阶段荷载-挠度曲线呈非线性变化,挠度发展较快,组合梁处于弹塑性阶段;④ 当荷载加至0.92Fu时,试验梁腹板开始出现局部屈曲,随荷载的增大,腹板屈曲变形急剧增大,同时各种伴随破坏不断产生并发展,直至组合梁达到极限承载力Fu,组合梁处于破坏阶段;⑤ 达到极限荷载后,随组合梁承载力的下降,挠度仍可继续增大,荷载-挠度曲线呈平缓下降趋势发展,组合梁处于承载力下降段。由图6可知,负弯矩区混凝土翼板开裂对试验梁刚度并无明显影响。

图6 荷载-挠度曲线
Fig.6 Load-deflection curves
监测腹板侧向变形可得到试验梁面外变形规律及屈曲特性。各试验梁腹板侧向变形规律较为相似,以试验梁NCTFCGS-2-2为例说明,该试验梁荷载-腹板侧向变形曲线见图7。由图7可以看出,试验梁并未发生分枝点屈曲,而是发生了类似于有初始缺陷的受压柱大变形极值点屈曲。受梁柱效应影响,随荷载的增加,腹板面内刚度减小,侧向变形呈线性增大。但因试验梁腹板面内刚度较大,故总体侧向变形很小。当荷载增至0.92Fu后,腹板侧向变形突然增大,增速急剧加快,试验梁腹板出现了显著的剪切屈曲面外变形。卸载后,腹板侧向变形除少量弹性部分恢复外,有较大塑性变形残余。
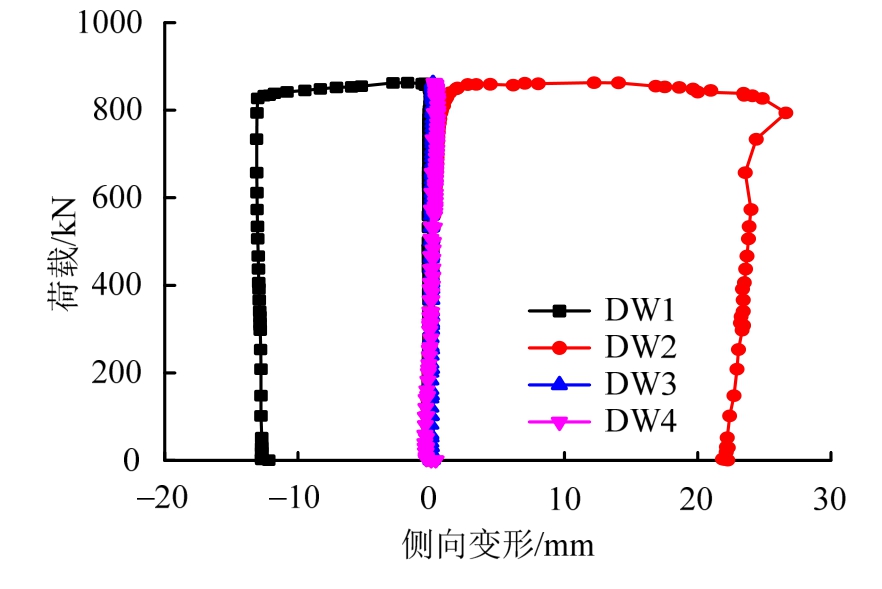
图7 试验梁NCTFCGS-2-2荷载-侧向变形曲线
Fig.7 Load-lateral deformation curves of NCTFCGS-2-2
由图4(c)试验梁梁端横截面受压屈曲破坏形态可以看出,腹板的受压屈曲形态类似于两端固结的欧拉柱的屈曲模态,这表明了圆管翼缘组合梁在翼缘-腹板交接处的边界条件更为近似固结状态。
试验测得各试验梁钢梁与混凝土翼板交界面相对滑移最大值为0.18 mm,此较小的滑移值表明了栓钉剪力连接件可确保组合梁的钢梁与混凝土翼板二者间较好的连接性能。同时也表明了负弯矩区混凝土翼板的受拉开裂对组合梁交界面的相对滑移无显著影响。
受压翼缘实测应变由弯曲应变和局部屈曲应变二者叠加而成,当试验梁受压翼缘发生局部屈曲时,实测翼缘压应变会有突变现象发生。从图8各试验梁跨中截面受压翼缘荷载-纵向应变曲线可看出,除NCTFCGS-2-2外,其他试验梁翼缘均未达屈服应变。NCTFCGS-1-1与 NCTFCGS-3-1荷载-纵向应变曲线在临近Fu时发生了应变转向,表明试验梁受压翼缘发生了局部屈曲,与观测试验现象是吻合的。而除这2根试验梁存在翼缘应变突变外,其余试验梁翼缘应变在试验梁发生剪切屈曲时并未出现显著变化。
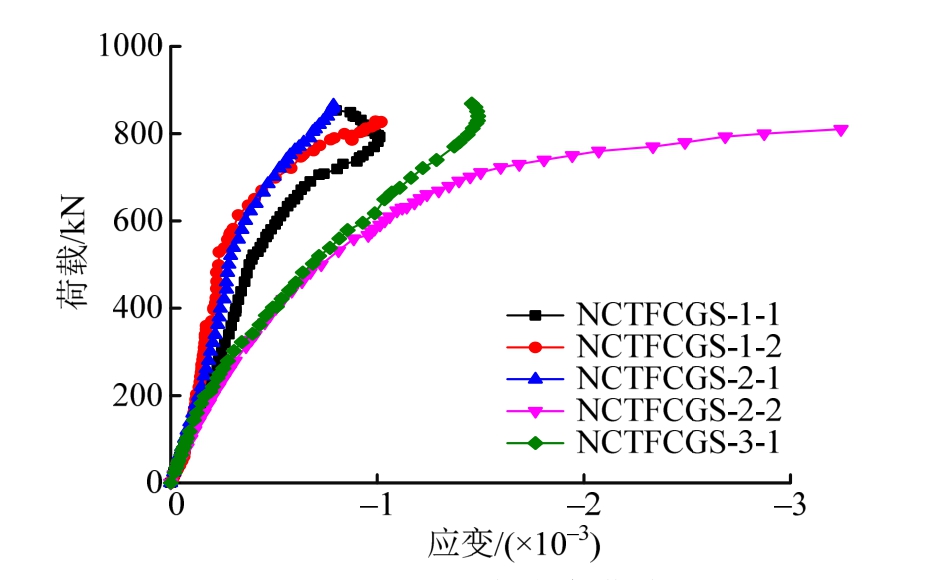
图8 荷载-纵向应变曲线
Fig.8 Load-longitudinal strain curves
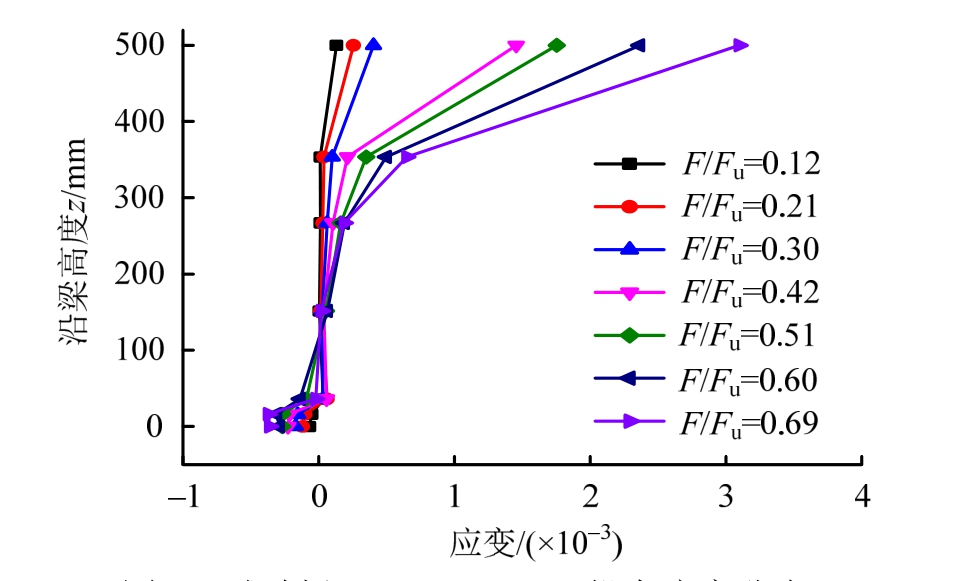
图9 试验梁NCTFCGS-2-1纵向应变分布
Fig.9 Longitudinal strains distribution of NCTFCGS-2-1
以 NCTFCGS-2-1为例说明。试验梁NCTFCGS-2-1截面 3沿梁高方向纵向应变分布如图9所示,图中z为距钢梁下翼缘底面高度。由图9可看出,试验梁纵向应变呈不均匀非线性分布,说明受小剪跨比构件剪切变形效应影响,截面变形已不能很好地符合平截面假定。
以 NCTFCGS-1-1为例说明,试验梁NCTFCGS-1-1截面2剪力-竖向剪切应变、沿梁高方向剪切应变分布曲线分别如图10、图11所示,图中V为剪力,r为竖向剪切应变。加载开始后,试验梁竖向剪切应变基本随剪力增加呈线性增长,腹板剪切应变发展速率显著高于圆管与混凝土翼板。当试验梁剪切应变大于理论剪切屈服应变后,应变增速加快,随荷载呈非线性增长。试验梁达极限承载力时,腹板各测点均进入剪切屈服状态,而圆管和混凝土翼板仍处于弹性受力状态。

图10 试验梁NCTFCGS-1-1剪力-剪切应变曲线
Fig.10 Shear force-shear strain curves of NCTFCGS-1-1
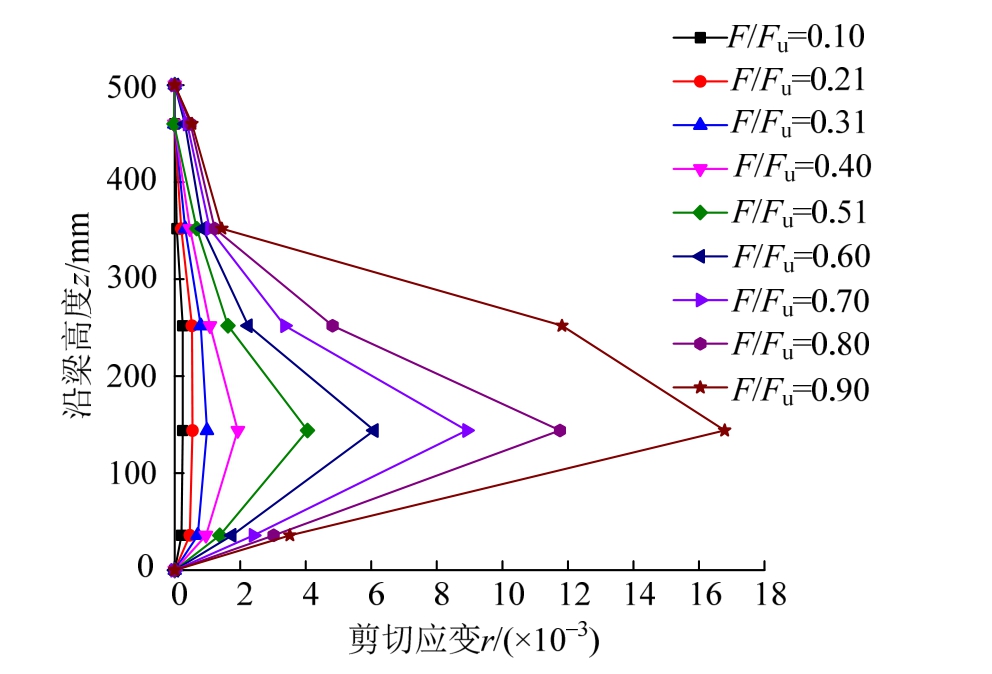
图11 试验梁NCTFCGS-1-1剪切应变分布
Fig.11 Shear strains distribution of NCTFCGS-1-1
在混凝土翼板受拉开裂后,为分析负弯矩区圆管翼缘组合梁混凝土的抗剪作用,采用考虑完全混凝土(弹性无开裂)的抗剪作用与不计混凝土的抗剪作用两种截面剪应变计算方法,对比试验梁NCTFCGS-1-1在腹板剪切屈服前F/Fu=0.4时沿梁高方向的剪应变分布如图 12所示。其中,竖向剪应变按下式计算:

式中:S为截面计算高度以外部分面积对中性轴的静矩;I为截面对中性轴的惯性矩;G为材料剪切模量;t为计算高度处截面宽度。
式(1)中,当考虑完全混凝土作用时按换算截面法计算公式参数,而不考虑混凝土作用时按纯钢梁计算公式参数。
由图 12计算与实测剪应变曲线比较可见,相较考虑完全混凝土作用的剪应变曲线,不计混凝土作用的剪应变曲线在总体应变分布趋势、各点剪应变数值及最大剪应变位置等特征方面均与试验曲线吻合更好。表明负弯矩区圆管翼缘组合梁在混凝土受拉开裂、截面特性发生改变后工作状态下,不计混凝土的抗剪作用较考虑完全混凝土的抗剪作用更为符合试验梁的抗剪特性。
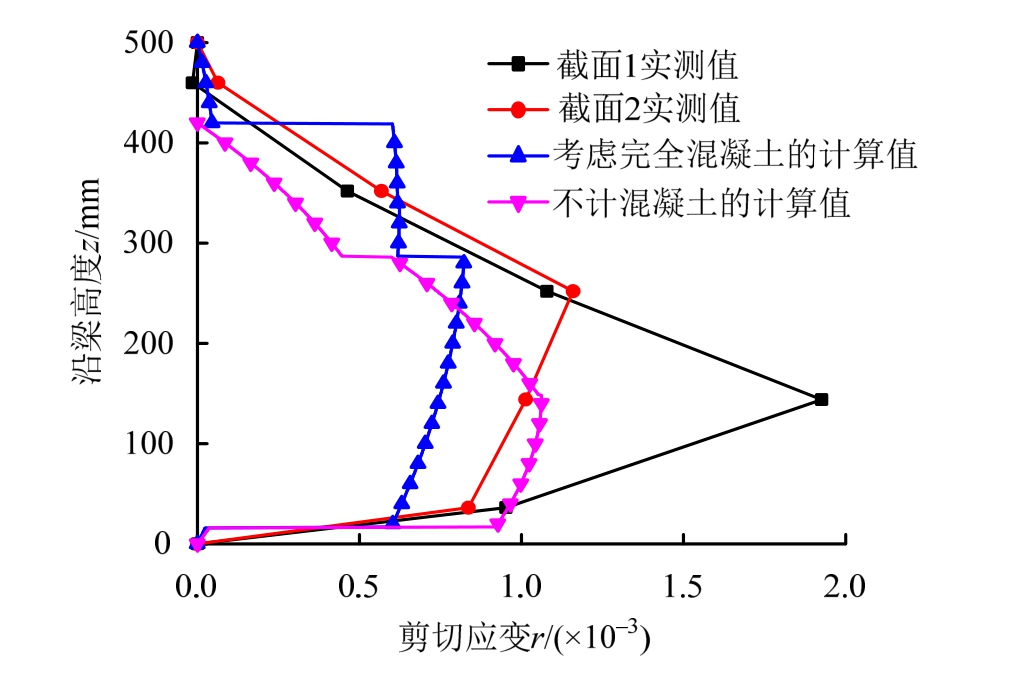
图12 试验梁NCTFCGS-1-1剪切应变分布比较
Fig.12 Comparison of shear strains distribution of NCTFCGS-1-1
连续组合梁负弯矩区荷载下受弯矩、剪力共同作用,由Von Mises强度理论可知,钢梁腹板存在的剪应力会引起截面极限抗弯承载力下降,反之,钢梁腹板存在的弯曲应力亦会导致截面极限抗剪承载力降低。欧洲EC4[20]、美国ASCE[21]、澳大利亚AS 2327.1[22]及中国《钢-混凝土组合桥梁设计规范》(GB 50917—2013)[23]等现行设计规范均使用弯剪相关方程计算承载力降低效应。在相关方程的极限抗弯承载力计算时均考虑了混凝土翼板和组合作用的贡献,但在相关方程的极限抗剪承载力计算时仅允许考虑腹板的抗剪强度。
根据弯剪相关特性,在计算弯剪共同作用下负弯矩区圆管翼缘组合梁极限承载力前,需首先计算负弯矩区圆管翼缘组合梁的纯弯承载力Mn及纯剪承载力Vn。
依据负弯矩区圆管翼缘组合梁试验结果,应用简化塑性理论计算其纯弯承载力时,可认为混凝土翼板内受拉钢筋,钢梁受拉、压钢材均达屈服强度,翼板混凝土受拉开裂退出工作。根据塑性中性轴所处位置可分为以下3种情况:
1) 塑性中性轴位于钢梁腹板内,即:
理论计算图式如图 13(a)所示。图 13(a)中,x为塑性中性轴至混凝土翼板顶面的距离;Ar为混凝土翼板纵筋截面积;At、Awt、Awc、Ab及y1、y2、y3、y4分别为圆管上翼缘、受拉腹板、受压腹板、钢板下翼缘截面积及相应截面形心至混凝土翼板内纵筋截面形心的距离。
则Mn可按如下计算:
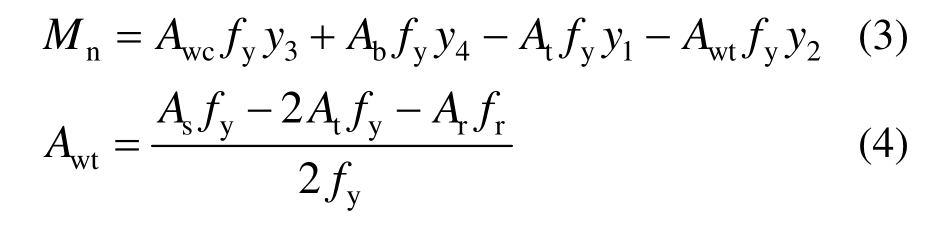
式中:Aw为钢梁腹板截面积;As为钢梁截面积。
2) 塑性中性轴位于圆管上翼缘内,即:
理论计算图式如图13(b)所示。图13(b)中,Att、Atc分别为受拉、受压圆管上翼缘截面积,y5、y6、y7分别为受拉、受压圆管上翼缘及腹板截面形心至混凝土翼板内纵筋截面形心的距离。
则Mn可按如下计算:
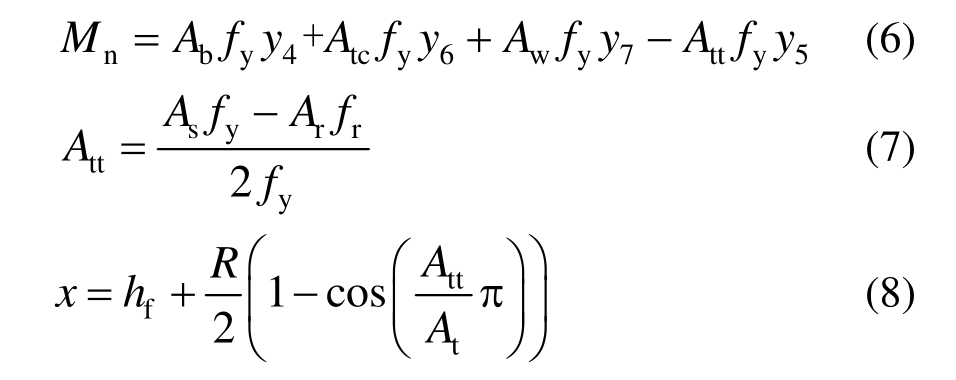
3) 塑性中性轴位于混凝土翼板内,即:
因翼板内受压混凝土与受拉钢筋的实际距离较近,其对截面抗弯承载力贡献较小,故可忽略翼板受压混凝土的抗弯承载力贡献[24]。此理论计算图式如图13(c)所示。
则Mn可按如下计算:

图13 负弯矩区圆管翼缘组合梁纯弯承载力计算图式
Fig.13 Ultimate strength under pure bending in negative
bending region of NCTFCGSs
混凝土翼板和组合作用对组合梁正弯矩区的竖向抗剪承载力贡献较大,而在组合梁负弯矩区,混凝土翼板因受拉开裂,其对竖向抗剪承载力的贡献相对并不显著。本文试验结果表明,负弯矩区圆管翼缘组合梁在混凝土开裂后,不计混凝土的抗剪作用较考虑完全混凝土的抗剪作用更符合试验梁的实际抗剪响应。圆管翼缘组合梁由于特殊的截面分布形式,在承载能力极限状态管翼缘并未达到完全剪切屈服,而腹板则可基本达到完全剪切屈服。本文在计算圆管翼缘组合梁纯剪承载力Vn时,忽略混凝土的抗剪作用,理论简化计算图式如图14所示。
Vn计算公式包含钢梁腹板与圆钢管上翼缘两部分的抗剪承载力贡献,即:
式中:Vw、Vt分别为钢梁腹板、圆钢管上翼缘的抗剪承载力。
对于密实截面组合梁,Vw可采用腹板塑性抗剪承载力,按下式计算:
因承载能力极限状态下钢管上翼缘未达完全剪切屈服,为合理简化Vt计算,引入钢管应力折减系数α,则Vt可采用折减的圆钢管上翼缘塑性抗剪承载力,按下式计算:
承载能力极限状态时,试验梁钢管混凝土上翼缘处于弹性状态,结合试验梁钢管混凝土上翼缘的计算弹性剪应变分布及钢管实测剪应变,可确定钢管的不均匀剪应力近似分布关系,之后对钢管剪应力进行应力积分,将各试验梁计算剪力分别与圆钢管的塑性剪力进行比较后,可确定α数值介于0.60~0.67之间,本文计算偏安全取值为0.60。

图14 负弯矩区圆管翼缘组合梁纯剪承载力计算图式
Fig.14 Ultimate strength under pure shear in negative moment region of NCTFCGSs
2005年之前AISC、AASHTO规范明确要求,当使用拉力场作用设计腹板时需考虑弯剪相关作用。White等[25]研究表明,采用AISC 2005、AASHTO 2004规范计算的抗弯、抗剪承载力偏于保守,且通常钢梁可发展屈曲后强度及应变强化作用来提供更大的承载力,因此在钢梁合理尺寸构造下,即使腹板设计需利用拉力场作用,弯剪承载力相关关系仍可忽略。此后的AISC[26]及AASHTO[27]修编规范均采用了White的研究成果而不再考虑弯剪相互作用。但需注意,密实截面钢梁较组合梁具有更好的延性能力,当施加剪力不大于腹板完全塑性剪切抗力时,这类构件通常具有比Mn更大的抗弯承载力。而组合梁受混凝土材料特性限制,纵使纯弯荷载下,也很难达到Mn。二者间抗剪承载力也具有类似特性。表1为试验梁忽略弯剪相关时承载力比较结果,表中,Mut为极限抗弯承载力试验值,Vut为极限抗剪承载力试验值。由表1可知,在高剪力、高弯矩荷载下,受弯剪相关作用影响,试验梁承载力降低显著,难以达到纯弯、纯剪承载力。忽略弯剪相关的承载力计算会高估试验梁的承载力,预测结果并不安全,因此,计算圆管翼缘组合梁负弯矩区承载力时考虑弯剪相关作用更为合理。
表1 忽略弯剪相关时承载力比较
Table 1 Comparison of strength regardless of moment-shear interaction
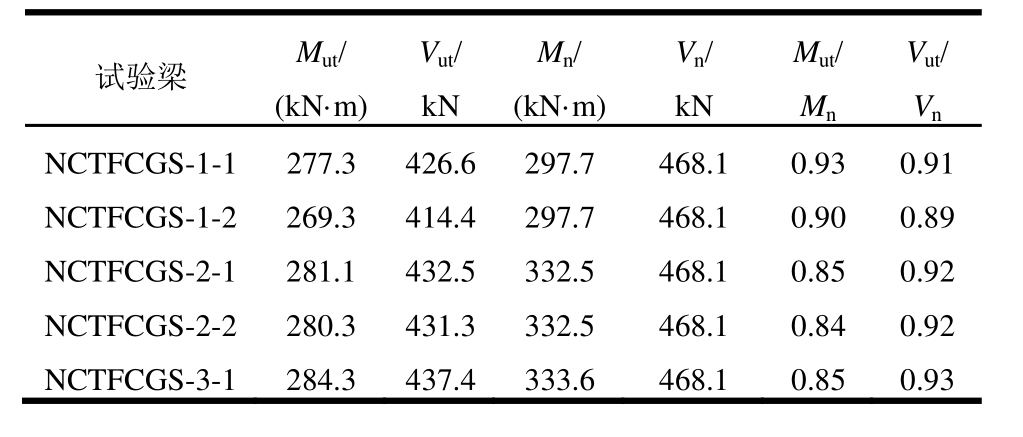
试验梁Mut/(kN·m)Vut/kNMn/(kN·m)Vn/kNMut/MnVut/Vn NCTFCGS-1-1 277.3 426.6 297.7 468.1 0.93 0.91 NCTFCGS-1-2 269.3 414.4 297.7 468.1 0.90 0.89 NCTFCGS-2-1 281.1 432.5 332.5 468.1 0.85 0.92 NCTFCGS-2-2 280.3 431.3 332.5 468.1 0.84 0.92 NCTFCGS-3-1 284.3 437.4 333.6 468.1 0.85 0.93
EC4规范要求当V>0 .5VRd时,组合梁需考虑剪力对抗弯承载力的降低影响,应根据受剪程度对钢梁腹板的抗弯承载力进行折减,其折减系数为(1-ρ)fyw,此处:
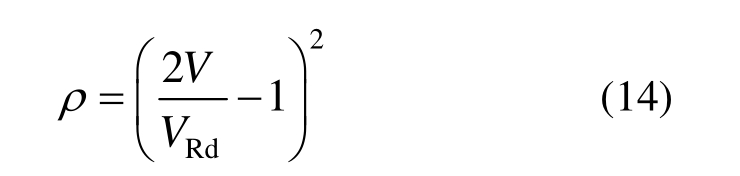
式中:VRd为抗剪承载力,取塑性抗剪承载力Vpl,Rd与剪切屈曲承载力Vb,Rd二者中的较小者;fyw为腹板拉压屈服强度。
当![]() 时,忽略钢梁腹板抗弯承载力贡献。
时,忽略钢梁腹板抗弯承载力贡献。
GB 50917—2013与AS 2327.1采用相同弯剪相关形式,同 EC4相关曲线仅有的区别是在![]() 之间时,抗弯承载力采用两种状态间的线性插值计算。
之间时,抗弯承载力采用两种状态间的线性插值计算。
ASCE 1998腹板开洞组合梁规范与Liang等[9]提出的负弯矩区组合梁弯剪相关承载力公式形式如下:
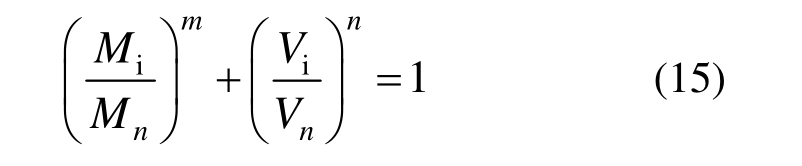
式中:Mi、Vi分别为弯剪共同作用下负弯矩区圆管翼缘组合梁极限抗弯承载力与极限抗剪承载力。式(15)在 ASCE 1998 中,m=n= 3;在Liang等公式中,m=0.6,n=6。
按以上弯剪相关形式计算试验梁在剪力影响下的抗弯承载力比较结果见表2。由表2可知,ASCE及 Liang等弯剪相关形式计算抗弯承载力较为保守,二者计算平均值分别为试验值的87%、82%。EC4规范采用的二次凸抛物线弯剪相关形式的计算抗弯承载力与试验结果最为接近,平均值为试验值的100%,但部分试验梁计算承载力略高于试验值,计算结果偏于不利。GB 50917—2013规范采用直线弯剪相关形式,其计算抗弯承载力较EC4规范略有降低,平均值为试验值的96%,且所有试验梁承载力的计算值均小于试验值。综上可知,GB 50917—2013规范的弯剪相关形式是满足计算精度与结果安全性二者组合的最适宜形式。因此,在应用本文推导的圆管翼缘组合梁负弯矩区纯弯、纯剪承载力公式的基础上,推荐采用GB 50917—2013规范给出的弯剪相关形式计算圆管翼缘组合梁负弯矩区的弯剪相关承载力。
表2 剪力影响下抗弯承载力比较
Tab.2 Comparison of flexural strength under the influence of shear
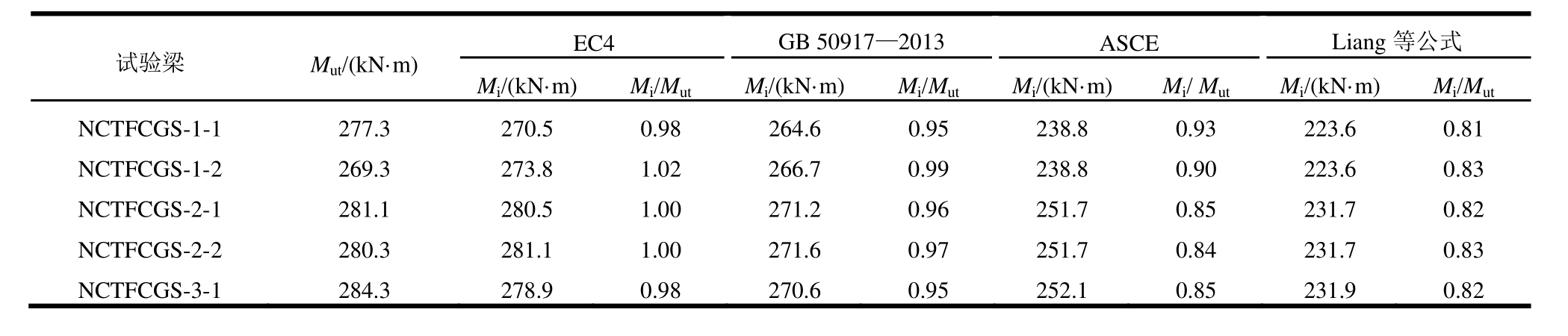
试验梁Mut/(kN·m) EC4 GB 50917—2013 ASCE Liang等公式Mi/(kN·m)Mi/MutMi/(kN·m)Mi/MutMi/(kN·m)Mi/MutMi/(kN·m)Mi/MutNCTFCGS-1-1 277.3 270.5 0.98 264.6 0.95 238.8 0.93 223.6 0.81 NCTFCGS-1-2 269.3 273.8 1.02 266.7 0.99 238.8 0.90 223.6 0.83 NCTFCGS-2-1 281.1 280.5 1.00 271.2 0.96 251.7 0.85 231.7 0.82 NCTFCGS-2-2 280.3 281.1 1.00 271.6 0.97 251.7 0.84 231.7 0.83 NCTFCGS-3-1 284.3 278.9 0.98 270.6 0.95 252.1 0.85 231.9 0.82
(1) 负弯矩区圆管翼缘组合梁的受力过程可划分为未开裂弹性阶段、开裂后弹性阶段、弹塑性阶段、破坏阶段及下降段等5个受力阶段。整个试验过程中,圆管翼缘组合梁表现出良好的稳定性和延性性能。
(2) 在混凝土翼板受拉开裂、截面特性发生改变后,相较考虑完全混凝土的抗剪作用,不计混凝土抗剪作用的计算弹性剪应变分布与实测剪应变曲线更为吻合,表明在负弯矩区圆管翼缘组合梁的抗剪性能分析时,可近似忽略混凝土的抗剪作用。
(3) 依据负弯矩区圆管翼缘组合梁承载能力极限状态下的工作特性,建立了圆管翼缘组合梁纯弯、纯剪承载力计算公式。在纯剪承载力公式中忽略混凝土的抗剪作用,并引入钢管应力折减系数α反映圆钢管的实际抗剪贡献。试验梁计算纯弯、纯剪承载力与试验结果对比表明,受高剪力、高弯矩相关效应影响,试验梁承载力降低显著,在计算负弯矩区圆管翼缘组合梁承载力时应考虑弯剪相关作用。
(4) 对比了EC4、GB 50917—2013、ASCE及Liang等公式的弯剪相关形式,计算了试验梁剪力影响下的极限抗弯承载力。计算结果比较表明,GB 50917—2013对试验梁极限抗弯承载力的平均计算精度为96%,是综合计算精度与结果安全性的最适宜形式。建议在应用本文推导的纯弯、纯剪承载力公式的基础上,采用GB 50917—2013规范给出的弯剪相关形式计算负弯矩区圆管翼缘组合梁弯剪相关承载力。
[1]聂建国, 陶慕轩, 吴丽丽, 等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报, 2012, 45(6): 100―122.Nie Jianguo, Tao Muxuan, Wu Lili, et al. Advances of research on steel-concrete composite bridges [J]. China Civil Engineering Journal, 2012, 45(6): 100―122. (in Chinese)
[2]陈齐风, 刘沐宇, 张强. 大跨径钢-混组合梁桥主梁负弯矩区腹板弯-剪弹性屈曲分析[J]. 工程力学, 2015,32(11): 180―188.Chen Qifeng, Liu Muyu, Zhang Qiang. Web buckling of girder in long-span steel-concrete composite bridge under shear and bending [J]. Engineering Mechanics,2015, 32(11): 180―188. (in Chinese)
[3]Vasdravellis G, Uy B, Kirkland B. Behaviour and design of composite beams subjected to negative bending and compression [J]. Journal of Constructional Steel Research, 2012, 79(79): 34―47.
[4]Ansourian P. Experiments on continuous composite beams [J]. Proceedings of the Institution of Civil Engineers, Part 2, 1981, 71(12): 25―51.
[5]樊健生, 聂建国. 负弯矩作用下考虑滑移效应的组合梁承载力分析[J]. 工程力学, 2005, 22(3): 177―182.Fan Jiansheng, Nie Jianguo. Effects of slips on load-carrying capacity of composite beams under negative bending [J]. Engineering Mechanics, 2005,22(3): 177―182. (in Chinese)
[6]White D W, Baker M G. Shear resistance of transversely stiffened steel-I girders [J]. Journal of Structural Engineering, 2008, 134(9): 1425―1436.
[7]薛建阳, 成果, 赵鸿铁, 等. 钢-混凝土在负弯矩作用下抗剪性能的试验研究[J]. 建筑结构学报, 2008, 29(增刊 1): 83―87.Xue Jianyang, Cheng Guo, Zhao Hongtie, et al.Experimental study on shear behavior of steel-concrete composite beams under negative moment [J]. Journal of Building Structures, 2008, 29(Suppl 1): 83―87. (in Chinese)
[8]周安, 戴航, 刘其伟. 钢箱-预应力混凝土组合梁负弯矩区结构性能试验研究[J]. 土木工程学报, 2009,42(12): 69―75.Zhou An, Dai Hang, Liu Qiwei. Experimental study of the structural behavior of the negative bending zone of steel box-prestressed concrete composite beams [J].China Civil Engineering Journal, 2009, 42(12): 69―75.(in Chinese)
[9]Liang Q Q, Uy B, Bradford M A, et al. Ultimate strength of continuous composite beams in combined bending and shear [J]. Journal of Constructional Steel Research, 2004,60(8): 1109―1128.
[10] 唐亮, 聂建国. 密实截面组合梁的竖向抗剪强度II: 受负弯矩作用的组合梁[J]. 土木工程学报, 2008, 41(3):15―20.Tang L, Nie Jianguo. Vertical shear strength of composite beams with compact steel sections. part II: composite beams subjected to hogging moment [J]. China Civil Engineering Journal, 2008, 41(3): 15―20. (in Chinese)
[11] Sause R. Innovative steel bridge girders with tubular flanges [J]. Structure and Infrastructure Engineering,2015, 11(4): 450―465.
[12] Kim B G, Sause R. High performance steel girders with tubular flanges [J]. International Journal of Steel Structures, 2005, 5(3): 253―263.
[13] Sause R, Kim B G, Wimer M R. Experimental study of tubular flange girder [J]. Journal of Structural Engineering, 2008, 124(3): 384―392.
[14] Dong J, Sause R. Flexural strength of tubular flange girders [J]. Journal of Constructional Steel Research,2009, 65(3): 622―630.
[15] Hassanein M F, Kharoob O F, Hadidy A M.Lateral-torsional buckling of hollow tubular flange plate girders with slender stiffened webs [J]. Thin-Walled Structures, 2013, 65(2): 49―61.
[16] Hassanein M F, Kharoob O F. Shear capacity of stiffened plate girders with compression tubular flanges and slender webs [J]. Thin-Walled Structures, 2013, 70(13):81―92.
[17] 王春生, 朱经纬, 翟晓亮, 等. 双管翼缘钢-混凝土新型组合梁抗弯性能试验[J]. 中国公路学报, 2017,30(3): 147―158.Wang Chunsheng, Zhu Jingwei, Zhai Xiaoliang, et al.Flexural behavior experiment of steel and composite girder with double tubular flanges [J]. China Journal of Highway and Transport. 2017, 30(3): 147―158. (in Chinese)
[18] 翟晓亮. 新型管翼缘组合梁桥静力性能研究 [D]. 西安: 长安大学, 2015.Zhai Xiaoliang. Static Performance study of tubular flange composite beam bridge [D]. Xi’an: Chang’an University, 2015. (in Chinese)
[19] 王春生, 常全禄, 翟晓亮, 等. 管翼缘组合梁桥设计与结构分析[J]. 钢结构, 2015, 30(6): 17―21.Wang Chunsheng, Chang Quanlu, Zhai Xiaoliang, et al.Design and structure analysis of tubular flange composite girder bridge [J]. Steel Construction, 2015, 30(6):17―21. (in Chinese)
[20] Eurocode 4: Design of composite steel and concrete structures Part 2: General rules and rules for bridges [S].London: British Standards Institution, 2005.
[21] ASCE 23-97, Specifications for structural steel beams with web openings [S]. Reston Virginia: American Society of Civil Engineers, 1998.
[22] AS 2327.1—2003, Composite structures Part 1: Simply supported beams [S]. Sydney: Standards Australia International Ltd, 2003.
[23] GB 50917—2013, 钢-混凝土组合桥梁设计规范[S].北京: 中国计划出版社, 2013.GB 50917—2013, Code for design of steel and concrete composite bridges [S]. Beijing: China Planning Press,2013. (in Chinese)
[24] 聂建国. 钢-混凝土组合梁结构—试验、理论与应用[M]. 北京: 科学出版社, 2005: 203―206.Nie Jianguo. Experiment, theory and application of steel-concrete composite girder structures [M]. Beijing:Science Press, 2005: 203―206. (in Chinese)
[25] White D W, Barker M G, Azizinamini A. Shear strength and moment-shear interaction in transversely stiffened steel I-girders [J]. Journal of Structural Engineering,2008, 134(9): 1437―1449.
[26] AISC 360-10, Specification for structural steel buildings[S]. Chicago: American Institute of Steel Construction,2010.
[27] AASHTO LRFD bridge design specifications [S].Washington D C: American Association of State Highway and Transportation Officials, 2010.
EXPERIMENTAL RESEARCH ON THE MECHANICAL PROPERTIES OF STEEL AND CONCRETE COMPOSITE GIRDERS WITH CIRCLE TUBULAR UP-FLANGE UNDER NEGATIVE BENDING