隔震支座在中国新建长联/多跨连续梁桥中的应用越来越多，如港珠澳大桥的非通航孔桥均安装了隔震支座；郑西高铁、沪昆高铁上多座连续梁桥也都安装了隔震支座。隔震桥梁主要通过隔震支座的非线性滞回特性，延长结构周期、减小地震作用下结构的响应，使桥梁主体结构在强震下仍保持弹性工作状态[1]。鉴于隔震支座恢复力的非线性特性、安装位置特点，地震动的非确定性及空间变异特性[1―2]，隔震桥梁在地震作用下的响应分析是典型的多输入局部非线性随机振动问题。由于叠加原理对非线性系统不再适用，即使在高斯过程激励下，非线性结构响应一般也不再是高斯过程，使得隔震桥梁非线性随机振动响应计算异常困难。
非线性随机动力学经过近半个世纪的发展形成了一系列经典方法，主要有FPK方程法[3]、随机平均法[4]、统计矩截断法[5]、随机摄动法[6]、等效线性化法[7]、等效非线性系统法[8]、随机模拟法[9－10]。近年来又发展出概率密度演化法[11]、尾部等效线性化法[12]、时域显式模拟法[13―14]等方法。其中时域显式模拟法具有较广的适用性、较高的计算效率。针对减震结构具有局部非线性特征，苏成等[15]在时域显式模拟法[13]的基础上进一步提出了时域显式降维迭代随机模拟法，改善了具有局部非线性特征结构的动力响应求解效率。
尽管非线性随机振动理论已取得上述进展，但对于多点激励下隔震桥梁的随机地震响应研究甚少，目前尚未提出系统可行的分析方法。本文针对隔震桥梁具有局部非线性特征，建立考虑多点激励下隔震桥梁随机地震响应分析模型并提出相应的时域显式迭代随机模拟法。
对于如图1所示有n个自由节点、m个地面支承节点、m′个隔震支座的隔震桥梁系统，受多点地震激励时，其运动方程可表示为[16]：
式中：下标s表示自由节点；b表示支承节点；M、C、K分别为集中质量矩阵、阻尼矩阵、刚度矩阵；Xs和Xb分别表示结构自由节点位移向量和支承节点处的地面强迫位移向量；D、 ′D表示隔震支座恢复力作用位置指示矩阵；
表示m′个隔震支座水平恢复力列向量；Xm′表示与隔震支座两端相连节点的相对位移向量；Pb表示m个支承节点受地面运动的地震力向量。
图1 隔震桥梁有限元模型
Fig.1 Finite element model of a seismically isolated bridge
将式(1)第一行展开，并忽略
可得：
鉴于此方程两端都含有与隔震支座相连节点的位移项，因此需迭代求解。
桥梁工程中常用的隔震支座包括铅芯橡胶支座LRB、高阻尼橡胶支座HDR和摩擦摆支座FPB。而采用的恢复力模型有：双线性模型、修正双线性模型、等价双线性模型、Bouc-Wen滞回模型等[17]，其中Bouc-Wen模型由于能较好地模拟隔震支座的滞回特性，且便于与运动方程一起求解，得到了广泛应用。
用Bouc-Wen模型描述的铅芯橡胶支座的恢复力Fr可表示为如下形式[17]：
式中：α为支座屈服后刚度与初始刚度的比值；
分别为支座的屈服位移、屈服荷载；Cb为
高阻尼橡胶支座的恢复力模型与铅芯橡胶支座恢复力模型的形式一致[17]。支座的粘滞阻尼系数；u、u˙分别为隔震支座端点相对水平位移、速度；Z为滞回特性分量：参数A、γ、β由铅芯橡胶支座的滞回曲线形状确定，通常取用Bouc-Wen模型描述的摩擦摆支座的恢复力模型可表示为[17]：
式中：μ为摩擦摆支座滑动摩擦系数；N为支座的竖向压力，通常将其视作恒载作用产生的支座反力[17―18]；R为滑动面的曲率半径；Zs为滞回特性分量；Y表示摩擦摆支座滑动前的弹性剪切变形，通常可取 0.13 mm~0.5 mm[17]；A、γ、β由摩擦摆支座的滞回曲线形状确定，通常亦可取A=1、
将隔震支座的恢复力表达式(3)或式(4)的第一行代入式(2)整理后可得：
式中：Kse、Kh、Cse为隔震支座的等效刚度矩阵、滞回刚度矩阵、等效阻尼矩阵；Z为隔震支座的滞回位移向量。由式(3)或式(4)的第二行知，可将Z的表达式改写为：
式中：U为隔震支座相对位移向量；
分别为全部隔震支座的顶、底节点的速度向量。
由式(5)计算隔震桥梁系统受多点地震激励的响应时，需已知Z；而求解式(6)时，需已知速度响应
因此需联合求解式(5)、式(6)。原问题含有相互耦合的两类变量，为了提高求解效率，将其转化为两个可独立求解的一类变量问题，再通过对两个问题进行交替迭代求解得到原问题的收敛解。
假定Z已知，将式(5)改写为状态方程的形式[19]：
其中：
假定
在时间步长Δt内随时间呈线性变化且初始条件
时，其解为[19]：
式中：
为各时刻激励的系数矩阵，是结构的固有属性；HΔtT=e 为指数矩阵。由式(9)~式(11)可知，仅需计算
即可求得各时刻响应对应的系数矩阵。
Bouc-Wen模型为微分型模型。研究发现，滞回位移Z迭代求解时，若使用低阶精度的积分算法，因算法计算精度不足，可能会产生非线性迭代震荡、收敛困难的现象。鉴于此，本文最终采用了具有高阶精度的龙格—库塔法对滞回位移方程式(6)进行求解。假定
已知，在第i个时间步步长
内，将其分为q个子步，子步步长为h=Δt/q，其递推格式可写为[20]：
式 中 ：sk=ti-1+kh(k= 1,2,… ,q)； 而ki(i= 1,2,3,4)可由下式计算：
至此，已获得关于结构响应V和滞回位移Z的递推公式，联合这两个公式即可求解当前时间步上结构响应，具体做法如下：
a) 给定Zi的初值
一般取上一时刻的收敛敛值
b) 把Zi的当前值代入式(9)，计算得到
进而可从中提取
代入式(12)，重新计算得到更新的
c) 把
d) 检验解Vi是否收敛，若收敛则停止并令
更新 a)，重新进行步骤 b)、c)、d)。收敛准则可取为
否则用步骤c)得到的
其中，ε为精度控制参数，符号
表示欧几里德范数。
上式求解过程可用以下迭代格式表示：
由式(14)可见，尽管在计算每一时刻的响应时需进行迭代计算，但主要计算全部可根据表达式通过矩阵与向量相乘完成，因此上述算法是一种显式迭代算法。系数矩阵Ai,i一旦生成后，在每个时间步的计算中并不需要更新，且每一个时间步内的迭代计算仅涉及因此，相对于在每个时间步内需不断更新有效刚度矩阵并反复计算其逆阵的一般数值积分方法，上述显式迭代算法具有较高的计算效率。
更进一步注意到式(9)中等式右端仅有与隔震支座相连节点力中含有滞回位移Z，其他节点力为确定值，而滞回位移Z仅与隔震支座顶、底节点速度相关。因此可将Vi分块表示，一部分为与隔震支座相连节点的速度响应值记为V~i，另一部分为除~i
V以外的结构响应值记为V^i，相应地式(9)中Vi的表达式可分成如下两部分：
由式(15)、式(16)可见，仅需对式(15)及式(12)进行迭代求解。求得Zi后代入式(16)即可得到其他响应V^i。上述迭代求解方法与2.3节的方法完全相同，即：
式(17)中所涉及的方程数远小于直接求解式(14)中的方程数。假若只关心隔震桥梁系统中除去与隔震支座相连节点或单元的某个响应量xi(如梁端位移)时，则可根据式(16)得到该响应的时域显式表达式：
式中
为系数矩阵
中对应于xi的行向量。通过式(18)可更进一步降低系数矩阵的存储规模。
隔震桥梁非线性随机地震响应统计值可在隔震桥梁运动方程时域显式求解方法的基础上采用随机模拟法获得，即对考虑空间变异性的随机地震动模型进行抽样，具体抽样方法可参考文献[12]、[21]。对于抽得的第k个激励样本
由式(17)可以获得第k次样本分析的显式迭代公式。对于不同的激励样本，系数矩阵不需要重新计算，因此计算效率可以大幅度提高。
对于任意结构响应r，求得其N个激励样本作用下的响应量
后，可求其统计矩。任意响应量r在不同时刻的均值和方差可分别表示为[22]：
而其峰值的平均值可按下式计算：
当激励样本数目足够大时，还可依据样本得到响应的概率分布[22]，获得隔震桥梁随机地震响应更全面的概率信息。
某一级公路上一座3×30 m等高预应力混凝土连续梁桥，桥型布置如图2，横断面布置如图3所示。主梁、桥墩、基础分别采用 C50、C40、C30混凝土，二期恒载为 63 kN/m，桥梁结构计算参数见表1。该桥每个桥台、桥墩上各布置2个铅芯橡胶支座，所用铅芯橡胶支座参数见表2。
分析时，结构阻尼矩阵由Rayleigh阻尼模型确定，质量比例因子α= 0.26088、刚度比例因子
铅芯橡胶支座模型采用式(3)，式中
迭代收敛误差限
图2 桥型布置图 /cm
Fig.2 The bridge layout
图3 桥梁横断面图 /cm
Fig.3 The cross section of the bridge
表1 桥梁结构基本参数
Table 1 Basic parameters of bridge structure
部位A/m2Iy/m4Iz/m4E/(N/m2) 密度/(kg/m3)主梁 12.49 6.70 228.91 3.45×1010 2549桥墩 2.01 0.32 0.32 3.25×1010 2549
表2 铅芯橡胶支座基本参数
Table 2 Basic parameters of lead rubber bearings
支座部位 屈服力Fy/kN 初始刚度K1/(kN/m) 屈服后刚度K2/(kN/m)桥墩处支座 384 25 900 4000桥台处支座 162 14 400 2200
假定②号桥墩坐落于坚硬场地上(soil1)，③号桥墩坐落于中硬场地上(soil2)，地震动从左至右传播，②号桥墩、③号桥墩处受到纵向部分相干地震动激励。地震动位移时程的自功率谱采用具有双重过滤特性的Clough-Penzien谱，其表达式为[2]：
式中：S0为谱强度，本文取为0.009 413 m2/s3(相当于抗震设防烈度8度，E2地震作用水准[21])；kω、kζ为土层的自振频率和阻尼比；ωsk、ζsk为滤波器参数。kω、kζ、ωsk、ζsk的取值见表3[2]。不同场地条件下位移自功率谱如图4所示。
表3 Clough-Penzien谱参数
Table 3 Parameters of Clough-Penzien Spectrum
场地类别 /(rad/s)kωkζ/(rad/ s)ωζsksk1 坚硬场地 15.0 0.6 1.5 0.6 2 中硬场地 10.0 0.4 1.0 0.6
图4 不同场地的位移自功率谱
Fig.4 Auto-power displacement spectrum of different sites
从图4可以看出，考虑局部场地条件时，各激励点的位移功率谱相差较大，这将导致生成的各激励点处位移时程的峰值相差较大。
空间相关性的地震动模拟时，任意两点间激励的相干效应函数ρ可表示为[22]：
式中：α为相干系数；vs为场地土剪切波速；d表示两点间的距离，其取值可根据实际情况确定。本文取α=0.2、vs= 600 m/s。多点地震动输入模拟依照文献[12]中的算法在 MATLAB上自编程序实现。模拟时截断频率
频率划分段数M=300，频率离散间隔
地震动持时
地震动持时离散时间间隔
共生成500组考虑空间相关性的地震动位移激励样本，图5为其中一组位移激励样本。需要注意的是，进行地震动模拟时，截断频率、地震动持时的选取需由所考察结构的动力特性确定。
从图5可以看出，soil1对应的地震位移时程与soil2对应的地震位移时程由于局部场地效应、相干效应的影响，无论是峰值还是随时间的变化情况都有明显不同。
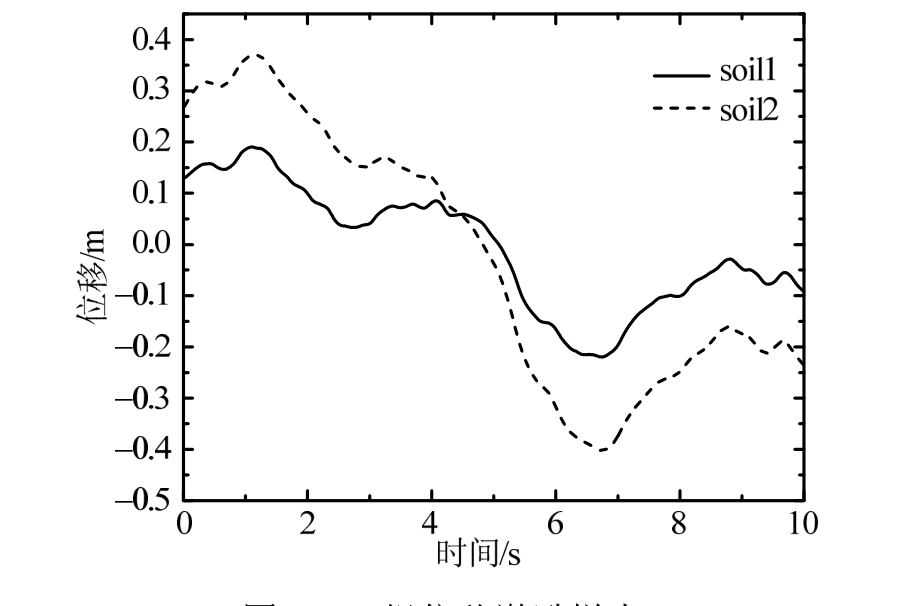
图5 一组位移激励样本
Fig.5 A displacement time history of ground motion
为了验证本文提出的多点激励下隔震桥梁时域显式迭代算法的有效性，分别采用本文方法、传统的基于 Newmark-β算法的直接迭代法[1―2]对任意选定的一组地震激励样本进行分析。传统的直接迭代法分别利用OpenSees、ANSYS实现，本文方法在 MATLAB平台上自编程序实现。将三种分析方法的计算结果进行对比，并对三种方法的耗时进行统计。表4为三种方法计算耗时对比，如图6所示为隔震桥梁①号桥台处梁端位移时程，如图7所示为隔震桥梁①号桥台处隔震支座恢复力。
由图6、图7可见，本文提出的时域显式迭代算法的计算结果与利用OpenSees和ANSYS进行非线性时程积分法的计算结果基本一致，验证了本文方法的正确性。
从表4可以看出，本文方法耗时最短，这是因为本文所建立方法根据隔震桥梁结构局部非线性特点将隔震支座的非线性恢复力作为等效荷载移动到运动方程的右端，然后使用显式、降维技术对其进行求解，避免了运动方程迭代求解时，对刚度矩阵的求逆，且求解时只需对含有隔震支座恢复力项进行迭代求解。随着隔震桥梁自由度数的增加，本文提出的方法优势更加明显。虽然由于三种分析方法各自预处理及存储结果耗时不同，使得这种比较不具有普遍意义，但其从侧面证实了本文方法在求解多点激励下隔震桥梁动力响应问题的高效性。
表4 三种方法计算耗时对比
Table 4 Comparison of computation time
方法 耗时/s本文方法 5.5 ANSYS非线性时程分析法 500 OpenSees非线性时程分析法 10
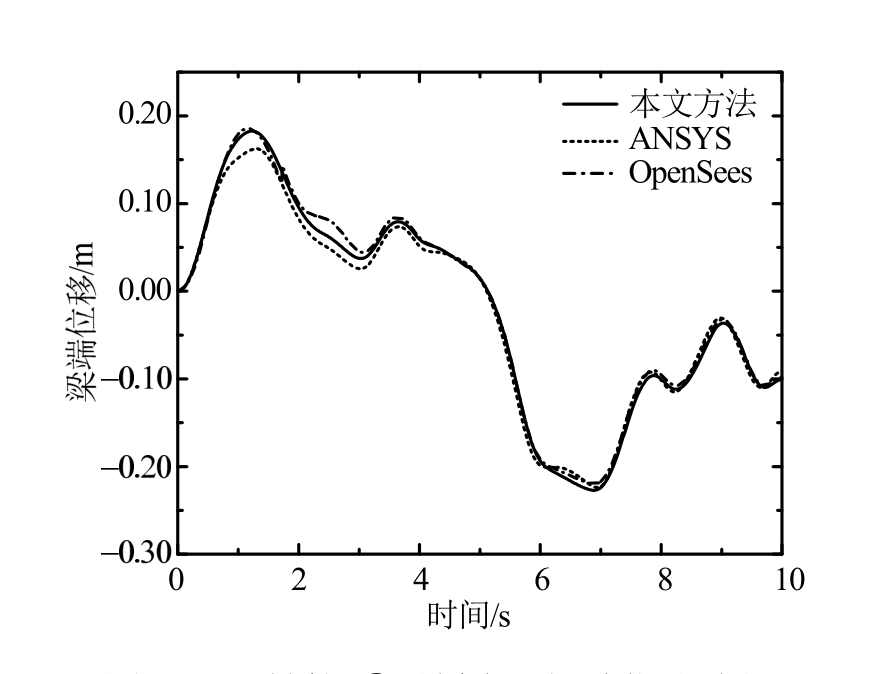
图6 隔震桥梁①号桥台处梁端位移时程
Fig.6 Time history of the beam end displacement at No. 1 abutment
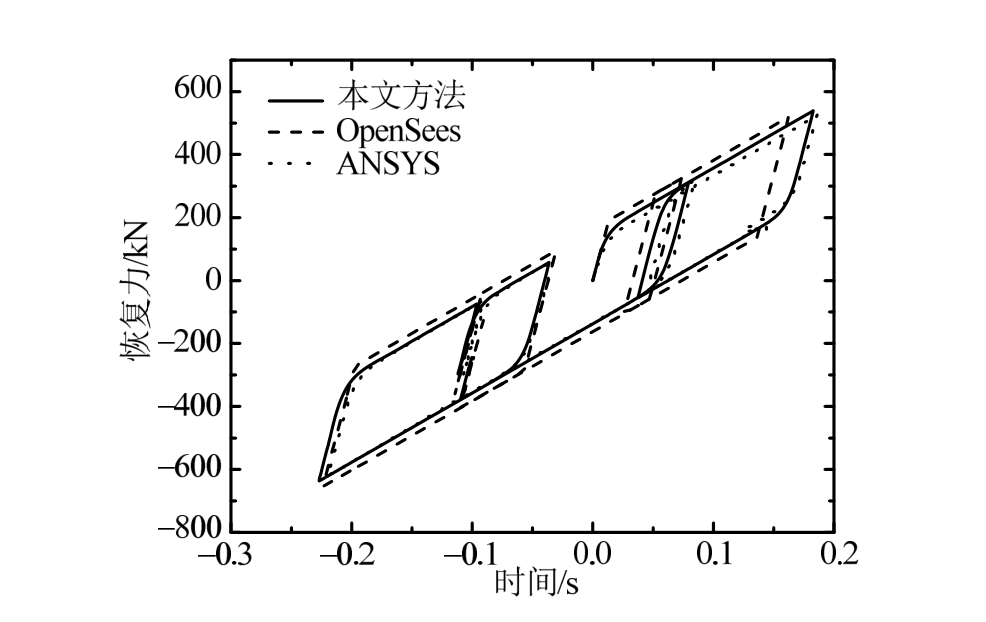
图7 隔震桥梁①号桥台处隔震支座恢复力
Fig.7 Time history of the restoring force of the isolation bearing at No.1 abutment
由图7可见，多点激励下隔震支座呈现出明显的非线性特征。这也证实了《公路桥梁抗震设计细则》(JTJ/T B02-01-2008)、《城市桥梁抗震设计规范》(CJJ 166-2011)中建议的进行隔震桥梁抗震性能验算时宜采用非线性时程分析方法。
将500组考虑空间相关性的地震动位移激励样本输入隔震桥梁模型进行分析。分析时分别采用本文提出的时域显式随机模拟法与传统随机模拟法[9]。传统随机模拟法分析时，每一次样本对应的时程分析采用ANSYS、OpenSees实现。
通过式(19)、式(20)可求得隔震桥梁结构各关心响应量的均值、标准差及最大值。表5列出了在500组位移时程激励下，隔震桥梁①号桥台处梁端位移标准差时程的均值及其绝对最大值的均值，表6列出了500次时程分析三种方法的计算耗时。
表5 ①号桥台处梁端位移统计值
Table 5 Statistics of the beam end displacement at No. 1 abutment
方法 标准差/m 绝对最大值的均值/m本文方法 0.084 6 0.171 4传统随机模拟法(ANSYS) 0.084 3 0.171 1传统随机模拟法(OpenSees) 0.084 6 0.172 6
表6 不同方法计算时间
Table 6 Summary of the computation time
方法 耗时/s本文方法 1 010 ANSYS非线性时程积分法 250 000 OpenSees非线性时程积分法 5 000
从表5可以看出三种方法计算结果基本一致，再次验证了本文方法的正确性。从表6中知本文方法计算耗时最少。这是因为进行非线性随机地震响应分析时，需多次重复计算。在ANSYS、OpenSees上采用的直接迭代法进行非线性随机振动分析时，每一样本时程分析时都需重新生成质量、刚度和阻尼矩阵并迭代求解整体平衡方程，而应用本文所建立的方法，由于响应具有显式表达且表达式中系数矩阵只需形成一次，接下来的每一样本时程分析的每次迭代都只需要进行局部迭代即可，因此分析效率有了极大的提高。
图8为应用本文方法求得的隔震桥梁①号桥台处梁端位移的标准差时程。从图8可以看出，起始段隔震桥梁结构响应呈现出明显的非平稳特性，响应标准差值急剧增大，一段时间后，结构响应的非平稳特性显著减弱。
图8 ①号桥台处梁端位移标准差时程
Fig.8 Standard deviation time history of the beam end displacement at No. 1 abutment
(1) 将时域显式迭代法应用于多点激励下隔震桥梁的非线性地震响应分析，针对隔震桥梁结构局部非线性特点使用降维迭代策略，可在保证求解精度的前提下，极大地提高隔震桥梁非线性地震响应分析效率。
(2) 基于所建立的动力时程分析方法进行非线性随机地震响应分析时，隔震桥梁结构的地震响应显式表达式中的系数只需生成一次，计算效率提高更加明显。
(3) 研究发现，采用Bouc-Wen模型表示隔震支座恢复力非线性特征时，滞回位移方程的时域积分需要选用具有较高计算精度的龙格—库塔法，以提高迭代算法的稳定性、改善收敛性。
[1]范立础. 桥梁抗震[M]. 上海: 同济大学出版社, 1997:281―283.Fan Lichu. Seismic design of bridges [M]. Shanghai:Tongji University Press, 1997: 281―283. (in Chinese)
[2]Clough R W, Penzien J. Dynamics of structures [M].New York: McGraw-Hill, 2003: 607―611.
[3]朱位秋. 非线性随机动力学与控制——Hamilton理论系统框架[M]. 北京: 科学出版社, 2003: 120―130.Zhu Weiqiu. Nonlinear stochastic dynamics and control -Hamilton theoretical framework [M]. Beijing: Science Press, 2003. (in Chinese)
[4]Roberts J B, Spanos P D. Stochastic averaging: An approximate method of solving random vibration problems [J]. International Journal of Non-Linear Mechanics, 1986, 21: 111―134.
[5]Levermore C D. Moment closure hierarchies for kinetic theories [J]. Journal of Statistical Physics, 1996, 83:1021―1065.
[6]Crandall S H. Perturbation techniques for random vibration of nonlinear systems [J]. Journal of the Acoustical Society of America, 1963, 35(11): 1700―1705.
[7]Iwan W D, Yang I M. Statistical linearization for nonlinear structures [J]. Journal of the Engineering Mechanics Division, 1971, 97(6): 1609―1623.
[8]Caughey T K. On the response of non-linear oscillators to stochastic excitations [J]. Probabilistic Engineering Mechanics, 1986, 1(1): 2―4.
[9]Shinozuka M. Monte Carlo solution of structural dynamics [J]. Computers and Structures, 1972, 2(5):855―874.
[10] Rubinstein R Y, Kroese D P. Simulation and the Monte Carlo Method [M]. New Jersey: John Wiley & Sons,2008: 6―12.
[11] Chen J B, Li J. A note on the principle of preservation of probability and probability density evolution equation[J]. Probabilistic Engineering Mechanics, 2009, 24(1):51―59.
[12] Wang Z, Der Kiureghian A. Tail-equivalent linearization of inelastic multi-support structures subjected to spatially varying stochastic ground motion [J]. Journal of Engineering Mechanics, 2016, 142(8): 322―338.
[13] 苏成, 徐瑞. 非平稳随机激励下结构随机振动时域分析法[J]. 工程力学, 2010, 27(12): 77―83.Su Cheng, Xu Rui. Random vibration analysis of structures subjected to non-stationary excitations by time domain method [J]. Engineering Mechanics, 2010,27(12): 77―83. (in Chinese)
[14] 徐瑞, 张加兴, 苏成. 非平稳随机激励下结构动力可靠度时域显式子集模拟法[J]. 工程力学, 2013, 30(7):28―39.Xu Rui, Zhang Jiaxing, Su Cheng. Time-domain explicit formulation subset simulation method for dynamic reliability of structures subjected to non-stationary random excitations [J]. Engineering Mechanics, 2013,30(7): 28―39. (in Chinese)
[15] 苏成, 李保木, 陈太聪, 等. 粘滞阻尼器减震结构非线性随机振动的时域显式降维迭代随机模拟法[J]. 计算力学学报, 2016, 33(4): 556―563.Su Cheng, Li Baomu, Chen Taicong, et al. Non-linear random vibration analysis of energy-dissipation structures with viscous dampers by random simulation method based on explicit time-domain dimensionreduced iteration scheme [J]. Chinese Journal of Computational Mechanics, 2016, 33(4): 556―563. (in Chinese)
[16] Chopra A K. Dynamics of structures: Theory and applications to earthquake engineering [M]. New Jersey:Prentice-Hall, 2001: 348―353.
[17] 王建强. 基础隔震结构多维及平—扭耦联地震反应分析[D]. 陕西: 西安建筑科技大学, 2003.Wang Jianqiang. Analysis on multi-dimensional and lateral-torsional coupled seismic response of baseisolated structures [D]. Shaanxi: Xi’an University of Architecture and Technology, 2003. (in Chinese)
[18] 叶爱君, 管仲国. 桥梁抗震[M]. 北京: 人民交通出版社, 2011: 71―80.Ye Aijun, Guan Zhongguo. Seismic design of bridges[M]. Beijing: China Communication Press, 2011: 71―80. (in Chinese)
[19] 钟万勰. 结构动力方程的精细时程积分方法[J]. 大连理工大学学报, 1994, 34(2): 131―136.Zhong Wanxie. On precise time-integration method for structural dynamic [J]. Journal of Dalian University of Technology, 1994, 34(2): 131―136. (in Chinese)
[20] Avriel M. Nonlinear programming: analysis and methods[M]. New York: Dover Publishing Inc., 2003.
[21] 杨庆山, 田玉基. 地震地面运动及其人工合成[M]. 北京: 科学出版社, 2008: 122―140.Yang Qingshan, Tian Yuji. Earthquake ground motions &artificial generation [M]. Beijing: Science Press, 2008:122―140. (in Chinese)
[22] 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 北京:高等教育出版社, 1998: 23―26.Mao Shisong, Wang Jinglong, Pu Xiaolong. Advanced mathematical statistics [M]. Beijing: Higher Education Press, 1998: 23―26. (in Chinese)
A SIMULATION METHOD BASED ON EXPLICIT TIME-DOMAIN ITERATION SCHEME FOR NONLINEAR RANDOM VIBRATION ANALYSIS OF ISOLATED BRIDGES UNDER MULTI-SUPPORT EXCITATION