空间结构的结构形式和形态特征与节点的空间位置分布(节点坐标)有关。在构件安装、结构拼装等施工过程中，各节点实际位置与其设计位置之间存在偏差，即结构初始几何缺陷[1－2]。初始几何缺陷是影响空间结构受力性态的重要因素，也是空间结构分析和设计中需要考虑的关键问题[3－7]。
现阶段，初始几何缺陷的引入方法主要有两种：1) 一致缺陷模态法[8]；2) 随机缺陷法[9－11]。在相同的缺陷幅值下，一致缺陷模态法使得空间结构的极限承载力下降较明显，是较不利的缺陷分布引入方法。由于该方法简单易行，已被纳入多个国家的结构设计规范[12－13]，但一致缺陷模态法引入的缺陷与荷载分布模式有关，并非结构真实的几何缺陷。随机缺陷法则是通过假定结构几何缺陷的统计规律服从某种概率分布，随机生成若干组节点位置偏差，将计算得到的极限承载力最小值作为结构的设计极限承载力[10－11]。由于随机缺陷法存在偶然性，将该最小值作为结构实际极限承载力是否合理，尚需进一步讨论。
事实上，在结构生命周期各阶段，结构的计算分析均需依据实测数据引入几何缺陷，以还原结构的真实几何位形。比如，在施工过程中，需要考虑前一施工阶段各节点的位置偏差对后续施工阶段的影响[14]；在检测评估中，难以测量空间结构所有节点，只能根据抽测的部分节点信息还原结构几何模型，进而分析和评估结构真实状态[15]。在现阶段的工程实践中，一般采用已测节点实际坐标和未测节点设计坐标建立修正模型[16]。然而，这种修正模型难以反映结构整体位形的真实状况。因此，如何合理地利用部分节点几何位置信息修正结构几何模型，并正确评估已知节点偏差对结构受力状态的影响，是空间结构施工和服役阶段计算分析中涉及的关键问题。针对这一问题，部分学者提出了结构位形反演推定[17－18]的概念，其基本思想是根据有限已知节点的位置偏差，基于随机理论推定其余节点的位置偏差。目前，关于空间结构随机缺陷的研究较多[19－21]，但关于结构整体位形反演推定的研究成果较少。
本文基于反演推定的概念，提出适用于空间结构的随机缺陷传播法，建立几何偏差在节点间的传播法则和随机偏差理论，利用已知(已测)节点几何位置信息，推定结构其余节点的位置偏差，并给出结构随机几何偏差的生成步骤。以某缩尺K6网壳模型为例，通过对比不同方法所引入的几何缺陷与结构实际缺陷的相似程度，分析基于不同方法得到的结构极限承载能力，验证了随机缺陷传播法的适用性和准确性。
节点间的偏差传播基于反演推定的概念，利用相邻节点的位置关系，将已知节点的位置偏差传播到相邻未知节点，进而逐步传播到离已知节点更远的节点，推定结构所有未知节点的位置偏差，最终确定结构的初始几何缺陷。
相邻节点的偏差传播是指由构件直接相连的节点间的偏差传播，其传播法则为：将已知偏差节点定义为主节点，与其相连的其他节点定义为从属节点，从属节点的位置偏差根据主节点偏差确定。
假定：节点未知偏差的计算可不考虑连接单元的轴向变形；相邻节点的相对偏差是由构件的转角偏差引起的；转角偏差引起的局部坐标系的改变可忽略。基于以上假定，从属节点的偏差可分为两部分：1) 由主节点偏差引起的刚体平动位移；2) 连接单元转角偏差引起的刚体转动位移。该刚体平动位移和刚体转动位移共同决定了从属节点的位置偏差，可按式(1)计算：
式中：TΔ表示刚体平动位移；RΔ表示刚体转动位移。
如图1所示，i、j分别为某一构件的两个端节点，其中i(xi,yi,zi)节点的位置偏差已知，j(xj,yj,zj)节点的位置偏差未知，故i节点为偏差传播的主节点，j节点为从属节点。i′、j′分别为i、j节点位置偏移后的实际位置。
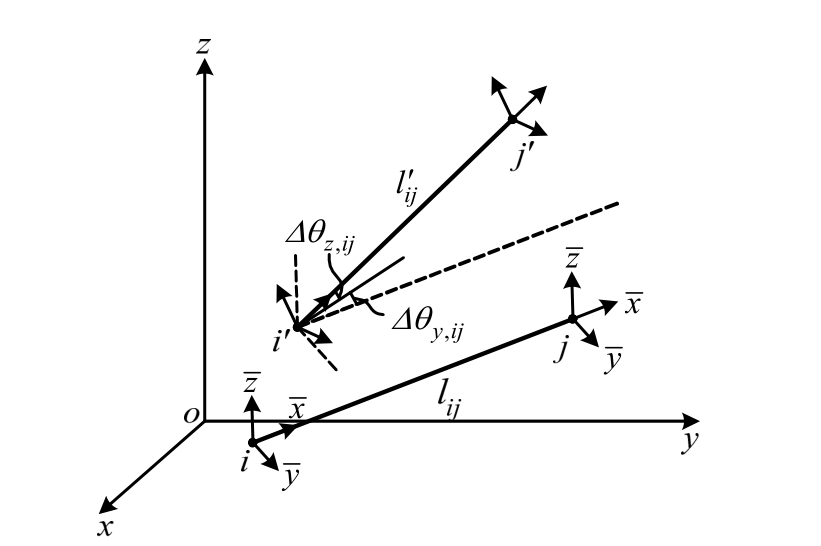
图1 相邻节点的偏差传播
Fig.1 Deviation propagation in adjacent nodes
在整体坐标系下，假设节点i位置偏移分别为Δxi、Δyi和Δzi，则局部坐标系下节点i的位置偏移可表示为：
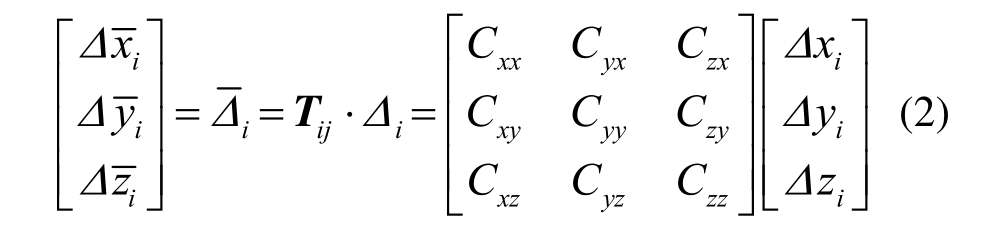
式中：
分别表示节点i在局部坐标系下3个坐标的位置偏移；Tij是单元坐标转换矩阵，Tij中各元素的计算如下：
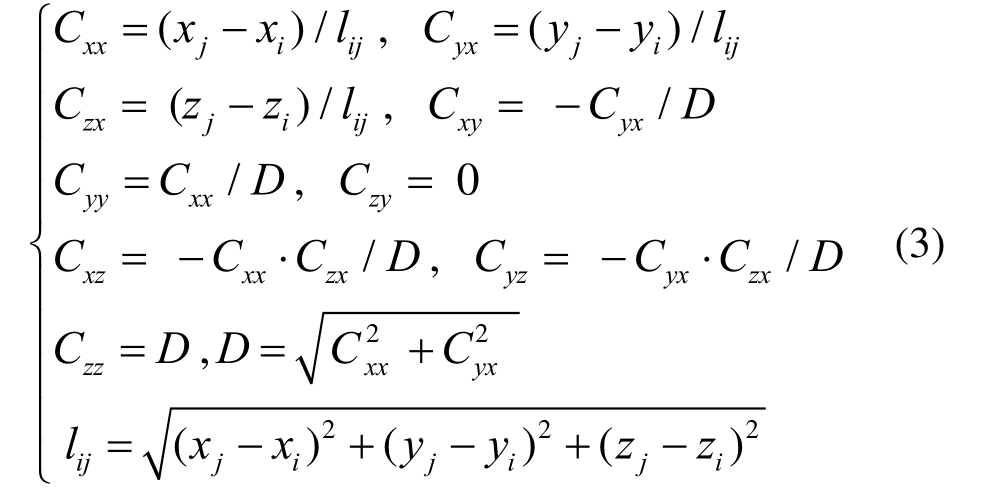
假设构件绕y轴和z轴的转角偏差分别为Δθy,ij和Δθz,ij，则局部坐标系下节点j的位置偏差可通过下式计算得到：
式中，lij表示构件的长度。
利用坐标转换矩阵，整体坐标系下节点j的位置偏差可表示为：
式(4)、式(5)可用来计算与已知偏差节点相邻的任意节点的未知偏差。
不相邻节点的偏差传播是指没有构件直接相连的节点间的偏差传播，其传播法则为：以已知偏差节点作为传播源，经过若干次相邻节点的传播，逐步传播至结构所有未知偏差的节点。其中每一次相邻节点的传播定义为一个传播步，上一传播步的从属节点定义为下一传播步的主节点。
如图2所示，假定节点1、节点20为已知偏差的节点，即传播源，在第1传播步中，节点1、节点20为主节点，节点2~节点7和节点21~节点26分别为节点1和节点20的从属节点，箭头的指向为偏差传播方向；在第2传播步中，节点2~节点7和节点21~节点26转变为该传播步中的主节点，节点8~节点19，节点27~节点38为从属节点；以此类推。对于第1传播步的任意从属节点，其在整体坐标系下的位置偏差可表示为：
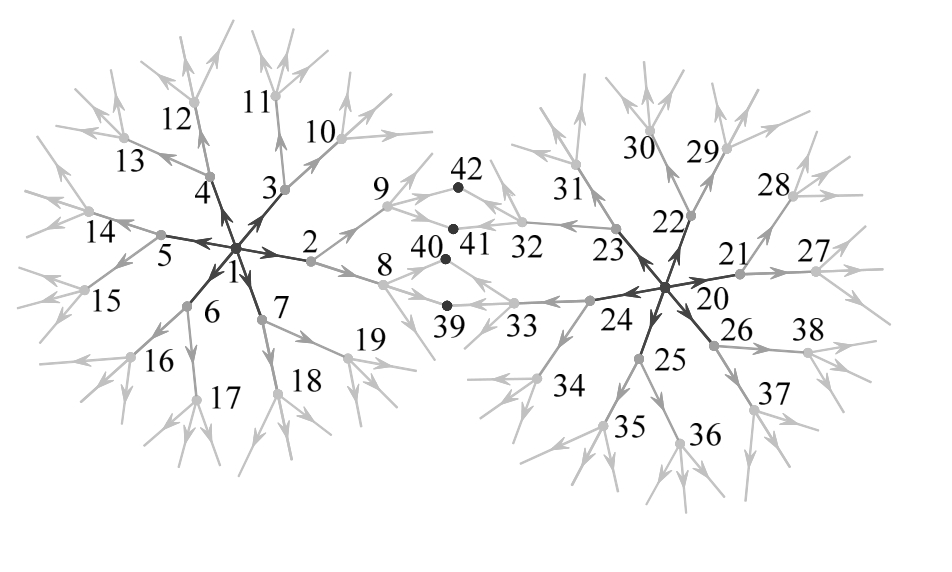
图2 不相邻节点的偏差传播
Fig.2 Deviation propagation in non-adjacent nodes
式中：下标“0”表示传播源；“1”表示第 1传播步。
类似的，对于第n传播步的任意从属节点，其在整体坐标系下的位置偏差可表示为：
式中：下标“n”表示第n传播步，相应节点为第n级节点；γn表示第n传播步的偏差修正系数(第2.1 节)。
在偏差传播过程中，如果结构有N个传播源，则存在一类特殊的未知偏差的节点，如本例节点39~节点 42，这类节点处于若干传播源的传播交界处，其位置偏差由相关传播源共同确定，即：
空间结构的节点数目较多，目前的研究和实测结果[11,18,22]表明，空间结构的节点位置偏差近似服从正态分布。在偏差传播理论中，确定节点位置偏差的统计分布规律及其参数是偏差传播理论的关键。由于主节点的位置偏差、构件的长度以及空间方位均为已知量，故从属节点位置偏差的不确定性由构件的转角偏差Δθy,ij和Δθz,ij产生。
假设构件的转角偏差Δθy,ij和Δθz,ij服从均值为0、方差为
的正态分布，即Δθy,ij,Δθz,ij~N(0,σ2)，则在局部坐标系下，主节点和从属节点在
方向的相对位置偏差服从正态分布，即：
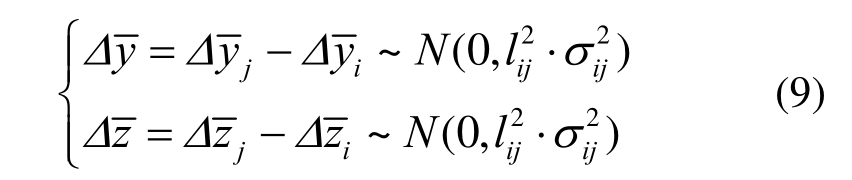
在整体坐标系下，主节点和从属节点的相对位置偏差可表示为：
由式(10)可知，主节点和从属节点三个主轴方向上的相对位置偏差均服从正态分布，即：
构件两端节点相对位置偏差的分布取决于转角偏差的方差，转角偏差的方差越大，节点的相对位置偏差越大。由于节点的相对位置偏差不能过大，且应满足已知节点偏差的统计分布规律，故整体坐标系下端节点相对位置偏差的标准差[σ]需满足式(12)约束方程，即：
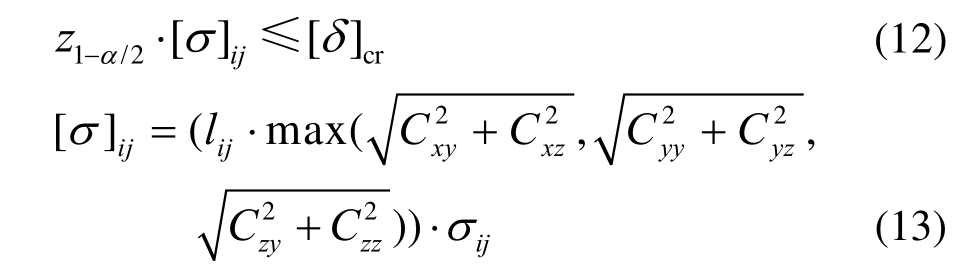
式中：z1-α/2表示正态分布 1-α/2的分位数，若
表示已知节点偏差的标准差，若已知偏差的节点数目较少，可取允许的最大施工误差作为临界值。
类似的，第n级节点与传播源的相对位置偏差也服从正态分布，即：
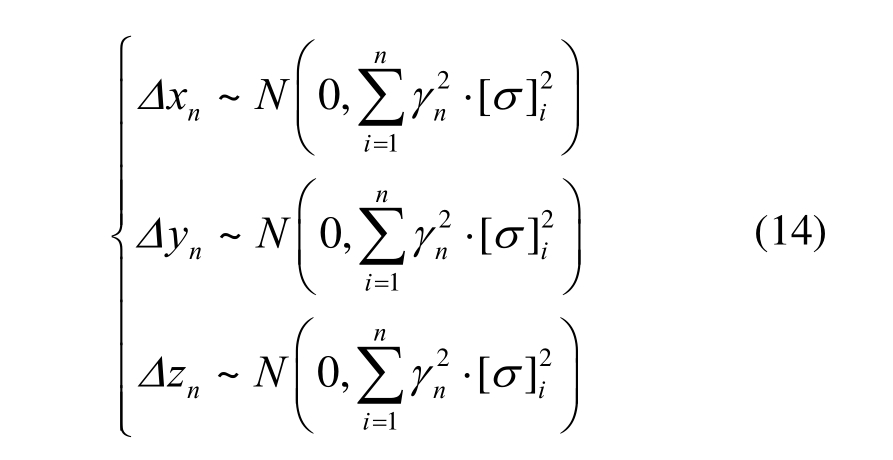
式(14)需满足如下约束方程：
因此，第n传播步的偏差修正系数
将节点随机偏差引入完善结构前，须对节点随机偏差分布进行假设检验，以验证其概率密度分布函数是否满足假定的偏差分布模型，而拟合优度检验是检验给定数据是否符合某种指定分布函数的有效方法。
2.2.1 已知节点偏差检验
在未知节点随机偏差生成前，需要分析已知节点或已测节点的偏差分布，同时为后续偏差生成提供相关参数。由于空间结构节点的位置偏差近似服从正态分布，Jarque-Bera检验[23]作为一个常用的拟合优度检验方法，适用于检验均值和方差都未知的数组是否服从正态分布，故本文采用 Jarque-Bera检验对已知节点的位置偏差分布进行检验。
已知节点偏差分布的原假设H0可表示为：
Jarque-Bera检验的统计量JB定义如下：
式中：n表示样本的个数；S、K分别表示样本的偏度和峰度；ˆjμ(j= 2,3,4)分别表示样本2阶、3阶和4阶中心矩的估计值。
由式(17)可知，统计量JB是两个渐进、独立的正态分布的平方和[23]，其分布可近似认为是两个自由度的χ2分布。在置信水平为α时，若原假设H0为真，近似地有
相应的，检验的拒绝域为：
若样本的统计量JB未落入式(19)的拒绝域，则接受H0，否则，则拒绝H0。
2.2.2 随机节点偏差分布检验
在未知节点随机偏差生成后，需要检验随机节点偏差的分布与已知节点偏差的分布是否一致。对于两个样本是否服从同一个分布的检验，可对其采用 Kolmogorov-Smirnov (K-S)检验[24－25]。
假设
是一个既定样本的累积分布函数，
是被检验样本的累积分布函数，则统计量Dn可表示为：
式中：N1、N2分别表示既定样本和被检验样本的样本容量；k1、k2分别表示两个样本中样本值小于或等于x的样本数。
假定α为检验的置信水平，若两个样本服从相同的分布，则统计量Dn需满足：
式中：p表示结构的相似度；dα(N2)表示统计量的临界值，可通过查表[25]得到。
基于偏差传播法则和随机偏差理论，空间结构随机缺陷传播算法可简述如下：
1) 确定若干个节点的位置偏差，计算已知节点偏差的均值μ和标准差σ；
2) 采用式(12)确定随机偏差的标准差限值[δ]cr，利用式(19)对已知节点偏差分布进行检验；
3) 根据均值μ和标准差限值[δ]cr，生成结构的随机转角偏差向量；
4) 以已知节点作为传播源，利用式(6)和式(7)计算所有未测节点的位置偏差；5) 重复4)生成满足要求的随机缺陷样本量；6) 利用式(20)对步骤 5)的样本进行拟合优度检验。
本文以缩尺K6网壳模型为例，分别采用一致缺陷模态法、随机缺陷法和随机缺陷传播法引入几何缺陷，将各方法引入的缺陷与结构实测缺陷进行对比，检验各方法的拟合优度，通过结构的整体稳定分析，研究不同方法引入的几何缺陷对结构承载能力的影响。
K6网壳缩尺模型的基本参数如下：跨度L=3.6 m，矢高f=0.9 m，矢跨比f/L=1/4，焊接球节点半径r=0.07 m，节点质量m=11.27 kg，结构杆件均采用ϕ6×1，材性为Q235钢材，结构实际模型如图3(b)所示。网壳的计算模型对原缩尺模型进行适当简化，其节点和支座的坐标采用缩尺模型节点和支座坐标实测数据；焊接球节点简化为位于球心位置的无体积质点，质点坐标采用缩尺模型节点坐标；构件截面采用缩尺模型的杆件截面，构件两端延伸至焊接球节点球心位置；模型的周边约束采用固端约束，各构件间节点连接形式均为刚接；材料本构采用理想弹塑性模型，弹性模量E0= 2.06×105N·mm−2，屈服强度fy= 235 MPa，泊松比ν=0.3。网壳结构计算模型如图3(c)所示。
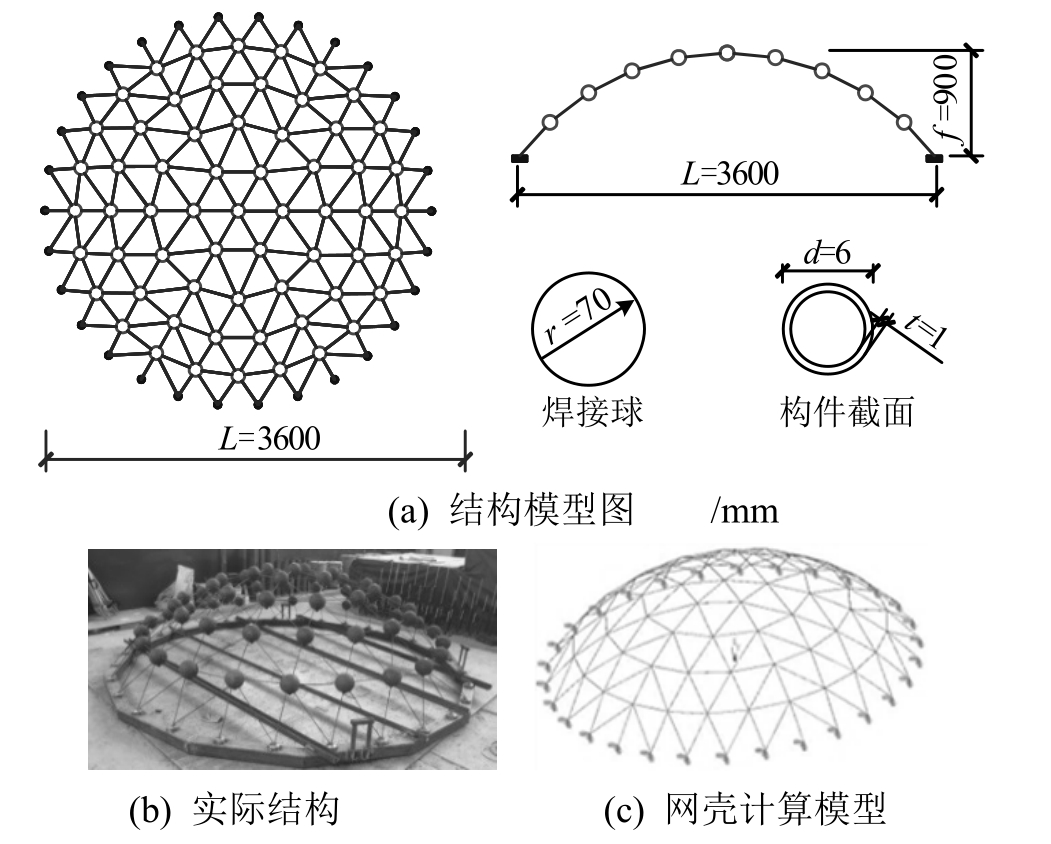
图3 K6网壳模型
Fig.3 K6 reticulated shell model
该结构的测点包含61个焊接球节点和30个焊接支座，共计91个测点，采用高精度全站仪(误差±1 mm)，对每个球节点分别测量6组球面坐标数据，在 6组数据中依次提取 4组数据进行球心坐标拟合，提取次数共计
次，再对拟合得到的15组球心坐标数据进行算数平均，将算数平均值作为该球节点球心的实测坐标数据，实测坐标数据和节点设计坐标的差值即为节点偏差，实测节点的偏差分布直方图如图4(a)所示，测点位置偏差的平均值为0.114 mm，标准差为3.682 mm，图4(b)、图4(c)和图4(d)分别表示测点位置偏差在x、y、z方向上的直方分布图。
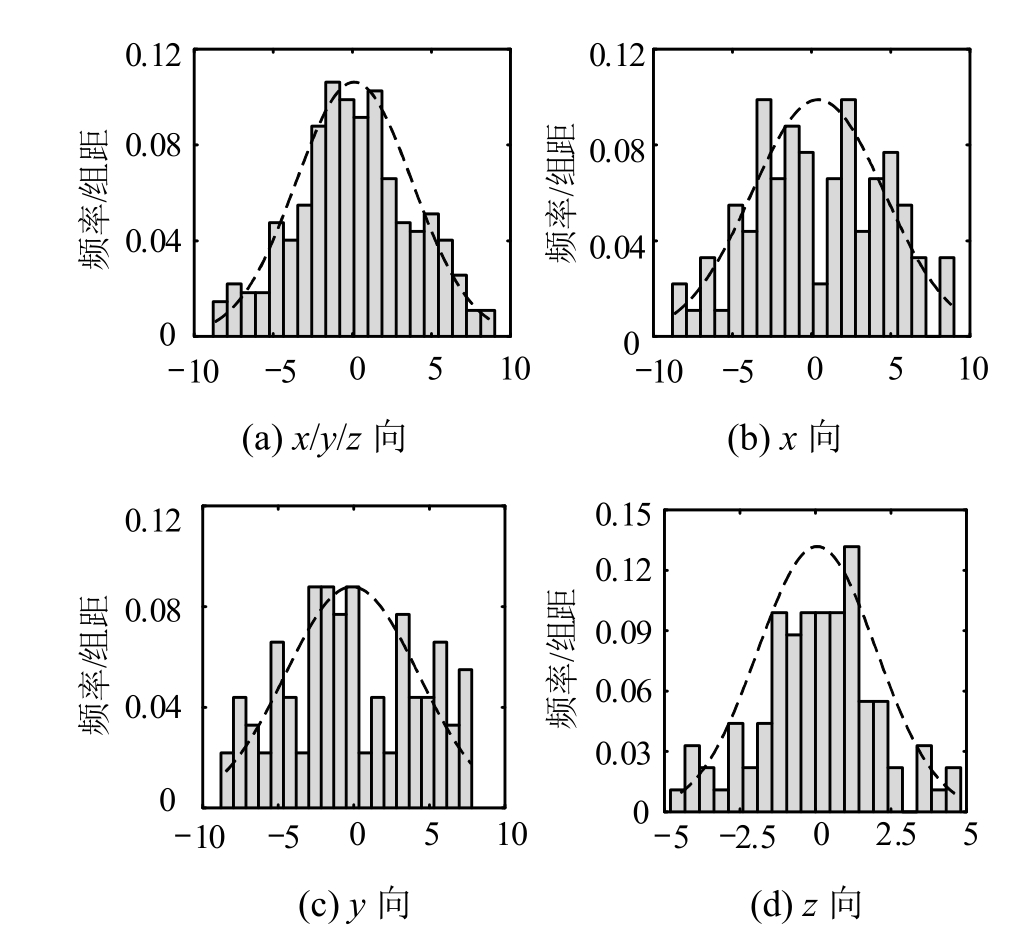
图4 实测节点偏差直方分布图 /mm
Fig.4 Histogram distribution of measured node deviation
表1 实测节点偏差检验结果
Table 1 Test results of measured node deviation
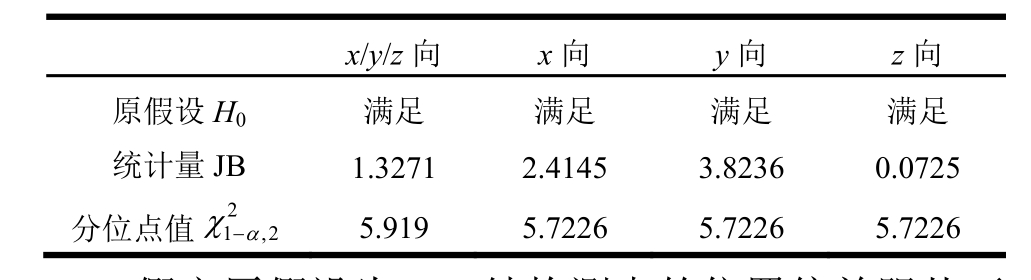
x/y/z向x向y向z向原假设H0满足 满足 满足 满足统计量JB 1.3271 2.4145 3.8236 0.0725分位点值21α,2χ-5.919 5.7226 5.7226 5.7226
假定原假设为H0：结构测点的位置偏差服从正态分布，对测点位置偏差样本进行 Jarque-Bera检验，其中置信水平α=0.05，检验结果如表1所示。由表1可知，y方向上的偏差分布统计量最大，为3.8236；z方向上的统计量最小，为0.0725，均小于临界值5.7226，未落入拒绝域，故接受原假设，该结构测点的位置偏差样本均服从正态分布。
3.3.1 节点间偏差传播
根据本文的偏差传播算法，在生成随机偏差前，需要确定已知位置偏差节点和偏差传播路径。为了探究已知偏差节点数目对结构缺陷拟合程度的影响，本文生成了14组已知节点偏差数N的偏差样本(其中N=0,1,3,5,7,9,18,27,36,45,54,63,72,81)，每组分别包含了500个样本，各样本中的已知偏差节点位置随机确定，当N=0时，生成的节点位置随机偏差与结构随机缺陷法生成的初始几何缺陷一致。
图5 K6网壳偏差传播路径示意图
Fig.5 Deviation propagation path in K6 shell
不同的已知偏差节点的数目和已知节点的分布对传播路径均有影响，本节分别列出了已知偏差节点数目N=1和N=9时，某样本的节点间偏差传播路径，如图5所示。当N=1时，覆盖全部节点需要经过6次传播图5(a)；当N=9时，节点间传播次数T减少为4次图5(b)；当N=9，而已知节点分布更均匀时，节点间的传播次数T减少为 2次(图5(c))。综上，当N越大，已知节点分布越均匀，则节点间的传播次数越少，传播模型引入的随机偏差累积越小，结构的节点位置偏差越接近实际状态。
3.3.2 随机偏差拟合优度检验
采用K-S检验方法对所生成的样本进行检验，原假设为H1：生成的样本与实际位置偏差服从相同分布，置信水平α=0.05。
表2给出了14组样本中各组满足原假设的样本数，由表2可知，当已知节点数目N较少时，满足原假设的节点随机偏差样本数较少；当N增加到节点总数的1/10，即N=9时，满足原假设的样本占比可达到75%左右；当N大于节点总数的1/5时，满足原假设的样本占比均大于90%。各组样本中原假设成立的概率密度分布曲线如图6所示，其中横坐标表示K-S检验的p值，红色虚线表示检验的置信水平。由图6可知，随着N的增加，满足原假设的样本显著增加，概率密度分布曲线形状发生变化，样本的p值从左侧集中逐渐变为右侧集中，且代表相似度水平的p值逐渐趋近于1，说明生成的节点位置偏差和节点实际的位置偏差相似度较高。采用随机缺陷法引入的缺陷，其缺陷分布与实际缺陷分布相同的样本占比14.8%，低于随机偏差传播法引入缺陷的样本占比；采用一致缺陷模态法引入的缺陷，其缺陷分布与实际缺陷分布的相似度p=0.0146，不满足原假设。
表2 随机缺陷样本K-S检验结果
Table 2 K-S test results of stochastic imperfection samples
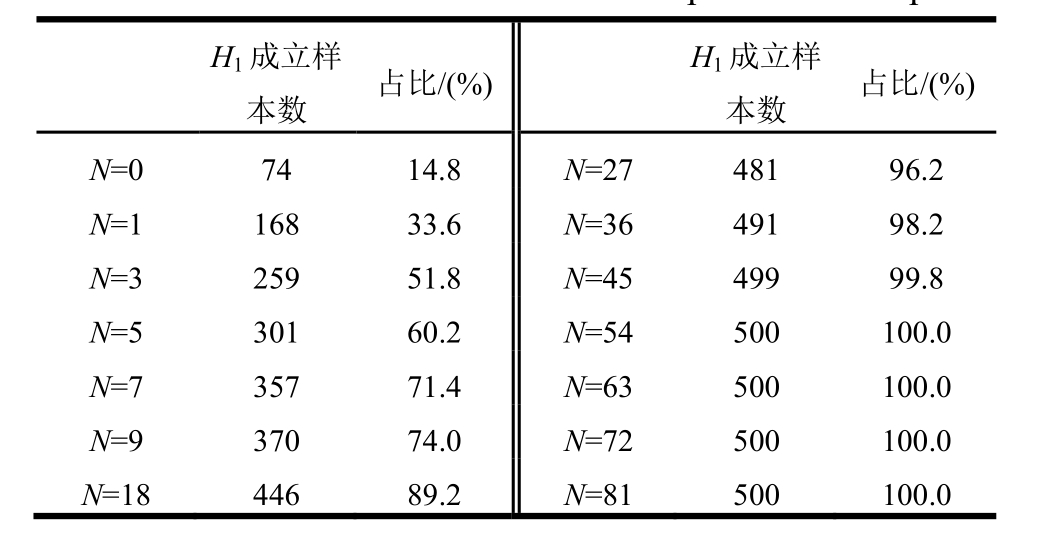
H1成立样本数 占比/(%)H1成立样本数 占比/(%)N=0 74 14.8N=27 481 96.2N=1 168 33.6N=36 491 98.2N=3 259 51.8N=45 499 99.8N=5 301 60.2N=54 500 100.0N=7 357 71.4N=63 500 100.0N=9 370 74.0N=72 500 100.0N=18 446 89.2N=81 500 100.0
从K-S检验的结果可知，随机缺陷传播法引入的缺陷比其他两种方法的拟合程度高。采用随机缺陷传播法引入几何缺陷，若要求满足原假设的样本占比高于 75%，则已知节点或待测节点需大于节点总数的 1/10；若要求满足原假设的样本占比高于90%，则已知节点或待测节点需大于节点总数的1/5。
图6 K-S检验p值概率密度分布曲线
Fig.6 Probability density distribution curve ofpvalue in K-S test
将实测的结构几何缺陷和各方法生成的几何缺陷分别引入结构计算模型，通过结构的极限承载力计算，可分析不同初始几何缺陷对结构承载能力的影响；将基于各方法计算得到的极限承载力与引入实测几何缺陷的模型得到的承载力进行对比，进而评估不同缺陷引入方法的有效性和准确性。假定网壳模型的恒载和活载均为 0.5 kN·m−2，满跨布置。采用通用有限元软件ANSYS v17.0进行建模分析，构件选用Beam188单元模拟。基于弧长法，计算网壳模型在给定静力荷载下的极限承载力。
按照结构实测节点位置偏差引入几何缺陷，计算可得结构的实际荷载因子为6.27。表3给出了14组缺陷样本计算得到的荷载因子中位数及其误差，当N=0时，样本荷载因子中位数的误差为5.15%，其余13组样本的误差均小于3%；当N大于节点总数的1/10后，各组样本极限承载力的中位数趋于稳定，故可将N等于节点总数1/10时的荷载因子中位数作为极限承载力代表值，即 6.21，其误差为0.96%。态法(RIMM)所得的样本中，最低的荷载因子值为4.38，若将此荷载因子作为极限承载力，其误差为30.16%，而若将荷载因子中位数作为极限承载力，其误差仅为 5.15%；采用一致缺陷模态法(CIMM)计算所得的荷载因子为5.54，误差为11.64%。
从稳定分析结果可知，随机缺陷传播法得到的荷载因子更接近结构的实际承载力理论值。在结构缺陷分布的统计参数(均值、方差)或较多节点位置偏差已知的情况下，建议采用基于随机缺陷传播法生成的几何缺陷进行稳定分析，并将样本计算得到的荷载因子中位数作为结构的实际承载能力代表值。
不同方法对结构极限承载力的影响如图 7所示，各组样本计算所得的荷载因子的分布比较集中，处于结构实际承载力理论值附近，存在个别荷载因子较低的样本，但数量不多。采用随机缺陷模
表3 14组随机缺陷样本承载力计算结果
Table 3 Results of load-carry capacity of stochastic imperfection samples for 14 groups
荷载因子中位数 误差/(%) 荷载因子中位数 误差/(%)N=0 5.95 5.15N=27 6.23 0.62N=16.14 2.13N=36 6.23 0.70N=36.14 2.05N=45 6.24 0.42N=56.18 1.44N=54 6.22 0.82N=76.21 1.00N=63 6.25 0.26N=96.21 0.96N=72 6.26 0.11N=186.20 1.15N=81 6.28 0.14
图7 不同方法对极限承载力的影响
Fig.7 Influence on ultimate load-carry capacity of structure by different methods
本文基于反演推定概念，提出了适用于空间结构的随机缺陷传播算法以及各节点间位置偏差的传播法则，该方法将若干实测节点的位置偏差逐级传播至结构所有节点，生成满足统计分布规律的结构几何缺陷。通过算例分析，得到以下结论：
1) 采用随机缺陷传播法所得的随机缺陷与结构实际缺陷分布相似度较高，当实测节点的数目达到节点总数的1/10时，满足相同分布的样本占比为74%，当实测节点数达到1/5时，满足相同分布的样本占比可达90%；
2) 采用随机缺陷传播法计算得到的荷载因子更接近结构实际承载力理论值，当实测节点的数目达到节点总数的1/10后，结构各组样本极限荷载因子的中位数趋于稳定；
3) 在结构缺陷分布的统计参数已知时，将样本计算得到的荷载因子中位数作为结构的实际极限承载能力代表值更符合实际。
[1]罗永峰, 韩庆华, 李海旺. 建筑钢结构稳定理论与应用[M]. 北京: 人民交通出版社, 2010.Luo Yongfeng, Han Qinghua, Li Haiwang. Stability of Steel Structures-The Theory and Implement [M]. Beijing:China Communications Press, 2010. (In Chinese)
[2]Papp F. Buckling assessment of steel members through overall imperfection method [J]. Engineering Structures,2016, 106(1): 124―136.
[3]Zhu Z C, Luo Y F, Xiang Y. Global stability analysis of spatial structures based on Eigen-stiffness and structural Eigen-curve [J]. Journal of Constructional Steel Research, 2018, 141(2): 226―240.
[4]Bruno L, Sassone M, Venuti F. Effects of the Equivalent Geometric Nodal Imperfections on the stability of single layer grid shells [J]. Engineering Structures, 2016,112(7): 184―199.
[5]何政, 胡意涛, 朱振宇, 等. 强震下网壳结构性能的多模态整体损伤演化[J]. 工程力学, 2016, 33(4): 104―113.He Zheng, Hu Yitao, Zhu Zhenyu, et al. Multi-modebased global damage evolution of lattice shells under strong earthquakes [J]. Engineering Mechanics, 2016,33(4): 104―113. (in Chinese)
[6]徐颖, 韩庆华, 练继建. 单层球面网壳抗连续倒塌性能研究[J]. 工程力学, 2016, 33(11): 105―112.Xu Ying, Han Qinghua, Lian Jijian. Progressive collapse performance of single-layer latticed shells [J].Engineering Mechanics, 2016, 33(11): 105―112. (in Chinese)
[7]蔡健, 贺盛, 姜正荣, 等. 单层网壳结构稳定性分析方法研究[J]. 工程力学, 2015, 32(7):103―110.Cai Jian, He Sheng, Jiang Zhengrong, et al. Investigation on stability analysis method of single layer latticed shells[J]. Engineering Mechanics, 2015, 32(7):103―110. (in Chinese)
[8]沈士钊, 陈昕. 网壳结构稳定性[M]. 北京: 科学出版社, 1999.Shen Shizhao, Chen Xin. Stability of grid shell [M].Beijing: Scientific Press, 1999. (in Chinese)
[9]金路, 刘丹, 贾连光. 考虑随机缺陷的钢框架-支撑结构试验研究与有限元分析[J]. 工程力学, 2016, 33(增刊1): 79―84.Jin Lu, Liu Dan, Jia Lianguang. Experimental study and finite element analysis on steel braced frame structures considering random imperfections [J]. Engineering Mechanics, 2016, 33(Supll 1): 79―84. (in Chinese)
[10] Liu H, Zhang W, Yuan H. Structural stability analysis of single-layer reticulated shells with stochastic imperfections [J]. Engineering Structures, 2016, 124(19):473―479.
[11] Chen G, Zhang H, Rasmussen Kim J R, et al. Modeling geometric imperfections for reticulated shell structures using random field theory [J]. Engineering Structures,2016, 126(21): 481―489.
[12] JGJ 7―2010, 空间网格结构技术规程[S]. 北京: 中国建筑工业出版社, 2011: 3.JGJ 7―2010, Technical specification for space frame structures [S]. Beijing: China Architecture Industry Press, 2011: 3. (in Chinese)
[13] EN 1993-1-6: 2007, Eurocode 3: Design of steel structures-Part 1-6: strength and stability of shell structures [S]. Brussels: European Committee for Standardization, 2007.
[14] 罗永峰, 王春江, 陈晓明, 等. 建筑钢结构施工力学原理[M]. 北京: 中国建筑工业出版社, 2009.Luo Yongfeng, Wang Chunjiang, Chen Xiaoming, et al.Mechanics Principle of Constructional Steel Structures[M]. Beijing: China Architecture Industry Press, 2009.(in Chinese)
[15] GB51008―2016, 高耸与复杂钢结构检测与鉴定标准[S]. 北京: 中国计划出版社, 2016.GB51008―2016, Technical standard for inspection and appraisal of high-rising and complex steel structures [S].Beijing: China Planning Press, 2016. (in Chinese)
[16] 洪丽霞. 实测缺陷对单层球面网壳结构性能的影响研究[D]. 西安: 长安大学, 2011.Hong Lixia. Influence analysis of lattice shell structure based on measured imperfection [D]. Xi’an: Chang’an University, 2011. (in Chinese)
[17] 罗立胜, 罗永峰, 郭小农. 考虑节点几何位置偏差的既有网壳结构稳定计算方法[J]. 湖南大学学报(自科版), 2013, 40(3): 26―30.Luo Lisheng, Luo Yongfeng, Guo Xiaonong. Overall stability of existing reticulated shells considering the effect of geometric position deviation of joints [J].Journal of Hunan University (Natural Science), 2013,40(3): 26―30. (in Chinese)
[18] 罗永峰, 刘俊. 既有空间结构位形推算的随机偏差方法[J]. 同济大学学报(自然科学版), 2017, 45(6): 791―798.Luo Yongfeng, Liu Jun. Stochastic Deviation method of reckoning geometric shapes of existing spatial structures[J]. Journal of Tongji University (Natural Science), 2017,45(6): 791―798. (in Chinese)
[19] 魏德敏, 涂家明. 单层网壳结构非线性稳定的随机缺陷模态法研究[J]. 华南理工大学学报(自然科学版),2016, 44(7): 83―89.Wei Demin, Tu Jiaming. Study on Stochastic Imperfection Modal Method for nonlinear stability of single-layer reticulated shells [J]. Journal of South China University of Technology (Natural Science Edition),2016, 44(7): 83―89. (in Chinese)
[20] 郭佳民, 董石麟, 袁行飞. 随机缺陷模态法在弦支穹顶稳定性计算中的应用[J]. 工程力学, 2011, 28(11):178―183.Guo Jiamin, Dong Shilin, Yuan Xingfei. Application of random imperfection mode method in stability calculation of suspend-dome [J]. Engineering Mechanics,2011, 28(11): 178―183. (in Chinese)
[21] 蔡健, 贺盛, 姜正荣,等. 单层网壳结构稳定分析中初始几何缺陷最大值的研究[J]. 建筑结构学报, 2015,36(6): 86―92.Cai Jian, He Sheng, Jiang Zhengrong, et al. Investigation on maximum value of initial geometric imperfection in stability analysis of single layer reticulated shells [J].Journal of Building Structures, 2015, 36(6): 86―92. (in Chinese)
[22] 刘学春, 张爱林, 葛家琪,等. 施工偏差随机分布对弦支穹顶结构整体稳定性影响的研究[J]. 建筑结构学报,2007, 28(6): 76―82.Liu Xuechun, Zhang Ailin, Ge Jiaqi, et al. Study on the influence of construction deviation random distribution on the integral stability of suspend-dome [J]. Journal of Building Structures, 2007, 28(6): 76―82. (in Chinese)
[23] Thadewald T, Buening H. Jarque-Bera test and its competitors for testing normality – a power comparison[J]. Journal of Applied Statistics, 2007, 34(1): 87―105.
[24] Massey Jr Frank J. The Kolmogorov-Smirnov test for goodness of fit [J]. Journal of the American statistical Association, 1951, 46(253): 68―78.
[25] Miller L H. Table of percentage points of Kolmogorov statistics [J]. Journal of the American Statistical Association, 1956, 51(273): 111―121.
STOCHASTIC IMPERFECTION PROPAGATION METHOD FOR SPATIAL STRUCTURES BASED ON INVERSION RECKONING