图1 边界约束钢筋混凝土板的荷载-挠度关系
Fig.1 Relationship of load-deflection for RC slabs with boundary constraints
为了分析方便，传统的结构计算通常将梁板构件抗力-变形曲线简化为弹塑性模型，计算结果仍然满足工程要求。然而，实际工程中梁板构件的极限抗力随挠度变化而出现明显波动，因而对于大变形构件采用理想弹塑性模型对抗力-挠度进行简化是欠妥当的。实际分析中，较多的采用经典屈服线理论来求解钢筋混凝土板的极限承载力。但是，不少试验结果表明[1―5]，由于钢筋混凝土板内的薄膜效应，无论板支承边界是否存在水平约束，其极限承载力都大于按屈服线理论得到的结果，导致计算结果与试验结果存在明显差别。文献[6―7]提出了一种附加承载力理论，将压力膜效应承载力看作纯弯曲作用下的弯曲承载力与三铰拱作用下的附加承载力之和的计算方法。文献[8]指出现行的设计规范(ACI440R-06)由于没有考虑板内受压薄膜效应的作用而严重低估了 GFRP筋混凝土板带的承载能力。文献[9]的试验结果表明，因受压薄膜效应的影响，当侧向约束刚度与试件自身刚度之比为0.022 1∶时，试件的极限承载力较上限方法得到的结果平均提高了38.3%。李国强等[10―11]论述了火灾下压型钢板组合楼板的薄膜效应产生机理，指出薄膜效应只在楼板变形相当大时对承载力的提高才起重要作用，不考虑板的受压薄膜效应。文献[12]对双向固支板耐火试验进行了数值模拟和分析，指出受拉薄膜效应能较大提高板的耐火极限。杨志年[13]和董毓利等[14―18]通过对钢筋混凝土单/双向板的理论分析和试验研究，结合屈服线理论提出了考虑受拉薄膜效应的板块平衡法。以上关于钢筋混凝土板的薄膜效应研究局限于单纯的受压或受拉薄膜效应分析，而完整的钢筋混凝土板压-拉薄膜效应常常被忽略。
事实上，对于大多数钢筋混凝土板，其灾难性破坏往往出现在大变形条件下的受拉薄膜效应阶段[19]。本文首先根据正截面抗弯的钢筋混凝土弹塑性模型得到基于受压薄膜效应的荷载-挠度全曲线，再利用经典的挠曲线近似微分方程并引入抗弯刚度软化系数对挠度进行修正，得到考虑压-拉薄膜效应的荷载-挠度全曲线。
根据经典的试验结果[2―4]，本文将钢筋混凝土板从开始加载到最后钢筋拉断破坏的全过程分为三个阶段(见图1)：① 板端部受压上升段(AB)；② 混凝土开裂剥落下降段(BC)及③钢筋拉伸上升段(CD)。
图1 边界约束钢筋混凝土板的荷载-挠度关系
Fig.1 Relationship of load-deflection for RC slabs with boundary constraints
由于板一般采用对称配筋，可假设矩形板在极限荷载作用下的屈服线模式如图2所示。
图2 矩形板屈服线模式
Fig.2 Yield line model of rectangular slab
在外荷载作用下，板块挠度不断增大，最终形成四个分块的破坏机制，各分块在外荷载和屈服线上内力的共同作用下处于平衡状态。根据虚功原理，可以得到：
式中：Wuj为均布面荷载；δ为对应点处的挠度；mu、
分别为单位宽度屈服线的正、负极限抵抗弯矩；θ为分块相对屈服线的转角；l为屈服线长度。
式(1)右边表示板分块绕屈服线转动所产生的内力做功：
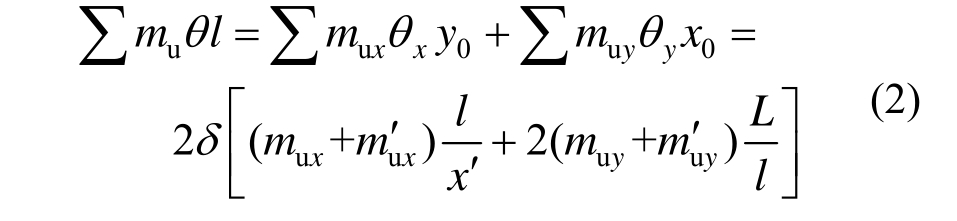
式(1)左边表示产生挠度δ时外荷载做功：
式中：xθ和yθ、mux和muy、mu′x和mu′y、x0和y0分别为θ、mu、l在x和y方向上的分量。
联立式(1)、式(2)、式(3)，可得单位面积上的极限均布荷载为：
由文献[2]可知：
式中：λ=L/l。当屈服线与配筋成直角时，由该配筋产生的单宽极限抵抗弯矩为[1]：
式中：h为板厚；xρ为x方向板底配筋率；yρ为y方向板底配筋率；fy为钢筋屈服强度；d为从受拉钢筋形心到混凝土最外边缘受压纤维的距离；fc为混凝土轴心抗压强度。
在竖向荷载作用下，板构件的受拉区混凝土开裂，宏观表现为构件端部向外移动，而四周围框约束限制了端部的侧向移动，有效控制了混凝土裂缝的开展，使得板的极限承载力大幅提高，这种因为端部挤压导致承载力提高的现象称为“受压薄膜效应”；当挠度继续增大时，跨中混凝土一部分受拉开裂一部分受压破碎而逐渐退出工作，使得跨中截面高度不断减小，板的承载力不断降低，直至跨中截面高度可忽略不计，此时荷载全部由钢筋承担，使得钢筋受拉板有向内移动的趋势，当板边受到侧向约束并且锚固良好时，会形成“悬链模型”[1]，随着跨中挠度增大，钢筋拉力的竖直分量越大，导致板的承载力再次提高，这种因为钢筋伸长导致承载力提高的现象称为“受拉薄膜效应”。
如图1所示，将板的上述受力全过程分为三段。AB段：随着跨中挠度增大，板向外移动趋势变得明显，受压薄膜效应增强，在B点增强效应达到最大并出现峰值荷载(即极限承载力)；BC段：当跨中挠度继续增加时，板内位移逐渐由向外转变为向内，此时受压薄膜力逐渐降低，压区混凝土压碎不断退出工作，截面的抗弯刚度减小，极限荷载降低，达到C点时可认为压区混凝土全部退出工作，钢筋受拉伸长并充分发挥作用，受拉薄膜效应出现；CD段：挠度进一步增大，钢筋产生的竖直向上分量不断提高，导致承载力有所提高，当板的极限承载力达到D点时，钢筋断裂，这一现象为受拉薄膜效应[16]。
1) 理论模型。
本文采用图3所示的板带体系，考虑到边界约束对板带承载力的提高作用，板的薄弱环节将出现在板中部，所以可以近似取x和y方向中间板带的承载力之和作为板的最终承载力。
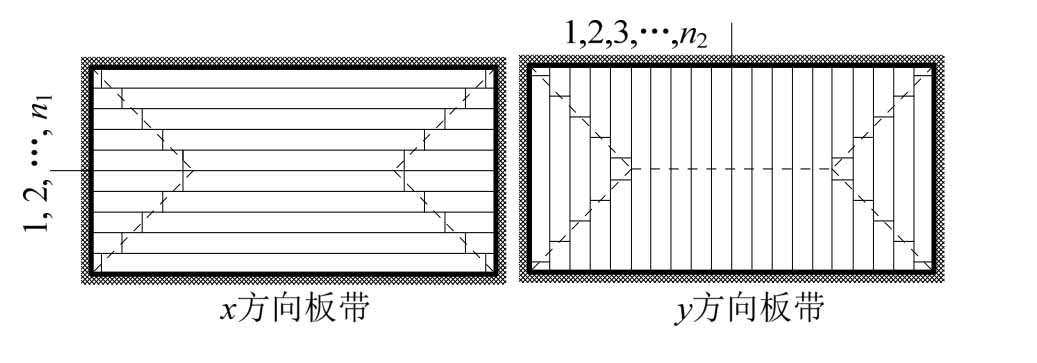
图3 板带体系
Fig.3 Strip of slabs
由于单一板带与梁式构件的受力特征相似，参考文献[20]中梁的受压面力效应理论，采用钢筋混凝土结构的弹塑性模型进行分析。如图1所示，AB段是受压薄膜效应不断发挥的过程，即弹性阶段逐渐向塑性阶段过渡的过程。一般情况下，围框约束的钢筋混凝土板的转动刚度较大，所以只考虑水平向刚度(以x方向板带为例)：
假定x方向的板带呈现如图4所示的三段式破坏模式[21]，其中N为受压薄膜力，t为板带向外位移，
和
分别为端部A点和跨中B点的截面抵抗弯矩。
① 弹性阶段。
受压薄膜力和跨中挠度的关系[17]：
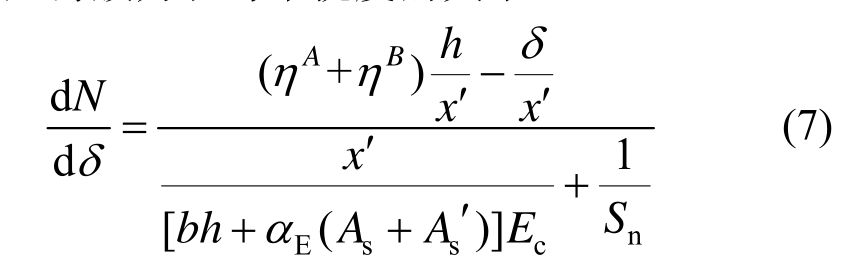
式中：Aη、Bη分别为A、B截面的中性轴高度系数；As′、As分别为截面受压和受拉钢筋的面积；b为板带宽度(本文取0.5h[20])。由于混凝土的压缩量很小，可以认为支座的向外位移等于板带的压缩量，则支座的水平向刚度Sn满足：
由力矩平衡条件得到截面抵抗弯矩，即：
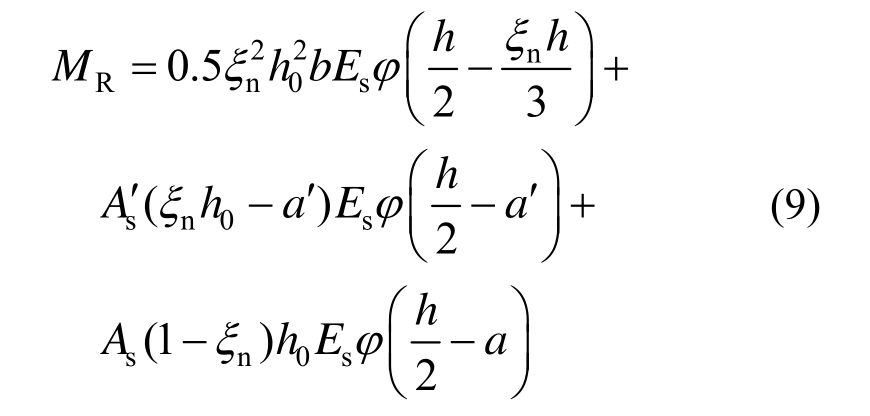
式中：φ为截面的平均曲率；nξ为相对压区高度系数；a′、a分别为受压和受拉钢筋的保护层厚度。
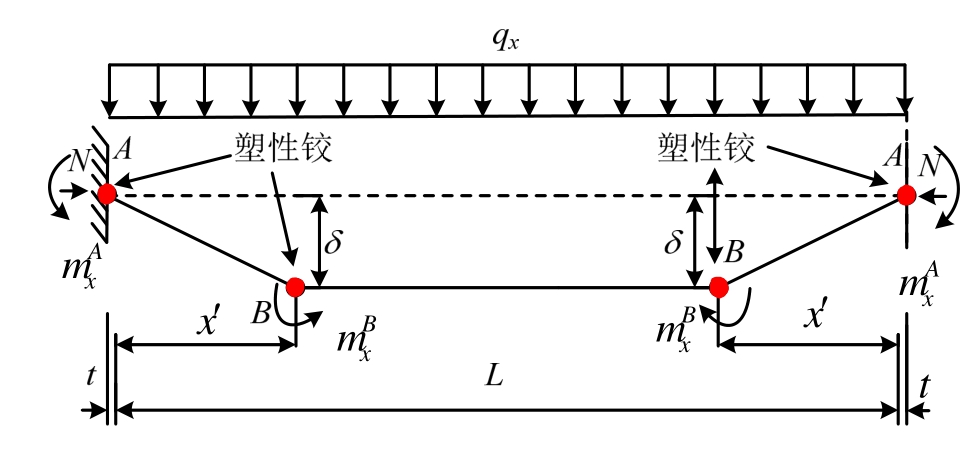
图4x方向板带计算简图
Fig.4 Calculation diagram of slabs along x-direction
② 塑性阶段。
考虑到塑性阶段压区混凝土不断被压碎，被包裹的受压钢筋无法充分发挥作用，本文偏于保守地不考虑受压钢筋对抗弯承载力的贡献，所以受压薄膜力和跨中挠度的关系变为：
其中：
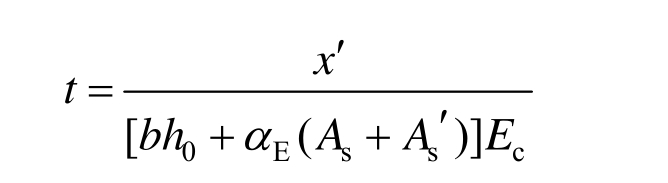
此时截面的抵抗弯矩为：
值得注意是，y方向跨中板带为两段式破坏模式，只需要将x′替换成l/2，然后将其他物理量对应替换，求解方法同上。
2) 抗力求解。
根据结构的静力平衡关系，可以得到x、y方向板带的均布线荷载：
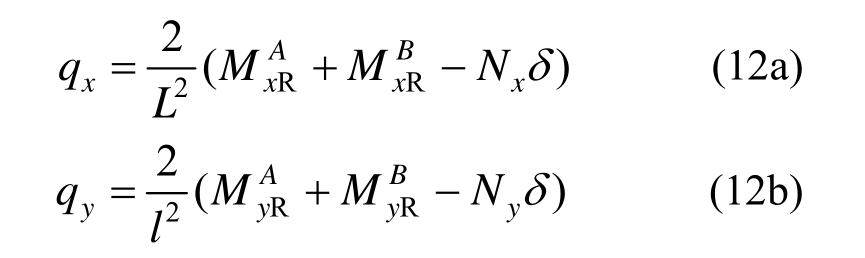
因而，板的最终承载力Wu(均布面荷载)为双向板带承载力之和，即：
3) 挠度修正。
按照(2)所述的方法得到板受压薄膜效应下的荷载-挠度曲线后，发现计算得到板的极限承载力与试验值吻合较好，但中心挠度的理论值约为0.1h[20,22]，远低于真实的试验值0.45h左右[2―4]，产生这种现象的原因主要有两个：① 三段(长跨)或两段(短跨)式破坏的板带模型为直线式，而实际的板由于受拉区混凝土开裂，板带变形后的轴线是一条曲线，导致基于直线式的弯曲破坏模式求到的挠度值明显偏小；② 塑性阶段一般不考虑混凝土的抗拉强度，而压区混凝土被压碎也逐渐退出工作，截面高度降低，实际的有效抗弯刚度在不断减小，因而在较小的荷载下也可能产生较大的挠度。
针对上述原因，本文进行再次修正。首先考虑实际变形，将求得的板带荷载值代入经典的挠曲线近似微分方程[23]，得到第一次修正后的挠度：
式中，
为板带截面的初始抗弯刚度。
为了简化计算，考虑到板达到峰值荷载(B点)时，混凝土板出现压碎，截面有效高度降低，受压薄膜效应逐渐减小，假定当塑性铰区板厚降为0.5h(C点)时，压区混凝土全部退出工作，整个压碎过程中截面的抗弯刚度逐渐减小(如图 5所示)，故引入抗弯刚度软化系数β。
图5 板带挠度和抗弯刚度的关系
Fig.5 Relationship of deflection-flexural rigidity for slabs
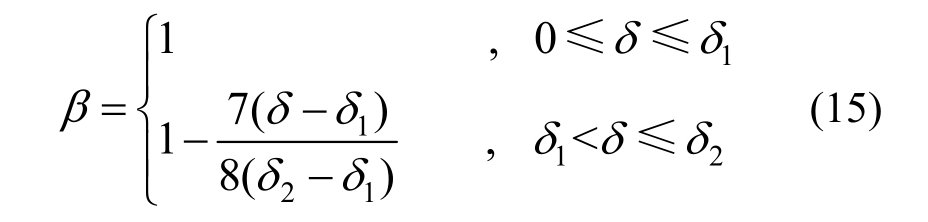
式中，1δ、2δ分别为未修正前B、C点的挠度值。
修正后的挠度为：
矩形板在大挠度下，压区混凝土全部退出工作(此时板的挠度为f2)，荷载由受拉钢筋独自承担(如图1中的CD段)形成受拉薄膜效应，外荷载q引起板块转动以及钢筋受拉伸长，该过程除了外荷载q做功W外，还有截面转动做功D1和钢筋伸长做功
根据能量原理：
外荷载做功，由式(3)得：
截面转动做功，由式(2)得：
钢筋伸长做功[14]：
其中，f2为产生受拉薄膜效应的起始挠度，由式(16)确定。
联立式(17)～式(20)可得到钢筋混凝土板受拉薄膜效应下的荷载-挠度关系：
通过式(13)求得受压薄膜效应下荷载-挠度关系，再经过式(14)、式(16)对挠度进行两次修正，然后运用式(21)得到受拉薄膜效应下荷载挠度关系，最后得到图 1所示的基于压-拉薄膜效应下边界约束钢筋混凝土板的荷载-挠度全曲线。
图6 塑性铰线形成后板块受力和挠度
Fig.6 Force and deflection at plastic hinge section
目前，关于专门梁板构件极限抗力的试验资料很少。本文选取Park的刚性围框约束的4块A组矩形钢筋混凝土板实测荷载-中心挠度曲线[1]作为对比验证试验。其中，混凝土弹性模量Ec=3.36×106psi，钢筋弹性模量Es=30.41×106psi，其他具体试验参数如表1所示。
表1 刚性围框约束的钢筋混凝土受荷板试验结果
Tabal 1 Test data of reinforced concrete slabs with rigid box constraints
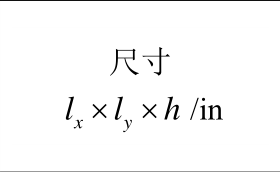
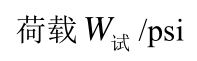
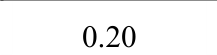
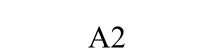
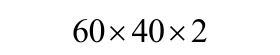
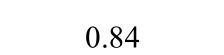
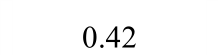
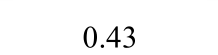
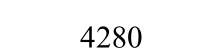
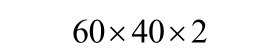
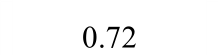
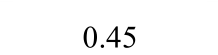
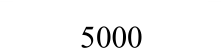
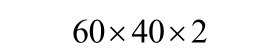
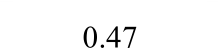
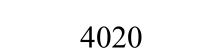
验值0.45h左右的试验结果吻合良好。由表2可知，本文计算得到的峰值荷载略小于试验值，原因主要有三个方面：① 忽略同向板带间的耦合作用，认为单个板带是独立工作，板的承载力为各板带承载力的简单叠加；② 没有考虑混凝土的受拉作用对承载力的贡献；③ 压区混凝土被压碎后，而破坏界面两侧混凝土存在摩擦咬合，仍然具有一定承载能力。但是，最终的理论结果和试验结果比较相近，说明本文将板划分为若干板带进行简化分析是合理的。计算得到的谷值挠度与试验结果最大相对误差为10%，远小于谷值荷载35%的最大相对误差，且谷值挠度出现在h左右。此外，A3矩形板出现较大误差，可能是因为实际混凝土强度偏高而配筋率偏低，在压区混凝土还未退出工作时，部分钢筋已经出现拉断，导致理论计算结果远大于试验值。从A2与A4板、A1与A3板、A1与A2板以及A3与A4板对比可知，混凝土抗压强度越高、配筋率越大，板中的受压薄膜效应就越明显，导致钢筋混凝土板的极限承载力与谷值承载力显著提高。
表2 本文计算结果与试验对比
Tabal 2 Comparisons of calculation results and test data
编号峰值荷载挠度f/h峰值荷载/psi 谷值挠度f/h谷值荷载/psi
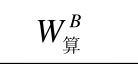
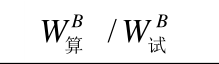
A1 0.50 0.53 1.06 30.8 28.95 0.94 1.26 1.22 0.97 7.09 8.52 1.20 A2 0.51 0.49 0.96 31.3 29.38 0.94 1.15 1.17 1.02 11.27 12.20 1.08 A3 0.46 0.53 1.15 37.8 37.59 0.99 1.16 1.20 1.03 13.89 18.74 1.35 A4 0.42 0.37 0.88 37.3 36.74 0.98 1.07 1.18 1.10 17.07 19.60 1.15
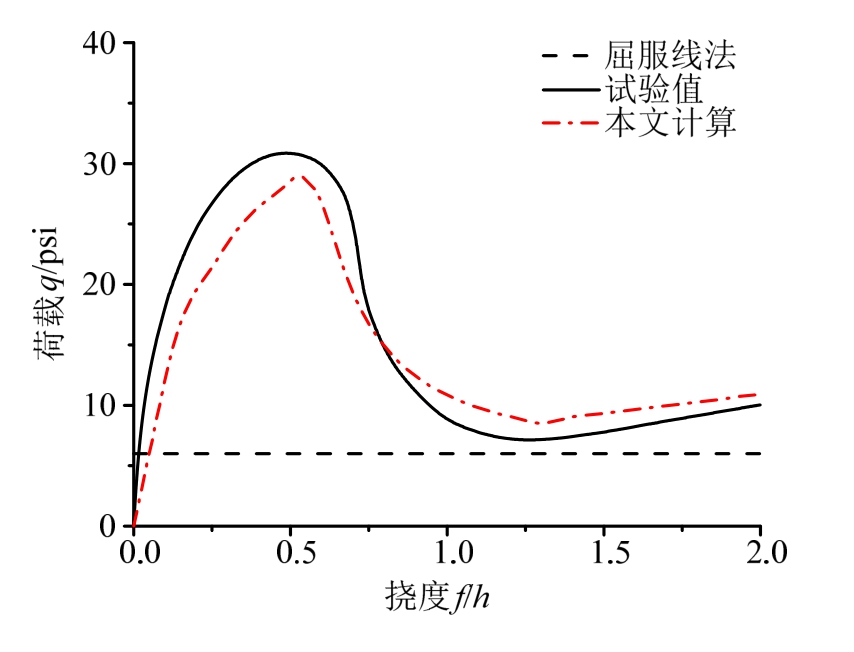
图7 A1板的荷载-中心挠度曲线
Fig.7 Load-center deflection curves of A1 slab
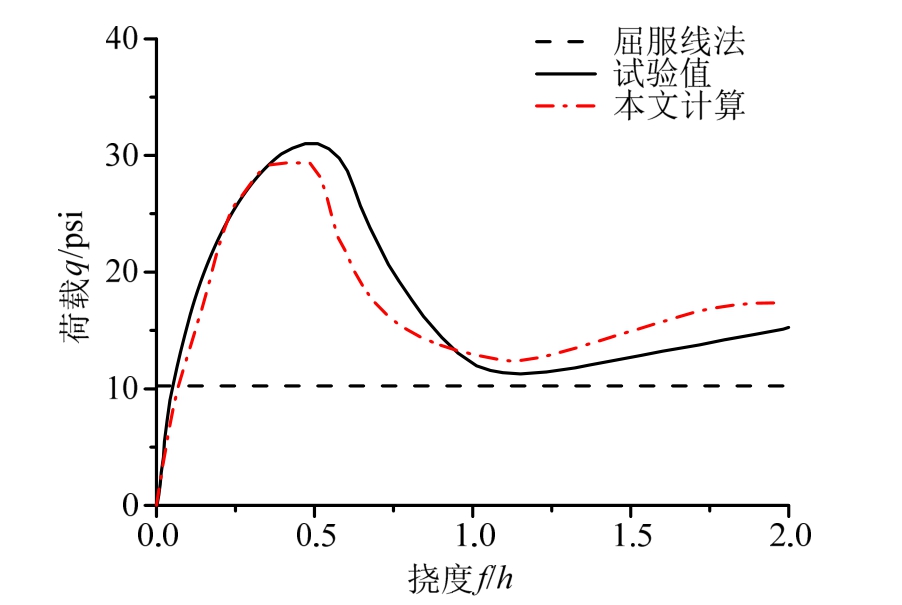
图8 A2板的荷载-中心挠度曲线
Fig.8 Load-center deflection curves of A2 slab
图9 A3板的荷载-中心挠度曲线
Fig.9 Load-center deflection curves of A3 slab
图10 A4板的荷载-中心挠度曲线
Fig.10 Load-center deflection curves of A4 slab
从图7～图10可以看出，本文理论方法得到的板带极限抗力与试验得到的抗力全过程吻合较好，充分体现了板带边界刚性约束产生的压-拉薄膜效应对极限承载力的影响，说明本文方法可以合理预测板带荷载-挠度全过程，为工程设计计算提供参考。此外，本文方法及Park试验结果充分说明压-拉薄膜效应对板带极限承载力有十分显著的影响，这种影响即使在板带受拉阶段也不能忽略。计算结果表明，通过屈服线理论得到的钢筋混凝土板极限承载力明显偏于保守，也无法反映板的承载力在挠度逐渐增大直至破坏全过程的变化规律，而本文同时考虑了板变形全过程中的压-拉薄膜效应，计算结果能较好地解释Park试验，揭示了矩形钢筋混凝土板从加载到破坏全过程的压-拉薄膜效应作用机理。不难发现，矩形板初始挠度较小时，受压薄膜效应明显，承载力迅速上升，在挠度约为0.45h时，承载力达到最大，随后板的极限荷载迅速下降接近屈服线理论荷载值后又开始产生受拉薄膜效应。此时，挠度约为h，之后板块的大转角导致钢筋竖向承载力分量不断增大，当挠度接近 2h时，钢筋拉断板块发生彻底分离破坏。
以上分析表明，边界刚性约束板带在外荷载作用下的荷载-挠度曲线呈起伏样变化，承载力峰值出现在受压薄膜效应阶段，混凝土被压碎后板带极限承载力迅速跌落，当挠度进一步增大时钢筋受拉作用逐渐发挥，板带出现受拉薄膜效应，板带极限承载力重新提高直至钢筋拉断破坏。考虑压-拉薄膜效应得到的板带第一峰值承载力和第二峰值极限承载力相对于基于经典屈服线理论分别提高了 195%和67%左右，说明当板带边界受到刚性约束时利用传统的屈服线理论对其极限抗力进行预测将严重低估板带的承载力能，结构分析中将其抗力模型简化为理想弹塑性模型是否合理值得商榷。
本文建立了围框约束钢筋混凝土矩形板基于压-拉薄膜效应的抗力求解方法，将计算结果分别与Park的4组试验结果以及屈服线理论计算的结果进行了比较，得出如下结论：
(1) 混凝土抗压强度越高、配筋率越大，压-拉薄膜效应越明显，钢筋混凝土板的极限承载力与谷值承载力越大，但是提高幅度逐渐减小；
(2) 板带极限抗力随挠度变化而变化，初始挠度较小时受压薄膜效应明显，挠度约为0.45h时板的极限承载力达到最大，当挠度达到h时出现受拉薄膜效应；
(3) 考虑压-拉薄膜效应得到的板带第一峰值承载力和第二峰值极限承载力相对于基于经典屈服线理论分别提高了195%和67%左右，说明利用传统的屈服线理论将严重低估围框约束RC板带的承载力能；
(4) 本文理论方法得到的围框约束 RC板带极限抗力与试验得到的抗力全过程吻合较好，充分体现了板带边界刚性约束产生的压-拉薄膜效应对极限承载力的影响，说明本文方法可以合理预测板带荷载-挠度全过程，为工程设计计算提供参考。
[1]R·派克, W·L·根勃尔著, 黄国桢, 等. 钢筋混凝土板[M]. 上海: 同济大学出版社, 1980: 365―367.Park R, Gambe W L. Reinforced concrete slabs [M].Wiley, 1980: 365―367.
[2]Wood R H, Drucker D C. Plastic and elastic design of slabs and plates [M]. London: Thames and Hudson,1961: 225―261.
[3]Park R. Ultimate strength of rectangular concrete slabs under short-term uniform loading with edges restrained against lateral movement [J]. Ice Proceedings, 1964,28(2): 125―150.
[4]Black M S. Ultimate strength study of two-way concrete slabs [J]. Struct. Div. ASCE, 1975: 311―324.
[5]沈聚敏, 王传志, 江见鲸. 钢筋混凝土有限元与板壳极限分析[M]. 北京: 清华大学出版社, 1993: 396―410.Shen Jumin, Wang Chuanzhi, Jiang Jianjing. Finite elements method of reinforced concrete and limit analysis of concrete slabs and shells [M]. Beijing:Tsinghua University Press, 1993: 396―410. (in Chinese)
[6]王刚, 王清湘, 刘士润. 钢筋混凝土板的压力膜效应承载力计算方法[J]. 吉林大学学报(工学版), 2010,40(3): 699―704.Wang Gang, Wang Qingxiang, Liu Shirun. Calculation method of load capacity compressive membrane effect of reinforced concrete slab [J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(3):699―704. (in Chinese)
[7]王刚, 司炳君, 康海贵. 考虑压缩薄膜效应钢筋混凝土板的变形分析[J]. 应用基础与工程科学学报,2017(4): 751―759.Wang Gang, Si Bingjun, Kang Haigui. Deflection calculation of reinforced concrete slab under compressive membrane action [J]. Journal of Basic Science and Engineering, 2017(4): 751―759. (in Chinese)
[8] 郑愚, 李春红. 侧向约束 GFRP筋混凝土板内压缩薄膜效应的研究[J]. 工程力学, 2014, 31(6): 203―211.Zheng Yu, Li Chunhong. Investigation of compressive membrane action inlaterally restrained GFRP reinforced concrete slabs [J]. Engineering Mechanics, 2014, 31(6):203―211. (in Chinese)
[9]王刚, 王清湘, 李中军, 等. 剪力墙结构中钢筋混凝土楼板膜效应试验研究[J]. 大连理工大学学报, 2012(1):66―73.Wang Gang, Wang Qingxiang, Li Zhongjun, et al.Experimental investigation of membrane action in reinforced concrete slab in shear-wall structures [J].Journal of Dalian University of Technology, 2012(1):66―73. (in Chinese)
[10] 李国强, 周昊圣, 郭士雄. 火灾下钢结构建筑楼板的薄膜效应机理及理论模型[J]. 建筑结构学报, 2007,28(5): 40―47.Li Guoqiang, Zhou Haosheng, Guo Shixiong.Mechanism and theoretical model of membrane action in slabs of steel buildings subjected to fire [J]. Journal of Building Structures, 2007, 28(5): 40―47. (in Chinese)
[11] 李国强, 郭士雄, 周昊圣. 火灾下钢结构建筑楼板的薄膜效应模型验证及实用方法[J]. 建筑结构学报,2007, 28(5): 48―53.Li Guoqiang, Guo Shixiong, Zhou Haosheng. Model validation and application of membrane action in slabs of steel buildings subjected to fire [J]. Journal of Building Structures, 2007, 28(5): 48―53. (in Chinese)
[12] 王志明, 张巍, 王浩, 施毅. 钢筋混凝土双向固支板的超长时间耐火极限研究[J]. 工业建筑, 2016, 46(2):52―57.Wang Zhiming, Zhang Wei, Wang Hao, Shi Yi. Study of fire resistance to reinforced concrete two-way fixed slabs for super long time [J]. Industrial Construction, 2016,46(2): 52―57. (in Chinese)
[13] 杨志年. 不同边界约束条件的混凝土双向板抗火性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2012, 50―54,51―71.Yang Zhinian. Research on fire resistance of two-way reinforced concrete slabs with different edge restraints[D]. Harbin: Harbin Institute of Technology, 2012, 50―54, 51―71. (in Chinese)
[14] 董毓利. 用变形和分解原理求混凝土板的受拉薄膜效应[J]. 力学学报, 2010, 42(6): 1180―1187.Do Yuli. Calculation of tensile membrane effects of concrete slabs using deformation additive decomposition theorem [J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1180―1187. (in Chinese)
[15] 王勇, 董毓利, 袁广林, 等. 考虑薄膜效应的钢筋混凝土双向板承载力分析[J]. 华中科技大学学报(自然科学版), 2014(3): 96―101.Wang Yong, Dong Yuli, Yuan Guanglin, et al.Load-carrying capacity analysis of reinforced concrete two-way slabs considering membrane effect [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition). 2014(3): 96―101. (in Chinese)
[16] 张大山, 董毓利, 吴亚平. 混凝土单向板的受拉薄膜效应计算[J]. 吉林大学学报(工), 2013, 43(5): 1253―1257.Zhang Dashan, Dong Yuli, Wu Yaping. Calculation of tensile membrane effect of one-way concrete slabs [J].Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1253―1257. (in Chinese)
[17] 王勇, 董毓利, 邹超英. 钢筋混凝土板的极限承载力计算[J]. 哈尔滨工业大学学报, 2013, 45(2): 8―13.Wang Yong, Dong Yuli, Zou Chaoying. Calculation of limit carrying capacity of reinforced concrete slabs [J].Journal of Harbin Institute of Technology, 2013, 45(2):8―13. (in Chinese)
[18] 张大山, 董毓利, 房圆圆. 考虑受拉薄膜效应的板块平衡法修正及在混凝土双向板中的应用[J]. 工程力学,2017, 34(3): 204―210.Zhang Dashan, Dong Yuli, Fang Yuanyuan. Modification of segment equilibrium method through considering tensile membrane effects and its application in two-way concrete slabs [J]. Engineering Mechanics, 2017, 34(3):204―210. (in Chinese)
[19] Park R. Tensile membrane behavior of uniformly loaded rectangular reinforced concrete slabs with fully restrained edges [J]. Magazine of Concrete Research,1964, 16(46): 39―44.
[20] 钱七虎, 王明洋. 高等防护结构计算原理[M]. 江苏:江苏科学技术出版社, 2009: 242―254.Qian Qihu, Wang Mingyang. Calculation theory for advanced protective structures [M]. Jiangsu: Phoenix Science Press, 2009: 242―254. (in Chinese)
[21] 陈力, 方秦, 龚自明, 等. 静载作用下钢筋混凝土梁板结构的面力效应(I)—理论模型[J]. 土木工程学报,2011(1): 29―35.Chen Li, Fang Qing, Gong Ziming, et al. Membrane action on reinforced concrete beam-slab structures under static load(I)—Theoretical model [J]. China Civil Engineering Journal, 2011(1): 29―35. (in Chinese)
[22] Roberts E H. Load carrying capacity of slab strips restrained against longitudinal expansion [J]. Concrete,1969, 3(9): 369.
[23] 孙训芳, 方孝淑, 关来泰. 材料力学(I)[M]. 北京: 高等教育出版社, 2009: 158―162.Sun Xunfang, Fang Xiaoshu, Guan Laitai. Mechanics of materials (I) [M]. Beijing: Higher Education Press, 2009:158―162. (in Chinese)
CARRYING-CAPACITIES OF RC SLABS WITH FULLY-FIXED SUPPORTS BASED ON THE COMPRESSIVE-TENSILE MEMBRANE EFFECT