表1 试验梁的参数
Table 1 Parameters of specimens
类型 先张梁编号 A组PA0 PA1 PA2 PA3预应力 0 0.25fpk0.5fpk0.75fpk类型 先张梁编号 B组PB0 PB1 PB2 PB3预应力 0 0.25fpk0.5fpk0.75fpk类型 后张梁编号 C组PC0 PC1 PC2 PC3预应力 0 0.25fpk0.5fpk0.75fpk
预应力混凝土(PC)具有跨越能力大、力学性能好等特点，目前已广泛应用于结构工程[1]。然而，随着服役时间的增长，在不利环境下PC结构性能劣化问题逐渐显现。其中，钢绞线锈蚀是造成结构性能退化的主要因素之一[2]。通常钢绞线具有较大的直径，一旦发生锈蚀极易造成混凝土的开裂和剥落，影响结构的耐久性[3－5]。因此，保护层锈胀开裂是评估结构耐久性的主要指标之一。
钢绞线锈蚀会对周围混凝土产生膨胀力，如何量化锈蚀产物的膨胀是预测混凝土锈胀开裂的关键因素之一。现有研究主要集中于普通钢筋的铁锈膨胀率，铁锈膨胀率定义为锈蚀产物体积与相应钢筋的体积比[6－7]。钢绞线的化学组成成分与普通钢筋不同，这会导致两者之间的铁锈膨胀率存在差异；再者，钢绞线的锈蚀速率随着预应力的增加而变快[8]，较快地锈蚀速率可能也会改变钢绞线锈蚀产物的组成成分，钢绞线锈蚀产物的膨胀率有待进一步研究。
混凝土锈胀开裂过程分为裂缝初始和扩展两个阶段[9－11]。裂缝初始阶段是锈蚀初始至保护层开裂，裂缝扩展阶段为保护层开裂到一定宽度。混凝土锈胀开裂过程大多采用厚壁圆筒理论进行模拟[6,12－14]，既有研究主要针对普通钢筋混凝土锈胀开裂，预应力混凝土锈胀开裂研究相对较少。预应力混凝土锈胀开裂过程中，混凝土会受到预应力和膨胀力的共同作用。Dai等[15]评估了预应力等因素对锈胀开裂的影响，但模型中钢绞线锈蚀产物的膨胀率依旧采用的是普通钢筋参数，同时也未考虑混凝土开裂损伤的影响，此外，预测模型分别采用了两个相对独立的理论去预测锈胀开裂初始和扩展阶段。如何合理地考虑以上因素对预应力混凝土锈胀开裂的影响仍需进一步研究。
本文旨在通过快速锈蚀方法开展预应力混凝土锈胀开裂试验，研究预应力钢绞线锈蚀产物的膨胀及混凝土开裂，分析预应力对混凝土锈胀开裂的影响。在此基础上，综合考虑预应力、铁锈膨胀率和混凝土开裂损伤等因素，建立开裂初始和发展全过程的锈胀裂缝预测模型，并通过试验结果进行验证。
为研究预应力对混凝土锈胀开裂的影响，试验设计制作了 12片混凝土梁。试验梁分为三组：A组、B组和C组；每组各4根，钢绞线的张拉应力分别为0、0.25fpk、0.5fpk和 0.75fpk，fpk为钢绞线抗拉强度标准值，其值为1860 MPa，各梁张拉应力参数如表1所示。A组和B组为先张预应力混凝土梁，C组为后张预应力混凝土梁。进行后张梁混凝土浇筑时，在钢绞线重心位置处预留直径为30 mm的橡胶棒，待混凝土达到养护龄期后，通过拉拔橡胶棒形成预应力筋孔洞，进而穿插钢绞线。为保证钢绞线与混凝土间的紧密接触，预应力张拉结束后采用高流动性的水泥浆对预留孔洞进行灌浆处理，水泥浆通过梁底预留孔注入预应力筋孔洞。
表1 试验梁的参数
Table 1 Parameters of specimens
类型 先张梁编号 A组PA0 PA1 PA2 PA3预应力 0 0.25fpk0.5fpk0.75fpk类型 先张梁编号 B组PB0 PB1 PB2 PB3预应力 0 0.25fpk0.5fpk0.75fpk类型 后张梁编号 C组PC0 PC1 PC2 PC3预应力 0 0.25fpk0.5fpk0.75fpk
梁截面的长×高×宽分别为 2000 mm×150 mm×130 mm。预应力筋采用1根φs15.2 mm(七股)钢绞线，梁顶架立钢筋采用2根直径为8 mm的HRB400钢筋，梁底受拉钢筋采用2根直径为6 mm的HRB400钢筋。箍筋为直径6 mm的HPB235钢筋，间距为100 mm。钢绞线和钢筋的保护层厚度分别为42.4 mm和30 mm。试验梁尺寸及配筋如图1所示。
图1 构件尺寸及配筋 /mm
Fig.1 Details and reinforcement of the specimens
混凝土采用 32.5级的硅酸盐水泥，水灰比为0.44，配合比∶水泥为 417 kg/m3，细骨料为676 kg/m3，粗骨料为1026 kg/m3。为加速锈蚀速率，混凝土内掺有NaCl，Cl-浓度为水泥质量分数的5%。先张和后张预应力混凝土 28 d抗压强度分别为44.1 MPa和43.4 MPa。表2给出了钢绞线和钢筋的化学成分。
表2 钢绞线和钢筋的化学成分 /(wt. %)
Table 2 Chemical compositions of strand and steel
类型 C Mn Si P S钢绞线 0.82 0.74 0.21 0.012 0.006变形钢筋 0.2 1.34 0.55 0.033 0.028类型 Cr Cu Ni Ti Al钢绞线 0.17 0.09 0.03 0.03 0.03变形钢筋 / / / / /
本试验通过电化学快速锈蚀方法得到不同宽度的锈胀裂缝。为单独研究预应力筋锈蚀的影响，利用环氧树脂对普通钢筋进行防锈处理。测试梁浸泡在质量分数为10%的NaCl溶液中，恒定直流电源的阳极与预应力筋连接，阴极与 NaCl溶液中的不锈钢连接，进而形成闭合回路。通电作用下，阳极释放出电子被氧化，预应力筋发生锈蚀。锈蚀电流为0.1A，电流密度为90 uA/cm2。A组、B组和C组的锈蚀时间分别为15 d、20 d和20 d，图2给出了加速锈蚀装置。
图2 加速锈蚀装置
Fig.2 Accelerated corrosion device
为研究钢绞线锈蚀产物的膨胀率，通过红外(IR)和热重(TG)分析对锈蚀产物样本的组成成分进行测量，其步骤如下：首先，收集裂缝中流出的钢绞线锈蚀产物；然后，利用烘干箱将锈蚀产物烘干，使用行星式研磨机将其研磨成粉末；最后，基于 IR和 TG分析对锈蚀产物的组成成分进行测量。红外分析使用的是Nicolet 6700 FTIR分析仪。热重分析使用的是DTG-60H综合热分析仪，测试环境为氮气环境，测试温度以10oC/min的速率从36℃上升到1000℃。
为研究预应力对混凝土锈胀裂缝扩展的影响，锈蚀过程中，利用精度为0.01 mm的裂缝观测仪观测裂缝随时间的发展。加速锈蚀后，利用裂缝观测仪对混凝土表面每10 cm位置处的纵向裂缝宽度进行测量。同时，测量每10 cm位置处的质量损失率来反映不同位置处钢绞线的锈蚀程度，测量步骤如下：首先，将钢绞线从混凝土中取出；然后，利用浓度为12%的盐酸对其表面的铁锈进行清洗，再利用石灰水进行中和；最后，将钢绞线切成10 cm每段，称量其残余质量。
钢绞线锈蚀产物的膨胀会导致混凝土开裂，锈蚀产物组成的不同会导致不同程度的体积膨胀率。本节首先利用 IR分析明确钢绞线锈蚀产物的组成成分；然后，使用TG分析明确锈蚀产物中氧化铁和氢氧化铁的含量；最后，分析得到钢绞线锈蚀产物的膨胀率。
IR分析是利用不同物质对红外光波的吸收存在不同，进而进行定性或定量分析[16]。图3给出了不同应力状态下钢绞线锈蚀产物样本的红外光谱。
表3 各铁锈的标准光谱和膨胀率
Table 3 The standard spectra and expansion ratio of rusts
注：S是强峰；M是中等峰；W是弱峰；B是宽带；VS是较强峰；VW是较弱峰；VB是较宽带。
类型 峰值/cm-1，(相对强度) 铁锈膨胀率α-FeOOH 1399(M), 1260(VM), 881(S), 793(S), 608(W), 463(B,VW) 2.95β-FeOOH 858(B,S), 670(B,S), (300～500) (B,S) 3.53 γ-FeOOH 1152(B,M), 1017(S), 737(VW), 487(VB,W) 3.07δ-FeOOH 1110(B,S), 880(S), 786(VW), 617(B,VW), 493(B,W) 2.99α-Fe2O3535(S), 464(M) 2.15γ-Fe2O3690(S), 682(S), 550(VS), 475(W), 437(W), 418(VW) 2.32 FeO 492(VB,W) 1.71 Fe3O4556(500～700)(B,W), 404(300～500)(VB,W) 2.10
Raman等[17]给出了不同种类铁锈的标准光谱，见表 3。由图 3和表 3可知，锈蚀产物样本中含有α-Fe2O3、Fe3O4、α-FeOOH、β-FeOOH 和γ-FeOOH，各锈蚀产物样本中的透射率存在不同。各样本透射率的差异性主要是由于锈蚀产物中铁锈的组成比例存在不同所造成的，这表明预应力对锈蚀产物的组成成份影响不大，但会改变各组成成分之间的比例。
图3 锈蚀产物的红外光谱
Fig.3 Infrared spectrums of corrosion products
钢绞线锈蚀产物主要由氧化铁和氢氧化铁组成。加热可以将氢氧化铁转化为氧化铁，进而导致锈蚀产物总质量的改变。根据这一特点，可以利用热重(TG)分析对样本中氧化铁和氢氧化铁的比例进行分析。基于热重(TG)分析曲线，进一步利用微商热重(DTG)法对锈蚀产物的质量损失率进行分析，图4给出了各样本的TG和DTG曲线。
图4 锈蚀产物的TG和DTG 曲线
Fig.4 TG and DTG curves of corrosion products
由图4可知，加热过程中有两个阶段出现了重量损失，锈蚀产物在 36℃～200℃的重量损失比200℃～400℃的重量损失要大。在 36℃～200℃，样本的重量快速下降，这阶段的重量损失主要是由于吸附水干燥的原因造成的。氢氧化铁中羟基的分解温度主要在 200℃～400℃[7]，在这一阶段，氢氧化铁会转化为氧化铁。由图4可以得到样本在200℃～400℃的重量损失，基于质量分数相等的原则，进而得到样本中氢氧化铁的质量分数，见表 4。由表4可知，预应力会增大锈蚀产物中氧化铁的比例，降低氢氧化铁的含量。
表4 锈蚀产物参数
Table 4 Parameter of corrosion products
预应力/MPa 200℃～400℃重量损失/(%)氢氧化铁质量分数/(%)氧化铁质量分数/(%)膨胀率0 7 69 31 2.96 0.25fpk4 40 60 2.68 0.5fpk4 40 60 2.68 0.75fpk5 49 51 2.78平均膨胀率 2.78
表3给出了各种铁锈对应的膨胀率[18]，α-Fe2O3和Fe3O4的膨胀率非常接近，而α-FeOOH、β-FeOOH和γ-FeOOH的膨胀率也类似。为简化分析，将氧化铁(α-Fe2O3和 Fe3O4)的 膨 胀 率 和 氢 氧 化 铁(α-FeOOH、β-FeOOH 和γ-FeOOH)的膨胀率分别取为平均值，进而根据氧化铁和氢氧化铁的含量确定各样本中锈蚀产物的膨胀率，见表4。由表4可知，不同应力状态下各样本的铁锈膨胀率相似，预应力对钢绞线铁锈膨胀率的影响并不显著。为此，对于电化学加速锈蚀试验得到的钢绞线锈蚀产物膨胀率可建议为平均值(2.78)。
锈蚀产物的膨胀会导致周围混凝土产生拉应力，当拉应力超过混凝土的抗拉强度时，混凝土内部会产生微裂缝。随着微裂缝的逐渐扩展，混凝土表面会出现裂缝。为评估预应力对混凝土保护层开裂临界时间的影响，表5给出了各试验梁保护层开裂的临界时间。
表5 保护层开裂的临界时间
Table 5 Critical time of cover cracking
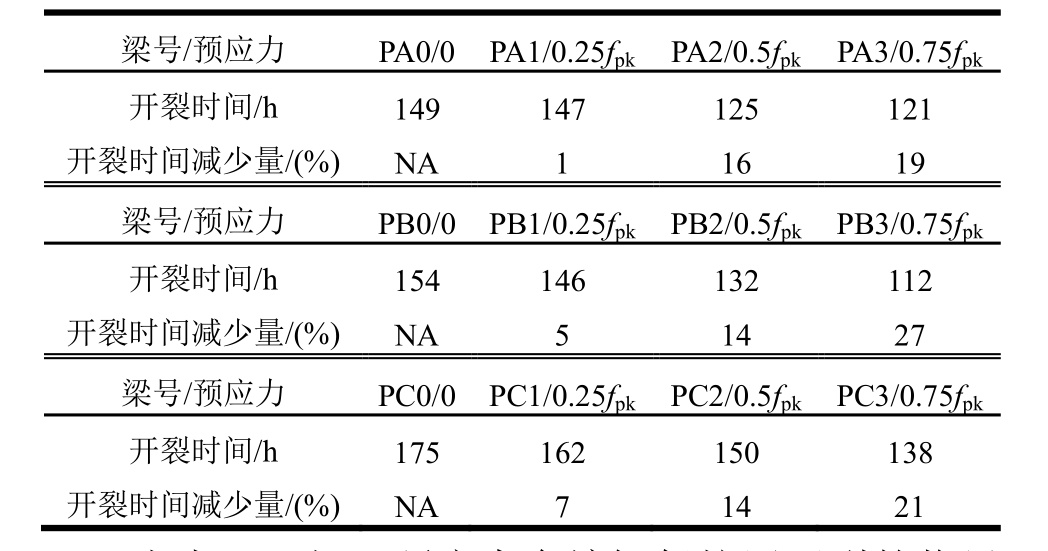
梁号/预应力 PA0/0 PA1/0.25fpkPA2/0.5fpkPA3/0.75fpk开裂时间/h 149 147 125 121开裂时间减少量/(%) NA 1 16 19梁号/预应力 PB0/0 PB1/0.25fpkPB2/0.5fpkPB3/0.75fpk开裂时间/h 154 146 132 112开裂时间减少量/(%) NA 5 14 27梁号/预应力 PC0/0 PC1/0.25fpkPC2/0.5fpkPC3/0.75fpk开裂时间/h 175 162 150 138开裂时间减少量/(%) NA 7 14 21
由表5可知，预应力会缩短保护层开裂的临界时间。当预应力为0.75fpk时，保护层开裂的平均临界时间降低了22%。随着锈蚀程度的增加，裂缝沿着锈蚀钢绞线位置逐渐扩展。为明确预应力对裂缝扩展的影响，图5给出了各试验梁最宽裂缝随时间的扩展规律。
图5 裂缝扩展
Fig.5 Crack propagation
由表5可知，先张预应力混凝土保护层的开裂时间较后张预应力混凝土早；由图5可知，在相同的锈蚀时间下，先张预应力混凝土的裂缝宽度也比后张预应力混凝土的大。造成以上现象的原因可能是先张梁中钢绞线与混凝土直接接触，保护层为连续介质，锈蚀产物引起的锈胀力可直接作用于混凝土，而后张梁中钢绞线与混凝土之间由水泥浆粘结，水泥浆的存在使得保护层为非连续介质，锈蚀力需先造成内部水泥浆的开裂才能作用于外部混凝土，水泥浆的存在延缓了混凝土的锈胀开裂。先张梁和后张梁两者之间锈胀开裂的差异性在今后的理论研究中将进一步开展。
由图5可知，锈胀裂缝宽度随预应力的增加而变大。当预应力为0.75fpk，A组、B组和C组的最大锈胀裂缝宽度分别增加了19%、30%和30%。加速锈蚀后，混凝土底部沿锈蚀钢绞线位置出现一条通长裂缝。相关研究表明质量损失率与锈胀裂缝宽度具有良好地线性关系[19]。为此，本试验对每10 cm位置的裂缝宽度和质量损伤率进行了测量，图6给出了不同应力状态下的裂缝宽度和锈蚀率。
图6 裂缝宽度与锈蚀率
Fig.6 Crack width and corrosion loss
由图6可知，轻微地钢绞线锈蚀会导致保护层开裂。裂缝宽度取决于预应力和锈蚀程度的共同作用，裂缝宽度随锈蚀率和预应力的的增加而增大。当预应力为0.75fpk时，裂缝扩展速率增加了9%。对于无预应力混凝土，钢绞线锈蚀率为10%时，对应的裂缝宽度为0.76 mm；当预应力分别为0.25fpk，0.5fpk和0.75fpk时，锈胀裂缝的宽度分别增加了3%，7%和11%。预应力的存在会加快裂缝扩展速率，同时也会增大锈胀裂缝宽度。
本文采用钢绞线均匀锈蚀对预应力混凝土锈胀开裂进行理论分析，理由有以下三点：1) 加速锈蚀后，观察钢绞线表面锈蚀情况，虽存在坑锈，但锈坑的体积较小，深度较浅；2) 对比裂缝宽度与锈蚀率数据(图6)可知，轻微地钢绞线锈蚀会导致保护层开裂；3) 既有研究表明，采用均匀锈蚀对混凝土锈胀开裂进行模拟具有一定的合理性[3,9,15,17]。轻微锈蚀下，锈蚀产物一般均匀地环绕在钢绞线周围，进而产生一个均匀地膨胀力。本模型将混凝土模拟为一个厚壁圆筒环，当锈胀力引起的拉应力达到预应力混凝土抗拉强度时，混凝土即产生微裂缝。
保护层完全开裂前，预应力混凝土保护层由两部分组成：即内环开裂混凝土和外环未开裂混凝土。通过开裂混凝土和未开裂混凝土交界面的变形协调关系，可以得到锈蚀率的表达式，进一步通过边界条件的设计，可以预测预应力混凝土从裂纹初始到扩展阶段的锈胀开裂过程。图 7给出钢绞线-混凝土交界面的应力分布和变形。
图7 交界面的应力分布和变形
Fig.7 Stress distribution and radial deformation at the strand-concrete interface
预应力钢绞线由一根内部钢丝和六根外部钢丝组成。试验结果表明，外围钢丝的质量损失是造成钢绞线锈蚀的主要原因，钢绞线的锈蚀率ρ为：
式中：R0为未锈蚀钢丝半径；Rρ为锈蚀后钢丝半径；Ap为钢绞线截面面积。
随着锈蚀程度的增加，锈蚀产物首先填充混凝土内的孔隙和裂缝，剩余部分则产生锈胀应力。根据体积相等原则，锈蚀产物的总体积为：
式中：ΔVr为锈蚀产物的总体积，
为锈蚀产物的膨胀率；ΔVw为钢丝的体积减小量，
为膨胀应力引起混凝土的体积变化，
Rt是包含锈蚀产物厚度的钢丝半径；ΔVp为填充孔隙和开裂混凝土的锈蚀产物，
Ru为开裂混凝土的半径。
联合式(1)和式(2)，得到混凝土的位移uc为：
锈蚀过程中，混凝土处于双向应力状态：即膨胀力产生的拉应力和预应力引起的压应力。混凝土所受的压应力，σ(y)为：
式中：Np为钢绞线的预应力；A为混凝土的截面面积；I为截面惯性矩；ep为钢绞线的偏心距；y为截面形心的高度。
双向应力状态下，混凝土的受力可表示为[21]
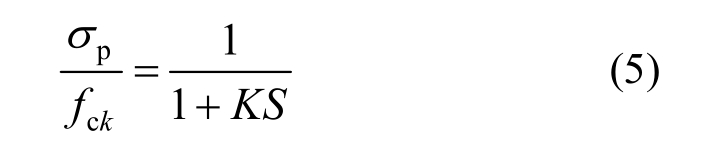
式中：
为双向应力状态下混凝土的抗拉强度；pσ为钢绞线位置处混凝土的压应力；fck为混凝土轴心抗压强度；ftk为混凝土轴心抗拉强度。
通过联立式(4)和式(5)，可得到双向应力状态下混凝土的抗拉强度ft。对于预应力混凝土，当拉应力超过双向应力状态下混凝土的抗拉强度时，混凝土内部产生微裂缝。本文假定内部微裂缝均匀、弥散地分布在开裂混凝土周围，进而引入一个刚度退化因子a，来考虑开裂混凝土的剩余刚度，其表达式为[22]：
其中：λ为材料参数，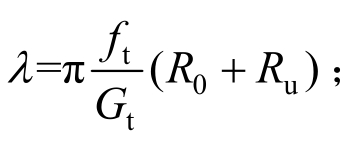
Gt为断裂能，Gt=0.88N/mm[20]；
为开裂混凝土的平均残余切应变；
为未开裂混凝土的平均切应变；Ec为混凝土的弹性模量。
混凝土开裂后变为各向异性材料，混凝土的径向弹性模量与切向弹性模量存在差异[20,22]。相应的径向应力和切向应力分别为：
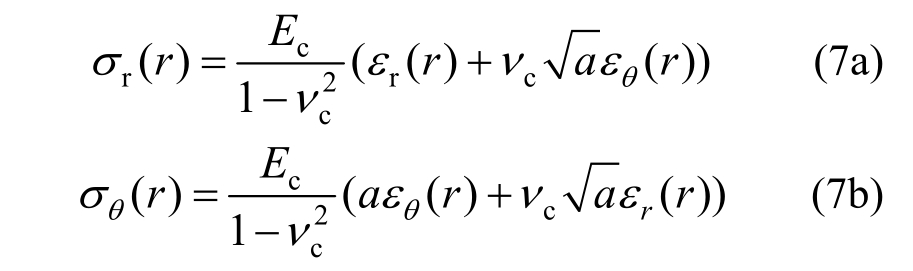
其中：r为开裂混凝土半径，
1ν和2ν分别为径向和切向的泊松比。
对于开裂混凝土，径向应力需满足以下平衡方程：
位移和应变的几何方程分别为
和
开裂混凝土的位移控制方程可写为：
求解式(9)，得到开裂混凝土的位移，u(r)为：
式中，b1(r)和b2(r)分别为相关参数。
将式(9)代入式(7)，式(7)中的径向应力和切向应力可重写为：
对于未开裂的外部混凝土，依旧可以利用弹性理论对其应力状态进行模拟。将未开裂混凝土模拟为厚壁圆筒环，基于圆环内压力轴对称情况，未开裂混凝土的切向将不存在位移。未开裂混凝土的径向应力，切向应力和径向位移分别为：
其中：t为未开裂混凝土半径，
为保护层厚度。
当裂缝尖端发展到Ru位置处时，式(12b)中的
等于双向应力状态下混凝土抗拉强度ft。由此，可取得Ru位置处的膨胀应力为：
开裂混凝土与未开裂混凝土交界面的位移和应力满足变形协调关系，即
b1(r)和b2(r)可表示为：
其中：
在[R0，Ru]区域内，式(6)中未开裂混凝土的平均切应变，
和开裂混凝土的平均残余切应变
分别为：
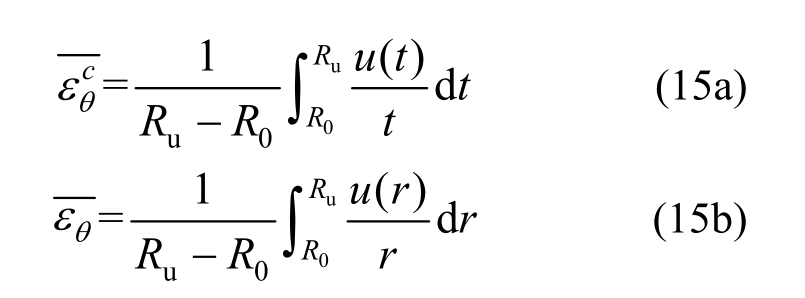
将式(15)代入式(6)，可以得到刚度退化因子，a。联立式(3)和式(10)，可以得到钢绞线锈蚀率ρ的表达式：
当裂缝扩展到混凝土表面时，保护层完全开裂。此时，Ru=Rc，进而求解式(16)可以得到保护层开裂的临界锈蚀率。
图8 裂缝扩展至混凝土表面
Fig.8 Crack propagates to concrete surface
保护层完全开裂后，混凝土表面可观测到可见裂缝。本文通过改变相应的边界条件，进而预测锈胀开裂从裂缝初始阶段到扩展阶段的全过程。保护层开裂后，裂缝在横断面呈现为梯形形态，如图 8所示。理论模型中厚壁圆筒的边界条件发生了改变，重新求解式(9)得：
式中，b3和b4为相关参数。
保护层开裂后，混凝土将不存在径向应力，边界条件可重新表示为：
求解式(18)可得参数b3和b4。混凝土表面的裂缝宽度可通过以下方程求得：
式中，
为混凝土表面的切应变。
联立式(17)和式(19)，得到混凝土表面的裂缝宽度为：
最后，通过联立式(3)和式(20)，得到了裂缝宽度和锈蚀率之间的关系。
综上所述，本文提出的预应力混凝土锈胀开裂预测模型可以考虑预应力、钢绞线锈蚀产物膨胀率和开裂混凝土剩余刚度等因素的影响。提高预应力和铁锈膨胀率会加速锈胀开裂过程，锈胀开裂计算对铁锈膨胀率和预应力等参数较为敏感。
利用本文提出的理论模型对本试验得到的锈胀裂缝宽度进行预测。模型中的部分参数如下：铁锈膨胀率和断裂能分别为2.78和0.088 N/mm。混凝土的弹性模量和泊松比分别为32.5 GPa和0.18。理论预测值和试验结果如图9所示。
由图9可知，预测结果的平均误差和标准差分别为10.98%和0.091，理论预测值与试验值较为吻合。预测误差可能是由于理论模型的简化，以及裂缝宽度和锈蚀率测量的不确定性等因素造成的。考虑到锈胀开裂的复杂性，相应的误差在可接受范围。综上所述，该模型可以合理地预测预应力混凝土的锈胀开裂过程。
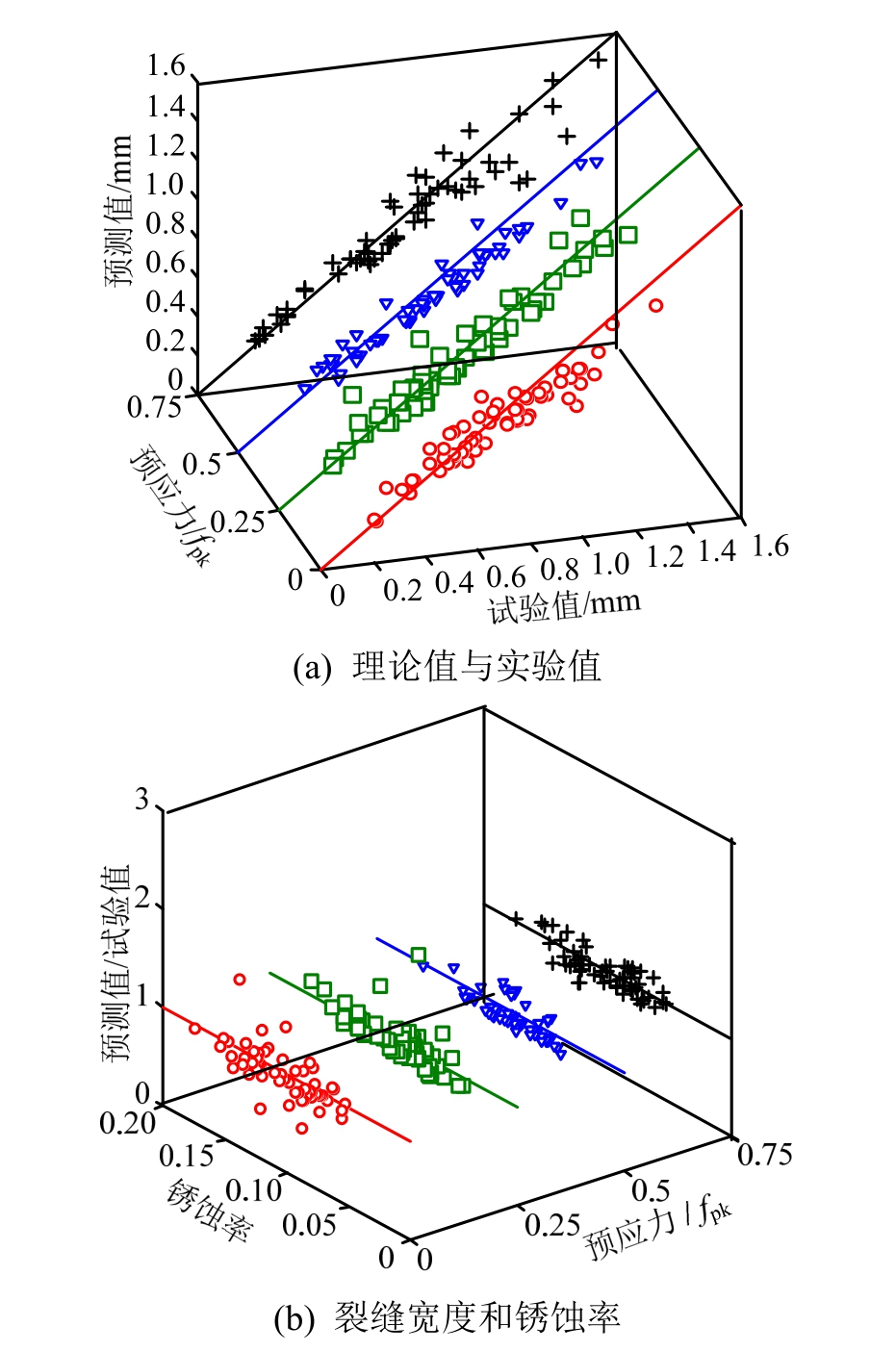
图9 模型验证
Fig.9 Model verification
本文试验研究了钢绞线锈蚀和预应力耦合作用下混凝土的开裂行为，分析了预应力钢绞线锈蚀产物的组成成分和膨胀率，建立了一个可以预测预应力混凝土锈胀开裂过程的理论模型。基于试验和理论分析，得到了以下结论：
(1) 预应力会加快锈胀开裂过程，当预应力达到钢绞线抗拉强度75%时，保护层开裂临界时间降低了22%，裂缝扩展速率增加了9%。
(2) 预应力的存在会增加锈蚀产物中氧化铁的含量，降低氢氧化铁的含量，但预应力的改变对钢绞线锈蚀产物膨胀率的影响不大，本文建议预应力钢绞线锈胀产物的膨胀率为2.78。
(3) 本文提出的理论模型可以合理地预测预应力混凝土锈胀开裂过程，锈胀开裂计算对预应力和铁锈膨胀率等参数较为敏感。
本试验的锈胀裂缝主要由快速通电锈蚀获得，这与自然环境下锈蚀引起的混凝土开裂可能存在差异性；此外，如何建立坑锈影响下预应力混凝土的锈胀开裂模型也有待进一步研究。
[1]Zhang W, Liu X, Gu X. Fatigue behavior of corroded prestressed concrete beams [J]. Construction and Building Materials, 2016, 106: 198－208.
[2]马亚飞, 王磊, 张建仁. 锈胀钢筋混凝土拱肋承载力试验与模拟 [J]. 工程力学, 2017, 34(7): 155－161.Ma Yafei, Wang Lei, Zhang Jianren. Experimental and numerical studies on reinforced concrete arch ribs with corrosion-induced cracks [J]. Engineering Mechanics.2017, 34(7): 155－161. (in Chinese)
[3] 张英姿, 范颖芳, 赵颖华. 混凝土保护层胀裂时刻钢筋锈蚀深度的理论模型[J]. 工程力学, 2010, 27(9):122－127.Zhang Yingzi, Fan Yingfang, Zhao Yinghua. Theoretical model to determine the depth of reinforcement corrosion at concrete cover cracking [J]. Engineering Mechanics,2010, 27(9): 122－127. (in Chinese)
[4]王治, 金贤玉, 付传清, 等. 基于损伤的钢筋混凝土锈胀开裂模型[J]. 建筑结构学报, 2014, 35(9): 115－122.Wang Zhi, Jin Xianyu, Fu Chuanqing, et al. Concrete cracking model for rust expansion based on damage [J].Journal of Building Structures, 2014, 35(9): 115－122.(in Chinese)
[5]Cao C, Cheung M M S, Chan B Y B. Modelling of interaction between corrosion-induced concrete cover crack and steel corrosion rate [J]. Corrosion Science,2013, 69: 97－109.
[6]Liu Y. Modeling the time-to-corrosion cracking in chloride contaminated concrete structures [J]. ACI Material Journal, 1998, 95(6): 675－681.
[7]Zhao Y, Ren H, Dai H, et al. Composition and expansion coefficient of rust based on X-ray diffraction and thermal analysis [J]. Corrosion Science, 2011, 53(5): 1646－1658.
[8]Li F, Yuan Y, Li C Q. Corrosion propagation of prestressing steel strands in concrete subject to chloride attack [J]. Construction and Building Materials, 2011,25(10): 3878－3885.
[9]王晓舟, 金伟良, 延永东. 混凝土结构锈胀开裂预测的路径概率模型 [J]. 浙江大学学报(工学版), 2010,44(6): 1191－1196.Wang Xiaozhou, Jin Weiliang, Yan Yongdong. Path probability model of corrosion-crack assessment for existing reinforced concrete structures [J]. Journal of Zhejiang University (Engineering Science), 2010, 44(6):1191－1196. (in Chinese)
[10] 吴灵杰, 寇新建, 周拥军, 等. 既有钢筋混凝土码头保护层锈胀开裂计算时长对比 [J]. 哈尔滨工业大学学报, 2016, 48(12): 51－55.Wu Lingjie, Kou Xinjian, Zhou Yongjun, et al.Propagation assessment of existing concrete dock based on concrete cover corrosion-crack [J]. Journal of Harbin Institute of Technology, 2016, 48(12): 51－55. (in Chinese)
[11] Khan I, François R, Castel A. Prediction of reinforcement corrosion using corrosion induced cracks width in corroded reinforced concrete beams [J]. Cement and Concrete Research, 2014, 56: 84－96.
[12] Bažant Z. Physical model for steel corrosion in concrete sea structures-theory [J]. Journal of the Structural Division, 1979, 105(6): 1155－1166.
[13] 毛江鸿, 陈佳芸, 崔磊, 等. 氯盐侵蚀钢筋混凝土锈胀开裂监测及预测方法 [J]. 建筑材料学报, 2016, 19 (1):59－64.Mao Jianghong, Chen Jiayun, Cui Lei, et al. Monitoring and predicting method for reinforced concrete expansion and cracking induced by chloride erosion [J]. Journal of Building Materials, 2016, 19 (1): 59－64. (in Chinese)
[14] Michel A, Pease B J, Peterová A, et al. Penetration of corrosion products and corrosion-induced cracking in reinforced cementitious materials: Experimental investigations and numerical simulations [J]. Cement and Concrete Composites, 2014, 47: 75－86.
[15] Dai L, Wang L, Zhang J, et al. A global model for corrosion-induced cracking in prestressed concrete structures [J]. Engineering Failure Analysis, 2016, 62:263－275.
[16] 李文钊, 陈晓楠, 王波, 等. 模拟海岛环境中弹药元件锈蚀产物红外光谱分析 [J]. 腐蚀与防护 [J]. 2013,34(3): 236－238.Li Wenzhao, Chen Xiaonan, Wang Bo, et al. IR analysis of corrosion products on amunition elements in simulate island environments. Corrosion and Protection [J]. 2013,34(3): 236－238. (in Chinese)
[17] Raman A, Kuban B, Razvan A. The application of IR spectroscopy to the study of atmospheric rust systems: I standard spectra and illustrative applications to identify rust phases in natural corrosion [J]. Corrosion Science,1991, 32(12): 1295－1306.
[18] Jaffer S J, Hansson C M. Chloride-induced corrosion products of steel in cracked-concrete subjected to different loading conditions [J]. Cement and Concrete Research, 2009, 39(2): 116－125.
[19] Zhang R, Castel A, François R. Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process [J]. Cement and Concrete Research, 2010, 40(3): 415－425.
[20] Pantazopoulou S J, Papoulia K D. Modeling cover-cracking due to reinforcement corrosion in structures [J]. Journal of Engineering Mechanics, 2001,127(127): 342－351.
[21] Tasuji M E, Slate F O, Nilson A H. Stress-strain response and fracture of concrete in biaxial loading [J]. Journal of the American Concrete Institute, 1978, 75(7): 306－312.
[22] Li C Q, Yang S T. Prediction of concrete crack width under combined reinforcement corrosion and applied load [J]. Journal of Engineering Mechanics, 2011,137(11): 722－731.
EXPANSION OF PRESTRESSED STRAND CORROSION PRODUCTS AND CONCRETE CRACKING PREDICTION