大量混凝土类材料动态压缩实验表明，在动载下，随着应变率的提高，混凝土类材料的抗压强度较准静态情况有明显的提高，这种现象被称为混凝土类材料的应变率效应，通常用混凝土动态强度峰值与准静态强度的比值(动态强度放大因子DIF)表示。DIF的测量有多种方法，Bresler和Bertero[1]、Takeda和 Tachikawa[2]利用液压试验机对试件进行加载，应变率可达到1 s-1；Hughes和Gregory[3]，Watstein[4]和 Hughes[5]通过落锤试验对试件进行加载，得到应变率10 s-1以下的动态压缩实验数据；Ross等[6―8]和 Malvern等[9]使用霍普金森压杆获得应变率为10 s-1～103s-1的动态压缩实验数据；Grote等[10]采用准静态强度为40 MPa～180 MPa的混凝土和砂浆，利用霍普金森压杆获得应变率为 250 s-1～1700 s-1的动态压缩实验数据。一系列实验数据表明，在高应变率下，DIFs随应变率增大的速率大于低应变率情况，文献[6－8]显示在应变率处于10 s-1～ 102s-1的范围内，混凝土类材料的DIFs随应变率变化曲线有一个转换应变率，超过这个转换应变率时，DIFs曲线会急剧上升。
对混凝土类大型结构在爆炸冲击荷载下的动态响应进行实验研究需要过高时间经济成本，而数值模拟无疑是一种经济省时的方法。在数值模拟中，准确输入混凝土类材料的真实应变率效应DIFε˙曲线对于研究混凝土结构在爆炸冲击等动载下的受力性能分析十分重要。
基于Bischoff和Perry[11]对1991年前前人实验研究的总结，CEB-FIP[12]给出了DIF随应变率变化的推荐公式，该公式已经广泛应用于数值模拟的材料模型中，但由于 1) 该公式的拟合是基于较陈旧的实验数据，实验设备和实验手段有限，高应变率下的实验数据不足；2) CEB[12]推荐公式是对混凝土类材料动态抗压实验获得DIFs数据的直接拟合，未去除动态抗压实验中试件包含的惯性效应，直接作为数值模拟的输入曲线会高估材料的抗力[13]。
本文通过收集 1990年以后最新的实验数据，并基于LS-DYNA软件对一系列SHPB实验所得动态强度放大因子DIFs进行惯性效应剥离，得到了混凝土类材料真实应变率效应引起的动态强度放大因子DIFε˙。分析了试件尺寸和准静态强度对惯性效应引起的动态强度放大因子DIFi的影响，分段对数据进行公式拟合，得到材料的真实应变率效应曲线。将本文拟合曲线、已有半经验公式[14]及动态抗压实验结果剥除惯性效应后的DIFε˙直接对比，可以看出，在高应变率下，本文拟合曲线比已有半经验公式[14]能更好地反映材料真实应变率效应；将数值模拟时输入本文拟合曲线与输入 CEB推荐公式的输出结果分别与实验结果对比，结果显示，本文拟合曲线能更好地反映混凝土类材料的真实应变率效应。
本节收集了 1990年以来最新的实验数据，通过不同形状，不同尺寸试件之间的强度转换，修正了由于准静态实验试件与动态实验试件之间试件尺寸差异带来的DIFs值误差，进一步与现有Bischoff和Perry[11]收集的1990年以前实验数据进行对比。
由于实验数据来自于不同文献，一般情况下，混凝土动态抗压实验采用圆饼状试件，用于测量混凝土准静态强度的试件形式却不尽相同，有的为立方体，有的为圆柱体，这也是早期 Bischoff和Perry[11]收集的实验数据存在很大离散性的一个原因。1966年，内维尔在大量资料研究的基础上，建立了目标试件强度与150 mm (6 in)的立方体试件强度之间的关系式，如式(1)所示[15]：
式中：fc为目标试件准静态抗压强度；fc6为150 mm(6 in)的立方体试件准静态抗压强度；v为目标试件的体积；h为试件的高度；d为试件的最大横向尺寸，该公式中所有尺寸均采用英制单位。
将式(1)进行转换可以得到任意两种不同形状不同尺寸试件之间准静态强度的转换关系式：
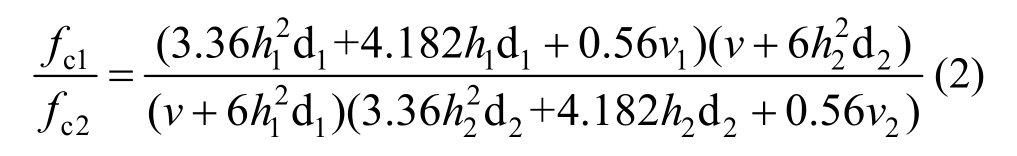
大部分实验数据采用的准静态测试试件都为直径与动态抗压实验试件长度相等，高度与动态抗压实验试件直径相等的圆柱体，这样可以保证准静态实验的试件与动态实验试件的强度测量结果最小程度上受试件尺寸影响，从而得到更准确的DIFs值。本文在计算DIFs时，将所有与动态实验测试试件关系不满足以上关系的准静态试件换算成与动态实验测试试件满足以上关系的情况。
1991年，Bischoff和Perry[11]分析比较了前人对混凝土类材料在不同应变率下抗压特性的诸多研究成果，总结出了DIF与应变率之间的关系(本文所定义的DIFs)，如图1(a)。由图1(a)可知，DIF随着应变率的增加而增大，且在低应变率时，这种增大较缓，在应变率位于 10 s-1～100 s-1之间处，DIF的增长曲线骤然变陡，出现转换应变率。欧洲国际混凝土委员会规范(CEB-FIP)[12]借鉴 Bischoff和Perry[11]的工作，给出了混凝土类材料的DIF与应变率关系的推荐公式，并将转换应变率定为30 s-1：
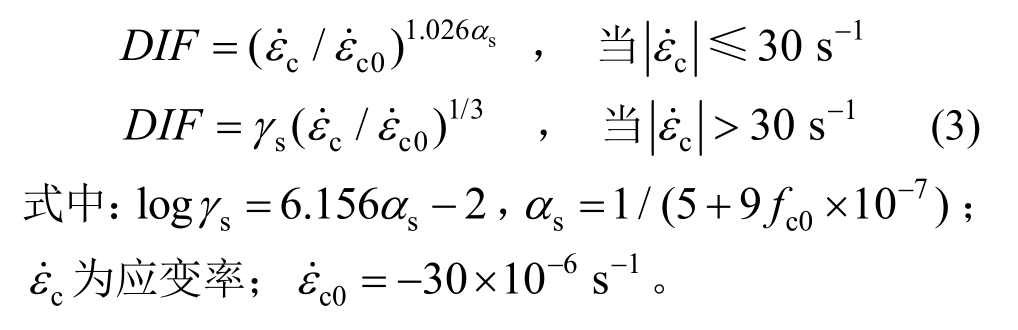
以上公式作为混凝土类材料应变率效应曲线，广泛运用于数值模拟中，但CEB推荐公式参考的实验数据过于老旧，高应变率情况的实验数据不足。
近二十年来，随着实验装置和实验手段及数据处理方法的不断进步，混凝土类材料动态力学性能研究方法取得了较多成果，测试精度也有所提高。本文参考了近二十年来关于混凝土类材料的动态抗压实验的文献[10―11,16―22](实验多针对新型材料混凝土，故选取其中的对照组实验数据—普通素混凝土进行研究)，对实验数据进行了整理。
将本文收集的近年实验数据经过式(2)转换后去除了准静态实验试件与动态抗压实验试件尺寸差异带来的影响，得到的DIFs值绘于图 1(b)，图1(b)较图1(a) Bischoff和Perry[11]的实验数据出现了更多应变率高于100 s-1的加载情况，因此，采用图1(b)数据拟合应变率曲线可以更好地反映混凝土材料高应变率情况下的DIFs。
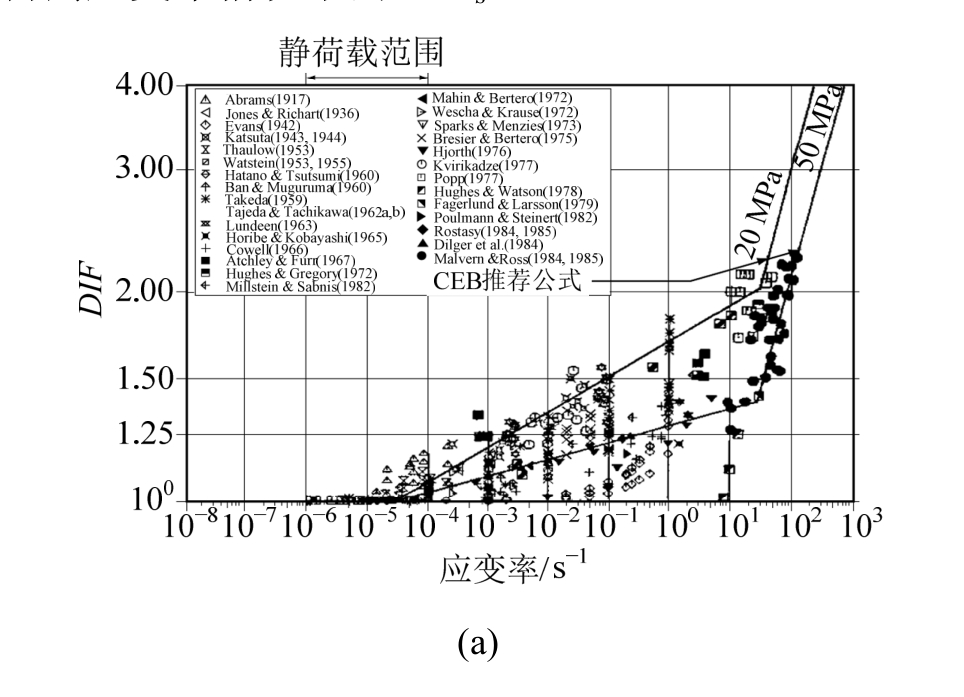
图1DIFs与应变率对数关系图
Fig.1DIFsobtained from present tests.
本节首先介绍了一种利用数值模拟剥离惯性效应的理论方法，在保证模拟准确性的前提下，建立简化模型，对上节实验数据进行惯性效应剥离，并分析了影响试件惯性效应的因素。
实验得到的混凝土类试件动态压缩强度提高不代表材料本身真实的应变率效应，而是试件的动态压缩强度提高，其中包含惯性效应作用。
Hao等[13]提出一种简单有效的惯性效应剥离方法，将由于试件横向惯性引起的应变率强化效应剥除，简要介绍如下：
实验得到的动态强度放大因子DIFs包含：
其中，fcd为材料动态抗压强度。Δfd是由于动载引起的强度提高，包括材料应变率效应及惯性效应，两者都是应变率的函数，可以认为两者是独立不耦合的[1]，则：
其中：Δfε˙为材料应变率效应引起的动态强度提高；Δfi为由于惯性效应引起的动态强度提高。将式(5)代入式(4)，得：
对于应变率不敏感材料，Δfε=0，此时的DIFs值即为DIFi：
在数值模拟时将材料应变率效应曲线输入设置为恒值1，得到的输出结果即为DIFi。材料真实动态强度放大因子计算如下：
完整的SHPB有限元模型包括压杆和试件，该完整模型计算耗时长。Hao等[13]提出一种简化模型，即忽略压杆而仅取试件部分建模，试件一端固定纵向位移，另一端采用速度加载，边界条件和有限元模型分别如图2和图3所示，单元类型采用3D Solid 164，材料模型采用 MAT-CONCRETE-DAMAGEREL3，材料参数采用72号模型，参数自动生成。该模型应用较为简单，只需输入fc即可生成所有参数，并且广泛应用于SHPB实验、爆炸冲击荷载下混凝土类材料动态响应的数值模拟中。根据不同实验的实际尺寸建模，直径在20 mm以下的试件采用1 mm×1 mm的单元尺寸，直径在20 mm以上的试件采用2 mm×2 mm的单元尺寸。
图2 试件边界条件示意图
Fig.2 Boundary condition
图3 有限元模型图
Fig.3 Finite element model
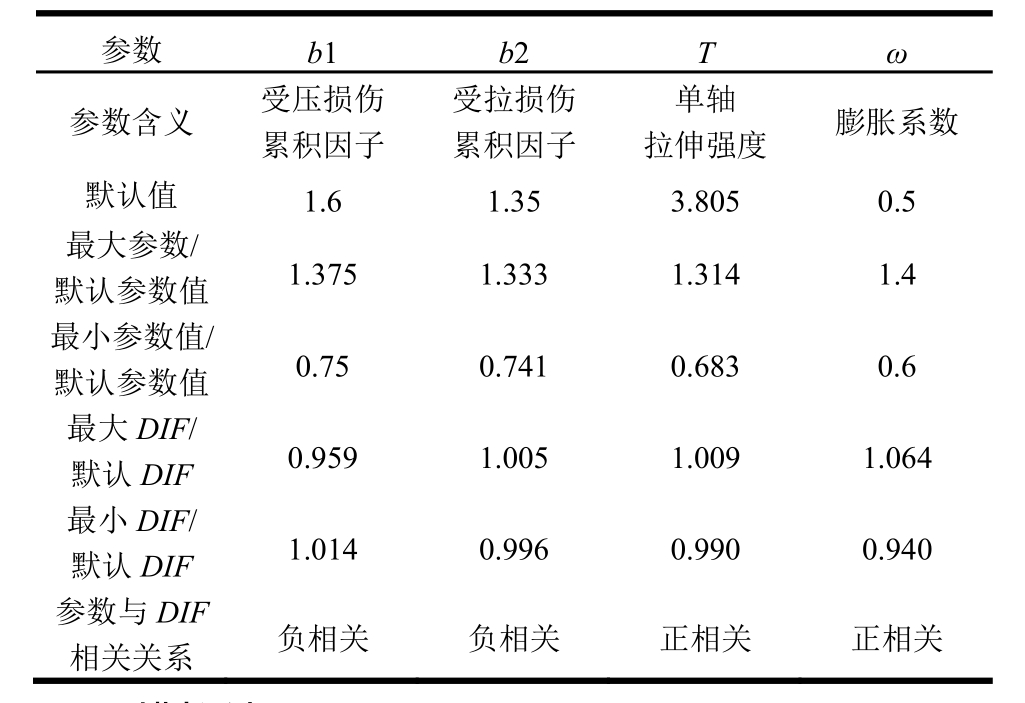
Release 3版本的K&C模型在输入混凝土材料准静态强度后会自动生成其他参数，分别讨论参数b1、b2、T、对数值模拟输出动态强度放大因子DIF的影响。各参数对数值模拟计算所得动态强度放大因子DIF的影响见表1。
由表1可以看出，受压损伤累积因子和膨胀系数对DIF的影响较大，且DIF与受压损伤累积因子呈负相关关系，与膨胀系数呈正相关关系。受拉损伤累积因子和单轴拉伸强度对DIF几乎没有影响。
表1 参数敏感性分析
Table 1 Analysis of parameters Sensitivity
参数b1b2Tω参数含义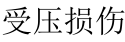
受拉损伤累积因子单轴拉伸强度 膨胀系数默认值 1.6 1.35 3.805 0.5最大参数/默认参数值 1.375 1.333 1.314 1.4最小参数值/默认参数值 0.75 0.741 0.683 0.6最大DIF/默认DIF0.959 1.005 1.009 1.064最小DIF/默认DIF1.014 0.996 0.990 0.940参数与DIF相关关系 负相关 负相关 正相关 正相关
图4为d=0.01 m，准静态强度为45 MPa试件的DIFi与应变率的关系图，由图可知，DIFi随应变率增大而增大。由于实验数据过于庞大，设定当惯性效应引起的DIFi小于1.05时，已足够小，可忽略DIFi对DIFs所起的作用，不对其按2.1节进行惯性效应剥离，此时对应的应变率即为临界应变率。
图4d=0.01 m试件DIFi与应变率关系图
Fig.4DIF-ε˙ of 0.01 m-diameter specimen
以d=0.01 m的试件举例，根据数值模拟结果，d=0.01 m 试件的DIFi达到临界值 1.05时的ε˙为59 s-1，采用2‰作为试件破坏应变[23]，试件破坏时波在试件内传播来回次数n计算如下：
其他尺寸的临界应变率计算结果见表2。
表2 混凝土试件临界应变率及对应n
Table 2 Critical strain rate andnof concrete specimen
试件d/m 长径比 临界应变率/s-1n0.01 0.5 59 6.27 0.016 0.5 35 6.61 0.02 0.5 28 6.61 0.037 0.5 16 6.25 0.05 0.5 12.6 5.69
由表2可以看出，虽然不同尺寸的试件临界应变率不同，但达到临界应变率时波在试件内传播的次数n都是6左右，即惯性效应对试件的影响与波在试件内传播次数有关。由于试件直径基本上都小于0.05 m，由表1中临界应变率可知，当应变率小于12.6 s-1时，可忽略DIFi的作用，因此对应变率小于12.5的实验数据不做惯性效应剥离处理，即视其DIFs为DIFε˙。将图 1(b)的数据按上述原则经过惯性效应剥离后得到的DIFε˙与应变率对数关系如图5所示。
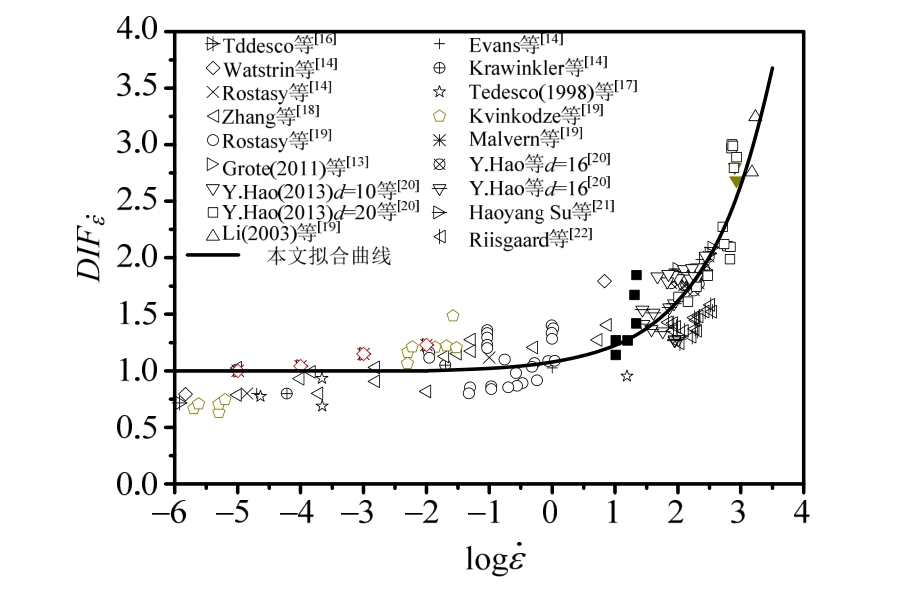
图5DIFε˙与应变率对数关系图
Fig.5 Curve ofDIFε˙-logε˙
由图5可知，当应变率小于10-2s-1时，DIFε˙基本上在1左右徘徊。DIFε˙理论上是大于1的，这是由于在准静态条件下混凝土中损伤是沿着材料中的“弱面”演化直至破坏的，因此其强度相对较低,在高应变率作用下，由于局部效应明显，使得损伤来不及找到整个材料中的“弱面”，只能在此局部“弱面”里演化，而且随着应变率的提高，此局部区域愈加小，“弱面效应”愈加不明显，宏观上就显示出压缩强度的提高[24]。但由于混凝土材料在准静态和较低应变率条件下的压缩强度变化不大，其试验误差远大于理论增加值，出现了部分实验结果小于1的情况，故将DIFε˙小于1的情况视为1。
采用与Xu和Wen[14]提出的半经验公式相同的公式形式，对去除惯性效应后的实验数据进行曲线拟合。
2.5.1 半经验公式[14]
半经验公式基于以下两个假设：1) 混凝土材料在动态抗拉实验中的强度提高不受横向惯性效应影响；2) 对于同一试件，在相同应变率下，材料应变率效应引起的受压动态强度放大因子DIFε˙和受拉动态强度放大因子DIFt有一定比例关系。
根据假设1)，由前人动态抗拉实验数据[14]可直接得到混凝土类材料受拉动态强度放大因子DIFt的拟合曲线公式如下：
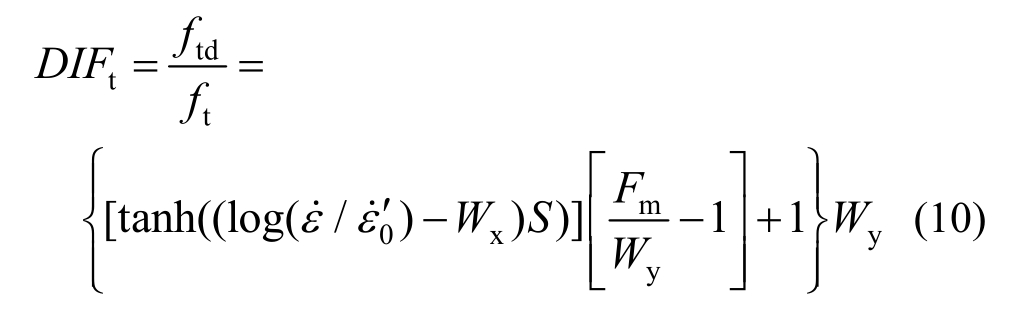
式中：ftd为材料动态受拉强度；ft为材料准静态受拉强度，实验中若没有数据，按
计算；
和S由实验获得，
′为参考应变率，一般情况下取
Wy=5.5。材料应变率效应引起的抗压动态强度放大因子DIFε˙计算如下：
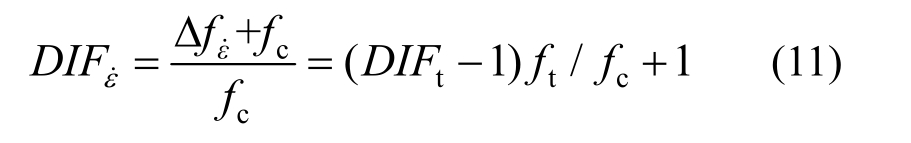
2.5.2 实验数据拟合
由图5可知，剥除惯性效应后，当应变率大于10-2s-1时，并没有出现如CEB推荐公式[12]一样的在30 s-1处出现明显转折，而是出现光滑上升的趋势。原因是图1(b)显示，当应变率大于30 s-1时，DIFs出现急剧的上升，但是由图4可知，DIFi也出现了同样的情况，所以从DIFs中除去DIFi得到的DIFε˙并没有在30 s-1的地方出现急剧上升，但图4显示DIFi在大于 100 s-1的情况下，上升趋势没有图1(b)中DIFs那么明显，故在高应变率下，DIFε˙仍呈现较大程度的上升趋势。为了与应变率小于10-2s-1的情况衔接，设置当应变率为 10-2s-1时DIFε˙为固定值1，参照Xu和Wen[14]半经验公式中计算DIFε˙的反三角函数形式，对应变率对数处于-2～3.5的范围内数据进行曲线拟合，如下：
当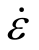
≤ 10-2时：
当
时：
2.6.1 试件尺寸对DIFi的影响
图6描绘了Hao等[20]实验中两种不同尺寸混凝土试件的DIFs、DIFi及DIFε˙。试件的准静态强度为45 MPa，试件长径比为0.5，直径分别为10 mm和20 mm，应变率范围为20 s-1～400 s-1。
由图6可知，在相同应变率下，混凝土试件的DIFs随着试件尺寸的增大而增大；将DIFs中的DIFi去除后，两种尺寸的DIFε˙结果十分接近，且DIFε˙增长趋势较平缓，说明在中高应变率下，混凝土材料真实应变率效应DIFε˙与试件尺寸关系不大，随应变率增加的提高程度也不大，这是因为惯性效应的去除，将应变率增加造成的抗压强度提高大大降低了；DIFi也随试件尺寸增大而增大，与惯性效应产生的原理[27]一致：惯性效应的产生，实质上是由于泊松效应的存在，轴向的加速度会导致径向加速度产生，而试件内部径向加速度的分布不均匀会使得外围部分对内核部分产生向内的惯性力，试件直径越大，这一约束力越大，类似于动载下围压对混凝土抗压强度的提高，围压越大，DIFi越大，故试件尺寸越大，DIFi越大。
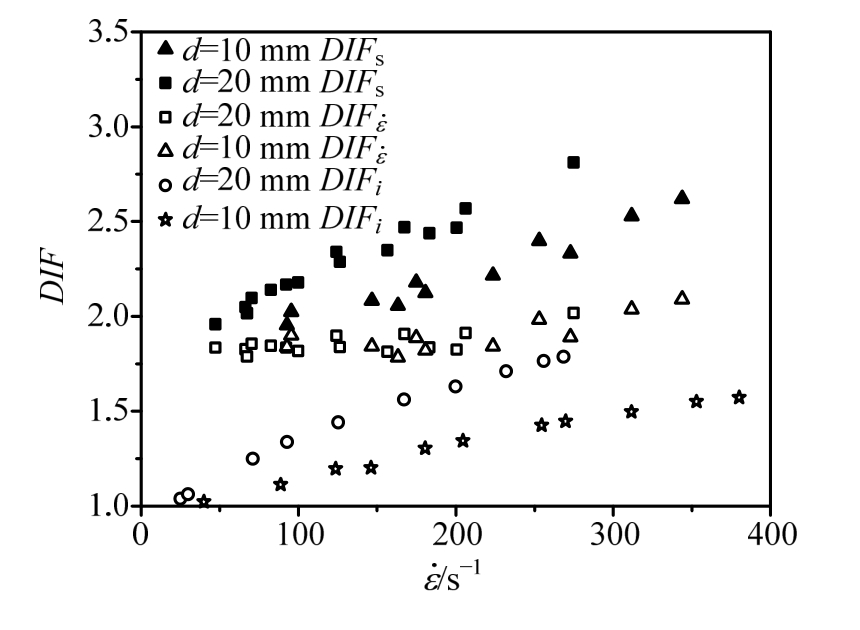
图6 试件尺寸对DIF的影响
Fig.6 The influence of specimen size onDIF
2.6.2 材料准静态强度对DIFi的影响
图7给出了具有相同尺寸、不同准静态强度的混凝土试件数值模拟得到的DIFi值。由图可知，在低应变率，尤其是接近0的时候两者的DIFi几乎一致，随着应变率提高，准静态强度差异引起的DIFi值的差异随着应变率的增加而增加。准静态强度越低的试件，DIFi随应变率增加的增加幅度越大。
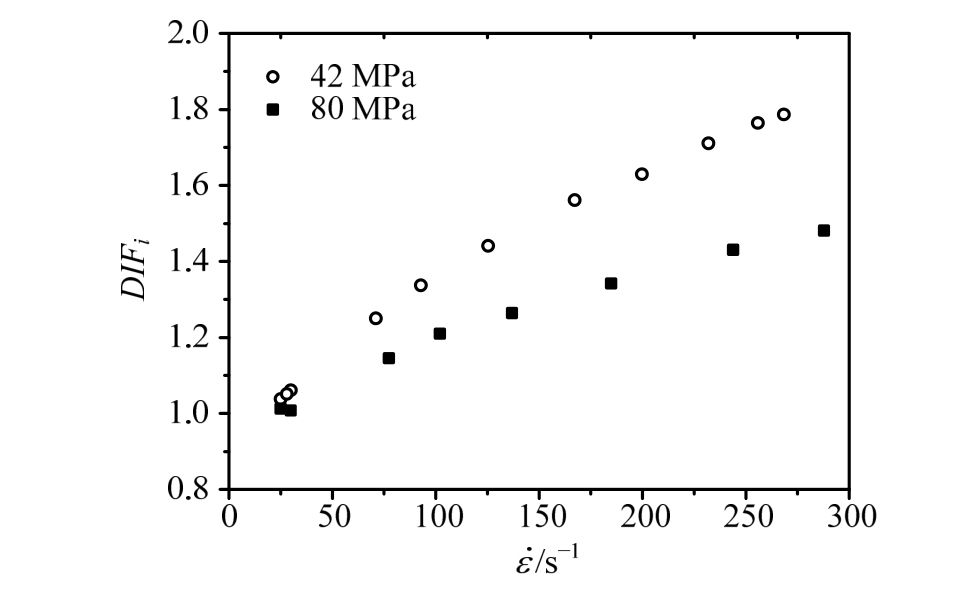
图7 混凝土准静态抗压强度对DIFi的影响
Fig.7 The influence of concrete quasi-static strength onDIFi
这是由于混凝土准静态强度越高，材料的初始缺陷就越少，与围压作用效果类似，惯性效应可以降低初始缺陷(裂纹、毛孔、破坏界面等)的影响。故在动态荷载下，惯性效应引起的抗压强度提高幅度对于低准静态强度来说会比高准静态强度混凝土更明显。
本节从两个方面验证 2.4节拟合曲线的优越性：1) 将本文拟合曲线直接跟由半经验公式[14]及实验数据剥离惯性效应后得到的DIFε˙对比 1)数值模拟时材料的应变率效应曲线分别输入本文拟合曲线和CEB推荐公式，对比两者的输出结果与DIFs的符合程度。
图8直接将本文拟合曲线与半经验公式[14]曲线及本文实验数据处理得到的DIFε˙进行对比，发现在低应变率下，两条曲线重合较好，而在高应变率下，半经验公式[14]会低估材料真实应变率效应，这是因为半经验公式[14]采用的实验数据达到的最高应变率有限，故在更高应变率下，本文拟合曲线能更好地反映材料真实的DIFε˙。
图8 本文曲线与半经验公式[14]对比
Fig.8 Comparison of new curve and semi-empirical formulas[14]
分别对混凝土试件的SHPB实验和弹体贯穿混凝土/钢复合靶板实验进行数值模拟，对比输入本文拟合曲线和 CEB推荐公式的输出结果，验证本文曲线相对于CEB公式的优越性。
3.2.1 SHPB实验
对图6中d=20 mm的试件SHPB实验进行数值模拟，利用Ansys建模时，分别在k文件中的K&C模型材料应变率效应曲线输入式(12)拟合曲线和CEB推荐公式(K&C模型默认)，将数值模拟输出的抗压动态强度放大因子DIFm与DIFs进行对比，结果如图9。由图9可知，在应变率较低(应变率对数小于 1.6 s-1)时，两种拟合曲线的输出结果基本重合，当应变率对数大于1.6 s-1时，随着应变率的增大，输入本文拟合曲线的输出结果逐渐小于输入 CEB时的输出结果，且与实验结果更加吻合。
图9 本文曲线与CEB公式对比
Fig.9 Comparison of new curve and CEB
3.2.2 弹体贯穿复合靶板实验
基于K&C模型，对团队Wu等[28]实验中弹体贯穿300 mm厚靶体实验进行数值模拟。将有限元计算结果与Wu等[28]实验中靶体破坏情况进行了对比。
因为靶体具有双轴对称的特性，为节约计算时间及空间，数值模拟采用1/4对称模型，如图10。弹体和复合靶体都采用3D Solid 164单元，钢筋采用梁单元，为了在保证计算精度的同时节约计算时间，采取了局部网格加密方法保证计算精度，采用面与面侵蚀接触算法计算弹与靶的接触。弹体视为刚体，钢筋和后覆钢板采用理想弹塑性材料模型，弹性模量为 210 GPa，屈服强度为 400 MPa，混凝土材料采用常用的K&C模型。
图10 有限元模型
Fig.10 Finite element model
数值模拟中混凝土材料应变率效应曲线分别输入本文改进的应变率效应曲线和CEB推荐公式，模拟结果见表3。
表3 本文曲线与CEB推荐公式的数值模拟结果对比
Table 3 Comparison of Numerical simulation results between CEB and new curve
类别 开坑深度 震塌深度 开坑宽度 震塌宽度实验 55 55 300 380输入CEB 42 68 180 410输入本文曲线 62 59 215 410
由表2记录的混凝土靶体开坑震塌尺寸可知，输入本文拟合曲线比输入 CEB推荐公式的输出结果与实验吻合更好。
本文通过收集 1990年以来最新的混凝土类材料动态抗压实验数据，并利用数值模拟将其惯性效应去除，得到DIFε˙与应变率对数的关系，发现：
(1) 去除惯性效应后的应变率效应曲线呈现光滑上升趋势。
(2) 对于同一种材料，试件的DIFs和DIFi都随试件尺寸的增大而增大，且去除DIFi后，混凝土类材料的DIFε˙与尺寸无关。
(3) 在同一应变率下，混凝土类材料准静态强度越大，材料的DIFi随应变率增长的增长幅度越小。
(4) 参考半经验公式[14]，采用反三角函数形式对DIFε˙与应变率对数的关系进行曲线拟合，该曲线较半经验公式[14]能更好地反映高应变率下的DIFε˙。
(5) 数值模拟时分别输入新的拟合曲线和CEB推荐公式，输出结果显示本文拟合曲线能更好地反映材料真实的应变率效应，验证了本文拟合曲线的优越性。
[1]Bresler B, Bertero V V. Influence of high strain rate and cyclic loading of unconfined and confined concrete in compression [C]// the 2nd Canadian Conference on Earthquake Engineering. Hamilton, Ont. McMaster University Bookstore, 1975: 1―13.
[2]Takeda J, Tachikawa H. The mechanical properties of several kinds of concrete at compressive, tensile, and flexural tests in high rates of loading [J]. Transactions of the Architectural Institute of Japan, 1962, 77: 1―6.
[3]Hughes B P, Gregory R. Concrete subjected to high rates of loading in compression [J]. Magazine of Concrete Research, 1972, 24(78): 25―36.
[4]Watstein D. Effect of straining rate on the compressive strength and elastic properties of concrete [J]. ACI Journal Proceedings, 1953, 49(4): 729―744.
[5]Hughes B P, Watson A J. Compressive strength and ultimate strain of concrete under impact loading [J].Magazine of Concrete Research, 1978, 30(105): 189―199.
[6]Ross C A, Tedesco J W. Split-Hopkinson pressure-bar tests on concrete and mortar in tension and compression[J]. Materials Journal, 1989, 86(5): 475―481.
[7]Ross C A, Tedesco J W, Kuennen S T. Effects of strain rate on concrete strength [J]. Materials Journal, 1995,92(1): 37―47.
[8]Ross C A, Jerome D M, Tedesco J W, et al. Moisture and strain rate effects on concrete strength [J]. Materials Journal, 1996, 93(3): 293―300.
[9]Malvern L E, Jenkins D A, Tang T, et al. Dynamic compressive testing of concrete [C]// Proceedings of 2nd symposium on the Interaction of Non-nuclear Munitions with Structures. Florida, USA. 1985: 194―199.
[10] Grote D L, Park S W, Zhou M. Dynamic behavior of concrete at high strain rates and pressures: I.experimental characterization [J]. International Journal of Impact Engineering, 2001, 25(9): 869―886.
[11] Bischoff P H, Perry S H. Compressive behavior of concrete at high-strain rates [J]. Material Structure, 1991;24(6): 425―450.
[12] CEB-FIP Model Code 1990, Bulletin D’ Information No.213/214 [S]. Lausanne, Switzerland: Committee International du Beton, 1993.
[13] Hao H, Hao Y, Li Z X. Numerical quantification of factors influencing high-speed impact tests of concrete material [J]. Advances in Protective Structures Research,2012, 1: 97―130.
[14] Xu H, Wen H M. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials[J]. International Journal of Impact Engineering, 2013,60: 76―81.
[15] 辛雁清. 混凝土圆柱体试件和立方体试件抗压强度关系的分析[J]. 中国水能及电气化, 2015 (7): 59―62.Xin Yanqing. Analysis of compressive strength relationship between concrete cylinder specimen and cube specimen [J]. China Mater & Electrification,2015(7): 59―62. (in Chinese)
[16] Tedesco J W, Powell J C, Ross C A, et al. A strain-ratedependent concrete material model for ADINA [J].Computers & Structures, 1997, 64(5/6): 1053―1067.
[17] Tedesco J W, Ross C A. Strain-rate-dependent constitutive equations for concrete [J]. Journal of Pressure Vessel Technology, 1998, 120(4): 398―405.
[18] Zhang M, Wu H J, Li Q M, et al. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part I: Experiments [J]. International Journal of Impact Engineering, 2009, 36(12): 1327―1334.
[19] Li Q M, Meng H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures, 2003, 40(2): 343―360.
[20] Hao Y, Hao H, Jiang G, et al. Experimental confirmation of some factors influencing dynamic concrete compressive strengths in high-speed impact tests [J].Cement and Concrete Research, 2013, 52: 63―70.
[21] Su H, Xu J, Ren W. Mechanical properties of ceramic fiber-reinforced concrete under quasi-static and dynamic compression [J]. Materials & Design, 2014, 57: 426―434.
[22] Riisgaard B, Ngo T, Mendis P, et al. Dynamic increase factors for high performance concrete in compression using split Hopkinson pressure bar [C]// Proceedings of the International Conference of Fracture Mechanics of Concrete and Concrete Structures. Ia-Framcos, Catania,Italy, 2007: 1―4.
[23] 杜修力, 窦国钦, 李亮, 等. 纤维高强混凝土的动态力学性能试验研究[J]. 工程力学, 2011, 28(4): 138―144.Du Xiuli, Dou Guoqin, Li Liang, et al. Experimental study on dynamic mechanical properties of fiber reinforced high strength concrete [J]. Engineering Mechanics, 2011, 28(4): 138―144. (in Chinese)
[24] 李潇, 方秦, 孔祥振, 等. 砂浆材料SHPB实验及惯性效应的数值模拟研究[J]. 工程力学, 2018, 35(7), 187―193.Li Xiao, Fang Qin, Kong Xiangzhen, et al. SHPB test and numerical investigation on the inertial effect of mortar material [J]. Engineering Mechanics, 2018, 35(7),187―193. (in Chinese)
[25] 沈蒲生, 梁兴文. 混凝土结构设计原理[M]. 北京: 高等教育出版社, 2012.Shen Pusheng, Liang Xinwen. Design principle of concrete structure [M]. Beijing: Higher Education Press,2012. (in Chinese)
[26] 高光发. 动态压缩下混凝土应变率效应压力与横向效应的影响与校正[C]. 第十一届全国爆炸力学学术会议论文全集, 2016.Gao Guangfa. Influence and revision of transverse inertia effect and pressure hardening effect on strain-rate hardening effect of compressive strength of concrete [C].Proceedings of 11th National Conference on Explosion Mechanics, 2016. (in Chinese)
[27] Forrestal M J, Wright T W, Chen W. The effect of radial inertia on brittle samples during the split Hopkinson pressure bar test [J]. International Journal of Impact Engineering, 2007, 34(3): 405―411.
[28] Wu H, Fang Q, Peng Y, et al. Hard projectile perforation on the monolithic and segmented RC panels with a rear steel liner [J]. International Journal of Impact Engineering, 2015, 76: 232―250.
MODIFICATION OF DIF-STRAIN RATE CURVE OF CONCRETE-LIKE MATERIALS IN NUMERICAL SIMULATION OF SHPB EXPERIMENTS