在我国，风力发电技术发展十分迅速，风电场建设已经逐渐由平坦内陆地区转向复杂山地地区。常用的商用风能资源评估软件，如WAsP，采用线性模型建立地形和风场的联系，对于复杂地形的风能资源评估有所不足，需要借助精细化 CFD(Computational Fluid Dynamics)模型才能得到较好的结果[1]。近十几年来，风工程研究者们围绕复杂地形风能评估的CFD方法开展了大量研究[2－5]。Blocken等[6]采用 RANS(Reynolds Averaged Navier-Stokes equations)模型对实际地形进行大气边界层模拟，对比了多种壁面函数，并探讨了模拟大气边界层的技术要求，为 CFD方法在复杂地形上的应用提供了一定的参考价值。Yan等[7]提出改进的k-ε湍流模型对复杂地形风场进行模拟，结果表明该模型可以很好地保证水平向平均风速和湍流强度的均匀性；然而，由于该方法基于时均的N-S(Navier-Stokes)方程，对于脉动风速的预测较差。Lopes等[8]采用LES(Large-eddy-simulation)模型对Askervein山地的流场进行了数值模拟，并与RANS进行对比，结果表明LES和RANS均能较好地预测平均风速加速因子，LES在迎风山坡上的湍动能预测结果优于RANS。Liu等[9]采用LES模型对具有植被的复杂地形风场进行了模拟，并与风洞试验结果进行对比，结果表明 LES模型能很好的预测该风场的平均风速和湍流强度分布。
现有成熟的CFD软件通常采用2阶精度格式的有限体积法，耗散和色散较大，对于复杂地形周围伴随的撞击、分离、环绕、再附着、漩涡脱落等多尺度流动现象的模拟很难给出正确的结果，为此CFD工作者发展了众多的高阶精度计算格式[10]。Patera[11]提出一种高阶数值方法—谱元法(Spectral Element Method, SEM)，它结合了有限元法和谱元法两方面的优点，不仅非常适合复杂外形的数值模拟，而且可以通过提高单元内插值阶数很方便地达到高阶精度，同时具有非常良好的指数收敛特性，因此十分适用于复杂地形的风场模拟[12]，目前已经应用于地震波传播、结构响应、浅水方程等多个领域[13－15]。
本文基于谱元法的开源平台Nek5000[16]，提出复杂地形下谱元法的建模方法，以 Askervein山为例，进行复杂地形风场大涡模拟，并与场地实测数据及其它数值模拟结果进行对比，验证谱元法在实际复杂地形风场模拟上的可行性与正确性，然后给出该区域附近的风能资源分布，为该区域风能资源评估及风机最优化排布提供参考。
谱元法是Patera和Maday提出的一种高阶数值方法，其基本思想是将计算区域划分为若干个单元，单元内的基函数取特殊的正交多项式，在特定的节点上展开，采用Galerkin法求解偏微分方程，得到全域的数值解。谱元法不仅能适应任意外形的数值模拟，而且能通过提高基函数的阶数很方便地增加精度，同时具有指数收敛特性，各个单元的内部节点之间不需要信息传递，并行效率非常高。目前，谱元法已经广泛应用于流体力学领域。
谱元法解流体力学N-S方程的基本思路为：将速度场和压力场用序列展开表示，如式(1)，代入时间离散后的不可压缩N-S方程中，得到方程的弱积分形式，采用伽辽金变分法，取特定的积分节点，得到矩阵形式方程，通过方程依次解出压力场和速度场的展开系数，从而得到全域的数值解。
式中：
为展开系数，是未知量
为单元内基函数，采用勒让德多项式，标准单元内一维基函数为：
式中：
为基函数；i为插值阶数，0≤i≤P；P为最大插值阶数；LP()ξ为勒让德多项式；LP′()ξ为LP()ξ的导数；ξ为节点坐标，在[-1,1]区间。
节点分为 GLL点(Gauss-Lobatto-Legendre)和GL点(Gauss-Legendre)，其中 GLL点为多项式
的零点，GL点为多项式LP(ξ)的零点。以P=6为例，二维GLL点和GL点分布如图1所示，可以明显看出，GLL点包含了边界点而GL点没有。
图1 GLL点和GL点分布
Fig.1 Distribution of GLL and GL points
根据速度场和压力场的网格节点是否同位处理，谱元法可分为PN×PN和PN×PN-2两种网格离散方案，前者表示速度场和压力场均用GLL节点，后者表示速度场用GLL节点而压力场用GL节点。PN×PN-2方案的优点是不需要给定压力边界即可求解，PN×PN方案的优点是时间迭代时不需要对压力场进行网格变换。本文出口为自由出口，不需要特定的压力边界，因此采用PN×PN方案。
为方便读者理解，下面给出采用高阶时间分裂离散、谱元法空间离散后得到的矩阵形式方程，通过式(3)～式(6)依次解出压力场和速度场的展开系数：
式中：i=1,2,3，分别表示纵向、横向、竖向3个方向；系数αq、βq和γ0为相关系数；M为质量矩阵；C为对流算子矩阵；Di为求导矩阵；L为拉普拉斯矩阵；
为已知时刻的速度展开系数；
为第 1个修正速度；
为第2个修正速度；
为未知时刻的压力展开系数，
为未知时刻的速度展开系数。
大涡模拟(LES)是 Smagorinsky[17]提出的一种数值方法，其基本思想是通过某种滤波函数将大尺度的涡和小尺度的涡分离开，大尺度的涡直接模拟，小尺度的涡用模型来封闭。滤波后的不可压缩N-S方程为：
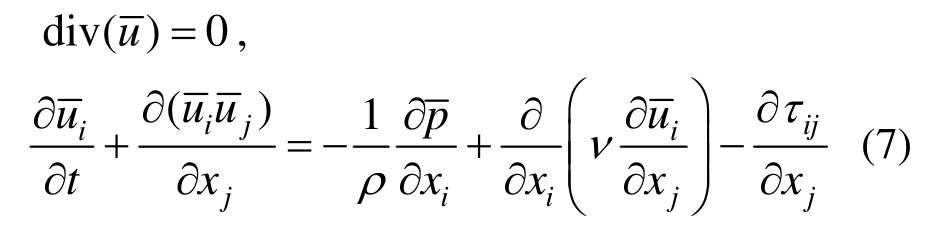
式中：ρ为流体密度；ui、uj为速度分量；p为压力；ν为流体运动粘度；上划线表示滤波后变量；
为亚格子应力。为使方程封闭，需要建立亚格子模型，常用的亚格子模型为Smagorinsky亚格子模型：
式中：Cs为 Smagorinsky常数，通常取 0.1；
为网格体积)为滤波尺度；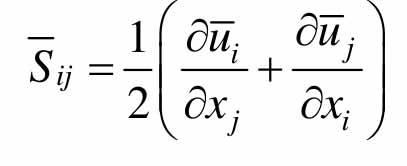
为应力张量的速率，
为了解决Smagorinsky常数为定值导致耗散过大的问题，Germano等[18]提出动态Smagorinsky模型计算Cs值，Lilly[19]提出最小二乘法对 Germano的模型进行了简单的修正：
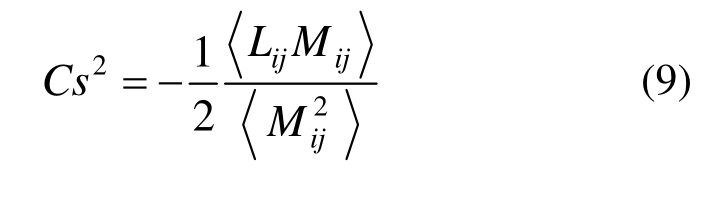
式中：
上划线
表示二次滤波后变量；符号
表示取横向平均。
本文的滤波函数采用文献[20]中设置：
式中：α为滤波权重；
为单元内插值节点数)为截断阶数；dk为κ阶转换函数的值。
以 Askervein山为例，自编程序完成复杂地形下谱元法的网格建模，设定计算域、边界条件等信息，添加大涡模拟求解器代码，进行复杂地形风场LES模拟。
1983年9月~10月，由国际能源协会风资源研究机构在苏格兰 Askervein小山上组织开展了大规模的测风项目[21]。Askervein小山高 116 m(海拔126 m)，位于苏格兰西海岸，属温带海洋性气候，盛行西南风。
如图2所示，该山及周围区域的地形等高线云图，整座山的形状似椭圆。粗糙度长度为 0.01 m~0.05 m，平均粗糙度长度为0.02 m~0.03 m。在此项目中，设立了分布于A、B和AA三条线上的约50座测风塔，其中大部分高度是 10m。line-A和line-AA的方向为 N43°，line-B的方向为 N313°。山顶点 HT的坐标为(075383，823737)，山体中心点CP的坐标为(075678，823465)，参考点RS的坐标为(074300，820980)，在HT点西南方向约3 km处。本文选用TU03-B实测数据作为对比数据，来流风向为N210°，该试验数据多次被应用于风场数值模拟研究[22―23]。
图2 Askervein山及测风塔分布
Fig.2 Askervein hill and locations of measurement towers
2.2.1 网格建模
对于真实地形建模，本文采用中国科学院计算机网络信息中心地理空间数据云平台的 ASTER GDEM V2地形数据(http://www.gscloud.cn)，水平分辨率为30 m，自编程序完成谱元法的复杂地形网格建模，具体流程如下：
1) 根据数值模拟需求，下载相应区域的地形数据。
2) 利用软件 globalmapper将下载的地形数据转换为模拟所需的坐标系，如本文采用的 British grid /OSGB36坐标系，并根据计算需要将指定区域的地形海拔数据导出，导出格式为.xyz，如图 3(a)所示。
3) 基于 matlab语言自编程序，根据风向对区域进行旋转，插值得到新的计算域的地形海拔信息，如图3(b)所示。
4) 将新的地形数据导入软件 IMAGEWARE，对点云进行光顺处理后，生成2.5D网格，导出.igs格式文件。
5) 利用软件Gambit读取该.igs文件，根据主计算域的地形特点，在四周添加一定长度缓冲区域后，进行网格划分，并导出.neu格式的网格信息文件。
6) 基于MATLAB语言，读取.neu文件，将单元节点按x-＞y-＞z(顺风向-横风向-竖向)顺序进行排序，生成Nek5000平台能够识别的单元信息、边界信息的文件格式，得到.rea文件。
7) 编译并运行Nek5000程序，校对网格质量，并将网格信息导出，核实地形海拔数据，如图3(c)，确定无误后进行下一步的模拟。
图3 地形海拔信息
Fig.3 Terrain elevation information
2.2.2 网格划分
本文以 HT点为坐标原点，主计算域大小为5 km×6 km×1 km，分别表示x方向(顺风向)、y方向(横风向)、z方向(竖向)。其中入口距离原点3 km，保证RS点在入口附近，出口距离原点2 km，两侧距离原点均为3 km，保证山体主体布置在主计算域中心，不受4个边界的影响。同时，将四周延伸到相同海拔平面，作为缓冲区域，保证出入口及两侧边界的稳定性。为尽量避免缓冲区域对主计算域的影响，缓冲区域的坡度应保证在20°以内，入口处的海拔高度变化不大，沿x方向增加200 m的过渡区域，保证入口的均匀性；出口处的海拔高度变化较大，沿x方向增加1 km的过渡区域及1 km的平坦地形，保证出口的均匀性与稳定性；左侧边界地形变化不大，沿y方向增加100 m的过渡区域；右侧边界地形变化很大，沿y方向增加500 m的过渡区域及500 m的平坦地形，保证两侧边界的稳定性。添加缓冲区域后的总计算域大小为7.2 km×7.1 km×1 km。
根据 Askervein山的地形特点，将计算域划分为36×44×15共23760个单元，考虑计算机条件限制，每个单元的插值阶数取为 4，即 109×133×46共 67万个网格节点。为验证网格无关性，划分42×48×17共 34272个单元的另一套网格，即127×145×52共96万个网格节点，二者模拟结果基本一致。
同时，为将谱元法与常用数值方法进行对比，利用商用软件Fluent对Askervein山进行了风场模拟，采用标准k-ε的RANS湍流模型，计算域划分为145×143×51共106万网格节点，并保证z方向第1个网格点距离地面1m，如图4。为验证网格无关性，划分180×143×61共157万网格节点的另一套网格，二者结果基本一致。
图4 Fluent中网格划分
Fig.4 Grid discretization in Fluent
2.2.3 边界条件
模拟区域入口给定均匀入口速度分布，其风速分布由采用测风点RS处测风数据拟合的对数函数来表示，速度垂直于入口边界：
式中：u/(m/s)表示入口风速；z/m表示离地高度；u*表示摩擦速度，取 0.6184 m/s；κ表示卡曼常数，取0.4；z0表示地面粗糙长度，取0.03 m。
出口边界采用自由出流，两侧及上边界采用对称边界，底部地面采用固壁边界。
Fluent中采用标准k-ε的RANS湍流模型[24]，入口除了给定式(11)的风速剖面外，还给定湍动能、耗散率剖面：
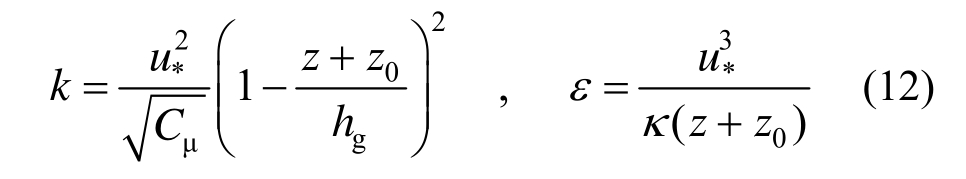
式中：hg表示大气边界层高度，取909.56 m；标准k-ε中湍流参数：Cμ=0.03，Cε1=1.21，Cε2=1.92，kσ=1，εσ=1.3。
出口边界和两侧边界的设置同谱元法，底部地面采用无滑移粗糙壁面，根据文献[25]建议，壁面粗糙高度采用 7.5×z0=0.225 m，粗糙常数取 0.4。空气密度ρ=1.225 kg/m3，空气运动粘度ν=1.4607×10-5m2/s。
2.2.4 Nek5000
Nek5000平台是基于C语言和Fortran语言编写的谱元法的开源平台，具有非常高的并行效率，可以方便地用于流体力学的数值模拟。首先经过多次处理，生成Nek5000可识别的.rea格式单元文件，参考文献[26]，处理随时间变化的湍流粘性项，最后通过修改源代码完成复杂地形风场的大涡模拟。
编写子程序eddy_visc，计算每个时间步的单元内所有节点的湍流粘性项。子程序 eddy_visc主要内容为：调用set_ds_filt、set_grid_spacing，分别定义滤波算子和滤波尺度；调用comp_gije、comp_mij、comp_lij分别计算
计算式(4)中的分子、分母，并取横向平均，从而得到Cs值；计算湍流粘性项
同时，为了尽量减少初始场的影响，添加子程序set_wall_spacing，以入口条件完成整个流场的初始化。经过测试，这样的初始化方法稳定性较高，不易发散。
基于以上设置，对 Askervein山进行风场数值模拟。Nek5000平台中，采用PN×PN网格方案，GMRES算法解压力场，3阶时间离散方案，对流形式处理对流项，速度场和压力场收敛的精度分别为 10-8和 10-5，采用非定常求解器，时间步长取0.2s，保证CFL数在1以内，每10步存储一次结果，流场趋于稳定后(6000个时间步)，对4000步的模拟结果进行采样及统计分析。Fluent平台中，采用SIMPLE算法，动量方程、湍动能和湍流耗散率均采用2阶迎风格式，采用定常求解器求解，连续方程和速度场的收敛精度分别为10-3和10-5，计算完成后输出结果。
本次模拟，谱元法的大涡模拟迭代10000步耗时 14 h(96万网格)，平均每步耗时 5.04 s，解压力场时平均每次内迭代 20步，因此名义上每步耗时0.252 s；Fluent的 RANS模拟迭代 3000步耗时1.77 h(106万网格)，平均每步耗时 1.76 s。从计算效率上看，RANS远高于LES；但从每一步内迭代耗时来看，谱元法优于Fluent。
将line-A上平均风速加速因子的数值模拟结果与场地实测数据进行对比，并研究 Askervein山上的平均风能资源分布。
为便于分析，引入无量纲参数平均风速加速因子SΔ，避免来流风速大小的影响直接反映该位置的平均风速因地形影响造成的风速变化大小，定义为：
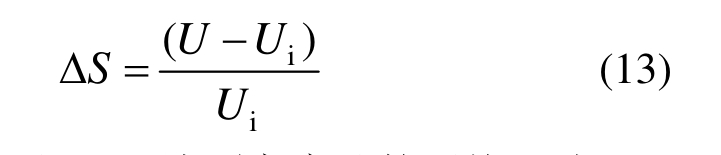
式中：Ui为入口处10m地面高度处的平均风速；U为某处的平均风速。
如图5所示，给出line-A上10 m高度处平均风速加速因子的数值模拟结果与实测结果，并与Castro等[27]数值结果进行对比。可以看出，平均风速加速因子的模拟值曲线与测量值基本吻合，趋势一致。大涡模拟在山顶风速加速因子误差为13%，在背风面最大误差为 10%。与低阶有限体积法相比，谱元法在较少的网格下，就能达到较高的精度，这是因为模拟瞬态的流动问题时，低阶数值方法在长时间积分后由于误差累积导致精度降低，而高阶数值方法在长时间积分后仍能保证较高的数值精度。
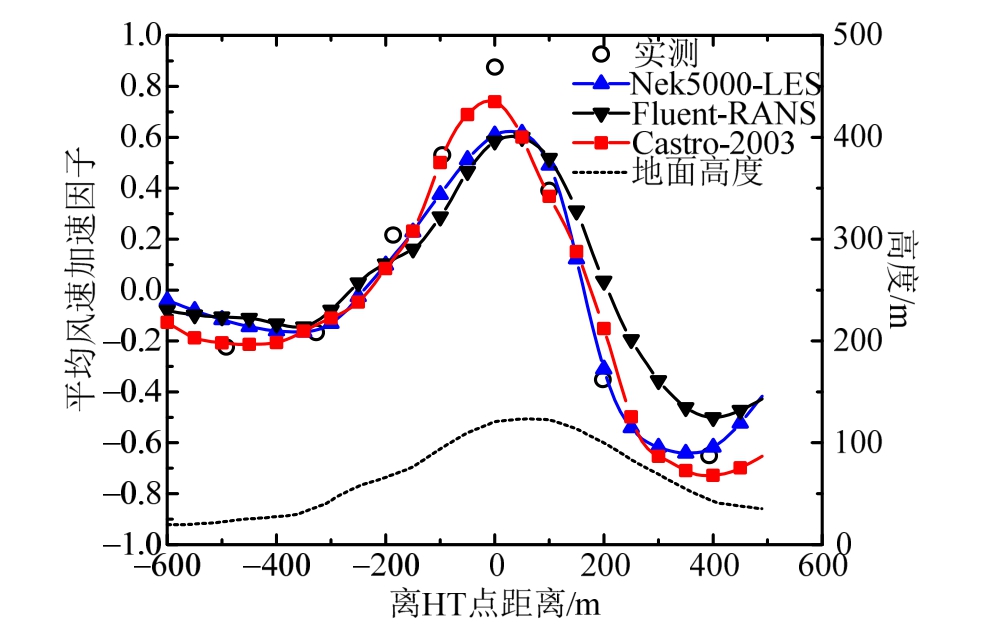
图5 line-A上各测风点10 m高度平均风速加速比
Fig.5 Comparison of wind acceleration factor along line-A at 10 m above ground
对比谱元法的LES与Fluent的RANS模拟结果可以发现， RANS对于背风坡的风速加速因子预测误差较大，这是因为RANS求解的是时均化流场，对于存在分离、再附等复杂流动现象的尾流区域模拟精度较低，而LES则非常好的捕捉到了尾流的脉动风速信息，能较好的再现尾流的旋涡分离再附现象，模拟精度较高。
风场的风速分布直接决定了风能资源的分布，从而最大程度决定了风机排布的最优方案。为研究Askervein山附近区域的风能资源分布，定义无量纲平均风能密度比：
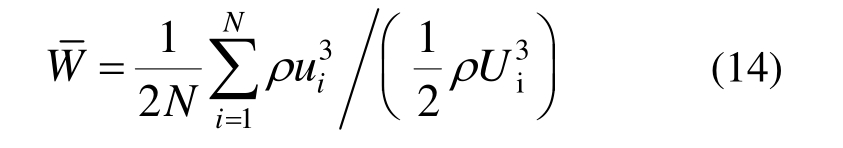
式中：ρ为空气密度；ui为第i个时刻的顺风向风速；N为统计的时刻数；Ui为入口10 m高度处平均风速。
图6 Askervein山的平均风能分布
Fig.6 Wind energy distribution on Askervein hill
现有的风机通常有70 m和150 m两种高度类型，根据Askervein山地形特点，主要对比70 m高度处的风能资源分布。图6给出70 m高度处Askervein山附近的平均风能资源分布图，从图中可以看出，风从入口进入，在山体前风速变小，可利用风能变小，随着山体的高度增加，风速逐渐增大，可利用风能增加，在山顶附近可利用风能最为丰富，从山顶到背风面，由于分离再附等现象，风速逐渐减小，可利用风能变少。对于本次工况而言，风机的最优布置区间为HT点的顺风向[-300 m,200 m]、横风向[-800 m,400 m]的范围内，作为为风机最优排布的参考。
本文基于谱元法开源平台Nek5000，进行平台二次开发，提出谱元法的复杂地形建模流程，以Askervein山为研究对象，对复杂地形风场进行大涡模拟，并与实测结果进行对比，得出以下结论：
(1) 将谱元法的 LES模拟结果和 Fluent的RANS结果对比发现，二者均能较好的预测line-A上10m高度处的平均风速加速因子；与RANS相比，LES对于尾流的模拟精度更高，预测更准；
(2) 根据数值模拟结果给出了 Askervein山附近的平均风能资源分布，评估山顶加速效应，为风机排布提供参考。
准确预测风场风速分布是复杂地形风能资源评估的前提，是风机最优化布置的保证。对比两种数值模拟结果发现，在网格较少的情况下，谱元法的LES模拟对于尾流的模拟精度仍然较高，非常适用于复杂地形的风场模拟，可应用于山区建筑物选址、复杂地形风能资源评估和风机最优化排布。
[1]靳晶新, 叶林, 吴丹曼, 等. 风能资源评估方法综述[J]. 电力建设, 2017, 38(4): 1－8.Jin Jingxin, Ye Lin, Wu Danman, et al. Review of wind energy assessment methods [J]. Electric Power Construction, 2017, 38(4): 1－8. (in Chinese)
[2]遆子龙, 李永乐, 廖海黎. 地表粗糙度对山区峡谷地形桥址区风场影响研究[J]. 工程力学, 2017, 34(6):73－81.Ti Zilong, Li Yongle, Liao Haili. Effect of ground surface roughness on wind field over bridge site with a gorge in mountainous area [J]. Engineering Mechanics, 2017,34(6): 73－81. (in Chinese)
[3]刘志文, 薛亚飞, 季建东, 等. 黄河复杂地形桥位风特性现场实测[J]. 工程力学, 2015, 32(增刊): 233－239.Liu Zhiwen, Xue Yafei, Ji Jiandong, et al. Field measure-ment of wind characteristics of a bridgesite with complex yellow river terrain [J]. Engineering Mechanics,2015, 32 (Suppl): 233－239. (in Chinese)
[4]Tse K T, Weerasuriya A U, Zhang X, et al. Effects of twisted wind flows on wind conditions in passages between buildings [J]. Journal of Wind Engineering &Industrial Aerodynamics, 2017, 167: 87－100.
[5]Bilal M, Birkelund Y, Homola M, et al. Wind over complex terrain – Microscale modelling with two types of mesoscale winds at Nygårdsfjell [J]. Renewable Energy, 2016, 99: 647－653.
[6]Blocken B, Stathopoulos T, Carmeliet J. CFD simulation of the atmospheric boundary layer: wall function problems [J]. Atmospheric Environment, 2007, 41(2):238－252.
[7]Yan B W, Li Q S, He Y C, et al. RANS simulation of neutral atmospheric boundary layer flows over complex terrain by proper imposition of boundary conditions and modification on the k-ε, model [J]. Environmental Fluid Mechanics, 2016, 16(1): 1－23.
[8]Lopes A S, Palma J M L M, Castro F A. Simulation of the Askervein flow. Part 2: Large-eddy simulations [J].Boundary-Layer Meteorology, 2007, 125(1): 85－108.
[9]Liu Z, Ishihara T, He X, et al. LES study on the turbulent flow fields over complex terrain covered by vegetation canopy[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 155: 60－73.
[10] 张来平, 贺立新, 刘伟, 等. 基于非结构/混合网格的高阶精度格式研究进展[J]. 力学进展, 2013, 43(2): 202－236.Zhang Laiping, He Lixin, Liu Wei, et al. High order accuracy scheme research based on unstructure/hybrid grid [J]. Advances In Mechanics, 2013, 43(2): 202－236.(in Chinese)
[11] Patera A T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion [J].Journal of Computational Physics, 1984, 54(3): 468－488.
[12] Korczak K Z, Patera A T. An isoparametric spectral element method for solution of the Navier-Stokes equations in complex geometry [J]. Journal of Computational Physics, 1986, 62(2): 361－382.
[13] Komatitsch D, Vilotte J P. The spectral element method:an efficient tool to simulate the seismic response of 2D and 3D geological structures [J]. Bulletin of the Seismological Society of America, 2012, 88(2): 368－392.
[14] Lee U. Spectral element method in structural dynamics[M]. Singapore: J. Wiley & Sons Asia, 2009.
[15] Giraldo F X, Warburton T. A nodal triangle-based spectral element method for the shallow water equations on the sphere [J]. Journal of Computational Physics,2005, 207(1): 129－150.
[16] Fischer P F, Lottes J W, Kerkemeier S G. Nek5000 Web Page [CP]. http://nek5000.mcs.anl.gov, 2008.
[17] Smagorinsky J S. General circulation experiments with the primitive equations [J]. Monthly Weather Review,1963, 91(3): 99－164.
[18] Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model [J]. Physics of Fluids,1991, 3(7): 1760－1965.
[19] Lilly D K. A proposed modification of the Germano subgrid-scale closure method [J]. Physics of Fluids,1992, 4(4): 633－633.
[20] Kanchi H, Sengupta K, Mashayek F. Effect of turbulent inflow boundary condition in LES of flow over a backward-facing step using spectral element method [J].International Journal of Heat & Mass Transfer, 2013,62(1): 782－793.
[21] Taylor P A, Teunissen H W. The Askervein hill project:overview and background data [J]. Boundary-Layer Meteorology, 1987, 39(1－2): 15－39.
[22] 梁思超, 张晓东, 康顺. 复杂地形风场绕流数值模拟方法[J]. 工程热物理学报, 2011, 32(6): 945－948.Liang Sichao, Zhang Xiaodong, Kang Shun. Numerical simulation for wind flow around complex terrain [J].Journal of Engineering Thermophysics, 2011, 32(6): 945－948. (in Chinese)
[23] Stangroom P. CFD modelling of wind flow over terrain[D]. Nottingham: University of Nottingham, 2004.
[24] 吕振峰. 复杂地形对风速分布影响的数值模拟研究[D]. 昆明, 昆明理工大学, 2015.Lü Zhenfeng. Research on influence of complex terrain on wind speed distribution of wind field [D]. Kunming:Kunming University of Science and Technology, 2015.(in Chinese)
[25] 邓院昌, 刘沙, 余志, 等. 实际地形风场 CFD 模拟中粗糙度的影响分析[J]. 太阳能学报, 2010, 31(12): 1644－1648.Deng Yuanchang, Liu Sha, Yu Zhi, et al. Research on roughness of CFD simulation on complex terrain [J].Acta Energiae Solaris Sinica, 2010, 31(12): 1644－1648.(in Chinese)
[26] Karamanos G S, Sherwin S J. A high order splitting scheme for the Navier-Stokes equations with variable viscosity [J]. Applied Numerical Mathematics, 2000,33(1–4): 455－462.
[27] Castro F A, Palma J M L M, Lopes A S. Simulation of the Askervein flow. part 1: reynolds averaged navier-stokes equations (k∈turbulence model) [J].Boundary-Layer Meteorology, 2003, 107(3): 501－530.
LARGE-EDDY-SIMULATION ON COMPLEX TERRAIN BASED ON SPECTRAL ELEMENT METHOD