
Q4单元是等参单元序列中最简单的单元,单元的形函数根据点协调条件可以直接建立,同时形函数自然满足单元边界的线性位移协调,单元形式简洁,概念清晰,但由于单元的精度较差,因此一般并不用于工程分析。
在Q4单元基础上,Wilson等[1]通过增加基于内部参数的附加位移场构造了非协调元 Q6,单元的位移场实现了等参坐标的二次完备,从而使单元的精度和抗网格畸变能力都得到大幅提升。
这一成功的尝试为人们提供了新的思路,但是这个位移模式对任意四边形不能通过强式分片检验。鉴于强式分片检验一直作为大家公认的判别非协调元是否收敛的标准,Taylor等[2]在Q6元的基础上提出了非协调元QM6,算例表明该单元有着良好的计算精度;Wachspress[3]提出了非协调元QP6;Pian等[4]采用近似分片检验提出 NQ6;龙驭球等[5]利用常应力和线性应力下的广义协调条件,提出了广义协调等参元GC-Q6;另外还有应力杂交元[6―7]、拟协调元[8]、应变元等[9]。这些单元都可以通过强式分片检验,取得了良好的结果。在此基础上,胡清元等[10]基于拟协调元提出了进一步弱化应变-位移关系的方法,李根等[11]在广义协调中引入罚因子以改善单元的协调性,岑松等[12―13]提出形状自由单元方法以兼顾单元收敛性和抗畸变能力。这些研究成果为新型单元的建立开拓了新的思路,也证实了对传统单元的改造仍然具有重要价值。
本文工作定位于把Q4、Q6以及QM6单元和广义协调理论进行更加深入的融合。一方面,广义协调理论自提出以来虽然被广泛应用于构造高精度的单元,但并未实现与Q4这样基本单元的自然沟通。另一方面,在处理基于内部参数的附加位移场时,QM6单元通过数值积分的方法消除附加位移场产生的非协调位移,从而使单元通过分片检验,虽然该数值积分方法还可应用于三维问题以强迫单元通过分片试验,但研究证明[14],这种方法仍有局限性,要使单元通过分片试验,可以从能量的角度出发基于广义协调理论选择适当的附加位移场。
首先采用优选的广义协调理论推导了 Q4单元,实现了广义协调理论在最基本等参元中的应用,其次通过选择满足广义协调条件的附加内参位移场[15]构造了单元GQM6,算例表明虽然新单元与QM6一样都只是满足等参坐标的二次完备,但GQM6单元表现出较QM6单元更好的性能,尤其抗网格畸变的能力,表明对这些传统的单元和理论进行深入融合仍然有着重要的意义。
广义协调条件包括点协调、边协调和周协调 3种类型。通常,为了降低单元的次数,大多数节点广义协调元采用54点协调与2个周协调相结合的方法,但这对于平面单元仍然会使位移场的次数达到二次。实际上,平面单元保证收敛只需要满足 3个刚体位移的协调和三3常应力下的协调,按照广义协调理论这六个协调条件可以表示为:
常应力xσ协调:

常应力yσ协调:
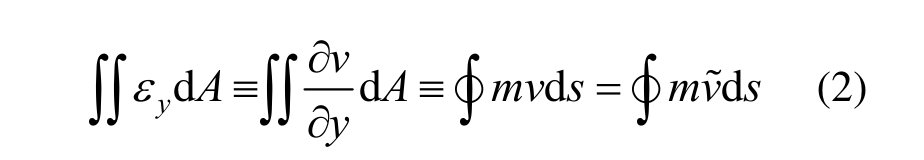
常应力τxy协调:

旋转协调:

沿x向平移的协调:

沿y向平移的协调:

其中:l、m为单元边界法线的方向余弦;u、v为单元两个方向的位移场;而u~、v~为相应的单元边界位移。
为了便于应用,协调条件式(3)、式(4)可以通过解耦等效替换为:

上面六个协调条件中对于u和v各有3个,虽然已经可以保证单元的协调性,但是对于四节点单元还需要为u和v各补充一个协调条件,这里选取点协调组合条件如下:

显然,u和v分别只包含4个协调条件,用于构造四节点单元时可以使节点位移场次数最低。
Q4单元的双向线性位移场为:

该位移场根据形函数特点,采用点协调条件可直接确定待定系数,最终得到边界协调的单元形函数为:
采用广义协调方法建立时,四个待定系数采用两个组合点协调条件和两个周协调条件可以确定,这里仅对位移u进行推导。其中,将式(11)位移场代入式(9)、式(10)两个组合点协调条件,可以直接解出1α和4α:

通过将式(11)所示位移场表达式代入周协调条件式(1)和式(7),则有:

式中:
联立式(15)、式(16)形成方程组,由此可以求得另外两个待定系数:

将iα(i=1,2,3,4)的结果代入式(11),则位移u的表达式可以整理为:


同样方法可以求得位移场v的表达式。显然式(19)中通过广义协调方法建立的形函数与式(12)中点协调方法得到的形函数相同。
为了改善Q4单元的性能,Wilson通过增加附加内参位移场的方法构造了非协调元Q6,Q6单元的附件内参位移场为:

附加内参位移项的增加,使Q6单元位移场实现了等参坐标的二次完备,大大提高了单元的精度和抗网格畸变能力,但对于任意四边形单元,由于破坏了边界协调,因此无法通过强式分片试验。采用Tailor提出的数值积分方法处理内参位移场可使单元通过分片检验,且效果良好,但该方法具有很强的局限性,因此文献[15]采用广义协调方法从理论出发,建立了平面问题附加内参位移的通用形式该通用形式从广义协调方法常应力下周协调出发:
即单元边界力在非协调位移上产生的非协调能力为0,其中![]() 为常应力下边界力
为常应力下边界力![]() cσ是常应力,n是单元外法线向量,则对于非协调位移部分有:
cσ是常应力,n是单元外法线向量,则对于非协调位移部分有:
由此建立的内参位移场的通用形式中部分特殊形式如下:
当n和m都为奇数时:
当n为奇数,m为偶数时:
当n为偶数,m为奇数时:

当n和m都为偶数时:

式中:

其中,bi、ci列于式(17),而:
在此,令Nλ=uλ,则对Q4单元可以选取如下附加二次内参位移项:

则最终的内参位移场为:
增加附加内参位移后,单元的刚度矩阵可以通过静力凝聚方法计算,即:
其中:

式中:t为单元的厚度;D为弹性矩阵,对于平面应力问题可以表示为:

其中,E和μ分别为弹性模量和泊松比。
式(32)中的应变矩阵可以表示为:
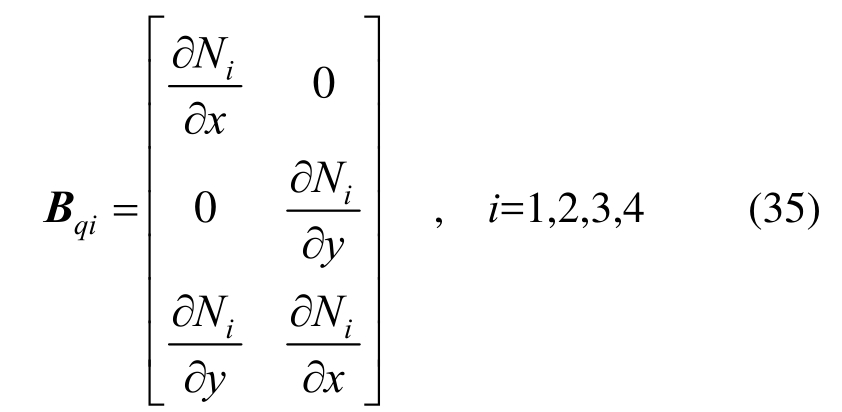
其中:
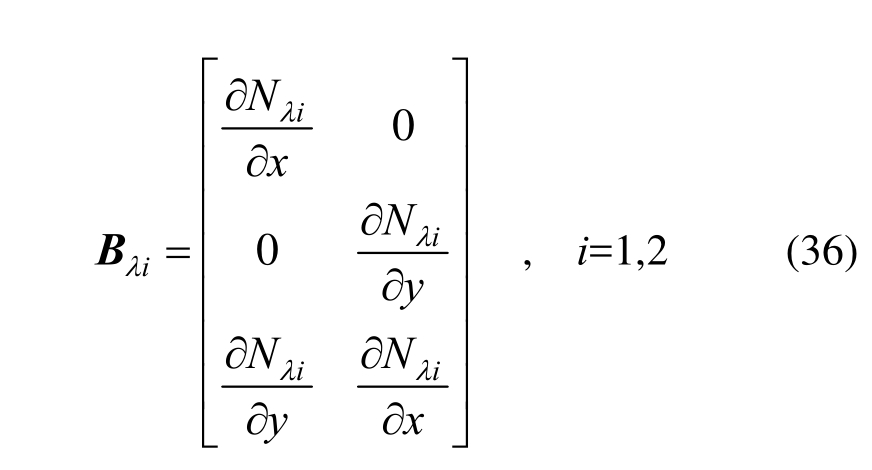
式(35)中节点位移形函数的偏导数可以表示为:

式(36)中附加内参位移形函数的偏导数可以表示为:

其中,J为单元的Jacobi矩阵。
在求得单元节点位移向量eq后,对于不含体积力的情况,单元的两个内部参数1λ和2λ可表示为:

则单元的应变和应力矩阵分别为:
该单元记为GQM6,可以看出GQM6单元的位移场与QM6相差无几,区别是:无论是节点位移场和内参位移场均采用广义协调方法来建立,尤其是在内参位移场,由于采用广义协调方法替代了QM6中的数值积分方法,降低了对单元边界的约束。
图1所示划分为任意网格的小片承受纯拉伸作用,GQM6可以给出精确解,结果如表1所示。

图1 分片检验
Fig.1 Patch test
表1 分片检验
Table 1 Patch test

结点uivi1 0.0 0.0 2 0.0 -0.25 3 0.0 -0.5 4 2.0 -0.125 5 2.5 0.0 6 4.0 0.0 7 4.0 -0.5
图 2所示不规则悬臂短梁在端部受剪问题(即Cook问题)。图示为典型网格 2×2,计算结果列于表2。

图2 Cook短斜梁
Fig.2 Cook’s skew beam
表2 Cook短斜梁计算结果
Table 2 Results of Cook’s skew beam

单元VCσAmaxσBmin2×2 4×4 8×8 2×2 4×4 8×8 2×2 4×4 8×8 Q4 11.80 18.29 22.08 0.1217 0.1873 0.2242 -0.0960 -0.1524-0.1869 QM6[2]21.05 23.02 — 0.1928 0.2243 — -0.1580 -0.1856 —HL[16]18.17 22.03 23.39 0.1582 0.1980 0.2205 -0.1335 -0.1770-0.1931 P-S[6]21.13 23.02 23.88 0.1854 0.2241 0.2364 — — —GQM6 21.05 23.02 23.69 0.1791 0.2287 0.2417 -0.2004 -0.2160-0.2087参考值 23.96 0.2362 -0.2023
图3所示悬臂梁,采用含4个单元的不规则网格。梁端A点和B点的挠度及其平均值的计算结果见表3。
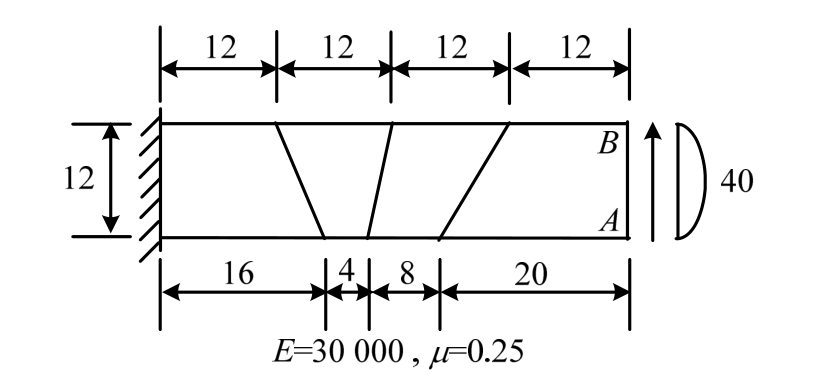
图3 不规则网格悬臂梁
Fig.3 Cantilever beam with four irregular meshes
表3 不规则网格悬臂梁梁端挠度
Table 3 Results of cantilever beam with irregular meshes

单元 梁端挠度 归一化结果A点B点 平均值A点B点 平均值Q4 0.2126 0.2131 0.2129 0.598 0.599 0.598 D-type[17]— — 0.3065 — — 0.861 Q4S[18]— — 0.2978 — — 0.837 GQM6 0.3291 0.3316 0.3304 0.925 0.932 0.929参考值 0.3558 1.000
图4所示为一厚曲梁受端部力作用,端点挠度结果列于表4中,并与QM6元、P-S元和PEAS7元进行了比较。

图4 厚曲梁弯曲
Fig.4 Curved thick beam
表4 厚曲梁端点挠度计算结果
Table 4 Results of curved thick beam

单元 QM6[2]P-S[6]PEAS7[9]GQM6 精确解VA83.61 84.58 84.58 84.61 90.1
图5所示薄曲梁受端部力作用。梁划分为5个单元。考虑两种尺寸:h/R= 0.03和h/R= 0.006。端点挠度计算结果列于表5中,并与Q4元、Q6元、QM6元和QUAD4元进行了比较。

图5 薄曲梁弯曲
Fig.5 Curved thin beam
表5 薄曲梁端点挠度计算结果
Table 5 Results of curved thin beams

h/RQ4 Q6[2]QM6[3]QUAD4[19]GQM6 精确解0.03 0.024 0.770 0.339 0.615 0.651 1.000 0.006 0.001 0.285 0.0220.163 0.173 1.000
图 6所示受纯弯作用的悬臂梁划分为 2个单元。图中e为畸变参数,弹性模量E=1500,泊松比µ=0.25。A点挠度随e的变化结果列于表6。

图6 网格畸变测试
Fig.6 Test of mesh distortion
表6 含畸变参数的纯弯梁梁端挠度结果
Table 6 Tip deflection of cantilever beams with distorted parameter e

e0 0.5 1 2 3 4 4.9 Q4 28.0 21.0 14.1 9.7 8.3 7.2 6.2 Q6[2]100 93.2 86.9 92.7 102 111 117 QM6[3]100 80.9 62.7 54.4 53.6 51.2 46.8 P-S[6]100 81.0 62.9 55.0 54.7 53.1 49.8 QE2[20]100 81.2 63.4 56.5 57.5 57.9 56.9 B-Q4E[20]100 81.2 63.4 56.5 57.5 57.9 56.9 GQM6 100 83.4 66.3 61.3 64.6 66.1 64.1精确解 100 100 100 100 100 100 100
基于等参坐标方法建立的四边形单元 Q6和QM6,通过在Q4单元的基础上引入基于内部参数的附加位移场,使单元的精度和抗网格畸变能力大幅提升,因此成为平面单元发展的里程碑。本文在此基础上对节点位移场和内部附加位移场均采用广义协调理论建立了GQM6单元,新单元虽然位移场同样只是达到等参坐标的二次完备,但数值算例结果表明GQM6单元除了在常规问题上表现出较高精度外,由于进一步放松了附加内参位移场的边界协调性,因此在抗网格畸变方面有着更突出的表现。
[1]Wilson E L, Taylor R L, Doherty W P, et al. Incompatible displacement models, numerical and computer methods in structural mechanics [M]. Numerical and Computer Methods in Structural Mechanics. Edited by Steven J.Fenves, Academic Press, New York, 1973: 43―57.
[2]Taylor R L, Beresford P J, Wilson E L. A nonconforming element for stress analysis [J]. Int. J. Num.Meth. Engng., 1976, 10(6): 1211―1219.
[3]Wachspress E L. Incompatible quadrilateral basis functions [J]. International Journal for Numerical methods in Engineering, 1978, 12(4): 589―595.
[4]Pian T H H, Wu Changchun. General formulation of incompatible shape function and an incompatible isoparametric element [C]. Proc. Of the Invitational China-American Workshop on FEM, Chengde, China,1986: 159―165.
[5]龙驭球,黄民丰. 广义协调等参元[J]. 应用数学和力学, 1988, 9(10): 871―877.Long Yuqiu, Huang Minfeng. A generalized conforming isoparametric element [J]. Applied Mathematics and Mechanics, 1988, 9(10): 871―877. (in Chinese)
[6]Pian T H H, Sumihara K. Rational approach for assumed stress finite elements [J]. International Journal for Numerical methods in Engineering, 1984, 20(9): 1685―1695.
[7]Chen W, Cheung Y K. Three dimensional 8-node and 20-node refined hybrid isoparametric elements [J].International Journal for Numerical Methods in Engineering, 1992(35): 1871―1889.
[8]陈万吉, 唐立民. 等参拟协调元[J]. 大连工学院学报,1981, 20(1): 63―74.Chen Wanji, Tang Limin. Isoparametric quasiconforming element [J]. Journal of Dalian University Technology, 1981, 20(1): 63―74. (in Chinese)
[9]Andelfinger U, Ramm E. EAS-elements for twodimensional, three-dimensional, plate and shell structures and their equivalence to HR-elements [J]. International Journal for Numerical Methods in Engineering, 1993(36): 1311―1337.
[10] 胡清元, 夏阳, 胡平, 等. 假设位移拟协调平面单元应变离散算法研究[J]. 工程力学, 2016, 33(9): 30―39.Hu Qingyuan, Xia Yang, Hu Ping, et al. Research on the strain discretization algorithm in assumed displacement quasi-conforming plane finite element method [J].Engineering Mechanics, 2016, 33(9): 30―39. (in Chinese)
[11] 李根, 黄林冲. 一种基于四边形面积坐标的四结点平面参变量单元[J]. 工程力学, 2014, 31(7): 15―22.Li Gen, Huang Linchong. A 4-node plane parameterized element based on quadrilateral area coordinate [J].Engineering Mechanics, 2014, 31(7): 15―22. (in Chinese)
[12] Cen S, Fu X R, Zhou G H, et al. Shape-free finite element method: The plane Hybrid Stress-Function(HS-F) element method for anisotropic materials [J].Science China: Physics, Mechanics & Astronomy, 2011,54(4): 653―665.
[13] 岑松, 尚闫, 周培蕾, 等. 形状自由的高性能有限元方法研究的一些进展[J]. 工程力学, 2017, 34(3): 1―14.Cen Song, Shang Yan, Zhou Peilei, et al. Advances in shape-free finite element methods: a review [J].Engineering Mechanics, 2017, 34(3): 1―14. (in Chinese)
[14] Xiaoming Chen, Song Cen, Yungui Li, et al. Several treatments on non-conforming element failed in the strict patch test. mathematical problems in engineering [J]. vol.2013, Article ID 901495, 7 pages, 2013.doi:10.1155/2013/901495
[15] 张春生, 龙驭球, 须寅. 内参型附加非协调位移基本项的推导和应用[J]. 工程力学, 2000, 17(5): 23―31.Zhang Chunsheng, Long Yuqiu, Xu Yin. Basic formulations of additional incompatible displacement on internal parameters: derivation and application [J].Engineering Mechanics, 2000, 17(5): 23―31. (in Chinese)
[16] Cook R D. Improved two-dimension finite element [J].Journal of the Structural Division, ASCE, 1974, 100ST9:1851―1863.
[17] Ibrahimgovic A, Taylor R L, Wilson E L. A robust quadrilateral membrane element with rotational degrees of freedom [J]. International Journal for Numerical Methods in Engineering, 1990, 30(3): 445―457.
[18] MacNeal R H, Harder R L. A refined four-noded membrane element with rotational degrees of freedom[J]. Computers & Structures, 1988, 28(1): 75―84.
[19] MacNeal R H, Harder R L. A proposed standard set of problems to test finite element accuracy [J]. Finite Elements in Analysis and Design, 1985, 1(1): 3―20.
[20] Piltner R, Taylor R L. A systematic constructions of B-bar functions for linear and nonlinear mixed-enhanced finite elements for plane elasticity problems [J].International Journal for Numerical Methods in Engineering, 1999, 44(5): 615―639.
A 4-NODE ISOPARAMETRIC ELEMENT FORMULATED WITH GENERALIZED CONFORMING CONDITIONS