张文元1,2,王 柯1,2,王 强1,2,陈 勇3,周 宇3,丁玉坤1,2
(1.哈尔滨工业大学,结构工程灾变与控制教育部重点实验室,哈尔滨 150090;2.哈尔滨工业大学,土木工程智能防灾减灾工业和信息化部重点实验室,哈尔滨 150090;3.中国建筑东北设计研究院有限公司,沈阳 110006)
摘 要:为研究高层或超高层大楼中拟采用的多腔钢板-混凝土组合剪力墙的抗震性能,对其进行拟静力试验及有限元模拟,分析了腔数对该类组合剪力墙的破坏模式、承载力、滞回曲线、骨架曲线、延性、刚度退化及耗能能力的影响。试验现象表明试件的破坏模式均为上部混凝土压碎、角部钢板屈曲。通过分析试验结果发现,该种类形式的组合剪力墙在较高轴压力作用下仍具有良好的水平变形能力和较强的耗能能力,3个试件的极限位移角平均值为1/61,且单腔长宽比的减小会降低试件的承载力、增加试件延性。通过有限元软件建立的该类组合剪力墙模型证明该计算结果与试验值吻合良好,同时发现当单腔长宽比减小到 1.94时,组合剪力墙的极限承载力基本不变。
关键词:多腔钢板-混凝土组合剪力墙;有限元分析;耗能能力;延性;单腔长宽比
目前钢-混凝土组合剪力墙主要有三种构造形式,包括内嵌钢板-混凝土组合剪力墙、单侧钢板-混凝土组合剪力墙以及双钢板-混凝土组合剪力墙。内嵌钢板-混凝土组合剪力墙的研究相对比较成熟,已提出了剪力墙受力的设计理论[1]。内嵌钢板-混凝土组合剪力墙与单侧钢板-混凝土组合剪力墙均采用一块钢板,它们相比于传统钢筋混凝土剪力墙承载力有了大幅提高,但是用于超高层建筑中主要存在以下不足[2]:1)位于钢板外侧的混凝土板在大变形的情况下可能会发生开裂剥落;2)混凝土开裂不能有效控制,裂缝外露影响剪力墙的正常使用。
国内外对双钢板混凝土剪力墙进行研究。聂建国等[3]对双层钢板-混凝土剪力墙进行试验和理论研究,但其墙体内仍配有钢筋。马恺泽等[4]对4个双层钢板-高强混凝土组合剪力墙进行试验研究,结果表明加劲肋比约束拉杆更能提高剪力墙的抗震性能。Eom等[5]对5组双钢板剪力墙进行试验研究,结果表明,剪力墙主要是由于钢板的局部屈曲破坏导致墙体破坏;高宽比大的试件更容易在墙端底部发生焊接破坏。Nie等[6]对12个双钢板剪力墙试件进行试验研究,结果表明,限制钢板的宽厚比可以有效的阻止钢板在屈服前局部屈曲。Chen等[7]对 4个双钢板剪力墙试件进行试验研究,结果表明较大的高宽比和剪切刚度导致试件呈现弯曲破坏的模式。Zhang等[8]对T型的双钢板进行试验研究,结果表明同样宽度的剪力墙,内部腔数越多,变形能力越强。Ji等[9]对5个内含钢管的双钢板组合剪力墙进行试验研究,结果表明有钢管柱的剪力墙性能优越,随着有钢管柱的腔体截面面积增加,剪力墙变形和耗能能力增加,力和刚度退化能力下降,最后得到了内含钢管的双钢板组合剪力墙的承载力公式。Wang等[10]对内嵌钢板组合剪力墙进行试验研究,结果表明试件的高宽比是影响试件破坏模式的重要因素。
上述研究表明,钢板混凝土剪力墙具有承载力高、延性好的特点,但是大部分的研究着眼于双钢板夹心混凝土,内部混凝土也需要配筋,混凝土与钢板通过栓钉传递剪力,双层钢板之间并没有形成稳固的连接,而两端增加钢管的做法施工较为繁琐。
本文在试验研究的基础上,提出多腔外包钢板混凝土剪力墙的截面形式,通过内部几道竖向的肋板将墙体分隔。利用有限元软件 ABAQUS进行数值模拟,通过模拟分析所得结果与试验所得结果进行比较。研究不同腔数对剪力墙性能的影响,总结腔体数量对剪力墙力学性能、变形能力以及耗能能力的影响规律,为其在高层或超高层大楼建筑中应用提供依据。
按某超高层建筑中拟设计使用的多腔钢板混凝土组合剪力墙,采用1∶5缩尺比例进行3个多腔钢板-混凝土组合剪力墙的试验研究,试件尺寸如图1所示。由于墙体两端的可以当做被钢板包围的混凝土柱,所以该种组合剪力墙本身就可以当做附带了边缘构件。多腔钢板内焊接直径为 6 mm,长度为20 mm的栓钉,用以增强钢板和混凝土之间的拉结作用,使钢板和混凝土能够更好地实现协同工作。栓钉的间距i根据“钢板剪力墙技术规程”中式(1)确定,i是组合墙体中钢板厚度。由公式可知,s≤ 85mm 。根据试件的实际尺寸制定栓钉的间距如图1所示。


图1 试件截面尺寸 /mm
Fig.1 Dimensions of specimens
试件的截面尺寸是120 mm×700 mm,高度为1050 mm,对应的剪跨比为0.75,设计轴压比为0.5。钢板的强度等级为Q345,厚度为3 mm,多腔钢板内混凝土强度等级为C40。正立面图和侧立面图如图4所示。
使用特制的大型加载装置对“全柱模型”的剪力墙试件施加轴力、弯矩和剪力,如图2所示。水平作动器(MTS)位置通过试件跨中,用来施加层剪力;试件上端和下端分别锚固在L梁和地梁上,在层剪力作用下可以形成对剪力墙上下端的约束弯矩;轴力由竖向两个200 t的MTS施加。加载中产生层间位移时,实时调整两个竖向MTS的轴压力,使它们之和维持不变,从而保证试件轴压比维持不变。
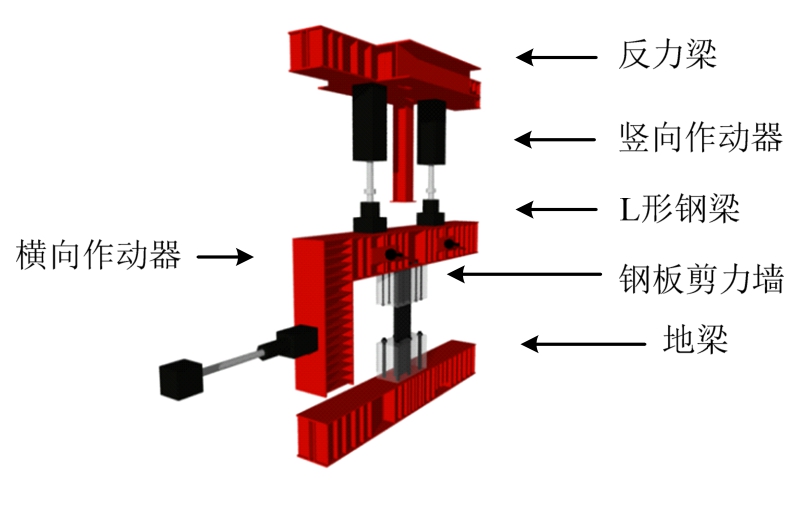
图2 试验加载装置
Fig.2 Test setup
本文中试验所用的钢材均为Q345级钢,厚度为 3 mm,弹性模量为 195500 MPa,屈服强度为467 MPa,极限强度为 558 MPa。C40混凝土抗压强度如表1所示。由于试件是在冬天浇筑的,其中5腔试件混凝土强度偏低。
表1 C40混凝土抗压强度 /MPa
Table 1 Concrete compression strength of C40

本试验采用拟静力试验方法,先在L形梁装置上部的两个竖向作动器施加轴力。所施加的轴力对应的设计轴压比为 0.5,设计轴压比按式(2)计算。式中fc为实测混凝土轴心抗压强度平均值,fy为实测的钢材屈服强度,系数1.25为重力荷载代表值产生的轴向压力分项系数;1.4和1.11分别为混凝土和钢材的材料分项系数[11]。
水平荷载的施加采用力控制和位移控制的混合加载方法,3腔试件和4腔试件的加载制度如图3所示。力控制阶段分2级加载,对应的水平荷载分别为300 kN、600 kN,每级荷载循环一次。当层间位移角达到1/400后,改用位移控制加载,每级位移增量为2.625 mm(对应1/400层间位移角),每级荷载循环两次。当试件不能维持施加的轴力或者层剪力下降到极限承载力的85%以下时,停止试验。
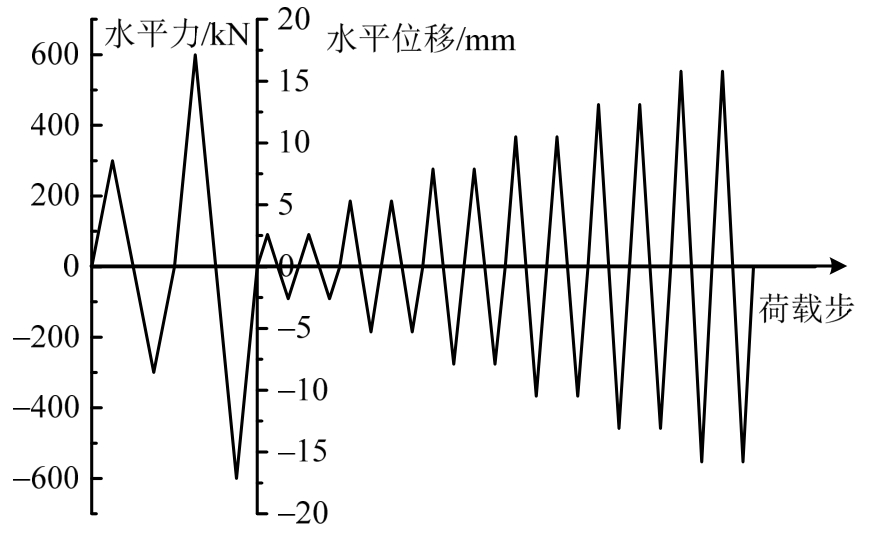
图3 试验加载制度
Fig.3 Test loading system
试验量测的内容包括:作动器施加的竖向和水平荷载;试件的层间位移;顶梁和底梁的转角位移;钢板测点的应变等。
3个试件的测点布置方案如图4所示。正面钢板布置了两排共 12个应变花,应变花分别处于肋板和腔体中间处。试件左右两端各布置四个位移计,其中四个水平的位移计监测试件的水平变形,四个竖向的位移计监测的是试件顶梁和底梁的转角变形。
试件的破坏过程以及形态可以分成3个阶段:
1)弹性阶段
从加载开始到水平荷载为600 kN,水平荷载较小,混凝土和钢板基本处于弹性阶段,试件的水平荷载-位移曲线呈线性增长,试件变形不明显。3腔、4腔、5腔达到弹性阶段最大位移分别是3.90 mm,4.96 mm和5.33 mm。

图4 试件测点布置 /mm
Fig.4 Instrumentation of the specimens
2)屈服和屈曲阶段
随着荷载逐渐增大,试件角部钢板应变超过2000 με,此时角部受压区正面钢板和侧面钢板开始发生局部鼓曲并且鼓曲现象逐渐严重。3腔试件达到此阶段时位移是10.5 mm,4腔、5腔试件达到此阶段时位移是7.9 mm。
3)破坏阶段
此时,正面钢板和侧面钢板出现多道鼓曲而且鼓曲现象严重;试件上部混凝土被压碎,失去竖向承载能力而发生破坏,试验结束后将外包钢板剖开,发现角部混凝土破碎程度严重,焊接在钢板表面的栓钉有的被拉断留在混凝土内,如图5所示。3腔、4腔、5腔试件达到此阶段的位移分别是18.4 mm、13.1 mm和23.5 mm。


图5 三种试件破坏形态
Fig.5 Failure modes of the specimens
3腔试件相比4腔、5腔试件破坏现象有所不同,在角部出现局部屈曲之后,3腔试件的正面和背面对接焊缝发生开裂,随着水平荷载的继续施加,开裂程度加深,如图5(b)所示。
三个试件的层剪力和层间变形曲线如图6所示。

图6 试件水平荷载-位移滞回曲线
Fig.6 Lateral force-displacement hysteresis loops
观察滞回曲线可以发现,5腔试件滞回曲线最为饱满,3腔试件滞回曲线捏缩最为严重。对比三种试件的骨架曲线可以发现,不同腔数模型的弹性承载力、弹性刚度、极限承载力以及延性系数等有着明显的差别,如表2所示。虽然试验中发现个别试件的地梁有少许滑移,但由于在试验中同时测量了顶梁和底梁的水平位移,位移数据使用上述两者的差值,因此加载装置的水平滑移并不会对试验结果产生实质影响。
对比三种试件的主要性能指标可以发现,5腔试件的延性最好,屈服位移角达到 1/164,峰值位移角达到1/50,极限位移角最大可以达到1/44;3腔试件的弹性段刚度最大,其负向加载的弹性段刚度可以达到269.74 kN/mm,其屈服荷载,极限荷载也最大;4腔试件的各方面性能居于3腔、5腔试件之间。由此可见,外包钢板内纵向肋板越多,对试件的延性贡献越大;腔数越少,试件的刚度越大,承载力也相应的提高。
表2 三种试件主要性能指标
Table 2 Test results of the specimens

4腔试件延性不高的原因在于四连杆L形梁的侧向支撑在层间位移为15.8 mm时,并没有提供可靠的面外转动约束,从而导致试件顶梁发生面外转动,试件顶部混凝土被局部压碎,影响整体受力性能,延性不高。但是对于4腔试件的其他性能指标影响不大。
3腔试件骨架曲线在-13.1 mm处下降较快的原因为四连杆装置地梁在此刻发生了滑移,试件因为短暂的剧烈振动加剧了内部损伤,从而导致骨架曲线在此刻下降较快,影响了后期的滞回性能。5腔试件滞回曲线饱满,骨架曲线也有明显的下降段,试件整体的性能较好。
三种试件外包钢板的应变发展规律类似,以 4腔试件为例进行说明。1号~6号应变花位于钢板上侧,7号~12号应变花位于钢板下侧。应变花最大、最小主应变与加载状态的关系曲线如图 7所示,钢板的屈服应变为2000 με。从关系曲线中可以看出:钢板上侧应力水平较大,钢板下侧应力水平较小。随着水平荷载的逐步加大,钢板表面应力也越来越大,并且角部的应力水平要大于钢板中部的应力水平。
刚度可以体现剪力墙抵抗变形的能力,是评价剪力墙抗震性能的重要指标。试件在水平往复荷载作用下,外包钢板会逐渐进入屈服,钢板内混凝土也会逐渐开裂,甚至压碎,试件的刚度便会逐渐降低。本文采用等效割线刚度 K[8]这个参数来分析试件在加载过程中刚度的变化,三种试件的刚度退化曲线如图8所示。


图7 外包钢板关键点的应变变化
Fig.7 Strain development on key points of steel plate

图8 三种试件刚度退化曲线
Fig.8 Stiffness degradation of specimens
对比三种试件的刚度退化曲线可以发现,正方向加载时,三种试件的刚度退化规律基本相同;负方向加载时,3腔试件比4腔试件刚度大,5腔试件次之,三种试件的刚度退化规律大致相同,3腔试件刚度退化程度相比其他两个试件更剧烈。对比每一种试件正向和负向加载的刚度退化曲线可以发现,刚度退化规律大致相同,但在同一荷载级别下,正向和负向的刚度又有些差别;先施加正方向荷载对试件负方向的刚度也存在影响。
剪力墙是高层建筑中重要的耗能构件,其耗能能力通常用能量耗散系数E[8]来评价。
三种试件的累积耗能和能量耗散系数与层间位移之间的关系曲线分别如图9和图10所示。三种试件的累积耗能均是随着层间位移的增加,累积耗能越来越大,并且三种试件的累积耗能与层间位移的关系曲线基本重合,说明三种试件的累积耗能能力基本相同。从试件的延性角度来看,5腔试件的延性优于4腔试件,3腔试件次之,所以对于最终的累积耗能,也是5腔试件最大,3腔试件最小,这也同时说明了试件的延性越好,累积耗能将会越大。三种试件能量耗散系数均随着层间位移的增加而增大,且数值大体相近,4腔试件的耗能能力要略强于5腔试件,从整体上来看3腔试件的耗能能力最差。分析其原因为3腔试件虽然刚度大,承载能力强,但其延性较差,故而耗能能力不如其他两个试件。

图9 累积耗能曲线
Fig.9 Accumulate energy dissipation curves of specimens

图10 能量耗散系数曲线
Fig.10 Energy dissipation coefficient curves of specimens
采用有限元分析软件ABAQUS建立分析模型,其中外包多腔钢板采用壳单元模拟,内部混凝土及栓钉均为实体单元。钢板和内部混凝土之间为摩擦接触,切向摩擦系数为 0.4[12],法向为硬接触;栓钉和钢板表面采用“Tie”约束连接,并嵌入混凝土内部。
由于试件模型较大,因此在保证计算精度的前提下对现有模型进行取半处理。取半的方法是沿着试件厚度的方向将模型取半,在截开的平面上施加限制z方向位移以及绕x轴和y轴转动的约束。有限元模型如图11(a)所示。图11(b)给出了取半模型与完整模型的结果对比,几乎完全重合的计算结果也证明了取半模型的可行性。

图11 有限元模型
Fig.11 Finite element model used in simulation
钢材的本构关系采用四折线等向强化力学模型,钢材的应力和塑性应变的具体取值如图12所示,分别由材性试验确定弹性段端点A、屈服平台端点B、极限抗拉强度点C以及破坏点D等关键点。

图12 钢材应力和塑性应变取值
Fig.12 Stress-plastic strain of steel plate
模型中混凝土的本构模型采用试验实测的混凝土强度,混凝土塑性损伤模型参考了张劲基于规范混凝土单轴本构关系[13]给出式(3):

其中k=t,c。αc取 1.94,αt取 2.47,βc取 0.7,βt取0.95。
把得到的层剪力-层间位移关系曲线与试验曲线进行对比,滞回曲线如图6所示,骨架曲线如图13所示。由图可知,有限元模拟的滞回曲线要比试验曲线更加饱满,捏缩程度相比试验滞回曲线弱一些。有限元模拟的骨架曲线和试验的骨架曲线吻合较好,极限承载力也十分接近,只是有限元模拟的弹性段刚度相对试验骨架曲线稍大一些。有限元模拟结果中极限位移和试验结果大致相同。

图13 三种试件骨架曲线对比
Fig.13 Skeleton curves compared with tests
由于混凝土是被钢板包围在里面,在试验过程中看不到混凝土的破碎情况,所以可以通过表面钢板的Mises应力表示试件在不同阶段的破坏情况。图14表示模拟四腔试件各个阶段钢板正面的Mises应力云图以及试验时对应的阶段。如图14(a)所示,当层间位移为2.625 mm时,钢板角部受压区(右上角和左下角)应力较大,小部分面积已经达到屈服。此时,试件刚刚达到屈服阶段,钢板此时并没有发生明显局部鼓曲。如图 14(b)所示,当层间位移为7.9 mm时,从正面钢板Mises应力云图中可以发现此时正面钢板屈服区域面积更大,且应力水平较高,达到450 MPa以上。同时,钢板表面发生了明显面外鼓曲,角部开始出现鼓曲。图14(c)表示,当层间位移为10.5 mm时,从正面钢板Mises应力云图中可以发现,此时正面刚板已经接近完全屈服,四个角部和钢板中间区域均达到极限抗拉强度。此时的面外鼓曲区域扩大,面外位移程度加深。图14(d)表示层间位移为 18.375 mm 时,从正面钢板Mises应力云图中可以发现,试件上部和下部区域屈服现象严重,且正面钢板大部分发生鼓曲,Mises应力分布不均匀。此时正面钢板和角部钢板出现多道鼓曲,并且鼓曲现象严重。从试验现象来看,有限元模拟和试验现象总体上吻合较好,能够较好的反应试验过程中钢板局部鼓曲等现象。

图14 四腔试件各个阶段试验现象
Fig.14 Performance of the four-tube specimen
在上述有限元模型验证的基础上,对影响多腔钢板-混凝土组合剪力墙性能的主要参数进行分析。参数分析的基本试件为试验的三种试件,单腔长宽比分别是 1.94、1.46、1.17,对应的腔数分别是 3腔、4腔、5腔,在此基本参数上开展对腔数的参数分析。在进行参数化分析建模时,钢材的本构关系改为双折线随动强化模型,弹性模量E=2.06×105MPa,屈服荷载为345 MPa,极限荷载为470 MPa,混凝土仍采用C40混凝土。
为探究腔数对试件极限承载力的影响,在原有模型的基础上,补充新建单腔长宽比为5.83、2.92、0.97的三种模型,对应的腔数分别是1腔、2腔、6腔,对比极限承载力的差别,六种不同腔数模型单向加载层剪力-层间位移关系曲线如图15所示。

图15 单腔长宽比对骨架曲线的影响
Fig.15 Influence of length to width ratio of single tube
从图中可以发现,随着单腔长宽比的减小(腔数的增加),组合墙体的极限承载力和弹性段刚度降低,而延性增加;而单腔长宽比为 0.97~1.94的模型,即腔数增长到3腔之后,无论是弹性段刚度还是极限承载力都十分接近,这说明当多腔钢板-混凝土组合剪力墙内单腔长宽比降低至1.94之后,剪力墙的极限承载力不会有显著的变化。
从受力机理角度分析,试件达到极限承载力时,正面钢板早已大面积屈服,角部受压区混凝土较大部分被压碎,而角部受压区混凝土较大部分被压碎是导致试件极限承载力下降的直接原因。墙体内的肋板将内部的混凝土分割成若干独立单元,单元之间依靠混凝土与肋板的粘结力和外包钢板的连续性维持共同工作,削弱了内部混凝土的整体性。由单腔时内部混凝土延性较差的整体受剪,转化为多腔时内部多个混凝土柱的弯剪共同作用,改变了组合墙体的受力模式。因此适当减小单腔长宽比(增加腔数),组合墙体的初始弹性刚度和承载力越低,而延性越好。
本文提出双钢板-混凝土组合剪力墙截面形式,对3个不同截面构成的剪力墙进行拟静力试验研究及有限元模拟分析,得到以下结论:
(1)三种试件的破坏模式基本相同,均为试件在加载后期,上部混凝土被压碎,角部钢板发生屈曲,竖向失去承载能力而发生破坏。在整个试验过程中,三种试件均表现出较好的力学性能和较强的耗能能力,其中3腔试件,即单腔长宽比为1.94的刚度及承载力最高,但延性较差;5腔试件,即单腔长宽比为 1.46的刚度及承载力最小,但延性最优;4腔试件,即单腔长宽比为1.17的力学性能和延性居于3腔和5腔试件之间,但耗能能力最强。
(2)在试验研究的基础上,建立了多腔钢板混凝土组合剪力墙有限元模型,有限元分析和试验的荷载-位移曲线吻合较好。说明本文建立的有限元模型能够较合理地模拟这类构件的受力性能,一定程度上可以代替部分试验,为建立多腔钢板混凝土组合剪力墙的抗震方法提供依据。
(3)对试件的单腔长宽比进行参数分析,结果表明,组合墙体的单腔长宽比越小(腔数的增加),极限承载力越小,延性越好,但随着单腔长宽比减少到 1.94时,剪力墙的极限承载力不会有显著的变化。
下一步会继续研究墙体厚度、钢板厚度、栓钉间距、剪跨比等因素对剪力墙性能的影响。
参考文献:
[1]Hitaka T,Matsui C,Sakai J.Cyclic tests on steel and concrete-filled tube frames with slit walls [J].Earthquake Engineering & Structural Dynamics,2010,36(6): 707―727.
[2]聂建国,陶慕轩,樊健生.双钢板-混凝土组合剪力墙研究新进展[J].建筑结构,2011,41(12): 52―60.Nie Jianguo,Tao Muxuan,Fan Jiansheng.Research advances of composite shear walls with double steel plates and filled concrete [J].Building Structure,2011,41(12): 52―60.(in Chinese)
[3]聂建国,卜凡民,樊健生.高轴压比、低剪跨比双钢板-混凝土组合剪力墙拟静力试验研究[J].工程力学,2013,30(6): 60―66.Nie Jianguo,Bu Fanmin,Fan Jiansheng.Quasi-static test on low shear-span ratio composite shear wall with double steel plates and infill concrete under high axial compression ratio [J].Engineering Mechanics,2013,30(6): 60―66.(in Chinese)
[4]马恺泽,刘伯权,鄢红良,等.高轴压比双层钢板-高强混凝土组合剪力墙抗震性能试验研究[J].工程力学,2014,31(5): 218―224.Ma Kaize,Liu Boquan,Yan Hongliang,et al.Experimental investigation on aseismic behavior of double steel high strength concrete shear walls with high axial load ratio [J].Engineering Mechanics,2014,31(5):218―224.(in Chinese)
[5]Eom T S,Park H G,Lee C H,et al.Behavior of double skin composite wall subjected to in-plane cyclic loading[J].Journal of Structural Engineering,2009,135(10):1239―1249.
[6]Nie J G,Hu H S,Fan J S,et al.Experimental study on seismic behavior of high-strength concrete filled double-steel-plate composite walls [J].Journal of Constructional Steel Research,2013,88(9): 206―219.
[7]Chen L,Mahmoud H,Tong S M,et al.Seismic behavior of double steel plate–HSC composite walls [J].Engineering Structures,2015,102(11): 1―12.
[8]Zhang X,Qin Y,Chen Z,et al.Experimental behavior of innovative T-shaped composite shear walls under in-plane cyclic loading [J].Journal of Constructional Steel Research,2016,120(1): 143―159.
[9]Ji X,Jiang F,Qian J.Seismic behavior of steel tube–double steel plate–concrete composite walls:experimental tests [J].Journal of Constructional Steel Research,2013,86(6): 17―30.
[10]Wang W,Wang Y,Lu Z.Experimental study on seismic behavior of steel plate reinforced concrete composite shear wall [J].Engineering Structures,2018,160(4):281―292.
[11]李盛勇,聂建国,刘付钧,等.外包多腔钢板-混凝土组合剪力墙抗震性能试验研究[J].土木工程学报,2013,46(10): 26―38.Li Shengyong,Nie Jianguo,Liu Fujun,et al.Experiment study on aseismic behavior of concrete filled double-steel-plate composite shear walls [J].China Civil Engineering Journal,2013,46(10): 26―38.(in Chinese)
[12]Gourley B C,Tort C,Denavit M D,et al.A synopsis of studies of the monotonic and cyclic behavior of concrete-filled steel tube members,connections,and frames [R].Newmark Structural Engineering Laboratory.University of Illinois at Urbana-Champaign,2008.
[13]张劲,王庆扬,胡守营,等.ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构,2008,38(8): 127―130.Zhang Jin,Wang Qingyang,Hu Shouying,et al.Parameters verification of concrete damaged plastic model of ABAQUS [J].Building Structure,2008,38(8):127―130.(in Chinese)
ASEISMIC BEHAVIOR OF COMPOSITE SHEAR WALL WITH STIFFENED DOUBLE STEEL PLATES AND INFILLED CONCRETE
ZHANG Wen-yuan1,2,WANG Ke1,2,WANG Qiang1,2,CHEN Yong3,ZHOU Yu3,DING Yu-kun1,2
(1.Key Lab of Structures Dynamic Behavior and Control of the Ministry of Education,Harbin Institute of Technology,Harbin,150090,China;2.Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of the Ministry of Industry and Information Technology,Harbin Institute of Technology,Harbin 150090,China;3.China Northeast Architectural Design & Research Institute Co.,Ltd.,Shenyang 110006,China)
Abstract:In order to study the aseismic behavior of shear walls in super high-rise buildings,the quasi-static test and finite element analysis on steel plate-concrete composite shear walls were conducted.The research focused on the effect of cavity on the aseismic performance,which included failure mode,bearing capacity,hysteresis curves,skeleton curves,ductility,rigidity degeneration and energy dissipation capacity.All specimens failed in the same failure mode,characterized by concrete crushing at the upper wall and local buckling of the steel plate in the corner.The results indicated that the composite shear wall exhibited excellent inter-storey deformation capacity and energy dissipation under high axial forces.The average value of the ultimate drift ratios for all the specimens was 1/61,and bearing capacity decreased with the decrease of length to width ratio of a single tube.A finite element model developed by ABAQUS is used to simulate the performance of this type of composite shear wall and the accuracy of the model is validated through the comparison with the experiment results.Meanwhile,it has been found that the ultimate bearing capacity of the composite shear wall is not significantly affected until the length to width ratio of a single tube decrease to 1.94.
Key words:composite shear wall; finite element analysis; energy dissipation capacity; ductility; length to width ratio
丁玉坤(1979―),男,内蒙巴盟人,副教授,工学博士,主要从事轻型钢结构研究(E-mail: dingykun@sohu.com).
周 宇(1987―),男,辽宁人,工程师,工学硕士,从事结构研究、结构设计与建筑施工工作(E-mail: zhouy.0407@163.com);
陈 勇(1966―),男,辽宁人,教授级高工,工学博士,从事结构研究与设计工作(E-mail: dr_cy@126.com);
王 强(1991―),男,黑龙江人,硕士生,主要从事高层钢结构和轻钢结构研究(E-mail:851280673@qq.com);
张文元(1972―),男,辽宁人,教授,工学博士,主要从事高层钢结构和轻钢结构研究(E-mail: hitzwy@163.com);
作者简介:
通讯作者:王 柯(1993―),男,广西柳州人,博士生,主要从事高层钢结构和轻钢结构研究(E-mail: wangke305@hit.edu.cn).
基金项目:国家自然科学基金青年基金项目(51108125);中建股份科技研发课题项目(CSCEC-2016-Z-41)
收稿日期:2017-06-21;修改日期:2018-03-28
文章编号:1000-4750(2018)11-0125-09
doi:10.6052/j.issn.1000-4750.2017.06.0482
文献标志码:A
中图分类号:TU398+.2