秦国华 1 ，林 锋 1 ，叶海潮 1 ，侯源君 1 ，陈雪梅 2 ，韩 雄 2 ，王华敏 1
(1.南昌航空大学航空制造工程学院，南昌 330063；2.成都飞机工业(集团)有限责任公司数控加工厂，成都 610092)
摘 要： 在毛坯成形过程中，材料力学性能的非均匀性导致铝合金厚板内产生残余应力，以致在后续切削加工过程中，随着材料的去除，残余应力的释放使得整体结构件发生变形，严重影响着整体结构件的尺寸稳定性。因此，定量化研究切削过程中残余应力释放的加工变形分析与预测是进行加工质量控制的核心环节，对于实现加工过程的高效化和精密化至关重要。通过铝厚板的材料去除转化为残余应力的释放，利用静力平衡条件将作用于整体结构件的残余应力等效为外力后，综合考虑铝厚板横向方向和轧制方向的残余应力，依据弯曲变形理论创新性地建立铝厚板内初始残余应力释放模型。残余应力释放模型不仅能够准确地计算整体结构件的加工变形，而且还能够方便地优化工艺参数完成加工变形的有效控制。根据模型计算值与有限元仿真值、实验测量值的相互比较，分析结果表明：无论是幅值还是变形曲线，计算值都与仿真值具有高度一致性，而与测量值相比，尽管在变形曲线上具有很好的吻合性，但由于残余应力的测量误差使得两者在幅值上亦存在一定误差。
关键词： 铝合金厚板；初始残余应力；加工变形；航空整体结构件；结构优化
零件的加工变形问题一直是困扰航空制造业的重要难题之一。波音公司通过分析四个飞机项目中加工变形造成的经济损失，认为加工变形导致零件返工和报废，直接或间接产生的经济损失超过2.9亿美元 [1] 。航空整体结构件一般由铝合金厚板材料进行90%～95%的材料切除后获得 [2] ，其加工变形问题显得尤为突出。尽管如此，但由于铝合金具有强度高、重量轻、刚度高、疲劳强度高、表面完善、成本低的优势 [3] ，在飞机机翼壁板、隔框、机身框、翼梁、翼肋等零件上进行了广泛使用 [4] 。
航空整体结构件加工变形很早便引起了欧美等发达国家的关注，空客公司自从20世纪90年代中期就开始了专门研究，在制造层面上实现了仅需要数控人员即可完成操作的成熟解决方案 [2] 。但是欧美的相关成果一般不对外宣布且进行了严格的知识产权保护，我国技术人员曾试图与波音公司就数控变形问题进行讨论，但因保密问题无果而终 [5] 。
航空整体结构件作为大型薄壁类零件，在高速加工已经普及航空业的情况下，切削力和切削热对加工变形的影响相比于毛坯中的初始残余应力已经可以忽略 [6] 。Huang等 [7] 利用有限元仿真方法，以毛坯初始残余应力为初始条件、以切削应力为动态边界条件，分析了整体结构件的加工变形规律，经化学铣削实验对比分析后认为在高速加工下毛坯初始残余应力对加工变形的影响占到90%以上。Zhang等 [8] 在测得板材厚度方向上的初始残余应力分布后，利用有限元方法研究了T形件在不同位置处的加工变形，总结出适当的厚度方向位置可以有效地降低零件变形。张以都等 [9] 通过有限元方法分析了不同走刀路径对加工变形的影响，认为在仅考虑毛坯初始残余应力的情况下，走刀路径对工件变形的影响可以忽略，同样归纳出在高速加工中可以忽略切削对加工变形的影响。这些研究的手段主要为有限元仿真分析，虽然能较为准确地预测加工变形，但难以系统地分析加工变形机理，确定初始残余应力释放影响工件变形的内在规律。
Naotake等 [10] 提出了残余应力幅值的概念，认为残余应力幅值(即残余应力最大值与最小值之差)与加工变形线性相关。Heymes等 [11] 提出了残余应变能的评价方法，认为板材类构件内存贮的弹性能越大残余应力引起的加工变形越大。这些方法主要在于评价残余应力引起加工变形的能力大小，但是无法直接对加工变形进行预测。当前的解析方法局限性较大，计算中仅能考虑单一方向应力，且材料去除必须为简单的厚板层削 [12] 和开单槽 [13] 情况。
为此，通过对毛坯初始残余应力的等效转化，以及横向和厚度方向的合成应力转化后，利用材料力学的弯曲变形分析模型，建立航空整体结构件材料去除引起的残余应力释放模型，实现整体结构件加工变形的显式精确计算。
为了实现复杂梁类整体结构件因残余应力释放引起加工变形的解析计算，必须进行等效受力和等效轧制方向应力的转化。
在尺寸为 R mm×T mm×H mm 的铝合金厚板内，其初始残余应力是力平衡和力矩平衡的整体，应满足下列方程：
其中：σ r 为轧制方向的分力；σ t 为横向方向的分力。
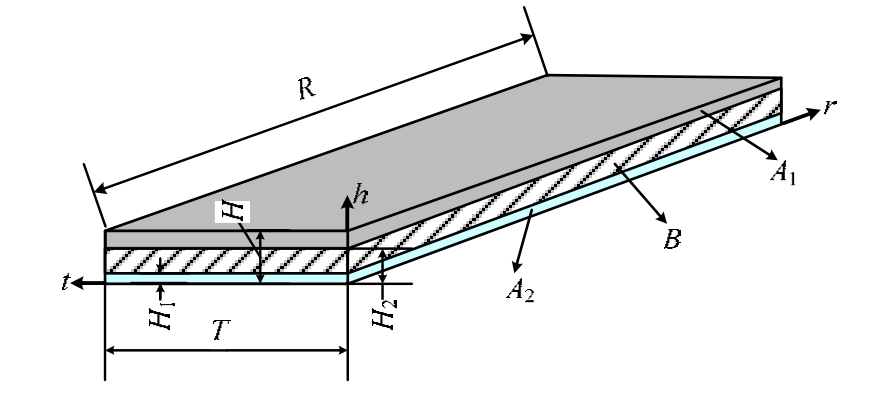
图1 零件在厚板中区域示意图
Fig.1 Area of the part in thick plate
图1为零件的三个区域，其中顶端部分A 1 和底部部分A 2 分别为材料去除区域，而中部的阴影部分B为铝合金厚板经材料去除后的成形零件。在材料去除的过程中，残余应力不断得到释放。相比于材料的屈服极限，残余应力较小，故残余应力的释放过程可以视为铝合金厚板的弹性变形过程。由此一来，残余应力释放过程可以认为材料是一步去除到位，不需要考虑材料去除的顺序。Robinson等 [14] 通过中子衍射法证明了材料去除可造成应力的重新分布，但不能造成应力驰豫现象，同样说明了在仅考虑残余应力情况下分析加工变形可以不考虑材料的去除顺序。
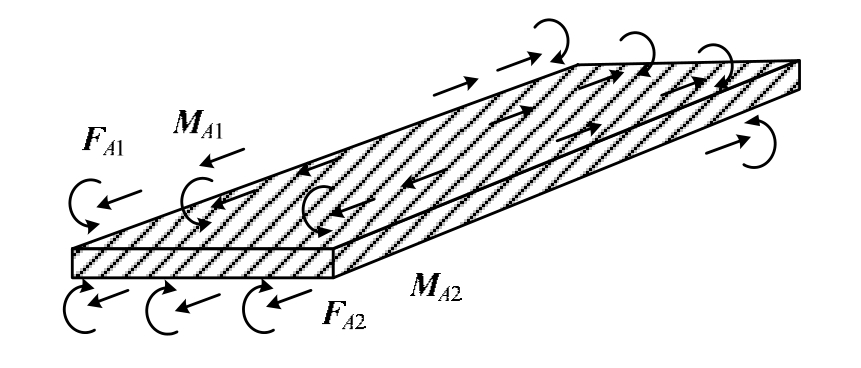
图2 作用B区的等效力
Fig.2 Equivalent loads on B zone
因此，可以将区域A 1 、B和A 2 分离看待，在加工前将区域B作为受区域A 1 、A 2 等效外力作用的薄层，如图2所示。因为铝厚板内残余应力满足式(1)和式(2)的力平衡和力矩平衡方程，所以区域B的内外力同样满足力平衡和力矩平衡，则有方程：
其中： F A1 、 M A1 和 F A2 、 M A2 分别为区域A 1 和区域A 2 作用于区域B的外力和外力矩； F B 和 M B 分别为区域B的内力和内力矩。
当区域A 1 和A 2 的材料去除后，其对区域B的作用力 F A1 、 M A1 和 F A2 、 M A2 也随之消除，故加工后的工件可以认为是仅受到由相应部位内初始残余应力所形成的 F B 和 M B 作用的受载变形体。而 F B 和 M B 在横向方向t和轧制方向r的分力分别为：
式中，H 1 和H 2 分别为工件在铝厚板厚度方向区域。
综上所述，残余应力释放引起的零件变形，可以等效为零件区域的残余应力作为外力施加在零件上引起的变形。
在类梁工件的变形分析中，同时考虑轧制方向和横向方向应力将使得计算难以进行。但是，轧制方向的变形受到横向方向作用力的影响，在分析轧制方向变形的过程中有必要将横向方向作用力考虑进去。
图3 零件受力图
Fig.3 Status of forces on workpiece
若工件在横向和轧制方向上的应力分别为σ t 和σ r ，如图3所示，那么由弹性理论可知，轧制方向的应变ε r 应为：
式中，v和E分别为工件材料的泊松比和弹性模量。
为了便于清晰地分析轧制方向的零件变形，定义轧制方向的等效应力如下：
式中，σ nr 为等效应力。
本文推导的变形计算解析式主要适用于梁类零件，这类零件变形的特征为，轧制方向的变形远大于其他方向的变形，且扭转变形极小。
图4 工件约束状态
Fig.4 Status of constraints on workpiece
工件在加工后的变形是在自由状态下产生的，其约束与简支梁基本相同，如图4所示，这样，工件可以自由伸缩、弯曲。
图5 力矩计算参数确定
Fig.5 Determination of parameters for torque calculation
在长度方向r上的不同位置上，整体结构件的横截面一般是不同的。因此，为了计算截面惯性矩I pi 和关于中心轴的力矩，需要将其进行分段，如图5所示。在确定了中性轴所在高度H vi 后，该截面的弯矩 M i 可表示为：
式中，t=T-T'为零件在高度方向 h上有材料部分的尺寸之和。
这样，由任意位置处截面上的弯矩 M i 引起的挠度ω i 可描述为：
因为力矩和截面惯性矩随横截面的不同而改变，依据式(9)求解挠度时需要进行二次积分，这个积分过程较为繁琐也比较困难。为此，可以通过对式(9)进行多项式拟合，即：
其中，系数A ij 为常数。
通过对式(10)、式(11)进行二次积分后，即可获得挠度ω i 的基本形式为：
其中，B i 和C i 为待定系数。
系数 B i 和 C i 可以通过边界条件求取，边界条件有三个，分别为：1)在 r=0处，存在 ω=0；2)在r=R处，存在ω=0；3)在i和i+1交接处，存在 ω i = ω i+1 和 
′ = 
。
这里选取两个典型实例，对推导的变形求解方法进行应用和验证。实例1为简单薄板类工件的实验和有限元比较验证，实例2为某主机厂的复杂框类整体结构件有限元验证。
薄板件的材料选用经过拉伸率为 δ=2.4%的7075-T73铝合金板材 [6] ，其弹性模量为E=70.5 GPa，泊松比为v= 0.33。毛坯尺寸为长R = 200 mm，宽T = 20 mm，高H = 6 mm，成品尺寸为200 mm ×20 mm × 4.5 mm，如图6所示，其中阴影部分为成品部分。薄板件的中性轴和截面惯性矩分别为H v =2.25 mm和I rp =151.875 mm 4 。
图6 零件与毛坯的关系 /mm
Fig.6 Relationship of workpiece and blank
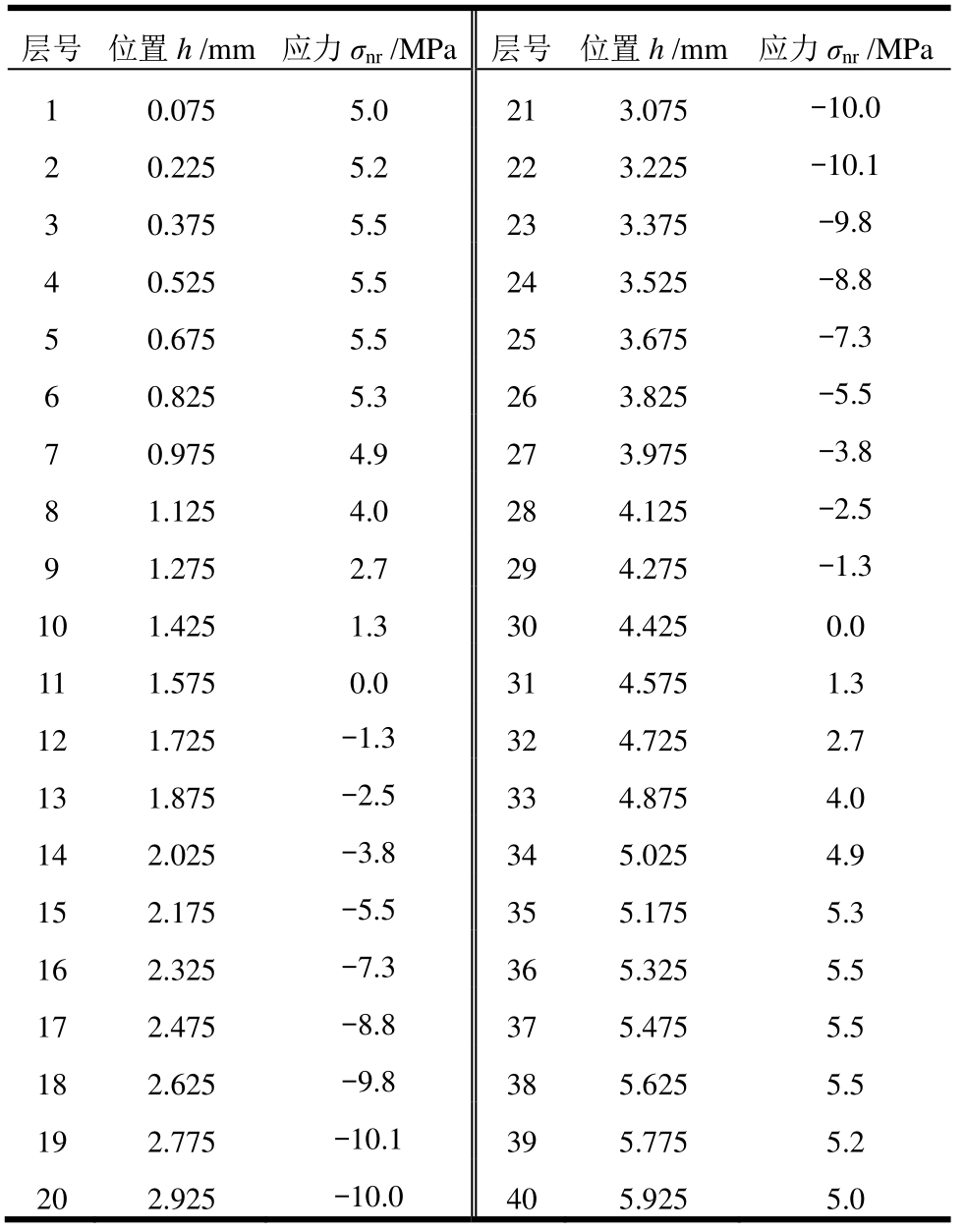
图7为毛坯内初始残余应力分布曲线 [6] ，沿厚度方向h对薄板件进行均匀分层，每层厚度为H i =0.15 mm。若选取每层中心的残余应力作为该层的应力值，则根据图7的初始残余应力分布状态，通过静力平衡条件求解出每层的应力值如表1所示。
该薄板件在任意位置r i 处加工表面的横截面均为相同的矩形，由式(8)可知截面力矩均为：
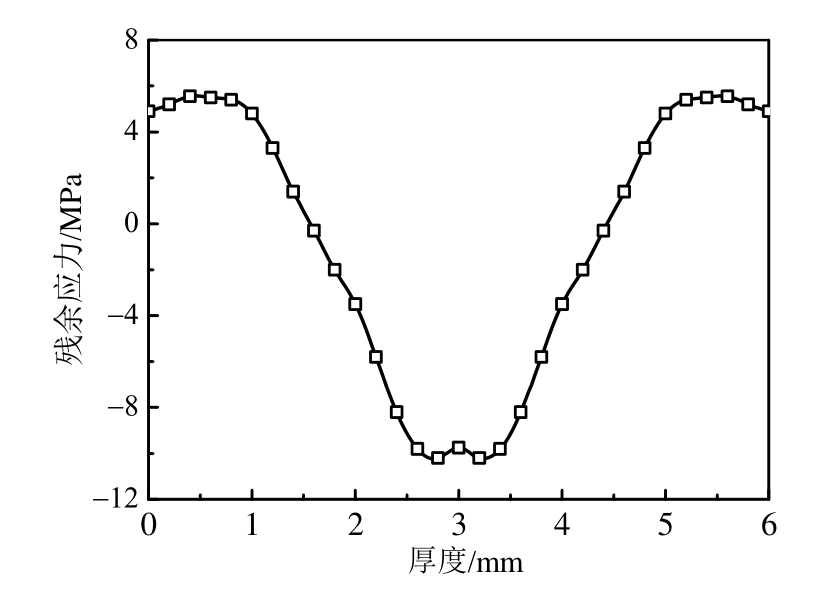
图7 初始残余应力
Fig.7 Distribution of initial residual stresses
因此，根据式(12)可得关于轧制方向的挠曲方程如下：
其中，A和B为由变形约束条件确定的待定系数。
表1 每层残余应力值
Table1 Residual stress in each layer
由图4可知，工件在首尾两端的变形均为0，则有：
代入式(14)求解得系数A和B的值为：
将系数A和B代入式(14)后，最终可得工件关于轧制方向的挠曲方程为：
接下来采用有限元方法解算工件变形。因为横向方向的残余应力很小，有限元分析中可不予考虑，故有限元分析采用二维平面单元。选择“Static，General”分析步类型，网格密度设定为0.15，总共有53320个单元，单元类型为CPS4R。在Interaction模块中使用 Model change进行“单元杀死”技术模拟材料的去除。图8为有限仿真得到的变形云图，在相同轧制方向位置的不同厚度上变形是一样的，可以用一条挠度曲线描述变形效果。加工变形测试实验分为材料去除、变形测量、数据分析等三个步骤。每次加工去除一层材料后，测量加工变形和工件厚度直到下一次加工准备完成，中间花费3 min～5 min，以使得加工测试过程与航空工业零件制造的现有工作流尽量吻合。
图8 仿真变形结果(放大100倍)
Fig.8 Simulated results (amplified 100 times)
图9 加工实验现场
Fig.9 Scene of machining experiment
选用Fadal VMC 3016L立式铣床进行加工，转速为5000 r/min，刀具直径为50 mm，如图9所示。高速铣削能够保证在动态加工过程中引入的残余应力水平很小 [6] 。变形测量在同一台铣床上进行，选用的测量头能够保证误差在3 μm以下，如图10所示。通过反复测量工件同一位置，并整理不同测量值。因此，可以认为预期精度在0.01 mm以下 [6] 。
图10 变形测量现场
Fig.10 Scene of deformation measurement
实验测量、有限元求解和解析式求解求得的挠度曲线比较如图 11所示，三者趋势完全一致，最大变形位置均发生在正中间位置，即在长度方向的100 mm处，实验测量值为0.18 mm，有限元仿真值为 0.22 mm，而解析计算结果也为 0.22 mm。解析计算值和有限元仿真值高度统一，两者与实验结果的相对误差为22.22%。
图11 挠曲变形对比
Fig.11 Comparison of deflection
虽然解析计算结果和有限元仿真值具有很高的吻合度，但是与实验数据相比，两者仍然存在25%左右的误差，主要原因分析如下：
1)残余应力测量和变形测量误差，测量过程中受到人为操作，设备条件和实验方法本身的限制不可避免地会带来误差；
2)厚板残余应力在同一厚度方向平面内并非完全相同，厚板在应力测量过程和变形分析过程中认为同一厚度方向平面内完全相同，但事实上同一平面内存在或多或少的不同，这也将使计算结果产生偏差；
3)有限元单元密度产生的误差，有限元仿真计算中，特别是大型复杂零件，受计算机硬件性能的限制，为了保证计算过程的顺利进行，其网格密度不能太高。这样，相对稀疏的网格密度将造成一定的计算误差。
图12 复杂框类结构件 /mm
Fig.12 Complex beam parts
某航空单面梁类结构件如图 12所示，长R=1005 mm，宽T=200 mm，高H=32 mm，壁板厚度均为 t=5 mm，材料为航空铝合金 7075，弹性模量为E=71.7 GPa，泊松比为v=0.33。残余应力的分布曲线如图13所示。
由于零件具有对称特征，计算时仅考虑一半，故将其分段为14个区域，如图12所示。
图13 残余应力分布曲线
Fig.13 Distribution curve of residual stresses
根据图 13的初始残余应力分布状态，通过公式(7)可知，等效轧制方向的应力可描述为厚度位置h的函数，即：
由于零件属于对称结构，自由释放状态下既有对称约束。因此，r=0 mm时ω=0，而r=502.5 mm时ω'=0。最终得到14段区域的挠度曲线方程如下：
其中：a i,j (1≤i≤14, 1≤j≤6)为系数，具体值如表2所示。
表2 挠度曲线的系数
Table2 Coefficient deflection equations
而在有限元仿真过程中，使用“Static，General”分析步类型，沿厚度方向平均分为 32层后，采用单元类型C3D10划分网格，总共有137797个单元，图14为计算后得到的工件变形云图。
图14 仿真变形结果(放大10倍)
Fig.14 Simulated results (amplified 10 times)
由图14可以看出，在确定的轧制方向位置上，不同横向方向位置和不同厚度方向位置的变形基本一致，因此可以用一条挠度曲线代表整体沿轧制方向变形的变化趋势。图 15为计算结果和仿真值的对比，二者有相同的变形趋势，最大变形均发生在502.5 mm处，分别为-9.573 mm和-9.264 mm，两者之间的误差仅为3.33%。
图15 挠曲变形对比
Fig.15 Comparison of deflection
结构优化的目的主要集中在体积、频率、柔度和模态等方面的控制 [15] ，鲜有针对残余应力引起的加工变形。由式(9)可知，改变梁类航空整体结构件的结构，将引起截面惯性矩I p 和作用力矩 M 的变化，从而实现航空整体结构件加工变形ω的控制。然而，截面惯性矩I p 和作用力矩 M 亦为长度位置r和厚度方向位置h的复杂函数，为了获得最小的加工变形ω，必须对式(9)进行一次积分求得ω'，并令其等于0，解算出r和h的值，这个求值过程将变得十分困难。为此，针对类似于梁的航空整体结构件，其简便的结构优化方法构造如下：
第一步，搜索隔板沿厚度方向的位置，使隔板的作用力矩最小化。
与截面惯性矩 I p 相比，作用力矩 M 的变化在幅值和梯度上都更加剧烈，而对作用力矩 M 影响最大的是隔板沿厚度方向的位置 h。基于力矩的解析式可知，有两种方法可以最小化力矩。一是在隔板内部，沿厚度方向寻找中性轴的位置 H rv (此时有h≤H rv ≤h+t/2)，使其上下的隔板内部作用力矩 M 1 相互抵消；另一则是，沿厚度方向寻找等于 0的等效残余应力，其相应位置h˙即可作为隔板位置(即h˙= h + t/2)，此时隔板上的作用力矩 M 1 为0。
第二步，调整中性轴的位置，使得隔板内部的作用力矩等于其余部分的作用力矩。
按照隔板内作用力矩最小化的目的，沿厚度方向选取中性轴后，零件结构基本确定。计算此时除隔板外的其余部分的作用力矩 M 2 ，然后通过沿厚度方向微调隔板的位置，使其产生作用力矩 M 1 ，以抵消其余部分的作用力矩 M 2 。因为隔板位置的少许变动对中性轴位置影响较小，可以认为其余部分的作用力矩基本不变。因此，微调后的位置所形成的结构，即可视为零件的最终结构。
这里，以上述方法对图 12的复杂零件进行结构优化，具体过程概述如下：
步骤1：确定隔板的初始位置。
隔板初始位置的选择方案包括：一是沿厚度方向的正中位置。当中性轴在隔板内部时，由于初始残余应力关于厚度方向对称(参见图 13)，因此有 
。二是等效残余应力为零的位置。如图13所示，当h˙=7.62 mm和h˙=24.38 mm，等效残余应力σ = 0。因此有h = 5.12 mm和h =21.88 mm。
步骤2：确定隔板的最终位置。当h = 13.5 mm时，由于结构件关于厚度方向对称，显然其余部分的作用力矩同样为零。因此最终位置依旧为厚度方向正中间位置。当h = 21.88 mm时，为了提高计算效率，选取此时各部分的平均中性轴位置作为整个零件的初始中性轴，计算除隔板之外其余部分的作用应力。通过计算得整体中性轴位置为H rv = 23.59 mm，则其余部分的作用力矩为 
345.7 N·mm。由于在厚度方向上隔板的截面积为S = 765.5 mm 2 ，故隔板内需额外产生应力为 σ =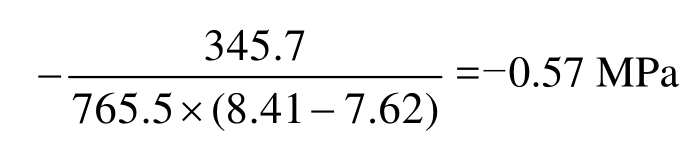 
。再由式(18)可知，最终位置仅需向外移动0.01 mm，即隔板的最终位置h = 21.87 mm。
同理，当h = 5.12 mm时，隔板的最终位置可确定为h = 5.11 mm。
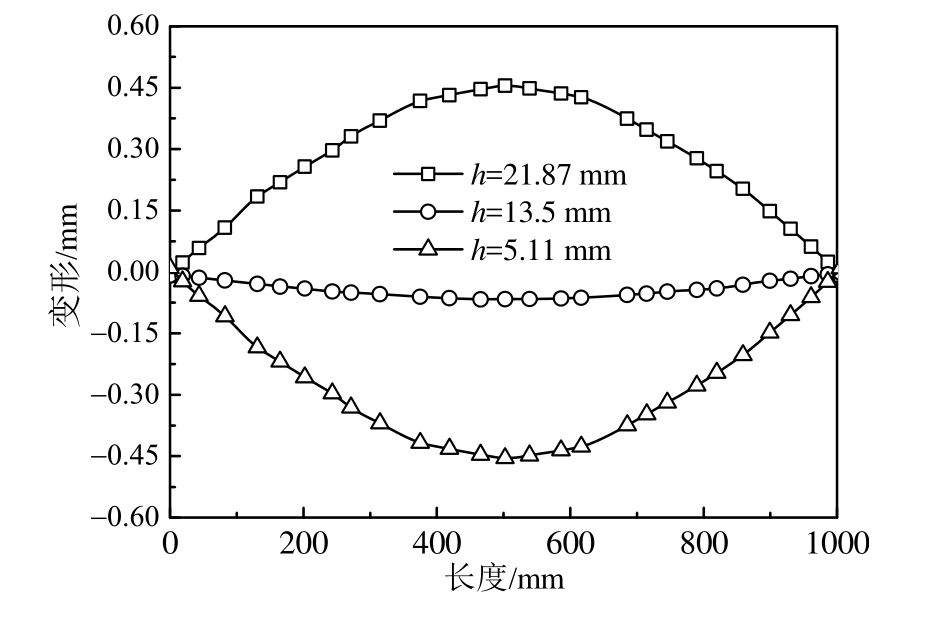
图16 结构优化后的变形比较
Fig.16 Comparison of deflection
利用有限元方法计算优化后的零件结构在残余应力释放时产生的加工变形，如图 16所示。当隔板位置为 h =5.11 mm时，加工变形的最大值为ω max =-0.455 mm；当隔板位置为h =21.87 mm时，加工变形的最大值为ω max = 0.455 mm；当隔板位置为 h =13.5 mm 时，加工变形的最大值为ω max =-0.067 mm。相比于隔板处于底面位置(即h=0)时，最大的加工变形分别降低了95.09%和99.28%。
(1)通过将毛坯内残余应力释放引起的零件变形，等效为零件内残余应力作为外力施加在零件上引起的变形，依据材料力学的弯曲变形计算方法推导出梁类航空结构件的残余应力引起加工变形的解析模型。
(2)通过将加工变形的模型计算值与有限元仿真值、实验测量值进行对比，分析后结果表明：计算值与仿真值无论是幅值还是变形曲线都具有高度一致性，而与测量值在变形曲线上具有很好的吻合度，但两者在幅值上则存在一定的误差。
(3)相比于有限元方法的建模繁杂，其计算精度受到网格密度的影响外，优化过程中采用有限元方法必受限于隔板位置的取值影响，导致在厚度方向上的仿真数量有限，得不到全局最优值。基于模型解析式建立的结构优化法，能够快速、精确的确定最低变形位置。
参考文献：
[1]Bowden D M, Halley J E.Aluminum reliability improvement program - final report 60606 [R].Chicago,IL, USA: The Boeing Company, 2001.
[2]Chantzis D, Van-der-Veen S, Zettler J, Sim W M.An industrial workflow to minimize part distortion for machining of large monolithic components in aerospace industry [C].Turin: Elsevier B.V, 2013: 281―286.
[3]刘静安, 王嘉欣.大型铝合金型材及其用途[J].有色金属加工, 2002, 31(3): 40―43, 46.Liu Jingan, Wang Jiaxin.Large aluminum alloy profiles and their applications [J].Nonferrous Metals Processing,2002, 31(3): 40―43, 46.(in Chinese)
[4]王祝堂.铝合金中厚板的生产、市场与应用[J].轻合金加工技术, 2005, 33(1): 1―20.Wang Zhutang.Production, market and application of aluminum alloy plate [J].Light Alloy Fabrication Technology, 2005, 33(1): 1―20.(in Chinese)
[5]王秋成.航空铝合金残余应力消除及评估技术研究[D].杭州: 浙江大学, 2003.Wang Qiucheng.Evaluation and relief of residual stresses in aluminum alloys for aircraft structures [D].Hangzhou: Zhejiang University, 2003.(in Chinese)
[6]Trummer V R, Koch D, Witte A, Santos J F, Castro P M S T.Methodology for prediction of distortion of workpieces manufactured by high speed machining based on an accurate through - the - thickness residual stress determination [J].The International Journal of Advanced Manufacturing Technology, 2013, 68(9/10/11/12): 2271―2281.
[7]Huang X M, Sun J, Li J F.Finite element simulation and experimental investigation on the residual stress - related monolithic component deformation [J].The International Journal of Advanced Manufacturing Technology, 2015,77(5/6/7/8): 1035―1041.
[8]Zhang Z, Li L, Yang Y F, He N, Zhao W.Machining distortion minimization for the manufacturing of aeronautical structure [J].The International Journal of Advanced Manufacturing Technology, 2014, 73(9/10/11/12): 1765―1773.
[9]张以都, 张洪伟.航空整体结构件加工变形有限元数值仿真 [J].北京航空航天大学学报, 2009, 35(2):188―192.Zhang Yidu, Zhang Hongwei.Finite element simulation of machining deformation for aeronautical monolithic component [J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(2): 188―192.(in Chinese)
[10]Naotake Y, Yoshimichi H.Removal technique of residual stress in 7075 Aluminum Alloy [C].Residual stress III: Science and Technology.Tokushima: Elsevier Science Publishers, 1192: 1140―1145.
[11]Heymes F, Commet B, DuBost B, Lassince P, Lequeu P,Raynaud G M.Development of new Al alloys for distortion free machined aluminum aircraft components[C].The 1st International Non-ferrous Processing and Technology Conference, Missouri: ASM International,1997: 249―255.
[12]Shang H S.Prediction of the dimensional instability resulting from machining of residually stressed components [D].LuBurke: Texas Tech University, 1995:1―128.
[13]刘秦龙, 华军, 贾瑞艳.开槽应力释放法优化整体结构件切削加工研究[J].机械设计与制造工程, 2014,43(4): 21―24.Liu Qinlong, Hua Jun, Jia Ruiyan.Study on the slotting monolithic components under residual stress and its optimization [J].Machine Design and Manufacturing Engineering, 2014, 43(4): 21―24.(in Chinese)
[14]Robinson J S, Tanner D A, Truman C E.Measurement and prediction of machining induced redistribution of residual stress in the aluminum alloy 7449 [J].Experimental Mechanics, 2011, 51(6): 981―993.
[15]王琥, 种浩, 高国强, 黄观新, 李光耀.重分析方法研究进展及展望 [J].工程力学, 2017, 34(5): 1―16.Wang Hu, Chong Hao, Gao Guoqiang, Huang Guanxin,Li Guangyao.Review of advances and outlooks in reanalysis methods [J].Engineering Mechanics, 2017,34(5): 1―16.(in Chinese)
MACHINING DEFORMATION MODEL AND STRUCTURAL OPTIMIZATION OF AERONAUTICAL MONOLITHIC COMPONENTS BASED ON RELAXATION OF INITIAL RESIDUAL STRESS
QIN Guo-hua 1 , LIN Feng 1 , YE Hai-chao 1 , HOU Yuan-jun 1 , CHEN Xue-mei 2 , HAN Xiong 2 , WANG Hua-min 1
(1.School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China;2.Numerical Control Machining Factory, Chengdu Aircraft Industrial (Group)Co., Ltd, Chengdu 610092, China)
Abstract: In the process of blank forming, the non-homogeneity of mechanical properties of material leads to the residual stress in a aluminum alloy thick plate.During the following cutting process, along with the removal of material, the release of residual stress makes the aeronautical monolithic component deformed, which seriouslyaffects the size stability of an aeronautical monolithic component.Therefore, the quantitative study on the analysis and prediction of deformation caused by the residual stress release during the cutting process is the core link of controlling the processing quality, and it is very important for the realization of machining process with high efficiency and precise.Through equaling the material removal of the aluminum thick plate to the residual stress release, the residual stress of the aeronautical monolithic component is converted to an external force on the basis of static equilibrium conditions.Then considering the residual stress in both the transverse and rolling direction of the plate, the deformation analysis model is established by using bending deformation theory.The comparison between calculated results of a model and the finite element simulated results and the experimental measurement data shows that: both the amplitude and deformation curve and the calculated results are highly consistent with the simulated results; when compared with experimental measurement data there is a deviation in the amplitude due to the measurement error, though the deformation curve of calculated results has a good agreement with them.
Key words: aluminum alloy thick plate; initial residual stress; machining deformation; aeronautical monolithic component; structural optimization
王华敏(1988―)，女，江西人，博士生，主要从事夹具的自动化设计、数控加工过程力学行为分析等方面的研究(E-mail: 910291556@qq.com).
陈雪梅(1969―)，女，四川人，研高工，硕士，主要从事机械加工、先进飞机制造技术、数字化装配及装备等方面的技术研究与管理工作(E-mail: Chenxm132@163.com);
韩 雄(1976―)，男，四川人，高工，博士，从事大型航空结构件数控加工工艺技术方面的工作(E-mail: xiong-han@163.com);
叶海潮(1979―)，男，河南人，讲师，博士生，主要从事工件装夹分析与优化、残余应力分析与预测、制造业信息化技术等方面的研究(E-mail: xxjy2000@163.com);
侯源君(1986―)，男，江苏人，博士生，主要从事振动辅助加工技术、工件装夹分析与优化等方面的研究(E-mail: hyj_1@139.com);
作者简介：
林 锋(1991―)，男，江西人，实验员，硕士，主要从事加工过程力学分析与仿真、残余应力分析与预测等方面的研究(E-mail: 317164178@qq.com);
基金项目： 国家自然科学基金项目(51765047，51465045)；江西省主要学科学术和技术带头人资助计划项目(20172BCB22013)；航空科学基金项目(2016ZE56011)；江西省自然科学基金项目(20161BAB206114)
通讯作者： 秦国华(1970―)，男，江西人，教授，博士，主要从事工件装夹分析与优化、切削加工基本力学行为分析与仿真、残余应力分析与预测、健康诊断与故障预测等方面的研究(E-mail: qghwzx@126.com).
文章编号： 1000-4750(2018)09-0214-09
收稿日期： 2017-06-06；修改日期：2017-12-04
文献标志码： A
doi: 10.6052/j.issn.1000-4750.2017.06.0433
中图分类号： V261.99