唐欣薇 1,2 ，黄文敏 1 ，周元德 2 ，张楚汉 2
(1．华南理工大学土木与交通学院，广州 510640；2．清华大学水沙科学与水利水电工程国家重点实验室，北京 100084)
摘 要： 层状岩石结构内部矿物之间的定向排列与胶结作用形成不同构造方向的细观结构，使岩石变形破裂及其力学性能存在明显的各向异性。该文以板岩为研究对象，通过构建空间相关函数，建立可表征不同片理方向的岩石细观颗粒离散元模型。基于细观力学参数反演，针对不同片理角度(θ)的巴西劈裂试验开展数值仿真分析，对板岩的各向异性行为进行了研究。结果表明，由于岩石受内部片理构造的影响，在劈拉荷载作用下，呈现三种破坏模式，当θ≤30°时主要发生矿物颗粒之间的拉伸破坏，当θ=45°～75°时为剪切与拉伸共同作用产生的破坏，当θ >75°时为沿着片理面的拉伸破坏；岩样破坏所耗能量及劈拉强度随片理角度的增大而逐渐降低。该文提出的方法能较好地模拟层状岩石的各向异性力学特征及变形破裂规律，与试验结果表现出良好的一致性。
关键词： 层状岩石；各向异性；空间相关特征；巴西劈裂；细观离散元
层状岩石内部存在大量由粘土矿物组成的层理、片理以及裂缝等软弱结构面，此处颗粒间的粘结力较小、强度较低，造成岩石力学性能在垂直于片理面、与片理面成一定夹角和平行于片理面方向存在明显的各向异性，以层状岩石作为基础的隧道、大坝、水库等工程的建设须考虑层状岩石的这一特性 [1―4] 。
巴西圆盘劈裂试验相比点荷载、多点弯曲、直接拉伸试验，具有操作简便快速、试验成本低等优点，是目前应用最广泛的岩石抗拉强度测试方法，已广泛应用于砂岩、板岩、页岩等层状岩石各向异性行为的研究中 [5―10] 。随着计算机技术的发展，数值仿真技术日新月异，逐渐形成反映岩石微细观组分及排列结构的细观力学模型。Debecker等 [11] 采用二维离散单元法对板岩进行了压缩与劈拉试验数值模拟，研究了板岩的破裂特征。谭鑫等 [12] 采用UDEC程序建立离散单元数值模型，利用随机分布的条状块体集合，通过设置层理界面和矿物颗粒之间的接触参数，模拟层理构造对片麻岩破坏的影响。Kim等 [13] 在数值模型中定义定向排列的层理结构，并赋予相应的微观参数，研究了砂岩在单轴压缩条件下的各向异性行为。Park等 [14] 在离散单元模型中设置平滑接头模拟岩石的片理结构，通过与片麻岩、板岩及片岩的试验结果比较，验证了模型的可靠性。但现有数值方法普遍定义矿物组分的力学属性为随机分布，或者将岩石的片理结构简化为某一方向的长条状分布形态，忽略了层状岩石结构本身的多相矿物组分、矿物成分含量及不同矿物定向排列形成的片理微观结构分布特征。
本文针对上述问题展开探讨，以板岩为研究对象，根据岩石内部的不同矿物及其矿物成分含量，采用空间相关方法，建立能够表征板岩不同片理方向分布特征的细观力学模型，结合细观力学参数反演技术，进行不同片理角度下的巴西劈裂数值试验，通过对比相关试验，探讨板岩在不同片理方向下的力学特性及变形破裂规律。本文的研究将为进一步探讨层状岩石类材料的变形破损机制提供了新的方法与参考。
层状岩石是一种典型的各向异性结构，岩石中不同矿物在空间上呈现定向排列特征，同种矿物在局部范围内存在一定的相关性和联系性，矿物之间的定向排列构成了不同方向的层理或片理结构。为表征岩石结构在空间上的分布特征，本文构建了运用于岩石类材料的空间相关函数并予以数值实现。
将二维随机场离散为n×n的矩阵，各单元之间存在相关性，引入空间相关函数 f(d)表征材料的关联程度，定义为空间内n×n个单元与距离为d的单元相关性的均值，即：
其中，d为ai, j与 a i + p , j + q 之间的距离，见图 1， 
代表单元ai, j与 
之间的属性，如式(2)所示，当两个单元为同种介质时， 
的值为1，当为不同介质时则为-1。
取岩石类材料的空间相关函数为 [15―16] ：
式中，L为空间相关长度(spatical correlation length)，用以描述空间两点之间的关联程度，空间相关长度L取决于材料结构特征，可开展相应的试验确定。
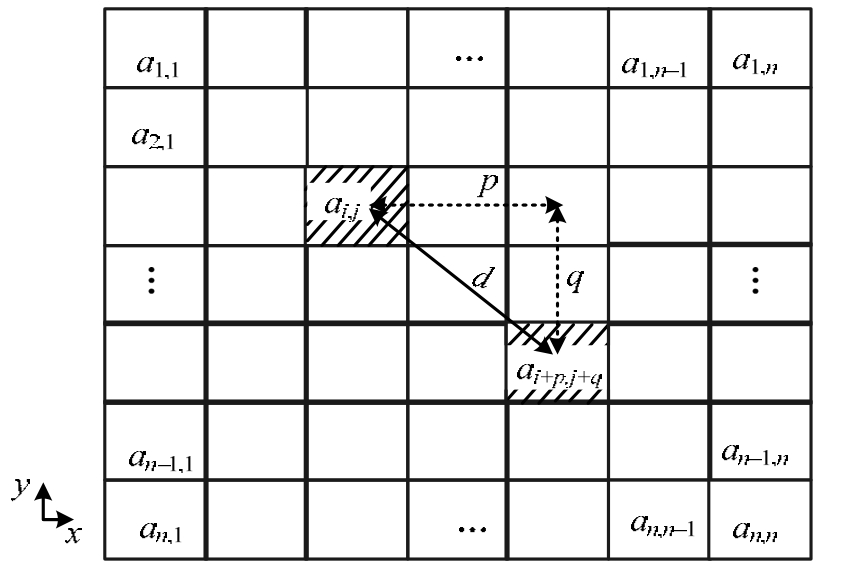
图1 二维连续随机场
Fig.1 Two-dimensional random field
假定二维空间内包含两相介质，生成随机的数组 A，数组内的单元 a i , j =±1， i = 1,2,…,n；j = 1 ,2,… ,n ，其中1和-1代表两相介质，假设两相介质含量不相等，分别为w和1-w(0<w<1)。两个单元之间的相关关系满足式(2)的条件，若为同一介质值为1，否则为-1，即：
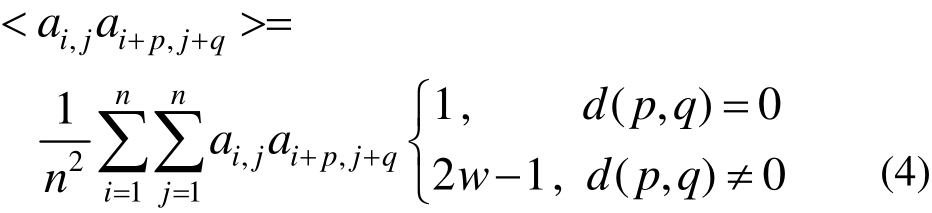
式中，d ( p, q)= 
之间的有效距离。对于各向异性情况，为体现空间相关函数在不同方向存在差异，需引入各向异性参数 s(anisotropy parameter)以表征各向异性，即：
式中，L x 和L y 为沿着x和y方向的空间相关长度，则有：
本文采用待定系数法求解具有特定空间相关特征的随机场，具体过程如图2所示。
图2 空间相关实现过程
Fig.2 The realization for spatial correlation
采用无空间相关的随机数组 A构造新的数组B，数组B内的单元b i, j 为：
式中：c d( p, q) 为待定数组C内的元素，为获得符合特定空间相关函数f (d )的随机场，则有：
综合式(7)和式(8)，可列出式(9)。式(9)为多元非线性方程组，共 ( n+1) 2 个方程，相应地，可求解出待定数组C，从而得到满足相关函数分布的数组B(这里给出的是没有各向异性情况的推导，考虑各向异性时只需要按照式(6)更新有效距离的计算即可)。根据给定的两相介质比例，对整个随机场进行修正，得到符合已知空间相关特性且满足既定两相介质比例w和1-w的数组B′。
采用1.2节方法构造随机场，空间相关长度和各向异性参数是关键性参数，为了探讨两者对两相材料细观结构表征的影响，本文基于 MATLAB计算获取相应的随机场，选取不同空间相关长度和各向异性参数进行了对比。
当不考虑细观结构的各向异性时(s=1，即L x 和L y 沿 x和 y方向的空间相关长度相同)，分别取L x =L y =1、3、6、9，随机生成的样本如图3所示。显然，不同空间相关长度对材料的细观结果具有显著影响。当空间相关长度较小(图 3(a))时，两相材料结构变化程度相当剧烈；随着空间相关长度的增大，材料的相关性增强，表现为随机场中同相材料的不断聚集，呈现一定的连续性(图3(b)～图3(d))。选取适宜的相关长度，可较好地表征诸如花岗岩、玄武岩等块状结晶岩石的细观结构。
为考虑不同各向异性参数对细观结构的影响，在图3(c)的基础上(取x方向的空间相关长度L x =6)，分别取各向异性参数 s=1、3、6、9，则根据式(5)可以确定y方向的空间相关长度L y =6、2、1、2/3，随机生成的样本如图4所示。可见，当各向异性参数s取1时，两相材料沿x、y方向的关联性保持一致，在随机场内形成块状聚集；随着各向异性参数的增大，两相材料沿y方向的关联性减小，变化程度逐渐剧烈，材料沿x方向仍保持原有的聚集程度，即随机场沿x、y方向为不同程度的凝聚，使得材料在空间内呈现明显的各向异性特征，各向异性参数愈大，这种特征愈为突出，可较好地表征诸如板岩、片麻岩等片状结晶岩石的细观结构。
图3 不同空间相关长度效果(s=1)
Fig.3 The results with different spatial correlation lengths (s=1)
注：图中不同颜色分别代表任意两种介质
图4 不同各向异性参数效果(L x =6)
Fig.4 The results with different anisotropy parameters (L x =6)
注：图中不同颜色分别代表任意两种介质
选取刘运思等 [9] 做的巴西劈裂试验，其中，试件直径为 50 mm(长径比 1∶1)，片理角度为 60°，试件选取湘西地区的板岩。基于上述思想和方法，建立具有片理构造特征的PFC 2D 颗粒离散元数值模型，结合细观参数反演技术，开展岩石破坏过程的仿真计算与分析。
湘西地区板岩具板状构造的浅变质岩石，由粘土岩、粉砂岩或中酸性凝灰岩经轻微变质所形成。外表呈致密隐晶质，内部矿物成分主要为绿泥石、伊利石等粘土矿物，夹杂石英、长石等矿物，其中，绿泥石与伊利石的含量可达80%以上。板岩内的片状矿物(如绿泥石、伊利石、绢云母等)呈定向排列，与胶结物中的变质矿物和泥质一起胶结紧密，使得板岩在宏观上呈现明显的片理构造，如图5(a)所示。
本次数值模拟将板岩视为由绿泥石和伊利石组成的各向异性材料，参考相关资料 [17] ，假定二者含量分别为60%和40%。对比岩石真实的微观结构，取L=6.0和s=6.0，按照1.3节的方法，随机生成9个具有板状特征的岩石细观结构，如图5(b)、图5(c)所示。可见，绿泥石与伊利石矿物有明显的聚集特征，且沿着某一方向延伸分布，不同矿物之间的定向排列构成了特定方向的片理结构，基于该方法构建的细观模型考虑了岩石不同矿物成分、矿物成分含量及岩石的微观结构分布特征，更接近真实结构。相对于常规的单独模拟出片理结构的方法，本文的方法可以更好地反映实际岩石结构分布特征，且该方法拓展至多相矿物具有良好的操作性。
图5 板岩微观结构
Fig.5 The meso-structure of slate
采用几何映射的方法，通过判断颗粒与矿物组分的位置关系确定各矿物组分的分布，建立可反映岩石材料细观结构的PFC 2D 颗粒元模型，如图6所示。所建立的数值圆盘试件直径为50 mm，颗粒单元粒径为0.2 mm～0.3 mm且满足高斯分布，单元数目约为11000个。其中，片理角度θ定义为片理方向与x轴之间的夹角。
图6 细观离散元模型
Fig.6 Meso-scale discrete element model
本文使用颗粒元平行粘结模型，在细观层面模拟岩石材料的力学性质。平行粘结模型假定颗粒间以接触点为圆心的圆盘上存在一系列平行弹簧，可以在颗粒间传递力和力矩，当作用在平行粘结上的最大拉应力达到法向粘结强度或最大剪应力达到切向粘结强度时即认为粘结断裂，颗粒发生破坏。颗粒单元间的作用及粘结模型的讨论可参考文献[18―19]。模型计算时需要利用参数反演技术确定岩样中各组矿物的细观力学参数，相应的步骤如下：
1)考虑到计算时间与效率，取颗粒单元半径R为 0.2 mm～0.3 mm。ρ为颗粒密度，由岩石材料密度及模型孔隙率计算得到，μ为颗粒间摩擦系数，取 μ=0.5。
2)根据绿泥石与伊利石矿物的宏观力学参数 [20] ，假定绿泥石、伊利石与交界面弹模 E n 的比为5∶6∶1，强度 
之比为3∶4∶1。
3)将颗粒刚度和粘结刚度换算成弹性模量E n = k n /2t ， 
= 
/(R A + R B )，且假定E n /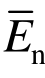 
= 1 ，根据法、切向刚度比 k n /k s 与泊松比v的关系可反演得到各组矿物的法、切向刚度比，然后由试验弹性模量E反演得到各组矿物的法、切向刚度k n 、k s 、 
、 
。
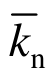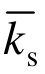4)假定法、切向粘结强度比为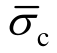 
∶ 
=1∶ 2 ，根据试验数据，反演得到各组矿物的法、切向粘结强度 
、 
。
反演得到的主要细观力学参数列于表 1，参数反演技术的介绍详见文献[21―22]。
表1 细观力学参数
Table1 Meso-mechanical parameters
在颗粒元模型中，为和试验结果进行对比，劈裂加载的应力计算公式如下：
式中： t σ为岩石劈拉强度；P为劈裂试验荷载；A为受拉断面面积。
图7与表2分别为基于表1参数计算所得的岩石开裂形态及劈拉强度，结果分析如下：
图7 试验与数值岩样破裂模式
Fig.7 Experimental and numerical fracture modes
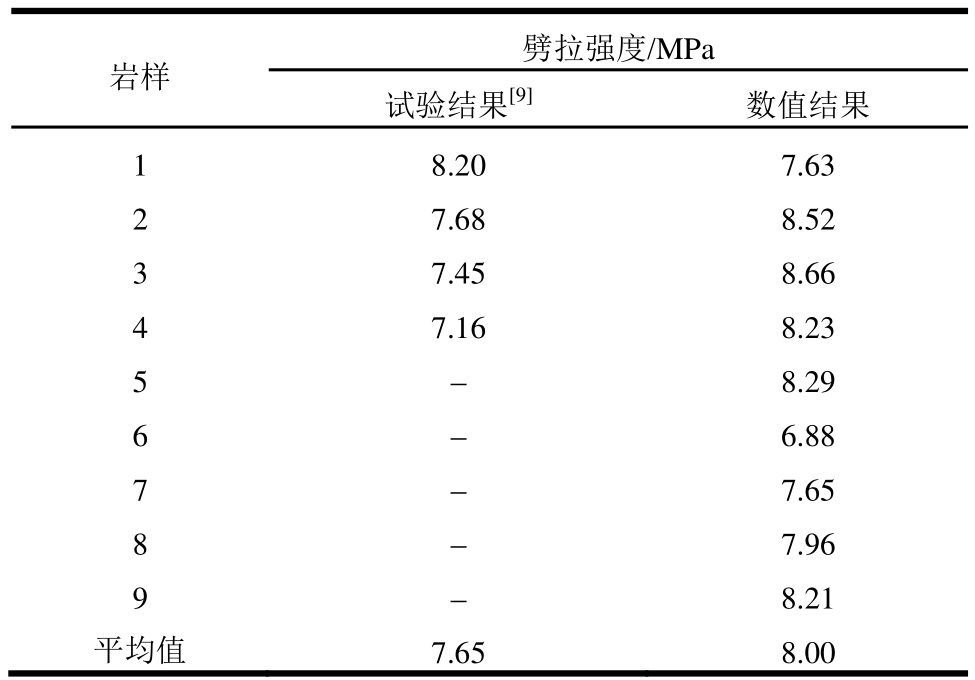
表2 试验与数值劈拉强度
Table2 Experimental and numerical splitting tensile strengths
1)基于本文的细观力学模型能反映微裂纹萌生、扩展直至出现宏观裂纹的全过程，在劈拉受载下，微裂纹从岩石加载端部与软弱片理面附近起裂，受板岩内部结构面的影响，裂纹的扩展具有一定的倾斜，与试验结果相近。
2)裂纹主要沿力学性能相对薄弱的矿物交界面扩展，当离开界面时，则从绿泥石、伊利石矿物中扩展，三者力学性能截然不同，矿物分布形态各异，不同试件的受力性能存在一定差异。
3)9个样本的劈拉强度与试验结果具有良好的可比性，岩样细观结构的矿物分布形态不同使得数值仿真结果呈现一定的离散性，其离散范围较好地反映了板岩劈拉强度的离散性。
为了研究片理角度对板岩劈拉力学行为的影响，本文基于上述巴西劈裂试验数值模拟方法，设计了7组不同片理角度，分别为θ = 0°、15°、30°、45°、60°、75°和 90°，每组片理角度按 Monte Carto法产生9个随机样本。
图8为不同片理角度板岩的劈裂破坏模式。可见，不同片理角度数值岩样的劈裂破坏模式差别较大，表现为以下3种主要形式：
1)当片理角度较小时(θ=0°～30°)，板岩开裂主要沿加载方向，圆盘破坏表现为矿物基质颗粒间的拉伸破坏。
2)随着片理角度的增大(θ=45°～75°)，裂纹在加载端处起裂，沿试件中部向一侧凸出，裂纹不再是规则地随加载方向发展，而是呈折线形式分布，除矿物基质颗粒间的劈拉破坏外，逐渐出现剪切破坏。
3)当片理角度增大至θ>75°时，裂纹的方向基本平行于片理的方向，岩样破坏表现为片理面的拉伸破坏。
综上所述，受内部片理结构特性的影响，板岩的破坏特征由矿物颗粒之间的拉伸破坏逐渐变化为剪切拉伸综合作用产生的破坏，最终转变为沿着片理面的拉伸破坏，文献[9]亦得到类似的试验现象。
图8 板岩劈裂破坏模式
Fig.8 Fracture modes of slate
在PFC 2D 中，可获取试件外力做功的总能量W，由此，得到不同片理角度下数值岩样达到失稳破坏时所消耗的总能量(见图9)，其中，耗损能量W的定义详见PFC用户手册 [23] 。可见，在外荷载的作用下，外力做功转变为颗粒间积累的能量，当积累能量超过片理面强度或不同矿物颗粒之间的粘结强度时，颗粒之间发生断裂。随着θ值的增加，岩样破坏所耗能量呈现整体下降趋势(由 53.49 J降至28.15 J)。当片理角度较小时(θ=0°～30°)，数值岩样的破坏需要突破矿物基质本身的粘结强度，而矿物之间的粘结强度大于片理结构面的强度，因此，岩样在这一片理角度下发生断裂破坏所消耗的能量较多，岩样的裂纹将穿越矿物基质与片理面，最终形成一条沿加载方向的裂纹。随着片理角度的增大(θ=45°～75°)，岩样的破坏是拉伸和剪切综合作用的结果，由于片理结构弱面的影响，岩石破裂所需消耗的能量会有所降低。而当片理角度增大至 θ=90°时，岩样为沿着片理面的拉伸破坏，此时消耗的能量最低，相对θ=0°时降低了45%。
图9 不同片理角度下岩样破坏所消耗能量
Fig.9 The fracture energy of slate with different θ
图10 劈拉强度与片理角度关系
Fig.10 Dependence of splitting tensile strength on θ
由式(10)得到板岩劈拉强度随片理角度 θ变化的曲线如图 10所示。可见，板岩巴西劈裂强度随片理角度θ的增大而逐渐降低，在θ=0°时，裂纹贯通坚硬矿物及片理面，需要克服最多的能量，因而，劈拉强度均值达到最大，为 10.69 MPa；在 θ=90°时，裂纹沿力学性能较为薄弱的片理面扩展，断裂能量最小，相应地，劈拉强度亦最小，为6.43 MPa，约为最大值的 60%。可见，片理角度对板岩劈拉强度的影响是十分显著的，呈现明显的各向异性特征。
(1)本文引入空间相关长度和各向异性参数，表征了层状岩石的空间局部连续程度和分布特性，以板岩为例，构建了不同片理角度的细观模型，更加真实地描述了岩石的结构特征，为进一步构建岩石材料细观结构提供了新的思路与参考。
(2)板岩随片理角度的增大，破坏模式由矿物颗粒间的拉伸破坏逐渐变化为拉剪破坏，最终转变为沿着片理面的拉伸破坏；岩石破坏所耗能量及其劈拉强度均随片理角度的增大而逐渐降低，呈现出明显的各向异性特征。
(3)应当指出，本文仅考虑了两相矿物组分，且只针对岩石巴西劈裂受载行为进行了探讨，后续将引入多相矿物组分，并对岩样的其他受载行为开展深入研究。
参考文献：
[1]Özsan A, Karpuz C.Geotechnical rock-mass evaluation of the Anamur dam site, Turkey [J].Engineering Geology, 1996, 42(1): 65―70.
[2]张卫东, 常龙, 高佳佳.横观各向同性地层井壁应力分析[J].工程力学, 2015, 32(11): 243―250.Zhang Weidong, Chang Long, Gao Jiajia.Stress analysis at the borehole wall in transverse isotropic formations[J].Engineering Mechanics, 2015, 32(11): 243―250.(in Chinese)
[3]王乐华, 陈星, 党莉.含显著沉积弱面砂岩加卸荷破坏试验研究[J].工程力学, 2013, 30(5): 181―187.Wang Lehua, Chen Xing, Dang Li.Experimental study on the failure of sandstone with notable bedding under loading and unloading [J].Engineering Mechanics, 2013,30(5): 181―187.(in Chinese)
[4]杨雪强, 李子生, 燕全会, 等.横观各向同性岩石类材料的破坏准则[J].工程力学, 2012, 29(12): 328―333.Yang Xueqiang, Li Zisheng, Yan Quanhui, et al.Failure criterion for transversely isotropic rock materials [J].Engineering Mechanics, 2012, 29(12): 328―333.(in Chinese)
[5]邓华锋, 张小景, 张恒宾, 等.巴西劈裂法在层状岩体抗拉强度测试中的分析与讨论[J].岩土力学, 2016(增刊2): 309―315.Deng Huafeng, Zhang Xiaojing, Zhang Hengbin, et al.Analysis and discussion on Brazilian tests on layered rock tensile strength [J].Rock and Soil Mechanics,2016(Suppl 2): 309―315.(in Chinese)
[6]Tavallali A, Vervoort A.Effect of layer orientation on the failure of layered sandstone under Brazilian test conditions [J].International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 313―322.
[7]Cho J W, Kim H, Jeon S, et al.Deformation and strength anisotropy of Asan gneiss, Boryeong shale, and Yeoncheon schist [J].International Journal of Rock Mechanics and Mining Sciences, 2012, 50: 158―169.
[8]Vervoort A, Min K B, Konietzky H, et al.Failure of transversely isotropic rock under Brazilian test conditions [J].International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 343―352.
[9]刘运思, 傅鹤林, 饶军应, 等.不同层理方位影响下板岩各向异性巴西圆盘劈裂试验研究[J].岩石力学与工程学报, 2012, 31(4): 785―791.Liu Yunsi, Fu Helin, Rao Junying, et al.Research on Brazilian disc splitting tests for anisotropy of slate under influence of different bedding orientations [J].Chinese Journal of Rock Mechanics and Engineering, 2012,31(4): 785―791.(in Chinese)
[10]杨志鹏, 何柏, 谢凌志, 等.基于巴西劈裂试验的页岩强度与破坏模式研究[J].岩土力学, 2015, 36(12):3447―3455.Yang Zhipeng, He Bai, Xie Lingzhi, et al.Strength and failure modes of shale based on Brazilian test [J].Rock and Soil Mechanics, 2015, 36(12): 3447―3455.(in Chinese)
[11]Debecker B, Vervoort A.Two-dimensional discrete element simulations of the fracture behaviour of slate [J].International Journal of Rock Mechanics and Mining Sciences, 2013, 61: 161―170.
[12]谭鑫, Heinz K.含层理构造的非均质片麻岩巴西劈裂试验及离散单元法数值模拟研究[J].岩石力学与工程学报, 2014, 33(5): 938―946.Tan Xin, Heinz K.Brazilian splitting tests and numerical simulation by discrete element method for heterogeneous gneiss with bedding structure [J].Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 938―946.(in Chinese)
[13]Kim K Y, Zhuang L, Yang H, et al.Strength anisotropy of berea sandstone: results of X-ray computed tomography, compression tests, and discrete modeling[J].Rock Mechanics and Rock Engineering, 2016, 49(4):1201―1210.
[14]Park B, Min K B.Bonded-particle discrete element modeling of mechanical behavior of transversely isotropic rock [J].International Journal of Rock Mechanics and Mining Sciences, 2015, 76: 243―255.
[15]Tang X W, Zhou Y D, Zhan C H, et al.Study on the heterogeneity of concrete and its failure behavior using the equivalent probabilistic model [J].Journal of Materials in Civil Engineering, ASCE, 2011, 23(4):402―413.
[16]Tang X W, Yang X B, Zhou Y D.An efficient algorithm for spatially-correlated random fields generation and its applications on the two-phase material [J].Solid State Communications, 2014, 182: 30―33.
[17]左清军, 吴立, 袁青, 等.软板岩膨胀特性试验及微观机制分析[J].岩土力学, 2014(4): 986―990.Zuo Qingjun, Wu Li, Yuan Qing, et al.Swelling characteristics test and micromechanism of soft slate [J].Rock and Soil Mechanics, 2014, 35(4): 986―990.(in Chinese)
[18]Potyondy D O, Cundall P A.A bonded-particle model for rock [J].International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329―1364.
[19]武明鑫, 张楚汉, 王进廷.基于细观颗粒元的混凝土弯曲试验模拟与率效应[J].清华大学学报: 自然科学版, 2014 (8): 999―1005.Wu Mingxin, Zhang Chuhan, Wang Jinting.Simulations of concrete bending and rate effects based on meso-scaled particle elements [J].Journal of Tsinghua University (Science and Technology), 2014, 54(8): 999―1005.(in Chinese)
[20]Wang Z, Wang H, Cates M E.Effective elastic properties of solid clays [J].Geophysics, 2001, 66(2): 428―440.
[21]Wu M X, Zhang C H.Influence of static pre-loading on the dynamic bending strength of concrete with particle element modeling [J].Science China Technological Sciences, 2015, 58(2): 284―296.
[22]Qin C, Zhang C H.Numerical study of dynamic behavior of concrete by meso-scale particle element modeling [J].International Journal of Impact Engineering, 2011,38(12): 1011―1021.
[23]Itasca C G I.Particle flow code in 2 dimensions (version 4.0), user’s manual: theory and background [M].Minneapolis, Minnesota: Itasca Consulting Group Inc,2008: 3―5.
TANG Xin-wei 1,2 , HUANG Wen-min 1 , ZHOU Yuan-de 2 , ZHANG Chu-han 2
(1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;2.State Key Laboratory of Hydroscience and Hydraulic Engineering, Tsinghua University, Beijing 100084, China)
Abstract: Various meso-scale representations of layered rock are formed by the directional arrangement and cementation of the minerals on a layered structure, which is obviously anisotropic in the mechanical behavior.This study presents a meso-scale particle discrete element model, which can demonstrate the meso-scale structure of slate by introducing a spatial correlation function.Based on the derivation of mechanical parameters on the meso-scale, the numerical simulations for slate Brazilian splitting tests with different bedding angles (θ)are conducted to investigate the anisotropic behavior.The simulation shows that there are three typical failure modes due to the various arrangements of bedding structures, including tensile failure at θ≤30°, combined shear and tensile failure at θ=45°～75°, and splitting-tensile failure at θ>75°.The splitting tensile strength and the fracture energy decrease with the increase of θ.The proposed method is able to describe the anisotropy characteristics and the deformation-fracture behavior for layered rocks, which is in a good agreement withcorresponding experiments.
Key words: layered rock; anisotropy; spatial correlation characteristics; Brazilian splitting test; meso-scale discrete element method
MESOSCALE STRUCTURE RECONSTRUCTION AND ANISOTROPIC BEHAVIOR MODELING OF LAYERED ROCK UNDER SPLITTING-TENSILE LOADING
张楚汉(1933―)，男，广东人，教授，中国科学院院士，博导，主要从事水工结构分析研究(E-mail: zch-dhh@tsinghua.edu.cn).
黄文敏(1992―)，男，广东人，硕士生，从事水工结构工程研究(E-mail: cthwenmin@mail.scut.edu.cn);
作者简介：
唐欣薇(1980―)，女，辽宁人，副教授，博士，硕导，从事岩土工程和水工结构方面的教学与研究工作(E-mail: cttangxw@scut.edu.cn);
基金项目： 国家自然科学基金项目(51109083，41572251)；清华大学水沙科学与水利水电工程国家重点实验室开放基金项目(2017C03)；国家自然科学基金委员会—中国铁路总公司高速铁路基础研究联合基金项目(U1434211)；国家重点研发计划项目(2016YFC1402800)
通讯作者： 周元德(1975―)，男，广东人，副教授，博士，博导，从事岩土破坏力学研究(E-mail：zhouyd@tsinghua.edu.cn).
文章编号： 1000-4750(2018)09-0153-08
收稿日期： 2017-06-02；修改日期：2017-11-20
文献标志码： A
doi: 10.6052/j.issn.1000-4750.2017.06.0419
中图分类号： TU452