图1 试验机整体视图
Fig.1 Global view of test machine
宋春明,苏 杭,姜红艳
(陆军工程大学爆炸冲击防灾减灾国家重点实验室,南京 210007)
摘 要: 梁受横向撞击时,其撞击力、局部变形和整体变形等动态响应受到撞击体质量、撞击速度、撞击位置以及梁刚度特性等因素的影响,研究这些参数对动力响应以及对撞击局部效应和整体效应的影响规律,是合理提出抗撞击防护手段的基础。该文利用低速落锤冲击试验装置进行了铝合金梁横向撞击试验,着重研究不同撞击速度、撞击位置和试件刚度等因素对铝合金梁所受撞击力、整体与局部变形、应变与能量等的影响规律。实验结果表明:随着撞击速度的增加,试件吸收能量的速率增大,撞击力幅值不断增加,撞击荷载主峰值段的持续时间减小;试件的整体变形和局部变形都明显增大,但局部效应相对增加更为显著;随着试件刚度(厚度)的增加,试件受相同速度撞击的吸收能量速率增大,撞击力荷载峰值显著增加;试件整体变形减小,而局部变形增加,说明试件刚度越大,其撞击整体效应减弱,而局部效应增强;试件受撞击后整体变形与撞击力相比明显具有滞后性,表明整体效应滞后于局部效应。
关键词: 振动理论;动态响应;低速撞击;梁;整体响应;局部变形
低速撞击下结构构件动态响应的研究对于工程结构的危险评估以及安全防护都具有重要意义。近年来梁动力响应的研究成果较多,有汪莲等 [1] 提出的一种基于应变模态的梁结构动挠度监测方法,还有耿少波等 [2] 对钢箱梁破坏形态及冲击波传递过程的实验研究等,但是针对低速撞击的研究较少。
低速撞击下梁动力响应的理论分析中,Hertz把撞击问题转化为刚体的相对运动问题 [3] ,Lausen和Simo [4] 建立了撞击过程的连续介质力学模型。王明洋等 [5] 分析了钢筋混凝土梁的准弹性阶段和塑性阶段计算方法,建立了梁动力响应的理论计算公式。周泽平等 [6] 采用刚性离散模型,推导出弹塑性状态下钢筋混凝土梁的不同计算方法。
影响梁动力响应的参数主要通过低速落锤实验进行研究。许斌和曾翔 [7] 研究了不同撞击体质量、速度和撞击能量对钢筋混凝土梁整体变形和支座反力等的影响。罗旗帜黄志斌 [8] 研究了不同支承条件对梁的撞击力、绝对位移、相对位移及弯矩的影响。闫秋实等 [9] 通过实验分析了不同套筒灌浆料饱满度和不同拼装位置的装配式钢筋混凝土梁的破坏形态和抗冲击力学性能。Mao和Barnett [10] 研究了梁纤维含量对超高性能纤维增强混凝土梁抗冲击性能的影响。Caliskan和Apalak [11] 研究了泡沫芯密度、高度和面板厚度对泡沫铝夹心梁动力响应的影响。
低速撞击下梁整体响应和局部破坏的单独研究较多,对于二者之间关系的研究和实验较少。本文基于低速落锤式冲击试验,研究分析了不同撞击速度、撞击位置及结构刚度对梁受撞击动力响应的影响规律,与理论计算结果进行了对比分析,同时分析了不同撞击参数下整体响应和局部破坏之间的关系。常见的钢筋混凝土构件或钢构件虽然材料性能与铝合金差异较大,但在遭受低速撞击时的局部与整体响应规律存在某些相似性,本文研究结果可以为相关针对性实验提供参考。
采用INSTRON的CEAST 9350低速落锤冲击试验机作为试验加载装置,图1为试验机整体视图,该仪器主要包含冲击塔、控制器和试验箱三个部分,其能够达到的最大冲能为1800 J。另外其具有的防回弹系统可在冲击后阻止冲击头再向试样方向运动,防止再次冲击试件。本次试验采用直径20 mm 的半球体锤头,冲击体(锤头加配重)质量为28.952 kg,由设备中自动称重系统量测得到。受撞击试件为铝合金梁,其材料含铝量 99.3%,含铁 0.35%,其他 0.35%,材料的弹性模量E=66.6 GPa,抗拉强度 150 MPa,屈服强度135 MPa。各试件宽度和材质均完全相同,试件厚度成为影响试件刚度的唯一变量,厚度可直接表述为刚度因素进行分析。

图1 试验机整体视图
Fig.1 Global view of test machine
对 6根铝梁试件进行冲击试验,分析 5 m/s、8 m/s和11 m/s三个撞击速度以及不同撞击位置对梁局部与整体响应的影响。试件编号及试验设计参数详见表1。对比试件B-1、B-2与B-3的破坏形态与相关参量可分析出撞击速度对梁动力响应的影响;对比试件B-2与B-4的破坏形态和动态参量可分析撞击位置对梁动力响应的影响;对比试件A-1、B-2与C-1的试验结果可分析不同结构刚度的影响。
表1 试件及试验设计参数
Table1 Specimens and test design parameters
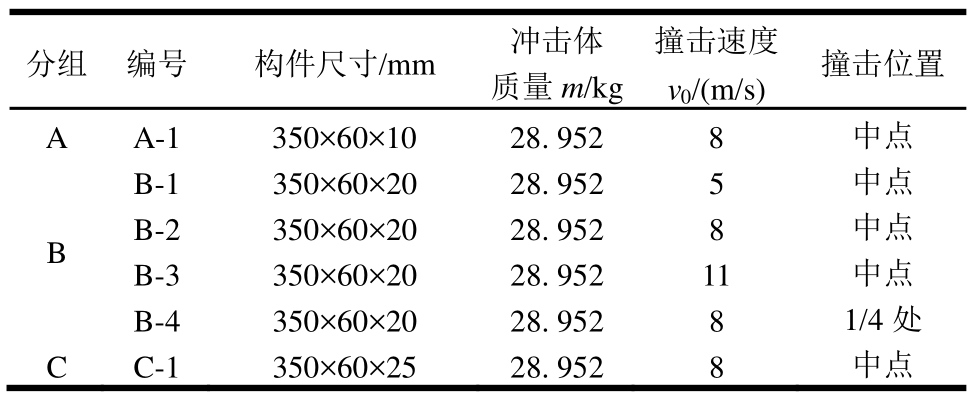
图2为铝梁的固定支架,其夹具和端部的辊轴保证了试件两端为简支支承条件,辊轴中心线之间的距离为33 cm。
试验的主要测量内容有:1)试件的残余变形;2)撞击力时程曲线;3)锤头的速度时程曲线;4)锤头的能量时程曲线;5)试件关键点处的应变时程曲线。量测方法主要利用低速落锤试验机自带的数据采集系统,记录整个冲击过程的撞击力时程曲线、锤头的能量及速度时程曲线。另外,在梁的底面中点及四分之一处粘贴应变片,由应变仪测量获得梁关键点的应变时程曲线。试件的局部(撞击坑)与整体(挠度)残余变形通过游标卡尺量测,并用相机拍摄记录试件最终的变形形态。

图2 铝梁的简支固定夹具
Fig.2 Clamping of the specimen
按照试验方案和流程,利用低速落锤实验装置依次对6根简支铝合梁进行低速撞击试验,为理论分析撞击速度、撞击位置等因素对梁低速撞击动力响应的影响规律提供依据。
本次试验的主要准备过程和试验流程如下:
1)用砂纸清理试件表面,在铝梁底面中点处和四分之一处粘贴纵向应变片,贴完后通过万用表量测电阻,检测是否绝缘,最后用环氧胶密封,防止撞击时应变片被振落。
2)固定试件,将试件放置在试件夹持装置的上盖与滚轴之间,并采用高强度螺栓拧紧。
3)检测试件粘贴后应变片的有效性,将应变片引出来的导线连接在应变仪上,并在试验开始前测试整个线路是否通畅,做好采集准备。
4)在落锤试验机的落锤架上添加配重。
5)对落锤试验机进行自检,查看锤头能够降落的最低高度,调节试件夹持装置下部的可调节支架,使试件与锤头之间保持适当的间距,保证在撞击过程中锤头与试件能很好的接触。
6)设置试验参数,如撞击速度、落锤重量等,释放锤头,进行撞击试验。
7)观察试件破坏形态,量测试件各点挠度,查看连接试验机的计算机所显示撞击力、速度与能量时程图以及应变时程图,初步分析数据是否可靠。
8)将落锤归位,拆卸试验后的试件,准备下个试件的冲击试验。
图3为不同撞击条件下铝梁最终的整体变形情况,可以看出6根试件均表现为弯曲变形模式。

图3 试件的整体变形
Fig.3 Global deformation of specimens
图3(a)为相同刚度和中心位置撞击,不同撞击速度条件下试件的变形图,明显可以看出,撞击速度越大,挠度越大,弯曲程度越明显。B-1、B-2、B-3的受撞击速度 v 0 分别为 5 m/s、8 m/s、11 m/s时,20 mm厚度铝梁挠度分别为 14.01 mm、23.36 mm、29.04 mm,对比表明当撞击速度分别由5 m/s增加0.6倍和1倍时,最大挠度分别增大67%和 107%,说明试件的整体变形与撞击速度并不成线性关系。
图3(b)为相同刚度和撞击速度,不同撞击位置时试验的最终变形图,撞击1/4跨度位置时梁的挠度明显减小,仅为15.36 mm,主要原因是梁在该点的变形刚度远大于跨中处的刚度。
图3(c)是相同撞击条件下三种不同厚度的铝梁在跨度中心处受撞击挠曲变形情况的对比。试件刚度越大,其变形越小。三种试件厚度比为1∶2∶2.5,最大挠度分别为33.35 mm、23.36 mm和13.64 mm,挠度比值为2.45∶1.71∶1,说明梁受撞击的变形能力与试件厚度(刚度)紧密相关。
局部变形是指撞击作用时冲击体头部侵入试件内部的深度,这个深度即表明冲击的局部效应。如图4所示,撞击坑基本为半圆形空腔,所测得深度如下:A-1为0.201 mm,B-1为0.187 mm,B-2为0.216 mm,B-3为0.287 mm,B-4为0.223 mm,C-1为0.266 mm。

图4 试件的局部变形
Fig.4 Local deformation of specimens
从图4(a)可以看出,随撞击速度的增加,形成的撞击坑尺寸越大,局部效应随撞击速度增加而越发明显。图4(b)为撞击条件相同而结构刚度不同时的局部变形,可以明显看出,试件刚度越大,其局部效应越明显,这与受撞结构整体效应随刚度的变化趋势正好相反,说明试件刚度增大时,其受撞击造成的整体效应减弱,而局部效应却增强。
比较试件B-2和试件B-4撞击坑深度的数值,发现相同撞击条件下,当撞击不同的位置时,撞击点处的局部变形相差不大。
利用低速落锤试验装置中自带的传感器可测得不同冲击条件下,从锤头最初接触试样到试样最终断裂整个过程中的详细数据。图5为刚度相同而冲击速度不同时各铝合金试件的撞击力时程曲线,可分为以下三个阶段。
第Ⅰ阶段为撞击力峰值阶段,也就是图5中撞击力曲线的第一个波峰,此阶段持续时间较短,约0.45 ms左右。首先冲击体锤头与梁开始接触,两者存在明显速度差,冲击体侵入到试件内部,撞击力快速增加,同时由于冲击体受相应的阻力作用,不断减速,两者之间的相对速度显著减小。当两者速度相同时,冲击体不能继续侵入试件内,此时局部变形达到最大值,同时撞击力达到峰值。接着冲击体与试件之间开始有脱开的相对运动,撞击力开始减小,直到两者完全脱开,撞击力减小为零。该阶段是实际的撞击力作用时间,也是撞击体和试件相互作用的时间。
第Ⅱ阶段为平台阶段,此阶段撞击力呈周期性振动,幅值大致保持稳定,形成平台。由各试件的撞击力时程曲线可以明显看出,此阶段持续时间较长,约为1.5 ms~3.5 ms。此阶段由于防回弹系统夹持住冲击锤体保持不动,而试件受撞击已产生了整体与局部位移,试件变形振动恢复;试件与冲击体发生接触撞击,然后局部变形增加,撞击力增大;试件受撞击力作用产生位移,逐步与冲击体脱离;然后不断重复“变形恢复-接触撞击-局部变形-整体变形-脱离”的过程,造成撞击力呈周期性振动,幅值大致保持稳定并不断下降的现象。
第Ⅲ阶段为缓慢下降段,此阶段试件振动基本结束,其和冲击锤头间的接触力不断下降,梁达到最终的塑性变形,最后落锤与试件接触力降为零。
由图5对比试件B-1、B-2与B-3的撞击力曲线,随着撞击速度v 0 逐渐增加,撞击力峰值不断增大。当撞击速度v 0 由5 m/s增加到8 m/s、11 m/s时,对应的撞击力峰值分别是25 kN、31.9 kN和46.45 kN,峰值增加明显。另外还可以看出,撞击荷载主峰值的持续时间随着撞击速度的增加逐渐减小。

图5 不同冲击速度的撞击力时程曲线
Fig.5 Impact force-time curve for different impact velocities
试件B-2和B-4的受撞击速度相同,但撞击位置不同,B-2梁撞击试件中点,而 B-4梁撞击 1/4跨位置,从图5可明显看出,两试件的撞击力曲线完全重合,说明对于低速撞击,撞击位置对撞击力的影响较小,但从图 3(b)知,撞击位置对结构的动力响应影响显著。图6为相同撞击速度下不同刚度(厚度)试件的撞击力时程图,对比试件A-1、B-2和 C-1,可明显看出随着试件自身刚度的增大,其所受的撞击荷载峰值越大。当试件厚度分别为10 mm、20 mm和25 mm时,所受撞击力峰值分别为26.4 kN、31.9 kN和40.6 kN,这种变化趋势与局部变形随试件厚度的变化趋势一致,说明了撞击力,即冲击体所受的阻抗力,主要取决于试件的局部变形。
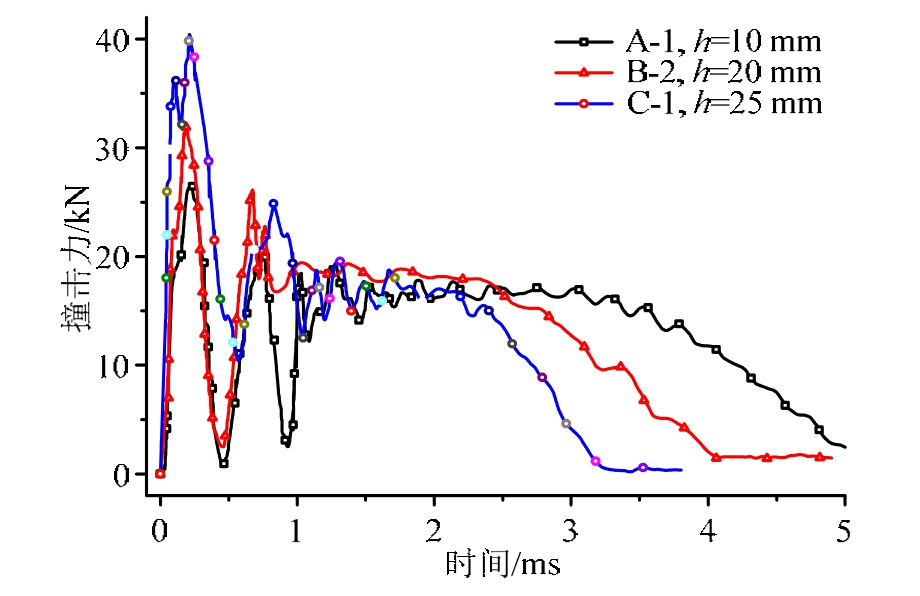
图6 不同刚度试件的撞击力时程曲线
Fig.6 Impact force-time curve of specimens with different stiffness
为反映结构整体的变形性,应变片主要粘贴于试件底部跨中位置(受冲击位置)。由于试件受冲击点位置处变形程度剧烈,该位置的应变片大都超过量程而失效。
图 7为梁的应变(反映试件整体变形)与撞击力时程(实际撞击力作用阶段)曲线图。可以看出撞击力作用时间0.47 ms,而试件的中点的应变达到最大值时间为1.16 ms,远大于实际撞击力的作用时间,说明位移具有明显的滞后性。当撞击力达到最大值的时间约为 0.28 ms,此时中点处的应变仅为2600 µε,是最大应变值的27%,意味着撞击力达到峰值时,而结构的整体变形很小;反过来说,结构整体变形(很小)对撞击力的影响非常有限。
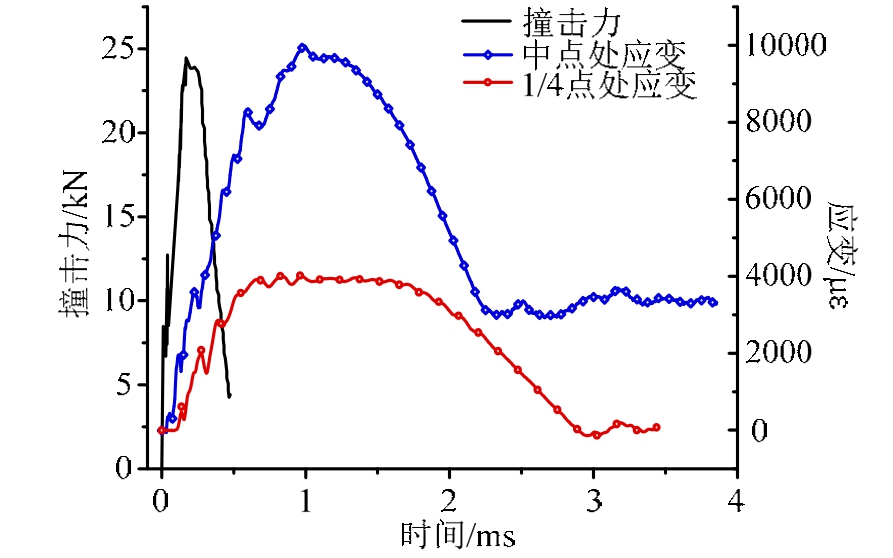
图7 B-1试件的应变与撞击力时程曲线(v 0 =5 m/s)
Fig.7 Strain&impact force-time curve of B-1(v 0 =5 m/s)
图8为测得的不同冲击条件下锤头的能量时程曲线,即锤头传递给试件能量随时间的变化曲线。
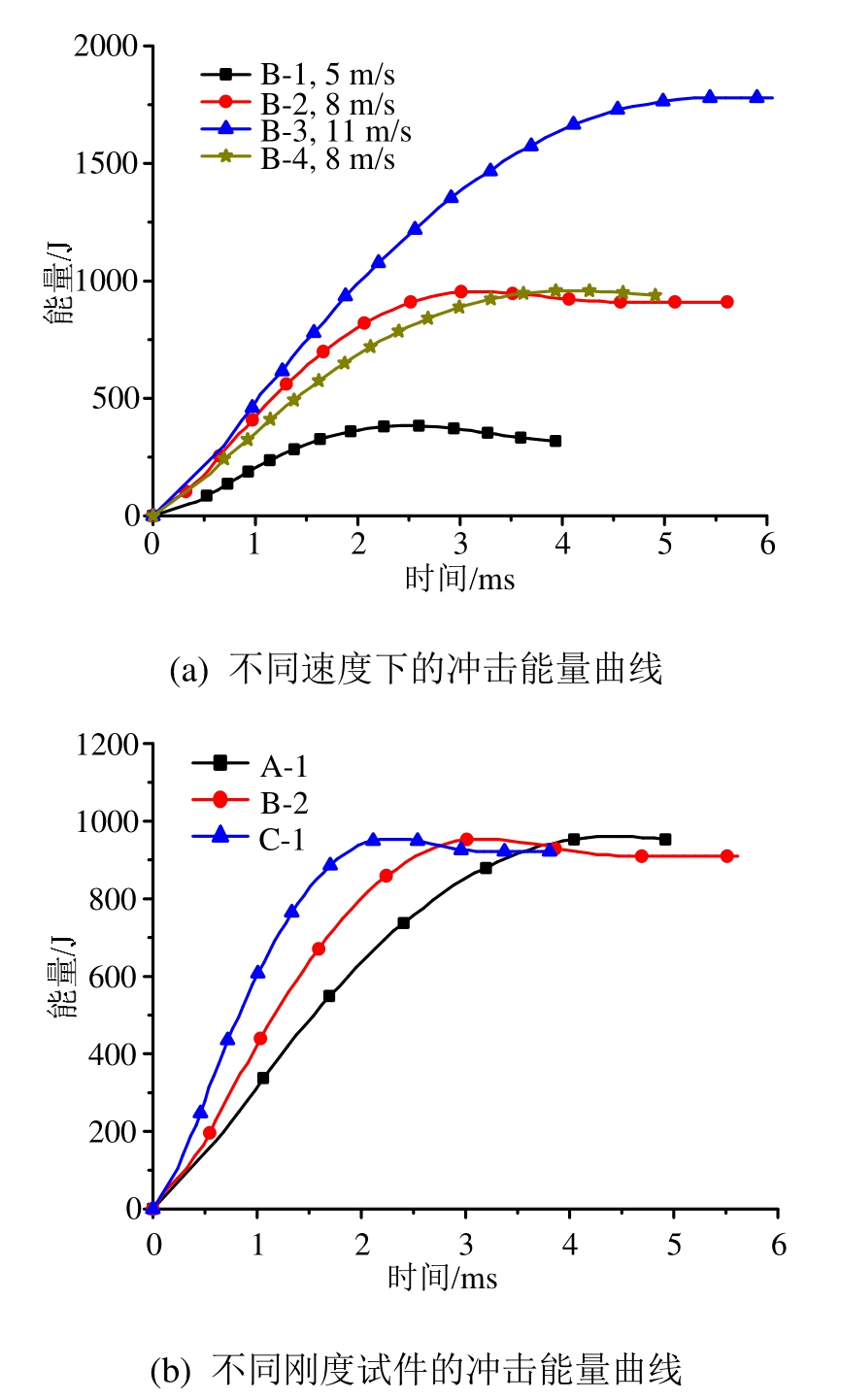
图8 锤头能量时程曲线
Fig.8 Energy-time curve of projectile
如图8(a)所示,冲击能量快速增加到最大值,然后趋于稳定,稳定值近似等于撞击动能。对比相同刚度的试件B-1、B-2、B-3所对应的能量曲线,发现撞击速度越大,能量曲线的斜率越大,说明试件吸收冲击能量的速率越高。B-2与B-4的冲击能量曲线非常接近,但跨度中点受撞击的B-2试件能量曲线斜率更大。图8(b)为撞击速度相同时,不同刚度试件的冲击能量曲线。由图可知,试件刚度越大,其冲击能量曲线斜率越大,说明刚度大的试件吸收能量更快。联系图3(c)和图4(b),刚度大的试件其整体变形越小,局部变形越大,而能量吸收速率却在增加,说明局部变形吸收的能量显著增大。
本次撞击试验的撞击力与结构响应等的详细结果如表2所示,其中局部与整体变形之比可以作为撞击作用的局部效应与整体效应对比的参考值。
表2 撞击试验结果
Table2 Test results

随着撞击速度的增加,结构的整体与局部破坏类型会发生变化,因此要重点分析冲击引起的整体变形和局部变形及其变化规律。如图9所示,整体变形主要由试件的中心挠度f表征,局部变形由撞击体侵入的深度α (t)表征。
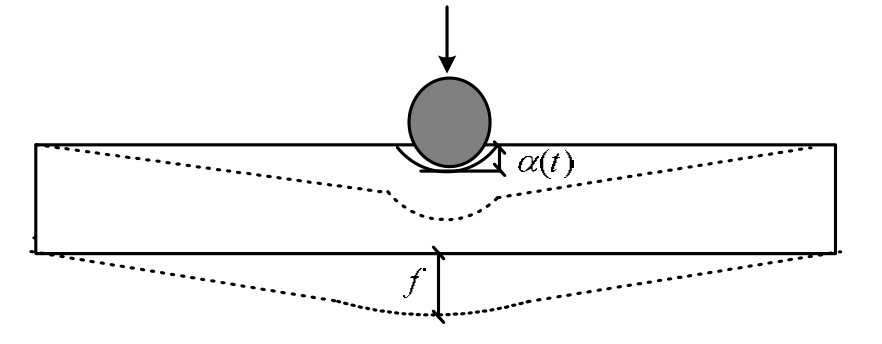
图9 整体与局部变形示意图
Fig.9 Global and local deformation diagram
局部效应与整体效应的相对变化趋势可直接由局部变形α(t)与整体变形 f的比值λ描述,即 ![]() 。由于撞击力与局部变形α(t)直接相关,低速撞击近似于准静态接触,根据Goldsmith的理论,撞击力与 α 3 /2 成正比;而整体变形f可直接由试件底部的应变来反映。
。由于撞击力与局部变形α(t)直接相关,低速撞击近似于准静态接触,根据Goldsmith的理论,撞击力与 α 3 /2 成正比;而整体变形f可直接由试件底部的应变来反映。
从撞击力与试件应变的时程图7可知,试件的整体变形具有滞后性,根源在于撞击力与加速度(变形的二阶导数)具有相同时间数量级,即: ![]() ,而整体变形
,而整体变形 ![]() ,即加速度的二次积分,需要一定的响应时间。当撞击速度增加时,撞击力增大但撞击力作用时间(撞击荷载的主峰值段约 0.45 ms)减小,而结构的整体来不及响应(未能达到最大位移)撞击过程就已结束,因此造成试件的局部效应显著增加。当速度增加到一定程度,结构的破坏类型开始转变为局部破坏形式。
,即加速度的二次积分,需要一定的响应时间。当撞击速度增加时,撞击力增大但撞击力作用时间(撞击荷载的主峰值段约 0.45 ms)减小,而结构的整体来不及响应(未能达到最大位移)撞击过程就已结束,因此造成试件的局部效应显著增加。当速度增加到一定程度,结构的破坏类型开始转变为局部破坏形式。
图10(a)表示的是撞击速度不同时,局部与整体变形比值的变化趋势,撞击速度越大,撞击局部变形与整体变形的比值就越大,局部效应相对显著增加。图10(b)表示梁厚度(抗弯刚度)不同时,撞击局部变形与整体变形的比值随着刚度的增加明显增大,结构响应模式由整体效应主导向局部效应增强方向转化。造成这种变化的主要原因是随着试件厚度的增加,其抗整体变形能力的增加更为明显。
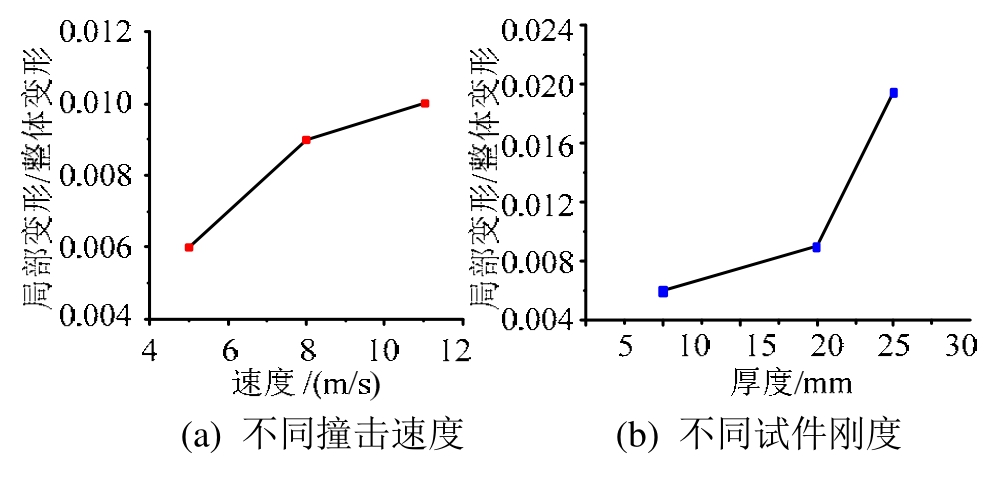
图10 试件局部与整体变形变化曲线
Fig.10 Trends for global and local deformation of specimens
利用文献[12]中低速撞击下梁的动力计算方程组,对于简支梁振型函数w i (x)可取为:
接触力按照Hertz接触理论 [1] 和简支梁进行计算:
式中:p为撞击接触力;T为撞击引起的梁的局部变形;k为接触刚度,由下式计算:
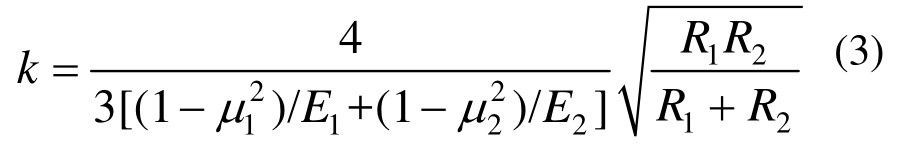
式中:R 1 、R 2 为曲率半径;μ 1 、μ 2 为泊松比;E 1 、E 2 为碰撞体的弹性模量。
铝梁试件可以视为理想的弹塑性材料,下面将理论计算与试验结果进行对比。相关计算参数如下:弹性模量E=66.6 GPa,密度ρ=2700 kg/m 3 ,梁的有效计算长度 l=0.33 m,梁的横截面尺寸b=0.06 m,厚度分别为0.01 m、0.02 m和0.025 m,刚性冲击体直径d=0.02 m,质量m=28.952 kg。
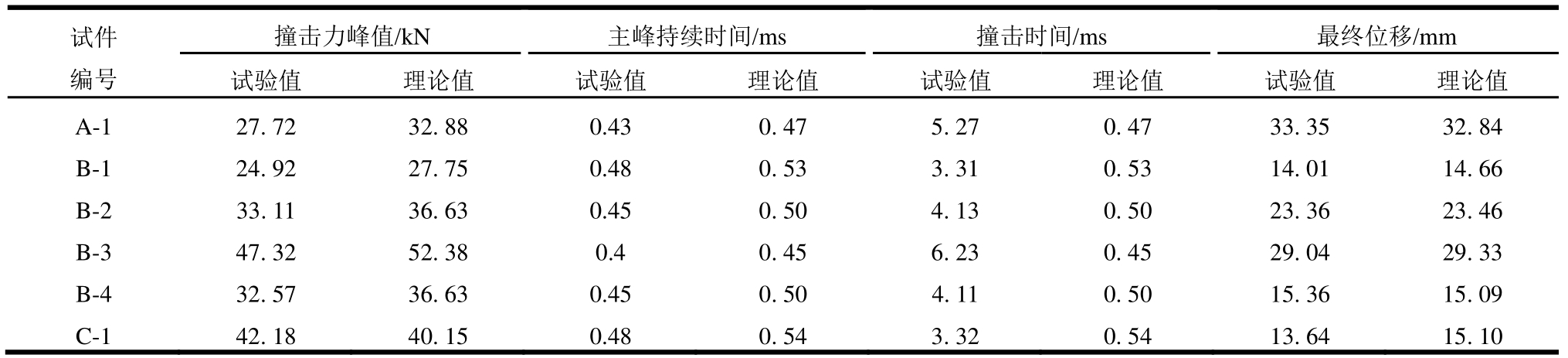
理论与试验的撞击力对比曲线如图 11所示。由于理论模型只考虑冲击体的一次撞击,即认为局部变形减小到α (t)=0时刻撞击结束,因此只能得到撞击力的主峰值段。从图中可以看出主峰值段撞击力的持续时间与理论计算结果基本一致,撞击力理论值与试验值基本吻合,理论值稍偏大。其中差别最大的为B-3试件,其撞击力的理论值大于试验值5.06 kN,偏差约10%。其主要原因是理论计算时采用Hertz理论,该理论为准静态的撞击接触理论,在保证试件挠度变形的条件后,造成撞击力的理论计算值偏大。
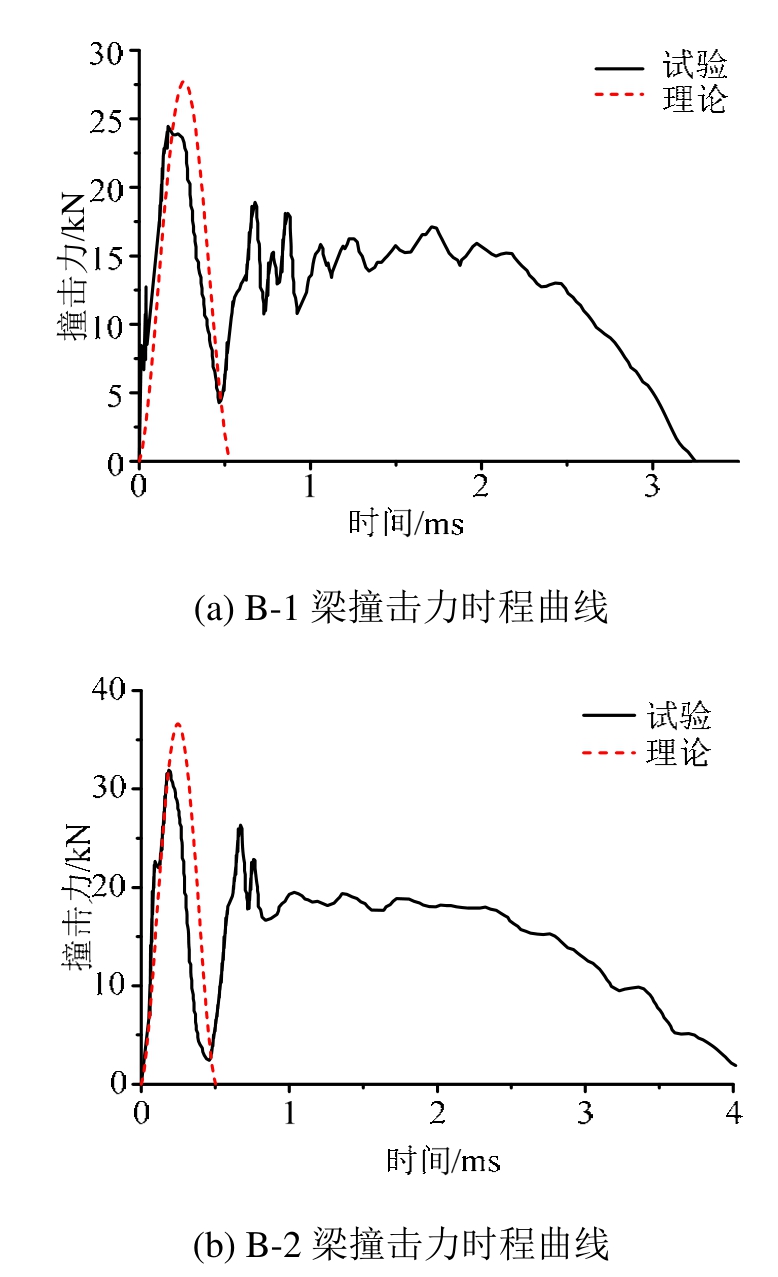
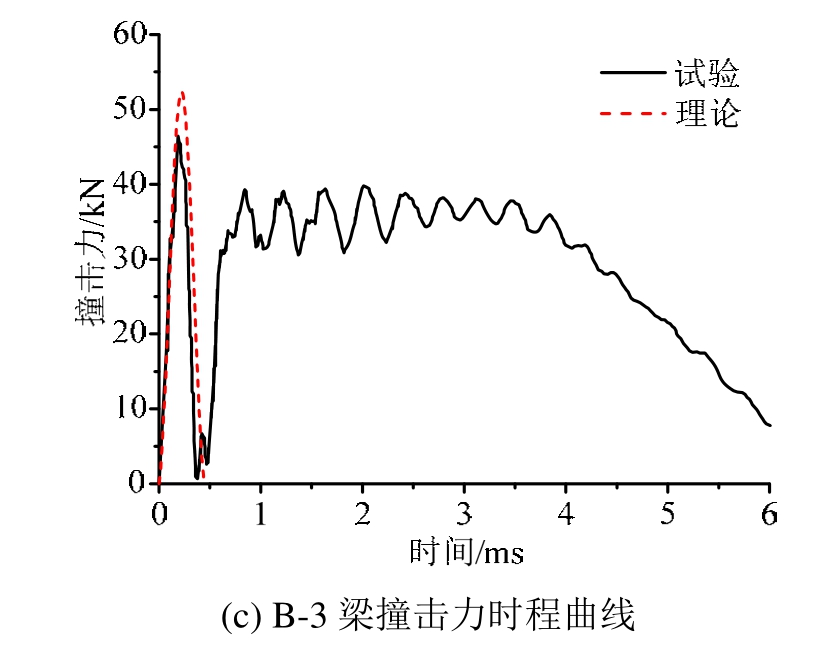
图11 撞击力时程的理论与试验值对比
Fig.11 Comparisons between theory and experiment results for impact force
另外还对不同撞击条件下试件的最终位移(挠度)进行了对比,具体如表3所示。其中位移理论值与试验值差别最大的 C-1试件,两者相差约1.46 mm,主要原因在于准静态的Hertz接触理论更适用于柔性撞击,而C-1试件刚度最大,柔度最小,所以理论计算偏差较大,而其他试件的数据均吻合良好。另外表中数值反映出的撞击局部效应和整体效应随速度、试件刚度的变化规律与试验完全一致,证明了试验数据的合理性。
表3 试件的动力响应计算结果
Table3 Dynamic response results of specimens
(1)利用低速落锤试验装置研究了不同冲击速度、撞击位置及试件刚度等因素对铝合金梁所受撞击力、整体与局部变形、应变与能量的影响规律。
(2)随撞击速度的增加,试件吸收能量的速率增大,试件承受的撞击力幅值不断增加,但撞击荷载的主峰值段持续时间减小;同时,试件的整体变形和局部变形都明显增大,但局部效应相对增加更为显著。
(3)相同撞击速度的条件下,随着试件刚度(厚度)的增加,试件受撞击吸收能量的速率增大,撞击力荷载峰值显著增加;同时,试件的整体变形明显减小,而局部变形增加,说明试件刚度越大,整体效应减弱,而局部效应增强。
(4)分析表明:铝合金梁在低速撞击作用下,其整体变形(挠度)与撞击力相比明显具有滞后性,即撞击的整体效应滞后于局部效应。
(5)通过理论计算与试验数据的对比分析,撞击力与试件位移响应等数据吻合良好,证明了试验所得规律的有效性。
参考文献:
[1]汪莲, 王佐才, 耿栋, 等.基于应变模态的连续梁动挠度识别[J].工程力学, 2017, 34(1): 130―138.Wang Lian, Wang Zuocai, Geng Dong, et al.Strain modes based dynamic deflection estimation of continuous beam structures [J].Engineering Mechanics,2017, 34(1): 130―138.(in Chinese)
[2]耿少波, 刘亚玲, 薛建英.钢箱梁缩尺模型爆炸冲击波作用下破坏实验研究[J].工程力学, 2017, 34(增刊 1):84―88.Geng Shaobo, Liu Yaling, Xue Jianying.Experimental studies on steel box girder scale model under blast load[J].Engineering Mechanics, 2017, 34(Suppl1): 84―88.(in Chinese)
[3]铁摩辛柯, 古地尔.弹性理论(第三版)[M].徐芝纶,译.北京: 高等教育出版社, 2013: 372―383.Timoshenko S P, Goodier J N.Theory of elasticity.3rd ed [M].Translated by Xu Z L.Beijing: Higher Education Press, 2013: 372―383.(in Chinese)
[4]Laursen T A, Simo J C.A continuum-based finite element formulation for the implicit solution of multibody, large deformation-frictional contact problems[J].International Journal for Numerical Methods in Engineering, 1993, 36(20): 3451―3485.
[5]王明洋, 王德荣, 宋春明.钢筋混凝土梁在低速冲击下的计算方法[J].兵工学报, 2006, 27(3): 399―405.Wang Mingyang, Wang Derong, Song Chunming.A calculation method of reinforced concrete beam under low velocity impact [J].Acta Armamentarii, 2006, 27(3):399―405.(in Chinese)
[6]周泽平, 王明洋, 冯淑芳.钢筋混凝土梁在低速冲击下的变形与破坏研究[J].振动与冲击, 2007, 26(5):99―103.Zhou Zeping, Wang Mingyang, Feng Shufang.Deformation and failure of a reinforced beam under low velocity impact [J].Journal of Vibration and Shock,2007, 26(5): 99―103.(in Chinese)
[7]许斌, 曾翔.冲击荷载作用下钢筋混凝土梁性能试验研究[J].土木工程学报, 2014, 47(2): 41―51.Xu Bin, Zeng Xiang.Experimental study on the behavior of reinforced concrete beams under impact loadings [J].China Civil Engineering Journal, 2014, 47(2): 41―51.(in Chinese)
[8]罗旗帜, 黄志斌.横向撞击下弹性支承轴向受力梁的动力响应[J].动力学与控制学报, 2010, 8(3): 207―212.Luo Qizhi, Huang Zhibin.Dynamic responses of axially-loaded beams with elastic supports subject to transversal impact [J].Journal of Dynamics and Control,2010, 8(3): 207―212.(in Chinese)
[9]闫秋实, 邵慧芳, 李亮.冲击荷载作用下装配式钢筋混凝土梁力学性能研究[J].工程力学, 2017, 34(4):196―205.Yan Qiushi, Shao Huifang, Li Liang.Study on the behavior of precast reinforced concrete beams under impact loading [J].Engineering Mechanics, 2017, 34(4):196―205.(in Chinese)
[10]Mao L, Barnett S J.Investigation of toughness of ultra high performance fibre reinforced concrete (UHPFRC)beam under impact loading [J].International Journal of Impact Engineering, 2017, 99: 26―38.
[11]Caliskan U, Apalak M K.Low velocity bending impact behavior of foam core sandwich beams: Experimental[J].Composites Part B: Engineering, 2016, 112: 158―175. .
[12]宋春明, 王明洋, 唐正国.柔性动边界梁在横向撞击下的动力响应[J].解放军理工大学学报(自然科学版),2008, 9(2): 151―155.Song Chunming, Wang Mingyang, Tang Zhengguo.Dynamic responses of beams with flexible supports subject to transversal impact [J].Journal of PLA University of Science and Technology (Natural Science Edition), 2008, 9(2): 151―155.(in Chinese)
EXPERIMENTAL INVESTIGATION ON RESPONSES OF ALUMINUM BEAMS TO LOW VELOCITY IMPACTS
SONG Chun-ming , SU Hang , JIANG Hong-yan
(State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact, Army Engineering University of PLA, Nanjing 210007, China)
Abstract: For beams under transverse impacts, the influences of the projectile’s mass and velocity, impact position and target stiffness, on the dynamic responses and impact effects of beams, such as impact force, global deformation and local deformation, is fundamental in anti-impact structural design.Six aluminum beams were transversely impacted by a low-velocity impact machine herein.Influences of parameters (i.e., velocity, impact position and specimen stiffness)on dynamic responses (i.e., impact force, global and local deformation, strain and energy)of beams were analyzed.The results revealed: with an increasing impact velocity, the specimen’s energy absorption speed and impact force amplitude increased, but the peak value duration of impact load reduced; both global and local deformation increased, but the increase in the local effects was more significant; with an increasing specimen stiffness (i.e., thickness), energy absorption speed and the peak value of impact force increased under the same impact velocity; the global deformation decreased while the local deformation increased,indicating that with an increasing stiffness, the global effect was weakened while the local effect was enhanced;compared with the impact force, the global deformation was obviously lagged, indicating that the global effect was lagged behind the local effect.
Key words: vibration theory; dynamic response; low velocity impact; beam; global response; local deformation
姜红艳(1990―),女,江苏人,硕士生,主要从事防护工程研究(E-mail: 1075416861a@sina.com).
作者简介:
宋春明(1979―),男,山东人,副教授,博士,研究室主任,主要从事防护工程研究(E-mail: ming1979@126.com);
基金项目: 国家创新研究群体科学基金项目(51021001)
通讯作者: 苏 杭(1993―),女,湖北人,硕士生,主要从事结构抗冲击效应及防护研究(E-mail: suhang_lillie@163.com).
文章编号: 1000-4750(2018)09-0145-08
收稿日期: 2017-05-27;修改日期:2017-11-01
文献标志码: A
doi: 10.6052/j.issn.1000-4750.2017.05.0409
中图分类号: O327