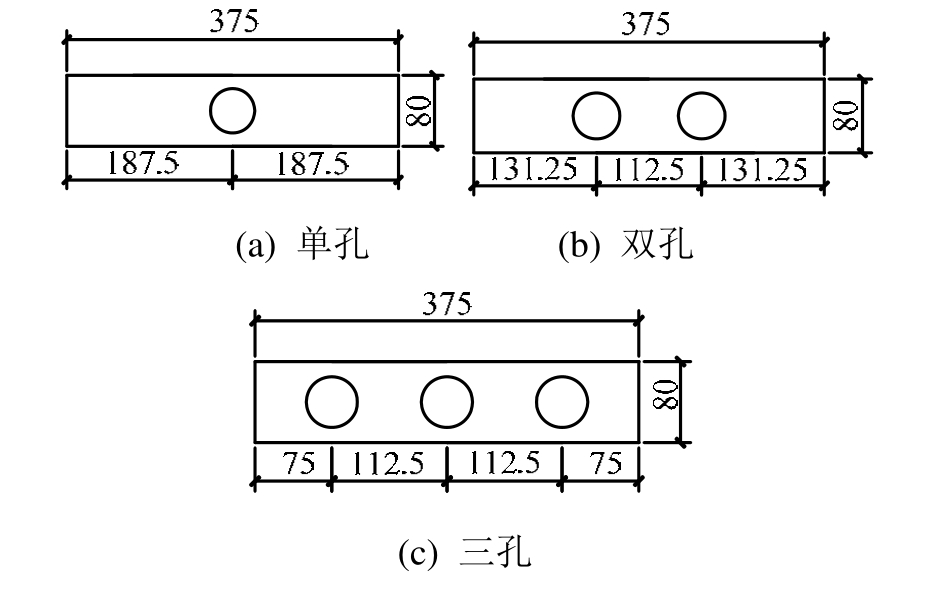
图1 PBL试件类型
Fig.1 Types of PBL connectors
杨 勇，陈 阳
(西安建筑科技大学土木工程学院，陕西，西安 710055)
摘 要： 为建立组合桥梁中开孔钢板剪力连接件(PBL)剪力连接件的抗剪承载力计算公式，开展8个PBL连接件的单调加载推出试验。着重研究静载下不同承压方式、混凝土强度、开孔数量和贯穿钢筋直径对连接件抗剪承载力的影响。基于变形协调条件分析端部混凝土、孔内混凝土榫和贯穿钢筋对单孔连接件极限承载力的贡献；多孔连接件的抗剪承载力则在考虑应力重分布的基础上将单孔连接件承载力进行叠加。试验结果表明：提出的 PBL连接件抗剪承载力计算模型物理意义明确，计算结果精度较高，可用于单排PBL剪力连接件的承载力计算。
关键词： 组合桥梁；PBL剪力连接件；推出试验；变形协调条件；抗剪承载力
钢-混凝土组合结构是在钢筋混凝土结构上兴起的一种新型结构，为了保证组合梁中钢与混凝土两种材料的共同作用，1987年，德国 Leonhardt等 [1] 教授首次开发出一种开孔钢板连接件，德文称为Perfobond Leiste (PBL)。PBL连接件是由开孔钢板、混凝土榫以及贯穿钢筋组成的剪力连接件 [2] ，通常布置在钢与混凝土组合梁的关键部位，将开孔钢板焊接于钢梁翼缘，不仅能够传递混凝土与钢梁之间的纵向剪切力，还能抵抗使两者分离的掀起作用。目前工程应用中使用最为广泛的连接件是栓钉 [3] ，但PBL剪力连接件却以抗剪刚度大、承载力高、抗疲劳性能好、施工方便 [4] 等优点成为最有前景的连接件。
目前，国内外学者已对开孔钢板连接件的受剪性能进行了大量试验研究与理论分析。Oguejiofor和Hosain [5] 以孔洞数目、孔洞间距、横向钢筋分布和混凝土强度为参数，提出了PBL连接件的承载力公式；Medberry和Shahrooz [6] 认为钢与混凝土之间的粘结作用对连接件承载力有一定的提高作用；Vianna等 [7] 提出了适用于不同混凝土强度的连接件承载力计算公式；Su等 [8] 利用一种新型的推出试验对PBL连接件的抗剪承载力进行推导。而国内已有PBL连接件计算模型均是在连接件沿钢梁翼缘通长布置的背景下提出的，宗周红和车惠民 [9] 提出了仅考虑混凝土榫和横向钢筋作用的抗剪承载力计算公式；胡建华等 [10] 认为应将横向普通钢筋和贯穿钢筋对抗剪承载力的贡献单独考虑，并且首次提出了考虑配筋率的 PBL连接件抗剪承载力公式；其后，石宵爽等 [11] 对3个PBL连接件的荷载-粘结滑移关系、破坏机理和极限承载能力进行了研究；柳扬清等 [12] 依据弹性地基梁理论分析了肋板间距对PBL连接件抗剪刚度的影响。由于目前实际工程应用中，连接件大都沿钢梁翼缘通长布置，钢板底部混凝土的承压力占总承载力的比例很小，因此抗剪承载力计算中均未考虑端部混凝土的承压作用。但如果连接件沿钢梁翼缘间断布置，即沿钢梁翼缘焊接n个连接件，由于每个连接件有2个端部，则共有2n个端部承压。单向受力过程中，会有n个端部来抵抗纵向剪力，因此会大大提高PBL连接件的纵向抗剪承载力。同时，由于该布置方式下连接件长度较小，不仅方便运输，还有利于减少施工过程中产生的焊接变形。
为建立端承型 PBL连接件的抗剪承载力理论计算公式，课题组完成了一批连接件推出试验(push-out test)，试验中通过在开孔钢板下部开槽的方式模拟端部不承压构件，通过在下部不开槽的方式模拟端部承压构件。同时，考虑孔洞数量、混凝土强度和贯穿钢筋直径等参数对 PBL连接件纵向抗剪性能的影响，并根据变形协调条件推导出单排连接件的极限承载力计算公式。
本文对单孔和多孔共8个PBL连接件进行了传统推出试验。所有试件的型钢规格为HW250 mm×HW250 mm×HW9 mm×HW14 mm，型钢与混凝土之间通过开孔钢板连接，其中开孔钢板厚15 mm，高 80 mm，孔洞间距 l=2.25d [5] ，即 l=2.25×50 mm=112.5 mm，如图1所示。为了分析端部混凝土承压作用对PBL剪力连接件承载能力的贡献，试验通过在钢板下部混凝土开槽来模拟不承压试件，不开槽来模拟承压试件，开槽尺寸为 100 mm×100 mm×125 mm，混凝土板中横向钢筋为■10，推出试件截面尺寸见图 2。该试验主要研究参数有端部承压方式、孔洞数量n、混凝土抗压强度f cu 以及贯穿钢筋直径d st ，具体如表1所示。
图1 PBL试件类型
Fig.1 Types of PBL connectors
图2 推出试件截面示意图 /mm
Fig.2 Cross-section of push-out specimens
表1 试件主要参数及试验结果
Table1 Main parameters of specimens and experimental results
表1中试件编号遵循以下规则：P代表PBL剪力连接件；第一个数字代表钢板上孔洞数目；第二个数字代表混凝土设计强度；最后一个数字代表贯穿钢筋直径；#代表无端部承压力。如试件P-1-45-14#表示只有一个孔洞、混凝土强度等级为C45且贯穿钢筋直径为14 mm的不承压PBL剪力连接件试件。
试验在2000 kN长柱试验机上进行，试验装置见图 3。试件底部用建筑结构砂浆坐浆并找平，加载端通过用修平胶找平的分配梁对型钢翼缘施加推压力，测试翼缘板上连接件的结构性能。加载过程中采用位移控制，以 1 mm/min的级差加载至试件破坏。钢板和混凝土之间的相对滑移采用4个高精度位移计测量，位移计布置在左右混凝土块的 2个侧面。同时量测试件承担的荷载，观察试件混凝土表面有无裂缝及连接件的破坏情况，所有试验数据均由计算机自动采集。
图3 推出试验加载装置
Fig.3 Push-out test loading device
端部承压试件在加载过程中，首先在混凝土板底部产生微小的裂纹，随着荷载的增加，混凝土板的竖向裂缝由下而上逐渐发展，最终在混凝土板侧面形成一条劈裂裂缝，如图4(a)所示，连接件由于没有受到混凝土的有效包裹而失去承载力。破坏时，开孔钢板前部的混凝土被压碎，孔内混凝土有明显的剪切破坏，横向钢筋也出现弯曲变形，但开孔钢板保持完好状态。
对于端部不承压试件，由于端部混凝土的承压作用很小，首先在槽口上方形成两条 45°斜裂缝，很快两快两条斜裂缝交汇成一个三角形楔块剥落，见图4(b)。当试件到达其极限承载力时，连接件与混凝土之间产生了明显的滑移现象，贯穿钢筋弯曲，孔内混凝土出现一定程度的剪切破坏。
图4 推出试件典型破坏形态
Fig.4 Typical failure modes of push-out specimens
2.2.1 端部承压方式的影响
图 5是端部承压和不承压试件的荷载-滑移曲线。可以看出，连接件在两种布置方式下的荷载-滑移曲线形状相似，但承压试件的初始斜率大于不承压试件，说明非连续布置连接件比连续布置具有更高的抗剪刚度。从表1可以看出端部不承压试件的纵向抗剪承载力仅占承压试件的44%，原因在于端部不承压试件没有底部混凝土的直接抗压作用，荷载主要由贯穿钢筋和开孔钢板孔内的混凝土提供，当达到极限承载力时，钢筋屈服、孔内混凝土出现一定的剪切破坏，PBL连接件充分发挥了其性能，但相对端承型试件来说，极限承载力较低，可见端部混凝土对 PBL连接件的纵向抗剪承载力具有很大的提高作用。由此可见，端承型试件在抗剪刚度和极限承载力方面都具有较大优势，建议在大跨桥梁中采用非连续布置的PBL连接件。
图5 端部承压方式的影响
Fig.5 Influence of end-bearing mode
2.2.2 开孔数量的影响
图 6是开孔钢板在连接件尺寸为 375 mm×80 mm×15 mm，孔洞数量分别为1、2、3时连接件极限承载力和孔洞数目的变化关系。观察发现PBL连接件的抗剪承载力随孔洞数量的增加有所提高。但开孔钢板上孔洞数量从2增加到3时，连接件的极限荷载仅增加了6.7%，这与文献[13]中提到的开孔钢板每多增加一个孔，连接件极限承载力提高5%的结论基本一致。说明孔洞数目大于2时，再增加孔洞对PBL连接件承载力的提高作用不明显。
2.2.3 混凝土强度的影响
PBL连接件在孔径为 50 mm，混凝土强度为49.4 MPa、52.6 MPa时的极限承载力分别为732 kN和802 kN，可以看出，PBL连接件的抗剪承载力随混凝土强度的提高而增加。
2.2.4 贯穿钢筋直径的影响
由表1可知，在三孔条件下，开孔钢板直径为50 mm时，P-3-45-14和P-3-45-20抗剪承载能力分别为732 kN和943 kN，PBL连接件的承载力提高了28%。由此可见，增加贯穿钢筋直径能显著提高PBL连接件的极限承载力。原因有两方面：1)贯穿钢筋靠自身的受拉来提供纵向抗剪承载力；2)贯穿钢筋、开孔钢板以及周围混凝土的共同作用使孔内混凝土处于三轴受压状态，一定程度上提高了孔内混凝土的抗压强度。但是应该注意到，PBL连接件的抗剪刚度与混凝土中粗骨料的进入比例密切相关 [14] ，如果钢筋直径过大，进入孔内的混凝土粗骨料将减少，一定程度上会降低PBL连接件的抗剪刚度。所以，在设计时应严格把控贯穿钢筋直径和粗骨料粒径比例，以便最大限度提高PBL连接件的力学性能。
图6 开孔数量的影响
Fig.6 Influence of the hole number
为了更直观地对PBL连接件承载力进行分析，图7给出了所有单孔连接件的荷载-位移曲线。
图7 标准单孔试件的分析图
Fig.7 Analytic chart of standard specimen with single hole
对于单孔标准试件 P-1-45-14来说，其抗剪承载力主要由端部混凝土的承压作用、孔内混凝土以及贯穿钢筋的抗剪作用提供。当其极限位移为6.43 mm时，极限承载力为533 kN，假定在该位移下，P-1-45-14、P-1-45-0、P-0-45-0和 P-1-45-14#的变形协调。因此，标准试件的端部混凝土承压力应该等于试件P-0-45-0在相对滑移为6.43 mm时对应的荷载305 kN；孔内混凝土的抗剪作用应该等于试件P-1-45-0和P-0-45-0在相对滑移为6.43 mm时的荷载差值 98 kN；贯穿钢筋的承载力可以通过P-1-45-14#在 6.43 mm时对应的荷载减去前面计算得到混凝土榫的作用，但考虑到贯穿钢筋占据孔内混凝土的面积，因此对混凝土榫的作用按照钢筋和孔内混凝土的面积比进行折减，最终得到贯穿钢筋的抗剪作用为123 kN。将以上三部分的作用进行叠加，得到标准试件 P-1-45-14的极限承载力为526 kN，和试验值 533 kN相差不大。同时，可以看出端部混凝土、孔内混凝土和贯穿钢筋分别占单孔PBL连接件承载力的56%、19%和25%，这与试件P-1-45-14#占P-1-45-14承载力的44%相吻合。
对于多孔连接件来说，由于在加载过程中，每个孔内混凝土的受力状态不同，当荷载较小时，一部分混凝土榫先坏，导致连接件应力重分布，随后其他孔才破坏。因此，多孔连接件的极限承载力远小于单孔连接件承载力的叠加。基于此，本文对多孔连接件孔内混凝土和贯穿钢筋在极限状态时的荷载进行折减，引入孔洞影响系数λ：
式中：n为开孔钢板上孔洞数目；d为孔洞直径；l为两个孔洞间间距，即两个圆心之间的距离，本文取2.25倍的孔洞直径。
在理论计算方面，Oguejiofor和Hosain [15] 认为PBL连接件的承载力(式(2))主要由三部分组成，第一部分是钢板下部混凝土的承压作用；第二部分是所有横向钢筋的抗滑移作用，包括开孔钢板孔中的贯穿钢筋和混凝土板中的横向钢筋；第三部分是孔中混凝土榫的抗剪切作用：
式中：P u /N为剪力连接件的抗剪承载力；h/mm为连接件高度；t/mm为连接件厚度；f ck /MPa为混凝土抗压强度；A tr /mm 2 为横向钢筋面积；f y /MPa为混凝土板中钢筋的屈服应力；D/mm为开孔钢板孔洞直径。
Medberry和Shahrooz [6] 在推出试验的基础上给出了考虑钢与混凝土之间粘结作用的强度公式：
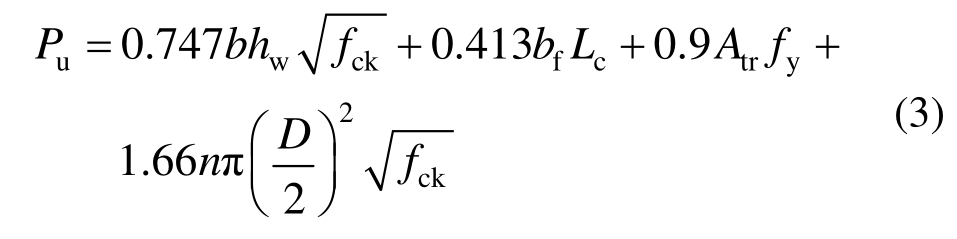
式中：b为混凝土板厚度；h w 为连接件下混凝土板的高度；b f 为型钢翼缘宽度；L c 为型钢翼缘与混凝土板的连接长度。Al-Darzi等 [16] 通过有限元模拟了PBL剪力连接件的结构性能，并且给出公式：
式中A sc 为孔洞中混凝土的面积。Veríssimo等 [17] 在Oguejiofor和Hosain的基础上，也通过推出试验得到一个较为精确的计算式：
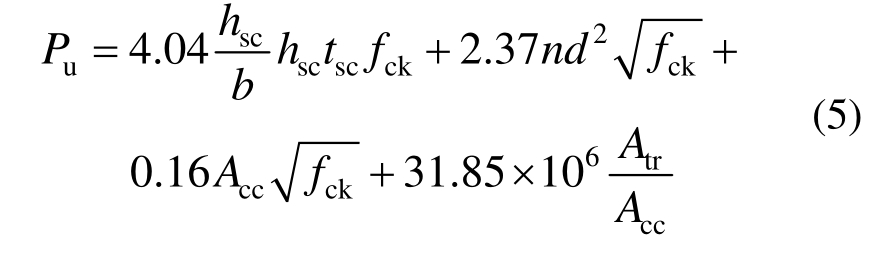
式中A cc 为每个连接件所分配的剪切混凝土面积。
此外，中国学者胡建华等 [10] 指出 PBL连接件的承载力由所有横向钢筋(贯穿钢筋和横向普通钢筋)和混凝土榫提供，并且明确区分了贯穿钢筋和混凝土板内横向钢筋的作用，其计算式为：
以上公式均是在线性回归基础上得到的，但对于每个试件来说，无论从加工制作还是试验加载过程中都存在很大的差异，通过表2对比可以看出，式(2)计算结果离散性较大，式(3)～式(6)计算结果都偏保守，因此有必要建立一个物理意义明确且更准确的PBL连接件承载力计算公式。
表2 试验结果和理论结果的对比
Table2 The comparison of experimental results and theoretical results
分析可知，PBL连接件承载力主要由端部混凝土的承压作用、孔内混凝土和贯穿钢筋抗剪作用三部分组成，因此，连接件的极限承载力可记为：
3.2.1 端部混凝土的承压作用P e
端部混凝土的承压作用主要由开孔钢板的横截面积和混凝土强度决定，因此，其大小可记为：
式中：A e 为开孔钢板的截面面积，A e =ht，h为开孔钢板高度，t为开孔钢板厚度；f cu 为混凝土立方体抗压强度。考虑到周围混凝土对该部分混凝土的约束作用，引入端部承压力提高系数φ e ，根据h=80 mm、t=15 mm、f cu =49.4 kN和试件 P-0-45-0在相对滑移为 6.43 mm时的荷载 305 kN求得φ e =5.15，则端部混凝土的承压作用为：
3.2.2 孔内混凝土的抗剪作用P c
孔内混凝土的受力见图 8，可以看出，混凝土榫受双剪力作用，因此，其抗剪作用可记为：
式中：A c 为孔内混凝土的面积，A c =π(d-d st ) 2 /4，d为孔洞直径，d st 为贯穿钢筋直径；τ c 为多向受力状态下混凝土榫的抗剪强度。
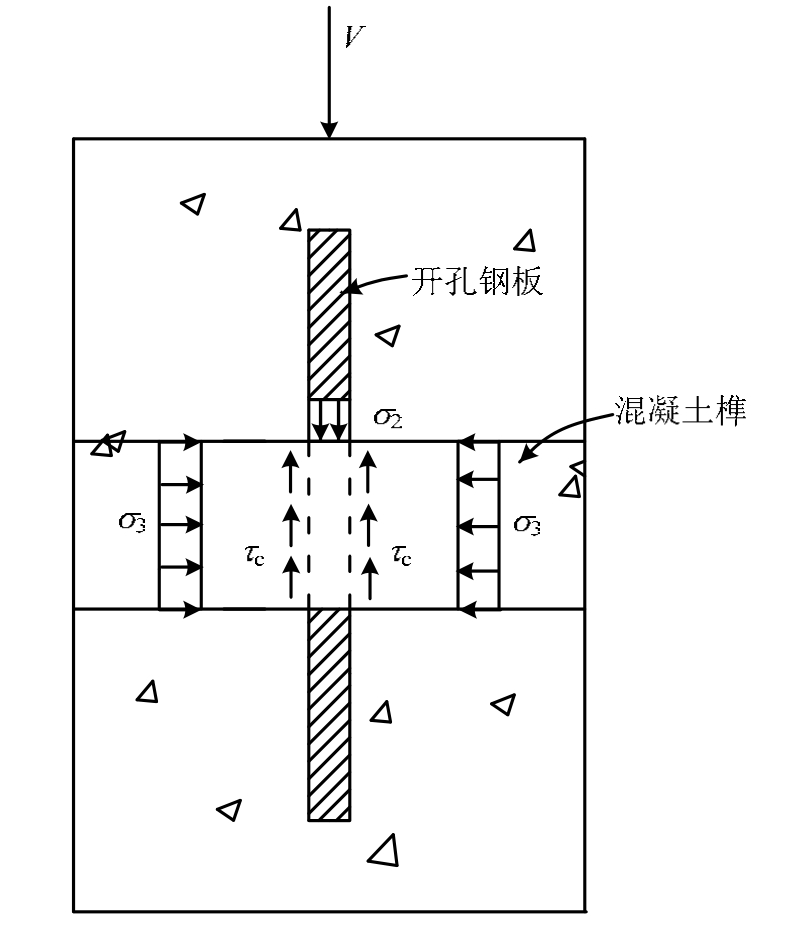
图8 混凝土榫受力图
Fig.8 Stress diagram of concrete dowel
参考文献[18]混凝土在纯剪状态下的剪切强度为τ = 0 .39f 0.57 ，但由于孔内混凝土处于贯穿钢筋
cv cu(σ 1 )、开孔钢板(σ 2 )和周围混凝土(σ 3 )的三轴受压状态，混凝土强度有一定的提高，因此引入混凝土榫强度提高系数φ c ，则：
φ c 通过试件P-1-45-0和P-0-45-0在相对滑移为6.43 mm时的荷载差 98 kN除以 2 A c τ c v 得到，即φ c =6.93。因此，混凝土榫的抗剪承载力为：
3.2.3 贯穿钢筋的抗剪作用q r
贯穿钢筋的受力见图9，其抗剪作用可记为：
式中：A r 为贯穿钢筋的截面面积， A r = 
/4；τ r 为贯穿钢筋的剪切强度。
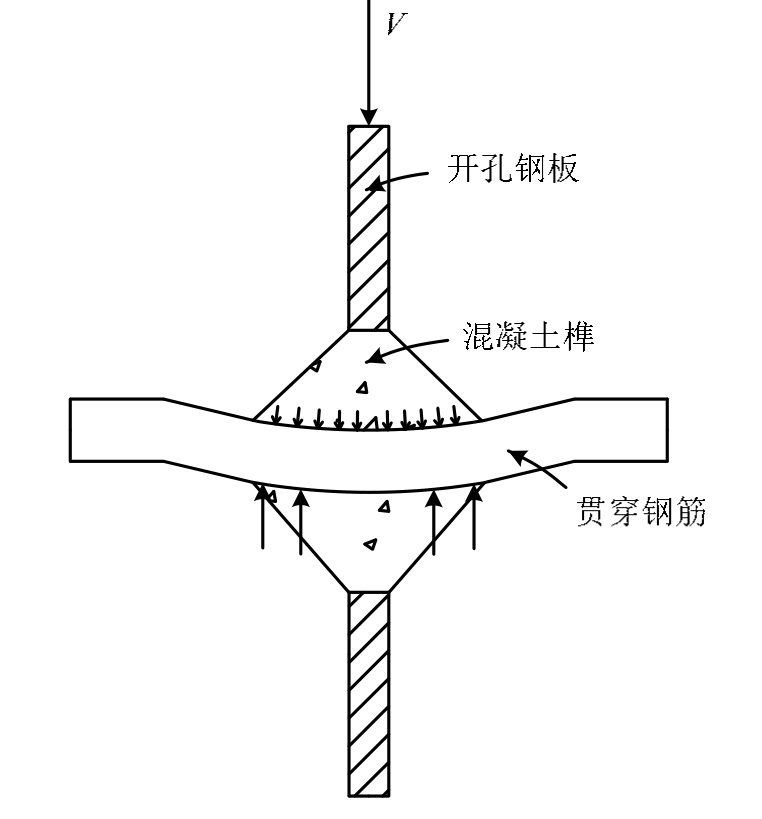
图9 贯穿钢筋受力图
Fig.9 Stress diagram of steel rebar through the hole
钢筋在纯剪状态下的剪切强度为τ r = f y /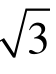 
，f y 为贯穿钢筋的屈服强度，但由图9可明显看出贯穿钢筋处于弯剪状态，且局部混凝土的支撑作用一定程度上可减小贯穿钢筋的变形，在此引入钢筋强度提高系数φ r ，则：
通过已知贯穿钢筋的抗剪承载力 123 kN和d st =20 mm、f y =357 MPa计算得到φ r =1.94。因此，贯穿钢筋的抗剪承载力为：
综上所述，标准单孔PBL连接件的抗剪承载力计算公式可记为：
多孔连接件的抗剪承载力计算则是在单孔连接件的基础上，保持端部混凝土的承压作用不变，将混凝土榫和贯穿钢筋的作用进行叠加。但考虑到开孔钢板上部分孔洞破坏之后连接件的应力重分布，在此对混凝土榫和贯穿钢筋所承担的抗剪作用按照孔洞数量、孔洞直径以及孔洞间距之间的关系(式(1))进行折减，则多孔PBL连接件的抗剪承载力计算式为：
根据提出的理论计算方法对本文8个试件的抗剪承载力进行计算，图 10为计算结果和试验结果的对比图，方差和变异系数分别为4.38%和4.53%，较其他已有计算公式更接近试验结果。图 11对其他相关试验的计算结果和试验值进行对比 [7,15,19―20] ，方差和变异系数分别为5.6%和6.2%，计算值和试验值吻合较好。该公式物理意义明确，能很好地预测PBL连接件的抗剪承载力。由于目前尚未有规范明确规定PBL连接件的抗剪承载力计算公式，且大多数学者根据试验拟合的公式也不具有广泛的应用性。因此，PBL连接件的抗剪承载力理论计算还需大量试验进行更全面的研究。
图10 试验结果和理论结果对比
Fig.10 Comparison of experimental results and theoretical results
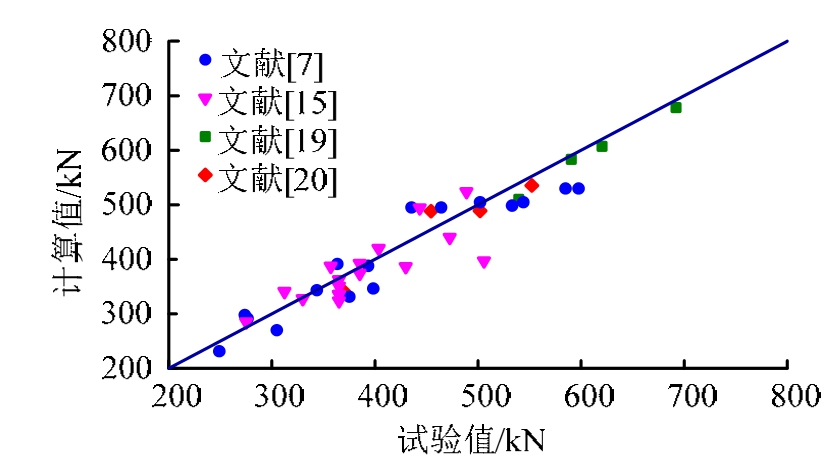
图11 试验结果对比
Fig.11 Comparison of experimental results
(1)端承型和非端承型试件的破坏形态有较大差异，前者是侧面混凝土板的劈裂破坏，后者是混凝土榫的剪切破坏；端部承压试件的抗剪承载力和抗剪刚度都高于端部不承压试件，建议在大跨组合桥梁中采用非连续布置的PBL连接件，不仅方便连接件的运输，也可以减少施工中连接件的焊接变形。
(2)端承型试件的承载力受多因素的控制，贯穿钢筋直径、开孔数目和混凝土强度都是影响其承载能力的主要因素，但当开孔钢板上孔洞数目多于2个时，再增加孔洞对PBL连接件的承载力提高作用不明显。
(3)本文基于变形协调条件对PBL连接件抗剪承载力进行分析，考虑了端部混凝土的承压作用以及孔中混凝土和贯穿钢筋的抗剪作用，并在多孔连接件中引入孔洞影响系数对混凝土榫和贯穿钢筋的承载力折减，提出的公式计算结果和实测结果吻合较好。说明本文提出的理论公式对预测单排PBL连接件的抗剪承载力有一定的参考价值。
参考文献：
[1]Leonhardt F, Andrä W, Andrä H, et al.Neues,vorteilhaftes Verbundmittel für Stahlverbund-Tragwerke mit hoher Dauerfestigkeit [J].Beton-Und Stahlbetonbau,1987, 82(12): 325―331.
[2]刘玉擎.组合结构桥梁[M].北京: 人民交通出版社,2005: 36―40.Liu Yuqing.Steel-concrete hybrid bridge [M].Beijing:China Communication Press, 2005: 36―40.(in Chinese)
[3]张猛, 汪洋, 张哲.钢-混凝土组合结构新型双钉头型栓钉剪力连接件抗剪承载力研究[J].建筑钢结构进展,2014, 16(2): 13―22.Zhang Meng, Wang Yang, Zhang Zhe.Analysis on the ultimate shear capacity of double-nut stud shear connector in composite structures [J].Progress in Steel Building Structures, 2014, 16(2): 13―22.(in Chinese)
[4]阳先全, 李艳.PBL剪力键承载能力试验研究[J].桥梁建设, 2015, 45(1): 85―90.Yang Xianquan, Li Yan.Test study of bearing capacity of PBL shear connectors [J].Bridge Construction, 2015,45(1): 85―90.(in Chinese)
[5]Oguejiofor E C, Hosain M U.A parametric study of perfobond rib shear connectors [J].Canadian Journal of Civil Engineering, 1994, 21(4): 614―625.
[6]Medberry S B, Shahrooz B M.Perfobond shearconnector for composite construction [J].Engineering Journal, 2002, 39(1): 2―12.
[7]Vianna J D C, Andrade S A L D, Vellasco P C G D S, et al.Experimental study of Perfobond shear connectors in composite construction [J].Journal of Constructional Steel Research, 2013, 81(81): 62―75.
[8]Su Q, Yang G, Bradford M A.Bearing capacity of perfobond rib shear connectors in composite girder bridges [J].Journal of Bridge Engineering, 2016, 21(4):06015009.
[9]宗周红, 车惠民.剪力连接件静载和疲劳试验研究[J].福州大学学报, 1999, 27(6): 61―66.Zong Zhouhong, Che Huimin.Experimental study of shear connector under static and fatigue loading [J].Journal of Fuzhou University, 1999, 27(6): 61―66.(in Chinese)
[10]胡建华, 叶梅新, 黄琼.PBL剪力连接件承载力试验[J].中国公路学报, 2006, 19(6): 65―72.Hu Jianhua, Ye Meixin, Huang Qiong.Experiment on bearing capacity of PBL shear connectors [J].Chinese Road Transaction, 2006, 19(6): 65―72.(in Chinese)
[11]石宵爽, 王清远, 欧阳雯欣.PBL剪力连接件粘结滑移性能的静载推出试验研究[J].工程力学, 2012, 29(1):168―175.Shi Xiaoshaung, Wang Qingyuan, Ouyang Wenxin.Push-out experimental study on bond-slip behavior of PBL shear connector under static loading [J].Engineering Mechanics, 2012, 29(1): 168―175.(in Chinese)
[12]柳扬清, 刘玉擎, 郑双杰.肋板间距对开孔板连接件抗剪刚度影响分析[J].工程力学, 2016, 33(9): 179―185.Liu Yangqing, Liu Yuqing, Zheng Shuangjie.Analysis on effect of plate spacing on shear stiffness of perfobond conncetors [J].Engineering Mechanics, 2016, 33(9):179―185.(In Chinese)
[13]Cândido-Martins J P S, Costa-Neves L F, Vellasco P C G D S.Experimental evaluation of the structural response of Perfobond shear connectors [J].Engineering Structures, 2010, 32(8): 1976―1985.
[14]肖林, 卫星, 强士中.两类 PBL剪力键推出试验的对比研究[J].土木工程学报, 2013, 46(11): 70―80.Xiao Lin, Wei Xing, Qiang Shizhong.Comparative study on two kinds of push-out tests of PBL shear connectors[J].China Civil Engineering Journal, 2013, 46(11): 70―80.(In Chinese)
[15]Oguejiofor E C, Hosain M U.Numerical analysis of push-out specimens with perfobond rib connectors [J].Computers & Structures, 1997, 62(4): 617―624.
[16]Al-Darzi S Y K, Chen A R, Liu Y Q.Finite element simulation and parametric studies of perfobond rib connector [J].American Journal of Applied Sciences,2007, 4(3): 122―127.
[17]Veríssimo G, Paes J L R, Valente I, et al.Design and experimental analysis of a new shear connector for steel and concrete composite structures [C]// 3rd International Conference on Bridge Maintenance, Safety and Management, Porto, Portugal, 2006.
[18]过镇海.钢筋混凝土原理[M].北京: 清华大学出版社,2013: 33―34.Guo Zhenhai.Reinforced concrete theory [M].Beijing:Tsinghua University Press, 2013: 33―34.(in Chinese)
[19]赵晨, 刘玉擎.开孔板连接件抗剪承载力试验研究[J].工程力学, 2012, 29(12): 349―354.Zhao Chen, Liu Yuqing.Experimental study of shear capacity of perfobond connectors [J].Engineering Mechanics, 2012, 29(12): 349―354.(in Chinese)
[20]Ahn J H, Lee C G, Won J H, et al.Shear resistance of the perfobond-rib shear connector depending on concrete strength and rib arrangement [J].Journal of Constructional Steel Research, 2010, 66(10): 1295―1307.
EXPERIMENTAL STUDY ON THE SHEAR CAPACITY OF PBL SHEAR CONNECTORS
YANG Yong , CHEN Yang
(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an, Shaanxi 710055, China)
Abstract: To establish the expression of shear capacity of PBL (Perfobond Leiste)connectors, monotonic loading push-out tests of eight PBL connectors were carried out.The influences of different bearing types,concrete strength, the number of hole(s)in the steel plate and the diameter of transverse rebar passing through the hole(s)on the shear capacity of PBL shear connectors in static loading were investigated emphatically.According to the deformation compatibility condition, the contribution of end concrete, concrete dowel and transverse rebar passing through the hole(s)to shear capacity of the shear connector with single hole were analyzed.The shear capacity of connectors with multiple holes were obtained by the superposition of the shear capacity of connectors with single hole on the basis of stress redistribution.Experimental results showed that the calculation model of the shear capacity had clear physical meaning and desired computational accuracy.The calculation model can be used to calculate the shear capacity of single row PBL shear connectors.
Key words: composite bridge; PBL shear connectors; push-out test; deformation coordination condition; shear capacity
作者简介： 杨勇(1976―)，男，江西人，教授，博士，博导，主要从事组合结构研究(E-mail: yyhhp2004@163.com).
基金项目： 国家自然科学基金项目(50708040，50978109)
通讯作者： 陈阳(1992―)，女，陕西人，博士生，主要从事组合结构研究(E-mail: xauatchenyang@126.com).
文章编号： 1000-4750(2018)09-0089-08
收稿日期： 2017-05-16；修改日期：2017-09-16
文献标志码： A
doi: 10.6052/j.issn.1000-4750.2017.05.0365
中图分类号： TU398+.9