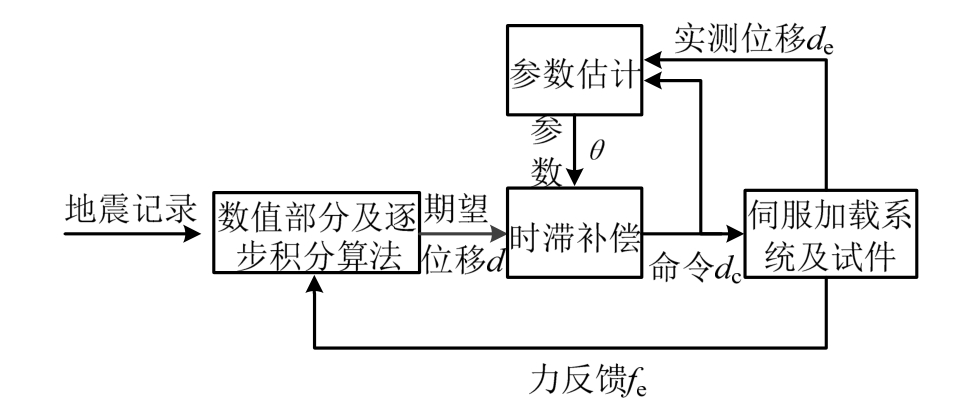
图1 自适应时滞补偿实时混合试验的原理
Fig.1 Principle of (RHT)with adaptive delay compensation
王 贞 1,2,3 ，李 强 1,2,3 ，吴 斌 1,2,3
(1．哈尔滨工业大学结构工程灾变与控制教育部重点实验室，哈尔滨 150090；2．哈尔滨工业大学土木工程智能防灾减灾工业和信息化部重点实验室，哈尔滨 150090；3．哈尔滨工业大学土木工程学院，哈尔滨 150090)
摘 要： 实时混合试验是由拟动力试验发展而来，时滞问题是实时混合试验的核心问题。传统时滞补偿方法往往假定试验中时滞不变，然而加载系统的非线性以及试件性能的变化可能导致系统时滞变化，使得此类方法性能不够理想。该文针对变时滞实时混合试验提出了基于模型参数识别的自适应时滞补偿方法。该方法将伺服系统简化为离散模型，通过在线参数估计确定系统状态，从而对伺服系统进行在线时滞补偿。该文首先阐述了该方法的原理，再通过数值模拟验证了方法的可行性与精度，并分析了不同模型对补偿的影响。
关键词： 实时混合试验；时滞补偿；自适应；离散模型；精度
自1992年Nakashima等 [1] 提出实时混合试验以来，各国学者开展了一系列研究工作，逐步确立了实时混合试验的核心问题—时滞。试验过程中伺服加载系统从接收命令到实现命令所需要的时间，即系统时滞 [2] 。不同于传统拟动力试验的慢速加载 [3] ，实时混合试验采用快速甚至实时加载。由于液压伺服加载系统是动力系统，试验中时滞不可避免。研究表明，时滞不仅影响试验的精度，在一定条件下甚至影响试验的稳定性 [4] ，威胁试验设备及试件的安全。
为解决时滞带来的问题，实时混合试验中需要补偿伺服加载系统时滞 [5] 。在各种时滞补偿方法中，最为常用的是基于位移预测的方法 [6－8] 。该类方法通常假定时滞为常数，并通过前期离线估计得到；试验过程中预测时滞时长后试验子结构的位移，并提前一个时滞时长发给作动器。事实上，由于试件以及伺服加载系统的非线性特征以及试件性能的变化，系统时滞往往是变化的。为解决变时滞补偿问题，文献[9－12]提出自适应时滞补偿方法；但是这些方法往往不具有较强的普遍性，很难得到大范围应用。与此不同，本文参照最小方差自校正控制，提出了基于加载系统离散模型参数在线识别的自适应时滞补偿方法。
自校正控制方法通过在线识别系统模型并进行相应的控制器调节，从而实现适应被控对象的时变特性，具有良好的控制性能。本文采用自校正控制方法 [13] 的基本原理，实现实时混合试验中加载系统时滞的自适应补偿，其原理如图1所示。
为了跟踪系统特性的变化，首先将试验系统简化为离散模型；在试验过程中，在线估计试验模型参数，该参数可以及时有效地反映系统时滞的变化；利用识别出的参数预测下一步命令，以达到自适应时滞补偿的目的。
图1 自适应时滞补偿实时混合试验的原理
Fig.1 Principle of (RHT)with adaptive delay compensation
系统模型就是为了建立试验加载系统输入、输出之间的关系，进而能够以此为基础预测加载系统对指定命令的响应。加载系统时滞是系统的一种特性，其改变的前提是加载系统参数的变化，因此，通过识别系统参数就能有效捕捉到时滞的变化。为了使用方便，这里采用差分模型，即：
式中：d c 与d m 分别为加载系统的命令与响应；θ c j 与 m k θ为对应模型参数；p与q为对应参数个数。为表述方便，式(1)可改写为矩阵形式，即：
式中：
细心的读者可能已经发现，式(2)中最新的命令被放在等号的左侧，其余项在右侧，这么做是为了采用该式预测命令。
将试验系统简化为离散模型后，为了实时跟踪系统特性的变化，需要在试验过程中在线估计式(2)中参数 θ 。本文采用带遗忘因子的递推最小二乘算法 [14] 估计参数，该算法存储量小、计算简便，可以有效克服“数据饱和”现象。该算法可表示为：
式中：λ为遗忘因子，一般取0.9≤λ≤1； I 为单位矩阵。至于方法启动值 P 0 及 θ 0 ，可以采用前期离线试验得到的相关数据进行一次完成(批处理)的最小二乘法 [14] 计算。具体算法如下：
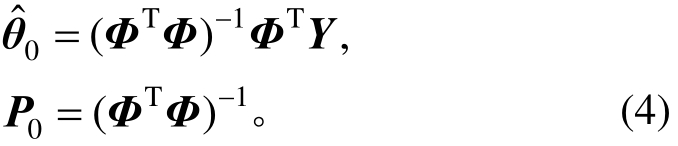
其中：
式中L为所用数据的组数。该算法得到的 θ 0 可以很好满足试验要求，但需要系统前期离线信号各频率成分充足，否则估计出的启动值 P 0 及 θ 0 可能误差过大，影响试验的精度及安全。也可以采用模拟得到结构位移响应作为期望位移开展前期参数识别试验。
在试验过程中，通过式(3)估计出的参数可以直接有效反映伺服系统当前的状态，实际上包含了系统时滞的特性。以离散模型的逆模型为基础，计算系统命令，在该系统模型有效的前提下，将实现理想的控制效果，包括实现良好的时滞补偿效果。因为该方法能够自动跟踪系统时滞变化，具有自适应特性，所以本文称之为自适应时滞补偿方法。该方法如下：
首先，在第t i+1 时刻，式(2)系统离散模型为：
其中：
假设模型参数在第 t i ～ t i+1 内变化不大，则可以用第i步估计的模型参数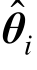 
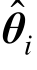近似 ，即：
在第i+1步，式(5)中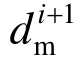 
未知， 
， …， 
， 
， 
， …， 
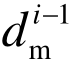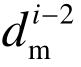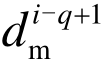均已知。另外，此时试件期望位移 d i+1 可由逐步积分算法(如中心差分法)计算得到。对于时滞补偿控制策略的目标是使实测位移尽量接近期望位移，因此，在计算命令时，可以假定：
即补偿方法为：
其中：
如果 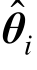足够接近真实模型参数 θ i+1 ，那么将式(9)得到的指令位移 
发送给伺服系统，试验子结构实测位移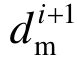 
就会接近期望位移 d i+1 ，从而达到时滞补偿效果。该自适应时滞补偿方法流程如图 2所示。
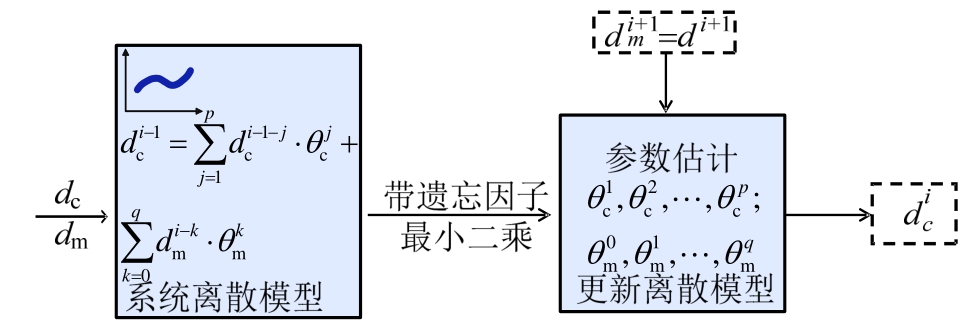
图2 自适应时滞补偿方法流程
Fig.2 Flow diagram of adaptive delay compensation
采用上述自适应时滞补偿方法的实时混合试验的试验流程如下：
1)确定系统系统离散模型，确定遗忘因子、积分步长等参数；
2)进行前期离线试验确定初值参数 θ 0 ；
3)在试验 t i 时刻采用带遗忘因子最小二乘法在线估计系统模型参数；
4)测量t i 时刻试验子结构实测位移及试件反力；
5)利用逐步积分算法求解结构下一步期望位移；
6)利用式(9)计算试验子结构的指令位移；
7)将指令位移发送给伺服系统；
8)i←i+1，返回第2)步，直到试验结束。
本节对所提出的基于模型参数识别的自适应时滞补偿方法进行数值模拟，检验方法的可行性与时滞补偿效果。
对图 3所示的单自由度结构体系进行数值模拟，质量取1000 kg，自振周期1 s，阻尼比为0%，因此试验子结构刚度为39.4784 kN/m。地震激励为El Centro (NS, 1940)地震波，峰值加速度调整为0.263 g。
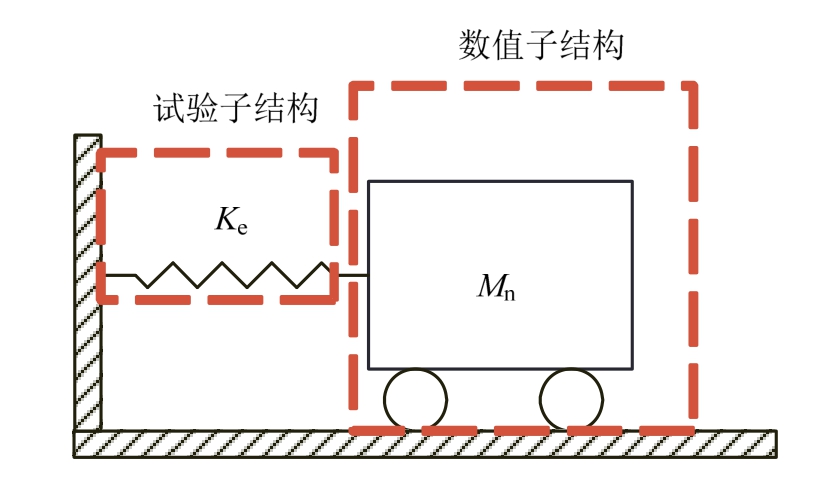
图3 结构示意图
Fig.3 Schematic of emulated structure
假定液压伺服系统传递函数为：
式中：系统圆频率ω=50 rad/s；阻尼比 ζ = 0 .80。采用中心差分法求解结构运动方程，积分步长取为0.01 s。
经反复计算分析发现，对于该混合试验，如下四参数伺服系统离散模型具有良好的时滞补偿性能：
式中θ 1 与指令位移有关，θ 2 ～θ 4 与实测位移有关。对于不考虑噪声的定常试验系统，以地震作用下纯数值模拟得到的结构位移作为输入，利用式(9)前期离线估计出的参数初值为：
采用该初值的实时混合试验模拟的参数估计值如图4，此时遗忘因子取为0.97。
图4表明，利用一次完成的最小二乘法所得的参数初值与稳定后的估计值存在一定偏差。该偏差对试验前3 s的时滞补偿效果产生了较大影响，此阶段响应位移与期望位移的差最大可达到3.556× 10 -3 mm。3 s后参数收敛到稳定值，响应位移与期望位移的差最大为 6 .103× 10 -6 mm。图5表明，试验系统时滞约为 27 ms，时滞补偿后实测位移与期望位移相位差对应时间约为0.003 ms，期望位移与结构纯数值模拟得到的试件位移(图中为参考位移)时间延迟约为 0.01 ms。可见本文所提出的时滞补偿方法具有良好的精度与补偿效果。
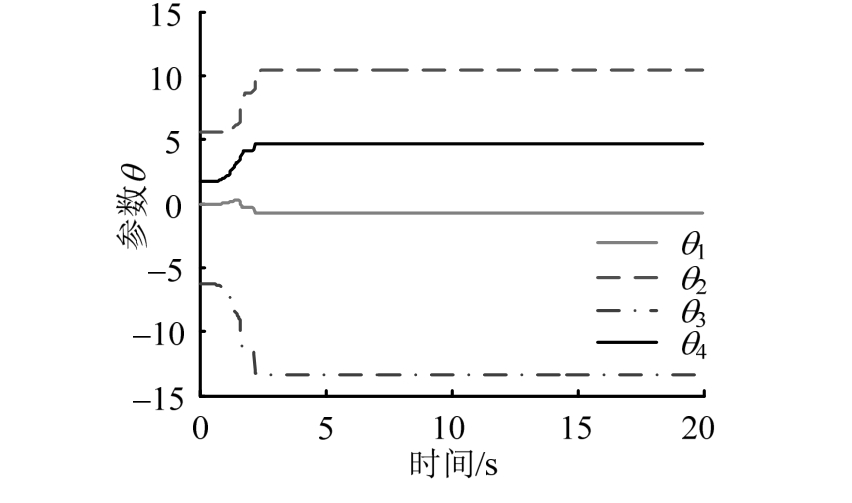
图4 定常系统参数估计值
Fig.4 Estimated parameters of invariant system
图5 定常系统实时混合试验模拟
Fig.5 Simulation of RHT with invariant system
为更加真实模拟实际实时混合试验以及分析补偿方法的抗噪能力，对响应位移 d m 加入方差为0.01 mm的白噪声，并完成实时混合试验模拟，其时滞补偿结果如图6、图7所示。
图6表明，考虑噪声后参数估计值变化幅度较大，表明参数估计值对噪声较为敏感。图7表明，试件实测位移与期望位移的差最大为0.1349 mm。实测位移与期望位移以及期望位移与结构纯数值模拟得到的试件位移的相对时间滞后均为0.2 ms左右。可见，即使参数估计不甚理想，时滞补偿效果仍然良好，说明时滞补偿本身对参数估计值波动不敏感。对于考虑噪声的定常系统，本文所提出的时滞补偿方法仍然具有良好的补偿效果。
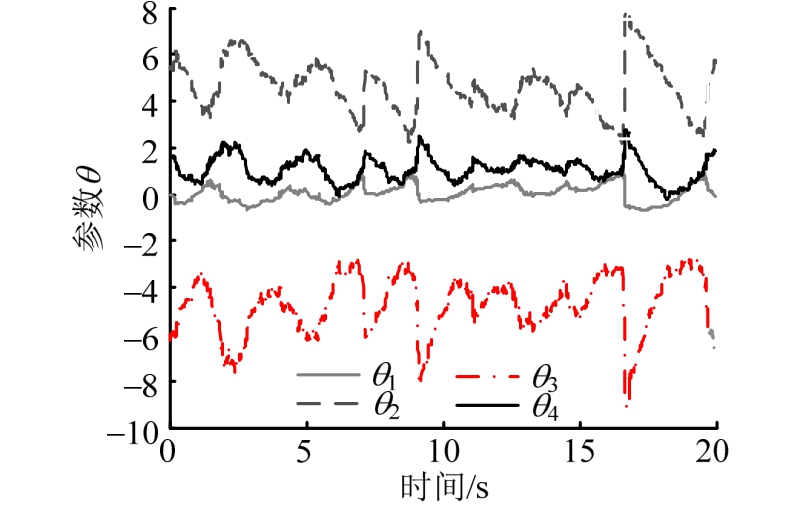
图6 考虑噪声的定常系统参数估计值
Fig.6 Estimated parameters of invariant system considering noise
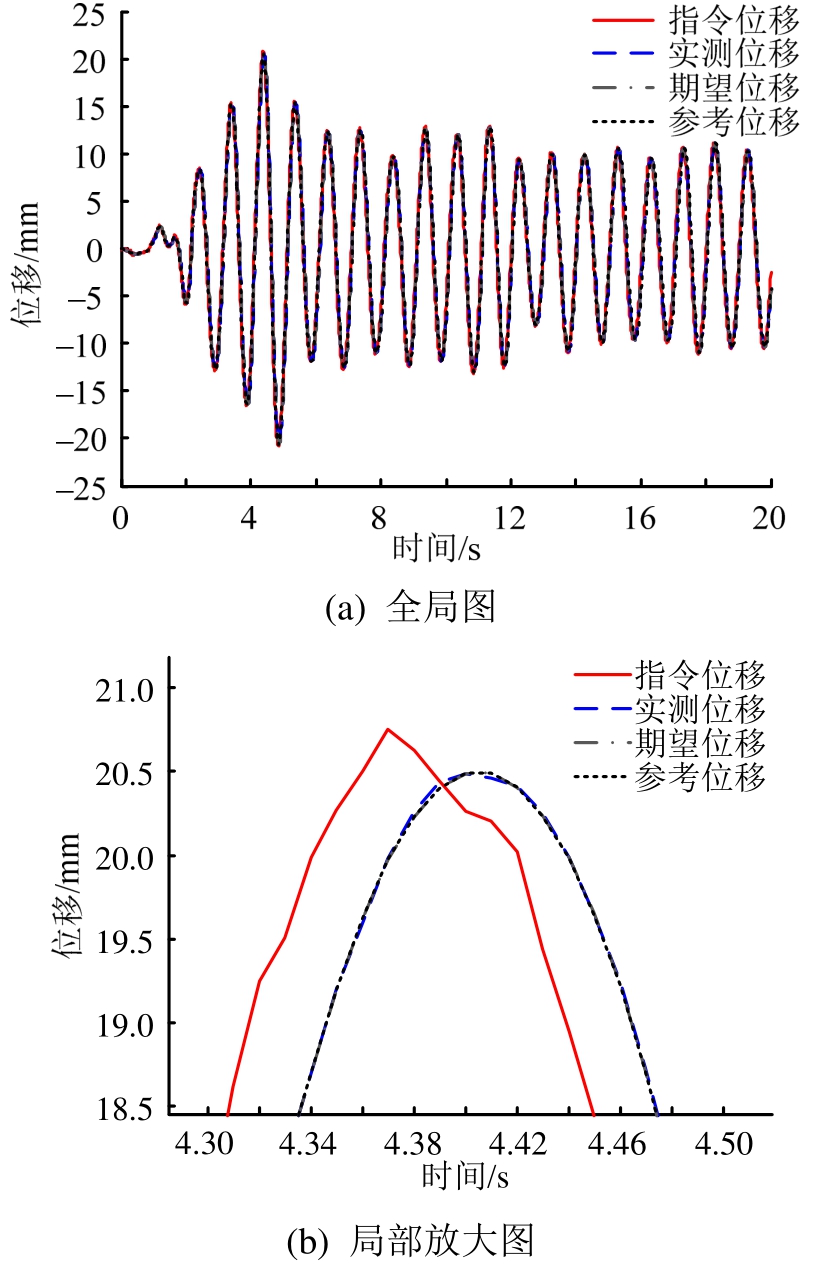
图7 考虑噪声的定常系统实时混合试验模拟
Fig.7 Simulation of RHT with invariant system considering noise
上述两节假定伺服加载系统的参数在试验中不发生变化，即定常系统。事实上，在实际实时混合试验中，加载系统特性、试件特性均可能发生变化，从而导致系统时滞也发生变化。许多时滞补偿方法往往假定定常时滞，无法准确补偿系统特性变化的时变系统时滞，使实时混合试验结果误差增大甚至不可靠。这也是本文尝试解决的问题，所提出的自适应时滞补偿方法在线识别系统模型参数，跟踪系统参数变化，以适应系统时滞的变化，取得较好补偿效果。
为了简单有效地模拟系统参数变化，本文假定式(11)中系统圆频率ω按照图 8所示正弦规律变化，阻尼比ζ调整为0.78。当ω取为峰值54及44时，系统时滞相差约为8 ms。
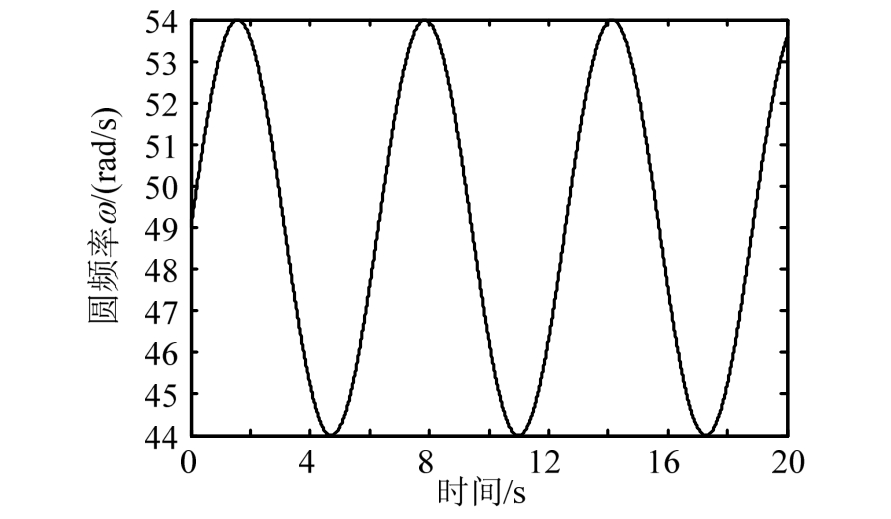
图8 时变系统圆频率ω的变化
Fig.8 Change of circular frequency ω of time-varying system
需要注意，应用递推最小二乘法识别时变参数，需要选取合适的遗忘因子。遗忘因子的作用是折减旧数据的影响权重，相对加大最近数据对参数估计的影响权重 [14] 。遗忘因子越小，就越能及时反映当前系统的模型参数，但是可能带来参数估计值的大幅波动，甚至可能威胁试验安全。通常情况下，遗忘因子一般取0.95～1。
对于上述实时混合试验，当遗忘因子 λ =0.963时，时滞补偿结果效果较好，实时混合试验的数值模拟结果如下：
由图9可知，参数θ 3 的估计值大致呈现出正弦变化，与假定的模型圆频率变化规律有一定相关性。而其他三个参数，基本不具有正弦波动趋势，表明与圆频率不直接相关。估计值还表现出小幅度振动。当该小幅度振动过大时，将会造成参数短时间内跳动过大，甚至威胁试验安全。通过调整遗忘因子可有效的减小该参数变化幅度。
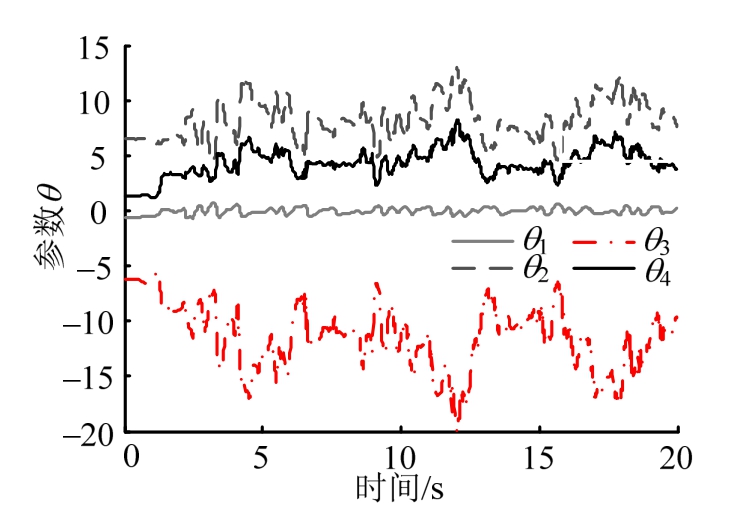
图9 时变系统参数估计值
Fig.9 Estimated parameters of time-varying system
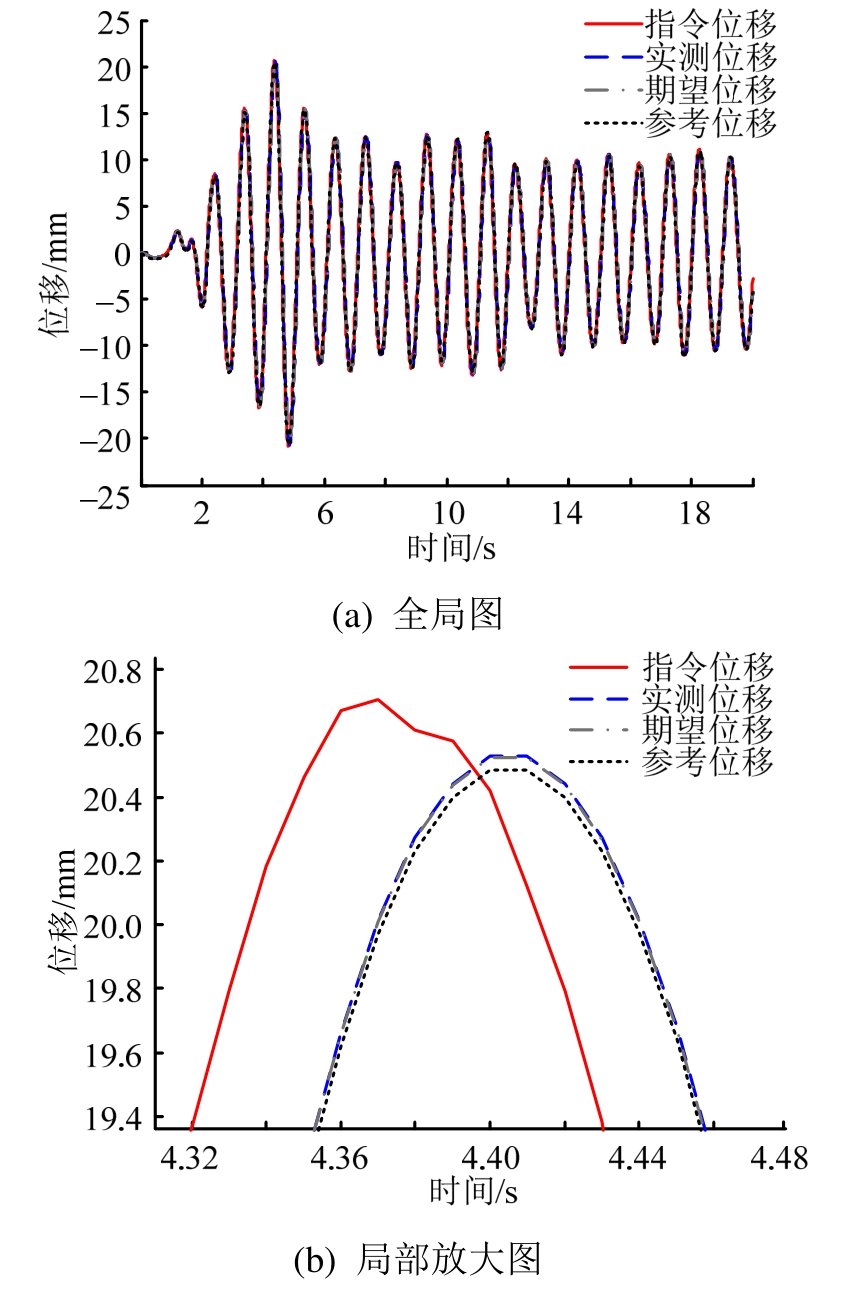
图10 时变系统实时混合试验模拟
Fig.10 Simulation of RHT with time-varying system
图 10表明，对于上述时变系统，经过补偿后试件实测位移与期望位移的最大差为0.0418 mm。试件实测位移与期望位移时间延迟约为0.2 ms，期望位移与结构纯数值模拟得到的试件位移时间偏差约0.25 ms。可见，真实参数的大幅度变化并未影响补偿效果。时滞补偿方法通过对参数不断地调节更新，使补偿过程更好地适应时变系统，达到良好的补偿精度。相较于传统补偿方法，该方法将更加适用于时变系统。
第 2节采用四参数模型取得了良好的补偿效果，接下来分别采用三参数模型和七参数模型进行模拟对比。三参数模型如下：当使用该模型对2.2节不考虑噪声的定常系统进行补偿时，参数估计值如图11所示。
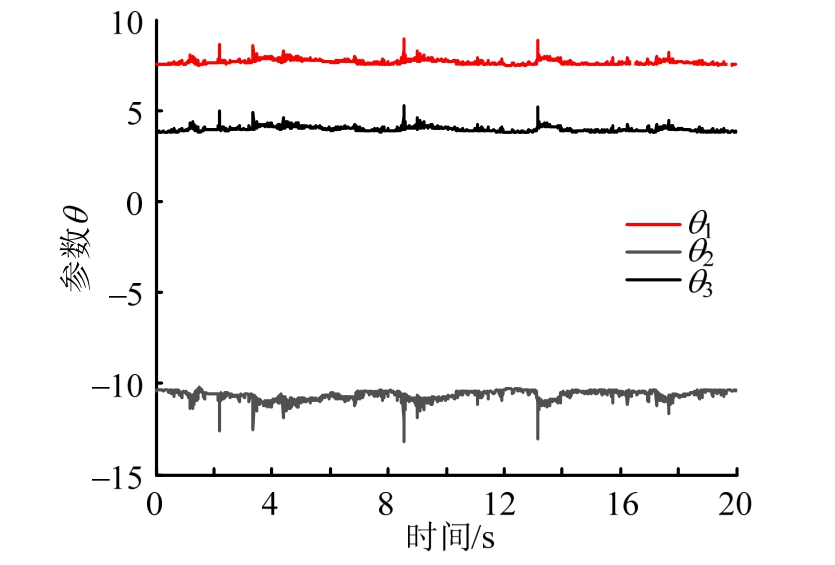
图11 三参数模型定常系统的参数估计值
Fig.11 Estimated parameters of three-parameter model for invariant system
由图11可知，参数估计值能够较好收敛。与四参数模型不同，三参数模型的参数估计值会出现小幅度振动。原因在于三参数模型减少了参数个数，其他参数在补偿过程中一定程度上会对选取的三个参数产生影响，从而使识别出的参数发生变化。
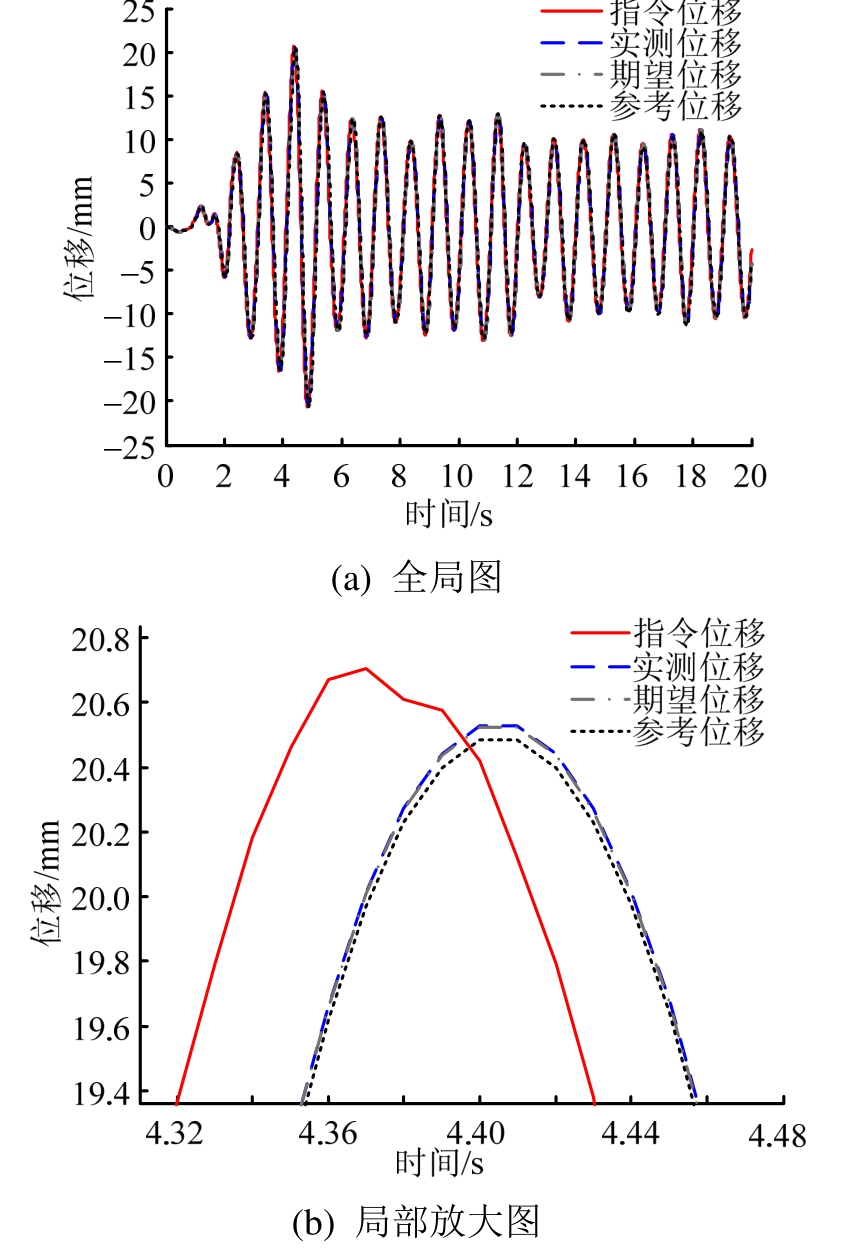
图12 三参数模型定常系统实时混合试验模拟
Fig.12 Simulation of RHT with three-parameter model for invariant system
三参数模型的时滞补偿效果如图12所示。补偿后试件实测位移与期望位移的差最大为0.01263 mm。响应位移与期望位移的时间延迟以及期望位移与真实位移的时间延迟均约0.02 ms。可见三参数模型补偿精度较四参数模型略差，但其稳定性良好，对试验安全威胁较小。实际实时混合试验中，该模型也是可以考虑采用的。
上述分析表明，离散模型参数越多，时滞补偿精度越高。然而，过多参数可能会降低时滞补偿方法的抗噪声能力。以如下七参数离散模型为例：
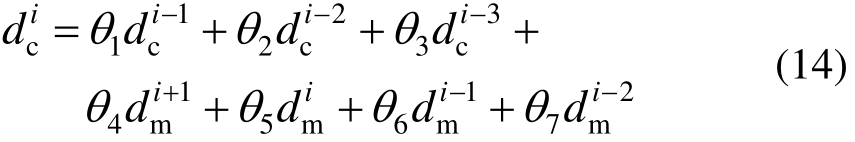
当使用该模型对2.1节考虑噪声的定常系统进行时滞补偿，其结果如图13所示。
图13 七参数模型定常系统实时混合试验模拟
Fig.13 Simulation of RHT with seven-parameter model for invariant system
由图13可知，时滞补偿过程中指令位移d c 发生大幅振动，振动的周期为两个积分步长2Δ t。可见过于复杂的系统离散模型不仅不能增加补偿精度，而且可能对试验安全造成很大的威胁。
综上，参数数目对时滞补偿效果、方法性能有较大影响，实际应用时宜谨慎选择参数。建议根据离线试验数据识别系统模型，比较不同模型参数的影响，从而合理选择参数。
本文以自校正控制理论为基础，提出了基于模型参数识别的自适应时滞补偿方法，并通过数值模拟验证了方法的可行性及时滞补偿效果。主要结论如下：
(1)不同试验工况下模拟结果表明，基于模型参数识别的自适应时滞补偿方法具有良好的抗噪能力，同时适用于时变系统，可以实现自适应时滞补偿的目的。
(2)系统离散模型的参数个数对补偿效果影响明显，参数过少会造成时滞补偿精度下降，参数过多会使补偿方法抗噪能力下降，试验存在安全隐患。基于模型参数识别的自适应时滞补偿方法需要选取适当的系统离散模型。
参考文献：
[1]Nakashima M, Kato H, Takaoka E.Development of real-time pseudodynamic testing [J].Earthquake Engineering and Structural Dynamic, 1992, 21(1): 79―89.
[2]Darby A, Williams M, Blakeborough A.Stability and delay compensation for real-time substructure testing [J].Journal of Engineering Mechanics, 2002, 128(12):1276―1284.
[3]邱法维, 钱稼茹, 陈志鹏.结构抗震实验方法[M].北京: 科学出版社, 2000: 72.Qiu Fawei, Qian Jiaru, Chen Zhipeng.Seismic test methodology for structures [M].Beijing: Science Press,2000: 72.(in Chinese)
[4]Mercan O, Ricles J M.Stability analysis for real-time pseudodynamic and hybrid pseudodynamic testing with multiple sources of delay [J].Earthquake Engineering and Structural Dynamic, 2008, 37: 1269―1293.
[5]王倩颖.实时子结构试验方法及其应用[D].哈尔滨:哈尔滨工业大学, 2007: 44―86.Wang Qianying.Real-time substructure testing method and its application [D].Harbin: Harbin Institute of Technology, 2007: 44―86.(in Chinese)
[6]唐贞云, 陈适才, 张金喜, 等.基于振动台的实时动力子结构实验系统稳定性预测研究[J].工程力学, 2016,33(12): 217―224.Tang Zhenyun, Chen Shicai, Zhang Jinxi, et al.Study on the stability prediction of real-time dynamic substructuring system based on shaking table [J].Engineering Mechanics, 2016, 33(12): 217―224.(in Chinese)
[7]Horiuchi T, Konno T.A new method for compensating actuator delay in real-time hybrid experiments [J].Philosophical Transactions of the Royal Society of London.Series A, 2001, 359: 1786―1893.
[8]Bonnet P A.The development of multi-axis real-time substructure testing [D].Oxford: University of Oxford,2006.
[9]Ahmadizadeh M, Mosqueda G, Reinhorn A M.Compensation of actuator delay and dynamics for real-time hybrid structural simulation [J].Earthquake Engineering and Structural Dynamics, 2008, 37(1): 21―42.
[10]Yunbyeong C, Kazemibidokhti K, Ricles J M.Adaptive time series compensator for delay compensation of servo-hydraulic actuator systems for real-time hybrid simulation [J].Earthquake Engineering and Structural Dynamic, 2013, 42: 1697―1715.
[11]Wang Z, Wu B, Bursi O S, et al.An effective online delay estimation method based on a simplified physical system model for real-time hybrid simulation [J].Smart Structures and Systems, 2014, 14(6): 1247―1267.
[12]Chae Y, Rabiee R, Dursun A, et al.Real-time force control for servo-hydraulic actuator systems using adaptive time series compensator and compliance springs[J].Earthquake Engineering and Structural Dynamics,2018, 47: 854―871.https://doi.org/10.1002/ eqe.2994
[13]周锐, 陈宗基.自适应技术的理论及应用—控制、滤波、预报[M].北京: 国防工业出版社, 2009: 134―189.Zhou Rui, Chen Zongji.Theory and applications of adaptive technique - control, filter, forecast [M].Beijing:National Defence Industry Press, 2009: 134―189.(in Chinese)
[14]庞中华, 崔红.系统辨识与自适应控制MATLAB仿真[M].北京: 北京航空航天大学出版社, 2009: 27―45.Pang Zhonghua, Cui Hong.Simulations of system identification and adaptive control using MATLAB [M],Beijing: Beihang University Press, 2009: 27―45.(in Chinese)
ADAPTIVE DELAY COMPENSATION METHOD FOR REAL-TIME HYBRID TESTING
WANG Zhen 1,2,3 , LI Qiang 1,2,3 , WU Bin 1,2,3
(1.Key Lab of Structures Dynamic Behavior and Control of the Ministry of Education, Harbin Institute of Technology, Harbin 150090, China;2.Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of the Ministry of Industry and Information Technology,Harbin Institute of Technology, Harbin 150090, China;3.School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)
Abstract: Delay and its compensation are key problems for Real-time Hybrid Testing (RHT), which was developed from the pseudo-dynamic testing method.Conventional compensation methods are mostly based on constant delay assumption.However, system delay changes during tests due to system nonlinearity and performance change of the specimen, which results in undesirable test results.This paper proposes an adaptive delay compensation method based on online model parameter identification for RHT.The proposed method uses discrete models to simulate the servo loading system, online parameter identification to attain the loading system state; then the system delay is compensated based on this model.This paper firstly describes the method, and then numerically validates the feasibility and the effectiveness.The effect of different models is demonstrated as well.
Key words: real-time hybrid testing; delay compensation; adaptive; discrete model; accuracy
吴斌(1970―)，男，湖北人，教授，博士，博导，主要从事结构振动控制和结构抗震试验方法研究(E-mail: bin.wu@hit.edu.cn).
作者简介：
李强(1994―)，男，黑龙江人，硕士，主要从事实时混合试验方法研究(E-mail: 923918245@qq.com);
基金项目： 国家重点研发计划项目(2016YFC0701106)；青年科学基金项目(51408157，51408080)；黑龙江省自然科学基金项目(LC201423)；高等学校博士学科点专项基金项目(20132302110065)；河北省交通运输厅科学技术项目计划项目(KT2)
通讯作者： 王贞(1983―)，男，安徽人，讲师，博士，主要从事结构抗震试验方法研究(E-mail: zhenwang@hit.edu.cn).
文章编号： 1000-4750(2018)09-0037-07
收稿日期： 2017-05-19；修改日期：2018-01-18
文献标志码： A
doi: 10.6052/j.issn.1000-4750.2017.05.0384
中图分类号： TU317+.9