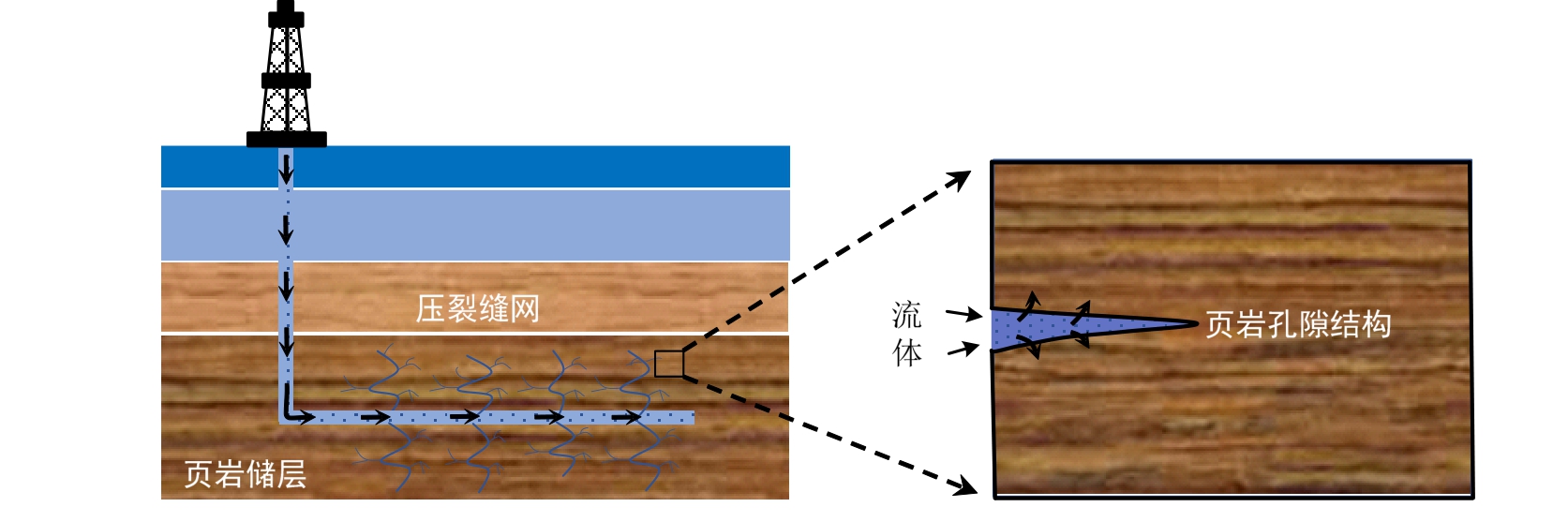
图1 页岩储层体积压裂改造
Fig.1 Stimulated reservoir volume of shale reservoir
王永亮 1,2 ，鞠 杨 1,3 ，陈佳亮 1,2 ，杨永明 1,2 ， Li CF 4
(1.中国矿业大学煤炭资源与安全开采国家重点实验室，北京 100083；2.中国矿业大学力学与建筑工程学院，北京 100083；3.中国矿业大学深部岩土力学与地下工程国家重点实验室，徐州 221116；4.Swansea大学Zienkiewicz工程计算中心，英国Swansea SA2 8PP)
摘 要： 该文介绍流体－固体－断裂耦合分析的自适应有限元(FE)－离散元(DE)算法，引进一款新近基于该方法研发的数值计算软件ELFEN，并将其应用于页岩分段体积压裂的三维数值计算和机理分析。该方法引入有限元应力恢复的超收敛拼片恢复(SPR)法，获得应力的超收敛SPR解，利用SPR解估计常规有限元解的误差，通过裂纹尖端局部区域的自适应网格重划分获得高精度应力解答并得以有效描述裂纹动态扩展，形成分析策略和求解方案。数值算例表明该算法和软件分析流体－固体－断裂耦合作用下单一、多水平井分段体积压裂的可靠性、有效性和实用性。
关键词： 自适应分析；有限元－离散元耦合；流体－固体－断裂耦合；体积压裂；ELFEN
我国页岩油气开发已经逐渐起步，诸多基础理论和关键科学(力学)问题正在攻关和深入研究。页岩油气规模开发主要依靠水平井和压裂改造两项核心技术，是面向重大工程需求的应用力学研究的重点课题。页岩气藏具有低孔隙率和低渗透率的特点，其压裂改造需要采用不同于常规天然气开采的技术，页岩储层“体破裂”的理论和技术构想应运而生 [1] ；该技术通过岩体在深部地应力作用下，利用水力或气体等体积压裂形成内部孔隙、层理裂隙和人工裂隙贯通的高密度缝网体系(图1)。有效、可靠的体积压裂数值计算方法和模拟技术成为需求。
图1 页岩储层体积压裂改造
Fig.1 Stimulated reservoir volume of shale reservoir
页岩体积压裂中的关键问题是流体驱动下的岩体破裂分析，流体―固体―断裂耦合机制是研究上的重点；岩石断裂的算法研究是其开展计算分析的重要基础，基于网格的数值方法中网格优化是技术上的难点。近年，国内外针对固体裂纹扩展的诸多计算方法得到建立和发展，如通过改进边界元法的位移间断方法 [2] ，裂纹扩展时重新剖分网格，用以描述裂纹面处位移间断来获得岩体内部的变形场；基于有限元和非连续变形分析的数值流行元方法 [3] ，在处理岩体内断层、节理等不连续面问题中具有一定优势，但其灵活高效求解三维问题尚有一定困难；基于解析或半解析裂缝模型的离散裂缝网方法 [4] ，采用简单的平面裂缝模型，求解时具有很高的效率，但简化模型同样难以处理三维问题、也未考虑材料各向异性、孔隙压力等因素，使其应用上受到限制。Dolbow和Belytschko [5] 提出扩展有限元法，通过改造传统有限元单元，实现无需重划网格即可实现裂纹在规则网格中的任意扩展，该方法在岩石断裂分析的计算中得到诸多应用：Mohammadnejad和Khoei [6] 将扩展有限元和粘结裂纹模型应用于水压驱动的裂纹扩展问题；Qing和Yao [7] 采用扩展有限元和有限差分法研究了裂缝性油气藏的裂纹开度和渗流问题；Zeng等 [8] 发展了岩体孔隙结构的流体―固体―断裂耦合扩展有限元法，将其用于页岩水平井水力压裂二维模型的数值模拟。Wang等 [9] 将有限元和离散元耦合来进行岩石的断裂分析，其利用有限元求解应力场并采用离散元进行破裂分析，形成基于连续介质力学的离散元方法(CDEM)，并将其用于页岩储层的水力压裂计算分析。本文作者及课题组针对低渗透性致密砂岩开展了水力压裂的实验研究和数值模拟分析 [10―11] ，讨论了不同地应力情况下水力压裂形成裂缝的形态；并利用模型重构技术建立了与实际岩石非均质性一致的三维数值模型，进一步采用CDEM对该模型进行裂缝网构型模拟分析；近期，发展了颗粒粘结方法和体积压裂模型，开展超临界二氧化碳(Supercritical CO 2 ，简称scCO 2 )的数值计算分析，讨论了天然裂纹对气体压裂的影响 [12] 。
在计算应用研究方面，涌现出针对体积压裂计算分析的平台和软件，如具有代表性的软件：FracpropPT、E-StimPlan、Meyer等，该软件均采用简化的裂缝模型对水力压裂实现模拟分析。FracpropPT、E-StimPlan引入解析或半解析的裂纹模型，仅能考虑储层为均质、各向同性材料；Meyer采用准三维模型，假设缝网为正交、平行且裂纹间距相等，难以描述复杂缝网。自适应有限元方法在振动、稳定、损伤分析等复杂问题中展现出很好的求解效力 [13―15] ，传统有限元因在裂纹尖端区域网格划分的限制，较难可靠、有效求解断裂问题，该自适应分析方法使其成为可能。Zienkiewicz和Zhu [16] 最早提出应力超收敛拼片恢复(Superconvergent Patch Recovery，简称SPR)法及其自适应分析方案。Azadi和Khoei [17] 基于SPR法的对二维断裂问题开展了有限元自适应求解，相比扩展有限元法，该法自动优化使用更少的单元和节点，便可获得精确的裂纹扩展路径并显著提高计算效率。英国Rockfield软件研发中心和Swansea大学研发的岩石力学计算分析软件 ELFEN [18] 针对致密性岩层的体积压裂开展分析，利用有限元和离散元耦合技术、并结合简单灵活的裂纹尖端局部网格自适应重划分实现裂纹扩展，更为精确、有效的网格重划分方法成为体积压裂新的研究内容。
本文将对该新型自适应有限元－离散元算法以及发展模型重构方法进行介绍，并引进ELFEN软件进行水力压裂数值计算分析，实现流体－固体－断裂耦合作用下三维岩体模型裂纹扩展的准确描述。
本文研究流体－固体－断裂耦合问题，耦合机制如图2所示，涉及的物理场和物理过程包括：
1)固体应力和孔隙压力在地应力、流体压力等外载荷作用下平衡—固体场；
2)岩体基质中孔隙流体流动—渗流场；
3)裂缝网络内流体流动—裂缝网络场。
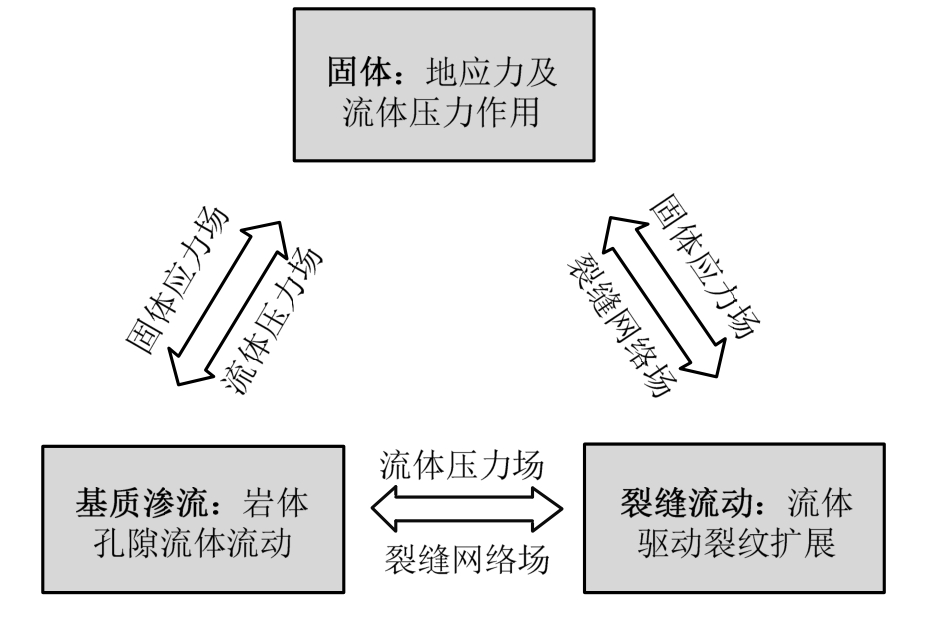
图2 流体-固体-断裂耦合机制
Fig.2 Fluidic-mechanical-fracture coupling mechanism
作为多孔介质的岩体，变形控制方程采用如下基本要求和假设：
1)利用合理的材料本构、强度方程，应力可有效分析拉压和剪切破坏。
2)裂缝内流体的质量守恒和流动方程可以描述平行板流动规律，导出熟知的裂隙渗流的立方定律。
假设流体加速度、对流项均不考虑，固体应力满足的动力平衡方程可表示如下 [19] ：
式中： L 为微分算子； σ ′为有效应力张量；α为Biot系数； m 为单位张量(二维问题时， m ={110} T ；三维问题时， m ={111000} T )。p 1 为岩体孔隙流体压力；ρ B 为岩体饱和容重，ρ B = ρ l φ+ ρ s (1 -φ)， φ为孔隙率，ρ l 、ρ s 分别为孔隙流体密度和岩体干密度)； g 为重力向量。
岩体基质内渗流的控制方程为 [19] ：
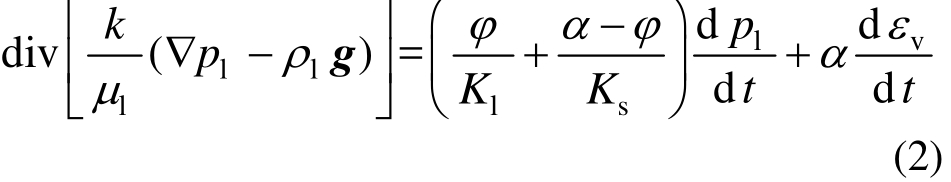
式中：k为岩体孔隙结构固有渗透率；μ l 为孔隙内流体速度；K l 为孔隙流体刚度；K s 为固体骨架刚度；ε v 为岩体孔隙结构体积应变；t为当前时刻。
裂缝内流体流动控制方程为 [19] ：
式中： k f r 为裂缝固有渗透率； μ n 为裂缝内流体速度；p n 为裂缝内流体压力；ρ fn 为裂缝内流体密度；S fr 为描述岩体在流体作用下可压缩性的参数；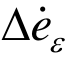 
为裂缝应变率。根据流体的平板理论，裂缝内流体的渗透率为：
式中，e为裂隙宽度。可压缩性的参数表示为：
式中：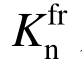 
为裂隙法向刚度； 
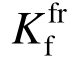为裂隙流体体积模量。
注入流体进入裂缝后会发生滤失，在页岩体积压裂的工程应用中有时高达 50%～80%，流体滤失对于准确描述断裂扩展具有重要影响，常采用如下流体滤失流速q 1 的计算方法：
式中：t sp 为流体从流至该截面到涌出到围岩的时间段；t exp 为流体流至该截面的时刻；t为流体流过该截面的时刻；V sp 为流体滤失体积；C为滤失参数。
流体驱动岩体断裂以张开型(I型)断裂为主，下面以此类型介绍断裂裂纹扩展的分析方法：
1)应力计算：计算最大主拉应力，自适应分析技术可确保该解答的可靠性。
2)损伤分析：根据各单元应力分析其损伤量d(0≤d≤1)，d达到1，将发生断裂。
3)裂纹扩展：裂纹沿垂直最大主拉应力方向扩展，该扩展方向不必沿单元边界。
记单元的抗拉强度和断裂能分别为σ t 、G f ，单元应力-应变关系如图 3所示 [18] ，当其最大主拉应力达到σ t ，则单元开始损伤(d=0)，主拉应力为 0时，单元损伤达到最大(d=1)。该应力-应变曲线与x轴所围面积即为断裂能G f ，应力-应变曲线在损伤阶段的斜率为：
式中，C l 为单元特征长度 [20] 。损伤阶段弹性模量可表示为：
式中，E为弹性阶段的弹性模量。
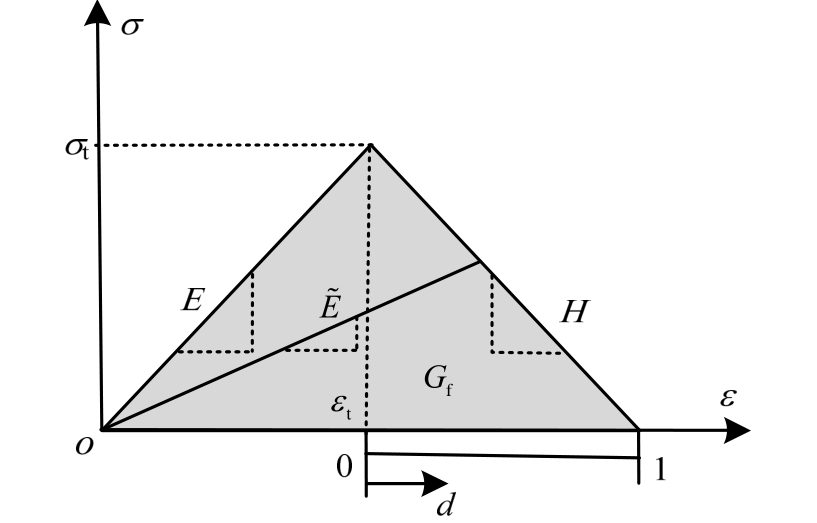
图3 应力-应变关系及损伤分析
Fig.3 Relationship of stress-stain and damage analysis
网格重分与裂纹扩展如图4所示：在流体驱动裂纹扩展过程中，在裂纹尖端出现应力集中，形成损伤区(d=1)(图4(a))；损伤区表示单元已经破坏，裂纹沿垂直最大主应力方向扩展，裂纹长度即该方向在损伤区的直线距离(图 4(b))；当裂纹预测长度达到提前给定的扩展长度时，采用常规离散元处理单元间破裂的方式进行裂纹扩展，扩展长度即裂纹预测长度，网格在裂纹尖端指定区域内进行重新划分，并计算得到新的损伤区(图4(c))。
图4 网格重分与裂纹扩展示意图
Fig.4 Remesh and fracture propagation
下面简述自适应分析的主要步骤：
1)有限元解：在当前网格(初始网格由用户提供)下，对含裂纹的岩体进行常规有限元计算，得到应力解答。
2)超收敛解：选取应力的自然超收敛点(高斯积分点)进行SPR法拼片得到单元节点的应力恢复，通过节点应力插值获得全域应力的超收敛解，并用其估计应力解答的误差。
3)网格重分：对误差超限的单元，估计单元新的尺寸并按其重划分，得到新网格，返回步骤(1)；如果所有单元均满足误差限，网格无需再重划分，求解过程结束。
按照上述自适应分析策略，以期得到岩体裂纹尖端处的优化网格及该网格下应力的高精度恢复解；随后，利用该高精度应力解答进行断裂判断，进一步利用离散元处理岩体断裂，可得具有一定精度保证的裂纹扩展路径。
将上述控制方程式(1)、式(2)和式(3)分别进行有限元离散：
式中： B u 、 B s 、 B n 分别为固体场、渗流场、裂缝流体场的形函数梯度矩阵(应变-位移矩阵)； N u 、 N s 、 N n 分别为各有限元形函数矩阵； L u 、 L s 、 L n 分别为各梯度算子。采用上述有限元离散，可得如下方程：
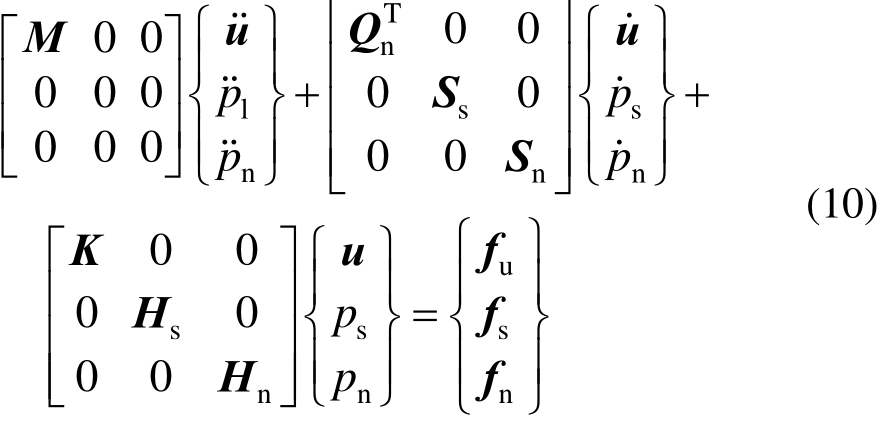
式(10)的推导过程及各参数矩阵含义可参考文献[19]、文献[21]。
SPR法 [16] 可以简单、有效地对应力进行精度恢复，获得断裂过程中应力的超收敛解。以图5所示的二维三角形和四边形单元为例，单元的高斯积分点是自然的应力超收敛点，即比其他位置的应力值具有更高的收敛阶、更高的精度，可以通过对各节点建立拼片得到应力场的拼片恢复：
式中： P (x, y)为给定的函数向量； a 通过恢复场在高斯积分点值与原解答的最小二乘拟合确定；通过该恢复场可得节点应力的高精度恢复值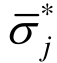 
(x, y),j= 1 ,2。按照式(11)，可得全域节点应力的恢复解，利用该节点应力进行有限元插值，即得全域的应力超收敛解：
式中， N i (x, y)为形函数。采用该法计算得到的超收敛解比原有限元解至少高一阶的收敛阶，可以用其作为原有限元解的误差估计和控制 [16] ，形成如下能量模误差估计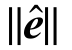 
式中： σ * 、 σ h 分别为矩阵形式表示的超收敛应力和常规应力解答； D 为弹性常数矩阵；Ω为求解域。利用上述误差估计，可以建立自适应分析目标：
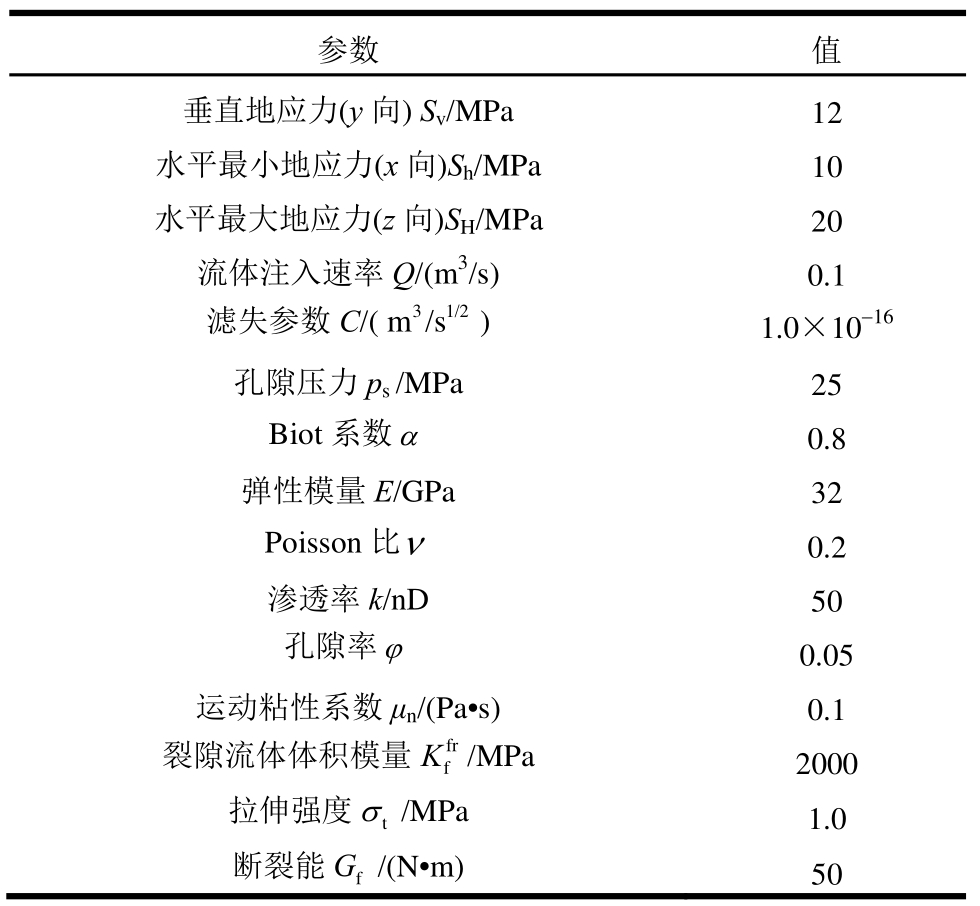
式中： 
表示域内所有单元的平均误差；Tol为用户给定的误差限；m为单元个数；|| e ||为所有单元的总误差。在每个单元K上定义误差估计参数：
则式(14)又可等价为：
如果式(16)不满足，表明原应力解答误差过大，需调整网格大小，估计新网格尺寸为 [16] ：
式中，h K 为单元K的当前网格尺寸。
需要指出的是，为了更合理地生成网格、高效地进行计算，可以只在裂纹尖端区域进行网格重划分。对裂纹尖端的单元进行误差估计和网格重划分，将对三维问题的自适应求解大大降低求解时间，同时也能保证很好描述裂纹扩展路径，ELFEN亦采取了该自适应网格重划分策略。
图5 单元节点的超收敛拼片应力恢复
Fig.5 Superconvergent patch recovery for nodal stresses of element
利用上述技术可形成流体-固体-断裂耦合核心求解方法，构成图6所示的整体算法。按照输入(前处理)、求解、输出(后处理)的主要步骤，实现流体驱动裂纹动态扩展。首先，需要输入模型的基本参数、流体加载、外部地应力以及自适应误差限、局部网格重划分区域等。
分析中，在当前载荷和岩体裂纹工况(如考虑初始天然裂纹，初始裂纹信息由用户提供)下，自适应求解得到固体应力场的数值精确解和裂纹扩展后的新缝网数值模型；在新缝网数值模型形成流体计算网格，引入当前的固体应力场进行求解，得到渗流压力场并在裂缝面处施加流体压力，增加流体流量载荷步，往复上述求解和分析；如果流体加载完成，求解过程结束，最终将输出满足误差要求全域解答及可靠的裂缝网构型。ELFEN软件采用该算法，发展了体积压裂模块 TGR(Tight Gas Reservoir) [18] 。
需要指出的是，该算法中模型重构为本文作者及其课题组在非均匀建模上的功能扩展，针对实际岩体(如页岩、砂砾岩)进行取样、切片、CT扫描，根据岩样的灰度图像和模型重构技术 [11] ，重构得到与其各矿物成分统计上一致的三维非均匀数值模型，本文仅列出该功能，相关方法、技术和研究成果将另文发表。
图6 整体算法流程
Fig.6 Flow chart of global algorithm
下面对典型的单水平井和多水平井体积压裂进行三维建模和计算分析，讨论自适应网格划分、流体－固体－断裂耦合技术的可靠性、有效性和实用性，研究分段压裂的压裂体积和孔隙压力的变化。以下数值算例均采用ELFEN进行计算分析。
图 7所示为单水平井分段压裂的初始几何模型，模型尺寸为a=250 m、b=100 m。压裂中设置5个射孔位置，分别沿水平井段起始端距离 85 m、95 m、105 m、115 m、125 m；为可靠描述起始阶段的裂纹起裂，在射孔区域进行初始网格细化，该区域为 75 m≤x≤135 m、100 m≤y≤150 m、40 m≤z≤60 m。图8所示为模型网格划分截面图，在每个射孔区域采用了更为细密的初始网格。模型的基本物理参数见表 1，部分选自文献[19]中页岩材料参数。
图7 初始几何模型
Fig.7 Initial geometric model
图8 初始网格
Fig.8 Initial mesh
表1 模型基本物理参数
Table1 Basic physical parameters of model
对该模型进行求解分析，各级压裂时间设置为220 s，得到如图9所示，各级压裂后的裂纹动态扩展形态及自适应网格，可见随着裂纹呈椭圆形向四周扩展、形成三维裂缝面；裂纹扩展过程中，网格不断细化，保证了求解的可靠性和有效性。
图9 裂纹动态扩展及自适应网格
Fig.9 Dynamic propagation of cracks and adaptive meshes
图10所示为各级压裂后的Mises等效应力结果，可见各裂缝面上应力相比围岩更高、变化更为复杂，同样要求相对细密的网格；随各级压裂的开展，由于井内流体的注入，Mises等效应力有增加的趋势。
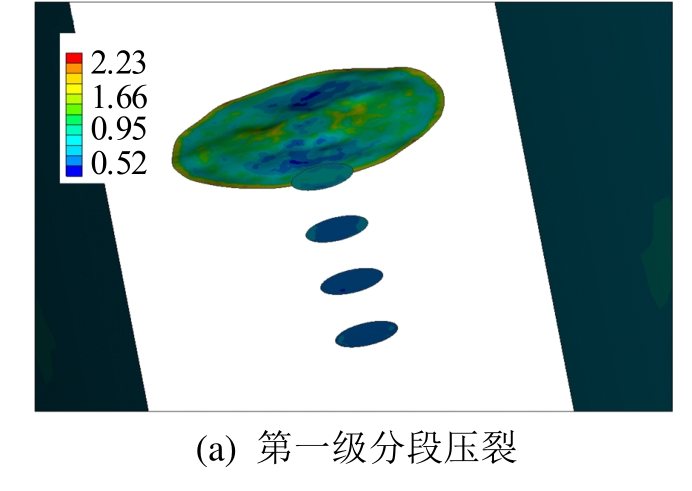
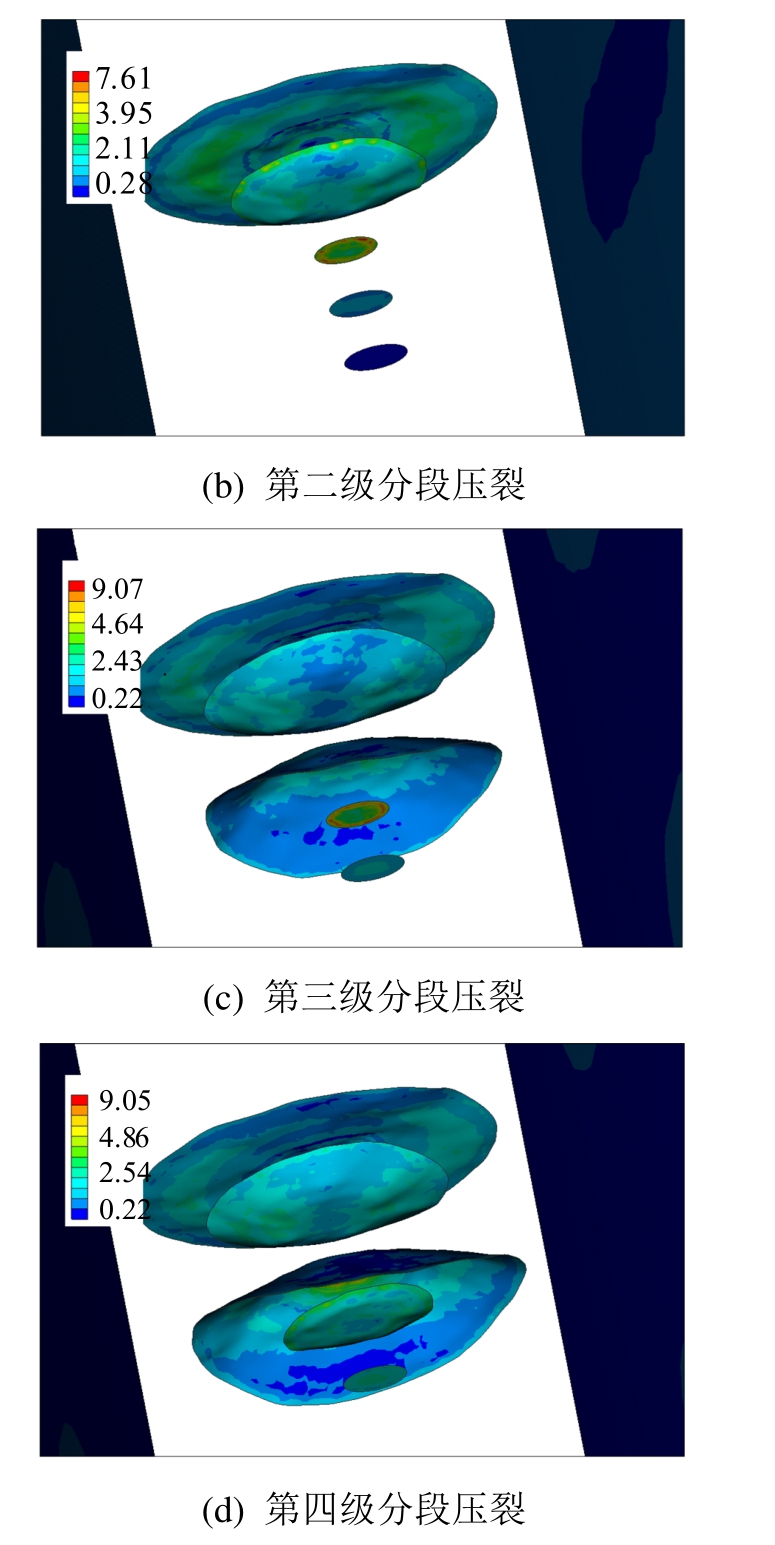
图10 Mises等效应力 /(×10 MPa)
Fig.10 Mises equivalent stress
图 11为压裂后压裂缝网体积随时间变化图，该结果可用于评价体积压裂的规模和效果。起始一段时间(约 40 s)，该水平井未裂纹扩展，当射孔内流体压力增加到一定程度，产生足够多的损伤区，才开始裂纹扩展；随后，射孔尖端起裂，各裂缝得到充分扩展，压裂缝网体积呈现线性增加的趋势，第四级压裂后达到约70 m 3 的裂缝体积，体现了分段压裂改造储层流通性的有效之处；曲线呈现波动变化，表明各级分段压裂会影响相邻裂缝的大小。图12为水平井起始处井壁孔隙压力随时间变化图，体现各级压裂与孔隙压力之间的相互影响：压裂前期，该孔隙压力增加，压裂之后，裂纹动态扩展造成该孔隙压力降低。
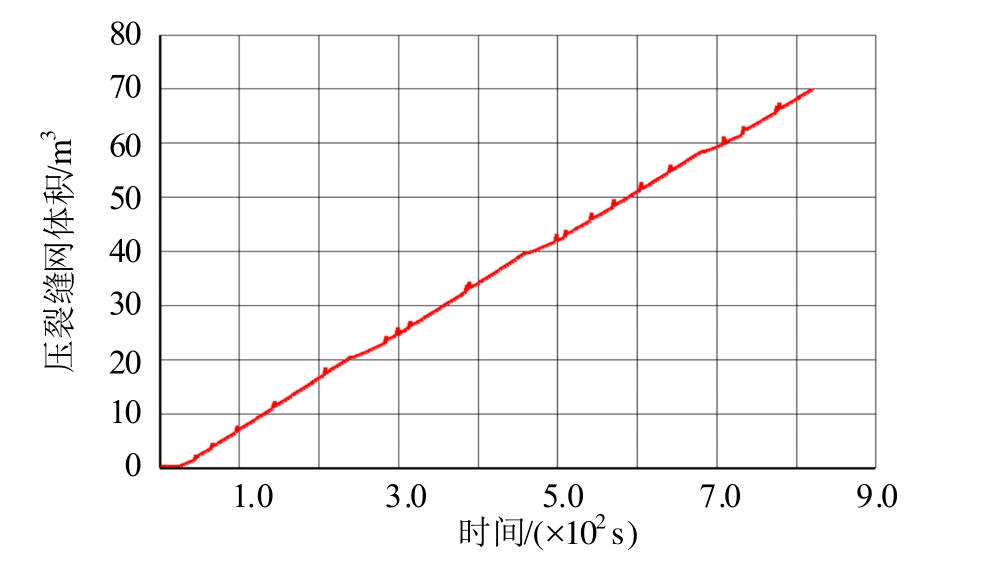
图11 压裂缝网体积变化
Fig.11 Evolution of total fracture volume
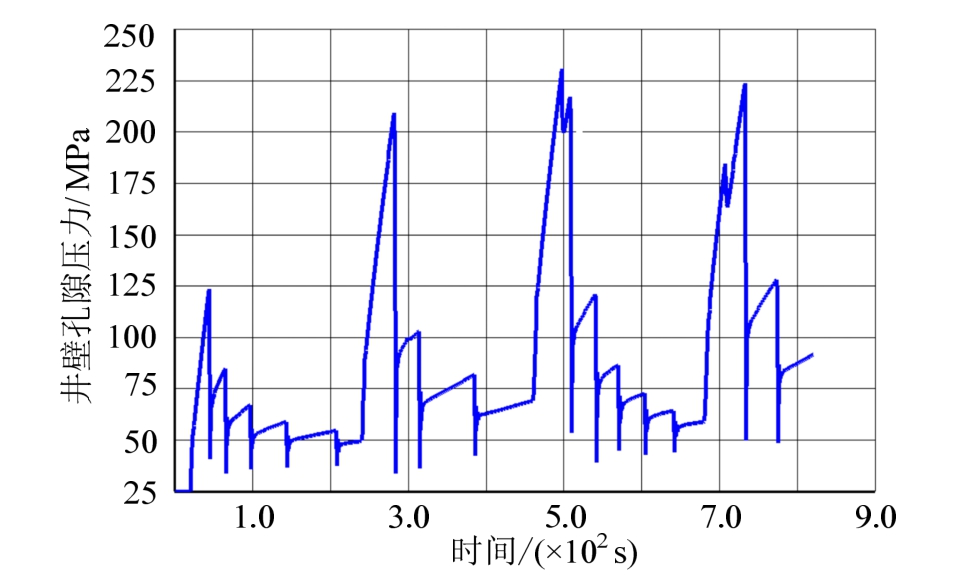
图12 井壁孔隙压力变化
Fig.12 Evolution of pore pressure on the wellbore
图13所示为多水平井(编号为I、II、III)分段压裂的初始几何模型，模型尺寸同4.1节中单一水平井模型情况。压裂中采用平行的3个水平井，各设置5个周向步孔的射孔位置，分别沿水平井段起始端距离85 m、95 m、105 m、115 m、125 m。为可靠描述起始阶段的裂纹起裂，在各射孔区域进行初始网格细化，各区域范围参见表2。图14所示为模型网格划分截面图，可见在各水平井的每个射孔区域均采用了较围岩更为细密的初始网格。模型的基本物理参数同4.1节中单一水平井模型情况。流体注入速率设置为0.5 m 3 /s，各级压裂时间为10 s。
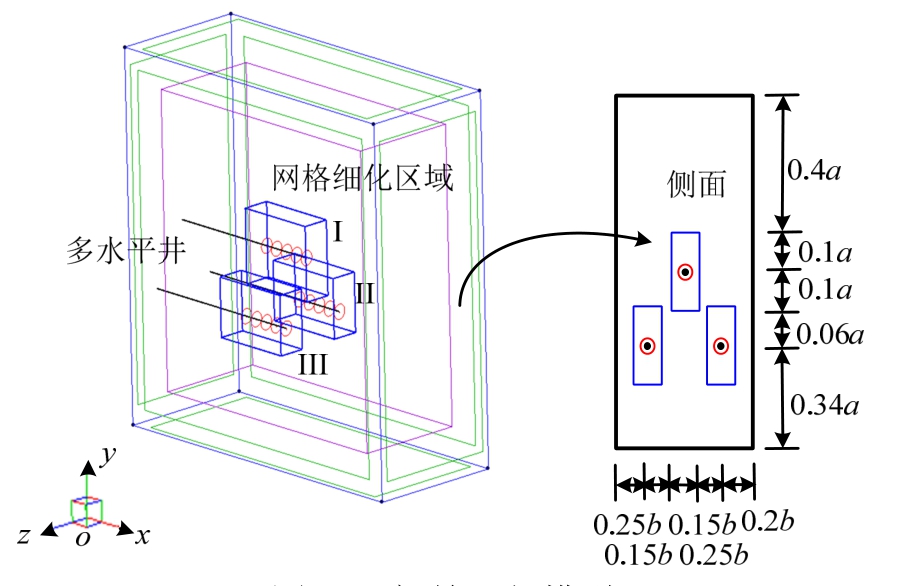
图13 初始几何模型
Fig.13 Initial geometric model
表2 多水平井射孔网格细化区域
Table2 Region of intensive mesh for multi-horizontal wells perforation
图14 初始网格
Fig.14 Initial mesh
对该模型进行求解分析，得到如图 15所示多水平井各级压裂后的裂纹动态扩展形态及自适应网格，可见各水平井平行同步向外扩展、形成三维裂缝面；裂纹扩展过程中，各裂纹尖端区域网格不断细化，保证了求解的可靠性和有效性。
图15 裂纹动态扩展及自适应网格
Fig.15 Dynamic propagation of cracks and adaptive meshes
图16所示为各级压裂后的第一主应力(拉应力)结果。可见各裂缝面外围应力集中明显，导致裂纹尖端区域损伤，向外均匀动态扩展；各级压裂进行中，各裂缝面仍出现相对较高的拉应力区。
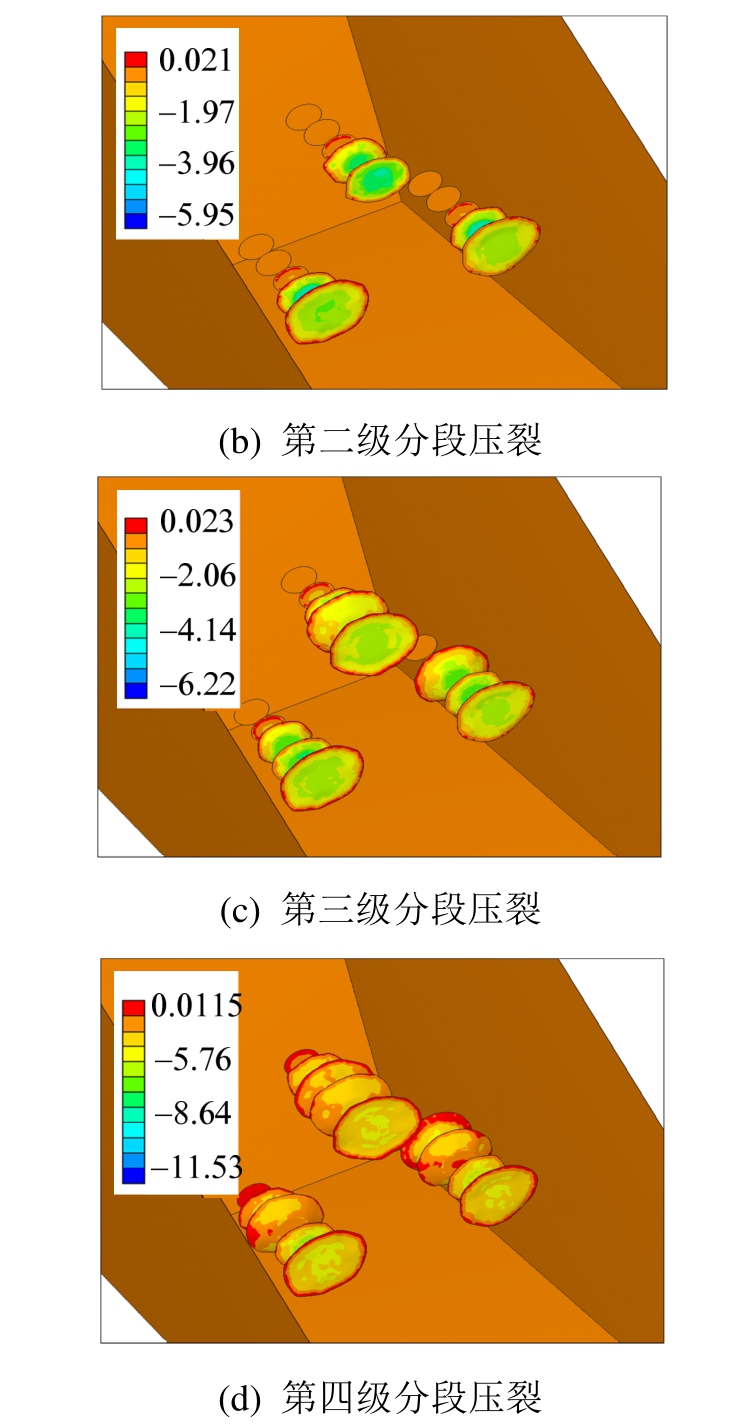
图16 第一主应力 /(×10 MPa)
Fig.16 First principal stressa
图17为压裂后压裂缝网体积随时间变化图，可见起始一段时间(约20 s)，各水平井并未裂纹扩展，当射孔内流体压力增加到一定程度，产生足够多的损伤区，才开始裂纹扩展；随后，各水平井同步压裂，压裂缝网体积呈线性增加趋势，在第四级压裂后产生约45 m 3 的裂缝体积；该曲线呈现波动变化，表明同一水平井各级分段压裂、不同水平井各级分段压裂对相邻裂缝大小均产生影响。图18为水平井I起始处井壁孔隙压力随时间变化图，各级压裂前期，该孔隙压力增加，压裂之后，裂纹动态扩展造成该孔隙压力降低；由于各水平井同步压裂，形成该曲线升降形式与图12所示的单水平井情况相似。本算例设置的各级压裂时间较短，未出现压裂裂纹间的交汇，否则造成各水平井压裂裂缝交汇，加之天然裂纹的影响，将会出现更为复杂的工况。
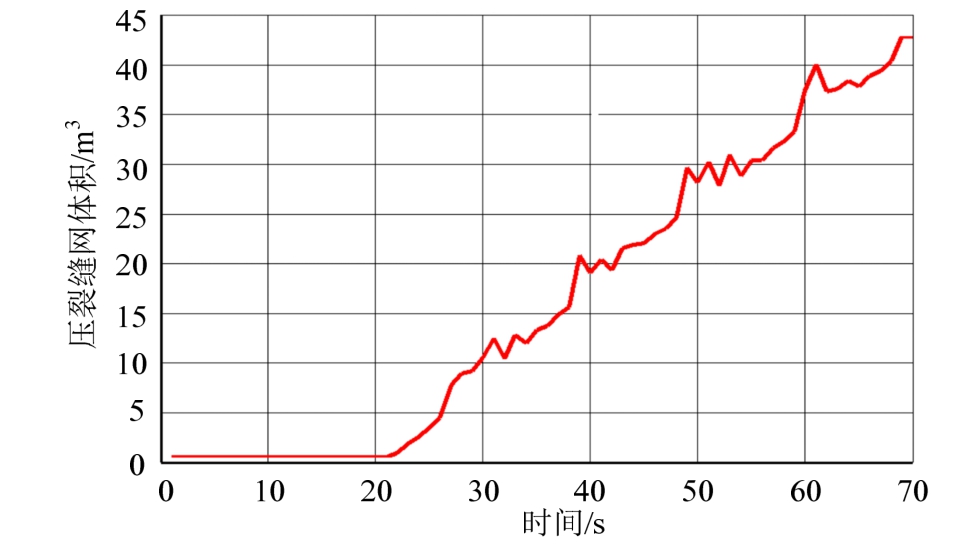
图17 压裂缝网体积随时间变化
Fig.17 Evolution of total fracture volume
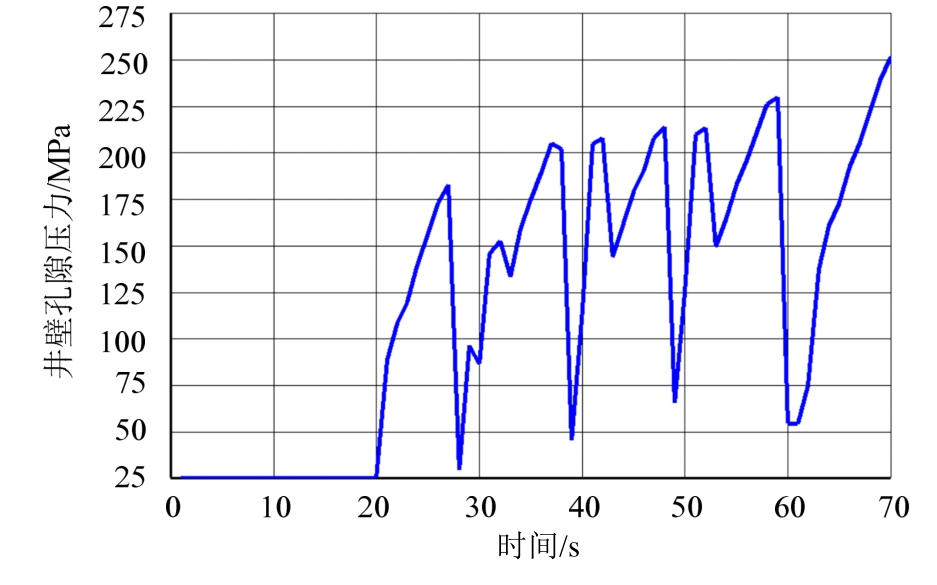
图18 井壁孔隙压力变化
Fig.18 Evolution of pore pressure on the wellbore
该文介绍固体断裂分析的自适应方法，以岩体的流体－固体－断裂耦合体积压裂进行分析，引进一款自适应有限元－离散元计算软件ELFEN，并以页岩体积压裂的三维数值算例进行简要介绍。数值算例得到单一、多水平井分段体积压裂中裂纹动态扩展及自适应网格、应力场演化、压裂缝网体积和井壁孔隙压力随时间的变化等结果。研究表明，灵活的网格自适应重划分是常规有限元破解断裂问题的可靠方法，合理的流固耦合分析是研究体积压裂的关键技术，简洁的局部网格重划分是提高大规模问题计算效率的有效策略。建立与实际岩体一致的数值模型，是保证计算结果有效性的前提，初始网格划分、模型重构、天然裂纹、流体滤失等，成为后续算法研究和数值计算的重点。
参考文献：
[1]谢和平, 高峰, 鞠杨, 等.页岩气储层改造的体破裂理论与技术构想[J].科学通报, 2016(1): 36―46.Xie Heping, Gao Feng, Ju Yang, et al.Novel idea of the theory and application of 3D volume fracturing for stimulation of shale gas reservoirs [J].Chinese Science Bulletin, 2016 (1): 36―46.(in Chinese)
[2]Ooi E T, Song C, Tin-Loi F, et al.Polygon scaled boundary finite elements for crack propagation modelling [J].International Journal for Numerical Methods in Engineering, 2012, 91(3): 319―342.
[3] Shi G H. Discontinuous deformation analysis: a new numerical model for the statics and dynamics of deformable block structures [J]. Engineering Computations, 1992, 9(2): 157―168.
[4] Dverstorp B，Andersson J．Application of the discrete fracture network concept with field data：Possibilities of model calibratin and validation [J]．Water Resources Research, 1989, 25(3): 540―550.
[5] Dolbow J, Belytschko T. A finite element method for crack growth without remeshing [J]. International Journal for Numerical Methods in Engineering, 1999, 46(1):131―150.
[6] Mohammadnejad T, Khoei A R. An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model[J]. Finite Elements in Analysis and Design, 2013, 73:77―95.
[7] Qing D Z, Yao J. Numerical simulation of shale hydraulic fracturing based on the extended finite element method [J]. Applied Mathematics & Mechanics, 2014,35(11): 887―1000.
[8] Zeng Q, Liu Z, Wang T, et al. Fully coupled simulation of multiple hydraulic fractures to propagate simultaneously from a perforated horizontal wellbore [J].Computational Mechanics, 2017: 1―19.
[9] Wang L X, Li S H, Zhang G X, et al. A GPU-based parallel procedure for nonlinear analysis of complex structures using a coupled FEM/DEM approach [J].Mathematical Problems in Engineering, 2013, 15(2): 1―15.
[10] Liu P, Ju Y, Ranjith P G, et al. Experimental investigation of the effects of heterogeneity and geostress difference on the 3D growth and distribution of hydrofracturing cracks in unconventional reservoir rocks [J]. Journal of Natural Gas Science & Engineering, 2016, 35: 541―554.
[11] Ju Y, Liu P, Chen J, et al. CDEM-based analysis of the 3D initiation and propagation of hydrofracturing cracks in heterogeneous glutenites [J]. Journal of Natural Gas Science & Engineering, 2016, 35: 614―623.
[12] Peng P H, Ju Y, Wang Y L, et al. Numerical analysis of the effect of natural micro-cracks on the supercritical CO 2 fracturing crack network of shale rock based on bonded particle models [J]. International Journal for Numerical and Analytical Methods in Geomechanics,2017, 41(18): 1992―2013.
[13] 袁驷, 王永亮, 徐俊杰. 二维自由振动的有限元线法自适应分析新进展[J]. 工程力学, 2014, 31(1): 15―22.Yuan Si, Wang Yongliang, Xu Junjie. New progress in self-adaptive FEMOL analysis of 2D free vibration problems [J]. Engineering Mechanics, 2014, 31(1): 15―22. (in Chinese)
[14] Yuan S, Wang Y L, Ye K S. An adaptive FEM for buckling analysis of non-uniform Bernoulli-Euler members via the element energy projection technique [J].Mathematical Problems in Engineering, 2013, 40(7):221―239.
[15] Wang Y L, Ju Y, Zhuang Z, et al. Adaptive finite element analysis for damage detection of non–uniform Euler–Bernoulli beams with multiple cracks based on natural frequencies [J]. Engineering Computations, 2017, 35(3):1203―1229.
[16] Zienkiewicz O C, Zhu J Z. The superconvergent patch recovery (SPR) and adaptive finite element refinement[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 101(1): 207―224.
[17] Azadi H, Khoei A R. Numerical simulation of multiple crack growth in brittle materials with adaptive remeshing[J]. International Journal for Numerical Methods in Engineering, 2011, 85(8): 1017―1048.
[18] ELFEN TGR user and theory manual [R]. Swansea United Kingdom: Rockfield Software Lted. 2016.
[19] Profit M, Dutko M, Yu J, et al. Complementary hydro-mechanical coupled finite/discrete element and microseismic modelling to predict hydraulic fracture propagation in tight shale reservoirs [J]. Computational Particle Mechanics, 2016, 3(2): 229―248.
[20] Lewis R W, Schrefler J Z. The finite element method in the static and dynamic deformation and consolidation of porous media [J]. Meccanica, 1999, 34(3): 231―232.
[21] Zienkiewicz O C, Taylor R L, Nithiarasu P. The finite element method (volume III): The finite element method for fluid dynamics [M]. Seventh ed. Singapore: Elsevier Private Limited, 2015: 423―449.
ADAPTIVE FINITE ELEMENT-DISCRETE ELEMENT ALGORITHM,SOFTWARE ELFEN AND APPLICATION IN STIMULATED RESERVOIR VOLUME OF SHALE
WANG Yong-liang 1,2 , JU Yang 1,3 , CHEN Jia-liang 1,2 , YANG Yong-ming 1,2 , Li C F 4
(1.State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology, Beijing 100083, China;2.School of Mechanical & Civil Engineering, China University of Mining and Technology, Beijing 100083, China;3.State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Xuzhou 221116, China;4.Zienkiewicz Centre for Computational Engineering, College of Engineering, Swansea University, Swansea SA2 8PP, UK)
Abstract: The adaptive algorithm of finite element (FE)-discrete element (DE)for fluidic-mechanical-fracture coupling analysis was introduced in this study.The novel computational software ELFEN based on this method was introduced and applied in a three-dimensional mechanism analysis of a staged stimulated reservoir volume of shale.The superconvergent patch recovery (SPR)method was used to obtain the superconvergent FE stress solutions, by which the error of conventional FE stress solutions was estimated.The adaptive local remesh for domains of crack tips was expected to be characterized by efficient analysis strategy and application for more accurate stress solutions and reliable crack propagation path.Numerical examples were given to show theeffectivity, reliability and practicability of the numerical algorithm and the software for staged stimulated reservoir volume of single- and multi-horizontal wells with fluidic-mechanical-fracture coupling.
Key words: adaptive analysis; FE-DE coupling; fluidic-mechanical-fracture coupling; stimulated reservoir volume; ELFEN
Li CF (1976―)，男，黑龙江人，英国Swansea大学教授，博士，博导，主要从事计算固体力学研究(E-mail: c.f.li@swansea.ac.uk).
陈佳亮(1989―)，男，河北人，博士生，主要从事矿山岩体力学和计算固体力学的研究(E-mail: chenjl@student.cumtb.edu.cn);
杨永明(1979―)，男，山西人，副教授，博士，硕导，主要从事矿山岩体力学研究(E-mail: yangym@cumtb.edu.cn);
作者简介：
王永亮(1985―)，男，河北人，助理研究员，博士，主要从事矿山岩体力学和计算固体力学的研究( (E-mail: wangyl@tsinghua.org.cn);
基金项目： 国家杰出青年科学基金项目(51125017)；国家自然科学基金项目(41877275，51608301，51374213)；国家自然科学创新研究群体科学基金项目(51421003)；国家重点研究发展计划项目(2016YFC0600705)；中国博士后科学基金项目(2018T110158，2016M601170)
通讯作者： 鞠 杨(1967―)，男，山东人，教授，博士，博导，主要从事矿山岩体力学研究(E-mail: juy@cumtb.edu.cn).
文章编号： 1000-4750(2018)09-0017-09
收稿日期： 2017-06-04；修改日期：2017-08-30
文献标志码： A
doi: 10.6052/j.issn.1000-4750.2017.06.0421
中图分类号： O34；TE37