宋子杰1,2，胡志强3
(1．上海交通大学海洋工程国家重点实验室，上海 200240；2．高新船舶与深海开发装备协同创新中心，上海交通大学，上海 200240；3．英国纽卡斯尔大学海洋科学与技术学院，纽卡斯尔，英国 NE1 7RU)
摘 要：该文介绍一个综合性解析计算程序，可用于预测船舶在碰撞和搁浅场景下的强非线性结构动力响应，包括结构变形阻力及能量耗散。解析计算方法具有使用方便，计算速度快，计算结果相对可靠的优点，易于工程应用。预测船舶碰撞与搁浅结构动力响应的程序包含两个模块，分别是船舶碰撞场景模块和船舶搁浅场景模块。船舶在碰撞和搁浅场景中，船体外板和内板等构件在外载荷作用下会出现弯曲、膜拉伸和撕裂的变形模式；船体桁材构件在外载荷作用下会出现弯曲和褶皱压溃变形模式。船体构件损伤失效所产生的结构变形阻力和能量耗散以解析的方式表达。此外，采用LS_DYNA程序开展数值仿真，验证解析计算程序的准确性和合理性。综合解析计算程序在结构设计阶段，对船体结构的耐撞性和船舶风险评估，都具有一定的工程应用价值。
关键词：船舶碰撞与搁浅；综合解析计算程序；变形机理；变形阻力；能量耗散；数值仿真
随着航运业的快速发展，海上航行的船舶数量越来越多。尽管人们做了许多努力来避免海上意外事故的发生，但海洋事故依然不可避免。据统计，近一半的事故是由船舶碰撞和搁浅引起的，此类事故导致船侧结构和底部结构破裂，漏油，进而造成经济损失，环境污染和人员伤亡。为了降低上述事故造成的损失，需要在设计阶段快速并准确地预测船舶的结构耐撞性。因此，预测船舶碰撞和搁浅场景中的结构动力响应具有重要意义。
为了分析船舶耐撞性，通常可以忽略船体构件之间的相互影响，将船体构件分成三类基本单元进行独立的研究：即板材结构，包括甲板、外底板、内底板、舷侧外板和舷侧内板；桁材和框架结构，包括纵桁、肋板和横框架结构；骨材结构：即依附在板材结构上的骨材。对于桁材结构，Wierzbicki和 Driscoll[1]，Wang 和 Ohtsubo[2]，Simonsen[3]，Zhang[4]以及Hong和Amdahl[5]等通过解析和实验的方法对桁材结构受压变形产生的阻力进行了研究。Gao和Hu[6―7]通过对这些学者的理论进行总结，并提出了新的理论模型。对于船体板，Wang等[8]，Zhang[4]，Simonsen 和 Lauridsen[9―10]，Haris 和Amdahl[11]通过对其变形模式的研究，提出了结构变形阻力解析计算方法。Sun和 Hu[12]，Haris和Amdahl[13]对椭球型撞头撞击舷侧外板的变形模式进行了研究，提出了球鼻艏撞击船侧场景下的结构变形阻力计算公式。
双层底船舶搁浅场景下的结构动力响应主要取决于场景尺寸，载荷性质和边界条件[14]。Alsos和 Amdahl[15]通过对一系列有限元模拟结果的观察分析，将礁石定义为三种类型，分别为“锥型”，“球面型”和“台型”。由于船舶搁浅于锥形礁石可能引发结构的局部撕裂，危害大，因而受到了广泛的关注。Wierzbicki和 Thomas[16]，Wang[17]及 Zhang[18]提出了板材撕裂在初始状态下的简化解析法。Zheng和 Wierzbicki[19]，Simonsen和 Wierzbicki[20]及Wang等[21]推导出了一系列适用于计算稳定状态下板材撕裂变形阻力的解析解。Zeng和Hu[22]指出Simonsen在计算摩擦力时所假定的接触面积有一定不足，并提出了一种新的简化解析法来计算船底外板受锥形礁石撕裂的变形阻力。此外，孙斌和胡志强等[23]提出了双层底搁浅于锥形礁石场景下肋板的变形机理及变形阻力的简化解析解。虽然船舶搁浅于台型礁石通常不会引起底板和横向构件的断裂，但这类搁浅会造成船底结构大面积的塑性变形，极大削弱船舶的整体强度，并可能由船舶剩余强度不足而引发中位断裂的严重后果。为了准确预测该场景下的结构动力响应，Hong和 Amdahl[24]针对该场景提出了一系列简化解析式，用于计算变形阻力及能量耗散。Hu等[25]和Yu等[26]用非线性有限元法对Hong和 Amdahl所提出的理论进行了验证。作为补充，于兆龙和胡志强等[27]对船底纵桁骨材的变形机理进行研究，并提出了用于计算其变形阻力及能量耗散的简化解析式。
本研究主要基于课题组近几年在船舶碰撞与搁浅解析计算方法研究基础上，利用 Fortran90语言开发了一个综合解析计算程序，用于预测船舶碰撞和搁浅场景下的结构变形阻力及能量耗散。在船舶碰撞模块中，定义撞击和被撞击船舶的主要船型参数，撞击速度，船艏形状，材料属性和主要构件的尺寸；在船舶搁浅模块中，定义礁石形状，滑移速度，材料属性及主要构件尺寸等参数。此外，通过数值模拟验证了程序的可行性。该综合分析程序在船舶的结构设计阶段对耐撞性设计具有一定的指导意义，且有助于船舶碰撞和搁浅场景下的快速风险评估。
船舶碰撞与搁浅过程中结构变形具有很强的非线性特征，解析计算方法主要基于塑性力学上限定理。在碰撞与搁浅过程中，船体结构发生一系列复杂的变形。为了简化计算过程，进行以下假设：
1)假定船体结构是理想刚塑性材料，忽略其弹性效应。
2)不同的能量耗散机制之间互不影响，在计算总的能量耗散时将各机制产生的能量耗散叠加。
3)不同构件之间无耦合作用，总的能量耗散及变形阻力值由各构件能量耗散及变形阻力相叠加得到。
4)假定结构的弯曲变形引起的能量耗散仅发生在塑性铰的形成上，忽略结构的连续弯曲变形引起的能量耗散。
5)假定损伤变形构件的边界由其周围未发生损伤的构件组成。
Wierzbicki[28]，Zhang[4]， Simonsen[14]，Wang和Ohtsubo[2]和Hong和Amdahl[29]运用上限定理和上述假设得出了大量的阻力和能量耗散公式，其可行性和准确性得到了验证。
根据塑性力学上限定理，外载荷做功的功率等于结构内部的能量耗散率，则：
式中：F(δ )为瞬时载荷；δ˙为外载荷加载速率；
为结构内部能量耗散率。对于变形损伤的板材结构而言，其变形能可划分为弯曲引起的变形能Eb及膜拉伸引起的变形能Em：
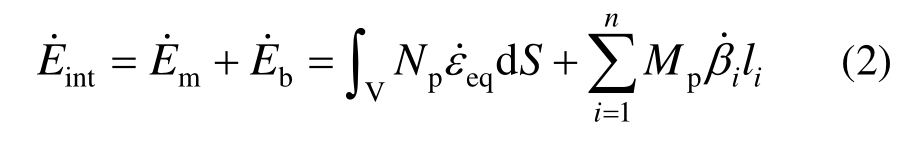
式中：Np和Mp分别为材料的极限塑性力和极限塑性弯矩；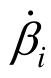
和li分别为第i根塑性绞线的曲率变化率和长度。平面应力状态下的等效应变εeq可由下式计算：
一旦确定了结构的位移场和速度场，就可以根据以上方法求解步骤，计算结构的变形阻力和能量耗散。
应变率变化对低碳钢的应力应变关系影响较大。应变速率对屈服强度的影响采用 Cowper-Symonds方程表示：
式中： σYd和σY分别为动态和静态的屈服应力；c和p为材料系数；β 为硬化参数；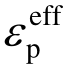
为有效塑性应变；Ep为塑性硬化模量。
解析计算程序包含两个模块，分别是碰撞模块和搁浅模块。
事故场景定义十分重要，场景参数决定了参与结构变形的船体构件数量。在碰撞场景定义中，撞击船艏形状可以设定为楔形艏或球鼻艏。楔形艏撞击船侧场景定义三个撞击位置；球鼻艏撞击船侧场景定义四个撞击位置，如图1所示。在搁浅场景定义中，礁石的形状定义为锥型或台型，礁石位置和搁浅深度的定义如图2所示。解析程序的流程图如图3所示。
图1 碰撞场景中的撞击位置
Fig.1 The typical collision positions
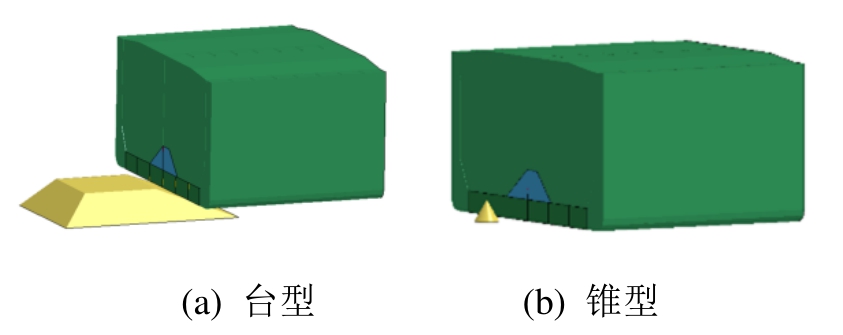
图2 两种典型的搁浅场景
Fig.2 The typical grounding scenarios
图3 综合解析程序的流程图
Fig.3 The flow chart of analytical tool
在楔形船艏撞击船侧场景中，船侧结构损伤变形如图4所示，其中，图4(b)为隐藏楔形船艏后结构变形损伤示意图，图4(c)为隐藏舷侧外板与甲板后结构变形损伤示意图。从图中可以看出，舷侧外板，桁材结构及骨材变形损伤严重。
图4 楔形船艏撞击船侧场景变形损伤模型
Fig.4 The deformation model of raked bow collision scenario
在楔形船艏碰撞模块中，舷侧外板变形理论模型如图5所示，船侧主要结构的变形损伤机理包括：
1)舷侧外板的两边塑性铰线处的塑性弯曲变形及中间部分的膜拉伸变形。
2)舷侧外板骨材两侧及中部的塑性弯曲变形和中间部分的膜拉伸变形。
3)桁材结构的受压及撕裂变形，包括甲板、横向肋板和纵桁。
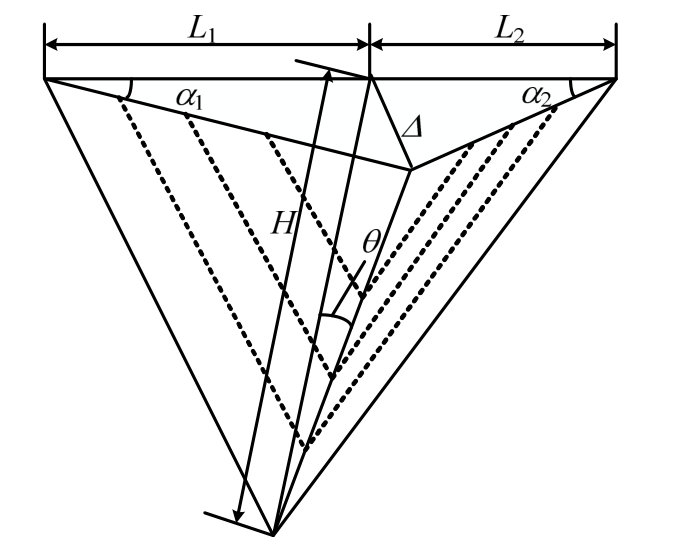
图5 舷侧外板变形的理论模型
Fig.5 Deformation model of the side plating
船侧外板结构变形阻力主要由外板结构膜拉伸变形，弯曲变形和撕裂变形产生，变形阻力为[30]：
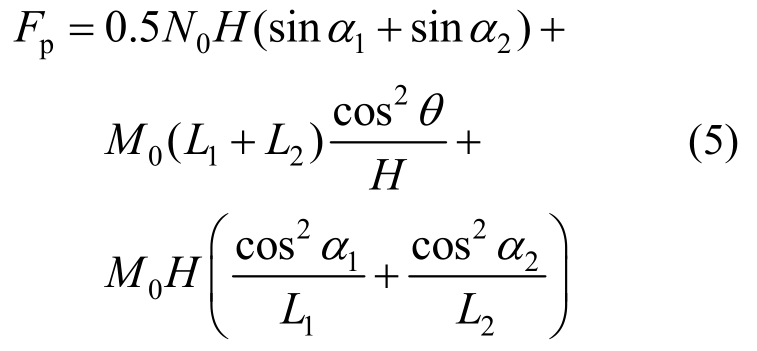
式中：L1和 L2为变形区域左右两侧的长度；H为变形区域的高度；1α和2α为变形区域左右两侧在纵向上的旋转角；θ为板在垂向上的旋转角。当板材发生撕裂时，裂缝上半部分不再发生变形，下半部分与撕裂前的变形机理相同，仍采用式(5)计算其变形阻力。
舷侧外板骨材的瞬时变形阻力为[30]：
式中：ts为骨材的厚度；l1和 l2是撞击点位置距离骨材左右两侧未发生严重变形的横肋板的纵向长度；θ1和θ2是骨材左右两端的瞬时转角。
桁材结构的变形主要为压溃屈曲变形。随着受压载荷的增加，桁材腹板屈曲失效。桁材腹板屈曲失效生成的褶皱波高度决定了桁材的压溃载荷，压溃变形和褶皱波高度如图6所决定。H为图6中褶皱变形高度，其表达式如下：
式中：b1、b2为桁材撞击点距左、右两侧变形横肋板的纵向距离；tw为其厚度。
桁材在第一个褶皱波形成过程中瞬时阻力为[6]：
图6 桁材结构受压变形的理论模型
Fig.6 Deformation model of the web girder
撞击深度的增加，桁材结构会发生撕裂变形，其变形阻力为[18]：
式中：σ0为流动应力； εu为材料的失效应变；β 为楔形撞头的半顶角； μ为摩擦力系数。结合式(5)、式(6)、式(8)、式(9)，则总的变形阻力可表示为：
楔形船艏碰撞模块的流程图如图7所示。其中，Δ为撞深，dΔ为步长，Δmax为最大撞深。
图7 楔形艏碰撞模块流程图
Fig.7 The flow chart of the raked bow collision module
在球鼻艏碰撞场景中，船侧结构损伤变形如图8所示，其中，图8(b)为隐藏椭球型撞头后结构变形损伤示意图，图8(c)为隐藏舷侧外板后结构变形损伤示意图。从图中可以看出，舷侧外板，桁材结构及骨材变形损伤严重。
图8 球鼻艏撞击船侧场景变形损伤模型
Fig.8 The deformation model of the bulbous bow collision scenario
在球鼻艏撞击船舶舷侧的模块中，舷侧主要结构的变形损伤机理包括：
1)船舶舷侧外板的膜拉伸变形及撕裂变形。
2)舷侧外板骨材的塑性弯曲变形及膜拉伸变形。
3)桁材结构的受压及撕裂变形。
图9 舷侧外板变形的理论模型
Fig.9 Deformation model of side plating
舷侧外板的变形阻力可由xoy和xoz两个方向上具有椭球形状的柱体撞击外板的变形阻力表达[12]，分别为：
式中：2a和2b分别为板的长和宽；lx、ly和lz分别为椭球撞头在空间坐标系x、y、z三个方向上的半径；α 和θ 分别为两个方向上外板两侧边缘的瞬时旋转角度。结合式(11)和式(12)，外板的瞬时变形阻力为：
随着撞深的增加，外板的变形机理由膜拉伸变形转化为撕裂变形。撕裂变形的瞬时阻力可表示为[6]：
式中：n为板材破裂后产生的裂缝条数；β 为椭球形撞头的半顶角；l为每条裂缝的长度。
在球鼻艏碰撞场景4中(如图1所示)，采用式(13)、式(14)计算舷侧外板变形阻力，采用式(6)计算外板上骨材变形阻力；在场景5及场景6中，采用式(8)、式(9)计算桁材变形阻力；在场景7中，横肋板与纵桁交叉形成十字构件抵抗撞击，此时不能简单地将横纵构件单独分开计算，这里采用 Yang和Caldwell[31]提出的十字构件轴向受压变形阻力计算公式：
式中：b和t分别为十字构件各个翼板的宽度及厚度；2H为十字构件每个褶皱的特征高度，其表达式为：
球鼻艏撞击船侧场景模块的流程图如图10所示。
图10 球鼻艏碰撞模块流程图
Fig.10 The flow chart of the bulbous bow collision module
在船舶搁浅于锥形礁石场景中，船底结构损伤变形如图11所示，其中，图11(b)为船底受损区域的局部示意图，图11(c)为船底外板及肋板受损区域俯视图。从图中可以看出，船底外板及肋板变形损伤严重。
图11 船舶搁浅于锥型礁石场景变形损伤模型
Fig.11 The deformation model of the rock-type grounding scenario
在双层底船舶搁浅于锥型礁石模块中，主要构件的变形损伤机理有：船底外板的膜拉伸变形，弯曲变形及撕裂变形；船底横肋板中部区域的膜拉伸变形及两侧塑性铰线处的弯曲变形。
图12 船底横肋板及外板的变形损伤理论模型
Fig.12 Deformation model of bottom floor and plating
各主要构件变形机理对应的变形阻力及能量耗散的简化解析表达式如下所示，详情请见文献[22―23]。
外底板的变形阻力为[22]：
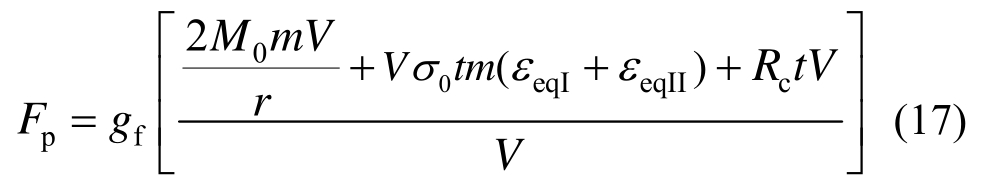
式中：gf为摩擦力影响因子；V为船舶搁浅时的速度； θ 为撕裂角度；h和φ分别为锥形礁石的撞深及半顶角；Rc为外底板材料的断裂韧度。
船底横肋板的变形阻力为[30]：
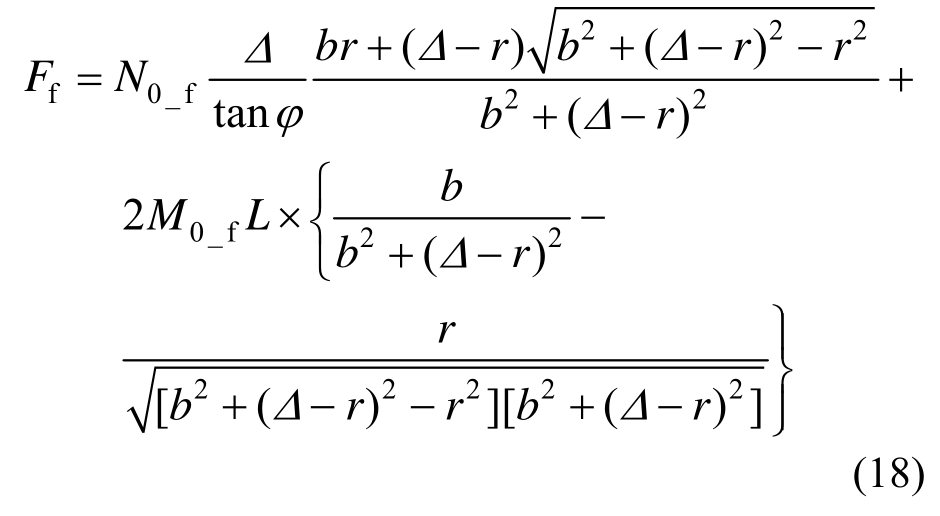
式中：Δ为礁石撞深；b为肋板两侧未发生严重变形的纵桁距离的1/2；r为锥形礁石底部半径；L为塑性绞线的长度。结合式(17)及式(18)，即可得船底结构在尖锐礁石搁浅场景下的总变形阻力：
船舶搁浅于锥型礁石模块的流程图如图13所示。式中：b0为船底肋板间距；u0为肋板发生撕裂时横向移动距离。
图13 船舶搁浅于锥型礁石模块流程图
Fig.13 The flow chart of rock-type grounding module
在双层底船舶搁浅于台型礁石模块中，主要构件的变形损伤机理有：
1)板两侧四条折现处的弯曲变形，板两侧折线间部分的膜拉伸变形，以及与礁石前表面接触的板的塑性滚动弯曲变形与膜拉伸变形。
2)纵桁的纵向滑移屈曲变形。
3)肋板的垂向挤压弯曲变形。
图14 船底肋板、纵桁及外板的变形损伤模型
Fig.14 Deformation model of bottom floor, longitudinal girder and plating
各主要构件变形机理对应的变形阻力及能量耗散的简化解析表达式如下所示，请参见文献[24]。
纵桁在半波长内能量耗散为：
平均变形阻力为：
式中，H和θ 分别为垂向压缩距离的 1/2和变形波角度的1/2，可表示为：
式中：D为撞深；α 为台型礁石倾角。
肋板的结构响应包含两部分：肋板中部的挤压变形及肋板两侧连带弯曲变形。其能量耗散及变形阻力为：
式中：C为礁石接触表面的半宽值；b可由上限定理获得，其表达式为：
船底外板的变形阻力及能量耗散为：
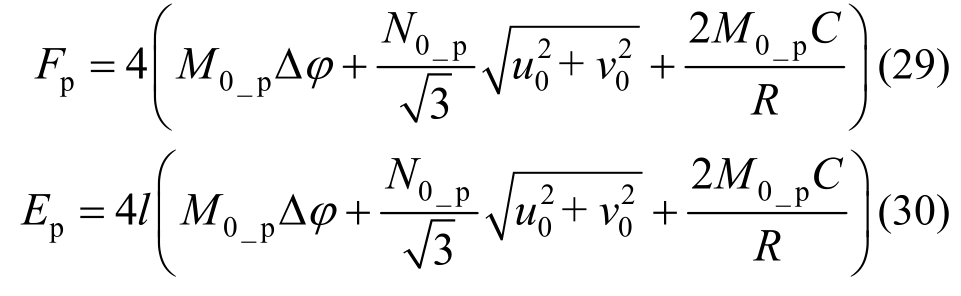
式中，R为塑性滚动半径。
双层底结构总的变形阻力及能量耗散为：
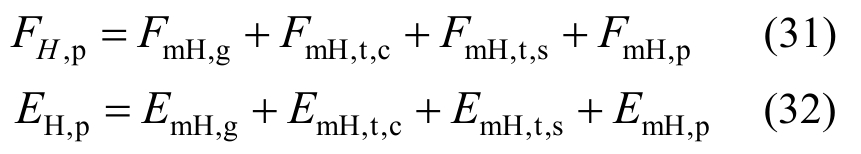
船舶搁浅于台型礁石模块的流程图如图15所示。其中，b0为船底肋板间距，u0为船底横肋板的最大挤压变形距离。
图15 船舶搁浅于台型礁石模块流程图
Fig.15 The flow chart of the shoal-type grounding module
为了验证综合解析程序计算结果的准确性，运用非线性有限元软件LS_DYNA对一系列工况进行分析。碰撞场景使用的油轮模型主尺度如表1所示；搁浅场景使用的油轮模型主尺度如表2所示。具体材料属性定义如表3所示。
表1 碰撞场景中油轮模型主尺度
Table 1 Main particulars of the tanker in collision scenario
表2 搁浅场景中油轮模型主尺度
Table 2 Main particulars of the tanker in grounding scenario
表3 数值模拟中两种材料的主要力学参数
Table 3 Major mechanic parameters of two kinds of materials
船舶在楔形艏撞击场景下的有限元模型如图16所示，其舷侧结构单元大小约为0.2 m，材料的失效应变定义为0.35。使用LS_DYNA数值仿真计算结果与综合解析程序的计算结果对比如图17及表4所示。
图16 楔形船艏碰撞场景有限元模型
Fig.16 Finite element model of the raked bow collision scenario
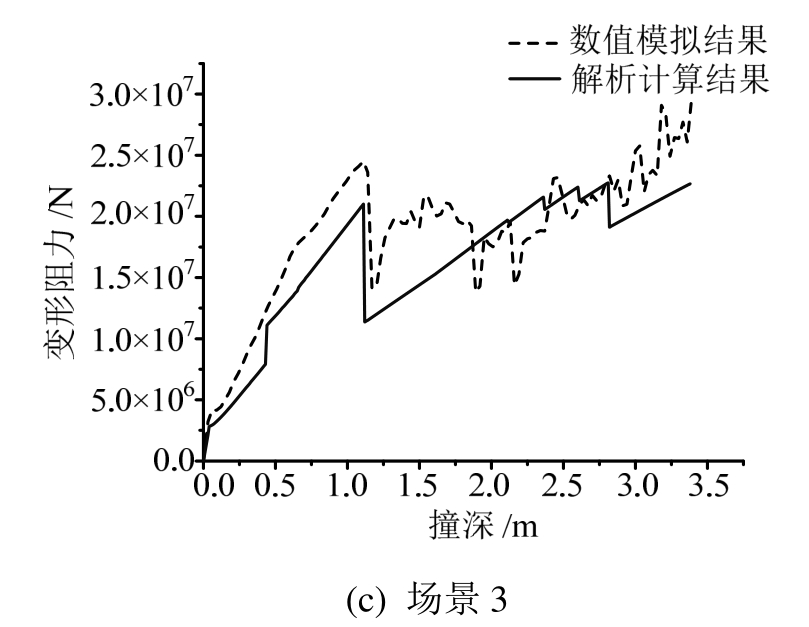
图17 船底结构变形阻力的计算及对比结果(场景定义如图1)
Fig.17 Comparison of resistance between analytical and numerical solutions (The scene definition is shown in Fig.1)
表4 船底结构能量耗散的计算及对比结果
Table 4 Comparison of energy dissipation.
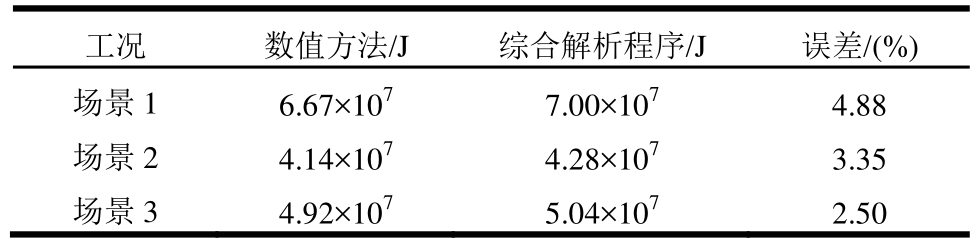
在场景1中，初始阶段参与变形的主要构件包括甲板，舷侧外板和舷侧外板上骨材。随着撞击深度的增加，横肋板及甲板上的骨材也参与到对撞击的抵抗中来。在场景2中，初始阶段只有舷侧外板及其上的骨材参与变形，随着撞击深度的增加，外板发生破裂。当撞击深度达到2.4 m时，舷侧纵桁开始参与抵抗撞击。在场景3中，舷侧外板，舷侧外板上骨材及纵桁参与了初始阶段对撞击的抵抗，当撞击深度达到0.3 m时舷侧肋板也参与到变形中来。随着撞击深度的不断增加，舷侧外板及纵桁将发生破裂。从图中可以看出，两种方法计算得到的变形阻力有一定的偏差，这是由于在解析程序中未考虑不同结构之间存在的耦合作用，且忽略了除主要构件外其他构件发生的相对较小的变形所致。但整体趋势是准确的，可被工程实践所接受。
船舶在球鼻艏撞击场景下的有限元模型如图18所示，其舷侧结构单元大小约为0.2 m，材料的失效应变定义为0.35。使用LS_DYNA数值仿真计算结果与综合解析程序的计算结果对比如图19及表5所示。
从图中可以看出，综合解析程序对场景4至场景6的能量耗散结果略有不足，这是由于忽略了除主要构件以外其他构件发生的相对较小变形，及忽略了不同构件之间的耦合效应所致。此外，变形阻力的对比结果也有一定的差异。在今后的研究中，需要对板被椭球型撞头撞击撕裂的变形机理进行进一步研究。然而，综合解析程序的计算结果的总体趋势准确的，可被工程实践所接受。
图18 球鼻艏碰撞场景有限元模型
Fig.18 Finite element model of bulbous bow collision scenario
表5 船底结构能量耗散的计算及对比结果
Table 5 Comparison of energy dissipation
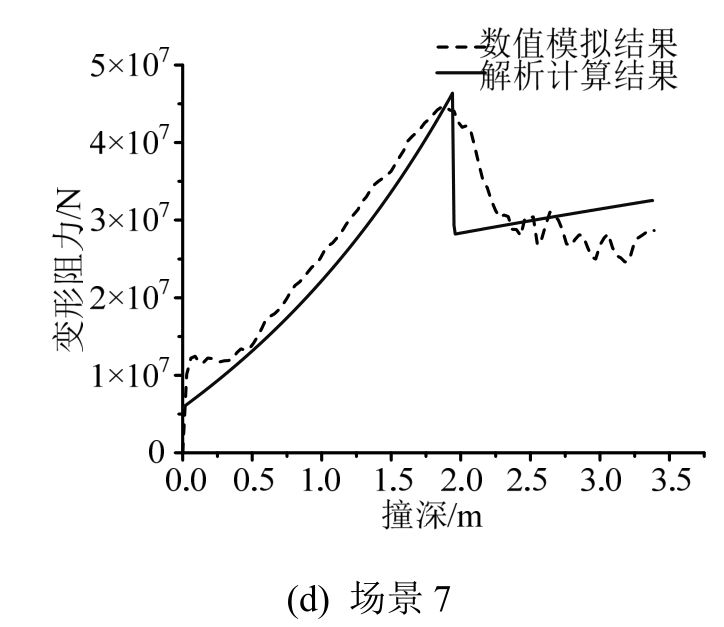
图19 船底结构变形阻力的计算及对比结果(场景定义如图1)
Fig.19 Comparison of resistance between analytical and numerical solutions (The scene definition is shown in Fig.1)
船舶在搁浅于锥型礁石场景下的有限元模型如图20所示。使用LS_DYNA数值仿真计算结果与综合解析程序的计算结果对比如图21所示，各工况的礁石倾角及撞深如表6所示。可以看出，综合解析程序较好地预测出肋板结构对搁浅损伤的抵抗作用，但对肋板发生破裂的撞击深度值的确定不十分准确，在今后研究中，需要对肋板发生撕裂的判定条件进行深入分析。
图20 船舶搁浅于锥型礁石场景有限元模型
Fig.20 Finite element model of rock-type grounding scenario
表6 各工况礁石的形状参数
Table 6 Rock parameters of different grounding cases.
图21 综合解析程序计算结果与数值模拟结果对比
Fig.21 Comparison of resistance between analytical and numerical solutions
船舶在搁浅于台型礁石场景下的有限元模型如图22所示。使用LS_DYNA数值仿真计算结果与综合解析程序的计算结果对比如图23所示。参与抵抗搁浅损伤的主要构件包括船底纵桁，肋板及外板。结果表明，综合解析程序的计算结果与数值仿真结果有一定的差异。在双层底船舶搁浅的初始阶段，变形阻力被明显的高估，这是由于在搁浅初期台型礁石并未完全进入双层底结构所致。此外，忽略结构之间的耦合作用导致在搁浅稳定阶段中变形阻力计算结果的差异。
图22 船舶搁浅于台型礁石场景有限元模型
Fig.22 Finite element model of the shoal-type grounding scenario
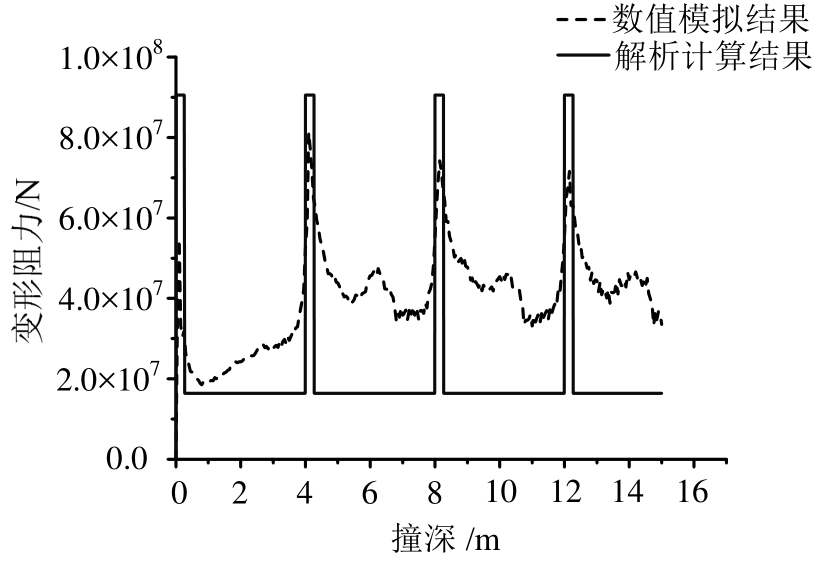
图23 综合解析程序计算结果与数值模拟结果对比
Fig.23 Comparison of resistance between analytical and numerical solutions
本文提出了一个综合解析程序，用于快速预测在船舶碰撞和搁浅场景中的变形阻力及能量耗散值。综合解析程序的计算结果与数值模拟结果的对比表明程序的可行性及准确性。
由于数值仿真法中模型的建立及有限元计算需花费大量人工及时间成本，因此，若需在船舶设计阶段或事故发生后进行快速计算并不容易。本文所提出的综合解析程序具有准确度较高，所需参数少，计算时间短等优点，很适用于船舶设计阶段的抗撞性能快速评估。通过在该综合解析程序中输入正确的船型及碰撞或搁浅参数，从而获得船舶各主要构件及总的变形阻力及能量耗散值，找到与已知的船舶初始动能相等的变形能所对应的撞击深度，即可对船舶耐撞性有初步的评估。此外，在相同的碰撞或搁浅环境中，船舶的变形阻力越大，其抗撞性能越好，因此可通过输入不同方案的船型参数，对综合解析程序计算得到的变形阻力或能量耗散值的对比，来决定具有更优防撞性的船舶设计方案。该综合解析程序对船舶耐撞性结构设计以及碰撞搁浅场景下的快速风险评估具有一定的指导意义。
参考文献：
[1]Wierzbicki T, Driscoll J C. Crushing damage of web girders under localized static loads [J]. Journal of Constructional Steel Research, 1995, 33(3): 199―235.
[2]Wang G, Ohtsubo H. Deformation of ship plate subjected to very large load [J]. Proc. of 16th Int. Conf. on Offshore Mech. and Arctic Eng. (OMAE), 1997, 2:173―180.
[3]Simonsen B C, Ocakli H. Experiments and theory on deck and girder crushing [J]. Thin-Walled Structures,1999, 34(3): 195―216.
[4]Zhang SM. The mechanics of ship collisions [D].Department of Naval Architecture and Offshore Engineering, Technical University of Denmark, 1999.
[5]Hong L, Amdahl J. Crushing resistance of web girders in ship collision and grounding [J]. Marine Structures,2008, 21(4): 374―401.
[6]Gao Z, Yang S, Hu Z. The resistance of ship web girders in collision and grounding [J]. Mathematical Problems in Engineering, 2014, 8(5): 1―13.
[7]高振国, 胡志强, 王革. FPSO舷侧结构抗撞性能的解析计算研究 [J]. 工程力学, 2014, 31(增刊1): 155―160.Gao Zhenguo, Hu Zhiqiang, Wang Ge. A simplified analytical method for prediction of anti-collision capability of FPSO side structures [J]. Engineering Mechanics, 2014, 31(Suppl 1): 155―160. (in Chinese)
[8]Wang G, Arita K, Liu D. Behavior of a double hull in a variety of stranding or collision scenarios [J]. Marine Structures, 2000, 13(3): 147―187.
[9]Simonsen B C, Lauridsen L P. Energy absorption and ductile failure in metal sheets under lateral indentation by a sphere [J]. International Journal of Impact Engineering,2000, 24(10): 1017―1039.
[10]Lee Y W, Woertz J C, Wierzbicki T. Fracture prediction of thin plates under hemi-spherical punch with calibration and experimental verification [J].International Journal of Mechanical Sciences, 2004,46(5): 751―781.
[11]Haris Sabril, Amdahl Jorgen. An analytical model to assess a ship side during a collision [J]. Ships & Offshore Structures, 2012, 7(4): 431―448.
[12]Sun B, Wang J, Hu Z. OMAE2015-41358 on prediction for structural performance of ship side structures in head-on collision scenario [C]// Omae. 2015.
[13]Haris S, Amdahl J. Analysis of ship–ship collision damage accounting for bow and side deformation interaction [J]. Marine Structures, 2013, 32(7): 18―48.
[14]Simonsen B C. Mechanics of ship grounding [D].Department of Naval Architecture and Offshore Engineering, Technical University of Denmark, 1997.
[15]Alsos H S, Amdahl J. On the resistance of tanker bottom structures during stranding [J]. Marine Structures, 2007,20(4): 218―237.
[16]Wierzbicki T, Thomas P. Closed-form solution for wedge cutting force through thin metal sheets [J]. International Journal of Mechanical Sciences, 1993, 35(3): 209―229.
[17]Wang Ge. Structural analysis of ships’ collision and grounding [D]. University of Tokyo, 1995.
[18]Zhang S. Plate tearing and bottom damage in ship grounding [J]. Marine Structures, 2002, 15(2): 101―117.
[19]Zheng Z M, Wierzbicki T. A theoretical study of steady-state wedge cutting through metal plates [J].International Journal of Fracture, 1996, 78(1): 45―66.
[20]Simonsen B C, Wierzbicki T. Plasticity, fracture and friction in steady-state plate cutting [J]. International Journal of Impact Engineering, 1997, 21(5): 387―411.
[21]Wang G, Ohtsubo H, Liu D. A simple method for predicting the grounding strength of ships [J]. Journal of Ship Research, 1997, 41(3): 241―247.
[22]Zeng J, Hu Z, Chen G. A steady-state plate tearing model for ship grounding over a cone-shaped rock [J]. Ships &Offshore Structures, 2014: 1―13.
[23]孙斌, 胡志强, 王晋. 船底肋板在尖锐礁石搁浅场景下的受力分析[J]. 工程力学, 2016, 33(增刊1): 266―269.Sun Bin, Hu Zhiqiang, Wang Jin. An analytical method for predicting the ship side structure response in raked bow collisions [J]. Engineering Mechanics, 2016,33(Suppl 1): 266―269. (in Chinese)
[24]Hong Lin, Amdahl Jørgen. Rapid assessment of ship grounding over large contact surfaces [J]. Ships &Offshore Structures, 2012, 7(1): 5―19.
[25]Hu Z, Jørgen A, Lin H. Verification of a simplified analytical method for predictions of ship groundings over large contact surfaces by numerical simulations [J].Marine Structures, 2011, 24(4): 436―458.
[26]Yu Z, Hu Z, Wang G. Plastic mechanism analysis of structural performances for stiffeners on bottom longitudinal web girders during a shoal grounding accident [J]. Marine Structures, 2015, 40: 134―158.
[27]于兆龙, 胡志强, 王革. 船舶搁浅于台型礁石场景下双层底外底板骨材变形机理研究[J]. 工程力学, 2014,31(9): 28―36.Yu Zhaolong, Hu Zhiqiang, Wang Ge. Plastic mechanism analysis of structural performances for stiffeners on bottom longitudinal web girders during a shoal grounding accident [J]. Engineering Mechanics, 2014,31(9): 28―36. (in Chinese)
[28]Wierzbicki T. Concertina tearing of metal plates [J].International Journal of Solids & Structures, 1995,32(19): 2923―2943.
[29]Hong L, Amdahl J. Plastic mechanism analysis of the resistance of ship longitudinal girders in grounding and collision [J]. Ships & Offshore Structures, 2008, 3(3):159―171.
[30]Sun B, Hu Z, Wang G. An analytical method for predicting the ship side structure response in raked bow collisions [J]. Marine Structures, 2015, 41: 288―311.
[31]Yang P D C, Caldwell J B. Collision energy absorption of ships' bow structures [J]. International Journal of Impact Engineering, 1988, 7(2): 181―196.
AN INTEGRATED ANALYTICAL METHOD TO PREDICT STRUCTURAL DYNAMIC RESPONSES OF SHIP STRUCTURE UNDER COLLISION AND GROUNDING SCENARIOS
SONG Zi-jie1,2, HU Zhi-qiang3
(1. State Key Lab of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;3. School of Marine Science and Technology, Newcastle upon Tyne, United Kingdom, NE1 7RU)
Abstract:An integrated analytical method is introduced in this paper, which can be used to predict the nonlinear structural dynamic responses for the ships under accidental collision and grounding scenarios. The structural dynamic responses include resistance and energy dissipation. Analytical method has the advantages of cost-effective and fast-calculation. The proposed analytical method contains two modules, one of which is the ship collision module and the other is the ship grounding module. In both scenarios, the deformation mechanisms of shell plating include plastic bending, membrane stretching and tearing, and the mechanisms of web girders include plastic bending and folding. Resistance and energy dissipation of the ship structural components are expressed by analytical formulas. Furthermore, numerical simulations were also conducted with code LS_DYNA,in order to prove the feasibility of the analytical method. This integrated analytical method can be used to predict crashworthiness capability and risk assessment of the ships under collision and grounding scenarios during structural design stage.
Key words:ship collision and grounding; integrated analytical tool; deformation mechanism; resistance; energy dissipation; numerical simulation
中图分类号：U661.4
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.03.0232
文章编号：1000-4750(2018)08-0245-12
收稿日期：2017-03-21；修改日期：2017-08-01
基金项目：深水浮式平台工程化设计验证试验研究(2016ZX05028-002-004)
通讯作者：宋子杰(1994―)，男，河南人，硕士生，从事船舶碰撞搁浅研究(E-mail: songzijie123@sjtu.edu.cn).
作者简介：胡志强(1975―)，男，上海人，副教授，博士，主要从事船舶碰撞搁浅研究(E-mail: zhiqiang.hu@ncl.ac.uk).