
图1 实验用正交各向异性板
Fig.1 Experimental orthotropic plate
胡君逸1,李跃明1,李海波2,程 昊2
(1.西安交通大学机械结构强度与振动国家重点实验室,陕西 710049;2.北京强度环境研究所可靠性与环境工程技术重点实验室,北京 100076)
摘 要:该文开展了热环境下正交各向异性板固有特性和激励响应的研究,通过实验测试与数值计算,分析了其固有频率随温度的变化规律、模态交换或突跳现象、以及激励作用下响应受温度的影响。结果表明:温度引起的热应力与热变形会改变板的动态特性,但两者在热屈曲前后对板刚度的影响机制不同,导致固有频率随温度先降低后上升,且它们的微小变化会导致正交各向异性板的模态交换或突跳现象;激励作用下整体响应曲线随温度升高向低频漂移。
关键词:正交各向异性板;热应力;热变形;模态振型;动态响应
热环境下正交各向异性板固有特性和响应规律的研究对于工程结构设计及其安全性评价具有重要意义。自20世纪90年代,国内外学者相继开展了各向同性板、壳,复合材料梁、板等结构动特性的研究。Matsunaga[1]研究了考虑剪切效应、厚度及旋转惯量复合材料角铺设层合板的振动特性和稳定性。Singha[2]用有限元法研究了复合材料板大范围的柔性自由振动,发现随着平板厚度和斜交角度的增加,非线性固有频率与线性固有频率的比值不断增加。Daneshjoo[3]用基于混合公式的有限元法研究了在横向载荷和热冲击同时作用下热弹耦合的各向同性和层状复合材料板的响应。Pradeep等[4]利用有限元研究了四边固支的粘弹性夹层板的热屈曲和振动特性。Jae-Sang等[5]采用有限元研究了带有形状记忆合金复合材料板的后屈曲振动特性,发现形状记忆合金会增加平板的热屈曲温度,减小热变形挠度。Anderson等[6]通过实验和有限元对比研究了不同铺设角复合材料板的固有频率和模态阵型。Ribeiro[7]研究了热载荷下四边固支的复合材料圆柱壳的振动特性。Cheng等[8]通过实验和数值计算研究了 1000℃高温环境下平板和加筋板固有振动特性,发现热应力的作用超过材料属性改变对模态的影响。Du等[9]研究了含有温度梯度层合板的振动特性,得到了较完整的基频变化规律。Jeyaraj等[10―11]建立有限元与边界元(FEA-BEA)联合仿真模型,分析了各向同性板及复合材料板在热环境下的振动及声响应特性。Kim[12]考虑结构热应力及材料的热属性,理论研究了热环境下功能梯度矩形板的振动问题。
Liu等[13]通过考虑一阶剪切变形效应的有限元法分析了存在热应变作用时复合材料层合板的振动特性。李世荣等[14]基于薄板大挠度理论建立了Winkler弹性地基上弹性圆板在均匀升温下的热过屈曲的控制方程,研究了由弹性地基刚度参数导致的临界屈曲模态跃迁。钮鹏等[15]通过建立热载荷作用下复合材料夹层梁受弹性地基约束时的几何非线性控制方程,研究了临界升温与地基弹性参数之间的关系曲线,并得到模态跃迁性质。杨雄伟等[16―17]通过建立X-43A结构与内声场的FEM-SEA混合模型,考虑材料热属性和结构热应力,研究了热环境对结构声-振特性的影响,得到了混响声场作用下结构在宽频范围内的响应。Geng和Li[18―20]等推导了考虑热应力作用下板的振动控制方程,针对各向同性简支及固支板在热环境下的振动及声辐射响应特性开展理论与实验研究。此外,还获得了热环境下层合板[21]、夹芯板[22]及夹芯梁[23]振动特性及声响应的半解析解。Zhao和Li等[24―25]还研究了湿环境下板和壳的振动问题,获得了湿环境下正交各向异性平板和圆柱壳的振动及声辐射特性。吴振强等[26]获得了热环境下各向同性加筋板的动特性。
关于热环境下各向同性板、壳结构振动特性的理论研究、数值分析、实验手段已有较多,且有关各向异性材料板固有特性的研究也有一定的基础,但考虑热效应的正交各向异性板固有特性变化及产生模态交换现象的研究还较少。本文以正交各向异性板为对象,开展热模态、热载荷及声/机械激励响应的实验研究;根据实验结果,实施考虑热应力及热变形效应的数值计算,解明了温度产生的热应力、热变形及材料参数对振动特性、模态交换的影响机制,以及温度变化对结构动响应的影响规律。
实验对象为正交各向异性单层板按[0°/90°]交替铺设的正交各向异性对称层合板,其中增强相为碳纤维,体积比例60%,基体相为环氧树脂,体积比例40%。实物如图1,材料结构铺层示意如图2,几何尺寸与材料属性如表1。中心面积0.3 ×0.2 m2的部分为测试区域,按顺序标记36个测试点。

图1 实验用正交各向异性板
Fig.1 Experimental orthotropic plate

图2 正交各向异性板材料结构示意图
Fig.2 Material and structure of orthotropic plate
表1 实验板的几何尺寸与材料属性
Table 1 Geometrical size and material parameter of specimen

注:因实验板有0.00108m(9层)和0.003m(25层)两种厚度,用“/”区分。
图3所示为实验装置,包括石英灯,实验夹具基座,支架,实验板(矩形板),工作灯,激振器,扬声器,滤波器,信号放大器,加速度传感器,力传感器和声传感器。测试设备包括红外测温计、力锤及LMS测试系统。

图3 实验装置
Fig.3 Experimental set
首先测得热环境下板的固有特性。热环境通过实验板下面的石英灯施加,利用红外测温仪获得实验板上具体测试点的温度。依据简单的数值分析结果,避开前五阶的振动不动点,将加速度传感器(PCB 333B32)布置在实验板的第 12测试点(见图1(b)),用于识别各阶振型、频率及阻尼比。采用LMS模态分析系统,通过力锤(PCB hammer 086C04)逐个激励各测试点、测试频率变化,同时为保证准确进行了相关性检测,最后利用LMS TEST.LAB处理实验数据。
其次,开展热载荷及声激励作用下正交各向异性板的动响应实验,通过 LMS振动测试系统输出线性周期调频信号(便于确定系统的频率响应),利用滤波器和信号放大器分别对激励信号进行有效滤除和放大,最后通过扬声器(Hivi SS6.5)将声激励施加在板上实现。加速度传感器布置在实验板第12测试点,声传感器(B&K type 4958)置于扬声器正下方0.05 m处,分别获取实验板的响应曲线和声源的声压。最后利用LMS TEST.LAB处理实验数据,获得实验板的频响曲线和声压。图4为热载及声激励实验的示意图。

图4 热载及声激励实验示意图
Fig.4 Sketch of thermal load and acoustic excitation experiment
之后,开展热载荷及机械激励作用下正交各向异性板的动响应实验,通过 LMS振动测试系统输出线性周期调频信号(便于确定系统的频率响应),利用滤波器和对激励信号进行有效滤除,最后通过激振器(MB Exciter Modal 2)和激振杆将机械激励施加在实验板上第 25点来实现。加速度传感器布置在实验板的第 12测试点,力传感器置于激振杆的末端,分别获取实验板的响应曲线和作用在实验板上的力信号。最后利用LMS TEST.LAB处理实验数据,获得实验板的频响曲线和力信号。图5为热载及机械激励实验的示意图。
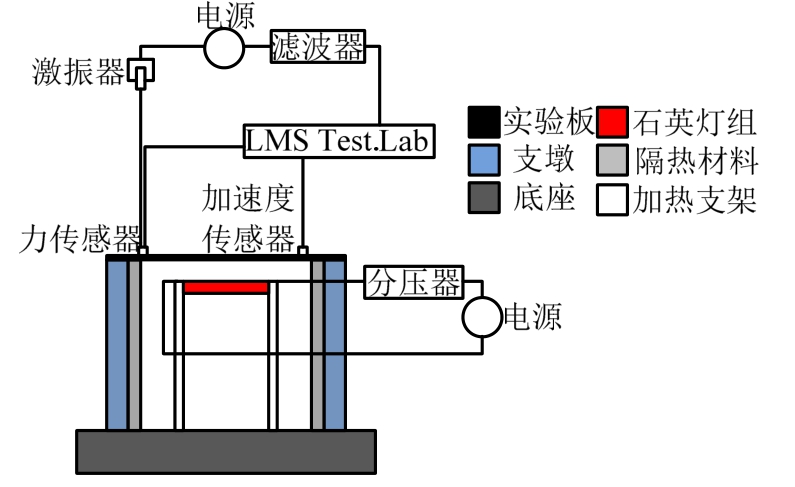
图5 热载及机械激励实验示意图
Fig.5 Sketch of thermal load and mechanical excitation experiment
1.2.1 固有振动特性
首先,对3块3 mm实验板进行模态实验,为避免实验板基体材料环氧树脂受热发生变化,实验温度仅升至 100℃左右,在此温度范围内材料弹性模量的变化很小,忽略其对板频率的影响。除去实验中奇异数据,表2为随中心温度变化的前三阶频率,依次下降了 9.9%、9.4%、6.2%。因为固支板受热产生的热效应削弱了板的刚度,导致了板固有频率的下降。
表2 3 mm实验板前三阶频率随中心温度的变化
Table 2 Frequency of 3 mm experimental plate with central temperature variation
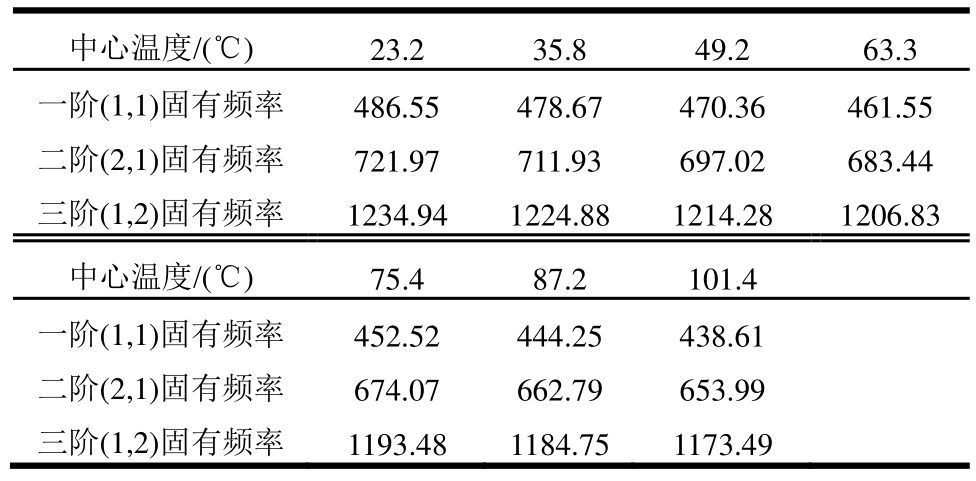

图6 固有频率随温度的变化百分比
Fig. 6 Frequency Decrease with Temperature Variation
图6为前三阶固有频率随温度下降按照此式![]() 处理的结果,式中 XS、XF、XT分别为初始温度、结束温度、中间任意温度时的固有频率。可见随温度升高,各阶下降速率不同,自然存在模态交换的可能。如图7所示给出了实验数据的误差统计,标准差的计算公式为:
处理的结果,式中 XS、XF、XT分别为初始温度、结束温度、中间任意温度时的固有频率。可见随温度升高,各阶下降速率不同,自然存在模态交换的可能。如图7所示给出了实验数据的误差统计,标准差的计算公式为:
式中:μ代表固有频率平均值;xi代表实验测得固有频率值。3块实验板所得实验数据绝对误差的标准差范围在0.6~1.6,表明实验整体数据分布均匀,可反映实验板在热载荷作用下固有频率的变化。

图7 前三阶固有频率绝对误差的标准差
Fig.7 Standard deviation of absolute error of frequency
其次,对1 mm实验板进行同样实验,表3为第1阶、2阶阶频率随温度变化的结果,图8为对应的曲线,图9为实验测试87.2℃和101.4℃的前二阶振型。第1阶频率随温度升高先降低而后上升,在100℃左右超过持续下降的第2阶频率,此时第1阶、第2阶振型发生了交换(见图9)。实验中第1阶频率无法降至0 Hz,可能由于平板的初始缺陷所导致,文献[16]中有对该现象的详细分析。
表3 1mm实验板前二阶固有频率随温度的变化
Table 3 Frequency of 1 mm experimental plate with temperature variation

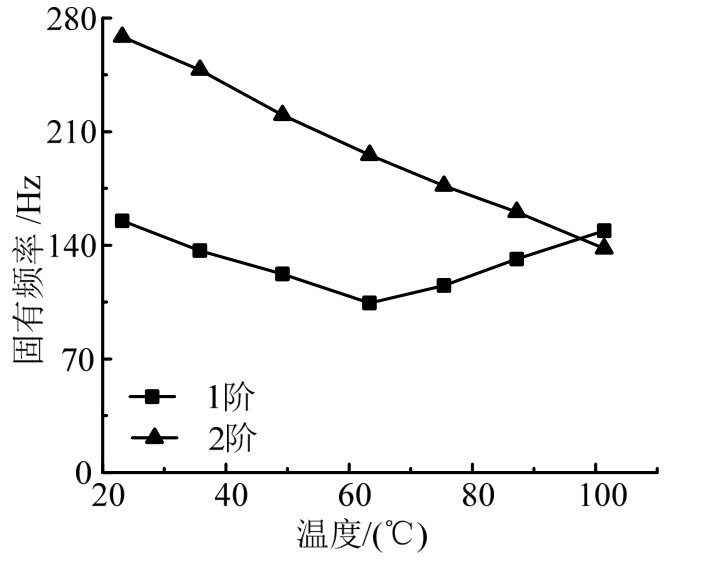
图8 1 mm实验板第1阶、2阶频率随温度的变化
Fig.8 Frequency of 1mm experimental plate with temperature variation


图9 温度87.2℃和101.4℃时1 mm实验板的前2阶振型
Fig.9 Mode shape of 1 mm experimental plate at 87.2℃ and 101.4℃
1.2.2 激励作用下的响应
最后,开展了声、机械激励作用下实验板的动响应实验,其中声激励选线性周期调频信号,范围0~3000 Hz,大小通过LMS以3 V电信号输出。图10是热环境下声激励作用的动响应曲线,可见,随温度升高频响曲线整体向低频漂移,整体特征基本不变。将第1阶频率峰值的局部放大,峰值随温度升高逐渐降低。因为受热板一方面因热效应削弱了刚度,使板的固有频率降低;另一方面热环境改变了结构阻尼比(见表4),第1阶阻尼比随温度升高而增大,使板的能量耗散增加,振动动能减小,所以频响曲线向低频漂移,第1阶响应幅值下降。
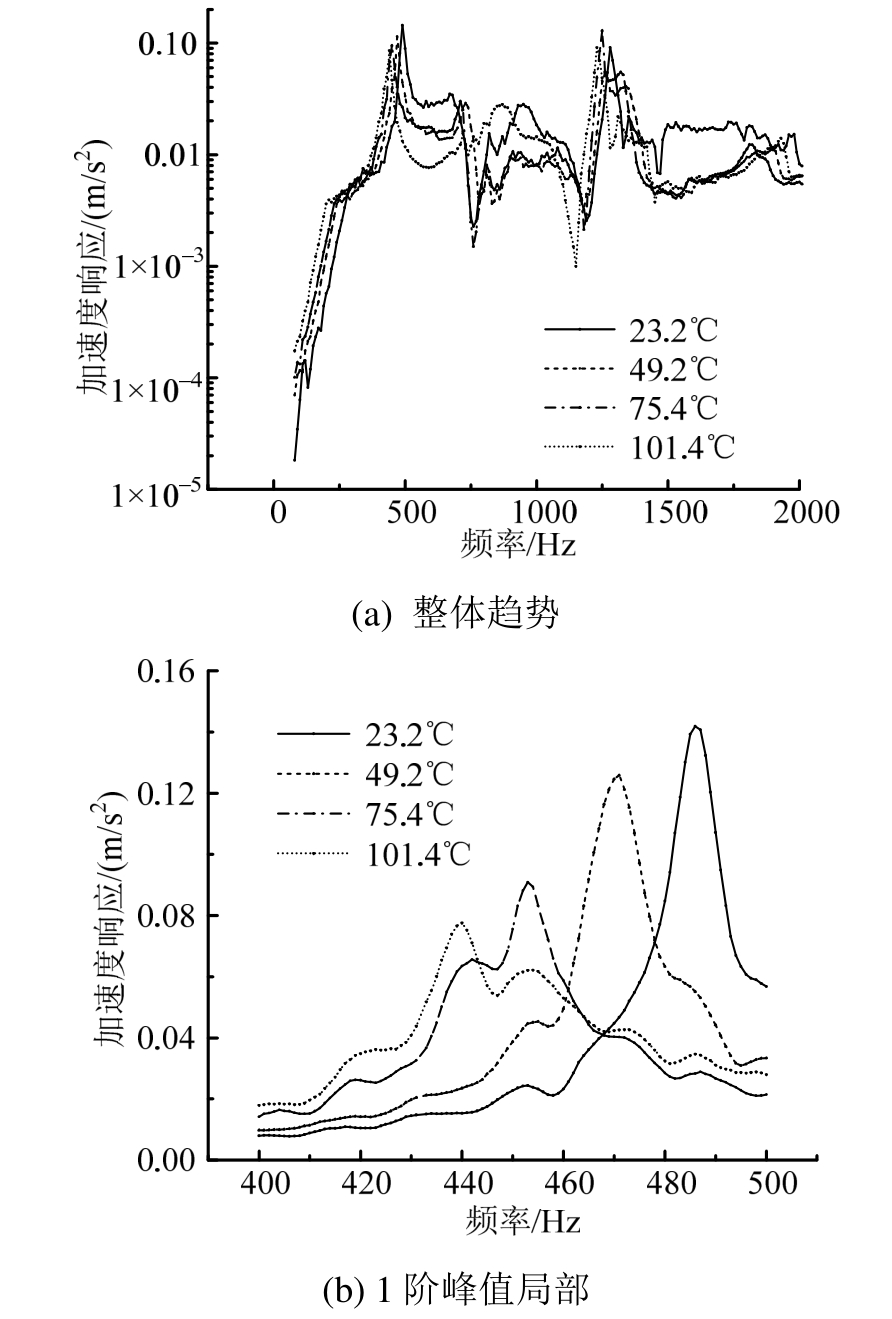
图10 热环境下实验板的声激励响应曲线
Fig.10 Response of experimental plate under thermal load and acoustic excitation
表4 3 mm实验板的前三阶模态阻尼比随温度的变化
Table 4 Damping ratio of 3 mm experimental plate with temperature variation

机械激励选择与声激励信号相同。图11是热环境下机械激励作用的动响应曲线,与声激励实验结果趋势相符,整体特征基本不变。不同激励作用下的响应曲线在共振频率和响应幅值存在差异,首先,声激励的1阶响应频率在440~490 Hz,而机械激励的1阶响应频率在355~395 Hz,因其机械激振器成了系统附加质量,使机械激励的峰值频率低于声激励的结果;其次,将1阶频率局部放大,发现响应峰值随温度升高逐渐增大,因为热载削弱了板的刚度,导致响应幅值增大。

图11 热环境下实验板的机械激励响应曲线
Fig.11 Response of experimental plate under thermal load and mechanical excitation
本节开展相关数值分析,进一步研究正交各向异性板频率、振型和频响曲线,并与实验结果比较。热结构的有限元分析需考虑由热应力产生的刚度阵Kσ和热变形产生的非线性刚度阵KNL的影响,由温度引起的材料属性变化此处暂不考虑。
热结构动力学行为可通过以下有限元方程求解:

其中:K0是结构原始刚度阵;Kσ是由热应力产生的刚度阵;KNL是由热变形产生的刚度阵;ω是结构固有频率;Ms是结构质量阵;Cs是结构阻尼阵,u是节点自由度的位移向量;Qs是激励向量。Kσ和KNL可表达为[27]:

其中:G是应变位移矩阵;S是应力矩阵;BL和BNL分别为几何矩阵B的线性和非线性部分;D为弹性矩阵;A是求解域。
激励作用下热结构声振响应可通过耦合系统的有限元方程求解。首先,耦合模型中内声场的动力学有限元方程[17]:
其次将声压及其他载荷作为结构的动力载荷,可得到耦合模型中结构的动力学有限元方程:
由此,获得内声场的声波传播和结构的振动特性,以声场空间位置处的声压p和结构节点自由度的位移u作为未知量,同时考虑热应力产生的刚度阵 Kσ和热变形产生的非线性刚度阵 KNL的作用,可得热结构的声-振耦合系统的有限元方程为:
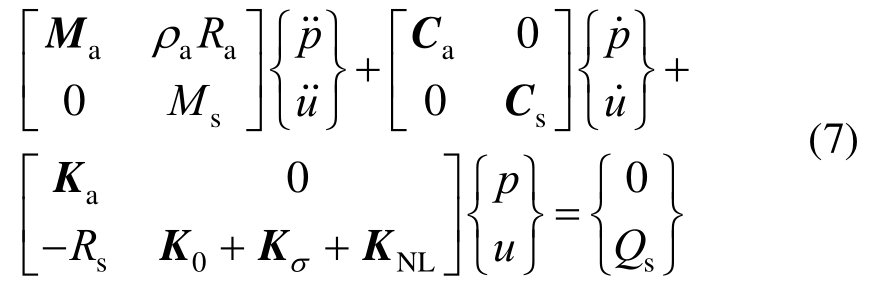
其中:Ka是内声场介质的刚度阵;Ma是质量阵,Ca是阻尼阵;p是空间位置处的声压;aρ是介质的密度。
2.2.1 固有频率变化规律
利用 NASTRAN求解热载产生的热效应包括热应力和热变形,将它们分别作为预应力和初始形变施加在原模型上,再进行模态分析。
采用四边形单元划分网格,四边固支。图12为3mm正交各向异性板前三阶频率考虑热效应(热应力及热变形)变化的计算结果与表2的对比,数值与实验结果均随温度的升高而下降且趋势相符,前3阶最大误差分别为6%、9%和3%。数值结果偏高可能是数值预测的刚度偏高及计算的理想化条件所致。

图12 3 mm正交各向异性板前三阶频率随温度变化的数值与实验对比
Fig.12 Frequency contrast between the test and numerical value of 3 mm orthotropic plate with temperature variation
进一步,我们给出了热应力单独作用下频率随温度的变化,如图13所示。对比图12与图13可见,两者几乎一致,表明热变形对频率变化几乎没有影响。这是因为3 mm平板未发生热屈曲,其热变形量很小,对刚度几乎没有影响,仅需考虑热应力对刚度的影响。热屈曲前热应力是影响板刚度的主要因素。
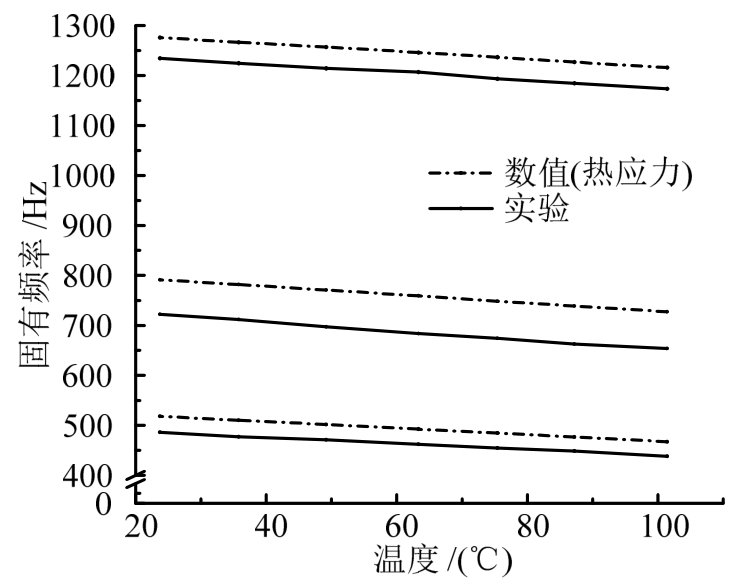
图13 热应力对正交各向异性板前三阶固有频率的影响与实验的对比
Fig.13 Frequency contrast between the test and effect of thermal stress on 3mm orthotropic plate
图14为1 mm正交各向异性板固有频率随温度变化的数值结果与图8结果的对比,图15为数值计算 87.2℃和 101.4℃的前二阶振型。为了准确对比实验结果,计算存在初始缺陷的平板模型,获得平板前二阶固有频率随温度的变化。通过对比,数值与实验结果整体趋势相符,1阶固有频率均随温度的升高先减小后增加,并在 100℃左右均超过持续下降的第2阶固有频率,1阶、2阶振型发生模态交换(见图15);说明此平板模型在实验温度范围内能合理地反映实验板的固有振动特性随温度的变化,可进一步计算分析热屈曲后热应力或热变形单独作用对板频率的影响。
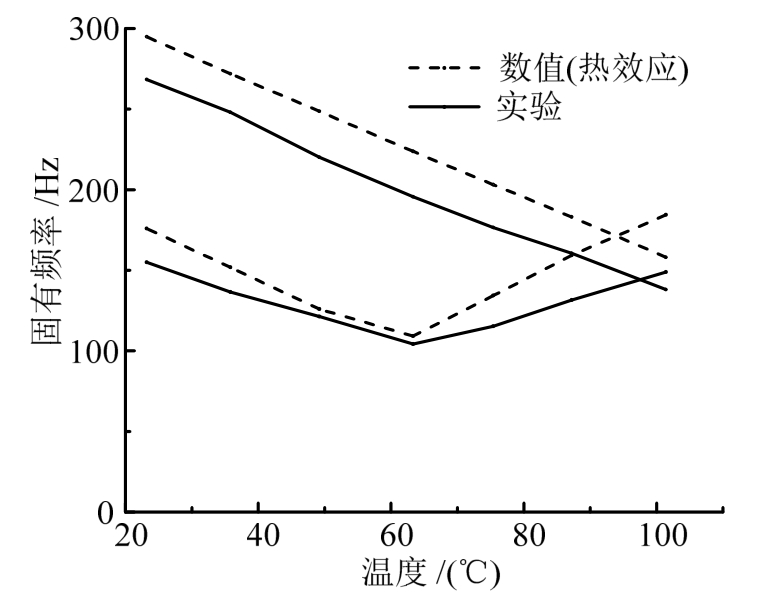
图14 1 mm正交各向异性板前二阶固有频率随温度变化的数值与实验对比
Fig.14 Frequency contrast between test and numerical value of 1 mm orthotropic plate with temperature variation
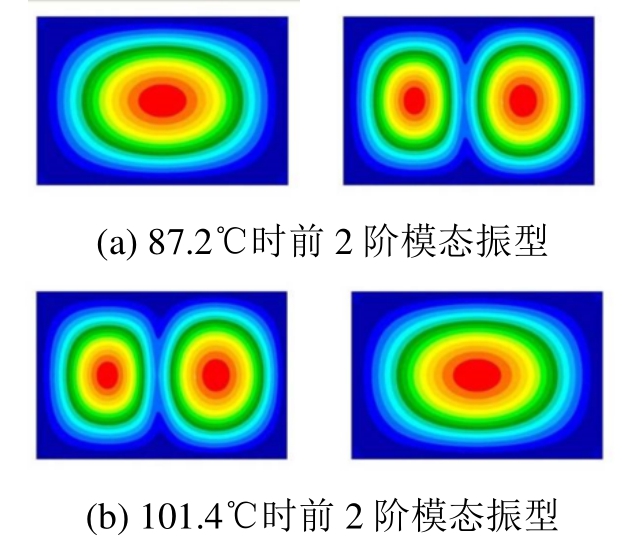
图15 环境温度为87.2℃和101.4℃时1 mm正交各向异性板的前2阶振型
Fig.15 Mode shape of 1 mm orthotropic plate at 87.2℃ and 101.4℃
图16为热应力或热变形单独作用对板频率特性的影响,其中方点线、圆点线分别代表热应力或热变形单独作用时固有频率的变化,虚线代表热屈曲后上述两者单独作用下频率的变化线,实线代表频率的实际变化线。热屈曲前,热应力起主要作用,固有频率呈线性下降;在屈曲温度附近热应力单独作用(方点实线)与实际频率(三角点线)相比有小幅差异,因为平板存在初始缺陷,在温度作用下产生了较小的热变形,使频率有小幅增加;热屈曲后,热应力单独作用时对频率的影响程度较之热变形单独作用时的程度小,频率转为增加,这是因为屈曲后由热变形产生的挠度大幅增加,热变形对初始刚度的影响超过热应力的影响。因此,发生热屈曲后需同时考虑热应力和热变形的效应,两者对初始刚度阵的影响程度在热屈曲前后不同。
通过对比,1 mm板在热屈曲前热应力起主要作用,其削弱了刚度,第1阶固有频率值随温度的升高减小;热屈曲后热变形起主要作用,其产生的挠度随温度升高不断增大导致结构刚度增大,因此频率值随温度升高而转为增加。

图16 热应力与热变形分别对正交各向异性板第1阶固有频率的影响
Fig.16 Effect of thermal stress and thermal deformation on frequency of 1mm orthotropic plate
2.2.2 模态交换
由以上实验和数值分析可见,热应力和热变形对正交各向异性板各阶频率产生影响且导致了模态交换,现讨论其机制。
考察正交各向异性板的材料参数和环境温度的变化对其固有特性的影响,计算对象几何尺寸和材料属性如表5,其中E1、E2分别为材料1、2的弹性模量,α1、α2分别为材料1、2的热膨胀系数。
表5 正交各向异性板几何尺寸与材料属性
Table 5 Geometrical dimensions and material parameter of orthotropic plate

首先,保持环境温度(室温)不变,固定材料 1的弹性模量 E1,调节弹性模量比值 E2/E1,观察正交各向异性程度对板各阶模态变化的影响。见图17和18,当E2/E1由3.5变至3.6时板的第6阶、7阶模态顺序发生了交换。
其次,保持材料各向异性程度不变(E2=2E1),考察温度改变对板各阶模态变化的影响。见图19和图20,当温度由51℃变至52℃时板的第3、4两阶模态出现了交换。
表6 正交各向异性板固有频率随材料各向异性程度的变化
Table 6 Frequency of orthotropic plate with orthotropy variation

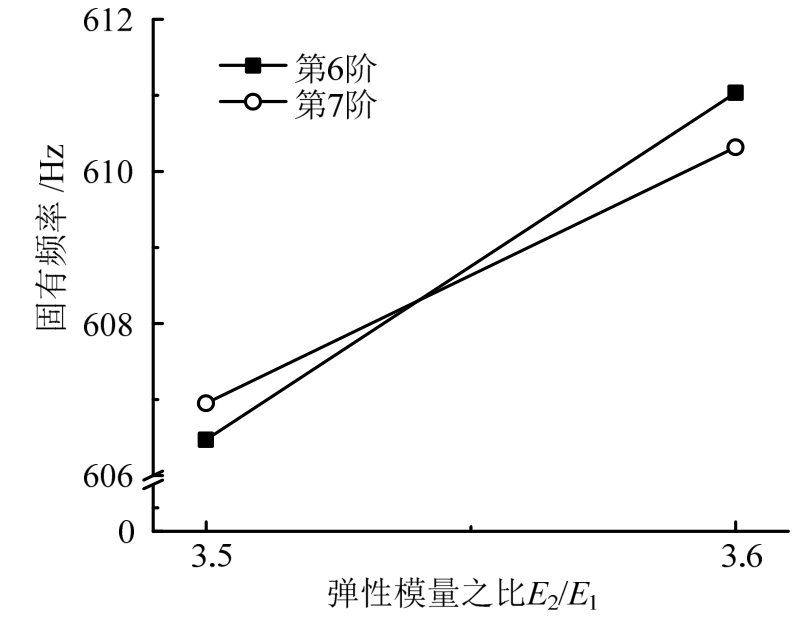
图17 正交各向异性板第6阶、7阶固有频率随材料参数的变化
Fig.17 Frequency of orthotropic plate with material parameter change

图18 正交各向异性板6阶、7阶振型随材料参数的变化
Fig.18 Interchange of mode shape of orthotropic plate with material parameter change
注:这里仅列出发生模态交换阶次的振型
表7 正交各向异性板固有频率随温度的变化
Table 7 Frequency of orthotropic plate with temperature variation

通过上述数值算例可见,无论是材料属性还是环境温度的微小改变,都会使正交各向异性板的模态发生交换。实质上,材料或温度的微小改变都是结构刚度阵受到了微小扰动。结构发生模态交换是
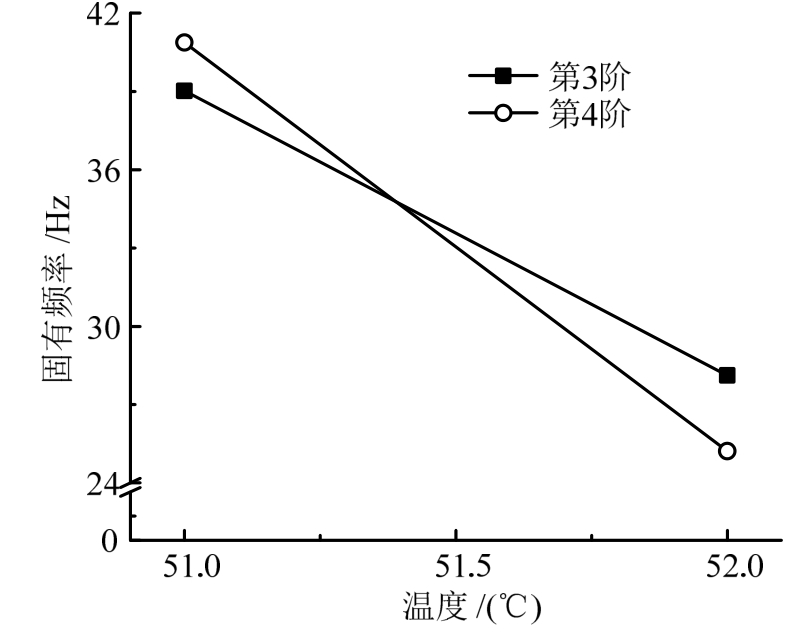
图19 正交各向异性板第3阶、4阶固有频率随温度的变化
Fig.19 Frequency of orthotropic plate with temperature change

图20 正交各向异性板3阶、4阶振型随温度的变化
Fig.20 Interchange of mode shape of orthotropic plate with temperature change
由于结构特征值的顺序交换而引起的[28―29],对于稳定结构的刚度矩阵,其元素受微小扰动导致特征值改变的问题可转化为研究一元高次方程的根与系数的关系。以3阶对称矩阵 aij(i, j = 1 ,2,3)为例,其特征值的方程为:

假设三个根为![]() 进一步可得根与系数的关系:
进一步可得根与系数的关系:

当aii不变,aij绝对值减小,则![]() 不变,
不变,![]() 增大,因此
增大,因此![]() 中,某些根增加,某些根减小;
中,某些根增加,某些根减小;
当aij不变,aii减小,则![]()
![]()
![]() 均减小,因此
均减小,因此![]() 均减小。
均减小。
由以上分析,3阶矩阵内的元素均减小时,由于对角线上元素和非对角线上元素扰动对解影响不同,则某些解不断减小且变化较快,某些解变化较慢或者保持不变,所以不同解变化趋势不同,可能出现某一种情况,当矩阵扰动后,某两个解的大小发生改变,即 λ1≥λ2或者 λ1≥λ3亦或者 λ2≥λ3,则发生了特征值的交换。对于更高阶的矩阵,可得相似的结论。
进一步,通过一弹簧质量系统如图21所示,来说明矩阵元素微小扰动可导致特征值的交换。
其中:k1=11.96 N/m,k2=6.03 N/m,k3=0.92 N/m,k4=0.03 N/m,k5=0.83 N/m,k6=15.96 N/m,m1=m2=m3=m4=m5=1kg。

图21 弹簧质量系统
Fig.21 Spring mass system
可计算得到原始系统的特征值和特征向量如表8。
表8 系统扰动前特征值和特征向量
Table 8 Eigenvalues and eigenvectors of the system before the turbulence

注:仅列出了发生模态交换相关阶次的特征值和特征向量。
假设系统弹簧刚度发生微小扰动:Δk1=-0.06 N/m, Δk2=-0.01 N/m, Δk3=-0.01 N/m, Δk4=-0.01 N/m, Δk5=-0.01 N/m, Δk6=-0.06 N/m。从而可获得系统扰动后的特征值和特征向量如表9。
表9 系统扰动后特征值和特征向量
Table 9 Eigenvalues and eigenvectors of the system after the turbulence

针对此结果,采用模态相关性的判别准则量化判定模态向量间相关度[30],计算获得弹簧质量系统在扰动前后的特征向量相关性结果见表10。
通过对弹簧质量系统的第4阶、5阶振型的特征向量进行相关性判断,确认弹簧质量系统扰动前第4阶振型与扰动后第5阶振型的相关度非常高,扰动前第5阶振型与扰动后第4阶振型的相关度非常高,说明弹簧质量系统扰动后第4阶模态与第5阶模态发生了交换。
表10 弹簧质量系统在扰动前后特征向量相关性检验
Table 10 Checkout on the relativity of eigenvectors of system between the turbulence

根据上述分析可知,热应力产生了削弱板原始刚度的效应,而热屈曲变形产生了增强加板原始刚度的效应,两者在不同温度区段(热屈曲前后)所发挥作用的强弱不同;当温度变化时,热应力和热变形的微小变化对原始刚度阵产生扰动,使得板的频率发生变化,相邻两阶频率值的大小顺序会发生改变,对应的模态振型发生交换。
热环境下正交各向异性板的声激励响应的数值计算采用软件VA one实施,声-振耦合系统计算模型与固有特性计算模型一致,因3 mm平板在实验中热应力起主要作用,故仅获得预应力的计算结果,施加在结构模型上,再实施数值计算。数值仿真中的声激励信号采用实验测试的激励信号,通过在边界元流场中板模型上方0.3 m处施加一个单极子来模拟,加速度传感器根据实验的实际情况安置在计算模型上,如图22为计算模型。

图22 声-振耦合系统计算模型
Fig.22 Calculate mode of SEA-FEM
图23为数值计算结果与图10的对比,可以看出不同温度下正交各向异性板数值和实验结果的整体趋势相符,计算结果大体上能反映正交各向异性板的实际响应。数值计算结果的频响曲线较光滑,可能是实验的外部环境并非理想消声环境,实验曲线存在小幅震荡。
由于正交各向异性板是由非单一材料构成,本小节考察增强相不同含量比对正交各向异性板的响应变化。

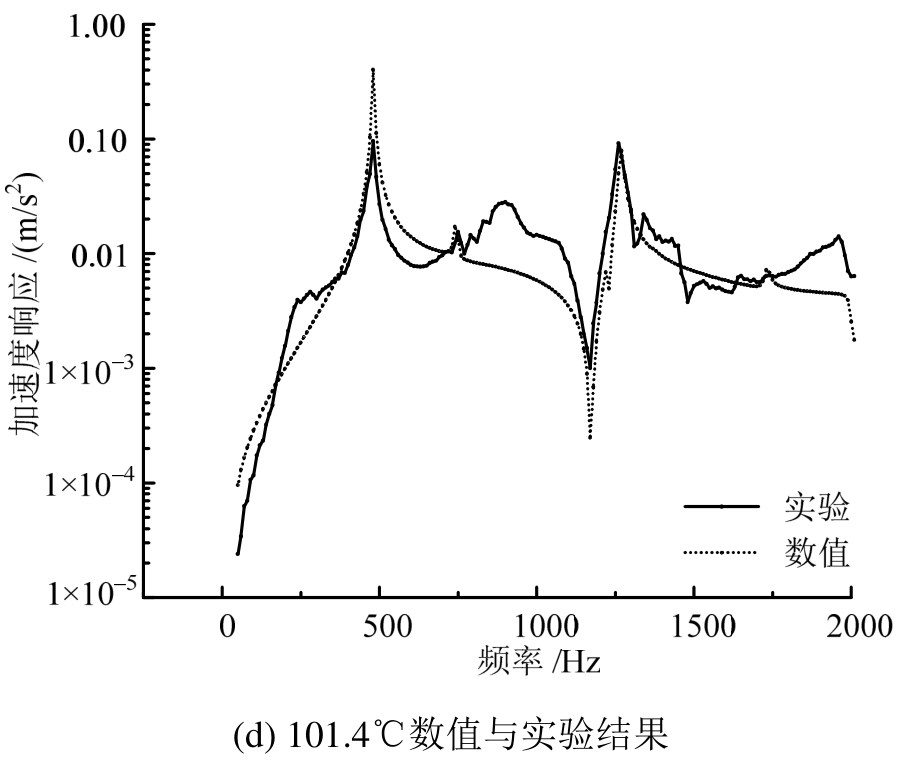
图23 热环境下正交各向异性板的声激励响应的数值与实验结果对比
Fig.23 Response of orthotropic plate under thermal load and acoustic excitation contrast between the numerical and test result
图24是正交各向异性板中增强材料含量比变化对其响应的影响,其中normal代表实验板,±5%代表增强材料含量比变化的计算对象。随着增强项含量比的变化频响曲线整体响应特性变化不明显,增强材料比例的增加增大板的刚度,固有频率上升,因此各阶响应峰值向高频漂移。

图24 正交各向异性板纤维比例改变对响应的影响
Fig.24 Effect of material ratio on response of orthotropic plate
本文以正交各向异性板为对象,采用实验与数值手段研究了四边固支热环境下其动特性与动响应的变化规律,明确了热应力与热变形对结构特性的影响效应,获得了正交各向异性板固有频率、振型和动响应的变化规律,并对模态交换现象开展了数值研究。结论如下:
(1)热环境引起板内热应力和热变形,热屈曲前热应力对原始刚度的变化起主要作用;热屈曲后热变形对原始刚度变化起主要作用;两者改变平板的固有振动特性,各阶频率的变化趋势不同,且会产生模态交换;
(2)依据热应力及热变形对结构刚度的效应实施数值模拟方法,开展了热环境下正交各向异性板固有特性和动响应的数值分析,与实验结果对比表明,两者符合良好,趋势一致,且验证了热应力与热变形在不同温度区域的效应;
(3)热环境温度、材料属性及几何构型的微小改变,均会导致结构刚度阵的特征值发生顺序变化,探讨了模态交换的机制;
(4)热环境、激励作用下板响应的整体特征变化较小,热屈曲前频响曲线向低频漂移,响应峰值受阻尼比的影响而发生变化;反之,热屈曲后频响曲线向高频漂移。
参考文献:
[1]Matsunaga H. Vibration and stability of angle-ply laminated composite plates subjected to in-plane stresses[J]. International Journal of Mechanical Sciences, 2001(43): 1925―1944.
[2]Singha M K. Nonlinear vibration of symmetrically laminated composite skew plates by finite element method [J]. International Journal of Non-linear Mechanics, 2007, 42(9): 1144―1152.
[3]Daneshjoo K. Classical coupled thermoelasticity in laminated composite plates based on third-order shear deformation theory [J]. Composite Structures, 2004, 64:369―375.
[4]Pradeep V, Ganesan N. Thermal buckling and vibration behavior of multi-layer rectangular viscoelastic sandwich plates [J]. Journal of Sound & Vibration, 2008, 310(1-2):169―183.
[5]Jae-Sang Park, Ji-Hwan Kim, Seong-Hwan Moon.Vibration of thermally post-buckled composite plates embedded with shape memory alloy fibers [J].Composite Structures, 2004,(63): 179―188
[6]Anderson T J, Nayfeh A H. Natural frequencies and mode shapes of laminated composite plates: experiments and FEA [J]. Journal of Vibration & Control, 1996, 2(2):381―414.
[7]Ribeiro P. Non-linear vibrations of laminated cylindrical shallow shells under thermomechanical loading [J].Journal of Sound and Vibration, 2008, 315: 626―640.
[8]Cheng H, Li H B, Zhang W, et al. Effects of radiation heating on modal characteristics of panel structures [J].Journal of Spacecraft and Rockets, 2015, 52(4): 1228―1235.
[9]Du M, Geng Q, Li Y M. Vibrational and acoustic responses of a laminated plate with temperature gradient along the thickness [J]. Composite Structures, 2016, 157:483―493.
[10]Jeyaraj P, Padmanabhan C, Ganesan N. Vibration and acoustic response of an isotropic plate in a thermal environment [J]. ASME Transaction Journal of Vibration and Acoustics, 2008, 130(5): 301―305.
[11]Jeyaraj P, Ganesan N, Padmanabhan C. Vibration and acoustic response of a composite plate with inherent material damping in a thermal environment [J]. Journal of Sound and Vibration, 2009, 320(1-2): 322―338.
[12]Kim Y W. Temperature dependent vibration analysis of functionally graded rectangular plates [J]. Journal of Sound and Vibration, 2005, 284(3-5): 531―549.
[13]Liu C F, Huang C H. Free vibration of composite laminated plates subjected to temperature changes [J].Computers and Structures, 1996, 60(1): 95―101.
[14]李世荣, 郁汶山. 弹性地基上加热弹性圆板的热过屈曲及临界屈曲模态跃迁[J]. 工程力学, 2007, 24(5):63―66.Li Shirong, Yu Wenshan. Thermal post-buckling and the critical buckling mode transition of heated elastic circular plates on elastic foundation [J]. Engineering Mechanics,2007, 24(5): 63―66. (in Chinese)
[15]钮鹏, 李旭, 李世荣, 等. 弹性地基上复合材料夹层梁的热过屈曲[J]. 工程力学, 2017, 34(增刊1): 26―30.Niu Peng, Li Xu, Li Shirong, et al. The thermal buckling of composite sandwich beams on elastic foundations [J].Engineering Mechanics, 2017, 34(Suppl 1): 26―30. (in Chinese)
[16]杨雄伟, 李跃明, 闫桂荣. 考虑材料物性热效应飞行器声振耦合动态特性分析[J]. 固体力学学报, 2010,31(增刊): 134―142.Yang Xiongwei, Li Yueming, Yan Guirong. Vibroacoustic dynamic analyze of aircraft with temperaturedependent material property [J]. Chinese Journal of Solid Mechanics, 2010, 31(Supll): 134―142. (in Chinese)
[17]耿谦, 李跃明, 杨雄伟. 热应力作用下结构声-振耦合响应数值分析[J]. 计算力学学报, 2012, 29(1): 99―104.Geng Qian, Li Yueming, Yang Xiongwei. Vibro-acoustic numerical analysis of thermal stressed aircraft structure[J]. Chinese Journal of Computational Mechanics 2012,29(1): 99―104. (in Chinese)
[18]Geng Q, Li H, Li Y M. Dynamic and acoustic response of a clamped rectangular plate in thermal environments:Experiment and numerical simulation [J]. Journal of the Acoustical Society of America, 2014, 135(5): 2674―2682.
[19]Geng Q, Li Y M. Analysis of dynamic and acoustic radiation characters for a flat plate under thermal environments [J]. International Journal of Applied Mechanics, 2012, 4(3): 1250028.
[20]Geng Q, Li Y M. Solutions of dynamic and acoustic responses of a clamped rectangular plate in thermal environments [J]. Journal of Vibration and Control, 2016,22(6): 1593―1603.
[21]Li W, Li Y M. Vibration and sound radiation of an asymmetric laminated plate in thermal environments [J].Acta Mechanica Solida Sinica, 2015, 28(1): 11―22.
[22]Liu Y, Li Y M. Vibration and acoustic response of rectangular sandwich plate under thermal Environment[J]. Shock and Vibration, 2013, 20(5): 1011―1030.
[23]李欢, 耿谦, 李跃明. 热环境下夹芯梁声振特性的理论与数值研究 [J]. 应用力学学报, 2015, 32(1): 40―45.Li Huan, Geng Qian, Li Yueming. Theoretical and numerical study on the thermal environment characteristics of Shengzhen sandwich beam [J]. Chinese Journal of Applied Mechanics, 2015, 32(1): 40―45. (in Chinese)
[24]Zhao X, Geng Q, Li Y M. Vibration and acoustic response of an orthotropic composite laminated plate in a hygroscopic environment [J]. Journal of the Acoustical Society of America, 2013, 133(3): 1433―1442.
[25]Xin Zhao, Yueming Li. Vibration and acoustic responses of an orthotropic composite conical shell in a hygroscopic environment [J]. Journal of Vibration &Control, 2015, 7(4): 190―217.
[26]吴振强, 程昊, 张伟, 等. 热环境对飞行器壁板结构动特性的影响[J]. 航空学报, 2013, 34(2): 334―342.Wu Zhenqiang, Cheng Hao, Zhang Wei, et al. Effects of thermal environment on dynamic properties of aerospace vehicle panel structures [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 334―342. (in Chinese)
[27]王勖成. 有限单元法[M]. 北京: 清华大学出版社,2003.Wang Xucheng. Finite element method [M]. Beijing:Tsinghua University Press, 2003. (in Chinese)
[28]陈塑寰. 结构动态设计的矩阵摄动理论[M]. 北京: 科学出版社, 1999.Chen Suhuan. Matrix perturbation theory for structural dynamic design [M]. Beijing: Science Press, 1999. (in Chinese)
[29]于岩磊, 高维成, 刘伟, 等. 密集模态结构模态跃迁分析的简化摄动法 [J]. 工程力学, 2012(3): 33―40.Yu Yanlei, Gao Weichen, Liu Wei, et al. A simplified perturbation method for modal transition analysis of dense mode Structures [J]. Engineering Mechanics,2012(3): 33―40. (in Chinese)
[30]Allemeng R J. The modal assurance criterion-twenty years of use and abuse [J]. Sound and Vibration, 2003,37(8): 14―21.
RESEARCHES ON VIBRATION CHARACTERISTIC AND DYNAMIC RESPONSE OF ORTHOTROPIC PLATE WITH THERMAL STRESS AND DEFORMATION
HU Jun-yi1, LI Yue-ming1, LI Hai-bo2, CHENG Hao2
(1. State Key Laboratory for Strength and Vibration of Mechanical Structures,Shaanxi Key Laboratory of Environment and Control for Flight Vehicle, Xi’an Jiaotong University, Shaanxi 710049, China;2. Science and Technology on Reliability and Environment Engineering Laboratory,Beijing Institute of Structures and Environment Engineering, Beijing 10076, China)
Abstract:This paper focuses on the study of the natural vibration characteristics and dynamic response of an orthotropic plate under thermal environment by means of experiment and numerical calculation. The variation of natural frequency as well as the interchange of the mode shape and response under excitation during thermal environment are the key points in this research. The result shows that the thermal stresses and thermal deformation due to thermal loading will change the dynamic characteristics of an orthotropic plate. The thermal stresses and thermal deformation are of different effects on the stiffness of the plate, will result in a trend that the fundamental frequency firstly lowers and then rises, and whose slight variation leads to a mode-shape interchange of the plate. The dynamic response curve shifts to the low frequency range with temperature rising.
Key words:orthotropic plate; thermal stress; thermal deformation; mode shape; dynamic response
中图分类号:O327
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.03.0258
文章编号:1000-4750(2018)08-0218-12
收稿日期:2017-03-30;修改日期:2018-01-23
基金项目:国家自然科学基金项目(11321062)
通讯作者:李跃明(1961―),男,江苏人,教授,博士,主要从事多场结构动力学研究(E-mail: liyueming@mail.xjtu.edu.cn).
作者简介:
胡君逸(1991―),男,湖北人,硕士,主要从事结构的热声振多场数值模拟与实验研究(E-mail:1014109224@qq.com);
李海波(1975―),男,湖北人,博士,主要从事飞行器结构动力学与可靠性技术研究(E-mail:haibo_lihb@aliyun.com);
程 昊(1983―),男,河北人,博士,主要从事飞行器结构动力学与力热复合试验技术研究(E-mail:chenghao613@126.com).