其中ne为随机场单元数目。用于随机场离散的方法较多，包括中点法、局部平均法和Karhunen-Loève展开方法[18－19]，鉴于基于乔列斯基分解的中点法计算简便易编程实现[7,20]，本文采用该方法离散相关非高斯参数随机场，可将所关注的边坡区域离散为ne随机场单元，随机变量X恰好与空间坐标点存在一一对应关系。随机向量X的联合概率分布可根据参数随机场的边缘概率分布、自相关函数和互相关系数来表征[19]。蒋水华，姚 池，杨建华，姜清辉，黄劲松
(南昌大学建筑工程学院，江西，南昌 330031)
摘 要：空间变异边坡可靠度计算需要进行多次重复性边坡稳定性分析，常用的边坡稳定性分析极限平衡方法(LEM)计算效率较高而有限元方法(FEM)可捕捉真实的边坡失效机制，边坡可靠度评价中如能充分利用这两者的优势将具有重要的工程价值。该文在发展考虑参数空间变异性边坡可靠度分析的一阶可靠度方法(FORM)基础上，提出基于模型修正的空间变异边坡可靠度分析方法，引入一修正系数将基于 LEM的简化极限状态面逐渐修正为基于FEM的准确极限状态面，最后基于修正系数和LEM安全系数计算公式采用线抽样法计算边坡失效概率。通过一个考虑参数空间变异性的摩擦/粘性土坡算例验证提出方法的有效性，并探讨土体参数空间变异性和黏聚力与内摩擦角之间互相关性对边坡可靠度的影响。结果表明：提出方法的边坡可靠度计算精度与基于 FEM 子集模拟方法一致，但是计算效率远远大于后者，尤其对于低概率水平边坡可靠度问题，从而为解决考虑土体参数空间变异性的低概率水平边坡可靠度问题提供一条新的途径。
关键词：边坡可靠度；空间变异性；有限元法；一阶可靠度方法；模型修正系数
天然土体由于受到沉积、后沉积、化学风化和荷载历史等影响，即便是均质岩土体，其特性参数也呈现一定的空间变异性[1―2]。考虑岩土体参数空间变异性的边坡稳定性问题日益受到岩土工程师的关注[3―8]。考虑岩土体参数空间变异性边坡稳定可靠度评价的前提是需对空间变异边坡进行多次重复性稳定性分析计算安全系数，目前常用的边坡稳定性分析方法主要有极限平衡方法(LEM)[4―10]和有限元方法(FEM)[3,8,11―13]。LEM计算简便，计算效率高，尤其对于瑞典圆弧法(OMS)，其边坡安全系数可表示为土体参数的显式函数关系。正如Griffiths和Lane[14]所指出，虽然LEM计算效率高，但是不能有效考虑边坡变形对稳定性的影响，并需要提前假设滑动面的形状(圆弧型)和位置，这些信息在边坡稳定性分析之前一般不得而知。因此，单采用 LEM 进行边坡稳定性分析可能会造成对边坡失效机制的不准确估计，单基于LEM进行边坡可靠度分析获得的失效概率会与工程实际存在偏差[3]。与LEM相比，FEM不仅不需要提前假定滑动面的形状和位置，而且能够考虑岩土体本身的应力-应变关系，自动搜索最危险滑动面，使得应力分布更加接近工程实际，且位移的兼容性可得到满足，从而能更加准确地评价边坡稳定性[12]。因而，基于 FEM的边坡可靠度计算方法能够更真实地评价边坡可靠度，但是该方法计算量通常非常大，尤其对于低概率水平边坡可靠度问题[3,8]。在此背景下，如果能够借助某种有效方法将 LEM(计算效率高)和FEM(可捕捉真实的边坡失效机制)的优点综合利用起来，以进行考虑土体参数空间变异性的边坡可靠度评价将具有重要的工程价值。目前李典庆等[15]和Xiao等[16]基于响应调节法(Response Conditioning Method)综合利用LEM和FEM优点协同式分析空间变异边坡可靠度问题，该方法虽然在保证边坡可靠度计算精度的基础上改善了计算效率，但是对于低概率水平(Pf＜0.001)边坡可靠度问题仍然需要进行成百上千次边坡稳定性有限元分析，这对于复杂的(三维)边坡可靠度问题来说计算量仍然较大。
为此，本文在发展空间变异边坡可靠度分析的一阶可靠度方法(First Order Reliability Method，FORM)基础上，提出了基于模型修正系数方法(Model Correction Factor Method，MCFM)[17]的空间变异边坡可靠度分析方法。借助修正系数v将基于LEM理想化的极限状态面逐渐逼近为基于FEM的准确极限状态面，使得基于计算效率较高的 LEM边坡可靠度估计逐渐修正为基于 FEM 的准确边坡可靠度估计。其中修正系数是通过从FORM计算获得的验算点作为输入参数进行边坡稳定有限元分析以确定。一旦获得修正系数，便可建立修正的边坡稳定性 LEM 模型，采用线抽样法计算空间变异边坡失效概率。为验证提出方法的有效性，本文分析了一个考虑土体参数空间变异性的摩擦/粘性土坡可靠度问题。
尽管一阶可靠度方法(FORM)目前已经在边坡可靠度计算中得到了一定的应用[4,9]，但是仍很少用于分析考虑岩土体参数空间变异性的边坡可靠度问题。下面将FORM拓展用于分析考虑参数空间变异性的高维边坡可靠度问题。
岩土体参数空间变异性通常利用随机场理论来描述[18]，即将某一参数随机场离散为一组与空间坐标相关的随机变量。如果在空间同一位置处存在多个相关联的土体参数(如黏聚力和内摩擦角)，则该参数随机场称作多变量随机场。为便于数值分析，通常将参数随机场离散为一组随机向量X=(X1,其中ne为随机场单元数目。用于随机场离散的方法较多，包括中点法、局部平均法和Karhunen-Loève展开方法[18－19]，鉴于基于乔列斯基分解的中点法计算简便易编程实现[7,20]，本文采用该方法离散相关非高斯参数随机场，可将所关注的边坡区域离散为ne随机场单元，随机变量X恰好与空间坐标点存在一一对应关系。随机向量X的联合概率分布可根据参数随机场的边缘概率分布、自相关函数和互相关系数来表征[19]。
基于 LEM 边坡可靠度分析的极限状态方程可表示为：
式中：FSLEM为采用简化LEM模型计算的边坡安全系数；gLEM(·)＜0 表示边坡失稳；
为随机向量 X的实现值，n为随机变量的数目，
其中nr表示参数随机场数目。在FORM计算中，需要将随机向量X转换到独立标准正态随机向量U，U = T(X)，这一转换过程可通过以下两步实现：
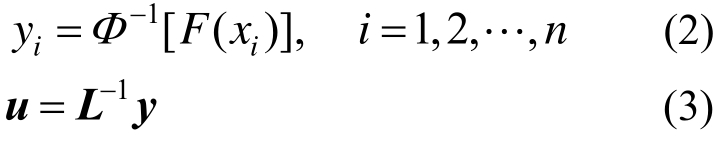
式中：y=(y1, y2,…, yn)T为相关标准正态随机向量实现值；F(·)为非高斯参数随机场边缘累积分布函数；Φ-1(·)为标准正态变量累积分布函数的逆函数。L为下三角矩阵，可通过乔列斯基分解得到：
式中R为考虑土体参数自相关性和互相关性的相关系数矩阵。假定每个土体参数都具有相同的自相关函数，R可通过式(5)构建：
式中：C为每个土体参数自相关系数矩阵；ρi,j表示第i和j个土体参数间的互相关系数。进而，独立标准正态 U空间中的极限状态方程可表示为
在基于FORM的边坡可靠度分析中，边坡失效区域是通过在验算点 u*附近进行一阶泰勒展开近似得到，其中验算点u*表示独立标准正态空间中极限状态面上概率密度最大的点，可通过求解如下有约束二阶非线性方程得到：
为了快速获得验算点u*，本文采用计算过程简便和收敛特性较好的 HLRF递归方法[21-22]求解式(6)所示非线性方程。哈弗林德和拉克维茨菲斯勒(Hasofer Lind and Rackwitz Fiessler，HLRF)递归方法是一个梯度优化方法，最早是由 Hasofer和Lind[21]提出，后来 Rackwitz和 Fiessler[22]通过Rosenblatt变换考虑了参数概率分布信息的影响。需要注意的是，在采用HLRF递归方法搜索验算点u*过程中，每一迭代步需计算极限状态函数相对于向量u的梯度向量 ∇ gLEM(u)。一旦获得验算点u*，还可获得原始X空间验算点x*=T-1(u*)以及原点到验算点之间的距离，即可靠指标β：
式中：α为独立标准正态空间参数u的敏感性因子，
进而根据可靠指标β可以近似解析计算边坡失效概率：
综上，所发展的考虑参数空间变异性边坡可靠度分析的FORM方法，无需提前单独离散参数随机场，便可有效地解决含多个相关非高斯参数随机场的边坡可靠度问题。然而，FORM方法毕竟是一阶近似方法，如果极限状态函数是输入参数的高阶非线性函数关系，FORM的计算精度值得商榷。另外基于 FORM 的边坡可靠度分析一般需要进行十几次甚至几十次迭代计算，相应地需要进行多次确定性边坡稳定性分析，即其计算效率与边坡稳定性分析计算量密切相关。本文将FORM方法与计算效率较高的 LEM 结合用于初步近似估计空间变异性边坡可靠度并搜索验算点。
最早由 Ditlevsen和Arnbjerg-Nielsen[17]提出的模型修正系数方法，能够综合利用简单模型(计算效率高)和复杂模型(计算精度高)的优点高效地计算较为准确的可靠度，已经在一些结构可靠度分析中得到了广泛应用[23－24]。MCFM 方法的关键是在概率框架下将一个较理想化的简单模型逐渐修正为计算量较大却接近工程实际的复杂模型。就边坡可靠度问题而言，可借助修正系数v(x)将计算效率较高的LEM模型逐渐修正为较真实的FEM模型，从而可将基于 FEM 边坡可靠度分析的极限状态函数表示为：
式中，FSFEM表示基于FEM计算的边坡安全系数。
一般来讲，完整求解修正系数v(x)的计算量有时甚至比基于 FEM 的直接边坡可靠度分析计算量大，为此Ditlevsen和Arnbjerg-Nielsen[17]建议首先利用简化模型进行可靠度分析获得验算点x*，再在x*附近采用零阶或一阶泰勒展开近似计算 v(x)。对于几何尺寸和土体特性相同的边坡，采用 LEM 和FEM计算的安全系数FSLEM和FSFEM之间常具有较大的相关性[15]，故本文在验算点x*附近采用零阶泰勒展开近似修正系数，即修正系数为一常数。基于MCFM 方法边坡可靠度分析的极限状态方程可表示为：
式中：
准确估计修正系数也需要进行迭代计算，第一步迭代计算中取修正系数初始值为 1.0，接着在每一迭代步中采用FORM方法对式(10)所示极限状态函数进行可靠度分析，搜索验算点
，并将所获的验算点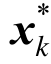
分别作为LEM和FEM模型输入参数计算边坡安全系数，进而估计修正系数
直至满足控制条件
或者
MCFM迭代计算终止，其中ε为收敛允许值，本文取ε=10-3，从中获得最终的验算点
、单位向量α和修正系数v(x*)。
在根据最终的修正系数v(x*)建立式(10)所示极限状态函数基础上，为考虑极限状态函数非线性的影响，本文提出采用线抽样法[25―27]计算边坡失效概率。值得指出的是，在 MCFM 基础上采用线抽样法计算边坡失效概率无需再进行额外的边坡稳定性有限元分析。线抽样法求解边坡失效概率的基本思想是在标准正态空间中沿重要方向(坐标原点指向验算点的方向)进行抽样，根据这些重要方向抽样获得的样本点对应的失效概率平均值来估算非线性极限状态函数的失效概率[25―27]。其中在MCFM分析中最后一轮 FORM 迭代计算的单位向量α可作为线抽样法失效概率计算的重要方向。基于线抽样法的失效概率计算中，常需通过式(11)旋转样本空间，使样本空间降低一维：
式中：V=[V0; Vn]，其中Vn表示平行于单位向量α的坐标；V0为与α垂直的超平面的样本空间；Σ为旋转矩阵，其第n+1行恰好为向量α。线抽样法计算流程如下：1)在垂直于向量α的超平面(vn=0)上随机产生Nl组V0的独立标准正态随机样本{v0k, k=1,2,…, Nl}；2)对于每组样本 v0k,，沿平行于α的方向进行线搜索，计算样本点到式(10)极限状态平面的距离dk；3)计算每个样本点对概率积分的贡献权重，其值恰好等于坐标vn处标准正态随机变量位于积分区域内的概率。由于独立标准正态分布的旋转对称性，第k组随机样本的概率为：
对Nl组随机样本对应概率取平均，便可获得边坡失效概率为：
综上，本文提出的基于模型修正的空间变异边坡可靠度分析方法共需进行两轮迭代计算，计算流程图如图1所示，主要计算步骤如下：
1)输入边坡几何信息、土体参数均值μ、变异系数 COV、分布类型和波动范围等，建立边坡稳定性模型，划分有限元单元网格和随机场单元网格。
2)根据土体参数自相关函数和互相关系数，利用式(5)构建相关系数矩阵R，并通过式(4)对R进行乔列斯基分解得到下三角矩阵L。
3)假定初始值：可靠指标β0=0，修正系数v0=1.0和验算点x0=μ。
4)根据土体参数分布类型、x0和矩阵L，利用式(2)和式(3)计算独立标准正态随机向量u。
5)将x0作为LEM模型输入参数计算边坡安全系数 FSLEM(x0)，并且估计梯度向量 ∇ gLEM(x0)和∇ gLEM(u)，再根据式(10)建立极限状态函数
6)采用 HLRF递归方法搜索新的验算点 x*和u*=T(x*)，并根据验算点 u*计算参数敏感性因子
和新的可靠指标β =αTu*。
7)判断计算结果是否满足如下控制条件：
如果满足，则提取验算点 x*；否则取 x0= x*和 β0= β，重复步骤 4)～步骤6)直至满足以上迭代收敛条件。
8)将验算点x*作为LEM和FEM模型输入参数，分别计算
获得新的修正系数
9)判断计算结果是否满足如下控制条件：|FSFEM(x*)－1.0|≤ε或者|v－v0|≤ε，如果满足，则提取修正系数v和重要方向α；否则取v0= v重复步骤4)～步骤8)直至满足以上迭代收敛条件。
10)利用最终修正系数 v建立极限状态函数gMCFM(x)=vFSLEM(x)-1.0，并根据重要方向α采用线抽样法通过式(11)～式(13)计算边坡失效概率Pf。
综上可知，提出方法的实现需要以 LEM 和FEM 协同联合计算为前提，本文直接通过MATLAB编程实现空间变异边坡稳定性的极限平衡分析，通过 MATLAB在 DOS环境下直接调用ABAQUS内核计算实现边坡稳定性的有限元分析。因篇幅所限，关于LEM和FEM的具体程序实现步骤详见文献[28]第 3章。在此基础上，通过模型修正系数方法便可将LEM和FEM的优点综合利用起来。总体来讲，提出方法程序和计算的复杂性较低、容易编程实现。
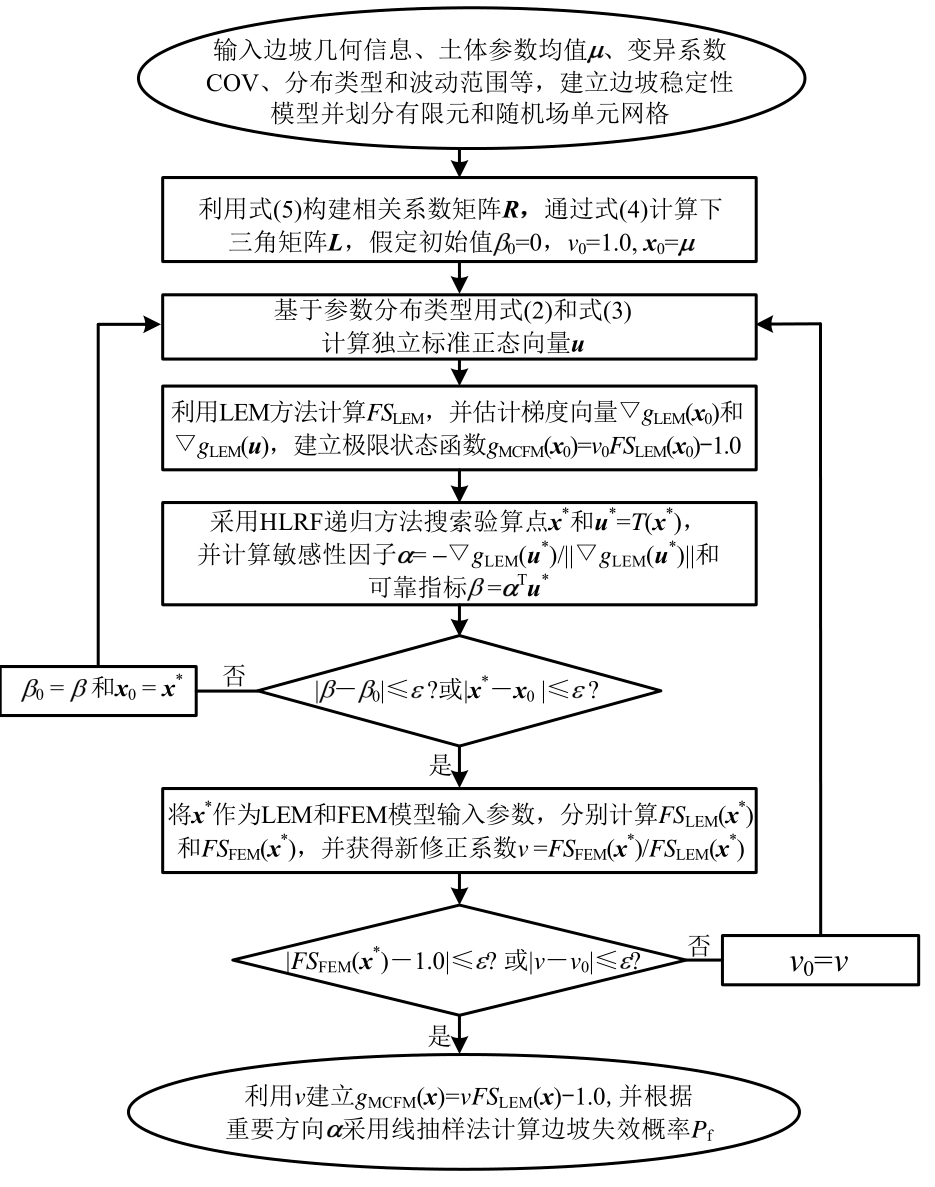
图1 基于模型修正的边坡可靠度分析方法的计算流程图
Fig.1 Flow chart of the model correction based slope reliability analysis approach
下面以文献[5―6]的均质摩擦/粘性土坡为例来验证本文提出方法的有效性，边坡计算模型如图2所示，坡高为10 m，坡度为1∶1。土体参数统计特征根据文献[5]选取，黏聚力c与内摩擦角φ均服从对数正态分布，它们的均值分别为10 kPa和30º，变异系数分别为 0.3和 0.2。土体容重γ=20 kN/m3视为确定值。取随机变量均值在 ABAQUS软件中按平面应变问题建立有限元模型，采用有限元强度折减方法分析边坡稳定性时，模型边界条件为边坡下部边界固定，左右两侧水平向约束，上部为自由边界。边坡区域共剖分了1190个边长为0.5 m的四节点四边形单元和坡面附近 20个三节点三角形单元，共有1281个节点，如图2所示。需要说明的是，所采用的有限元单元是一次单元类型，以保证边坡稳定有限元与极限平衡分析之间的一致性以及有限元网格与随机场网格之间的一致性。当然有限元单元也可拓展采用二次单元类型以提高计算精度，但是相应的计算量会明显增加。此外，采用理想弹塑性模型和Mohr-Coulomb失效准则，初始应力场采用重力加载法对边坡所有区域施加重力荷载计算得到[29]。最后边坡失稳判据较多[30]，为计算方便，本文将在给定最大迭代计算步(即在一个时间步中总的迭代步数为 500)下有限元计算不收敛作为边坡失稳判据。此外，按照Griffiths和Lane[14]的建议，取土体弹性模量E=100 MPa和泊松比ν=0.3。基于输入土体参数均值采用瑞典圆弧法和有限元法计算的边坡安全系数分别为1.15和1.174。图2还比较了由OMS获得的边坡临界滑动面和FEM计算的塑性应变云图。显然，通过极限平衡分析获得的边坡临界滑动面与有限元分析获得的边坡最大塑性应变存在一定的差别。
图2 边坡稳定性模型及计算结果
Fig.2 Slope stability model and the results
为了考虑土体参数空间变异性和 c与φ间互相关性对边坡可靠度的影响，采用相关对数随机场模拟 c与φ固有的空间变异性，基于乔列斯基分解的中点法[7]离散c与φ相关对数随机场。按照文献[5]，采用指数型自相关函数模拟抗剪强度参数空间自相关性，其中水平和垂直波动范围分别取 40 m和4.0 m；c与φ间互相关系数ρc,φ取-0.5作为基准值，并且考虑-0.7≤ρc,φ≤0进行参数敏感性分析。为了保证基于OMS和FEM的边坡稳定性分析之间的一致性，离散的随机场网格尽可能与有限元单元网格完全保持一致，如图2所示，这样共需采用n= 2420个随机变量模拟 c与φ相关对数随机场实现值。根据第3节提出方法计算流程首先采用FORM方法进行第一轮含2420个随机变量的边坡可靠度FORM迭代计算并搜索验算点x*，其中边坡安全系数采用OMS方法计算，在OMS计算中通过“剪入剪出方法”随机产生了可覆盖整个边坡可能的失稳区域的4387条圆弧潜在滑动面。接着进行第二轮 MCFM迭代计算，每个迭代步中将第一轮迭代计算获得的验算点x*作为LEM和FEM模型输入参数，分别计算安全系数 FSLEM(x*)和 FSFEM(x*)，直至修正系数满足收敛条件，从中获得最终的修正系数和重要方向α。最后，利用最终的修正系数和OMS安全系数计算公式建立极限状态函数，见式(10)，并根据重要方向α采用线抽样法计算边坡失效概率。
为了验证提出方法的有效性，同时分别采用了基于OMS和FEM的10次独立子集模拟[15,31]计算边坡失效概率，其中子集模拟每层样本数目为500，条件概率为0.1[31]。表1比较了三种方法计算的边坡失效概率Pf，失效概率变异系数 C OVPf，计算时间ts和边坡稳定性有限元分析次数NFEM。计算时间ts是指在同一配置内存为 32 GB、处理器为 Intel Xeon E5和主频为3.5 GHz的台式机上的运行时间。对于工况1，COVc=0.3和COVφ=0.2，提出方法只需要进行NFEM= 5次边坡稳定性有限元分析，获得的Pf=2.53×10-2(COVPf=10.0%)与基于FEM子集模拟方法计算的 Pf=2.4×10-2( C OVPf=14.2%)非常吻合。然而，基于 FEM 子集模拟方法所需的计算时间为29194.1 s，远远大于提出方法所需的计算时间(688.8 s)。说明提出方法能够有效综合LEM和FEM的优势准确估计考虑空间变异性的高维边坡可靠度。相比之下，基于OMS子集模拟方法明显高估了边坡失效概率，主要由于OMS方法需要提前假定边坡滑动面的形状(圆弧型)和位置。
为了进一步验证提出方法的有效性，图3给出了边坡失效概率随 c与φ间互相关系数ρc,φ的变化关系，图3中还列出了MCFM方法计算结果用于比较。需要说明的是，图3中MCFM方法表示在MCFM最后一轮迭代中采用FORM计算边坡失效概率，不借助线抽样法修正边坡失效概率。同样将基于 FEM 子集模拟方法计算结果近似视作“精确解”，由图3可知，在ρc,φ由-0.7变化到0的过程中，边坡失效概率Pf逐渐增加，提出方法计算结果与精确解基本保持一致，但是基于OMS子集模拟方法和 MCFM 方法均明显高估了边坡失效概率。进一步表明提出方法可以有效地分析考虑参数空间变异性的边坡可靠度问题。对比提出方法和MCFM方法计算结果可知，十分必要在 MCFM 分析的基础上考虑极限状态面非线性的影响，采用线抽样法计算边坡失效概率。
表1 边坡可靠度计算结果(ρc,φ=-0.5)
Table 1 Slope reliability analysis results with ρc,φ=-0.5
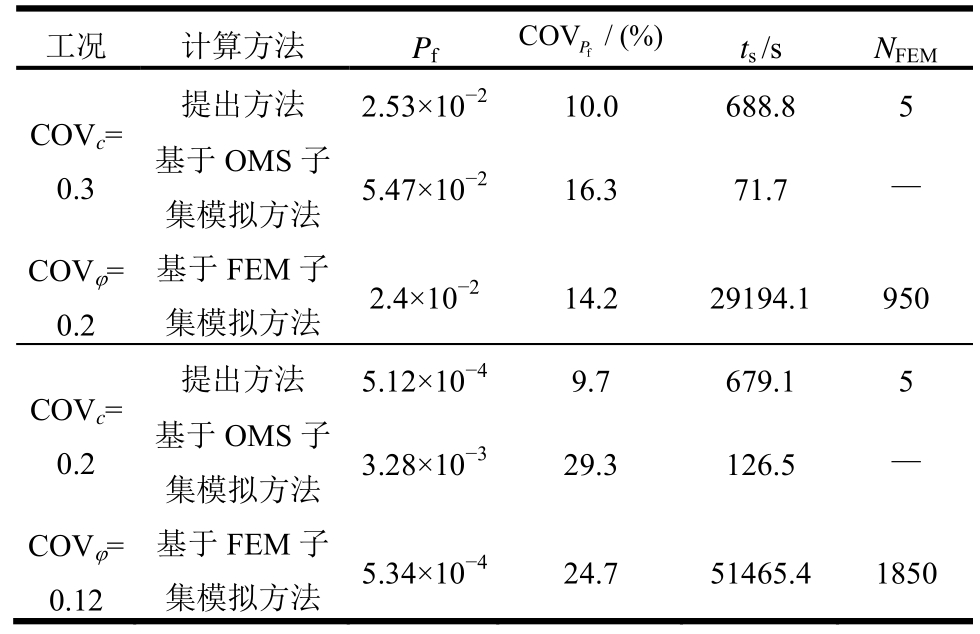
注：表中基于OMS和FEM子集模拟方法的结果是对10次独立子集模拟计算结果统计求平均得到。
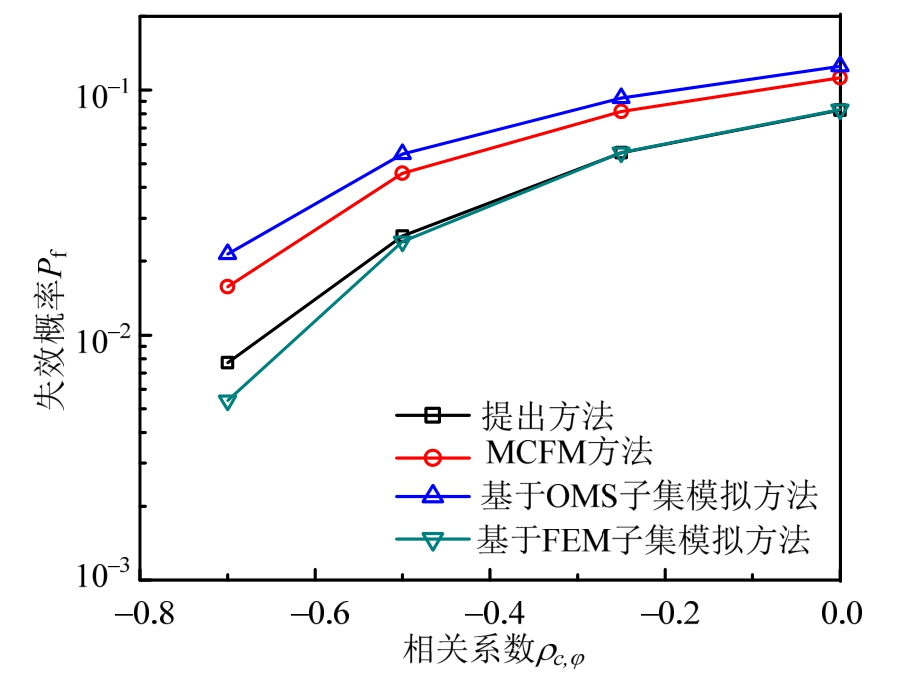
图3 边坡失效概率随黏聚力和内摩擦角间相关系数变化关系
Fig.3 Variation of probability of failure with cross-correlation coefficient between cohesion and friction angle
上面边坡可靠度分析获得的失效概率总体偏大(Pf＞0.001)，理论上来说可以采用直接蒙特卡洛模拟(Monte-Carlo Simulation，MCS)和子集模拟方法计算。相比之下，低概率水平边坡可靠度问题(Pf＜0.001)在岩土工程实际中更为常见，更受岩土工程师关注，下面分别将 COVc和 COVφ降低至 0.2和0.12，采用不同方法进行边坡可靠度分析以进一步显示提出方法的优越性。由表1工况2可知，提出方法计算的 Pf=5.12×10-4(COVPf=9.7%)仍然与精确解 Pf=5.34×10-4(COVPf=24.7%)保持一致。然而，基于 FEM 子集模拟方法获得精确解需进行NFEM=1850次边坡稳定有限元分析，共耗时51465.4 s，相比之下提出方法只需进行 NFEM=5次边坡稳定有限元分析，共耗时679.1 s，约为前者的1/76，极大地提高了计算效率。可见，相比于基于OMS子集模拟方法提出方法对计算精度的改善和相比于基于 FEM 子集模拟方法提出方法对计算效率的改善均非常明显，进一步表明提出方法能够有效地分析考虑参数空间变异性的低概率水平边坡可靠度问题。
为充分利用边坡稳定性分析极限平衡方法计算效率高和有限元方法可捕捉真实的边坡失效机制的优点，本文提出了基于模型修正的空间变异边坡可靠度分析方法，以一个考虑参数空间变异性的摩擦/粘性土坡算例验证了提出方法的有效性，并探讨了土体参数空间变异性和黏聚力与内摩擦角间互相关性对边坡可靠度的影响。主要结论如下：
(1)提出方法的边坡可靠度计算精度与基于有限元分析的子集模拟方法一致，但是计算效率却远远大于基于有限元分析的子集模拟方法，尤其对于低概率水平边坡可靠度问题(Pf＜0.001)，只需进行10次以内的边坡稳定性有限元分析，从而为解决考虑土体参数空间变异性的低概率水平边坡可靠度问题提供了一条新的途径。
(2)相比于基于有限元分析的子集模拟方法，基于瑞典条分方法的子集模拟虽然计算效率较高，但是明显高估了边坡失效概率，主要由于瑞典条分计算需要提前假定滑动面的形状(圆弧型)和位置，而有限元方法无需这些假设便可准确捕捉真实的边坡失效机制。
(3)通过对比提出方法和MCFM方法计算结果可知，在模型修正系数方法迭代计算的基础上，十分必要考虑最终极限状态面非线性的影响，采用线性抽样法重新校正边坡失效概率。
(4)提出方法的实现需要保证由LEM与FEM计算的安全系数之间具有一定的相关性，其计算精度一般随着该相关性的增大而增加。例如对于含软弱夹层的复杂边坡，由LEM与FEM计算获得的边坡最危险滑动面可能相差较大，导致相应的边坡安全系数之间的相关性较小。对于类似这样的复杂边坡，提出方法的有效性还有待进一步验证。
参考文献：
[1]Phoon K K, Kulhawy F H. Characterization of geotechnical variability [J]. Canadian Geotechnical Journal, 1999, 36(4): 612―624.
[2]张继周, 缪林昌, 王华敬. 土性参数不确定性描述方法的探讨[J]. 岩土工程学报, 2009, 31(12): 1936―1940.Zhang Jizhou, Miao Linchang, Wang Huajing. Methods for characterizing variability of soil parameters [J].Chinese Journal of Geotechnical Engineering, 2009,31(12): 1936―1940. (in Chinese)
[3]Griffiths D V, Fenton G A. Probabilistic slope stability analysis by finite elements [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(5): 507―518.
[4]Low B K, Lacasse S, Nadim F. Slope reliability analysis accounting for spatial variation [J]. Georisk, 2007, 1(4):177―189.
[5]Cho S E. Probabilistic assessment of slope stability that considers the spatial variability of soil properties [J].Journal of Geotechnical and Geoenvironmental Engineering, 2009, 136(7): 975―984.
[6]Jiang S H, Li D Q, Cao Z J, et al. Efficient system reliability analysis of slope stability in spatially variable soils using Monte Carlo simulation [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015,141(2): 04014096.
[7]蒋水华, 李典庆, 周创兵, 等. 考虑自相关函数影响边坡可靠度分析[J]. 岩土工程学报, 2014, 36(3): 508―518.Jiang Shuihua, Li Dianqing, Zhou Chuangbing, et al.Slope reliability analysis considering effect of autocorrelation functions [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 508―518. (in Chinese)
[8]Javankhoshdel S, Luo N, Bathurst R J. Probabilistic analysis of simple slopes with cohesive soil strength using RLEM and RFEM [J]. Georisk, 2017, 11(3): 231―246.
[9]Low B K, Zhang J, Tang W H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope [J]. Computers and Geotechnics, 2011, 38(2):196―204.
[10]张浮平, 曹子君, 唐小松, 等. 基于蒙特卡罗模拟的高效边坡可靠度修正方法[J]. 工程力学, 2016, 33(7):55―64.Zhang Fuping, Cao Zijun, Tang Xiaosong, et al. Efficient slope reliability updating method based on Monte Carlo simulation [J]. Journal of Engineering Mechanics, 2016,33(7): 55―64. (in Chinese)
[11]谭晓慧, 王建国. 边坡的弹塑性有限元可靠度分析[J].岩土工程学报, 2007, 29(1): 44―50.Tan Xiaohui, Wang Jianguo. Slope reliability analysis using elastoplastic finite element method [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(1): 44―50.
[12]Duncan J M. State of the art: limit equilibrium and finite-element analysis of slopes [J]. Journal of Geotechnical Engineering, 1996, 122(7): 577―596.
[13]孙玉进, 宋二祥, 杨军. 基于非线性强度准则的土工结构安全系数有限元计算[J]. 工程力学, 2016, 33(7):84―91.Sun Yujin, Song Erxiang, Yang Jun. Finite element analysis of earth structure stability with general nonlinear failure criterion [J]. Chinese Journal of Engineering Mechanics, 2016, 33(7): 84―91. (in Chinese)
[14]Griffiths D V, Lane P A. Slope stability analysis by finite elements [J]. Géotechnique, 1999, 49(3): 387―403.
[15]李典庆, 肖特, 曹子君, 等. 基于极限平衡法和有限元法的边坡协同式可靠度分析[J]. 岩土工程学报, 2016,38(6): 1004―1013.Li Dianqing, Xiao Te, Cao Zijun, et al. Auxiliary slope reliability analysis using limit equilibrium analysis and finite element analysis [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(6): 1004―1013. (in Chinese)
[16]Xiao T, Li D Q, Cao Z J, et al. Three-dimensional slope reliability and risk assessment using auxiliary random finite element method [J]. Computers and Geotechnics,2016, 79: 146―158.
[17]Ditlevsen O, Arnbjerg-Nielsen T. Model-correction-factor method in structural reliability [J]. Journal of Engineering Mechanics, 1994, 120(1): 1―10.
[18]Vanmarcke E H. Random fields: analysis and synthesis.Revised and expanded new edition [M]. Beijing: World Scientific Publishing, 2010.
[19]Li C C, Der Kiureghian A. Optimal discretization of random fields [J]. Journal of Engineering Mechanics,1993, 119(6): 1136―1154.
[20]Jiang S H, Huang J S, Yao C, et al. Quantitative risk assessment of slope failure in 2-D spatially variable soils by limit equilibrium method [J]. Applied Mathematical Modelling, 2017, 47: 710―725.
[21]Hasofer A M, Lind N C. Exact and invariant second-moment code format [J]. American Society of Civil Engineers, Journal of Engineering Mechanics,1974, 100: 111―121.
[22]Rackwitz R, Fiessler B. Structural reliability under combined random load sequences [J]. Computers and Structures, 1978, 9(5): 489―494.
[23]Franchin P, Ditlevsen O, Der Kiureghian A. Model correction factor method for reliability problems involving integrals of non-Gaussian random fields [J].Probabilistic Engineering Mechanics, 2002, 17(2): 109―122.
[24]Leander J, Al-Emrani M. Reliability-based fatigue assessment of steel bridges using LEFM–A sensitivity analysis [J]. International Journal of Fatigue, 2016, 93:82―91.
[25]Hohenbichler M, Rackwitz R. Improvement of second-order reliability estimates by importance sampling [J]. Journal of Engineering Mechanics, 1988,114(12): 2195―2199.
[26]陈磊, 吕震宙, 宋述芳. 模糊可靠性灵敏度分析的线抽样方法[J]. 工程力学, 2008, 25(7): 45―51.Chen Lei, Lü Zhenzhou, Song Shufang. Line sampling algorithm for fuzzy reliability sensitivity analysis [J].Chinese Journal of Engineering Mechanics, 2008, 25(7):45―51. (in Chinese)
[27]吕召燕, 吕震宙, 张磊刚, 等. 基于条件期望的改进线抽样方法及其应用[J]. 工程力学, 2014, 31(4): 34―39.Lü Zhaoyan, Lü Zhenzhou, Zhang Leigang, et al. An improved line sampling method and its application based on conditional expectation [J]. Chinese Journal of Engineering Mechanics, 2014, 31(4): 34―39. (in Chinese)
[28]李典庆, 蒋水华. 边坡可靠度非侵入式随机分析方法[M]. 北京: 科学出版社, 2016: 73―106.Li Dianqing, Jiang Shuihua. A non-intrusive stochastic method for slope reliability analysis [M]. Beijing:Science Press, 2016: 73―106. (in Chinese)
[29]Smith I M, Griffiths D V, Margetts L. Programming the finite element method [M]. 5th ed. Chichester, UK: John Wiley & Sons, 2014.
[30]Tu Y, Liu X, Zhong Z, et al. New criteria for defining slope failure using the strength reduction method [J].Engineering Geology, 2016, 212: 63―71.
[31]Au S K, Beck J L. Estimation of small failure probabilities in high dimensions by subset simulation [J].Probabilistic Engineering Mechanics, 2001, 16(4): 263―277.
MODEL CORRECTION FACTOR METHOD BASED APPROACH FOR RELIABILITY ANALYSIS OF SPATIALLY VARIABLE SLOPES
JIANG Shui-hua , YAO Chi , YANG Jian-hua , JIANG Qing-hui , HUANG Jin-song
(School of Civil Engineering and Architecture, Nanchang University, Nanchang, Jiangxi 330031, China)
Abstract:Reliability analysis of spatially variable slopes involves repeatedly evaluating the slope stability using a deterministic analysis method such as the limit equilibrium method (LEM) or the finite element method (FEM).The LEM is conceptually simple and computationally efficient, while the FEM tends to give a more realistic prediction of slope failure mechanism, particularly when considering the spatial variability of soil properties.Thus, it is of great interest to adopt advantages of both LEM and FEM in estimating the reliability of slope stability. This paper aims to propose a model correction factor method (MCFM) based approach for reliability analysis of spatially variable slopes. In this approach, first-order reliability method is adopted for slope reliability analysis considering spatial variation. A model correction factor is introduced to modify the idealized LEM-based limit-state surface to the more accurate FEM-based limit-state surface. Finally, a line sampling is adopted to estimate the probability of slope failure based on the corrected LEM model with the model correction factor. The reliability assessment of a cohesive-frictional slope example is studied to investigate the performance of the proposed approach considering the spatial variability of the soil strength parameters. The results indicate the proposed approach not only provides an accurate estimation of probability of failure consistent with that obtained from the FEM-based subset simulation, but also significantly reduces the number of finite element analyses of slope stability. Thus, it provides an effective and versatile tool for slope reliability analysis at low-probability levels considering the spatial variability of the soil strength parameters.
Key words:slope reliability; spatial variability; finite element method; first order reliability method; model correction factor
中图分类号：TU311；TU432
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.04.0308
文章编号：1000-4750(2018)08-0154-08
收稿日期：2017-04-25；修改日期：2017-09-22
基金项目：国家自然科学基金项目(51509125，51679117，U1765207)；江西省自然科学基金项目(20171BAB206058，20161BAB216117)
通讯作者：姜清辉(1972―)，男，江西人，教授，博士，博导，主要从事边坡渗流与稳定性分析方面的研究(E-mail: jqh1972@ncu.edu.cn).
作者简介：
蒋水华(1987―)，男，江西人，副教授，博士，主要从事岩土工程可靠度分析与风险控制研究(E-mail: sjiangaa@ncu.edu.cn);
姚 池(1986―)，男，湖北人，副教授，博士，主要从事裂隙岩体水力耦合数值模型研究(E-mail: chi.yao@ncu.edu.cn);
杨建华(1986―)，男，湖北人，副教授，博士，主要从事岩石动力学与工程爆破方面研究(E-mail: yangjianhua86@ncu.edu.cn);
黄劲松(1967―)，男，湖北人，教授，博士，主要从事岩土工程可靠度分析与风险控制研究(E-mail: jinsonghuang@ncu.edu.cn).