图1 碟簧装置试验
Fig.1 Test of disc spring device
肖水晶，徐龙河，卢 啸
(北京交通大学土木建筑工程学院，北京100044)
摘 要：为减轻混凝土剪力墙墙脚处的严重破坏，提高混凝土结构延性并控制震后残余变形，提出一种具有复位功能的钢筋混凝土剪力墙。该自复位剪力墙(SC-SW)通过两侧墙脚设置的碟簧装置提供复位力，利用墙体自身变形耗散地震能量。基于相同的几何尺寸和配筋以及相似的加载规则，建立普通钢筋混凝土剪力墙 SW1和自复位剪力墙SC-SW有限元模型，对比分析两者的承载能力，耗能能力及变形能力。结果表明，SC-SW的承载能力略高于SW1，累积滞回耗能大于SW1，并且SC-SW的延性性能相比SW1提高约40.95%。新型SC-SW墙脚处放置碟簧装置可提供必要的抗侧刚度减轻墙脚的破坏，并提供较好的复位能力，能基本消除构件的残余变形，使结构在地震后具有可恢复的功能。
关键词：新型自复位剪力墙；自复位能力；延性性能；耗能能力；残余变形
钢筋混凝土剪力墙构件是高层建筑中的主要抗侧力构件，其刚度大、承载力高，但变形能力受到了较大限制，在地震作用下墙脚处会产生较大损伤，最终导致震后结构残余变形过大而无法继续使用，甚至引起结构突然倒塌[1]。因此，提高钢筋混凝土结构的延性，减小震后残余变形，使结构震后功能可恢复非常具有研究意义和价值。
从20世纪90年代开始，基于性能的抗震设计逐渐成为了抗震研究的主流方向之一，可恢复功能结构和构件的研究也成为抗震研究的热点问题[2－3]。目前，应用于可恢复功能结构中的剪力墙大多采用摇摆和自复位结构形式，主要配合框架结构使用[4－5]。国内外学者对自复位剪力墙结构的研究取得了较多成果，吕西林等[6－7]提出可更换墙脚的概念，可使剪力墙震后功能恢复；Kurama等[8]提出了无粘结预应力自复位剪力墙，由混凝土墙片通过水平节点叠合而成，墙片内置无粘结预应力钢绞线，通过墙片与基础间缝隙张开闭合的效果，有效减小地震对结构的作用，结构的自重及预应力则提供自复位能力；Kurama等[9]还提出在结构中附加粘滞阻尼器来提高结构的非弹性耗能能力，结构通过裂缝张开时阻尼器变形来消耗地震能量；Holden等[10]在预制预应力自复位剪力墙墙肢与基础连接处增设了软钢棒消能装置，并通过试验与相同尺寸的传统现浇混凝土剪力墙的抗震性能进行了对比；Marriott等[11]出可以将预应力自复位剪力墙的耗能装置设计成外置形式，以方便震后更换；吴浩等[12]针对自复位剪力墙结构耗能不足的特点，在墙身与基础交界处增加软钢阻尼器；党像梁等[13]进行了底部水平开缝预应力自复位剪力墙的试验研究与数值模拟。
本文针对地震作用下墙脚损伤严重，延性性能和残余变形大的缺点，提出一种新型自复位钢筋混凝土剪力墙(Self-centering Shear Wall，SC-SW)，在两侧墙脚处设置碟簧装置提供复位能力，并通过墙体自身变形耗散地震能量。用 OpenSees软件对具有复位功能的SC-SW和普通混凝土剪力墙SW1进行模拟，对比分析了两者的承载能力，耗能能力及变形能力，并通过改变碟簧装置刚度分析了不同刚度对SC-SW复位能力的影响，验证了SC-SW具有良好的复位能力和延性性能，基本消除结构残余变形，可以满足震后结构功能可恢复的要求。
碟簧装置为多片无支撑面碟簧叠合与对合共同组成，碟簧叠合能提供较大的恢复力，碟簧对合能提供较大的行程。为了验证组合碟簧的复位能力，徐龙河等[14－17]对其进行了拟静力试验，试验装置如图1所示。
图1 碟簧装置试验
Fig.1 Test of disc spring device
图2给出了碟簧装置在低周往复荷载作用下的力-位移曲线。可以发现，碟簧装置具有良好的复位能力，减小甚至消除残余变形。由于各碟簧片之间及碟簧与挡板之间存在相对摩擦，在加载-卸载循环过程中碟簧装置存在少量摩擦耗能。碟簧的刚度及变形能力能够按照实际工程需要灵活设计，实现结构功能可恢复的性能需求。
图2 碟簧装置力-位移曲线
Fig.2 Force-displacement curve of disc spring device
在地震作用下钢筋混凝土剪力墙墙脚损伤较大，破坏严重。为了改善墙体的性能，本文提出在墙脚设置碟簧复位装置形成自复位钢筋混凝土剪力墙，其构造形式如图3所示。根据墙片厚度确定单片碟簧尺寸，再根据所需要提供的恢复力大小确定碟簧组合形式和碟簧数量，得到墙脚处预留高度。
按承载能力极限状态设计时，碟簧装置承受的压力Ns和拉力Nt分别按式(1)和式(2)计算：
式中：α1为混凝土应力图形系数，随混凝土强度等级的提高而减小；fc为混凝土抗压强度；fy和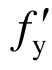
分别为受拉钢筋和受压钢筋的屈服强度；As和
分别为受拉钢筋和受压钢筋的面积；bw为墙脚洞口长度，根据碟簧的外径确定；bs为墙脚洞口宽度，即为墙肢的厚度。
图4给出了碟簧装置工作原理图，墙顶受到侧向水平荷载F作用时，墙脚一侧碟簧偏心受压，另外一侧内套碟簧钢管受拉，卸载时，预压后的碟簧可提供恢复力，协助墙体恢复到平衡位置，减小残余变形；墙顶反向加载时，工作原理同前。在墙脚两侧，碟簧装置与墙体和支座分别通过预埋件连接，墙脚端和支座端分别设有墙脚挡板和支座挡板，碟簧两端设有自由的碟簧挡板，在荷载作用下，碟簧挡板压缩碟簧变形，提供恢复力。剪力墙两侧放置碟簧装置能保护墙脚，改善普通剪力墙墙脚破坏严重的缺点。
图3 SC-SW构造图
Fig.3 Configuration of SC-SW
SC-SW的耗能机理如下：在弹性阶段，结构的变性较小；屈服阶段，结构变形增大，两侧碟簧装置分别受压和受拉，受压侧碟簧可通过碟簧摩擦耗散部分能量，受拉侧碟簧可通过内套碟簧钢管耗散能量，因此可防止墙体过早发生塑性变形而破坏，碟簧装置成为 SC-SW 的第一道防线；当结构变形很大时，墙体会发生部分塑性变形与碟簧装置共同耗散地震能量，由于碟簧装置具有较好的复位能力，可避免墙体发生严重破坏，保护墙脚，实现功能可恢复的需求。
图4 碟簧装置工作原理图
Fig.4 Operation principle of disc spring device
图5给出了由剪力墙墙体耗能和碟簧装置复位(忽略碟簧之间摩擦)叠加后的 SC-SW 理论滞回曲线模型。剪力墙墙体耗散地震能量时，塑性变形后存在很大残余变形，即使结构未倒塌也可能由于功能不可恢复而无法继续使用。附加碟簧复位装置后，碟簧压缩后提供恢复力可使墙体恢复到原来的位置，不仅避免了因墙脚破坏而使剪力墙过早退出工作，而且能减小甚至消除残余变形，使剪力墙发生塑性变形后仍能保持原有的功能。
图5 SC-SW理论滞回曲线
Fig.5 Theoretical hysteresis curve of SC-SW
普通钢筋混凝土剪力墙试件 SW1的几何尺寸参见图3，其墙体和约束边缘配筋及材料参数均见参考文献[18-19]。图6给出了试件SW1试验加载规则示意图，试件屈服后，试验采用位移控制加载，加载位移按不同位移角控制，每级加载循环2次。
在 OpenSees软件中建立试件 SW1有限元模型，定义多维混凝土材料、多维钢筋材料和分层壳截面，应用分层壳界面定义 ShellMITC4单元生成分层壳剪力墙单元[20]。边缘约束区加强钢筋通过桁架单元定义。
图6 试件SW1试验加载规则
Fig.6 Loading rules of specimen SW1
试件 SW1的裂缝分布与试验破坏形态如图7所示。加载位移较小时，在墙与基础梁连接的交界面出现水平裂缝，但试件最外侧竖向钢筋尚未屈服；随着加载位移增大，竖向受压钢筋屈服，受拉混凝土开裂，水平力-位移曲线出现比较明显的弯曲；随着加载位移继续增大，试件的水平裂缝逐渐扩展并延伸，水平裂缝发展为斜向裂缝，底部压区混凝土压碎剥落，试件的最终破坏形态为弯曲破坏以及底部混凝土压溃而丧失竖向承载力。
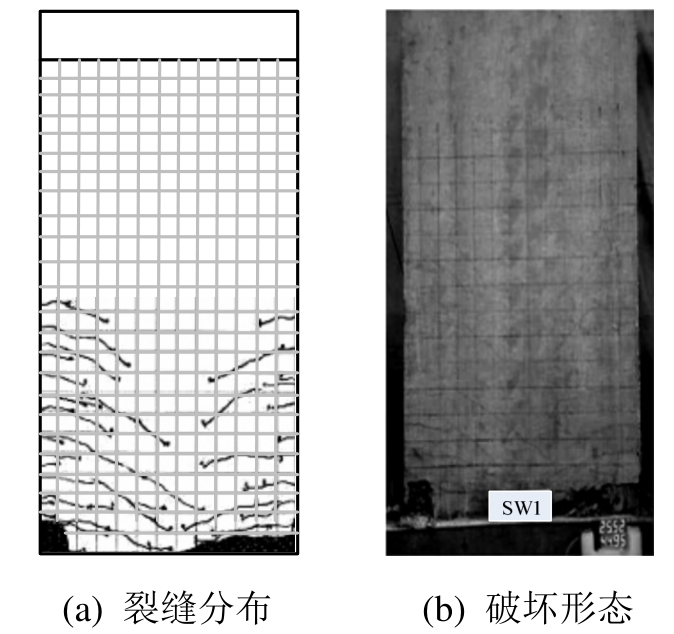
图7 SW1裂缝分布与破坏形态
Fig.7 Crack distribution and failure form of SW1
图8为试件SW1试验与模拟滞回曲线对比结果。由对比可知，正向加卸载时，模拟得到的试件屈服荷载、峰值荷载和破坏荷载均能与试验值吻合较好，误差值分别为9.23%、0.86%和10.52%；反向加卸载时，由于试验误差导致反向加卸载与正向加卸载不对称，而模拟时为理想的完全对称，因此模拟的峰值荷载与试验峰值荷载误差较大，但仍小于20%。试件正向卸载与反向卸载时的残余位移均能与试验结果吻合。因此，本文采用的模拟方法能用于分析试件 SC-SW 的力学性能，滞回性能和延性性能。
图8 试件SW1试验和模拟滞回曲线对比
Fig.8 Comparison of hysteresis curve of SW1 between simulation and tests
预留墙脚尺寸为160 mm×200 mm，其宽度根据墙厚确定，高度根据碟簧需要提供的复位能力确定。由确定的预留墙脚尺寸选择单片碟簧参数如表1所示。根据单片碟簧参数计算每侧墙脚可放置叠合碟簧共 23片，因此，每侧碟簧受轴向荷载完全压并时可提供最大恢复力为 1584 kN，刚度为480 kN/mm。受拉侧碟簧装置中，内套碟簧钢管可承受拉力，保证墙脚处抗拉承载力与SW1相同。
表1 单片碟簧参数
Table 1 Parameters of disc spring
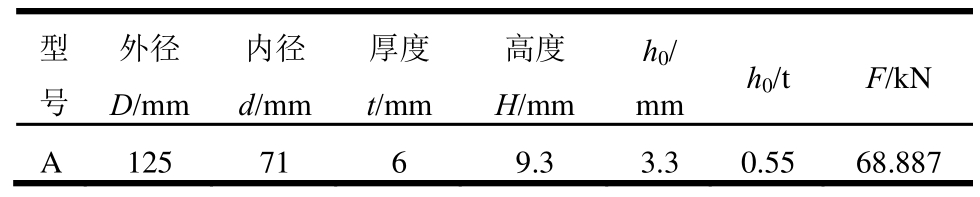
注：h0为无支承面碟簧压平时变形量的计算值；F为碟簧压平时的恢复力。
根据试验得到的碟簧特性(不考虑碟簧间的摩擦耗能)，选择OpenSees中的桁架单元模拟碟簧只受压不受拉的性能。由模拟构件 SW1得到的墙脚竖向最大承载力F′与Ns的最大值及去除预留墙脚时能达到的最大竖向位移Δ计算得到墙脚理论需要的恢复力值，即可确定碟簧刚度。按
计算得到最大数值为100 kN/mm，由于墙体在侧向荷载作用下，碟簧装置处于偏心受压状态，能提供的最大恢复力值实际低于轴向受力数值。当设置碟簧刚度为100 kN/mm时，碟簧装置侧压得到的力位移曲线如图9所示，当碟簧处于受压状态时，其力-位移曲线为线性变化，其斜率即是碟簧装置实际能提供的刚度。根据图示结果可知，碟簧侧压刚度比轴压刚度降低50%左右。因此，模拟输入碟簧刚度应比理论计算得到的轴压时刚度大，按本文预留墙脚尺寸放置碟簧装置实际能提供的最大刚度满足需求。模拟时选择实际需求刚度理论值设置，其刚度值大小设为150 kN/mm，只需选择两组7片碟簧与4片碟簧对合即可满足需求。
图9 墙脚碟簧装置侧压时力-位移曲线
Fig.9 Force-displacement curve of disc spring device in eccentric compression
在OpenSees中模拟SC-SW时，墙体配筋和材料强度及设置的参数均与模拟 SW1时一致，预留墙脚两侧放置碟簧，通过桁架单元模拟。加载规则与SW1类似，在加载至位移角为1/75后，继续加载至1/50，每级加载位移循环两次。
图10 SC-SW力-位移曲线
Fig.10 Force-displacement curve of SC-SW
图10为SC-SW力-位移曲线，其滞回环相对比较饱满。结果表明，墙脚设有碟簧复位装置的SC-SW 基本没有残余变形，加载后位移角能达到2.2%。在加载阶段，加载初期由墙体提供抗侧刚度，初始刚度较大，墙体屈服后，墙脚一侧碟簧压缩，组合后 SC-SW 刚度降低，碟簧装置很好的保护了墙脚，避免墙脚先损伤破坏，因此 SC-SW 刚度无下降趋势；卸载时，碟簧装置提供复位能力，协助墙体恢复到平衡位置，由于碟簧复位能力强，可使墙体基本保持恒定的卸载刚度恢复到平衡位置，基本消除了残余变形。
图11为SC-SW与SW1力-位移曲线对比，可以看出两者的承载能力变化。图示表明，SC-SW与SW1的屈服荷载，峰值荷载和极限荷载均差别较大，位移也差别较大，特征点处的荷载和位移对比结果如表2所示。其中，采用能量法确定屈服荷载和屈服位移，极限荷载为85%的峰值荷载，极限位移即为极限荷载对应的位移。对于SW1，因为没有明显的下降段，按位移角达到塑性限值 2%的位移作为极限位移。
图11 SC-SW与SW1力-位移曲线对比
Fig.11 Comparison of force-displacement curves of SC-SW and SW1
表2 SC-SW与SW1特征点处的荷载和位移对比
Table 2 Comparison of force and displacement at feature points of SC-SW and SW1
由表2数值对比知，SC-SW的峰值荷载略高于SW1的峰值荷载，极限位移也高于SW1的极限位移。SC-SW没有明显的下降段，位移角超过2%时，仍能继续承受荷载，对提高结构延性具有明显的优势。
图12为SC-SW与SW1在不同加载幅值下累积耗能对比，图示表明SC-SW与SW1累积耗能均随着加载位移幅值的增大而增加。当位移角达到1.5%时，普通钢筋混凝土剪力墙 SW1由于墙脚损伤严重而破坏，而 SC-SW 墙脚设置碟簧复位装置能减小墙脚部位损伤，可继续加载至位移角达到2.2%。位移角小于1.5%时，每级加载位移处SW1的累积耗能大于SC-SW，由于SC-SW损伤小，不完全通过自身塑性变形耗散能量，因此 SC-SW 的耗能能力要弱于SW1。继续加载至位移角达到2.2%时，SC-SW 耗能继续累积，最终累积耗能略大于SW1破坏时的累积耗能，因此，新型SC-SW的累积耗能相比SW1只是在同等位移下低于SW1，破坏时总的累积耗能要略高于SW1。
图12 SC-S W与SW1不同加载幅值下累积耗能对比
Fig.12 Comparison of accumulative hysteretic energy dissipation of SC-SW and SW1
图13为SC-SW与SW1在不同加载幅值下的等效粘滞阻尼比对比结果，等效粘滞阻尼比可反应构件的耗能能力，根据滞回曲线拉或者压半圈所消耗的能量与拉或压最大位移下的弹性应变能的比值计算得到。由对比结果可知，正向加卸载与反向加卸载的耗能能力基本一致，加载位移小于40 mm时，SC-SW与SW1的等效阻尼比相差很小，加载位移大于等于40 mm时，SC-SW的等效阻尼比明显小于SW1的等效阻尼比，即SC-SW的耗能能力要弱于SW1。由于加载位移小于40 mm时，SC-SW与 SW1均未产生较大的塑性变形，主要墙体自身耗散能量，因此两者耗能能力相差不大。产生较大塑性变形后，SW1通过墙体自身塑性变形耗散能量，墙脚损伤严重，残余变形较大，耗能能力没有明显下降；而 SC-SW 延性较好，能继续加载至大位移，墙体破坏不严重，但由于承载能力不断提高，残余变形很小，其弹性应变能不断增加，因此等效阻尼比下降明显。SC-SW具有很好的复位能力和延性性能，保护了墙体本身，因此在加载到较大位移时其耗能能力有所下降，但仍能满足结构需求。
图13 SC-SW与SW1等效粘滞阻尼比对比
Fig.13 Comparison of equivalent viscous damping ratio of SC-SW and SW1
为了研究不同复位能力的碟簧装置对 SC-SW的影响，本文设置了三种不同的工况进行对比，每种工况的参数设置如表3所示。
表3 不同加载工况参数设置
Table 3 Parameters of different loading cases
按相同的加载规则对不同工况下的 SC-SW 加载，三种不同工况下的滞回曲线对比结果如图14所示。图示表明，随着碟簧装置刚度的增大，SC-SW的峰值荷载增大，但 SC-SW 的残余变形随着碟簧刚度的减小而增大，三种工况下的残余位移分别为2.04 mm、6.13 mm、19.66 mm，当碟簧刚度不足以抵抗竖向荷载时，墙体残余变形很大，没法消除。由于加载初期主要由墙体承载和耗能，三种工况下刚度基本一致，加载后期随着碟簧理论刚度K的减小，组合墙体刚度降低。因此，碟簧理论刚度是影响 SC-SW 复位能力的主要原因，设置刚度时需要根据墙体的实际需求进行计算。
图14 不同工况的SC-SW力-位移曲线对比
Fig.14 Comparison of force-displacement curves of SC-SW under different cases
延性性能是评价剪力墙性能的一个重要性能指标，其数值可通过位移延性μ衡量，计算公式如下：
其中：Δu为构件的极限位移，可定义为荷载下降为85%的峰值荷载对应的位移；Δu为构件的屈服位移，可用能量法计算得到。
表4给出了SC-SW和SW1的延性性能对比结果，SC-SW的位移延性比SW1提高约40.95%。说明本文提出的新型复位剪力墙可以有效地改善剪力墙的变形能力，使混凝土剪力墙达到预期的延性需求。
表4 SC-SW与SW1位移延性对比
Table 4 Comparison of displacement ductility of SC-SW and SW1
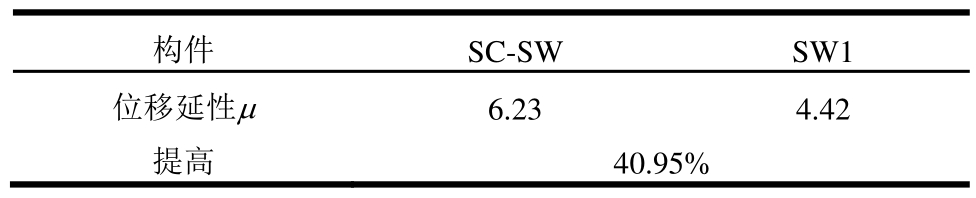
图15给出了SC-SW与SW1的残余变形对比结果。图中等效残余位移角为残余位移与构件的高度的比值。图示结果表明，SC-SW与SW1的残余位移值均随着加载位移的增大而增加。SC-SW的残余位移值要远小于 SW1的残余位移值，由等效残余位移角的数值说明 SC-SW 的残余位移相对于构件的的高度可忽略不计。因此，本文提出的新型SC-SW具有较好的延性性能，为改善结构过早进入严重破坏提供保障。
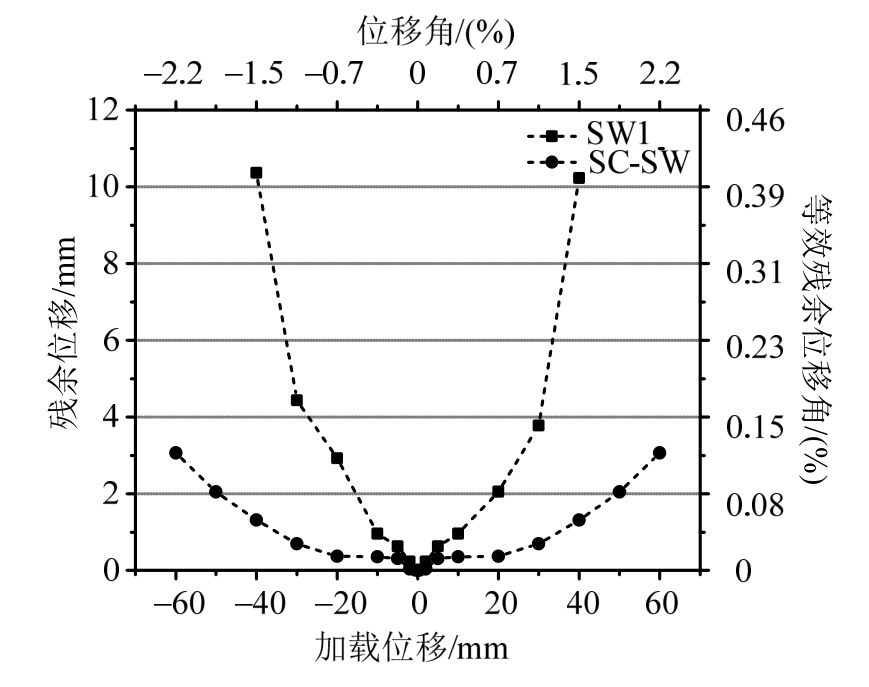
图15 SC-SW与SW1残余变形对比
Fig.15 Comparison of residual deformation of SC-SW and SW1
本文设计了一种新型自复位钢筋混凝土剪力墙，介绍了其构造和工作原理。通过有限元模拟对比分析了新型自复位墙与普通钢筋混凝土剪力墙的性能，得出了主要结论如下：
(1)试验表明，碟簧受压后可提供恢复力，减小甚至消除残余变形。在墙脚两侧设置碟簧复位装置，碟簧偏心受压，提供的刚度约为轴心受压时碟簧刚度的2/3。
(2)设置合理的碟簧刚度K，模拟得到SC-SW的滞回曲线相对饱满，随着加载位移的增大，其抗侧刚度没有明显下降，能提供较大的承载能力。碟簧刚度与理论需求刚度一致时，复位剪力墙具有良好的复位能力。
(3)与相同尺寸及配筋的钢筋混凝土剪力墙相比，SC-SW能达到普通剪力墙的承载能力和耗能能力，其延性性能提高了约40.95%，并消除了结构残余变形，使结构具有可恢复的功能。
参考文献：
[1]徐龙河, 肖水晶, 卢啸, 等. 钢筋混凝土剪力墙基于变形和滞回耗能非线性组合的损伤演化分析 [J]. 工程力学, 2017, 34(8): 117―124.Xu Longhe, Xiao Shuijing, Lu Xiao, et al. Damage evolution analysis of reinforced concrete shear wall based on nonlinear combination of deformation and hysteretic energy [J]. Engineering Mechanics, 2017,34(8): 117―124. (in Chinese)
[2]Kam W Y, Pampanin S, Palermo A, et al. Self-centering structural systems with combination of hysteretic and viscous energy dissipations [J]. Earthquake Engineering& Structural Dynamics, 2010, 39(10): 1083―1108.
[3]周颖, 吕西林. 摇摆结构及自复位结构研究综述[J].建筑结构学报, 2011, 32(9): 1―10.Zhou Ying, Lü Xilin. State-of-the-art on rocking and self-centering structures [J]. Journal of Buiding Structures, 2011, 32(9): 1―10. (in Chinese)
[4]蒋欢军, 刘其舟. 可恢复功能剪力墙结构研究进展[J].振动与冲击, 2015, 34(7): 51―58.Jiang Huanjun, Liu Qizhou. State-of-the-art of the research advances on resilient shear walls [J]. Journal of Vibration and Shock, 2015, 34(7): 51―58. (in Chinese)
[5]纪晓东, 钱稼茹. 震后功能可快速恢复联肢剪力墙研究[J]. 工程力学, 2015, 32(10): 1―8.Ji Xiaodong, Qian Jiaru. Study of earthquake-resilient coupled shear walls [J]. Engineering Mechanics, 2015,32(10): 1―8. (in Chinese)
[6]吕西林, 陈聪. 带有可更换构件的结构体系研究进展[J]. 地震工程与工程振动, 2014, 34(1): 27―36.Lü Xilin, Chen Cong. Research progress in structural systems with replaceable members [J]. Earthquake Engineering and Engineering Vibration, 2014, 34(1):27―36. (in Chinese)
[7]毛苑君, 吕西林. 带可更换墙脚构件剪力墙的低周反复加载试验[J]. 中南大学学报 (自然科学版), 2014,45(6): 2029―2040.Mao Yuanjun, Lü Xilin. Quasi-static cyclic tests of RC shear wall with replaceable foot parts [J]. Journal of Central South University (Science and Technology),2014, 45(6): 2029―2040. (in Chinese)
[8]Kurama Y, Sause R, Pessiki S, et al. Lateral load behavior and seismic design of unbonded post-tensioned precast concrete walls [J]. Structural Journal, 1999,96(4): 622―632.
[9]Kurama Y C. Unbonded post-tensioned precast concrete walls with supplemental viscous damping [J]. ACI Structural Journal, 2000, 97(4): 648―658.
[10]Holden T, Restrepo J, Mander J B. Seismic performance of precast reinforced and prestressed concrete walls [J].Journal of Structural Engineering, 2003, 129(3): 286―296.
[11]Marriott D, Pampanin S, Bull D, et al. Dynamic testing of precast, post-tensioned rocking wall systems with alternative dissipating solutions [J]. 2008, 41(2): 90―103.
[12]吴浩, 吕西林, 蒋欢军, 等. 预应力预制混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报, 2016, 37(5):208―217.Wu Hao, Lu Xilin, Jiang Huanjun, et al. Experimental study on seismic performance of prestressed precast concrete shear walls [J]. Journal of Buiding Structures,2016, 37(5): 208―217. (in Chinese)
[13]党像梁, 吕西林, 钱江, 等. 底部开水平缝预应力自复位剪力墙有限元模拟[J]. 工程力学, 2017, 34(6): 51―63.Dang Xiangliang, Lu Xilin, Qian Jiang, et al. Finite element simulation of self-centering pre-stressed shear walls with horizontal bottom slits [J]. Engineering Mechanics, 2017, 34(6): 51―63. (in Chinese)
[14]徐龙河, 樊晓伟, 逯登成, 等. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J]. 工程力学, 2016,33(10): 116―122.Xu Longhe, Fan Xiaowei, Lu Dengcheng, et al. Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation brace[J]. Engineering Mechanics, 2016, 33(10): 116―122. (in Chinese)
[15]Xu L H, Fan X W, Lu D C, et al. Hysteretic behavior studies of self-centering energy dissipation bracing system [J]. Steel and Composite Structures, 2016, 20(6):1205―1219.
[16]Xu L H, Fan X W, Li Z X. Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace [J]. Engineering Structures, 2016, 127: 49―61.
[17]Xu L H, Fan X W, Li Z X. Cyclic behavior and failure mechanism of self-centering energy dissipation braces with pre-pressed combination disc springs [J].Earthquake Engineering and Structural Dynamics, 2016,46(7): 1065―1080.
[18]钱稼茹, 江枣, 纪晓东. 高轴压比钢管混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报, 2010, 31(7):40―48.Qian Jiaru, Jiang Zao, Ji Xiaodong. Experimental study on seismic behavior of steel tube-reinforced concrete composite shear walls with high axial compressive load ratio [J]. Journal of Buiding Structures, 2010, 31(7):40―48. (in Chinese)
[19]Qian J, Jiang Z, Ji X. Behavior of steel tube-reinforced concrete composite walls subjected to high axial force and cyclic loading [J]. Engineering Structures, 2012, 36:173―184.
[20]Mazzoni S, McKenna F, Scott M H, et al. OpenSees users manual [J]. PEER, University of California,Berkeley, 2004: 131―184.
DESIGN AND BEHAVIOR STUDY ON REINFORCED CONCRETE SHEAR WALLS WITH SELF-CENTERING CAPABILITY
XIAO Shui-jing , XU Long-he , LU Xiao
(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract:An innovative reinforced concrete shear wall with self-centering capability, which can reduce serious damage at the foot parts of the wall and improve the ductility capacity and control the residual deformation of structures during earthquakes, was developed in this study. The self-centering force of the self-centering shear wall (SC-SW) was provided by the combination disc spring device installed at both sides of the wall, and the seismic energy was dissipated by the deformation of the wall. The finite element models of SC-SW and the general reinforced concrete shear wall SW1 were establilished based on the same geometric dimensions and reinforcement, as well as the similar loading rules. The bearing capacity, energy dissipation and deformation capabilities were compared between the two models. Results indicated that the innovative SC-SW exhibited better energy dissipation capability and bearing capacity, and the ductility capacity of SC-SW was increased by 40.95%compared with SW1. The innovative SC-SW with disc spring device can also provide the necessary lateral stiffness and the restoring force to reduce serious damage at the foot parts of the wall and even eliminate the residual deformation of components, so that the structure has a recoverable function after the earthquakes.
Key words:innovative self-centering shear wall; self-centering performance; ductility capacity; energy dissipation capability; residual deformation
中图分类号：TU352.1+1
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.04.0296
文章编号：1000-4750(2018)08-0130-08
收稿日期：2017-04-18；修改日期：2017-09-05
基金项目：国家自然科学基金项目(51578058，51408034)；北京市自然科学基金项目(8172038)
通讯作者：徐龙河(1976―)，男，黑龙江人，教授，博士，博导，从事结构抗震与健康监测研究(E-mail: lhxu@bjtu.edu.cn).
作者简介：
肖水晶(1991―)，女，江西人，博士生，从事高层建筑结构抗震研究(E-mail: 14121117@bjtu.edu.cn);
卢 啸(1986―)，男，湖南人，副教授，博士，从事高层建筑结构抗震研究(E-mail: luxiao1018@gmail.com).