刘亭亭1,2,于晓辉1,2,吕大刚1,2
(1.哈尔滨工业大学,结构工程灾变与控制教育部重点实验室,哈尔滨 150090;2.哈尔滨工业大学,智能防灾减灾工业和信息化部重点实验室,哈尔滨 150090)
摘 要:采用主成分分析方法,考虑多个地震动强度参数,综合分析多元地震动强度参数主成分与结构损伤之间的相关性。以单自由度体系为研究对象,使用三种恢复力模型,选择 80条真实地震动记录作为输入,分析得到体系在地震作用下的最大位移和滞回能量。采用挑选的 10个地震动强度参数,基于主成分分析方法,构造地震动强度的主成分线性组合,并对地震动强度参数主成分与结构损伤之间的相关性进行分析。结果表明:由于考虑了多个地震动强度参数,相比于单个地震动强度参数与结构损伤之间的相关性,地震动多元强度参数主成分与结构损伤之间的相关性更为稳定。
关键词:主成分分析;地震动强度参数;结构损伤;单自由度体系;相关系数
在地震工程研究中,选择合理的地震动强度参数是一个非常重要的研究课题。地震动强度参数是连接地震危险性与结构损伤的关键环节,也是量化地震动破坏势的关键参数。从不确定性分析的角度,选择与结构损伤相关性较高的地震动强度参数将有助于减小结构地震损伤预测结果的不确定性,从而通过选择较少数量的地震动记录,合理量化地震动记录的不确定性,进而减小结构地震损伤分析所需的计算资源。
近年来,国内外研究学者针对不同地震动强度参数与结构损伤之间的相关性开展了一系列研究。例如:韩建平等[1]基于汶川地震数据,对地震动强度参数与中长周期单自由度系统最大响应的相关性进行了研究。叶列平等[2]基于单自由度系统和多自由度系统,采用不同学者提出的 33个地震动强度指标,分析研究了单个地震动强度指标与主要结构地震响应之间的相关性,并对用于结构抗震分析的地震动强度指标提出了建议。Elenas和Meskouris[3]以及 Elenas[4]以一榀钢筋混凝土平面框架结构作为研究对象,对地震动峰值参数、谱参数和能量参数与结构整体损伤之间的相关性进行了研究。研究结果表明:相比于地震动峰值参数,地震动能量参数和谱参数与结构损伤之间的相关性更强。李雪红等[5]基于单自由度体系和实际减隔震桥梁结构,对地震动强度指标与结构响应之间的相关性进行了研究,并对各地震动强度指标的敏感性进行了分析。李爽等[6]分别针对近场地震动和远场地震动,对地震动参数之间的相关性以及地震动参数与结构整体损伤之间的相关性进行了研究。卢啸等[7]针对超高层建筑结构,分析了不同地震动强度指标与结构抗震设计控制指标的相关性、离散度及其随结构基本周期的变化规律。
尽管已有上述关于地震动强度参数与结构损伤之间相关性的研究成果,但值得指出的是,上述研究均针对的是单个地震动强度参数与结构损伤之间的相关性。综合不同研究结果可以发现:尚不存在唯一最优地震动强度参数,使其与结构损伤之间具有最强相关性。造成这一现象的主要原因是:对于地震作用这一复杂的事件,单个地震动强度参数无法描述所有地震特性,因此,无法全面、准确地评估地震动强度与结构损伤之间的相关性[8]。鉴于此,有必要综合考虑多个地震动强度参数,全面评估地震动强度与结构损伤之间的相关性。为实现这一研究目的,该文基于多元统计学中的主成分分析方法[9],将多个地震动基本强度参数线性组合成为一个新的地震动强度综合指标,对地震动多元强度参数综合指标与结构损伤之间的相关性进行全面研究。基于上述思路,该文以单自由度体系为研究对象,选择80条真实地震动作为输入,挑选10个与地震动加速度、速度和位移相关的强度参数作为基本参数,开展了地震动多元强度参数主成分与结构损伤的相关性分析,以期为全面、准确地了解地震动强度与结构损伤之间的相关性提供帮助。
主成分分析(Principal Component Analysis,PCA)是多元统计学中一种常用的数据降维方法[9],目的是以最少的信息丢失为前提,将众多的原有变量(或“指标”)综合成较少的几个互不相关的综合变量(称为“主成分”)。假设有 p个具有一定相关性的原有变量![]() ,希望用一组较少个数的互不相关的综合变量
,希望用一组较少个数的互不相关的综合变量![]() 代替。
代替。
设p维随机向量![]() 的协方差矩阵为
的协方差矩阵为![]() 在多元统计学中可以证明[9]:求总体主成分可以归结为求X的协方差矩阵Σ的特征值和特征向量问题。将Σ的特征值按从大到小的顺序排列为
在多元统计学中可以证明[9]:求总体主成分可以归结为求X的协方差矩阵Σ的特征值和特征向量问题。将Σ的特征值按从大到小的顺序排列为![]() ,相应的正交归一化特征向量为e1,e2,…,ep,则X的第k个主成分可表示为:
,相应的正交归一化特征向量为e1,e2,…,ep,则X的第k个主成分可表示为:
式中![]() 。此时有:
。此时有:

在实际应用中,通常选取m<p,选取原则是前m个主成分的累积贡献率达到85%的比例,其表达式如下:

式中,第k个主成分Yk的方差贡献率为:
在实际问题中,总体X的协方差矩阵通常是未知的,需要用样本观测数据进行估计。
该文选取 80个地震动记录,基于主成分分析构造地震动强度参数的主成分线性组合,然后利用三种滞回材料建立的 4个单自由度体系(SDOF)作为研究对象,得到结构的2个损伤指标,综合分析多元地震动强度参数主成分与结构损伤之间的相关性研究,其基本流程如图1所示。

图1 基本流程图
Fig.1 The basic flow chart
该文选择最简单的SDOF体系以及最基本的地震动强度参数作为载体,有助于获得地震动多元强度与结构损伤之间相关性的更为一般性的结论。通过Pearson相关系数、Spearman相关系数、Kendall相关系数来度量两者的相关性大小,并且为了避免研究结果的特殊性,通过改变单自由度体系的模型特性以及强度折减系数,研究结构模型参数对地震动多元强度与结构损伤之间相关性的影响。然后对比多元地震动强度参数主成分、单个地震动强度参数和结构损伤的相关性,虽然采用多元地震动强度与结构损伤之间的相关性,要比传统的单地震动强度与结构损伤之间相关性分析过程复杂,但由于主成分分析的方法本身并不复杂,且相比于有限元分析所耗费的计算资源几乎可以忽略不计。
鉴于该文研究所采用的结构体系为具有不同周期的单自由度结构,采用文献[10]中提供的地震动集合有利于获得更为一般性的结果。选择文献[10]附录A中的set#1B地震动集合作为地震动输入。该地震动集合包含有40组两方向地震动记录,共计获得80条地震动记录。该地震动记录不针对具体结构和具体场地,因此具有较好的适用性和实用性,广泛应用于其后的相关研究中[11―13]。详细地震动记录列表及地震动挑选过程可参见文献[10],在此不作赘述,仅给出地震动的反应谱,如图2所示。

图2 所选地震动的反应谱
Fig.2 Response spectra of the selected ground motions
选择 OpenSees平台进行单自由度体系的建模和非线性时程分析。分别采用理想弹塑性模型、双线性模型和滞回模型作为单自由度体系的恢复力模型。图3给出了上述三种恢复力模型所对应OpenSees中的材料。
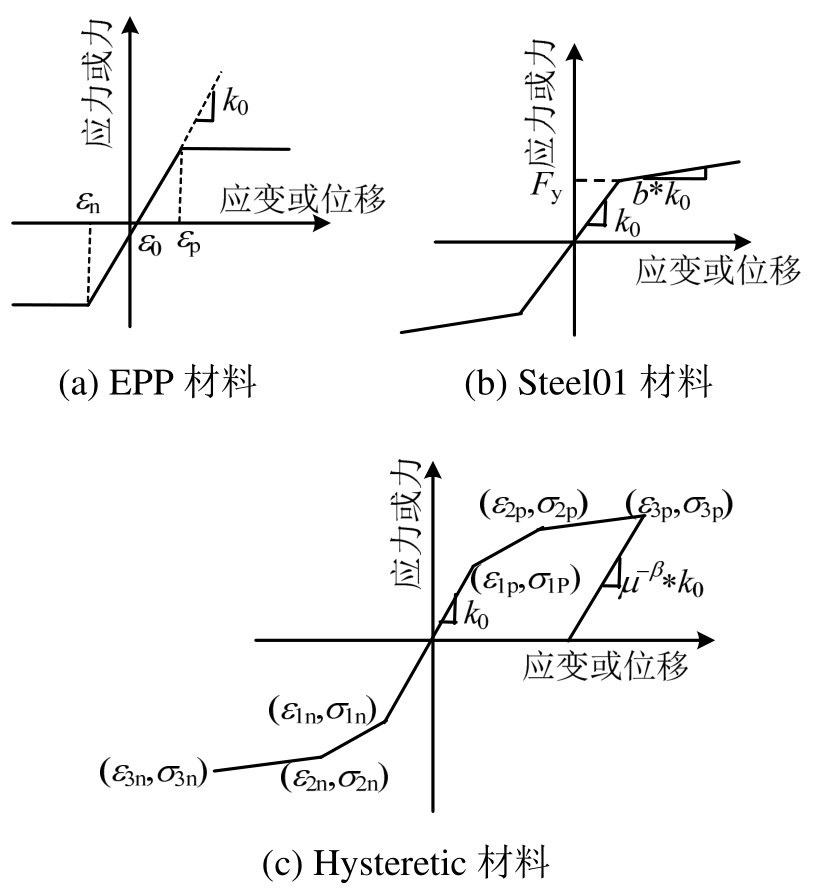
图3 基于OpenSees的单自由度体系建模
Fig.3 SDOF models based on OpenSees
表1对上述三种材料在OpenSees中的控制参数进行了说明。根据退化和捏缩特性控制参数的不同,将 Hysteretic材料分成考虑捏缩效应和不考虑捏缩效应对应的两种滞回模型。为方便以后应用,将上述三种材料对应的四种单自由度模型分别简称为模型 1~模型 4(见表1)。假定单自由度体系的阻尼比为5%,周期T范围为:T=0.1 s~6.0 s,在此范围内选取25个结构周期。
考虑不同强度折减系数 R=2~5确定单自由度体系屈服强度的影响,其中R定义为:
式中:Fe为地震作用下结构保持线弹性的强度;Fy为结构的屈服强度。
表1 SDOF体系模型编号和所对应的OpenSees材料特性
Table 1 Number of SDOF models and the corresponding material characteristics in the OpenSees flatform

该文采用 Newmark线性加速度法进行非线性时程分析,选取地震作用下结构的最大位移反应um ax和结构在地震作用下的累积滞回能量EH作为结构损伤指标。其中滞回能量的表达式如下:
式中:F(u)为滞回恢复力时程;ü(t)为地震动速度时程;m为结构体系的质量。
根据文献[14]的分类方法,将地震动强度参数划分为加速度相关参数、速度相关参数和位移相关参数。其中,加速度相关参数与短周期(加速度敏感区)结构相关性较强,速度相关参数与中长周期(速度敏感区)结构相关性较强,位移相关参数与长周期(位移敏感区)结构相关性较强。选择文献[14]中的23个地震动强度参数作为基本参数。其中,加速度相关、速度相关和位移相关的地震动强度参数定义见表2。其中,Tf表示地震动总持时;![]() 表示重要持时;t95和t5分别表示 95%和 5%的 Arias强度所对应的时间。
表示重要持时;t95和t5分别表示 95%和 5%的 Arias强度所对应的时间。
表2 所选地震动强度参数
Table 2 The selected ground motions intensity measures
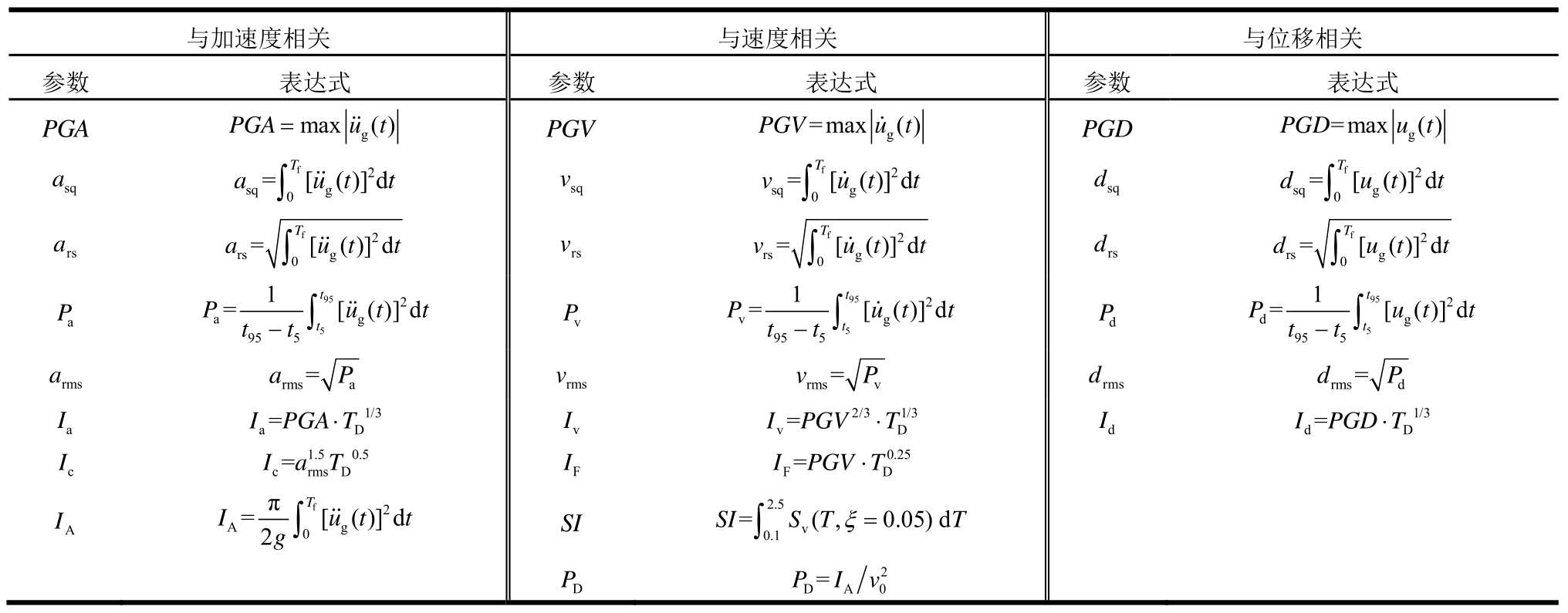
由于所挑选的地震动强度参数存在不同参数表达式相近的情况,会造成主成分分析的共线性问题[15]。因此,不能为了避免遗漏信息而选取过多重叠信息的变量,而应对所挑选地震动强度参数进行有效筛选。具体来说,ars、vrs、drs分别和asq、vsq、ds q在表达式上只相差一个指数;arms、vrms、drms分别与 Pa、Pv、Pd在表达式上也只相差一个指数;asq和IA在表达式上只相差一个常数;Ic、Ia、IF、Iv、Id在对数坐标系下是重要持时和其他地震动强度参数的线性组合。此外,主成分分析一般要求原始变量的相关系数在0.3以上。综上,该文选择10个地震动强度参数作为主成分分析的原始变量,即
采用4.1节中的10个地震动强度参数作为基本变量,利用主成分分析方法构造地震动多元强度参数主成分,其综合考虑了多个地震动强度的影响,更全面地考虑地震动本身的特性,使得其与结构损伤之间相关性的评估结果更为客观。按照主成分分析的基本原理,计算 80条地震动的样本协方差矩阵Σ和特征矩阵e如下所示,特征向量对应的特征值如图4所示。
从图4可以看出,第四个及第五个特征值变化的趋势已经开始趋于平稳。为了保留地震动强度参数的更多信息,该文提取前五个主成分进行分析。


图4 不同主成分的特征值
Fig.4 Eigen values of different principal components
前五个主成分的方差贡献率分别为:79.4%、13.2%、3.5%、1.6%、1.1%,上述五个主成分的累积贡献率为98.8%。这一结果表明:选取前五个主成分几乎可以完全解释所选地震动强度指标的方差。进一步将所挑选的前五个主成分进行线性组合,以每个主成分的方差贡献率作为权重,构造一个新的综合强度指标:
并将其作为分析相关性的地震动多元参数的主成分计算值。
该文采用三种相关系数来度量地震动强度与结构损伤之间的相关性,包括:Pearson相关系数[16]、Spearman相关系数[17]以及Kendall相关系数[18]。其中,Pearson相关系数用来衡量变量之间线性相关性,但其无法描述变量间非线性相关性。Spearman相关系数为秩相关系数,用来衡量两个变量间是否单调相关,可以描述变量间非线性相关关系。Kendall相关系数是衡量等级变量相关程度的一个统计量,根据两个变量间序对的一致性来判断其相关性。
上述三个相关系数的取值都在−1和 1之间。Pearson相关系数为1时,表示两个变量成正线性相关;Pearson相关系数为−1时,表示两个变量负线性相关;当Pearson相关系数取值为0时,表示两个变量不存在线性相关关系。Spearman相关系数为1时,表示两个变量严格单调递增;Spearman相关系数为−1时,表示两个变量严格单调递减;当Spearman相关系数取值为0时,表示两个变量不存在单调相关关系。当Kendall相关系数为1时,表示两个变量有一致的等级相关性;当Kendall相关系数为为−1时,表示两个变量有完全相反的等级相关性;当Kendall相关系数取值为0时,表示两个变量是相互独立的。
鉴于地震动强度与结构损伤近似服从对数线性关系[19],为此,该文首先对地震动强度参数和结构损伤参数进行对数变换。Pearson相关系数、Spearman相关系数以及Kendall相关系数的计算公式为:

式中:i为地震动编号;N为地震动样本容量;ln I MP CA,i为第i条地震动多元强度参数主成分计算值;lnDMi为第i条地震动引起结构损伤的对数值;![]() 和
和![]() 分别为 ln I MP CA,i和ln D Mi的平均值; Pi和Qi分别为 ln I MP CA,i和ln D Mi的秩次;sgn(·)为符号函数。
分别为 ln I MP CA,i和ln D Mi的平均值; Pi和Qi分别为 ln I MP CA,i和ln D Mi的秩次;sgn(·)为符号函数。
该文采用最大位移 umax和滞回能量 EH作为结构损伤参数。采用第2节中所挑选的地震动记录作为输入,对模型1~模型4进行时程分析,获得结构损伤的分析结果。仅选取对应加速度敏感区(T=0.2 s)、速度敏感区(T=1.0 s)和位移敏感区(T=5.0 s)三个结构周期,以模型 1为例,在折减系数R=2条件下,获得地震动多元强度参数主成分与结构损伤之间的相互关系,如图5所示。

图5 地震动多元强度参数主成分与结构损伤的散点图
Fig.5 Scatter plots of principal components of multivariate earthquake intensity measures and structural damage
以折减系数R=2所对应的模型分析结果为例,进一步采用Pearson相关系数、Spearman相关系数以及Kendall相关系数,对地震动多元强度参数主成分与结构损伤之间相关性进行分析,分别给出模型1~模型4对应的基于主成分地震动强度参数与以um ax为参数的结构损伤之间的相关系数分析结果,如图6所示。由图可见,针对不同结构模型,采用不同的相关系数,地震动多元强度参数主成分与结构损伤之间的相关系数均随着结构周期的增加而增加。其中,在T<1 s时,相关系数上升较快,而T>1 s之后相关系数趋于平缓。将Pearson相关系数、Spearman相关系数以及Kendall相关系数的分析结果对比,可以发现:模型1~模型4对应的Pearson相关系数最大,Spearman相关系数次之,Kendall相关系数最小。此外,针对不同结构模型的Pearson相关系数和Spearman相关系数分析结果都在0.5以上,表明:地震动多元强度参数主成分与umax之间存在较强的相关性。

图6 地震动多元强度参数主成分和ln umax的相关系数
Fig.6 Correlation coefficients between principal components of multivariate earthquake intensity measures and ln umax
图7(a)~图7(d)分别给出了模型1~模型4的地震动多元强度参数主成分与以 EH为参数的结构损伤之间的相关系数分析结果。由图可见,地震动多元强度参数主成分与 EH之间的相关系数均随着结构周期的增加而增加,且在T<1 s时,相关系数上升较快,而T>1 s之后相关系数趋于平缓。此外,Pearson相关系数最大,Spearman相关系数次之,Kendall相关系数最小,且 Pearson相关系数和Spearman相关系数分析结果都在0.5以上,表明:地震动多元强度参数主成分与 EH之间也存在较强的相关性。

图7 地震动多元强度参数主成分和ln EH的相关系数
Fig.7 Correlation coefficients between principal components of multivariate earthquake intensity measures and ln EH
对比图6和图7可见,无论采用umax或EH作为结构损伤参数,由于考虑多个地震动强度参数的影响,使得地震动强度参数主成分与结构损伤的相关系数随时间增加而增加,且在T<1 s时,相关系数上升较快,而T>1 s之后相关系数趋于平缓。为此将在后续的研究中,以多自由度体系为研究对象,通过开展广泛的有限元分析,对多元地震动强度与结构损伤之间的相关性进行进一步的评价和验证。
为更好理解地震动多元强度参数主成分与结构损伤之间的相关性,本文仅以 PGA、PGV、dsq为例,给出了基于单个地震动强度参数与以 EH为参数的结构损伤之间的Pearson相关系数分析结果并作对比(如图8所示)。由图可见,PGA在加速度敏感区(T=0~0.5 s)与EH的Pearson相关系数最大,然后逐渐减小;PGV在速度敏感区(T=0.5 s~3.0 s)与EH的Pearson相关系数达到峰值,然后逐渐减小;dsq与EH的Pearson相关系数随周期的增大而增大,在位移敏感区(T>3.0 s)达到峰值。上述分析结果与文献[5]的研究结果一致,表明:单个地震动强度参数与结构损伤的相关性会在不同结构周期范围内发生较大变化。对比图7和图8可见,地震动多元强度参数主成分与结构损伤之间的相关性在 T>1 s后趋于稳定,这也体现了采用多个地震动强度参数可以更加全面地考虑地震动的信息,从而与结构损伤建立更为稳定的相互关系。

图8 单一地震动强度参数与ln EH的Pearson相关系数
Fig.8 Pearson correlation coefficient between a single earthquake intensity measure and ln EH
为了研究模型参数对相关系数的影响,图9(a)给出了模型1~模型4在R=2条件下,基于主成分的地震动强度与EH的Pearson相关系数。图9(b)给出了模型4在R=2~5条件下,地震动多元强度参数主成分与EH的Pearson相关系数。

图9 模型参数对相关性结果的影响
Fig.9 Effects of model parameters on correlation results
由图9(a)可以发现,采用不同结构模型分析得到的相关系数较为接近。由图9(b)可以发现,不同折减系数对相关系数的影响也并不明显。综合图9可以得到结论:模型参数对地震动多元强度参数主成分与结构损伤之间的相关性影响不大。
基于多元统计学中的主成分分析方法,以单自由度体系作为研究对象,挑选 80条真实地震动作为输入,采用10个地震动强度参数作为原始变量,分别以最大变形umax和滞回能量EH作为结构损伤参数,对地震动多元强度参数主成分与结构损伤之间的相关性进行研究,主要结论如下:
(1)地震动多元强度参数主成分与结构损伤之间的Pearson相关系数最大、Spearman相关系数次之、Kendall相关系数最小。
(2)模型参数对地震动多元强度参数主成分与结构损伤之间的相关性影响较小。采用不同折减系数使相关性相差不大,并且采用不同模型也使相关性相差不大。
(3)地震动多元强度参数主成分与结构损伤之间相关系数在 T=1.0 s之前的结构周期范围内增加幅度较大,其后的增加幅度很小。而单个地震动强度与结构损伤之间的相关性则随着结构周期的变化而发生较大变化。这说明由于考虑了多个地震动强度参数,地震动多元强度参数主成分与结构损伤之间的相关性更为稳定。
参考文献:
[1]韩建平, 周伟, 李慧. 基于汶川地震数据的地震动强度指标与中长周期 SDOF 体系最大响应相关性[J].工程力学, 2011, 28(10): 185―196.Han Jianping, Zhou Wei, Li Hui. Correlation between ground motion intensity indices and SDOF system responses with medium-to-long period based on the wenchuan earthquake data [J]. Engineering Mechanics,2011, 28(10): 185―196. (in Chinese)
[2]叶列平, 马千里, 缪志伟. 结构抗震分析用地震动强度指标的研究[J]. 地震工程与工程振动, 2009, 29(4):9―22.Ye Lieping, Ma Qianli, Miu Zhiwei. Study on earthquake intensities for seismic analysis of structures [J]. Journal of Earthquake Engineering and Engineering Vibration,2009, 29(4): 9―22. (in Chinese)
[3]Elenas A, Meskouris K. Correlation study between seismic acceleration parameters and damage indices of structures [J]. Engineering Structures, 2001, 23(6): 698―704.
[4]Elenas A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings [J]. Soil Dynamics and Earthquake Engineering, 2000, 20(1): 93―100.
[5]李雪红, 李晔暄, 吴迪, 等. 地震动强度指标与结构地震响应的相关性研究[J]. 振动与冲击, 2014, 33(23):184―189.Li Xuehong, Li Yexuan, Wu Di, et al. Correlation between ground motion intensity and structural seismic response [J]. Journal of Vibration and Shock, 2014,33(23): 184―189. (in Chinese)
[6]李爽, 谢礼立, 郝敏. 地震动参数及结构整体破坏相关性研究[J]. 哈尔滨工业大学学报, 2007, 39(4): 505―509.Li Shuang, Xie Lili, Hao Min. Correlation between seismic ground motion parameters and their relationship with overall damage to structure [J]. Journal of Harbin Institute of Technology, 2007, 39(4): 505―509. (in Chinese)
[7]卢啸, 陆新征, 叶列平. 超高层建筑地震动强度指标探讨[J]. 土木工程学报, 2012, 45: 292―296.Lu Xiao, Lu Xinzheng, Ye Lieping. Discussion on the ground motion intensity measures for super high-rise buildings [J]. China Civil Engineering Journal, 2012, 45:292―296. (in Chinese)
[8]Housner G W, Jennings P C. The capacity of extreme earthquake motions to damage structures [J]. Structural and Geotechnical Mechanics, 1977: 102―116.
[9]Jolliffe I T. Principal Component Analysis [M]. New York: Springer-Verlag,1986.
[10]Baker J W, Lin T, Shahi S K, et al. New ground motion selection procedures and selected motions for the PEER transportation research program [R]. Peer Report 2011, 3.
[11]Ramanathan K, Padgett J E, DesRoches R. Temporal evolution of seismic fragility curves for concrete box-girder bridges in California [J]. Engineering Structures, 2015, 97: 29―46.
[12]Konstantinidis D, Nikfar F. Seismic response of sliding equipment and contents in base-isolated buildings subjected to broadband ground motions [J]. Earthquake Engineering & Structural Dynamics, 2015, 44(6): 865―887.
[13]Wang Z, Dueñas-Osorio L, Padgett J E. Influence of scour effects on the seismic response of reinforced concrete bridges [J]. Engineering Structures, 2014, 76:202―214.
[14]Riddell R. On ground motion intensity indices [J].Earthquake Spectra, 2007, 23(1): 147―173.
[15]Narasimhan S, Wang M, Pandey M. Principal component analysis for predicting the response of nonlinear base-isolated buildings [J]. Earthquake Spectra, 2009,25(1): 93―115.
[16]Pearson K. Notes on the history of correlation [J].Biometrika, 1920, 13(1): 25―45.
[17]Croux C, Dehon C. Influence functions of the Spearman and Kendall correlation measures [J]. Statistical Methods& Applications, 2010, 19(4): 497―515.
[18]Kendall M G. A new measure of rank correlation [J].Biometrika, 1938, 30(1/2): 81―93.
[19]于晓辉, 吕大刚, 王光远. 关于概率地震需求模型的讨论[J]. 工程力学, 2013, 30(8): 172―179.Yu Xiaohui, Lü Dagang, Wang Guangyuan. Discussions on probabilistic seismic demand models [J]. Engineering Mechanics, 2013, 30(8): 172―179. (in Chinese)
ANALYSIS OF CORRELATION BETWEEN PRINCIPAL COMPONENTS OF MULTIVARIATE EARTHQUAKE INTENSITY MEASURES AND STRUCTURAL DAMAGE
LIU Ting-ting1,2, YU Xiao-hui1,2, LÜ Da-gang1,2
(1. Key Lab of Structures Dynamic Behavior and Control of China Ministry of Education, Harbin Institute of Technology, Harbin 150090, China;2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of the Ministry of Industry and Information Technology,Harbin Institute of Technology, Harbin 150090, China)
Abstract:The correlation between multivariate earthquake intensity measures and structural damage was comprehensively studied by incorporating multiple earthquake intensity measures and adopting the principal component analysis method. The single degree of freedom systems were used as the study objects, which were defined by three kinds of constitutive models. A set of 80 real ground motion records were selected as the inputs,and the structural responses in terms of maximum displacement and hysteretic energy were calculated. Ten earthquake intensity measures were selected, and the principal component analysis method was adopted to construct the principal linear combination of the earthquake intensity measures. Then the correlation between the principal components of multivariate earthquake intensity measures and the structural damage was studied. The results show that, compared with the correlation between a single earthquake intensity measure and structural damage, the correlation between the principal components of earthquake intensity measures and the structural damage is more stable since it considers multiple earthquake intensity measures.
Key words:principal component analysis; earthquake intensity measures; structural damage; single degree of freedom system; correlation coefficient
中图分类号:P315.9
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.04.0289
文章编号:1000-4750(2018)08-0122-08
收稿日期:2017-04-14;修改日期:2017-06-18
基金项目:国家自然科学基金项目(51678209,51408155,51378162);国家科技支撑计划课题项目(2013BAJ08B01)
通讯作者:吕大刚(1970―),男,黑龙江人,教授,博士,博导,副院长,主要从事结构可靠度、地震工程等研究(E-mail: ludagang@hit.edu.cn).
作者简介:
刘亭亭(1987―),女,黑龙江人,博士生,主要从事地震易损性和地震危险性研究(E-mail: liutingtinghit@163.com);
于晓辉(1982―),男,辽宁人,副研究员,博士,硕导,主要从事地震易损性和概率风险分析研究(E-mail: yxhhit@126.com).