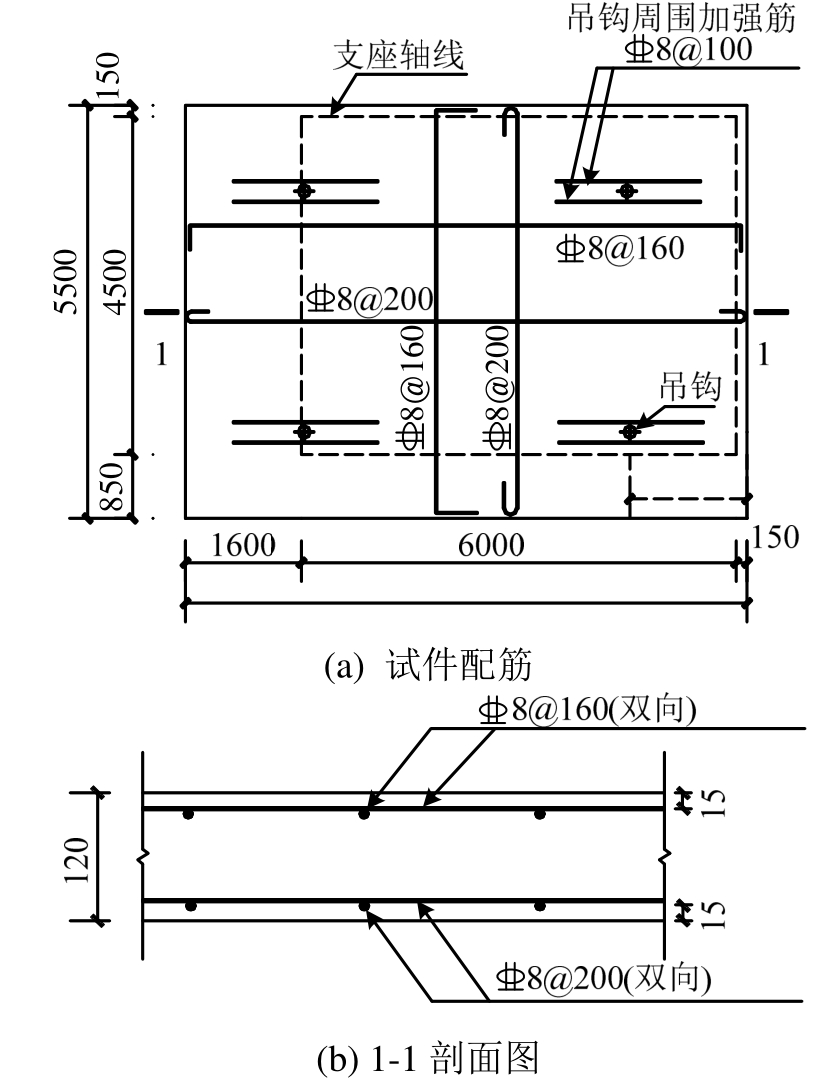
图1 试件尺寸及配筋
Fig.1 Dimension and reinforcement arrangement of specimen
朱崇绩1,董毓利2
(1.济南大学土木建筑学院,山东,济南 250022;2.华侨大学土木工程学院,福建,厦门 361021)
摘 要:对2个足尺邻边简支邻边固支钢筋混凝土双向板试件进行了抗火试验,介绍了试验炉及试件设计、试验方案及观测内容和方法,描述了试验现象、裂缝及邻边简支邻边固支钢筋混凝土双向板的破坏特征,研究了受火过程中沿板厚度的温度场分布规律及板的竖向和水平变形,分析了受火过程中固支边的内力重分布;试验结果表明,未受火面裂缝最终形成半椭圆形破坏模式。在试验基础上,给出了火灾作用下邻边简支邻边固支钢筋混凝土双向板极限承载力的新能量法计算模型,该模型假定火灾作用下板的张拉薄膜效应在塑性铰线形成后出现,且张拉薄膜效应为塑性铰线上屈服钢筋伸长所做塑性功提供。该模型计算结果与试验结果吻合很好,而基于塑性铰线理论的传统能量法计算值偏保守。
关键词:双向板;邻边简支邻边固支;半椭圆形破坏模式;极限承载力;能量法;塑性铰线理论
火灾作用下钢筋和混凝土的材料力学性能随温度升高不断劣化、钢筋与混凝土之间的粘结强度随温度升高不断降低以及在混凝土板内沿板厚度产生不均匀温度场[1-4]等,这些因素导致钢筋混凝土板在火灾作用下承载力随温度升高而不断降低,甚至引起板失效。1995年~1996年试验结果被广泛发表的Cardington火灾试验说明火灾作用下整体结构中钢筋混凝土组合楼板具有非常显著的薄膜效应,这一现象引起了国内外学者的极大关注[5―10]。
国内外对钢筋混凝土板在火灾作用下力学行为及其薄膜效应进行了大量的试验及理论研究。Bailey[11―12]对 48个水平方向没有约束的缩尺钢筋混凝土板试件进行了常温静力试验和恒载升温试验,通过试验指出常温下板的静力破坏形式包括钢筋拉断和角部混凝土压碎,且具体破坏形式与配筋率有密切关系;高温作用下钢筋混凝土板的破坏形式主要为钢筋拉断,配筋率增大时有可能发生角部混凝土的压碎破坏。Lim等[13]利用BRANZ耐火试验炉进行了3个足尺钢筋混凝土简支双向板试件的抗火试验,试验对板的四个角部进行了约束,而水平方向没有进行约束。试验表明:板的竖向位移达到270 mm(短跨的1/12)时并没有出现坍塌现象,其耐火极限远高于按屈服线理论计算的结果[14]。西安建筑科技大学的王滨[15―16]对四边简支和四边固支2种形式的钢筋混凝土双向板进行了抗火试验,给出了各种形式板火灾作用下的破坏模式。目前,钢筋混凝土板在火灾作用下的薄膜效应和极限承载力的计算主要有Bailey等[17]提出的和Usmani等[18―19]提出的2种方法,这2种方法的不同在于Bailey提出的方法假设钢筋混凝土板没有水平约束,而Usmani提出的方法则假设钢筋混凝土板的水平方向完全被约束;这2种方法的缺点是假设过多、物理意义不明确、与传统塑性铰线理论不统一且计算复杂。本文在对四边简支双向板[15]、四边固支双向板[16]及平板无梁楼盖[1]等进行试验及理论研究的基础上,对足尺邻边简支邻边固支双向板的抗火性能进行了试验研究,并提出了基于传统塑性铰线理论的火灾作用下邻边简支邻边固支双向板极限承载力的能量计算方法。
试验共设计2个钢筋混凝土邻边简支邻边固支双向板试件TL1和TL2,且2个试件的参数设置相同。试件轴线尺寸为4500 mm×6000 mm,板厚为120 mm。考虑板的搁置长度及火灾作用下板的竖向变形引起的板简支边滑动,将板的2相邻简支边各沿轴线外伸 150 mm;考虑固支边的嵌固及反力架的位置,将长固支边沿短跨方向向外延伸了850 mm,短固支边沿长跨方向向外延伸了1600 mm,试件的最终尺寸为 5500 mm×7750 mm×120 mm,试件尺寸及配筋见图1。试件TL1和TL2同时制作,同一批钢筋的屈服强度为384 MPa,极限抗拉强度为535 MPa。

图1 试件尺寸及配筋
Fig.1 Dimension and reinforcement arrangement of specimen
试件采用C30商品混凝土浇筑,试件TL1养护38d,试验时与试件同等条件养护的标准混凝土立方体试块(150 mm×150 mm×150 mm)的抗压强度为30 MPa;试件2养护68d,试验时与试件同等条件养护的标准立方体试块抗压强度为31.7 MPa。
试验采用水平火灾试验炉,试件在试验炉上的布置如图2所示。试验升温系统由对称布置在试验炉长边方向的8个燃烧器组成,燃烧器之间间距为1 m。除去支承轴线内侧耐火砖墙和岩棉防火墙所占面积,试件实际受火面积为3800 mm×5400 mm。

图2 试件布置
Fig.2 Specimen arrangement
根据混凝土结构试验方法标准[20],简支边支座采用钢球和钢滚轴,钢球和钢滚轴的直径均为100 mm;固支边支座采用焊接在钢板上的钢滚轴,为避免支座过于沉重造成试验不便,固支边支座采用直径40 mm的钢滚轴,10 mm厚的钢板,固支边与简支边的支座高度差通过砖与砂浆找平。支座布置如图3所示,简支边沿AD、DC方向,固支边沿AB、BC方向。
固支边约束反力由反力装置实现,每一套荷载施加装置包括 1个液压千斤顶,1根截面尺寸为 I126×74×5的工字钢分配梁,分配梁长1500 mm,2根直径40 mm长400 mm的钢滚轴,1块尺寸为10 mm×300 mm×2100 mm的钢板和1个量程为5 t的BHR-4型荷重传感器,反力装置组合方式如图4所示。长固支边布置4套反力装置,短固支边布置3套,如图5所示。通过BHR-4型荷重传感器在试验前准确施加约束荷载并在试验过程中实时监测约束荷载变化,其数值由静态电阻应变仪(DH3815N)采集和记录。
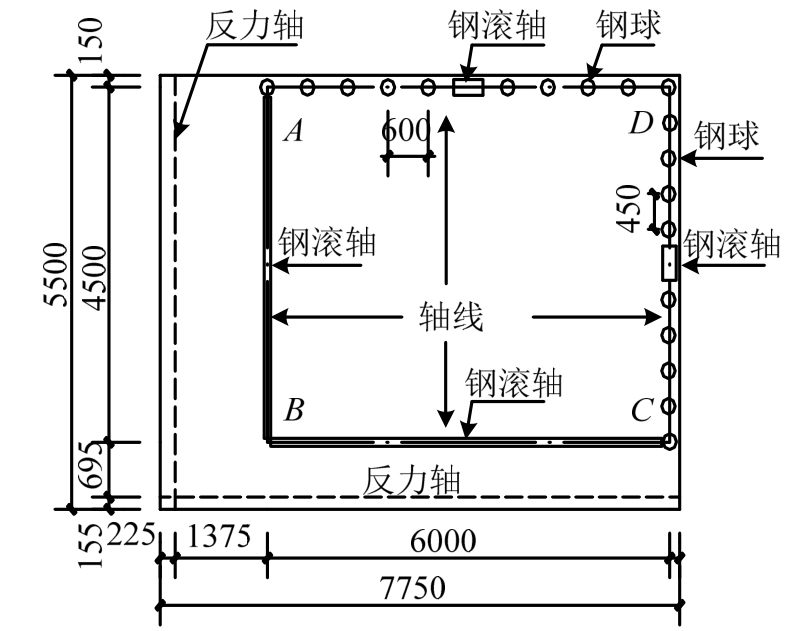
图3 支座布置
Fig.3 Configuration of edge-support

图4 固支边约束荷载施加装置
Fig.4 Constrict loading apparatus of clamped edges

图5 固支边约束详图
Fig.5 Details of clamped edges
本试验为恒载升温,在支承轴线内的板面上均布2.0 kN/m2活荷载。用20 kg的铁砝码在板面上均匀布置以模拟活荷载,铁砝码不足时用沙袋补充,如图6所示。

图6 均布活荷载布置
Fig.6 Arrangement of live loads
板的平面外(竖向)和平面内(水平)位移均由差动式位移传感器(LVDT)测量,位移传感器的测点布置见图7,LVDT的数据由安捷伦数据采集仪(Agilent 34980A)进行采集。
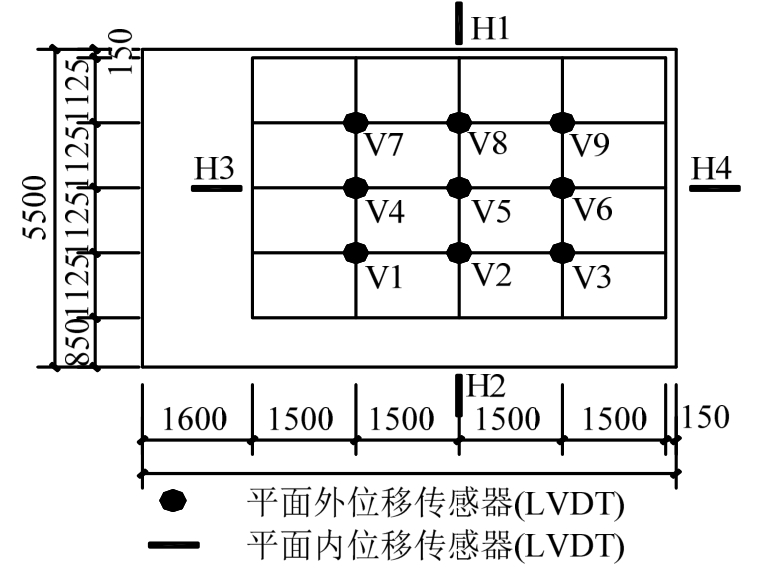
图7 位移计布置
Fig.7 Arrangement of LVDTS
混凝土和钢筋的温度由预埋在板内的自制 K型热电偶测量,热电偶测点布置如图8所示。共布置了9组热电偶,每组热电偶包括7片K型热电偶,第1片热电偶位于板底,第7片热电偶位于板顶,其余热电偶均匀布置,间距20 mm。钢筋温度由K型热电偶与各测点底层和顶层钢筋直接连接测得。热电偶数据由数据采集仪(Agilent 34980A)采集。

图8 热电偶布置
Fig.8 Arrangement of thermal couples
为便于描述试验现象,以L代表长跨,l代表短跨。4 min时,在固支边AB、BC支承轴线处形成了沿固支边轴线发展的裂缝①和②。固支边轴线处混凝土开裂后,轴线内侧板的负弯矩增大,6 min时,在距离长固支边BC轴线300 mm~400 mm处出现裂缝③,裂缝由从短固支边 AB向短简支边 CD发展,至距短简支边CD约1/4L时改为沿与长固支边轴线成30°角的方向继续向短简支边 CD发展,裂缝宽度为4 mm。30 min时,在长固支边BC轴线附近出现了主要裂缝①、③和④,其中裂缝①沿轴线方向发展,裂缝③和④都是在距短简支边CD约1/4L处斜向短简支边发展;在短固支边AB轴线附近共出现了主要裂缝②和⑤,且裂缝在距长简支边AD约1/4L处斜向长简支边发展。恒载升温作用下简支板双向板的角部会向上翘起[12],本试验没有对两相邻简支边角部进行约束,58 min时,两相邻简支边角部开始向上翘起,出现平行于短跨方向由长简支边AD中央向长固支边BC方向发展的裂缝⑥,裂缝发展到距长固支边BC约1/4L处。118 min时,两相邻固支边AB、BC角部弧形裂缝的最大宽度达到了6 mm~7 mm。试件TL1在243 min时停止试验,试件TL2在280 min时停止试验。板顶裂缝的开裂形式如图9所示,最终形成一半椭圆型的破坏模式。试验过程中,12 min时在板顶裂缝处开始出现水渍;18 min时板顶水分增加的速率明显变快,且在沿板厚贯通的裂缝处开始出现水分蒸发;68 min时板面凹陷处积蓄的水分达到最大量,同时伴有大量水分蒸发;183 min时板顶水分蒸发完毕,只在轴线处及轴线外裂缝处存在少量水渍。


图9 板顶裂缝形式
Fig.9 Top crack pattern of the Specimen
试验升温曲线如图10所示,实际升温曲线与ISO834标准升温曲线基本一致。试验停止时,试件TL1的炉温为1155℃,试件TL2的炉温为1177℃。
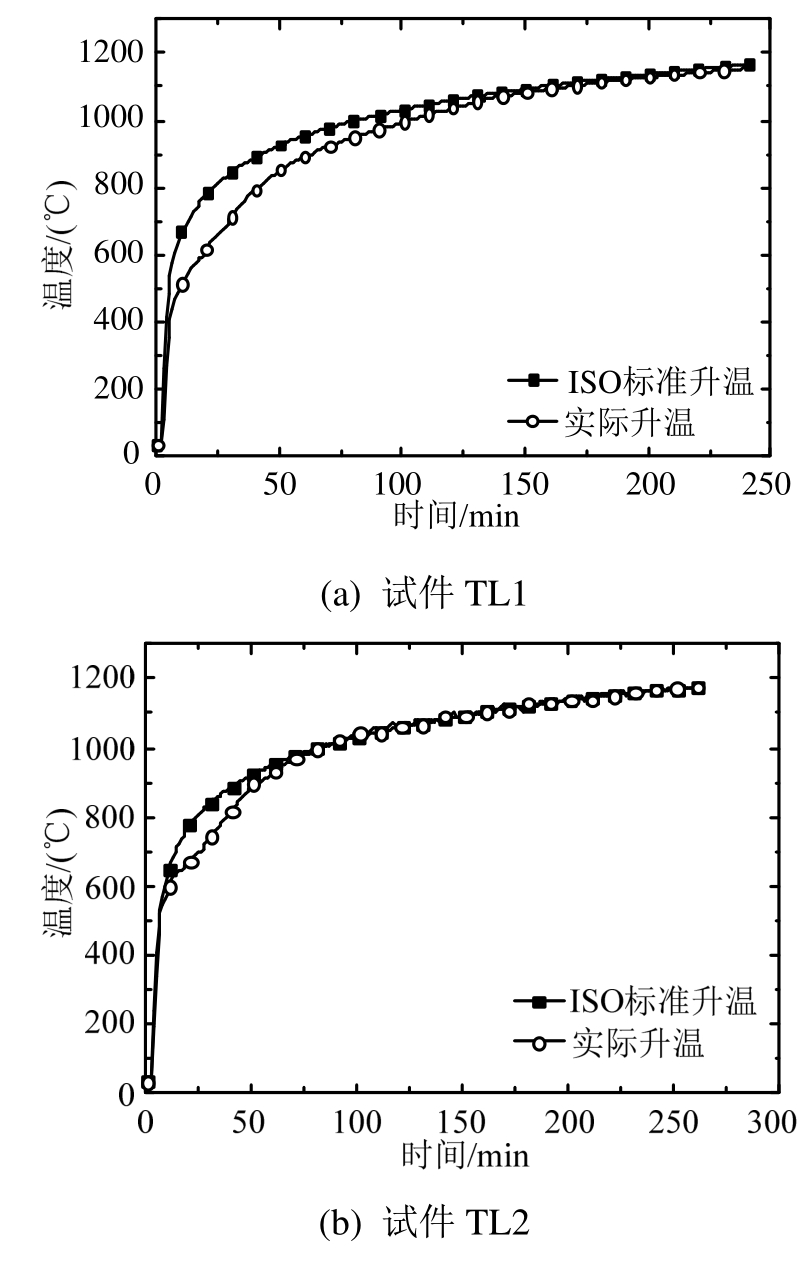
图10 试验炉炉温-时间曲线
Fig.10 Temperature-time curves of furnace
升温阶段沿板厚混凝土温度随时间的变化曲线如图11所示。由试验结果可知,试件 TL1和TL2板底混凝土最高温度分别为921℃和914℃,板顶混凝土的最高温度分别为166℃和160℃。由于水分的影响,升温过程中除板底混凝土外,其它高度处混凝土的温度都在 100℃时出现了明显的恒温段。

图11 截面混凝土温度-时间曲线
Fig.11 Temperature-time curves of concrete along depth of the specimen
图12为试件底层和顶层钢筋的温度-时间关系曲线,可以看到,由于水分的影响,顶层钢筋在100℃时出现了明显的升温水平段。试件底层钢筋与顶层钢筋的温差不断增大,100 min时,试件TL1和TL2底层和顶层钢筋的温差分别达到了541℃和502℃;试验结束时,试件TL1和TL2底层和顶层钢筋的温差分别达到了 609 ℃和 591 ℃,可以看出从100 min起,水分对顶层钢筋升温的影响开始不明显。
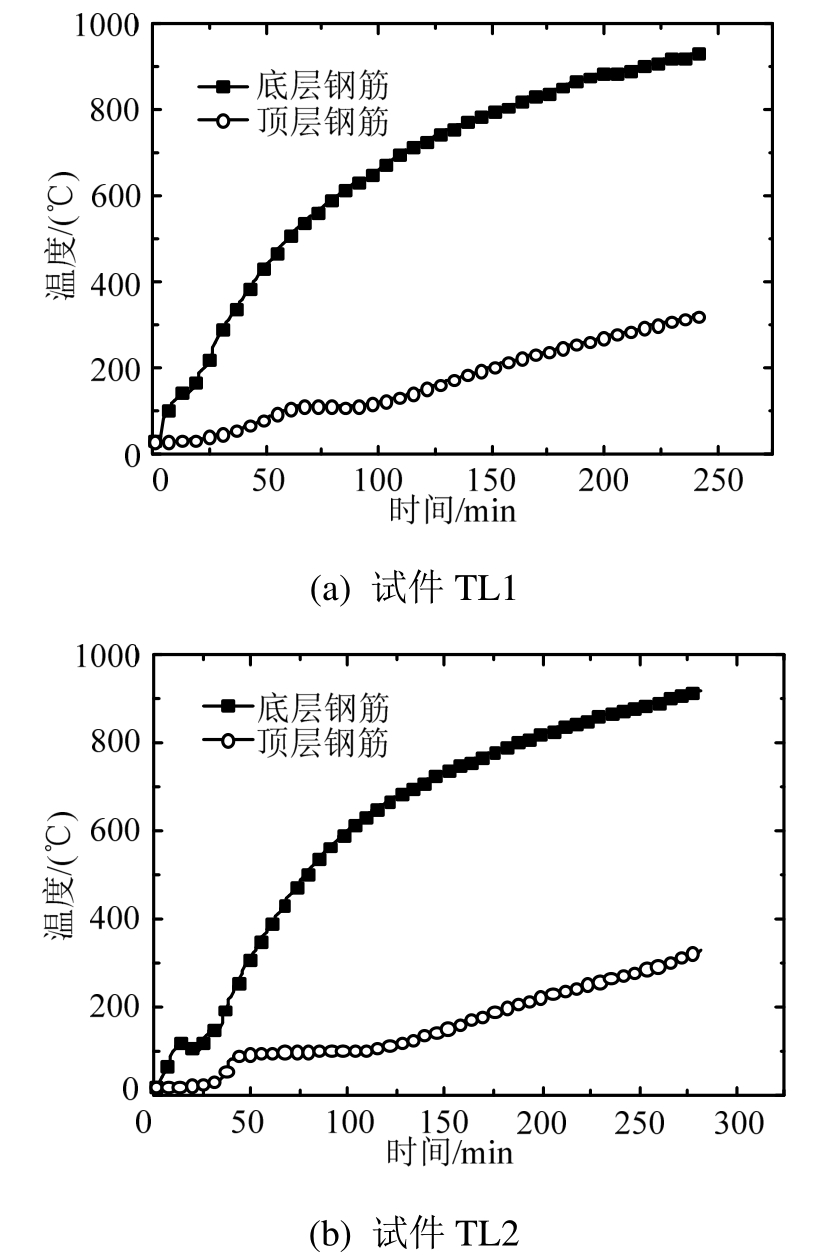
图12 试件内钢筋温度-时间关系曲线
Fig.12 Temperature-time curves of top and bottom bars in the specimen
图13为试件各测点的平面外(竖向)位移随时间的变化关系曲线,图中位移为负值表示板的平面外位移位于初始中平面以下,为正值表示板的平面外位移位于初始中平面以上。60 min之前,板的平面外位移增长很快,中点位移V5达到了-77.59 mm,相当于以-1.29 mm/min的速率增长;60 min之后,中点位移V5基本上以-0.44 mm/min的速率增长。9个测点中,V1紧挨着两个固支边,其竖向位移最小;V2、V3、V4和V7点的最终位移在-70 mm左右,均是靠近某一固支边的测点;V6、V8和 V9的最终位移为-120 mm左右,均是靠近某一简支边的测点;试件TL1和TL2的中点位移V5最终分别为-173 mm和-175 mm。由于板的边界条件不对称,中点位移V5并不是整个板面的最大平面外位移,由试验观测知,整个板面平面外最大位移为中点偏向两简支边附近的某一点。

图13 平面外位移-时间曲线
Fig.13 Vertical deflection-time curves
图14为平面内(水平)位移随时间的变化曲线,图中位移为负表示板的位移沿轴线向外发展,为正表示沿轴线向内发展。图中H1为长简支边的位移,H2为长固支边的位移,H3为短固支边的位移,H4为短简支边的位移。由图可知,H2总是正的,且其最终为-0.90 mm;H1、H3和H4均是负值,H1最终为-6.85 mm,H3最终为-3.37 mm,H4最终为-25.51 mm。可以看出,固支边的平面内位移远小于简支边的。
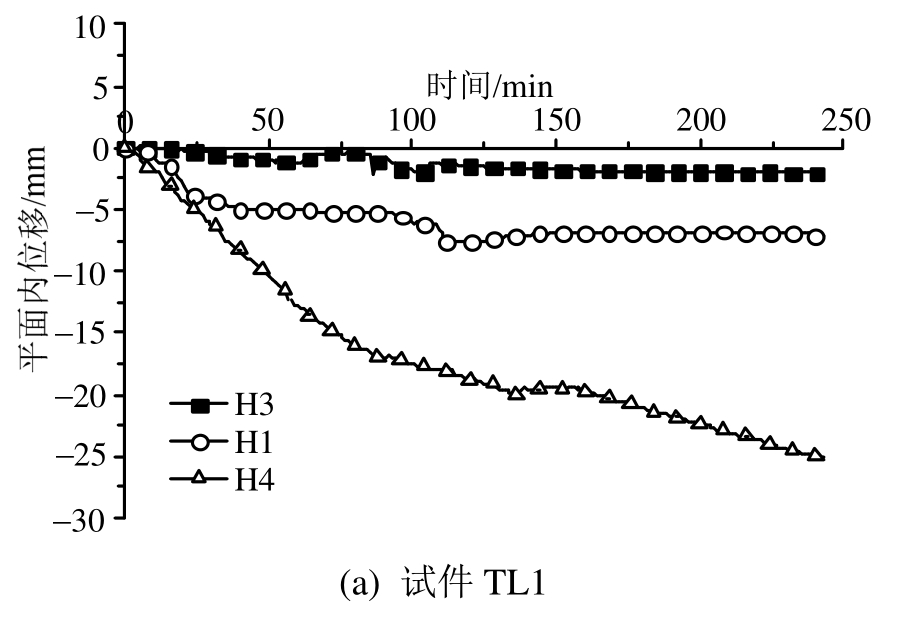

图14 平面内位移-时间曲线
Fig.14 Horizontal displacement-time curves
图15为两固支边AB、BC的约束荷载平均值随时间的变化曲线。4 min时,裂缝①和②出现使应力释放,板的约束荷载有所降低,内力重分布之后约束荷载继续增加。试件TL1和TL2长固支边BC的约束荷载分别在第27 min和第31 min时达到最大值19.12 kN/m和16.63 kN/m,短固支边AB的最大值分别为6.68 kN/m和6.32 kN/m,此时板面主要裂缝为裂缝①~⑤。峰值过后,短固支边的约束荷载基本维持在 1.62 kN/m,而长固支边的约束荷载则持续降低,试件TL1和TL2的最终值分别为10.50 kN/m和9.32 kN/m。
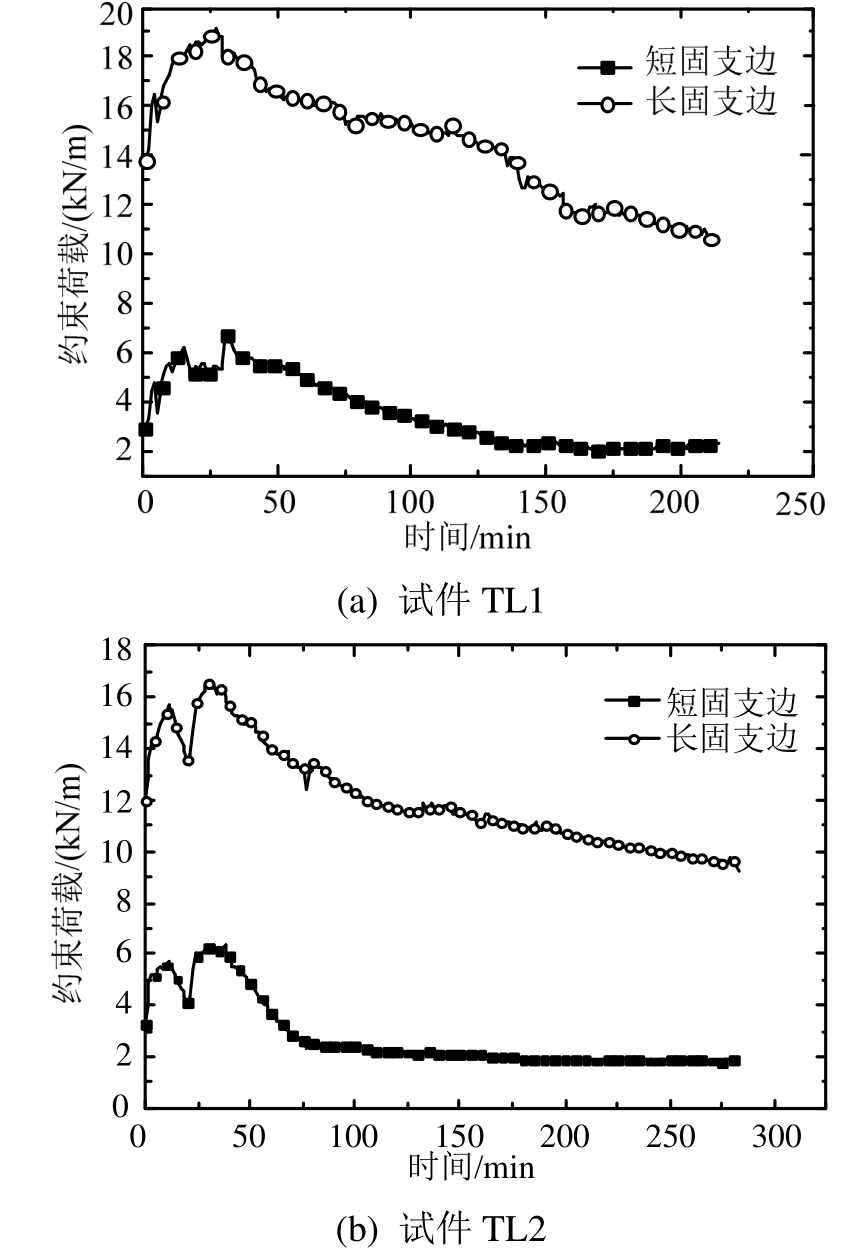
图15 固支边约束荷载-时间曲线
Fig.15 Constraint force-time curves of clamped edges
由试验知,火灾下邻边简支邻边固支板的破坏模式与传统塑性铰线理论破坏模式相似,见图16,所以假设其破坏模式符合传统塑性铰线理论的破坏模式。
极限承载力的计算与传统塑性铰线理论一样作出如下假设:
1)塑性绞线上沿板厚度方向混凝土的开裂贯通;
2)塑性铰线上钢筋均达到屈服,并且随温度升高屈服强度降低;
3)没有出现钢筋硬化。
板的平面内位移远小于平面外位移,在板的极限承载力计算中不考虑板的平面内位移。
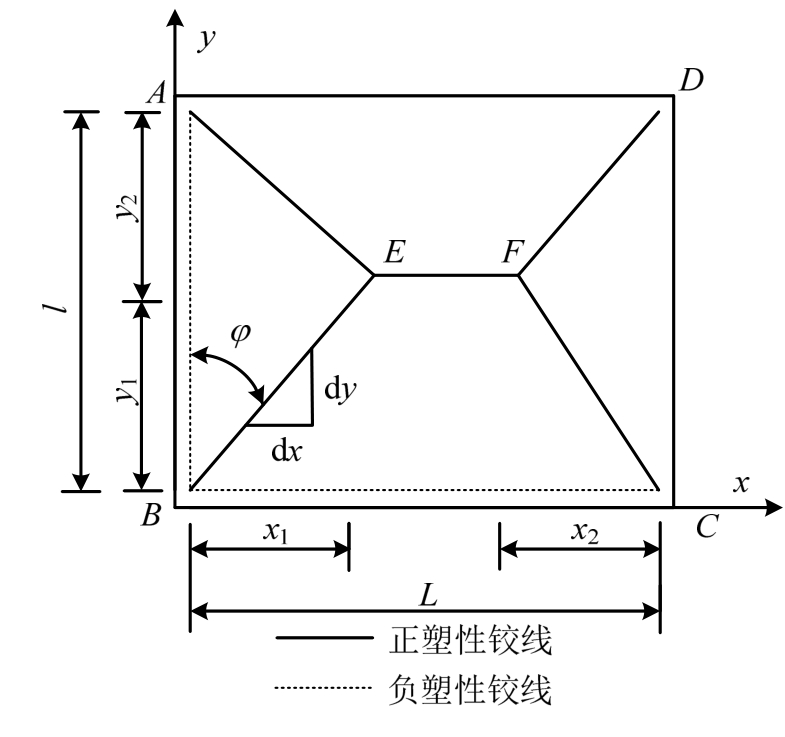
图16 板的塑性铰线模式
Fig.16 Plastic hinge line configuration of the slab
假设火灾作用下塑性铰线EF段竖向位移为z,则塑性铰线AE沿x向和y向的竖向位移分别为![]() 和
和![]() ,沿x方向钢筋的长度为
,沿x方向钢筋的长度为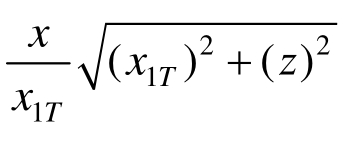 ,沿y方向钢筋的长度为
,沿y方向钢筋的长度为![]() ;塑性铰线BE沿x向和y向的竖向位移分别为
;塑性铰线BE沿x向和y向的竖向位移分别为![]() ,沿x方向钢筋的长度为
,沿x方向钢筋的长度为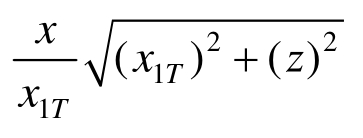 ,沿y方向钢筋的长度为
,沿y方向钢筋的长度为![]() ;塑性铰线CF沿x向和y向的竖向位移分别为
;塑性铰线CF沿x向和y向的竖向位移分别为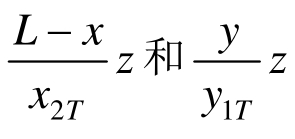 ,沿x方向钢筋的长度为
,沿x方向钢筋的长度为![]() ,沿y方向钢筋的长度为
,沿y方向钢筋的长度为![]() ;塑性铰线DF沿x向和y向的竖向位移分别为
;塑性铰线DF沿x向和y向的竖向位移分别为![]() ,沿x方向钢筋的长度为
,沿x方向钢筋的长度为![]() ,沿y方向钢筋的长度为
,沿y方向钢筋的长度为![]() 。其中 xiT、 yiT为考虑混凝土线性膨胀引起的位置参数 xi、 yi随温度的变化值,分别按式(1a)和式(1b)计算:
。其中 xiT、 yiT为考虑混凝土线性膨胀引起的位置参数 xi、 yi随温度的变化值,分别按式(1a)和式(1b)计算:
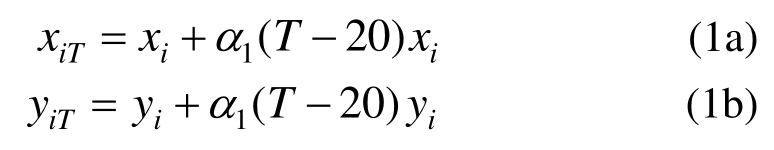
式中,α1为混凝土的热膨胀系数,根据欧洲规范EN1992-1-2: 2004(E)采用。
大挠度时塑性铰线处的截面力见图17。由能量法知,板的内力做功等于外荷载做功,传统塑性绞线理论认为板的内力做功为塑性铰线截面上混凝土压应力CT与钢筋拉力TT组成的截面抵抗弯矩做功;而大挠度时屈服钢筋被拉伸长度较大,耗费的外力功不能忽略,所以此处认为与外荷载做功平衡的内力做功包括两部分:一是截面抵抗弯矩做功;二是屈服钢筋被拉长做功。正是由于屈服钢筋伸长做功,使大挠度时板的极限承载力比按传统塑性绞线理论的计算值高,这也是火灾作用下大变形板出现薄膜效应的原因。
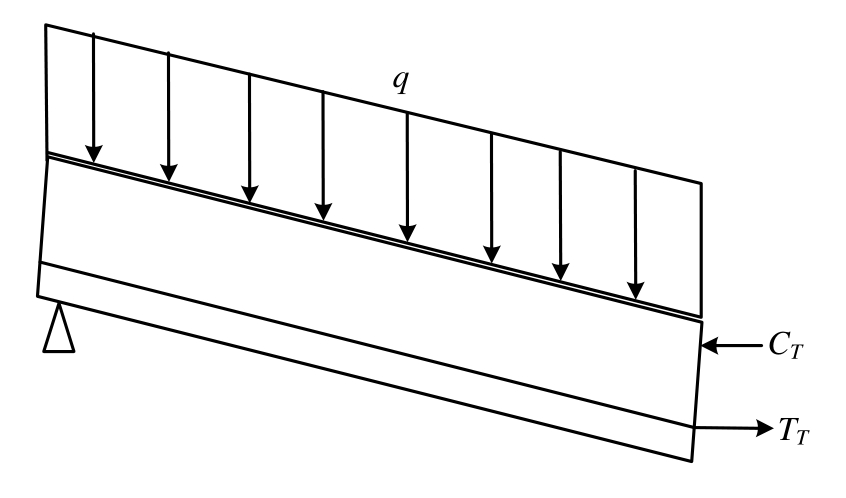
图17 大挠度时塑性铰线处的截面力
Fig.17 Forces at the yield hinge section of the slab with large displacement
假设形成塑性铰线后T时刻塑性铰线EF的挠度为v,图16中的塑性铰线BE绕轴线AB转动时钢筋伸长所做功为:

同理可得塑性铰线AE绕轴线AB转动时、CF绕轴线CD转动时和DF绕轴线CD转动时钢筋伸长所做的功分别为:
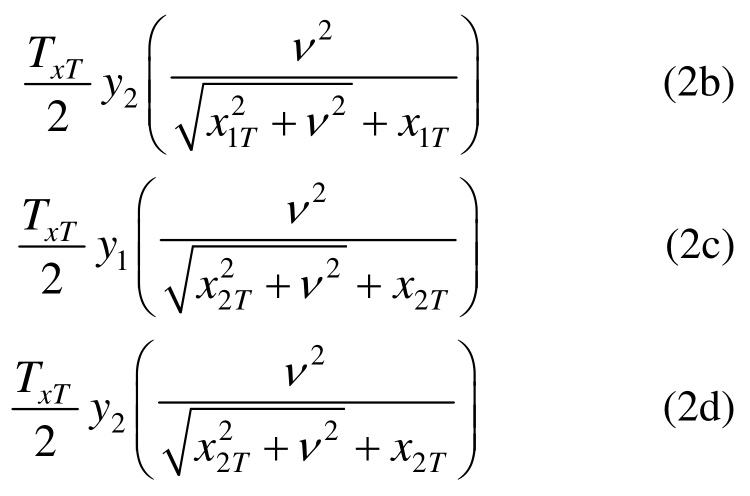
式中,TxT为塑性绞线上钢筋沿x方向的分力。
塑性铰线BE绕轴线BC转动时钢筋伸长所做功为:

同理可得塑性铰线AE绕轴线AD转动时、CF绕轴线BC转动时和DF绕轴线AD转动时钢筋伸长所做的功分别为:
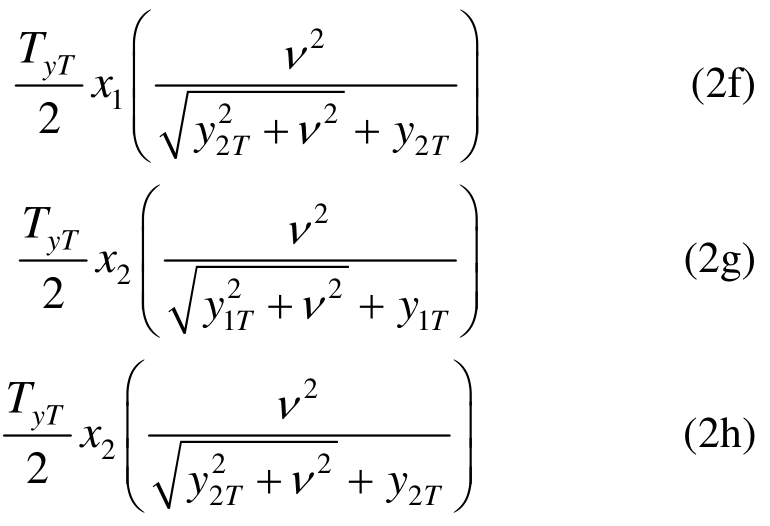
式中:TyT为塑性绞线上钢筋沿y方向的分力。塑性铰线EF绕轴线AB转动时钢筋伸长所做的功为:

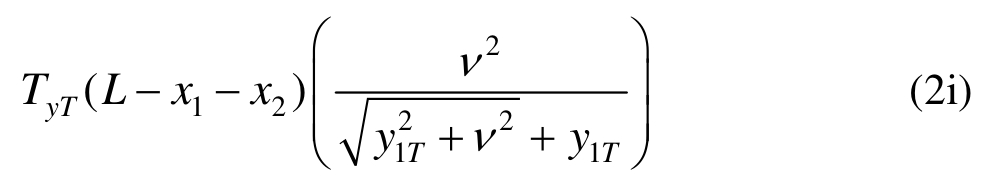
同理可得塑性铰线EF绕轴线CD转动时钢筋伸长所做的功为:
根据板块平衡,图16中区块AEFD绕AD转动的平衡方程为:
同理可得区块AEB、BCEF和FCD绕各自支承轴转动的平衡方程分别为:

式中:mx、my为常温下塑性铰线处x方向和y方向的截面抵抗矩;m′xe、m′ye为x方向和y方向固支边轴线处的负弯矩;q为混凝土板的承载力,包括板的自重及板的均布活荷载。
计算得:
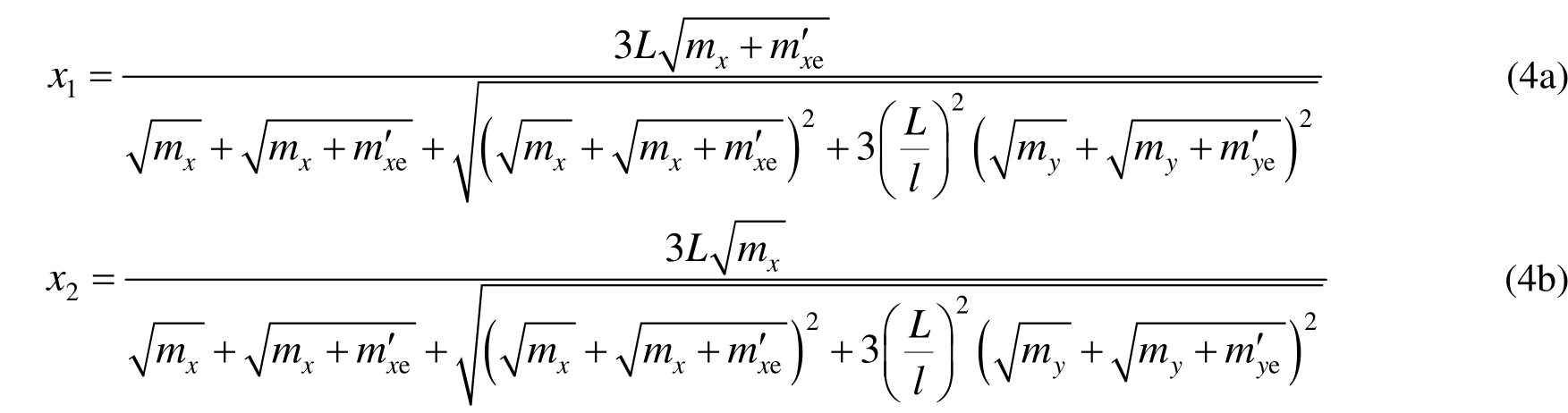

荷载q做功为:

内力做功包括截面抵抗弯矩转动做功和屈服钢筋伸长做功两部分,截面抵抗弯矩转动做功为:

屈服钢筋伸长所做功为:

由外力做功与内力做功相等,即 W =D1+D2,得:
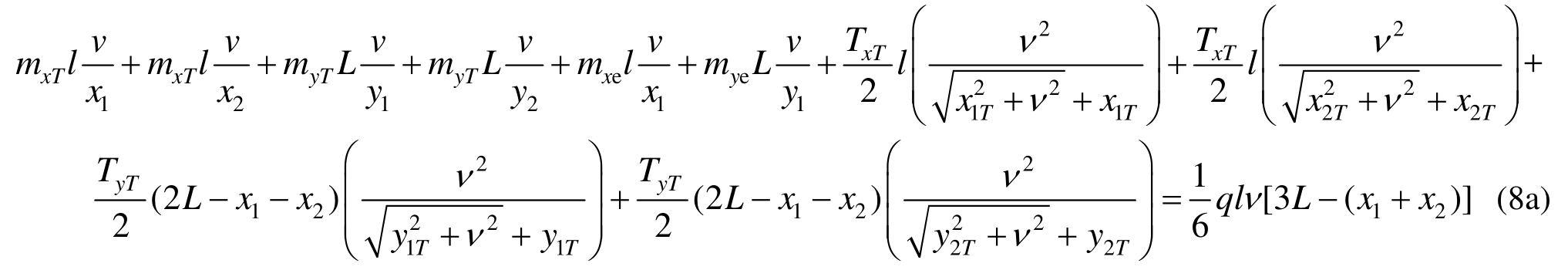
整理得:
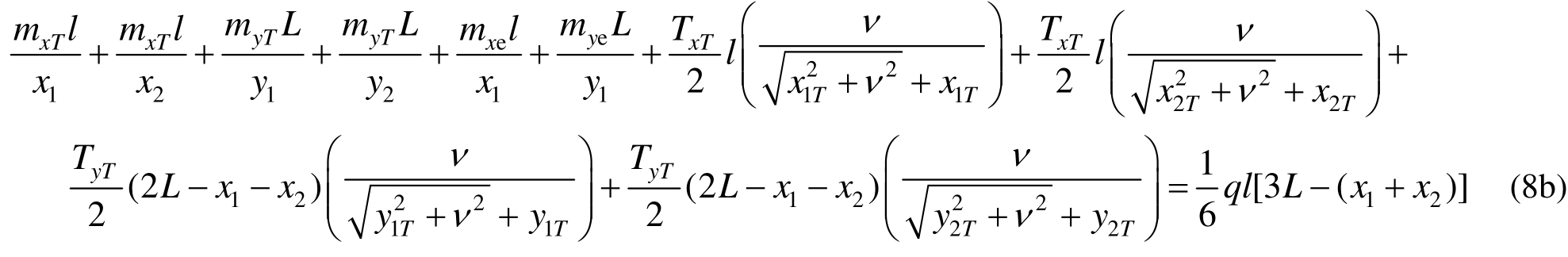
薄膜效应在塑性铰线形成后才出现,且钢筋此后一直处于屈服状态,但火灾作用下其屈服强度随钢筋温度的升高而降低。所以式(8b)改为:
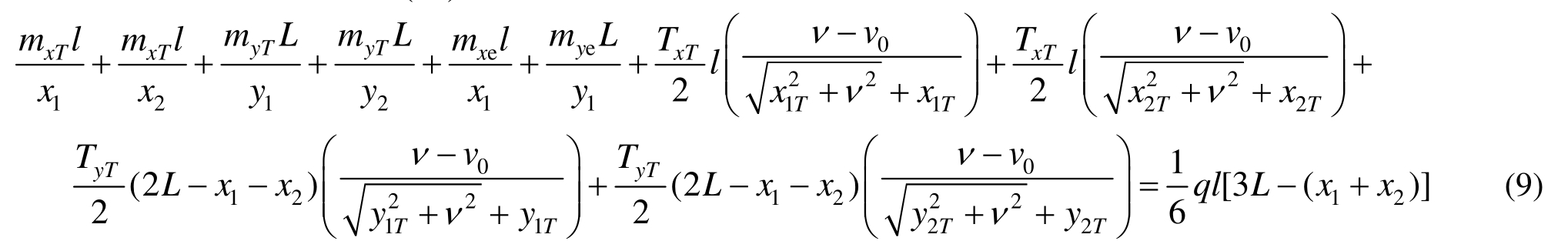
式中:v0为形成塑性绞线时塑性绞线EF的挠度。
由式(9)可求得荷载q为:

该计算模型与基于塑性绞线的传统能量法计算模型是统一的,板的竖向位移小于v0时,式(10)即为传统能量法的计算模型。
Bailey提出的计算模型[11―12,17]中对v0的取值偏于保守,基于以前的试验结果,建议v0取值为:

式中:fy常温下钢筋的屈服强度;E为常温下钢筋的弹性模量。
给定板的参数,利用板平面外位移和底层钢筋温度的试验结果,根据式(10)可以得出板的承载力与底层钢筋温度的变化关系。试件TL1和TL2火灾作用下承载力与底层钢筋温度变化的关系曲线见图18,可以看出,根据传统能量法,试件 TL1在底层钢筋温度为 720℃时破坏,而根据本文提出的新能量法,底层钢筋温度为 750℃时试件还没破坏。根据传统能量法,试件TL2在底层钢筋温度为730℃时破坏,而根据新能量法,试件在底层钢筋温度为770℃时破坏,与试验结果一致。

图18 极限承载力-温度曲线
Fig.18 Load-carrying capacity-time curves of specimen
利用板的竖向位移和钢筋温度的试验结果,使按式(10)计算的承载力等于施加在板上的荷载,用二分法可得到底层钢筋的临界温度。当底层钢筋达到此临界温度时,外部荷载做功等于板的内力做功。底层钢筋临界温度的计算值与试验结果的对比见图19。可以看出,试件TL1和TL2分别在其竖向位移为170 mm和162 mm时底层钢筋达到临界温度,临界温度分别为 760℃和 772℃,与试验结果一致。

图19 底层钢筋温度计算与试验对比曲线
Fig.19 Predicted reinforcement temperatures compared to tests

图20 不同平面外位移下板的极限承载力变化
Fig.20 Variation of load-carrying capacity at different deflection levels
板的竖向位移给定,可根据板底层钢筋的温度,利用式(10)计算板的极限承载力。图20为板的竖向位移分别为板的长向跨度的1/30,1/25和1/20时板的极限承载力随底层钢筋温度的变化。可以看出,底层钢筋温度低于400℃时,极限承载力基本上为一常数,当底层钢筋的温度超过400℃以后,极限承载力呈线性降低。按传统能量法计算,板在底层钢筋的温度为700℃时破坏,根据新能量法计算,板在底层钢筋温度超过780℃时才发生破坏。
本文通过足尺两邻边简支两邻边固支钢筋混凝土双向板抗火性能的试验研究和火灾作用下极限承载力的计算,主要得出以下结论:
(1)火灾作用下邻边简支邻边固支钢筋混凝土双向板的板顶裂缝形成半椭圆形破坏模式;板的最大平面外位移出现在板中心偏向两简支边附近;板的固支边产生了明显的应力重分布,沿板厚度混凝土温度场呈非线性分布。
(2)大挠度情况下,板的张拉薄膜效应在塑性铰线出现后产生,且产生薄膜效应的原因是塑性铰线截面处屈服钢筋伸长所做塑性功。
(3)火灾作用下板的破坏模式与常温下板的破坏模式一致,所以本文提出与传统能量法计算模型相统一的新能量法计算模型,该模型计算板的极限承载力与试验结果吻合很好,而传统能量法计算结果偏保守。
参考文献:
[1]朱崇绩, 董毓利, 朱崇钊. 足尺平板无梁楼盖抗火性能的试验研究[J]. 建筑结构学报, 2013, 34(3): 12―19.Zhu Chongji, Dong Yuli, Zhu Chongzhao. Experimental Study on Fire Resistance Properties of Full-scale Flate-plate Floor Subjected to Fire [J]. Journal of Building Structures, 2013, 34(3): 12―19. (in Chinese)
[2]王勇, 袁广林, 李志奇, 等. 钢筋混凝土双向板火灾行为的数值分析[J]. 工程力学,2 015, 32(11): 218―250.Wang Yong, Yuan Guanglin, Li Zhiqi, et al. Numerical analysis of fire behavior of two-way reinforced concrete slabs[J]. Engineering Mechanics, 2015, 32(11): 218―250. (in Chinese)
[3]杨志年, 董毓利. 钢框架结构中钢筋混凝土双向板火灾试验研究[J]. 工程力学, 2013, 30(4): 337―344.Yang Zhinian, Dong Yuli. Experimental study of two-way reinforced concrete slab subjected to fire in a steel-framed building [J]. Engineering Mechanics, 2013,30(4): 337―344. (in Chinese)
[4]Yong Wang, Guanglin Yuan, Zhaohui Huang, et al.Experimental study on the fire behaviour of reinforced concrete slabs under combined uni-axial in-plane and out-of-plane loads [J]. Engineering Structures, 2016,128(10): 316―332.
[5]Vassart O, Bailey C. G, Hawes M, et al. Large-Scale Fire Test of Unprotected Cellular Beam Acting in Membrane Action [J]. Journal of Structural Fire Engineering, 2011,2(3): 259―268.
[6]李兵, 董毓利, 娄永杰, 等. 足尺钢框架中连续板格火灾实验研究[J]. 工程力学, 2015, 32(1): 145―153.Li Bing, Dong Yuli, Lou Yongjie, et al. A fire test of continuous panels in a full-scale steel-framed structure[J]. Engineering Mechanics, 2015, 32(1): 145―153. (in Chinese)
[7]陈适才, 仁爱珠, 王静峰, 等. 钢筋混凝土楼板火灾反应数值计算模型[J]. 工程力学, 2008, 25(3): 107―112.Chen Shicai, Ren Aizhu, Wang Jingfeng, et al. Numerical modeling of reinforced concrete Slabs subjected to fire[J]. Engineering Mechanics, 2008, 25(3): 107―112. (in Chinese)
[8]Omer E, Izzuddin B. A, Elghazouli A. Y. Failure of unrestrained lightly reinforced concrete slabs under fire,Part I: Analytical models [J]. Engineer Structural, 2010,32(9): 2631―2646.
[9]王勇, 王腾焱, 袁广林, 等. 基于不同混凝土本构模型的混凝土双向板火灾行为分析[J]. 工程力学, 2016,33(11): 208―219.Wang Yong, Wang Tengyan, Yuan Guanglin, et al.Analysis of fire behavior of two-way concrete Slabs based on different constitutive models [J]. Engineering Mechanics, 2016, 33(11): 208―219. (in Chinese)
[10]Bailey C. G, Lennon T, Moore D. B. The behaviour of full-scale steel framed buildings subjected to compartment fires [J]. The Structural Engineer, 1999,77(8): 15―21.
[11]Bailey C. G, Toh W. S. Behaviour of Concrete Floor Slabs at Ambient and Elevated temperatures [J]. Fire Safety Journal, 2007, 42(6-7): 425―436.
[12]Bailey C. G, Toh W. S. Small-scale Concrete Slab Tests at Ambient and Elevated Temperatures [J]. Engineering Structures, 2007, 29(10): 2775―2791.
[13]Lim L, Wade C. Experimental fire tests of two-way concrete slabs [R]. University of Canterbury and BRANZ Ltd, New Zealand, 2002.
[14]Lim L, Buchanan A, Moss P. Numerical modeling of two-way reinforced concrete slabs in fire[J]. Engineering Structures, 2004, 26(8): 1081―1091.
[15]王滨, 董毓利. 四边简支钢筋混凝土双向板火灾试验研究[J]. 建筑结构学报, 2009, 30(6): 23―33.Wang Bin, Dong Yuli. Experimental research of four-edge simply supported and four-edge fixed two-way reinforced concrete slab under fire [J]. Journal of Building Structures, 2009, 30(6): 23―33. (in Chinese)
[16]王滨, 董毓利. 钢筋混凝土双向板火灾试验研究[J].土木工程学报, 2010, 57(4): 53―62.Wang Bin, Dong Yuli. Experimental study of two-way reinforced concrete slabs under fire [J]. China Civil Engineering Journal, 2010, 57(4): 53―62. (in Chinese)
[17]Bailey C G, White D S, Moore D B. The tensile membrane action of unrestrained composite slabs simulated under fire conditions [J]. Engineering Structures, 2000, 22(12): 1583―1595.
[18]Usmani A S, Cameron N J K. Limit capacity of laterally restrained reinforced concrete floor slabs in fire [J].Cement and Concrete Composites, 2004, 26(2): 127―140.
[19]Cameron N J K, Usmani A S. New design method to determine the membrane capacity of laterally restrained composite floor slabs in fire. Part 1: Theory and method[J]. The Structural Engineer, 2005, 83(19): 28―33.
[20]GB 50152-1992, 混凝土结构试验方法标准[M]. 北京:中国建筑工业出版社, 1992: 15―18.GB 50152-1992, Standard Methods for Testing of Concrete Structures [M]. Beijing: China Architecture &Building Press, 1992: 15―18. (in Chinese)
AN ENERGY METHOD FOR CALCULATION THE LOAD-CARRYING CAPACITY OF TWO-WAY SLABS WITH TWO EDGES SIMPLY SUPPORTED AND TWO EDGES CLAMPED IN FIRE
ZHU Chong-ji1, DONG Yu-li2
(1. School of Civil Engineering and Architecture, University of Jinan, Jinan, Shandong 250022, China;2. College of Civil Engineering, Huaqiao University, Xiamen, Fujian 361021, China)
Abstract:Fire-resistant experiments were conducted on two full-scale reinforced concrete two-way slabs with two edges simply supported and two edges clamped. This paper presents the design of the furnace and specimens,the test plan, the measuring contents and methods. The test phenomena, cracking and failure characteristics of the tested reinforced concrete two-way slabs were described. The temperature distribution along the depth of the slab,vertical deflection and horizontal displacement have been studied.Internal force redistribution of the clamped edges has been analyzed. The results indicated that the cracks on the unfired side of the slab formed a semielliptical pattern. Based on the experimental results, a new energy method for the limit load-carrying capacity calculate of concrete slabs with two edges simply supported and two edges clamped in fire conditions was presented. The model assumed that the tensile membrane effect of the slabs showed only after the formation of plastic hinge lines, and was caused by the plastic work done by the reinforcement elongation at the yield line section. Comparison between the developed model and test results showed good correlation, while the classical energy method based on the yield line theory gave a conservative value.
Key words:two-way slab; two edges simply supported and two edges clamped were employed; semielliptical pattern; limit load-carrying capacity; energy method; yield line theory
中图分类号:TU375.2
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.04.0266
文章编号:1000-4750(2018)08-0067-12
收稿日期:2017-04-06;修改日期:2018-06-11
基金项目:国家自然科学基金项目(50578078)
通讯作者:朱崇绩(1980―),男,山东人,讲师,博士,从事结构抗火性能化设计研究、结构健康监测研究(E-mail: zhuchongji@163.com).
作者简介:董毓利(1965―),男,江苏人,教授,博士,博导,从事结构抗火性能化设计研究(E-mail: dongyl@hqu.edu.cn).