王 峰1,2，林 皋3，周宜红1,2，赵春菊1,2，周华维1,2
(1．湖北省水电工程施工与管理重点实验室(三峡大学)，宜昌 443002；2．三峡大学水利与环境学院，宜昌 443002；3．大连理工大学水利工程学院，大连 116024)
摘 要：该文基于滑动Kriging插值法，提出了求解含夹杂非均匀材料问题的扩展无单元Galerkin法。该方法利用水平集函数对滑动 Kriging插值形函数进行扩展，从而来反映材料交界面的几何形状和不连续位移场。相比传统的移动最小二乘法形函数，滑动Kriging插值形函数由于满足Kronecker delta函数性质，因此能准确施加位移边界条件。在含夹杂非均匀材料问题求解时，阐述了扩展无单元Galerkin法位移模式的构造以及控制方程的建立。最后通过单夹杂和多夹杂算例表明，扩展无单元Galerkin法相比扩展有限元法，计算精度更高、收敛速率更快。
关键词：非均质材料；扩展无单元Galerkin法；滑动Kriging插值；无网格法；水平集方法
随着复合材料为代表的新兴材料行业成为国家重点培育战略性新兴产业，复合材料得到了广泛应用，如市政建设、新能源的利用、汽车工业发展、大飞机项目等。复合材料作为一种多相材料，复合材料的弹性模量、强度等力学性能受到各相材料的影响，目前研究其力学性能主要有两种方法[1]：宏观方法和微观方法。微观方法是通过研究复合材料组成，建立材料性能与细观结构参数之间关联，并分析复合材料荷载作用下力学性能的一种方法。影响复合材料力学性能的因素有两种，一种是每一相材料的弹性常数，另一种是复合材料内部的微结构特征，主要包括夹杂的形状、几何尺寸、基体中分布情况，其中对夹杂问题的研究一直是材料界和力学界的研究热点。
无网格法[2―3]作为一种新兴的数值计算方法，其利用一组散布在问题域及域边界上的节点来构造场函数近似表达式，该方法不需利用预定义的网格对域进行离散，因此在求解涉及网格畸变或网格重构等问题时具有明显优势。在处理含夹杂复合材料问题时，传统的无网格法主要通过修正权函数法[4]、修正变分法[5]和虚实转换法[6]来处理，这类方法简单易于编程，计算效率较高，但是破坏了无网格法形函数的高阶光滑特性，计算精度较低。
扩展的无单元 Galerkin法(extended elementfree Galerkin method，XEFG)作为一种新兴的无网格法，是 Ventura等[7]受扩展有限元法(extended finite element method，XFEM)[8－11]的启发，基于单位分解思想提出来的。该方法对满足单位分解条件的近似函数实施扩展，利用水平集方法(level set method，LSM)表征不连续体几何形态。马文涛等[12]在不连续近似函数中引入 Heaviside阶跃函数和裂尖 Westergaard 扩展项来描述裂纹两侧的不连续位移场和裂尖奇异场，并将XEFG法应用于裂纹扩展分析。目前扩展的无单元Galerkin法主要用于裂纹体强不连续问题的求解，而对含杂质非均质材料这类弱不连续问题的求解很少。
同时，XEFG法选用传统的移动最小二乘法(moving least squares，MLS)构造形函数，然而MLS形函数不具有插值性，不满足Kronecker delta特性，因此在本质边界条件施加上存在困难。为了弥补这一缺点，马文涛等[13]、Nguyen等[14]将径向点插值法(radial point interpolation method，RPIM)与 XEFG法结合提出了扩展径向点插值无网格法，并将其用于断裂问题的求解。滑动 Kriging插值法(moving Kriging，MK)[15―16]是一种基于随机过程的统计预测方法，其对区域化变量进行线性无偏和最优估计，具有平滑、方差最小统计特性，而且构造的形函数满足Kronecker delta函数性质。Watts等[17]将MK插值与无单元 Galerkin法(element-free Galerkin method，EFG)结合对四边形复合板进行了非线性分析，Bui等[18]将MK插值与EFG法结合对结构动力学问题进行了求解，Li等[19]将MK插值与无网格边界积分方程相结合对二维位势问题进行了求解，Zheng等[20]将 MK插值与无网格局部 Petrov-Galerkin法(meshless local Petrov-Galerkin method，MLPG)结合对弹性力学问题进行了求解。本文将MK插值引入XEFG法并将其用于含夹杂复合材料问题的求解，同时利用水平集方法描述夹杂材料的几何界面。
水平集方法[21―22]是1988年Osher和Sethian为了解决火苗外形变化过程而提出的一种用于界面追踪和形状建模的数值技术。其基本思想是将界面看成高一维空间中水平集函数φ(x,t)的零水平集，将界面的速度也扩充到高一维的水平集函数上，然后写出水平集函数所满足的发展方程，求解此方程，推进水平集函数，计算到要求时刻，找出此新时刻水平集函数的零水平集从而得到界面的形状。该方法的优点是水平集函数建立在离散节点上，而不是固定网格，能很自然地处理界面拓扑变化；水平集演化方程与界面维数无关，易于求解高维问题。
水平集一个重要的用途便是对空洞和夹杂进行描述，例如对圆形夹杂、椭圆形夹杂和多边形夹杂的描述。对于圆形夹杂，可以通过如下水平集函数来表示：
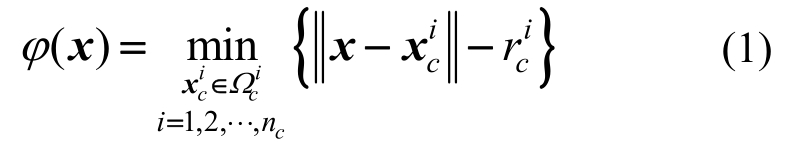
式中：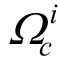
为第i个夹杂所占的区域；nc为圆形夹杂的个数；
和
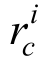分别为第i个夹杂的中心和半径。很明显可以看出，在圆形区域之外水平集为正，在圆形区域之内水平集为负。图1给出了单一圆形夹杂水平集函数表示。
对于椭圆形空洞，若长半轴和短半轴分别为 a和 b，两个焦点坐标分别为
和
则椭圆形空洞水平集函数表示为：
式中：nc为椭圆形空洞的个数；
和 ai分别为第i个椭圆形空洞的两个焦点坐标和长半轴。
图1 单一圆形夹杂水平集函数表示
Fig.1 Level set function for single inclusion
Kriging插值是以南非矿业工程师Kriging D. G.名字命名的一种最优内插法，它以变异函数理论和结构分析为基础，在有限区域内对区域化变量进行无偏最优估计。Gu[15]最早将 Kriging插值引入到EFG法中，从而扩展了无网格法形函数，跟 MLS类似，这里我们称作滑动 Kriging插值法(moving Kriging，MK)。由于MK插值所构造的形函数具备Kronecker delta特性，因此用其构造近似函数具有很大的优势。考虑定义在问题域Ω及其边界Γ上的场函数u(x)，设问题域通过N个场节点离散，在任意点x的支持域内有n个场节点，若已知节点的场函数值为 u ( x1) ,u ( x2),… ,u (xn)，则点x处的近似场函数可以通过MK插值来逼近：
式中，矩阵A和B分别表示如下：
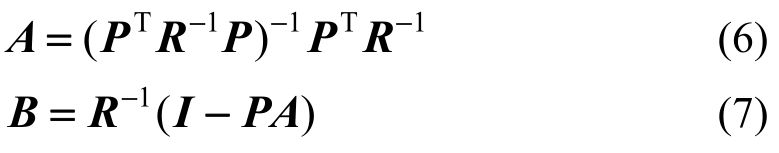
式中：I为n×n的单位矩阵；p(x)是一组完备多项式基，表达式为：
对于线性基：
这里选用线性基，节点处基函数值所形成的矩阵P表示为：
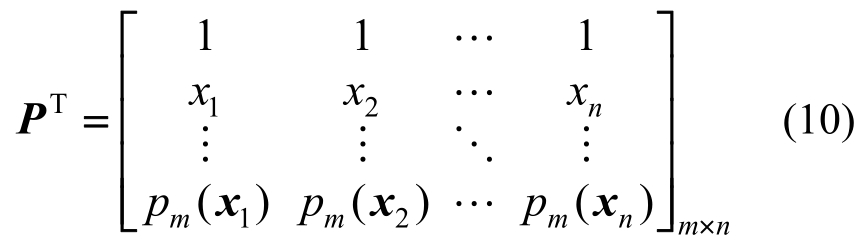
矩阵R和矢量r(x)为：
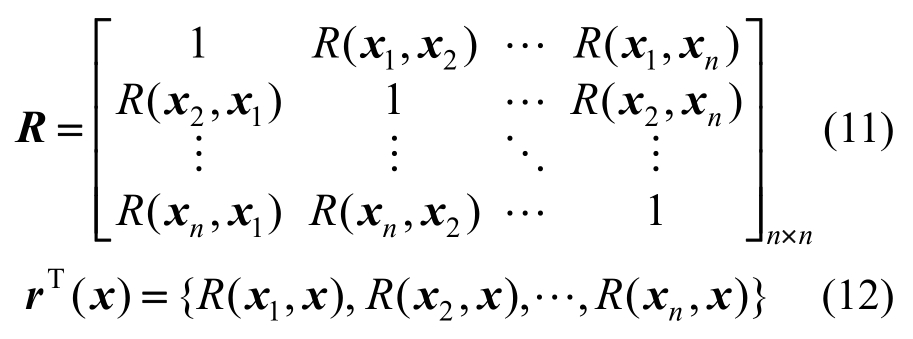
其中：R为对角线为1的对称相关矩阵；R (xi, xj)为节点xi和xj之间的相关函数，这里我们取Gaussian型函数：
其中，θ＞0为模型相关参数，这里我们按照文献[20]所示方法选取θ=0.1，
式(5)形函数最重要的一条性质就是满足Kronecker delta函数性质，即：
单位分解法[23](partition of unity method, PUM)基本思想是从局部数值分析到整体分析，即先分片建立尽可能精确的局部逼近函数，然后再将各片“粘合”，从而形成全局逼近函数。设函数集{φI( x ) }(I = 1 ,2,… ,n )称为从属于开覆盖On的单位分解，在每个节点的覆盖上函数集{φI(x)}满足以下条件：
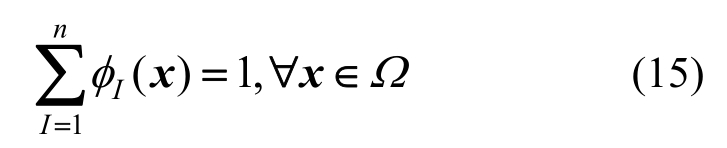
本文选取MK形函数作为单位分解函数，从而弱不连续问题通过XEFG法表示为：
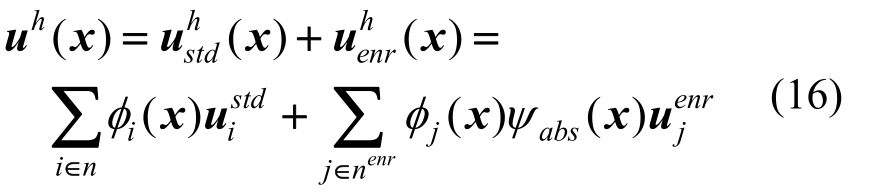
式中：n是节点总数；nenr是支撑与不连续面交叉的节点数；φ是MK形函数；ψabs(x)是增强函数；ustd是标准连续节点位移场函数；uenr是扩展节点的位移场函数。由于扩展的节点一般只限制在特定较小的计算区域内，因此并不会增加太多的附加自由度，具有较高的计算精度。
增强函数ψabs(x)表达式如下：
式中，增强函数是水平集函数的绝对值[24]，在界面上其导数不连续。另外一种增强函数表达式如下[25]：
考虑物理域Ω，其边界Γ由位移边界uΓ和面力边界Γt组成，由虚功原理可得二维线弹性力学控制方程的等效弱形式为：
式中：u={uv}T是位移向量；σ是应力向量；ε是应变向量；b是体力向量；
是面力边界Γt上的已知面力分量。
将式(3)代入式(19)，并考虑位移变分的任意性，可得如下节点离散方程：
为了简化，上标u代表连续部分，e代表不连续增强部分。跟节点i和 j有关的刚度矩阵K和外荷载向量f可表示为：
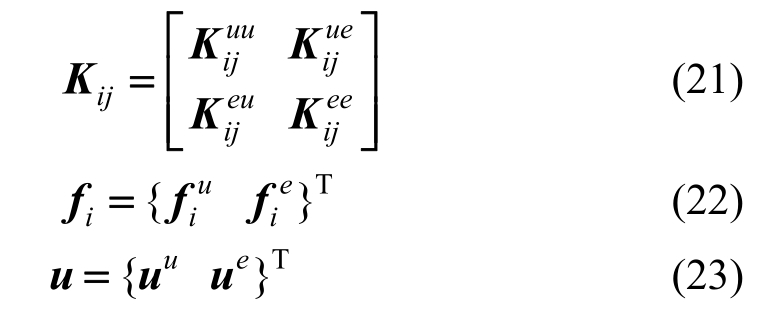
式中，Kuu、Kee和Kue是跟标准EFG插值、增强插值和两者都有关的刚度矩阵，它们分别表示如下：
B矩阵是形函数导数组成的矩阵：
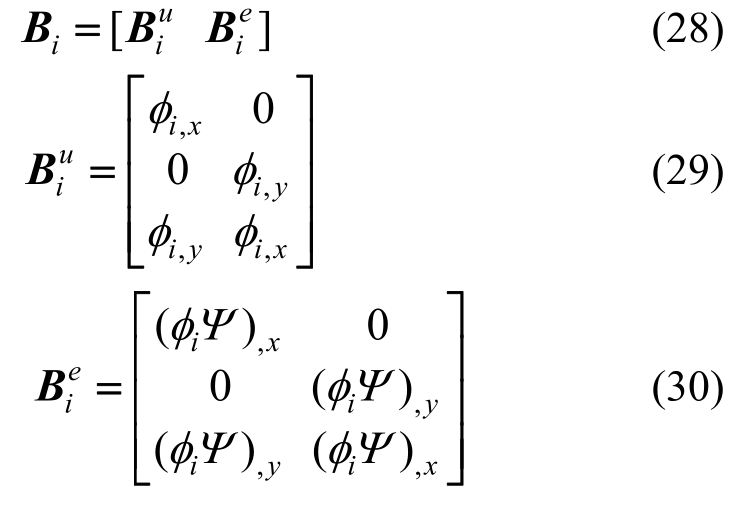
考虑如图2所示的双材料板[24]，材料参数在材料交界面
处不连续，取无量纲材料参数。
内的Lame常数为：
内的Lame常数为：
。材料参数为：弹性模量
，泊松比
；弹性模量
，泊松比
。按平面应变问题进行计算，在边界
上施加位移：
。该问题可以简化为：
该问题的精确解为：
这里，
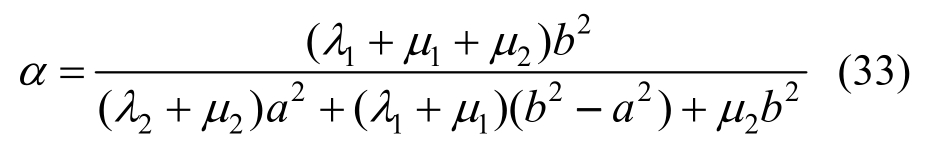
径向(εrr) 和环向(εθθ)应变为：
径向(σrr) 和环向(σθθ)应力为：
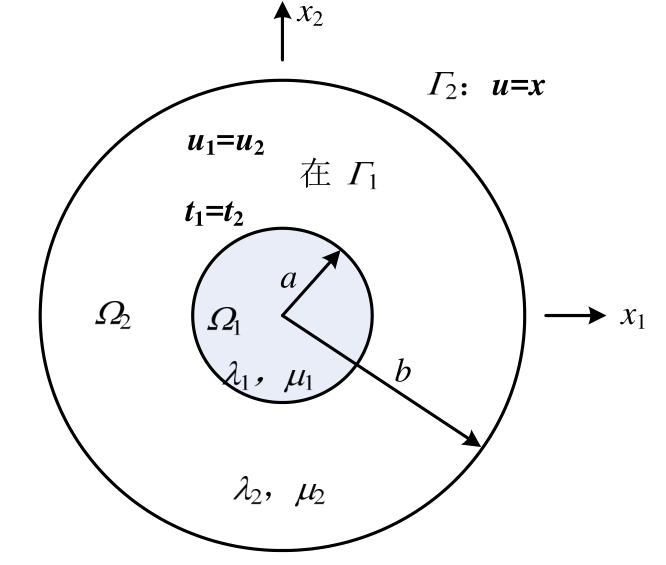
图2 双材料边值问题
Fig.2 Bimaterial boundary-value problem
在计算过程中，我们取2×2的方板，方板中心有一半径a=0.4的圆形夹杂1Ω。通过均匀布置的21×21个节点来离散问题域，方板增强节点如图3所示，每个背景网格里面布置6×6个高斯点，节点影响域半径取为1.5，图4给出了XEFG位移计算结果与解析解比较图，很容易可以看出，XEFG计算结果与解析解非常吻合。
图3 双材料板节点离散
Fig.3 Domain discretization with enriched nodes
图4 双材料板位移变形图
Fig.4 Numerical deformed shape for the bimaterial plate
为了进行误差和收敛性分析，这里我们定义位移相对误差范数L2：
式中：unum为位移数值解；uexact为位移解析解。这里取节点间距(h=0.2、0.1、0.05、0.025、0.0125)进行误差收敛性分析，并与XFEM(每个有限元网格里面布置6×6个高斯点)误差进行对比，如图5所示。很明显可以看出，XEFG和XFEM精度随着自由度的增加均提高，然而在相同节点间距下，XEFG误差更小、精度更高。图6给出了通过XEFG法计算得到的x方向应力，可以看出，x向应力在材料交界面处变化很明显，交界面上下相比交界面左右x向应力更大。
为了与XFEM在计算时间作对比，本文选用同样的节点间距(h=0.1)，在Intel Core i5-4590 Win7系统 MATLAB2015上进行计算，XEFG计算时间为16.2 s，XFEM计算时间为3.9s，可以看出XEFG法由于可以共享更多的节点信息，因此增加了计算时间。
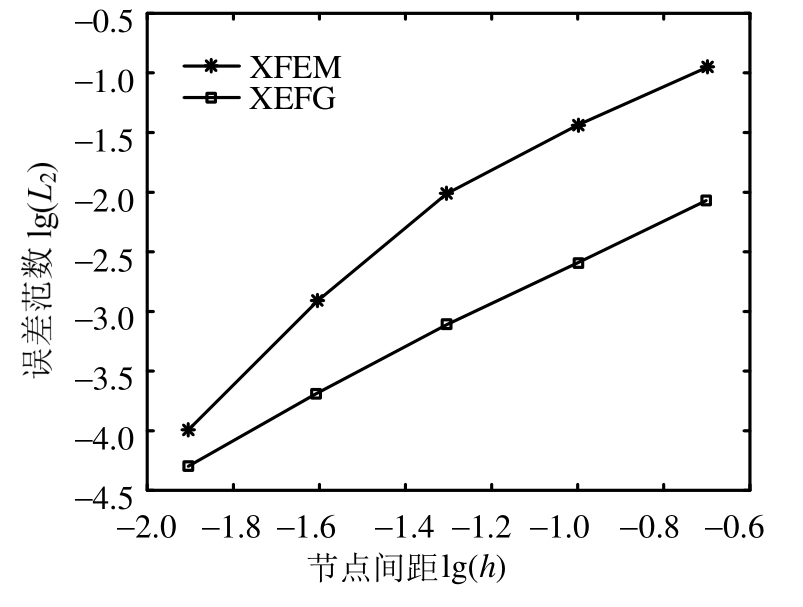
图5 位移范数收敛图
Fig.5 Rate of convergence in displacement norm
图6 x向应力
Fig.6 Stress contour in the x-direction
取无量纲边长为L=2的方形板，考虑如图7所示的含四个圆形夹杂(半径r=0.2)和图8所示的含九个圆形夹杂(半径 r = 0 .133)两种情况，方板下端固定，上端施加均布荷载p=1。方形板弹性模量E1=1，泊松比ν1=0.3；夹杂弹性模量E2=10，泊松比ν2=0.3，按平面应力问题进行计算。节点影响域半径取为 1.5，每个背景网格里面布置6×6个高斯点。
图7 含四个圆形夹杂方形板节点离散
Fig.7 Distribution of nodes and location of enriched nodes for four inclusions
图8 含九个圆形夹杂方形板节点离散
Fig.8 Distribution of nodes and location of enriched nodes for nine inclusions
在含四个圆形夹杂方形板计算过程中，每个背景网格里面布置6×6个高斯点，节点影响域半径取为1.5，图9给出了XEFG和XFEM计算得到x=1处竖向位移分布，很明显节点间距(h=0.1)一致的情况下，XEFG相比XFEM精度更高。
而在含九个圆形夹杂方形板计算过程中，每个背景网格里面布置6×6个高斯点，节点影响域半径分别取1.4(h=0.1)和1.2(h = 0 .05)，图10给出了XEFG和XFEM计算得到x=1处竖向位移分布，很明显节点间距(h=0.1)一致的情况下，XEFG相比XFEM精度更高。
通过含四个圆形夹杂方板和含九个圆形夹杂方板x=1处竖向位移分布，可以看出位移随着夹杂数目的增多，竖向位移出现小幅度的波动，这是由于圆形夹杂的作用。图11给出了含九个圆形夹杂方板竖向位移分布，由于方板下端固定，方板下端竖向位移最小，同时受材料夹杂界面的影响，竖向位移等值线图呈现波浪状分布。
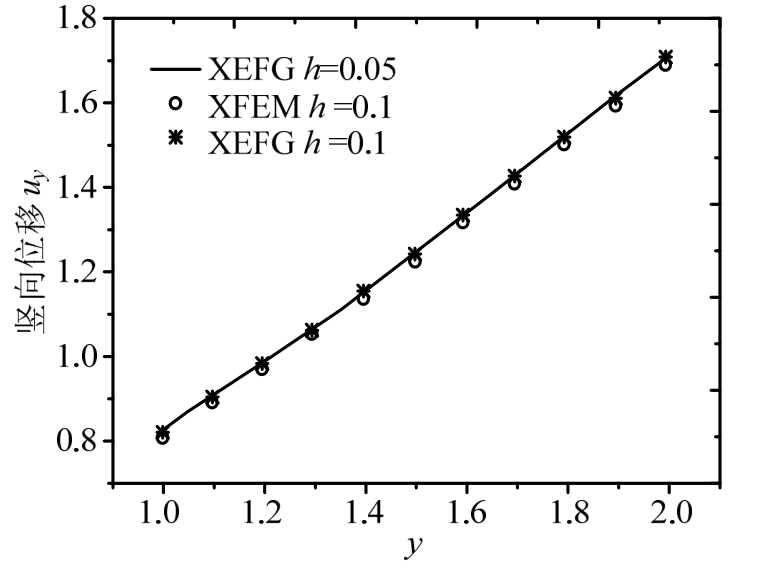
图9 含四个圆形夹杂方形板x=1处竖向位移分布
Fig.9 Comparison of the y-displacement along x=1 between XEFG and XFEM for four inclusions
图10 含九个圆形夹杂方形板x=1处竖向位移分布
Fig.10 Comparison of the y-displacement along x=1 between XEFG and XFEM for nine inclusions
图11 含九个圆形夹杂方形板竖向位移分布
Fig.11 Displacement contour in the y-direction of nine inclusions
(1)本文将滑动Kriging插值引入到XEFG法中提出了一种改进的XEFG法，并将其应用到含夹杂非均质材料问题。夹杂不连续界面通过水平集方法进行描述，同时利用无网格法的单位分解性质，构造了无网格不连续近似函数，其扩展项由水平集函数确定，并基于伽辽金法推导了弹性力学方程的离散弱形式。
(2)由于MK形函数具有Kronecker delta函数性质，因此在位移边界条件的施加上更为方便。同时相比有限元基函数，MK形函数更加光滑连续，因此在相同节点分布的情况下，XEFG相比XFEM精度更高，收敛速度更快。
参考文献：
[1]程丽. 带有夹杂的非均质体扩展有限元程序研制及应用[D]. 南京: 河海大学, 2007.Cheng Li. Extended finite element method program research and application for in-homogeneous material with inclusions [D]. Nanjing: Hohai University, 2007. (in Chinese)
[2]马文涛, 许艳, 马海龙. 修正的内部基扩充无网格法求解多裂纹应力强度因子[J]. 工程力学, 2015, 32(10):18―24.Ma Wentao, Xu Yan, Ma Hailong. Solving stress intensity factors of multiple cracks by using a modified intrinsic basis enriched meshless method [J]. Engineering Mechanics, 2015, 32(10): 18―24. (in Chinese)
[3]邵玉龙, 段庆林, 李锡夔, 等. 功能梯度材料的二阶一致无网格法[J]. 工程力学, 2017, 34(3): 15―21.Shao Yulong, Duan Qinglin, Li Xikui, et al.Quadratically consistent meshfree method for functionally graded materials [J]. Engineering Mechanics, 2017, 34(3): 15―21. (in Chinese)
[4]Organ D, Fleming M, Terry T, et al. Continuous meshless approximations for nonconvex bodies by diffraction and transparency [J]. Computational Mechanics, 1996, 18(3):225―235.
[5]Cordes L W, Moran B. Treatment of material discontinuity in the element-free Galerkin method [J].Computer Methods in Applied Mechanics and Engineering, 1996, 139: 75―89.
[6]蔡永昌, 朱合华. 在无单元法里直接准确施加位移边界条件和材料不连续条件[J]. 计算力学学报, 2004,21(6): 740―745.Cai Yongchang, Zhu Hehua. Direct imposition of essential boundary and material discontinuity conditions in the meshless method [J]. Chinese Journal of Computational Mechanics, 2004, 21(6): 740―745. (in Chinese)
[7]Ventura G, Xu J X, Belytschko T. A vector level set method and new discontinuity approximations for crack growth by EFG [J]. International Journal for Numerical Methods in Engineering, 2002, 54(6): 923―944.
[8]刘学聪, 章青, 夏晓舟. 一种新型裂尖加强函数的显式动态扩展有限元法[J]. 工程力学, 2017, 34(10):10―18.Liu Xuecong, Zhang Qing, Xia Xiaozhou. A new enrichment function of crack tip in XFEM dynamics by explicit time algorithm [J]. Engineering Mechanics,2017, 34(10): 10―18. (in Chinese)
[9]王振, 余天堂. 模拟三维裂纹问题的自适应多尺度扩展有限元法[J]. 工程力学, 2016, 33(1): 32―38.Wang Zhen, Yu Tiantang. Adaptive multiscale extended finite element method for modeling three-dimensional crack problems [J]. Engineering Mechanics, 2016, 33(1):32―38. (in Chinese)
[10]江守燕, 杜成斌. 弱不连续问题扩展有限元法的数值精度研究[J]. 力学学报, 2012, 44(6): 1005―1015.Jiang Shouyan, Du Chengbin. Study on numerical precision of extended finite element methods for modeling weak discontinuities [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6):1005―1015. (in Chinese)
[11]应宗权, 杜成斌, 王友元. 颗粒增强复合材料的扩展有限元模拟方法[J]. 水利学报, 2011, 42(2): 198―203.Ying Zongquan, Du Chengbin, Wang Youyuan.Numerical simulation of particle reinforced composite using extended finite element method [J]. Journal of Hydraulic Engineering, 2011, 42(2): 198―203. (in Chinese)
[12]马文涛, 师俊平, 李宁. 水平集和无网格耦合法在裂纹扩展中的应用[J]. 岩土力学, 2012, 33(11):3447―3453.Ma Wentao, Shi Junping, Li Ning. Coupling of level set and meshless method and its application to crack propagation [J]. Rock and Soil Mechanics, 2012, 33(11):3447―3453. (in Chinese)
[13]马文涛, 李宁, 师俊平. 基于单位分解的扩展径向点插值无网格法[J]. 岩土力学, 2012, 33(12):3795―3800.Ma Wentao, Li Ning, Shi Junping. An enriched radial point interpolation meshless method based on partition of unity [J]. Rock and Soil Mechanics, 2012, 33(12):3795―3800. (in Chinese)
[14]Nguyen N T, Bui T Q, Zhang C, et al. Crack growth modeling in elastic solids by the extended meshfree Galerkin radial point interpolation method [J].Engineering Analysis with Boundary Elements, 2014, 44:87―97.
[15]Gu L. Moving kriging interpolation and element-free Galerkin method [J]. International Journal for Numerical Methods in Engineering, 2003, 56(1): 1―11.
[16]王峰. 改进的无网格法求解温度场和温度应力及其在水工结构分析中的应用[D]. 大连: 大连理工大学,2015.Wang Feng. Improved meshless method for the solution of temperature field and thermal stress and its application to hydraulic structure analysis [D]. Dalian: Dalian University of Technology, 2015. (in Chinese)
[17]Watts G, Pradyumna S, Singha M K. Nonlinear analysis of quadrilateral composite plates using moving kriging based element free Galerkin method [J]. Composite Structures, 2017, 159: 719―727.
[18]Bui T Q, Nguyen M N, Zhang C. A moving Kriging interpolation-based element-free Galerkin method for structural dynamic analysis [J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(13/14/15/16): 1354―1366.
[19]Li X G, Dai B D, Wang L H. A moving Kriging interpolation-based boundary node method for two-dimensional potential problems [J]. Chinese Physics B, 2010, 19(12): 120202.
[20]Zheng B J, Dai B D. A meshless local moving Kriging method for two-dimensional solids [J]. Applied Mathematics and Computation, 2011, 218(2): 563―573.
[21]Osher S, Sethian J A. Fronts propagating with curvaturedependent speed: Algorithm based on Hamilton-Jacobi formulation [J]. Journal of Computational Physics, 1988,79(1): 12―49.
[22]Osher S, Fedkiw R P. Level set methods: an overview and some recent results [J]. Journal of Computational Physics, 2001, 169(2): 463―502.
[23]刘欣. 无网格方法[M]. 北京: 科学出版社, 2011.Liu Xin. Meshless method [M]. Beijing: Science Press,2011. (in Chinese)
[24]Sukumar N, Chopp D L, Moës N, et al. Modeling holes and inclusions by level sets in the extended finite-element method [J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190: 6183―6200.
[25]Moës N, Cloirec M, Cartraud P, et al. A computational approach to handle complex microstructure geometries[J]. Computational Methods in Applied Mechanics and Engineering, 2003, 192: 3163―3177.
NUMERICAL SIMULATION OF INHOMOGENEOUS MATERIAL USING EXTENDED ELEMENT-FREE GALERKIN METHOD
WANG Feng1,2, LIN Gao3, ZHOU Yi-hong1,2, ZHAO Chun-ju1,2, ZHOU Hua-wei1,2
(1. Hubei Key Laboratory of Construction and Management in Hydropower Engineering, China Three Gorges University, Yichang 443002, China;2. College of Hydraulic & Environmental Engineering, China Three Gorges University, Yichang 443002, China;3. School of Hydraulic Engineering, Dalian University of Technology, Dalian 116024, China)
Abstract:Extended element-free Galerkin method (XEFG) is proposed to solve inhomogeneous materials with inclusions based on moving Kriging interpolation. Level set functions are used to represent the geometric interfaces of inclusions and to enrich moving Kriging shape functions in constructing a discontinuous displacement field. The displacement boundary condition can be enforced exactly as the shape functions constructed from the moving Kriging interpolation possess the Kronecker delta property, compared with traditional moving least square shape functions. The key techniques of XEFG are presented, including the construction of displacement pattern, and the establishment of the displacement governing equation. Finally, the examples of single inclusion and multiple inclusions show that XEFG method have higher accuracy and better convergence, compared with the extended finite element method.
Key words:inhomogeneous material; extended element-free Galerkin method; moving Kriging interpolation;meshless method; level set method
中图分类号：TU599
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.04.0291
文章编号：1000-4750(2018)08-0014-07
收稿日期：2017-04-17；修改日期：2018-01-18
基金项目：国家自然科学基金项目(51479103)；中国博士后科学基金项目(2013T60283)
通讯作者：王 峰(1987―)，男，山东人，讲师，博士，主要从事水工结构温控及抗震数值计算研究(E-mail: wangfeng@mail.dlut.edu.cn).
作者简介：
林 皋(1929―)，男，江西人，教授，博导，中科院院士，主要从事核电与水工结构抗震研究(E-mail: gaolin@dlut.edu.cn);
周宜红(1966―)，男，湖北人，教授，博士，博导，主要从事水工施工组织和管理研究(E-mail: zyhwhu2003@163.com);
赵春菊(1974―)，女，湖北人，教授，博士，博导，主要从事水工施工组织管理与系统仿真研究(E-mail: chunju.zhao@163.com);
周华维(1988―)，女，湖北人，博士生，主要从事大体积混凝土温度控制研究(E-mail: zhouhuawei1988@163.com).