线性元时程积分按最大模自适应步长公式的证明

袁 全1，袁 驷2，李 易1，闫维明1，邢沁妍2

(1．北京工业大学建筑工程学院，工程抗震与结构诊治北京市重点实验室，北京 100124；2．清华大学土木工程系，土木工程安全与耐久教育部重点实验室，北京 100084)

摘 要：该文对运动方程时程积分解法曾提出一种线性有限元自适应步长求解的算法，给出了按最大模自适应步长的计算公式，其中含有步长h的5/2阶的分数阶次。该文对该公式给出数学证明，并通过单自由度和多自由度的数值算例验证了其5/2分数阶次是最优的。

关键词：有限元法；时程积分；线性单元；自适应步长；最大模

结构动力响应问题归结为时域上的常微分方程初值问题，最常用的方法是时程积分的方法[1―3]。此类方法的收敛精度、数值稳定性、计算效率等都强烈依赖于时间步长的选择和优化。因此，自适应步长的研究就自然地成为近些年的研究热点[4―7]。纵观现有的自适应步长方法，大都是针对时域上离散点的解答，可在一定程度上控制其误差扩散、改善计算精度，但尚未见到能够在时域上逐点按最大模严格控制误差的自适应步长求解。

袁驷等在文[8]中提出一种线性有限元时程积分的自适应步长解法。该法采用最简单的线性单元，构建了单步法递推公式，进而基于EEP(单元能量投影)超收敛计算技术[9―11]，实现了自适应步长求解，可在整个时域上得到误差分布均匀且逐点按最大模满足给定误差限的解答；其中的自适应步长的计算，简单高效，一般不超过2次迭代即得到优化的步长。文[8]给出了步长计算公式，但没有给出证明。本文给出该公式的数学证明，并通过数值试验验证该式中5/2阶的分数阶次是最优的。

1 公式证明与评述

1.1 步长公式的数学证明

文[8]的自适应步长求解的目标为，在精确解未知的情况下，事先给定误差限Tl，寻求一个优化的步长h，使得在该单元e上有限元解答uh按最大模度量满足给定的误差限 Tl，即满足。对于单自由度问题，设已给定初始步长h0并已求得其上的线性有限元解uh和EEP超收敛解u*，文[8]中给出的步长计算公式为：

其中，α≤1是乘以 Tl的一个安全系数。以下将给出式(1)的数学证明，然后将其推广到多自由度问题。

首先，根据有限元数学理论[12]，对于线性元解的误差在全时域Ω上有如下的最大模估计：

其中：

考虑到本文方法是在一个单元上求解，其定义域Ω应代换为单元e，因此当前单元上的最大模估计为：

又注意到式(3)右端的积分定义于局部单元区间[t1,t2]上，所以其值与单元长度 h=t2- t1有关，根据积分中值定理可得：

对于较小的h，ü在单元上近似为常数(即略掉h阶及更高阶微量)，与常数C1合并，则式(3)变为：

即在单个单元上，线性元解uh一般按步长h的5/2阶收敛，此为分数阶次的来源。实际求解中，其精确解u用EEP超收敛解u*代换，式(5)可写成更为实用的。

则用式(6)可估算常数：

而新的单元长度 h应尽量使得即再对Tl乘以安全系数α，便有式(1)。

1.2 几点评述

1)以上证明中，最本质的是有限元解答的最大模估计式(2)，而这个估计是很常规的、一般性的，同样适用于 n(＞1)个自由度体系的问题。实际计算时，用单自由度问题的公式(1)计算出每一个位移分量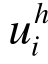应该调整的步长：

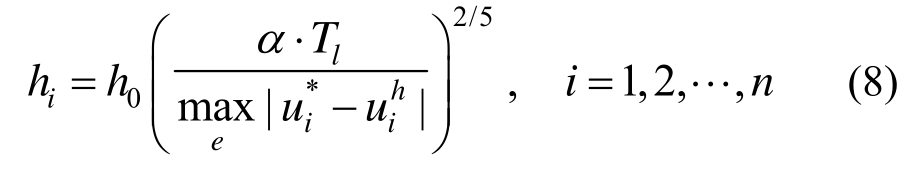
最终的步长取其最小值，即：

2)证明并不依赖EEP超收敛解u*，只要能够有效地估计误差，用其他方法获得超收敛解代替u*亦可。

3)安全系数α的引入是实施上的考虑，使得计算出来的步长偏保守一些，与数学证明也无直接关系，以下数值算例中总取α = 1。

2 数值算例

式(5)和式(6)的估计是自适应步长调整的关键，式(5)是理论公式，式(6)是实用公式。本节给出单自由度和多自由度算例，用以验证上述两个估计式中的分数5/2阶为最优。

以下分别记最大模误差对于多自由度问题，取各个位移分量最大模误差的最大者。对于给定的误差限Tl入误差比

2.1 单自由度算例

考虑有阻尼体系在简谐荷载作用下的反应，其运动方程为：u(0)=0和ü ( 0) = 1 。取第一个单元计算，用理论公式和实用公式求其最佳步长，亦即使误差比取Tl=1/1000，分别用2阶、5/2阶和3阶的估计式计算，初始步长分别取为h0=0.2和h0=0.3。

数值结果列于表1和表2，可以看出无论是用精确解还是 EEP解计算，二者的结果是高度一致的：1)都是5/2阶收敛最快，验证了理论公式的正确性；2)二者数值精度的差别仅在小数点后第3位上，表明实用公式是有效和可靠的。有鉴于此，以下仅给出用EEP解计算的结果。图1和图2给出了不同阶数收敛的情况。

表1(a) 不同阶数的收敛情况(h0=0.2，精确解)
Table 1(a) The result of convergence wisth different orders (h0=0.2, exact solution)

迭代次数i 2阶 5/2阶 3阶0 1 2 3 4 5 6 7 8 h max h e hmax h e hmax h e 0.200000 0.597275 0.200000 0.597275 0.200000 0.597275 0.258787 1.188146 0.245788 1.034636 0.237486 0.943672 0.237415 0.942913 0.242462 0.997553 0.242120 0.993784 0.244496 1.020127 0.242701 1.000175 0.242624 0.999333 0.242072 0.993253 0.242684 0.999987 0.242678 0.999929 0.242893 1.002301 0.242685 1.000001 0.242684 0.999992 0.242614 0.999220 0.242685 1.000000 0.242685 0.999999 0.242709 1.000265 0.242685 1.000000 0.242676 0.999910

表1(b) 不同阶数的收敛情况(h0=0.2，EEP解)
Table 1(b) The result of convergence with different orders (h0=0.2，EEP solution)

迭代次数i 0 1 2 3 4 5 6 7 8 2阶 5/2阶 3阶h e*hm axh e*hm axh e*hmax0.200000 0.600658 0.200000 0.600658 0.200000 0.600658 0.258057 1.189217 0.245233 1.036451 0.237040 0.945886 0.236639 0.941592 0.241746 0.997250 0.241476 0.994258 0.243868 1.020984 0.242013 1.000211 0.241940 0.999407 0.241349 0.992844 0.241992 0.999984 0.241988 0.999939 0.242217 1.002485 0.241994 1.000001 0.241993 0.999994 0.241916 0.999142 0.241994 1.000000 0.241994 0.999999 0.242020 1.000297 0.241994 1.000000 0.241984 0.999898

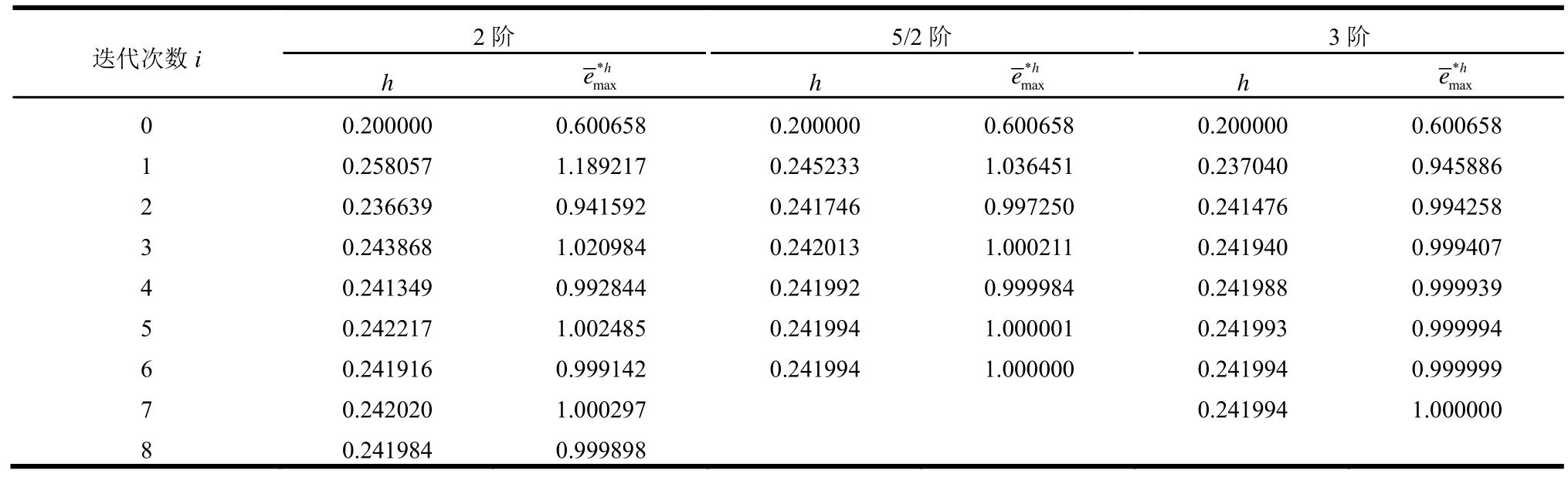
表2(a) 不同阶数的收敛情况(h0=0.3，精确解)
Table 2(a) The result of convergence with different orders (h0=0.3, exact solution)

迭代次数i 0 1 2 3 4 5 6 7 8 2阶 5/2阶 3阶h max h e hmax h e hmax h e 0.300000 1.769769 0.300000 1.769769 0.300000 1.769769 0.225509 0.821797 0.238756 0.957238 0.248018 1.059998 0.248760 1.068532 0.242967 1.003116 0.243247 1.006220 0.240651 0.977709 0.242664 0.999777 0.242745 1.000663 0.243379 1.007679 0.242686 1.000016 0.242691 1.000071 0.242449 0.997406 0.242684 0.999999 0.242685 1.000008 0.242765 1.000882 0.242685 1.000000 0.242685 1.000001 0.242658 0.999701 0.242685 1.000000 0.242694 1.000102

表2(b) 不同阶数的收敛情况(h0=0.3，EEP解)
Table 2(b) The result of convergence with different orders (h0=0.3, EEP solution)

迭代次数i 2阶 5/2阶 3阶h e h*h e h*h*h max max emax 0 0.300000 1.789069 0.300000 1.789069 0.300000 1.789069 1 0.224289 0.815462 0.237723 0.953231 0.247122 1.058104 2 0.248374 1.072606 0.242321 1.003646 0.242514 1.005794 3 0.239820 0.976018 0.241969 0.999721 0.242047 1.000594 4 0.242749 1.008420 0.241996 1.000021 0.241999 1.000061 5 0.241733 0.997105 0.241993 0.999998 0.241994 1.000006 6 0.242084 1.001002 0.241994 1.000000 0.241994 1.000001 7 0.241962 0.999654 0.241994 1.000000 8 0.242004 1.000120

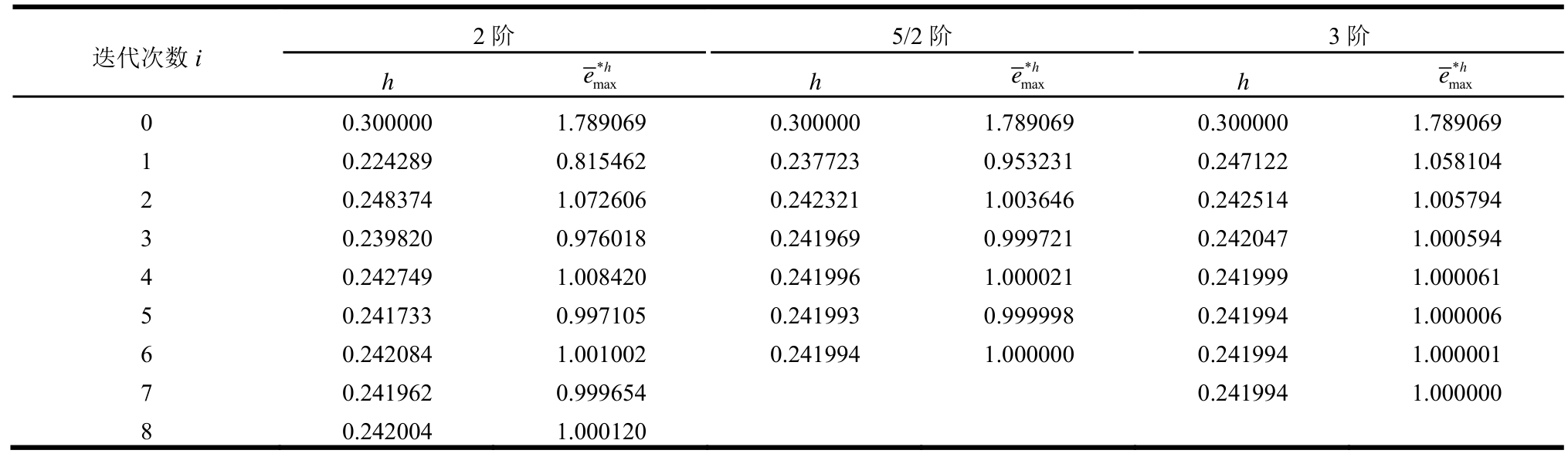
图1 初始步长h0=0.2的收敛结果
Fig.1 The result of convergence with h0=0.2

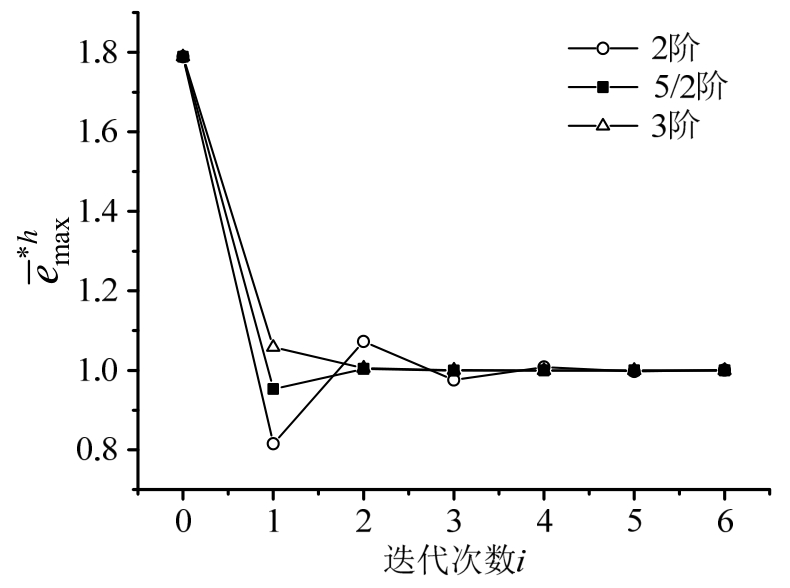
图2 初始步长h0=0.3的收敛结果
Fig.2 The result of convergence with h0=0.3

2.2 多自由度算例

考虑三层剪切型框架结构体系，其状态用三质点离静止位置的位移表示。其质量矩阵、阻尼矩阵、刚度矩阵为：

简谐荷载向量为，初始位移取零，初始速度为，误差限，初始步长分别取0.02和0.01，收敛结果分别如图3和图4所示。可见，无论初始步长偏大或偏小，5/2阶均为最快收敛，与单自由度算例是一致的。通常来说，在收敛效率上，5/2阶优于3阶，3阶优于2阶。

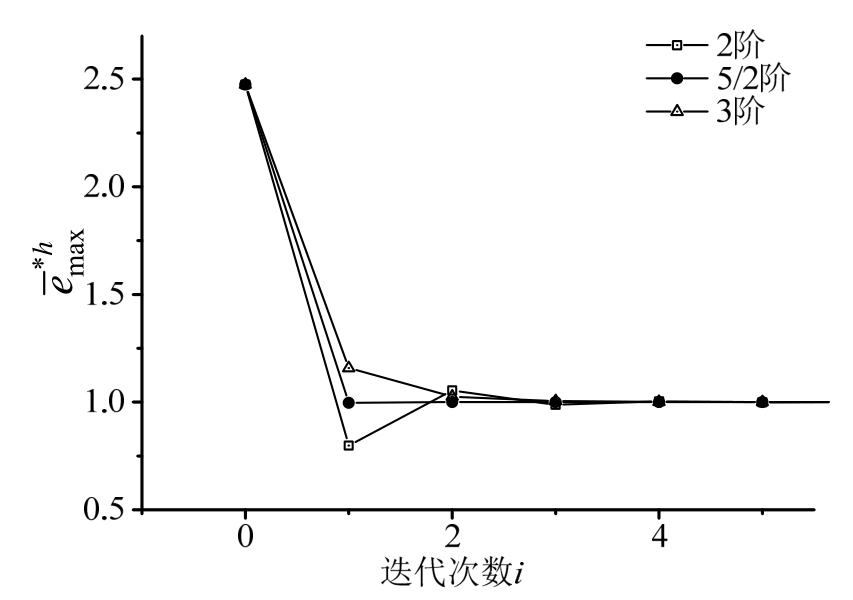
图3 初始步长h0=0.2的收敛结果
Fig.3 The result of convergence with h0=0.2

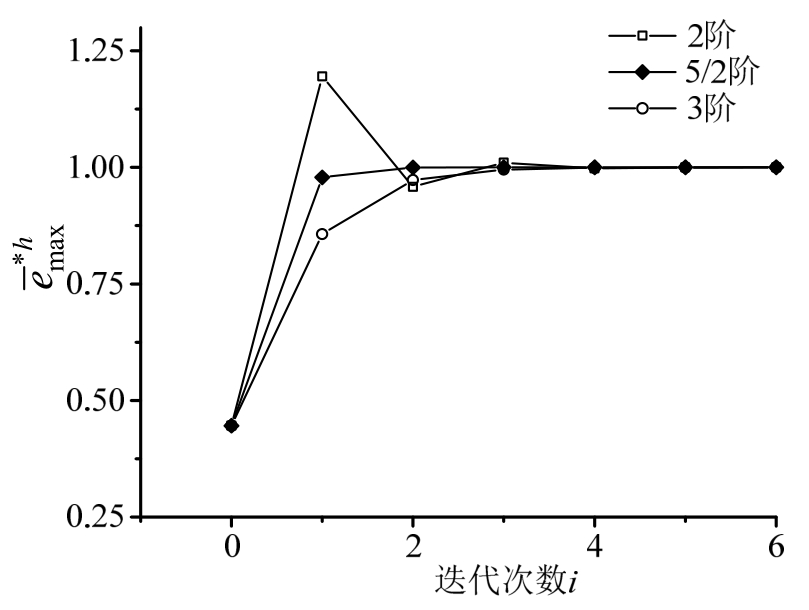
图4 初始步长h0=0.01的收敛结果
Fig.4 The result of convergence with h0=0.01

3 结论

经本文证明以及数值试验验证，文[8]提出的自适应步长公式(1)不失为一个简洁、合理、高效的自适应步长计算方案。

参考文献：

[1]Clough R W. Dynamics of structures [M]. New York:McGraw-Hill, 1995.

[2]刘晶波, 杜修力. 结构动力学[M]. 北京: 机械工业出版社, 2005.Liu Jingbo, Du Xiuli. Structural dynamics [M]. Beijing:China Machine Press, 2005. (in Chinese)

[3]Zhong W X, Williams F W. A precise time step integration method [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1994, 208(6): 427―430.

[4]Hibbitt H D, Karlsson B I. Analysis of Pipe Whip [R].Palo Alto: Electric Power Research Institute, 1979.

[5]Bergan P L G, Mollestad E. An automatic time-stepping algorithm for dynamic problems [J]. Computer Methods in Applied Mechanics and Engineering, 1985, 49(3):299―318.

[6]Zienkiewicz C, Xie Y M. A simple error estimator and adaptive time stepping procedure for dynamic analysis[J]. Earthquake Engineering & Structural Dynamics,1991, 20(7): 871―887.

[7]Lages E N, Silveira E S S, Cintra D T, et al. An adaptive time integration strategy based on displacement history curvature [J]. International Journal for Numerical Methods in Engineering, 2013, 93(12): 1235―1254.

[8]袁驷, 袁全, 闫维明, 等. 运动方程自适应步长求解的一个新进展——基于EEP超收敛计算的线性有限元法[J]. 工程力学, 2018, 35(2): 13―20.Yuan Si, Yuan Quan, Yan Weiming, et al. New development of solution of equations of motion with adaptive time-step size — linear FEM based on EEP super convergence technique [J]. Engineering Mechanics, 2018, 35(2): 13―20. (in Chinese)

[9]袁驷, 王枚. 一维有限元后处理超收敛解答计算的EEP法[J]. 工程力学, 2004, 21(2): 1―9.Yuan Si, Wang Mei. An element-energy-projection method for post-computation of super-convergent solutions in one-dimensional FEM [J]. Engineering Mechanics, 2004, 21(2): 1―9. (in Chinese)

[10]袁驷, 林永静. 二阶非自伴两点边值问题 Galerkin有限元后处理超收敛解答计算的EEP法[J]. 计算力学学报, 2007, 24(2): 142―147.Yuan Si, Lin Yong-jing. An EEP method for post-computation of super-convergent solutions in one-dimensional Galerkin FEM for second order non-self-adjoint boundary-value problem [J]. Chinese Journal of Computational Mechanics, 2007, 24(2): 142―147. (in Chinese)

[11]Yuan Si, Xing Qinyan, Wang Xu, et al. Self-adaptive strategy for one-dimensional finite element method based on EEP method with optimal super-convergence order[J]. Applied Mathematics and Mechanics (English version), 2008, 29(5): 591―602.

[12]Strang G, Fix G J. An analysis of the finite element method [M]. 2nd ed. Wellesley MA: Wellesley-Cambridge Press, 2008: 39―50.

PROOF OF ADAPTIVE TIME-STEP SIZE FORMULA BASED ON MAXIMUM NORM IN TIME INTEGRATION OF LINEAR ELEMENTS

YUAN Quan1, YUAN Si2, LI Yi1, YAN Wei-ming1, XING Qin-yan2
(1. Beijing Key Laboratory of Earthquake Engineering and Structural Retrofit, Beijing University of Technology, Beijing 100124, China;2. Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry,Department of Civil Engineering, Tsinghua University, Beijing 100084, China)

Abstract:An algorithm for time integration of motion equations using linear finite elements with adaptive time-step size had been proposed by the authors, in which a formula for the calculation of adaptive time-step size h based on maximum norm, characterized by containing a term of 5/2 order of h, was also presented. This paper gives a mathematical proof for the proposed formula. In addition, the numerical examples of both single and multiple degreed systems are obtained to verify that 5/2 order is optimal.

Key words:FEM; time integration; linear element; adaptive time-step size; maximum norm

中图分类号：TU311; O241.81

文献标志码：A

doi:10.6052/j.issn.1000-4750.2018.03.0106

文章编号：1000-4750(2018)08-0009-05

收稿日期：2017-11-12；修改日期：2018-06-25

基金项目：国家自然科学基金项目(51378293，51078199，51508305)

通讯作者：袁 驷(1953―)，男，北京人，教授，博士，从事结构工程研究(E-mail: yuans@tsinghua.edu.cn).

作者简介：

袁 全(1993―)，男，北京人，硕士生，从事结构工程研究(E-mail: quanyuan_002@163.com);

李 易(1981―)，男，湖北人，副教授，博士，从事工程结构防灾减灾研究(E-mail: yili@bjut.edu.cn);

闫维明(1960―)，男，黑龙江人，研究员，博士，从事工程结构减震控制研究(E-mail: yanwm@bjut.edu.cn);

邢沁妍(1981―)，女，辽宁人，讲师，博士，从事结构工程研究(E-mail: xingqy@tsinghua.edu.cn).