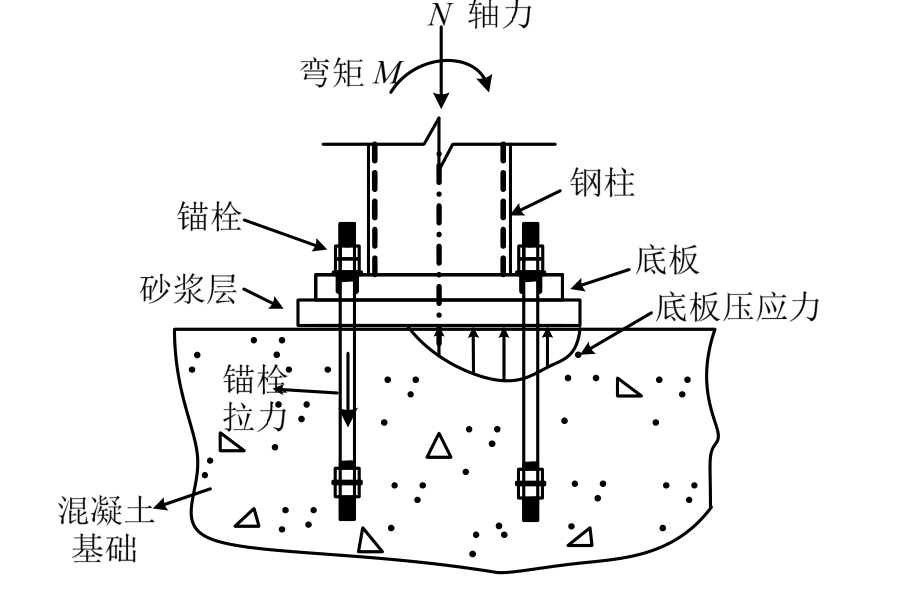
图1 外露式柱脚受力机制
Fig.1 Resistance mechanisms of exposed column base
崔 瑶1,李 浩1,刘 浩1,王晶秋1,唐贞云2
(1. 大连理工大学海岸和近海工程国家重点实验室,大连 116024;2. 北京工业大学城市与工程安全减灾教育重点实验室,北京 100124)
摘 要:该文在外露式柱脚拟静力试验的基础上总结了柱脚在压弯和拉弯状态下的受力机理,提出了两种受力状态下柱脚的屈服承载力、极限承载力及转动刚度的计算公式。该文提出的承载力及转动刚度计算结果与试验结果的误差在10%左右,具有较高的计算精度。在试验研究的基础上还提出了两种状态下柱脚的恢复力模型:在压弯状态下,柱脚的滞回曲线呈“旗帜型”,骨架曲线由不考虑强度退化的双折线模拟;在拉弯状态下,柱脚的承载力大幅度下降,滞回曲线为饱满曲线,骨架曲线为不考虑锚栓屈服后强度增加的理想弹塑性模型。恢复力模型与试验曲线吻合较好,可有效地反映出不同受力状态及不同锚栓布置下的外露式柱脚的弯矩转角行为,可有效用于分析整体框架的抗震性能。
关键词:外露式钢柱脚;锚栓;抗弯承载力;抗弯刚度;恢复力模型
外露式钢柱脚常常应用于中低层钢框架结构中[1―2]。外露式柱脚主要由钢柱、底板、混凝土基础、锚栓和砂浆层组成,如图1所示。柱脚承受弯矩时,一侧锚栓受拉,另一侧底板承压,在混凝土基础配筋合适且底板较厚的情况下,外露式柱脚的力学行为主要由锚栓控制[3]。

图1 外露式柱脚受力机制
Fig.1 Resistance mechanisms of exposed column base
我国外露式柱脚的设计主要参考《钢结构连接节点设计手册》(第2版)[4]和《钢结构设计手册》(上册)[5],对柱脚承载力进行验算和构造设计,但是设计承载力以屈服承载力为标准进行计算并未给出极限承载力的计算以及柱脚的延性要求。
美国规范[6]对于底板的设计采用悬臂板模型,底板压应力假设为矩形分布,锚栓达到抗拉强度时即为柱脚极限抗弯承载力;欧洲规范 Eurocode3[7]规定柱脚的抗弯承载力由分别对受拉锚栓中心与受压柱翼缘中心取矩的最小值来得到;日本采用无限刚性底板假设,同美国类似考虑柱脚极限承载力,并且由锚栓控制[8]。
国内外对钢框架抗震性能展开大量研究[9―17]。钢柱脚作为重要节点,学者对其抗震性能展开大量试验[8, 11―13]和有限元[14―16]研究,主要研究外露式柱脚在轴压力下的抗震性能。而在地震作用下,框架边柱有可能处于受拉状态,因此外露式柱脚在轴拉力下的抗震性能需要进一步的试验研究。部分学者通过试验与理论分析给出了柱脚承载力计算公式[11―14]以及转动刚度的计算公式[11―12, 14],但多数仅研究了小变形下的屈服承载力,未考虑大变形下柱脚行为以及极限承载力。而多数震害研究表明,大震作用下柱脚容易出现较大变形,其变形行为及承载力会对结构整体在大震作用下的行为产生较大影响。因此,也需对柱脚大变形行为进行研究。
通常情况下在抗震设计及抗震验算时并未考虑外露式柱脚实际的滞回性能,但已有的研究指出外露式柱脚的力学行为对钢框架的整体抗震性能有重要的影响[17―18]。外露式柱脚的力学行为主要由锚栓来控制,提高锚栓延性可以有效提高柱脚的延性,柱脚延性的提高可以使结构更多构件参与到变形耗能中去,从而提高结构的整体耗能能力[17―18]。
针对以上问题,该文在外露式柱脚受弯试验结果[19]的基础上进一步展开理论分析,通过传力机制分析柱脚在循环荷载下的受力特点,建立骨架线模型,并给出柱脚在屈服状态和极限状态下承载力计算公式以及转动刚度公式,根据试验结果给出柱脚卸载和滞回特性,最终得到外露式柱脚恢复力模型,可为整体框架弹塑性分析提供参考。
通过5个试件研究了锚栓数量、锚栓布置方式、轴压比等参数对外露式柱脚抗弯性能的影响。试件由高 1200 mm 的方钢管(200 mm×12 mm)和底板(350 mm×350 mm×40 mm)组成,钢柱和底板均采用Q235钢。锚栓直径为20 mm,总长为600 mm,其中螺纹段长度90 mm,采用热轧与冷拔两种材料,其应力-应变曲线如图2所示,其中,热轧锚栓屈服强度276 MPa,抗拉强度486 MPa;冷拔锚栓抗拉强度 651 MPa。基础梁高 600 mm,采用商品混凝土,混凝土强度等级为C40,为避免基础梁破坏配置了足量钢筋。在试件浇筑的同时,按照规范要求制作了混凝土轴心受压标准试件,在相同养护条件下,标准试件28 d的抗压强度平均值为41 MPa。在底板和基础梁间灌注40 mm厚的砂浆垫层。试件参数见表1,锚栓的具体布置如图3。
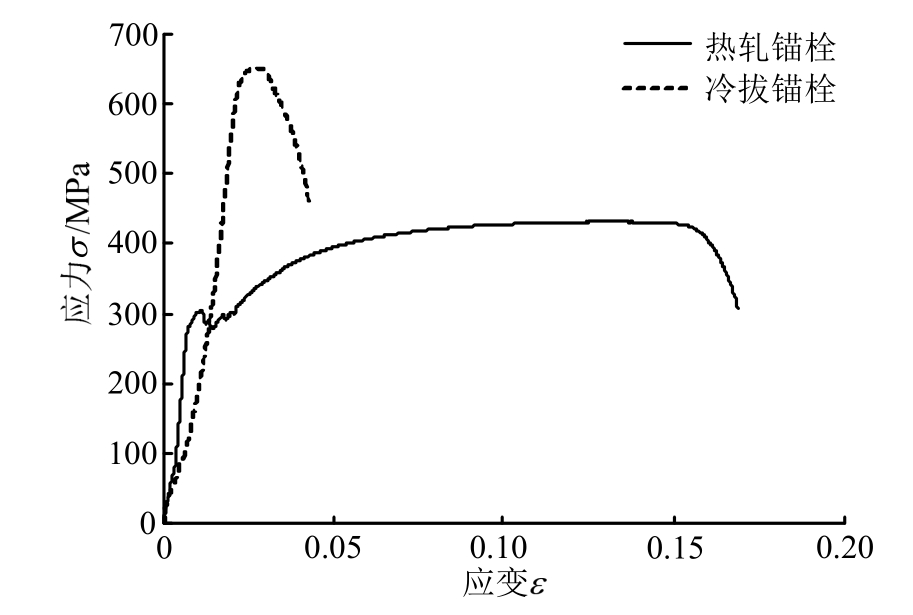
图2 锚栓材料的应力-应变关系
Fig. 2 Strain-stress curves of anchor rods
表1 试件参数
Table 1 Parameters of specimens
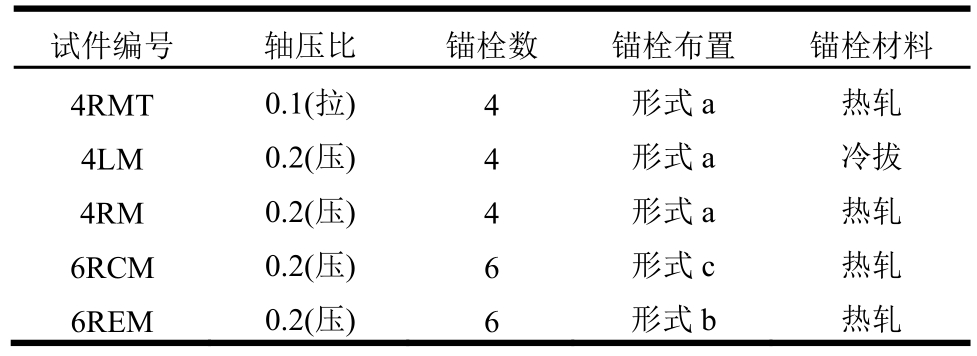
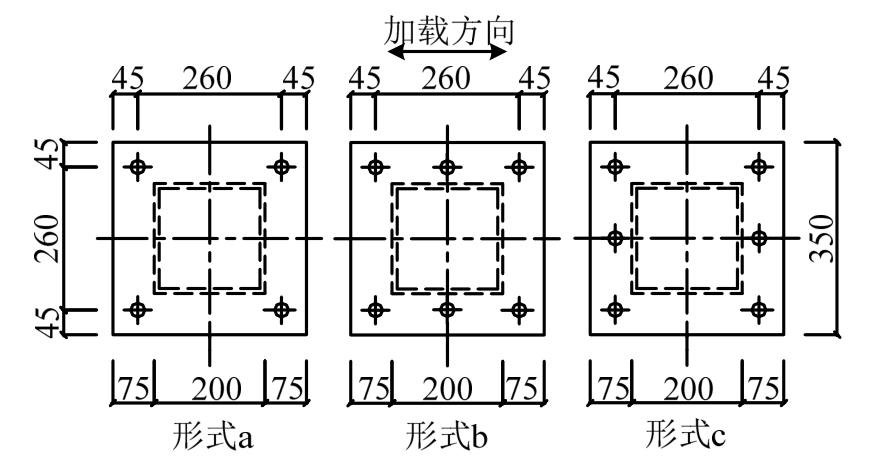
图3 锚栓布置示意图 /mm
Fig.3 Arrangement of anchor rods
本次试验旨在研究中低层钢框架中柱的力学性能,采用2/3缩尺模型,竖向荷载与水平荷载均施加于钢柱顶部(相当于底层钢柱的反弯点处),钢柱与底板焊接,通过锚栓与基础梁连接,基础梁固定在地面,并在钢柱顶部安装侧向滚动支撑,有效防止加载过程中试件出现面外变形。
加载装置如图4所示。竖向荷载通过1000 kN液压作动器在柱顶施加,水平荷载通过 500 kN电液伺服作动器施加。
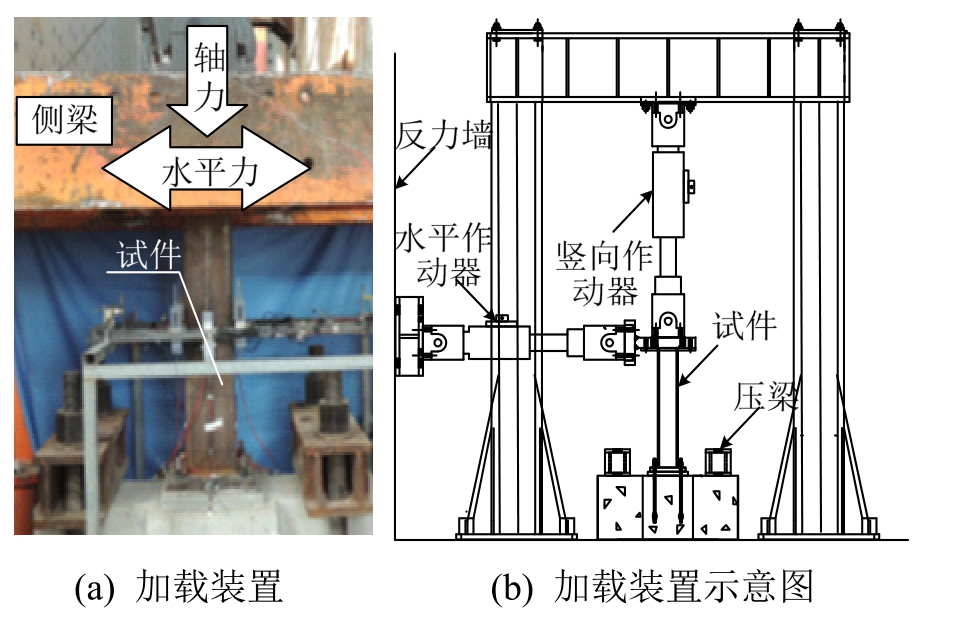
图4 试验加载装置图
Fig.4 Test setup
正式加载时,首先施加目标竖向荷载,受压试件为540 kN(轴压比为0.2),受拉试件为270 kN(轴压比为-0.1),然后利用 500 kN电液伺服作动器施加水平荷载,采用位移控制的加载方式,加载的位移角分别为0.25%、0.5%、1%、2%、3%、4%、6%、8%和10%,每级循环2次。
整个试验过程中,钢柱没有屈服,破坏集中在柱脚连接处。根据试件承受的轴力及锚栓材料的不同,破坏模式主要分为3种,如图5所示。

图5 试件破坏形态
Fig.5 Failure mode of specimens
当试件承受压力、采用热轧锚栓(4RM、6RCM及6REM)时,柱顶转角达到3%锚栓屈服,锚栓屈服后柱脚能够继续传递荷载,加载结束锚栓依然没有被拉断;当试件承受压力、采用冷拔锚栓时(4LM),柱顶转角加载至6%的过程中,锚栓突然被拉断,试验结束;当试件承受拉力、采用热轧锚栓时(4RMT),柱顶转角达到 0.5%时,底板与砂浆层已经完全分离,位移角为3%时即被突然拉断。
图6给出了所有试件的弯矩转角曲线,可以看出4个受压试件为“旗帜型”曲线,捏缩效应明显,而受拉试件近似于平行四边形,表明轴力方向的改变使柱脚的受力性能发生本质变化,接下来的讨论都将分压弯状态和拉弯状态展开。
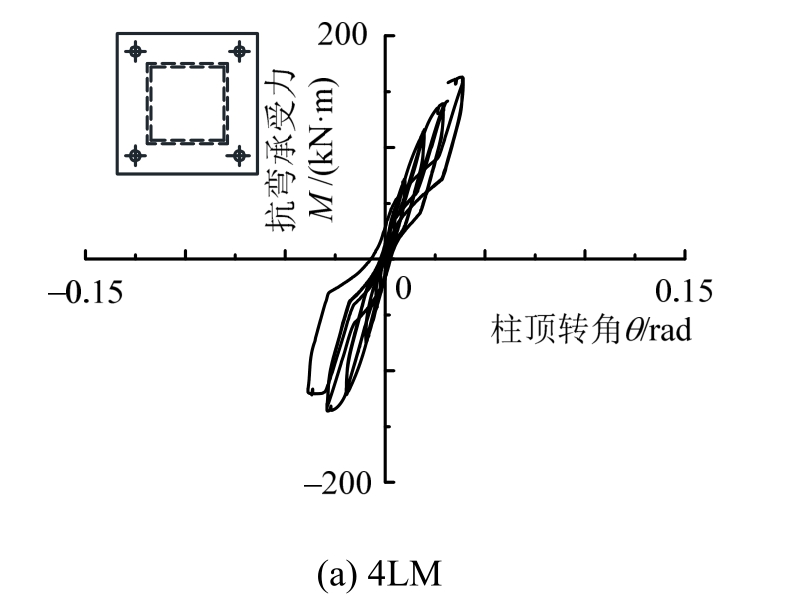

图6 M-θ滞回曲线
F i g.6 M-θ h y s t e r e t i c l o o p s
结合试验得到压弯状态下外露式柱脚滞回曲线模型如图7所示,图中My为屈服抗弯承载力,为锚栓达到屈服时柱脚的抗弯承载力;Mu为极限抗弯承载力,为锚栓达到极限强度时柱脚的抗弯承载力;θy为锚栓屈服时柱顶转角,θu为锚栓达到极限强度时的柱顶转角。柱脚节点具体过程的受力状态如图8所示。
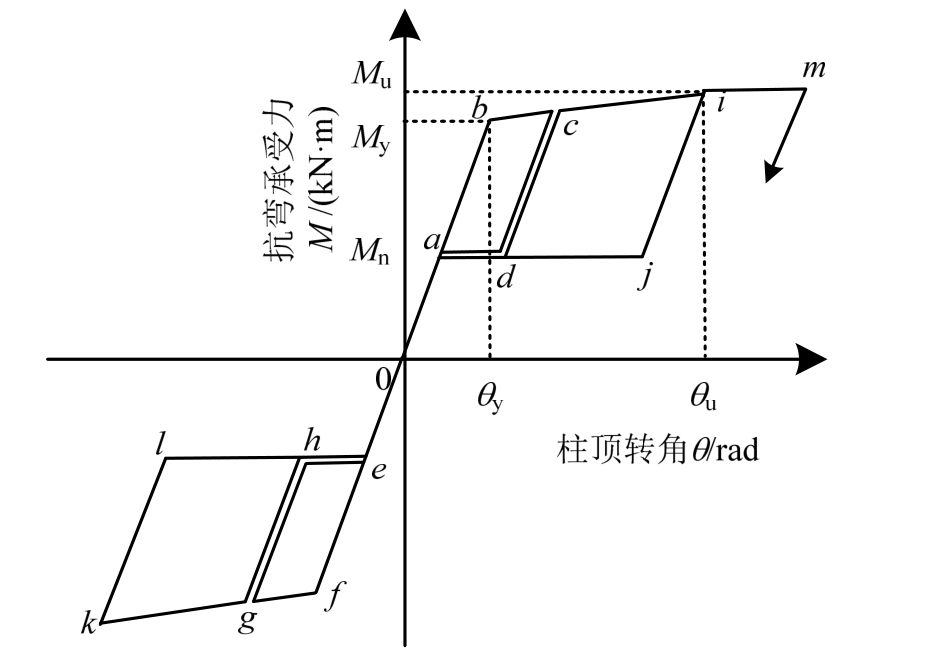
图7 外露式钢柱脚受压弯状态下恢复力模型
Fig.7 Hysteretic model of exposed column base under compressive axial force

图8 外露式钢柱脚压弯状态下受力机制
Fig.8 Resistance mechanisms of exposed column base under compressive axial force
在循环荷载作用下恢复力模型的具体路径为:0→a→b→c→d→a→0→e→f→g→h→e→0→a→d→c→i→j→a→0→e→h→g→k→l→e→0→。
其中,0→a段:锚栓不受力,此时水平荷载产生的弯矩由轴力平衡,Mn为由轴压力产生的平衡弯矩,对于特定的轴力和特定的柱脚几何尺寸该值为定值,由式(1)计算:
式中:N为轴压力;d0为钢柱轴线到钢柱翼缘外侧的距离,即此时假定底板转动点位于受压侧钢柱翼缘处。
a→b段:由a点开始,锚栓开始受力,达到b点时,锚栓开始屈服;b→c段:锚栓开始产生塑性变形,变形量为bc段水平距离;c→d段:在c点处开始卸载,卸载刚度与 0b段的加载刚度相同;d→a段:锚栓不受力,锚栓产生的塑性变形导致柱脚产生空转动,da段与bc段的变形量相同;a→0段:柱脚底板在轴力N的作用下自然回落,在荷载减为0的过程中,转角恢复到0。反向加载与正向加载呈中心对称。需要注意的是再次正向加载时,路径不再是0→a→b→c,而是变为0→a→d→c,主要是由于锚栓产生的塑性变形使再次加载时柱脚产生空转动,此时锚栓不受力,达到d点时,锚栓开始受力,此后的行为与第1圈相似。
结合试验得到拉弯状态下外露式柱脚恢复力模型如图9。

图9 外露式钢柱脚受拉弯状态下恢复力模型
Fig.9 Hysteretic model of exposed column base under tensile axial force
图中 My为屈服抗弯承载力,为锚栓达到屈服时柱脚的抗弯承载力。循环荷载作用下恢复力模型的具体路径如下:0→a→b→c→d→e→f→g→h。
柱脚节点具体过程的受力状态如图10,为描述方便,假设从左到右为水平荷载加载正向,两侧锚栓为右侧锚栓和左侧锚栓。由于柱脚承受轴向拉力,锚栓很快达到屈服,因此在外露式钢柱脚拉弯状态下的恢复力模型中不考虑锚栓屈服后增加的强度,仅用锚栓的屈服强度进行讨论。
其中,0→a→b段:加载初期,两侧锚栓均匀受拉,正向加载后,左侧锚栓受力增加,右侧锚栓卸载,在a点处,左侧锚栓屈服,柱脚承载力达到正向屈服弯矩,之后左侧锚栓产生塑性变形;b→c→d段:柱脚先卸载再反向加载,左侧锚栓受力减小,右侧锚栓受力增加,由于初始加载从正向开始,左侧锚栓有部分残余变形,反向加载时,右侧锚栓受力继续增加左侧锚栓受力继续减小,弯矩方向发生改变,在d点处,右侧锚栓屈服,柱脚承载力达到负向屈服弯矩;d→e段:继续反向加载,此时左侧锚栓受力为零,弯矩保持不变;e→g段:柱脚先负向卸载再正向加载,卸载时底板与左侧锚栓再次接触,右侧锚栓受力迅速减小,左侧锚栓开始受力,回到一定转角时,两侧锚栓产生的力矩再次平衡,正向加载时,左侧锚栓受力超过右侧锚栓,弯矩变为正值,转角回零后正向弯矩达到极值;g→h段:继续正向加载,此时左侧锚栓的残余变形再次增加,由于模型中不考虑锚栓屈服后上升的强度,此时柱脚传递弯矩没有增加。
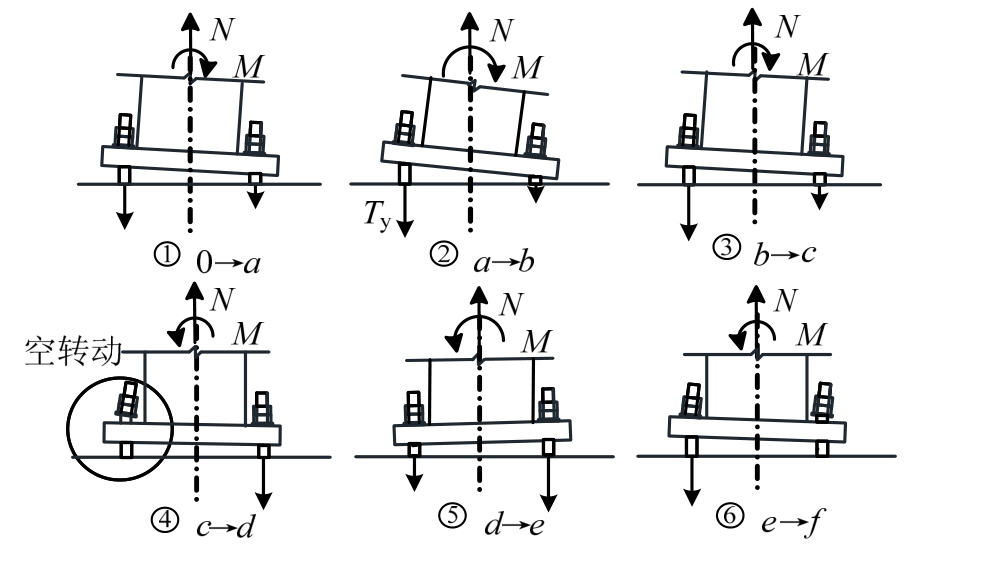
图10 外露式钢柱脚拉弯状态下受力机制
Fig.10 Resistance mechanisms of exposed column base under tensile axial force
综上所述,当柱脚破坏由锚栓破坏控制时,压弯状态下,外露式柱脚的滞回曲线为“旗帜型”;拉弯状态下,则为饱满的曲线,但其承载力大幅下降。造成二者不同的原因主要是压弯状态下,卸载时底板在轴压力作用下回落,锚栓的塑性变形使柱脚产生一段空转动,da段与bc段水平距离相同,再加载时ad段锚栓不受力,d点之后底板与螺帽接触,锚栓开始受力;而在拉弯状态下,由于轴拉力的作用,锚栓一直处于拉伸状态,塑性变形不断累积,底板与基础顶面间距不断加大。
该文提出压弯和拉弯两种状态下的外露式柱脚恢复力模型由骨架线模型与其卸载及滞回特性组成。该模型假设:1) 骨架曲线为不考虑强度退化的双折线模型;2) 各控制点的加载卸载刚度均与屈服荷载之前的加载刚度相同。
外露式柱脚骨架曲线模型如图11。a点、b点分别为屈服点和极限点,My为屈服抗弯承载力,Mu为极限抗弯承载力;θy为柱脚屈服时柱顶转角,可由锚栓屈服时变形几何关系求解,θu为柱脚达到极限状态时的柱顶转角,θy和θu满足以下关系:
式中μ为延性系数。由试验结果可知,采用热轧锚栓时,柱脚延性系数约为 4,采用冷拔锚栓时,柱脚延性系数约为2。
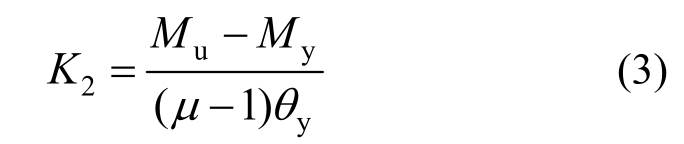
图11 外露式柱脚骨架曲线模型
Fig.11 Skeleton curve model of exposed column base
图11中K1为柱脚达到屈服时的割线刚度,K2为强化刚度。由试验结果可知,压弯状态下柱脚延性较好,可考虑锚栓的强化作用:
拉弯状态下锚栓进入强化段后很快被拉断,因此滞回曲线模型中不考虑强化刚度,K2为0。
3.2.1 压弯状态
压弯状态下,以锚栓拉断为破坏形态的外露式柱脚承载力计算,可通过对受压侧压力合力点位置取矩建立平衡关系求解。
根据试验中底板位移计采集的数据,结合几何关系,绘制出加载过程中柱脚连接的转动点位置随柱顶位移的变化情况[19]。如图 12所示,其中横轴为转动点相对于底板中轴线的距离dc,纵轴为柱顶位移δ,数据点均为各加载循环的极值点。

图1 2 转动点位置变化
F i g.1 2 V a r i a t i o n o f r o t a t i o n p o i n t o f b a s e p l a t e
由图12及图13可知,柱脚屈服时柱顶位移约为24 mm(图中横向虚线处),此时转动点位置大致位于锚栓处(图中纵向虚线处),与试验现象一致,因此计算中可假设柱脚达到屈服承载力时转动点位于锚栓处;当变形继续增加时观察到转动点位置稍向内移,主要原因为砂浆层达到承载极限被压碎。计算极限承载力时根据塑性分析方法假设压应力为矩形分布,利用荷载平衡关系求出转动点位置。

图13 压弯状态下外露式柱脚转动点示意图
Fig.13 Observed rotation point of base plate under compressive axial load
图13和图14分别给出了压弯状态下柱脚屈服和极限状态的转动点示意图和受力简图,对转动点求矩由力的平衡关系式可得到柱脚抗弯承载力。
屈服状态下,假设底板下压应力分布为三角形且压力合力点位于受压侧锚栓处,对该点求矩得到柱脚屈服抗弯承载力:
对于6REM试件,考虑三排锚栓布置,由之前文章对于试验数据的分析中得出中间一排锚栓的受力近似为外排锚栓受力的1/2,故承载力公式为:
式中Ty为受拉侧外排锚栓屈服时的总拉力:
式中:dt为受拉侧锚栓到中轴线的距离;dc为反力合力R的作用点距中轴线的距离;N为轴压力;n为受拉侧锚栓数量;fy为锚栓屈服强度;Ae为锚栓有效截面面积。

图14 压弯状态下外露式柱脚受力简图
Fig.14 Force diagram of exposed column base under compressive axial load
极限状态下,假设底板下压应力分布为矩形分布,下部砂浆层达到抗压强度,由荷载平衡求得反力 R,根据底板下单位长度砂浆的抗压强度 q,可计算得到底板压应力分布长度x,并确定反力R的作用位置,对底板中轴线求矩得出极限抗弯承载力:
对于6REM试件,相应的承载力计算公式为:

Tu为受拉侧外排锚栓达到极限强度时总拉力:
式中fu为锚栓抗拉强度。q为底板下单位长度砂浆的抗压强度:
式中:fc为砂浆的抗压强度;B为底板宽度。
需要注意的是,循环加载中存在加载先后顺序,如图15所示,试件6REM中排锚栓在正向加载时发生变形,在反向加载时,由于锚栓产生的残余变形以及正向加载时砂浆垫层被压碎,导致中排锚栓受力较小或不受力,反向承载力降低。因此计算试件6REM的正向加载极限承载力考虑中排锚栓变形的影响,按式(8)计算。计算反向加载极限承载力时不考虑中排锚栓的贡献,按式(7)计算。
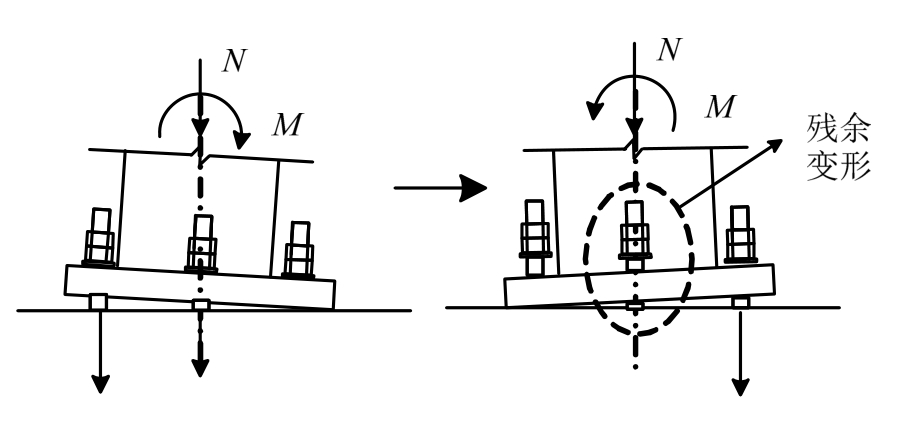
图15 循环荷载下6REM的不对称性
Fig.15 Asymmetry of 6REM in cyclic loading
3.2.2 拉弯状态
由于柱脚承受轴向拉力,两侧锚栓一开始便受拉,在循环水平荷载作用下锚栓产生的残余变形不断累积,底板逐渐脱离砂浆层,锚栓承受所有的剪力,且同时承受拉力、剪力以及弯矩作用,柱脚的抗弯承载力几乎全部由锚栓提供。如图 16所示,屈服状态和极限状态下转动点位于锚栓处。
图 17给出了拉弯状态下承载力计算简图,对转动点求矩得到屈服和极限承载力公式:

式中:l为两侧锚栓之间的距离;N为轴向力。

图16 拉弯状态下柱脚底板转动点示意图
Fig.16 Schematic of bserved rotation point of base plate under tensile axial load
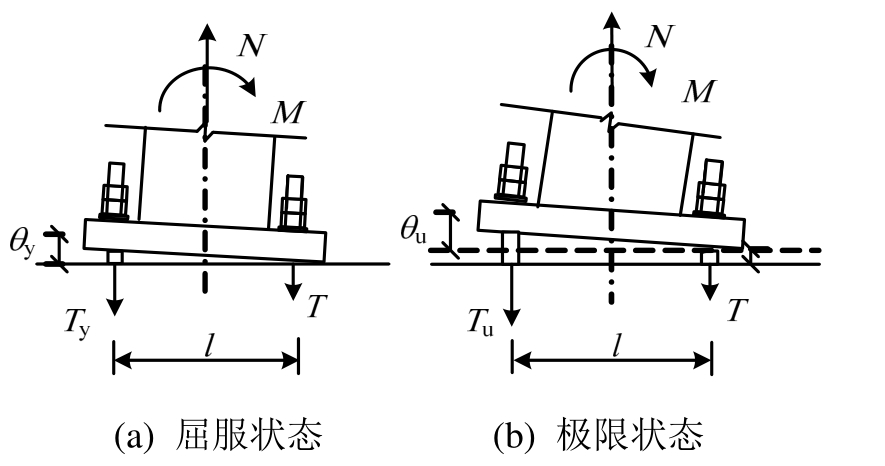
图17 拉弯状态下外露式柱脚受力简图
Fig.17 Force diagram of exposed column base under tensile axial load
由于在极限状态下,锚栓处于拉、弯、剪荷载共同作用,锚栓存在较大的剪应力,故抗拉强度会有所降低,为了考虑这种影响,需要对锚栓的抗拉强度进行折减。由第四强度理论等效应力为:
此时设折减后的抗拉强度为σuz,由Von-Mises应力准则,剪应力![]() ,令等效应力等于抗拉强度σu,代入式(13)为:
,令等效应力等于抗拉强度σu,代入式(13)为:
解得![]() 即折减系数应取为
即折减系数应取为![]()
式(12)考虑强度折减后应为:
式中,μ为锚栓抗拉强度折减系数,取为![]()
3.2.3 计算值比较
表2比较了外露式钢柱脚抗弯承载力的计算结果与试验结果(4RMT极限承载力考虑强度折减)。可以看出,压弯状态下计算屈服抗弯承载力时取受压侧锚栓处为反力合力作用点得到的结果与试验值较为接近,误差基本在10%左右,满足一定的精度要求。对于计算极限抗弯承载力采用的矩形压应力分布假设得到的结果误差基本在10%以内。
表2 承载力计算值与试验结果对比
Table 2 Comparison of calculated moment resistance and measured moment resistance
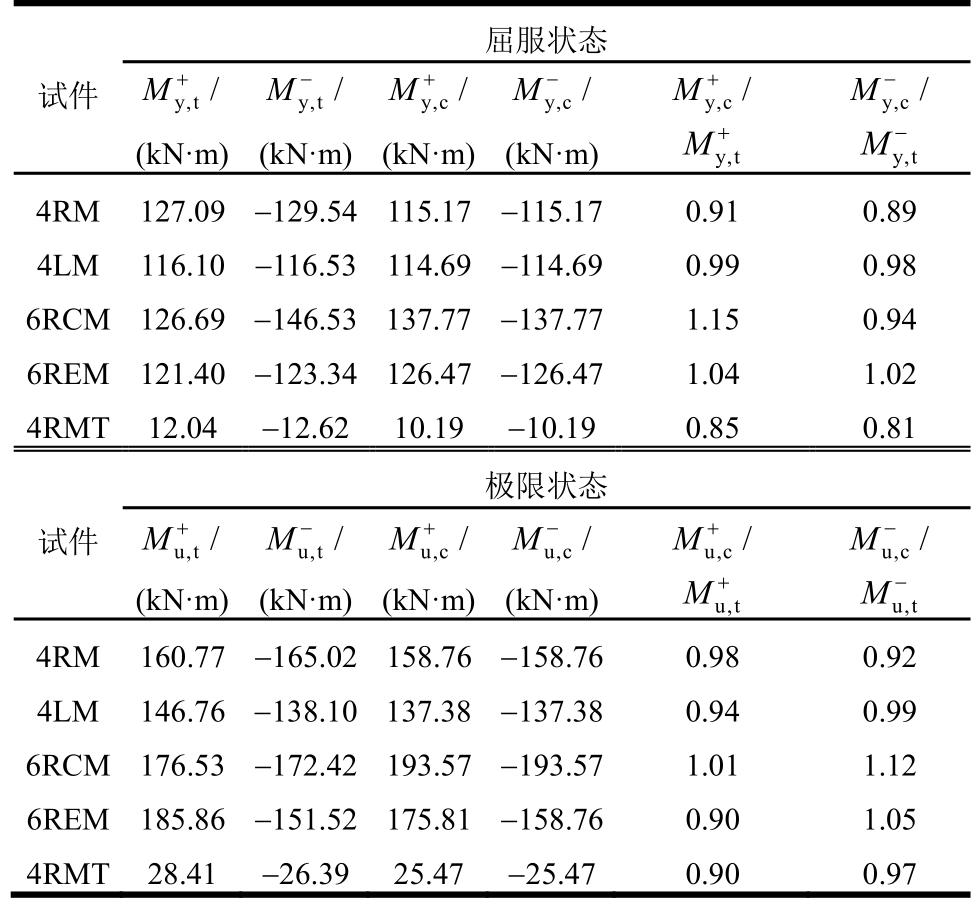
注:My,t为屈服弯矩试验值;My,c为屈服弯矩计算值;Mu,t为极限弯矩试验值,Mu,c为极限弯矩计算值。“+”、“-”代表正向加载和反向加载
考虑6REM由于中排锚栓塑性变形导致反向承载力降低,故其反向承载力按照式(7)进行计算,计算结果与试验值较为接近,误差在5%左右。
拉弯状态下,计算得到屈服抗弯承载力偏于保守,误差为15%,主要因为屈服状态时底板与砂浆层并未完全脱离,存在的接触反力并未考虑到计算公式中,因此导致计算结果偏小。而对于极限承载力,考虑强度折减后计算值与试验值的比值为0.9,计算满足较好的精度,且偏于保守。
为简化计算,定义柱脚初始转动刚度为锚栓屈服时的抗弯承载力与屈服柱顶转角的比值。前文已经给出了柱脚在压弯以及拉弯状态下的屈服抗弯承载力 My,因此只需要得到柱顶转角 θy的计算方法便可以间接求得抗弯刚度K。
试验测得的柱顶位移主要包括底板转动引起的位移量δyb、底板滑移量δslip、钢柱弯曲产生的位移量δco。如图18所示。

图18 柱顶位移组成
Fig.18 Component parts of top displacement
减去底板滑移量后柱顶转角 θy主要包括底板转角θyb和钢柱弯曲转角θyco两部分:
钢柱弯曲转角θyco按照悬臂梁模型进行计算:
式中:My为柱脚的屈服抗弯承载力;h为钢柱高度;Eco为钢柱弹性模量;I为钢柱截面惯性矩。
3.3.1 压弯状态
压弯状态下,柱脚一侧锚栓受拉,另一侧底板承压,假定转动点位于受压侧锚栓处,图 19给出了柱脚的受力以及几何变形关系。
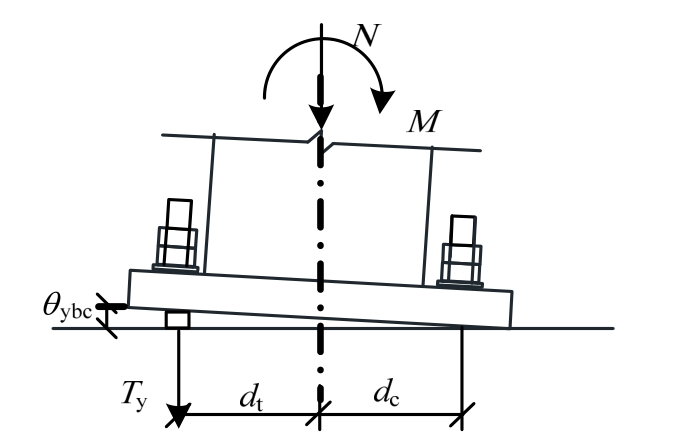
图1 9 θybc计算简图
F i g.1 9 C a l c u l a t i o n d i a g r a m o f θybc
底板屈服转角为:
式中:σy为锚栓屈服应力;le为锚杆长度;E为锚栓弹性模量。考虑到柱脚底板、砂浆层等其他部件的变形需要对上述给出的计算结果乘以一个放大系数 Rc,放大系数 Rc参考文献[13]及文献[18]取为4。
因此,压弯状态下的柱顶转角θyc为:
可以得到压弯状态下转动刚度K1c:

3.3.2 拉弯状态
拉弯状态下,底板与砂浆层很快分离,柱脚转动刚度基本由锚栓提供,可不考虑其他部件变形的影响,由柱脚的受力以及几何变形关系(图20),得到底板转角θybt的计算公式为:
式中:Ty为受拉侧锚栓屈服时总拉力;N为轴力;le为锚杆长度;n为受拉侧锚栓个数;Ae为锚杆的有效截面面积;l为锚栓间距;E为锚栓弹性模量。
因此,拉弯状态下的柱顶转角θyt为:

计算得到拉弯状态下转动刚度K1t:
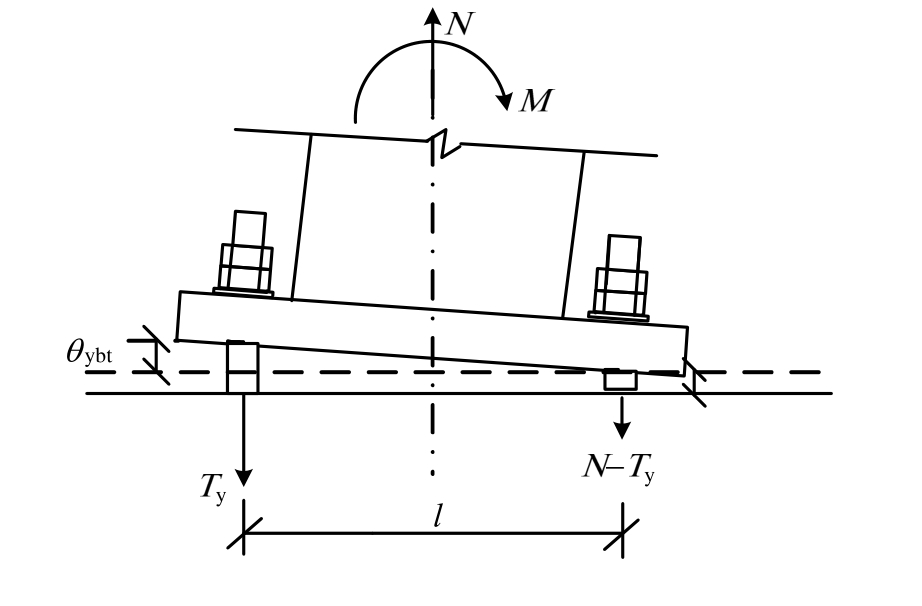
图 20 θybt计算简图
Fig.20 Calculation diagram of θybt
3.3.3 计算值比较
表3是抗弯刚度计算结果与试验结果的对比。
表3 抗弯刚度计算值与试验结果对比
Table 3 Comparison of calculated and measured stiffness
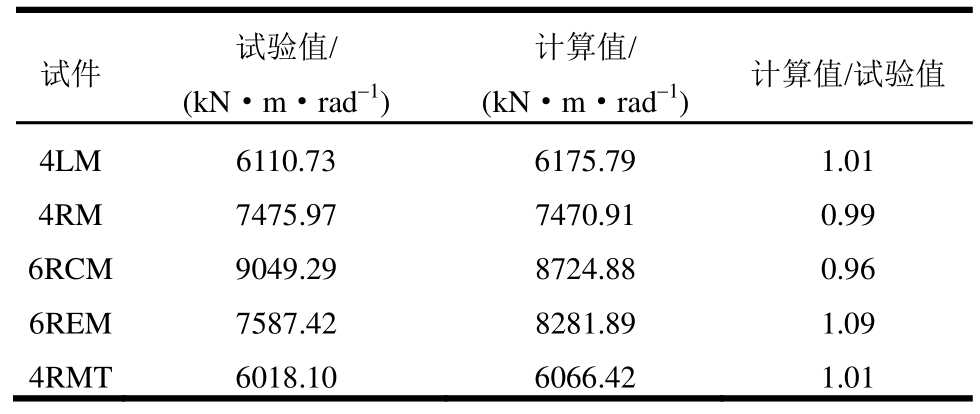
从表3可看出,无论压弯状态还是拉弯状态计算得到的抗弯刚度与试验结果均吻合较好,精度在10%以内,可较准确地量化外露式柱脚的半刚性。
图 21比较了通过该文提出的外露式柱脚恢复力计算模型和计算公式得到的滞回曲线与试验测得的柱脚弯矩转角滞回曲线。
从图中可看出,压弯状态下计算曲线与试验曲线吻合较好,尤其是屈服点、极限点以及加载卸载刚度的计算都有较高的吻合度,计算滞回曲线可以反映出由于底板空转动引起的捏缩效应。
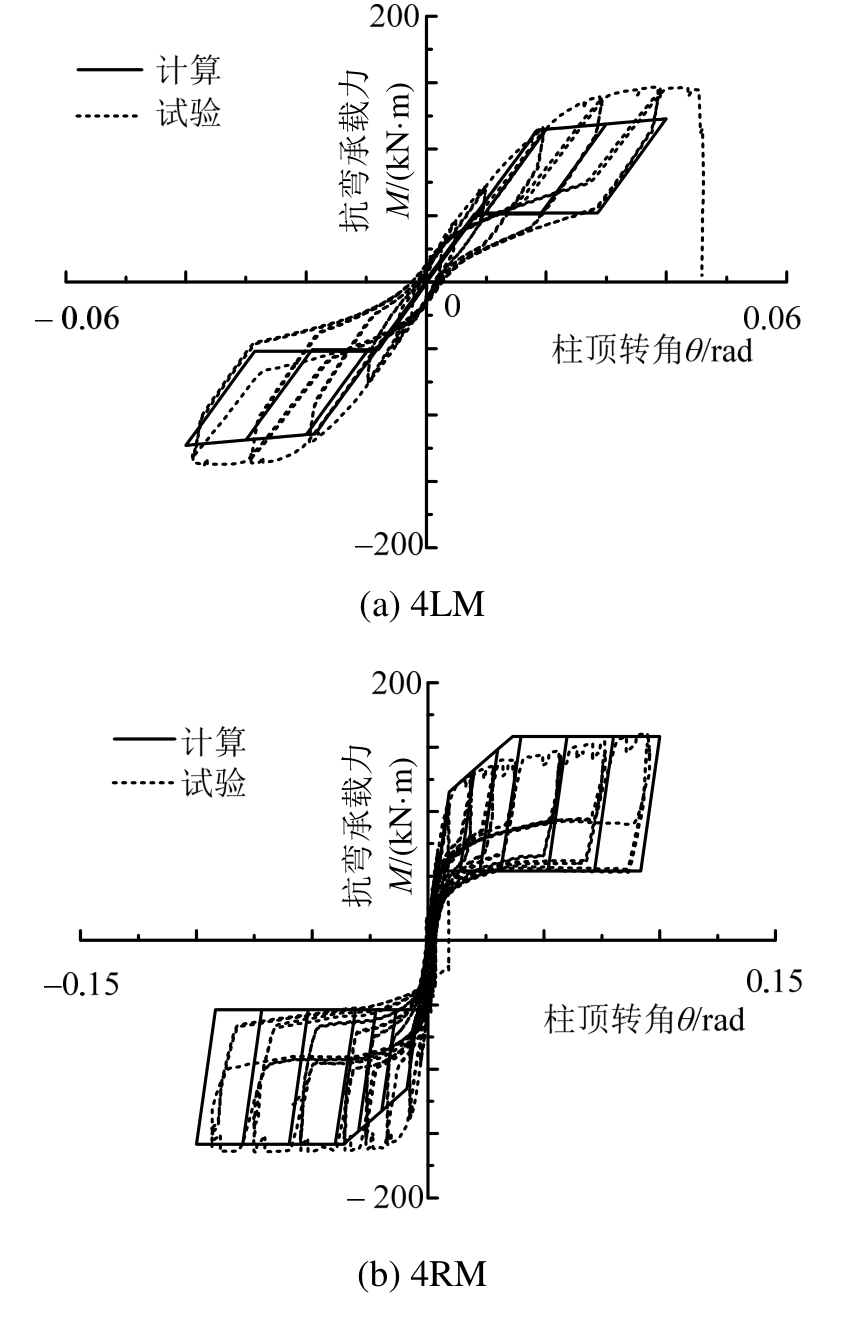
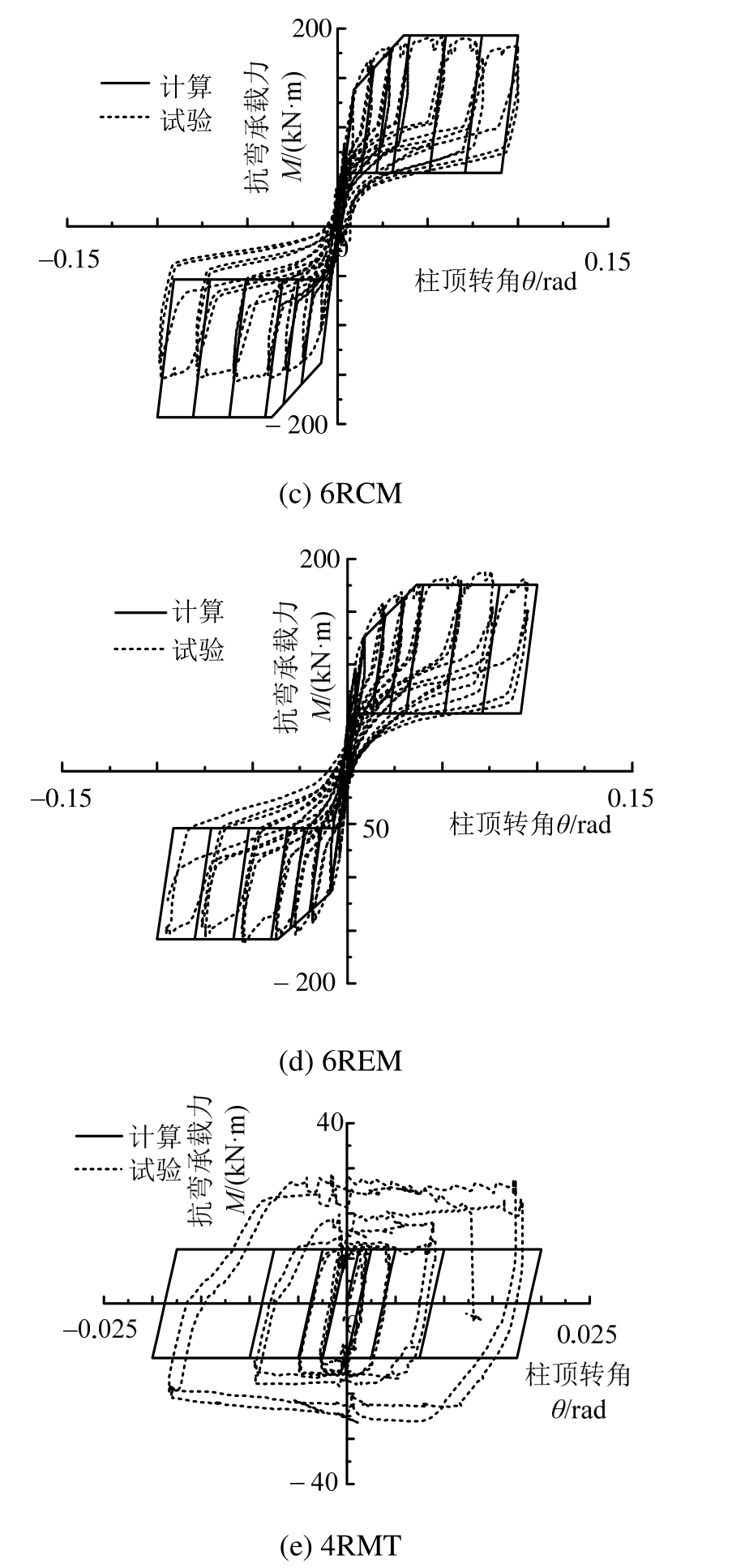
图21 计算滞回曲线与试验曲线对比
Fig.21 Comparison of restoring force models with test curves
拉弯状态下,由试验结果可知,锚栓进入强化段后很快被拉断,因此计算模型中未考虑锚栓强化的影响。如图 21所示,锚栓强化前的计算结果与试验结果吻合较好。该文提出的柱脚拉弯状态下的极限承载力可用于判断柱脚在拉弯状态下的安全冗余度。
(1) 压弯状态下,外露式钢柱脚的滞回曲线为旗帜型;拉弯状态下,滞回曲线则为饱满形状,但承载力大幅度降低。
(2) 压弯状态下,外露式钢柱脚屈服承载力计算,可假设底板压力合力点位于锚栓处,底板压应力为三角形分布;极限承载力计算时,底板下压应力分布可简化为矩形分布,根据平衡条件计算转动点位置,承载力计算值均为试验值的90%左右。
(3) 拉弯状态下,柱脚底板与砂浆层分离,锚栓受轴拉力,外露式钢柱脚在屈服状态和极限状态时的转动点均可取在锚栓处。计算极限承载力时,采用折减系数1/2考虑复杂应力下锚栓受拉强度降低。屈服承载力和极限承载力的计算值分别为试验值的85%和90%。
(4) 为简化计算,定义柱脚初始转动刚度为锚栓屈服时的抗弯承载力与屈服柱顶转角的比值。计算屈服转角时,压弯状态下除考虑锚栓变形外,还需考虑柱脚底板、砂浆层等部件变形的贡献;拉弯状态下,柱脚底板较早脱离砂浆层,可仅考虑锚栓变形。计算转动刚度大致为试验值的90%。
(5) 滞回曲线模型由双折线骨架线模型及其卸载刚度和滞回特性组成,卸载刚度与加载刚度一致。该模型可有效地反映出不同受力状态及不同锚栓布置的外露式钢柱脚的弯曲转角滞回曲线,可用于整体框架的抗震性能分析。
参考文献:
[1] GB 50017―2003, 钢结构设计规范[S]. 北京: 中国建筑工业出版社, 2003.GB 50017―2003, Code for design of steel structures [S].Beijing: China Architecture Industry Press, 2003. (in Chinese)
[2] GB 50011―2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB 50011―2010, Code for seismic design of buildings[S]. Beijing: China Architecture Industry Press, 2010. (in Chinese)
[3] Thambiratnam D P , Pazamasivam P. Base plates under axial loads and moment [J]. Journal of Structural Engineer, ASCE, 1986, 112(5): 1166―1181.
[4] 李星荣, 魏才昂, 丁峙崐, 等. 钢结构连接节点设计手册 [M]. 第2版. 北京: 中国建筑工业出版社, 2005.Li Xingrong, Wei Cai'ang, Ding Zhikun, et al. Joint design manual for steel structures [M]. 2nd ed. Beijing:China Architecture & Building Press, 2005. (in Chinese)
[5] 《钢结构设计手册》编辑委员会. 钢结构设计手册(上册)[M]. 北京: 中国建筑工业出版社, 2004.Editorial Committee of Steel Structure Design Manual.Design manual for steel structures (Volume one) [M].Beijing: China Architecture & Building Press, 2004. (in Chinese)
[6] AISC, Base plate and anchor rod design (2nd Edition)[S]. Chicago: American Institute of Steel Construction Inc, 2006.
[7] BS EN 1993-1-8 Eurocode 3, Design of steel structure:Part 1-8: design of joints[S]. London: British Standards Institution, 2005.
[8] Sato K A. Research on the aseismic behavior of steel column base for evaluating its strength capacity and fixity [R]. Tokyo, Japan: Kajima Institute of Construction Technology, 1987.
[9] 李慎, 苏明周. 基于性能的偏心支撑钢框架抗震设计方法研究[J]. 工程力学, 2014, 31(10): 195―204.Li Shen, Su Mingzhou. A performance-based seismic design method for eccentrically braced steel frames [J].Engineering Mechanics, 2014, 31(10): 195―204. (in Chinese)
[10] 施正捷, 李全旺, 樊健生. 偏心钢结构节点梁柱-核心区受力机理研究[J]. 工程力学, 2017, 34(5): 68―77.Shi Zhengjie, Li Quanwang, Fan Jiansheng. Interaction effect between a beam or column and the core area of an eccentric steel joint [J]. Engineering Mechanics, 2017,34(5): 68―77. (in Chinese)
[11] 于安麟, 永毓栋, 郭在田, 等. 露出型钢柱脚抗剪性能的研究(I)[J]. 工业建筑, 1992, (5): 24―26.Yu Anlin, Yong Yudong, Guo Zaitian, et al. Research on behavior of shearing resistance in steel column base (I)[J]. Industrial Construction, 1992 (5): 24―26. (in Chinese)
[12] 于安麟, 永毓栋, 郭在田, 等. 露出型钢柱脚抗剪性能的研究(II)[J]. 工业建筑, 1992 (6): 29―33.Yu Anlin, Yong Yudong, Guo Zaitian, et al. Research on behavior of shearing resistance in steel column base (II)[J]. Industrial Construction, 1992 (6): 29―33. (in Chinese)
[13] Cui Y, Nagea T, Nakeshima M. Hysteretic behavior and strength capacity of shallowly embedded steel column bases [J]. Journal of Structural Engineering, ASCE, 2009,135(10): 1231―1238.
[14] Kanvinde A M, Grilli D A, Zareian F. Rotational stiffness of exposed column base connections: experiments and analytical models [J]. Journal of Structure Engineering,ASCE, 2012, 138(5): 549―560.
[15] Rodas P T, Zareian F, Kanvinde A. Hysteretic model for exposed column–base connections [J]. Journal of Structural Engineering, 2016, 142(12): 04016137-1-14.
[16] 丁敏, 李潇, 马倩, 等. 基于 Winkler弹性地基梁模型的半刚性轻钢柱脚底板受力分析[J]. 工程力学, 2014,31(5): 158―165.Ding Min, Li Xiao, Ma Qian, et al. Mechanical analysis of the sole plate of semi-rigid light steel column footing based on winkler model of elastic foundation beam [J].Engineering Mechanics, 2014, 31(5): 158―165. (in Chinese)
[17] Picard A, Beaulieu D. Behavior of a simple column base connection [J]. Canadian Journal of Civil Engineering,1985, 12(1): 126―136.
[18] 崔瑶, 王枫智, 于贵书. 强震作用下柱脚连接刚度对钢框架性能的影响[J]. 地震工程与工程振动, 2016,36(3): 162―169.Cui Yao, Wang Fengzhi, Yu Guishu. Effect of column base stiffness on seismic behavior of steel frame under severe earthquake [J]. Earthquake Engineering and Engineering Dynamics, 2016, 36(3): 162―169. (in Chinese)
[19] 刘浩, 崔瑶. 外露式钢柱脚受弯性能试验研究[J]. 钢结构, 2017, 32(217): 40―44.Liu Hao, Cui Yao. Experimental study on bending behavior of exposed column base [J]. Steel Construction,2017, 32(217): 40―44. (in Chinese)
HYSTERETIC RESISTANCE MECHANISM OF EXPOSED STEEL COLUMN BASES
CUI Yao1, LI Hao1, LIU Hao1, WANG Jing-qiu1, TANG Zhen-yun2
(1. State Key laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China;2. The Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology , Beijing 100124, China)
Abstract:Based on quasi-static test results of exposed columns, the lateral resistance mechanisms of the exposed columns under compressive or tensile axial loads are summarized. The method for predicting the yield moment, ultimate moment, and initial stiffness of exposed column bases under compressive or tensile axial loads is proposed; and the errors of the resulting predictions are within 10% of the experimental tests. A hysteretic model of exposed columns under compressive or tensile axial loads is proposed. Under compressive axial loads,the hysteresis curves of exposed column bases are “flag-shaped”, and the backbone curve is simulated using a bilinear model without strain hardening. Under tensile axial loads, the resistance of exposed columns is reduced significantly, and the hysteresis is full. The backbone curve is simulated by an idealized elastic-plastic model which does not consider the strain hardening of the anchor rod. The hysteresis curves from the model agree well with the experimental results. The hysteretic model can represent the bending behavior of exposed column bases with different anchor rod arrangements well, and thus can be used to analyze the seismic performance of whole frames in future research.
Key words:exposed column base; anchor rods; moment resistance; flexural rigidity; hysteretic mechanism
中图分类号:TU391
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.04.0288
文章编号:1000-4750(2018)07-0232-11
收稿日期:2017-04-14;修改日期:2017-11-12
基金项目:国家自然科学基金项目(51208076, 51678106);中央高校基本科研业务费专项资金项目(DUT14LK04)
通讯作者:崔 瑶(1983―),女,辽宁人,副教授,博士,主要从事钢结构抗震方面研究(E-mail: cuiyao@dlut.edu.cn).
作者简介:
李 浩(1992—),男,内蒙古人,硕士生,主要从事钢柱脚抗震性能研究(E-mail: lihao1992dut@163.com);
刘 浩(1991—),男,山东人,硕士生,主要从事钢柱脚抗震性能研究(E-mail: liuhaoxylf@mail.dlut.edu.cn);
王晶秋(1994—),女,山东人,硕士生,主要从事钢柱脚抗震性能研究(E-mail: wangjingqiu@mail.dlut.edu.cn);
唐贞云(1983—),男,重庆人,副研究员,博士,主要从事结构抗震实验技术研究(E-mail: tzy@bjut.edu.cn).