
图1 断层错动试验装置
Fig.1 Faulting model test device
石吉森1,2,凌道盛1,2,徐泽龙3,黄 博1,2
(1.浙江大学软弱土与环境土工教育部重点实验室,杭州 310058;2.浙江大学岩土工程研究所,杭州 310058;3.东京大学工业科学研究所,日本 1538505)
摘 要:基于设计的断层错动装置和PIV技术,研究了倾斜场地条件下逆断层错动导致上覆土体破裂的过程,重点分析了场地倾斜对破裂带的扩展规律、土体变形和地表变形等的影响。研究结果表明:随着场地倾斜程度增大,破裂带露头时的基岩错动位移也随之增大;不同倾斜场地的破裂带露头倾角均与Rankine理论预测结果更为一致,而Roscoe理论和Vermeer理论的预测结果均有较大误差;断层错动过程中上盘土体应变(剪应变、正应变和等效应变)均大于下盘土体;随着地表倾斜程度增加,露头时刻地表位移和地表位移梯度均随之增大;同时,结合现场实测数据,对建构筑物与断层的避让距离的研究表明:相较于下盘,上盘地表建构筑物的断层避让距离应更大;而随着场地倾角由正变为负,上盘地表建构筑物的避让距离还应增大。
关键词:倾斜场地;模型试验;逆断层错动;破裂带;粒子图像测速技术(PIV)
目前地球正处于地壳活动的活跃周期,全球地震灾害频发。单列近十年来所发生的特大地震(死亡1000人及以上)就有2008年汶川地震、2010年海地地震、玉树地震、2011年东日本大地震等,这些地震均造成了巨大人员伤亡和难以估量的财产损失[1-3]。显然,该地壳活跃周期内,我国及周边地区地震活动最为剧烈频繁。就地理条件而言,我国长期受到太平洋板块和亚欧板块碰撞、喜马拉雅造山运动等强地质活动的影响。无论从短期还是长期来看,我国地震发生频率高、强度大的现象将一直存在,对地震的相关研究刻不容缓。
根据致灾机理不同,地震作用主要可分为断层上下盘之间的错动和地震波传播产生的振动[4]。前者对岩土体和建构筑物的破坏主要是由于活动断裂位错产生的剪切或撕裂破坏,如断层错动造成管道、隧道等错断即是典型的例子;而远离断层错动区域,主要是通过地震波传播产生的振动造成循环累积变形、地基液化等诱发的破坏。以往的研究主要集中在对地震波传播过程的研究,相对而言,对断层错动破坏机理的研究仍然不够深入。
断层错动方面的理论研究主要有弹性位错理论[5]和三角剪切模型[6],弹性位错理论将上覆岩土体简化为弹性半空间,而三角剪切模型中三角形速度场对土体是否适用仍有待研究。实际上,断层错动与建构筑物的相互作用过程是复杂的动态过程,这两种理论在研究断层错动与建构筑物的相互作用时仍存在困难。
除了理论研究外,对断层错动的研究也有较多采用了模型试验的方式,主要包括常重力模型试验和离心模型试验两种,研究重点多放在破裂带扩展的影响因素及破裂带扩展与建(构)筑物的相互作用上。Cole等[7]采用常重力模型试验研究了正、逆断层错动引起上覆土层破裂,提出了一个可预测破裂带形状和位置的理论模型。Lin等[8]将常重力模型试验与有限元分析结合,研究了断层错动速率、断层倾角、剪胀角、尺寸效应、弹性模量、泊松比、粘聚力、内摩擦角、荷载的位置等因素对破裂带扩展的影响。杨杰等[9]、徐泽龙[10]也开展了相关模型试验研究工作。在离心模型试验研究方面,Bransy等[11-12]利用离心机研究了正、逆断层错动对自由场地和浅基础的影响,骆冠勇等[13-14]则重点探讨了断层错动作用下上覆砂土、粘土层变形特性。Ng等[15]、蔡奇鹏等[16]则利用离心机研究了胶结粘土中的正断层错动。Anastasopolous等[17]采用应变软化摩尔-库伦模型,通过修正硬化模量在一定程度上消除了计算结果的网格依赖性,并将断层错动的数值模拟结果与Bransy的离心机试验结果作了对比。需要指出,断层的深度往往可深达几十、上百公里(可参考震源深度),模型尺寸相较真实断层均较小,即使是离心机试验,受条件限制,目前也仅能模拟埋深几十米深的断层[11-12],与实际断层错动过程的应力水平存在巨大差别,因此应该认为模型试验的结果更加适用于近地表处土体。但考虑到绝大部分建构筑物均位于近地表区域,该区域也是研究中关注的重点,因此模型试验的研究成果仍然具有不可忽视的参考价值。
以往的研究均是基于水平场地,对倾斜场地条件下断层错动过程的研究还未见报道。相较于平坦水平场地,倾斜场地是更为一般的情况,水平场地的研究结果在倾斜场地条件下的普适性如何值得考虑。此外,我国山区多、面积广,在这些地区建成、在建和备建的基础设施也日益增多。倾斜的地形将会对地下构筑物形成偏压,偏压侧的构筑物更容易受到损伤,目前对这类地下偏压结构的研究也不完善。三角剪切模型中均假设原生地表为水平,而原生地表倾斜时速度场的分布情况、褶皱的性状如何也值得研究。因此,对倾斜场地条件下断层错动过程的研究具有不可忽视的现实意义。本文首先设计了常重力条件下的断层错动模型试验装置,利用该装置并结合 PIV技术(粒子图像测速技术,一种数字图像测量技术,本试验中用于测量土体位移场),研究了逆断层错动对地表倾角不同的上覆砂土层的影响,试验结果有助于揭示倾斜场地下断层错动的基本规律。
本文设计的断层错动模型试验装置如图 1所示。试验装置由土箱、导向模块、加载系统等组成。土箱内净空间的大小为 1600 mm×300 mm×800 mm(长×宽×高),土箱前壁为透明有机玻璃,便于高分辨率相机拍摄断层错动引起的土层破裂过程。土箱后壁覆盖一层薄聚四氟乙烯(摩擦系数仅约 0.04)作光滑处理,以使断层模型尽量接近平面问题(即不考虑断层错动过程在土箱宽度方向的变化)。土箱底部由两块刚性底板构成,左侧为固定底板,长1100 mm;右侧底板长500 mm,与土箱右侧壁连成整体,在试验过程中可沿导向模块所设置角度上升或下降。两块底板交界位置即为模型断层的错动面,基岩断点如图1(a)中A点。
导向模块为角度可调节导轨结构,布置于土箱右侧和底部,以保证断层错动方向,导向模块的角度调节范围为0°~90°。加载系统由一台螺旋丝杆升降机和一台伺服电机组成,位于土箱右下方,并固定在底座上。升降机最大出力为24.5 kN,丝杆行程200 mm,减速比24,输入轴容许转速为1500 r/min。伺服电机额定输出功率为 2.3 kW,可调转速为0~1000 r/min。在伺服电机带动下,升降机可实现稳定匀速上升(模拟逆断层)或下降(模拟正断层),速率可变范围为0~6 mm/s(竖向)。

图1 断层错动试验装置
Fig.1 Faulting model test device
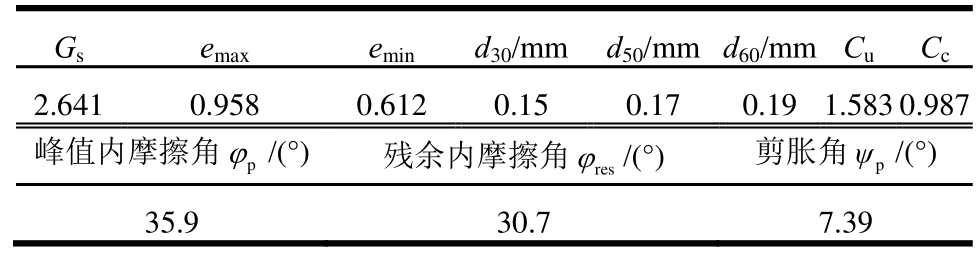
本文所有试验均采用相对密实度Dr为60%(中密)的福建标准细砂,正式试验前先利用一组直剪试验获得该种砂的基本物理力学参数,直剪试验结果如图 2。试验得到的福建标准细砂各项物理力学参数列于表 1,考虑到直剪试验的固有缺陷及提高试验结果精度,表中福建标准细砂的峰值剪胀角pψ为采用 Shibuya等[18]总结的相关公式(式(1))的计算结果。

图2 直剪试验结果
Fig.2 Results of direct shear test
表1 福建标准细砂物理力学参数
Table 1 Parameters of Fujian standard fine sand
浇筑好的倾斜场地模型如图3所示,土层下方为一个倾角为θ的隐伏逆断层,虚线所示为断层错动引发土体中产生的破裂带,破裂带露头处倾角为β。α为场地地表倾角,规定地表由水平绕顺时针旋转(此时下盘地表高于上盘地表)时地表倾角α为正,逆时针旋转α为负,图中所示为α=5°的情况。本文分别对 α 为 5°、10°、0°、-5°、-10°五种场地倾角情况下的逆断层错动进行了试验,各试验在模型制备时控制基岩断点处砂土层厚度H=600 mm。
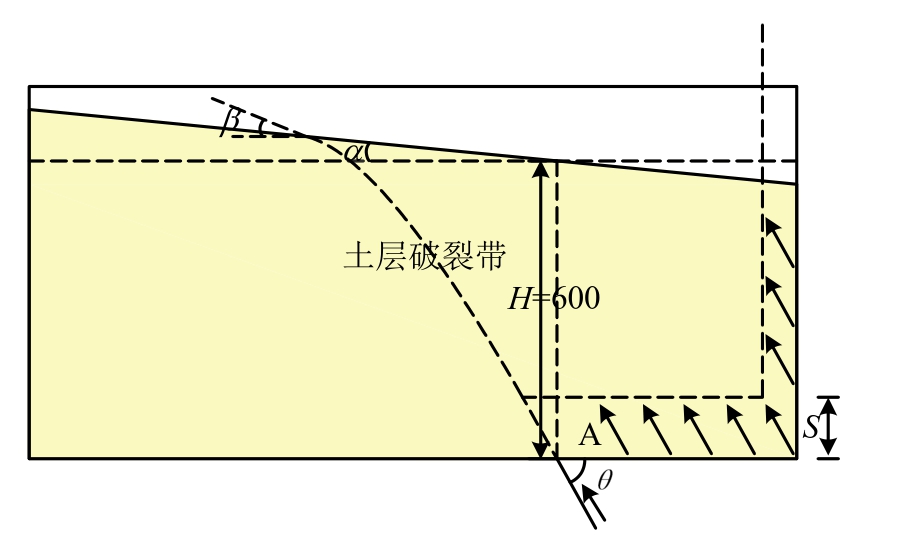
图3 α=5°倾斜场地模型示意图
Fig.3 Inclined ground model with α=5°
所有试验均控制土箱内初始试样的相对密实度 Dr=60%,由于地表为倾斜,给试样制备和密实度的控制带来不便。经过多次试探性模型制备,在正式试验时采用密度控制法控制所浇砂的相对密实度,遵循“定量称取,分层浇筑,严控体积,界面刮毛,多缺少补”的原则,即:1) 首先根据所需的地表倾角α计算得到需装入砂的总体积V和砂的总质量M;2) 同时计算出土箱中100 mm厚砂的质量m,将总质量M的砂按质量m分为若干份浇筑;3) 每层刚浇筑完的土样表面难以避免的会出现起伏不平,采用刚度较大、宽度略小于土箱宽度的钢条初步找平,再用面积较大的刚性平板分区域来回反复按压,直到该层各处厚度均匀,均为100 mm;4) 为保证先后浇筑的两层砂接触良好,不产生人工节理,用软毛刷将表面刷到平整并适当刮毛;5) 当所有砂浇注完成后,用软毛刷沿土箱侧壁事先绘制好的边界线将地表按所需场地倾角α刷成一个斜面,多缺少补。
试验的监测系统布置见图 4,监测系统由高分辨率相机和线性位移传感器(LVDT)等组成。高分辨率相机选用Nikon D3,拍摄时分辨率设置为4256×2832(像素)。试验时将高分辨率相机布置于土箱有机玻璃正前方,按 1 s间隔拍照记录断层错动引起的土体破裂过程,供后续PIV分析使用。PIV技术是一种基于高分辨率照相和数字图像处理的面测量技术[19],其以物体自身纹理为跟踪对象,克服了传统点测量技术测点少的缺点,具有分析结果精度高(误差达到亚像素量级)、操作方便等特点,目前已经被广泛用于岩土工程试验领域[20-21]。

图4 监测系统布置
Fig.4 Setup of monitor system
模型右侧壁布置1个线性位移传感器(LVDT),直接测量右侧壁的竖向位移,由于右侧壁与可动底板为一整体,该值即为基岩的竖向错动。LVDT采用Macro Sensors公司,型号PR750 2000传感器,量程为100 mm,测量精度为0.01 mm。
试验前,先调整导向模块至所需的断层倾角,同时按断层错动类型(正/逆)和错动速率设置伺服电机的转向和转速;然后启动监测系统记录土层变形并开始试验;当观察到破裂带出露地表后(地表出现明显突起),停止试验。本文所有试验均为逆断层错动,断层倾角取为60°,断层错动速率为0.5 mm/s(竖向位移)。
断层错动将产生破裂带,破裂带附近剪切错动变形最为剧烈,也是地下建构筑物应该避开的区域。以往有关断层错动对建构筑物影响的研究很多都是基于土体中已有破裂带[22-24],此时建构筑物避让距离较好判断,抗震及加固措施实施也相对容易。而对于本文所研究的隐伏断层的情况,上覆土体在历史上并未出现破裂带,则其避让距离需要根据破裂带的扩展规律来预先判断,因此对破裂带扩展规律的研究显得尤为重要,这也是本文的研究重点之一。
图 5 给出了 α=10°、0°、-10° 三种不同场地中破裂带的扩展过程,α=5°、-5°为中间情况,扩展规律类似。从单一场地随时间轴的横向比较可知,破裂带的扩展行为基本呈现如下规律:在断层错动初期,破裂带近似直线扩展,且破裂带倾角接近断层倾角(本试验中约为60°),随着断层错动的进行,破裂带的扩展方向逐渐向下盘偏转。而从多个场地(不同地表倾角)的纵向比较可发现,随着地表倾角 α由正值向负值变化,破裂带的扩展方向将明显地偏向下盘。


图5 倾斜场地破裂带扩展
Fig.5 Fault ruptures propagation in inclined grounds
为进一步定量化研究,记基岩竖向错动位移为S,破裂带露头倾角(即破裂带露头处与水平向夹角)为 β,如图 3所示,对竖向错动位移归一化处理S=S / H× 100%[25]。表2和图6给出了破裂带露头时归一化竖向位移S、破裂带露头倾角β随地表倾角α的变化。
表2 露头时破裂带相关参数
Table 2 Relative parameters of fault rupture at time of outcropping

可以看出,水平场地露头时归一化竖向位移S最小,约为7.4%。随着场地地表倾斜程度增加,露头时刻S 也不断增加,当 α=±5°时S约为8.5%,当α=±10°时S约为10%。这个结果似乎表明露头时刻的错动位移仅与地表倾斜程度有关,而与倾斜方向无关。造成该现象的根本原因可能与露头时刻破裂带长度有关(见表2),水平场地时破裂带露头长度最小,约为 819 mm,而随着地表倾斜程度增加,破裂带露头长度Lr均有所增长,如果认为破裂带近似以均匀的速率扩展,则倾斜场地破裂带露头时间也将随之延迟。但鉴于本试验的地表倾斜程度较小,该规律在地表倾斜较大时是否适用仍然有待研究。

图6 露头时归一化竖向位移S和破裂带露头倾角β随α的变化
Fig.6 Variation of normalized vertical displacement of bedrockSand dip angle β with α
破裂带露头倾角β则呈现出很明显的规律性:α=10°时,破裂带露头倾角β最大约为37°,而随着地表倾角α由正变为负,β的值逐渐减小。由于逆断层错动过程中上盘土体对下盘土体的挤压,破裂带露头处土体将呈现被动状态[26](第2.2节的PIV分析也显示了这一结果),即大主应力方向平行于地表。此时可以采用一些经典的土压力理论来预测近地表破裂带的方向,包括Rankine理论、Roscoe理论[27]或Vermeer理论[28]等。按照Rankine理论,土体的破裂面和最大主应力的夹角λ与土体的峰值摩擦角φp有关,Roscoe理论认为λ仅与土体的峰值剪胀角Ψp有关,而Vermeer则认为λ的值与φp和Ψp两者均有关,三种理论的λ的计算公式为:

考虑地表倾角 α,则破裂带与水平向的夹角 β可按照式(3)计算:
表3给出了三种理论预测的β值与实测β值的对比。显然,Rankine理论的预测结果与模型试验的结果吻合的更好,误差远小于Roscoe理论和Vermeer理论的预测值。但考虑到土体在较大围压下会产生明显的剪胀性,而本模型试验的尺寸较小,上覆土层厚度仅为600 mm,最深处土压力也仅为12 kPa(土重度按照20 kN/m3计算),试验时土体剪胀性的影响可能并未完全发挥。
表3 不同理论预测的β值与试验结果对比
Table 3 Comparison of β predicted by different theories and model test

断层错动过程中土体的变形剧烈程度与地下构筑物的安全直接相关,设计及建造地下建构筑物时的选址均应位于土体变形较小的区域。土体的变形场不能直接得到,需通过对位移场做进一步处理获得。基本流程是先通过PIV技术分析得到土体的位移场,然后选取合适的插值函数(经典且方便的插值函数如有限元的形函数)拟合位移场,最后对位移函数求一阶导数得到土体的应变场。
图7给出了五种不同地表倾角下,通过PIV分析得到的破裂带露头时土体位移场。可以看出,较为“明显”的位移矢量均集中在上盘,而下盘土体在试验过程中基本保持静止,理论上下盘土体位移矢量的值应为零,但在PIV分析结果中呈现出系统误差之内的某些小值。破裂带附近的位移矢量呈现出从上盘到下盘由大变小逐渐过渡的过程,上盘土体靠近右侧边界处的土体的位移矢量趋于恒定,由于该部分土体受到了很明显的边界效应的影响,土体自上而下呈现出均匀的位移矢量。

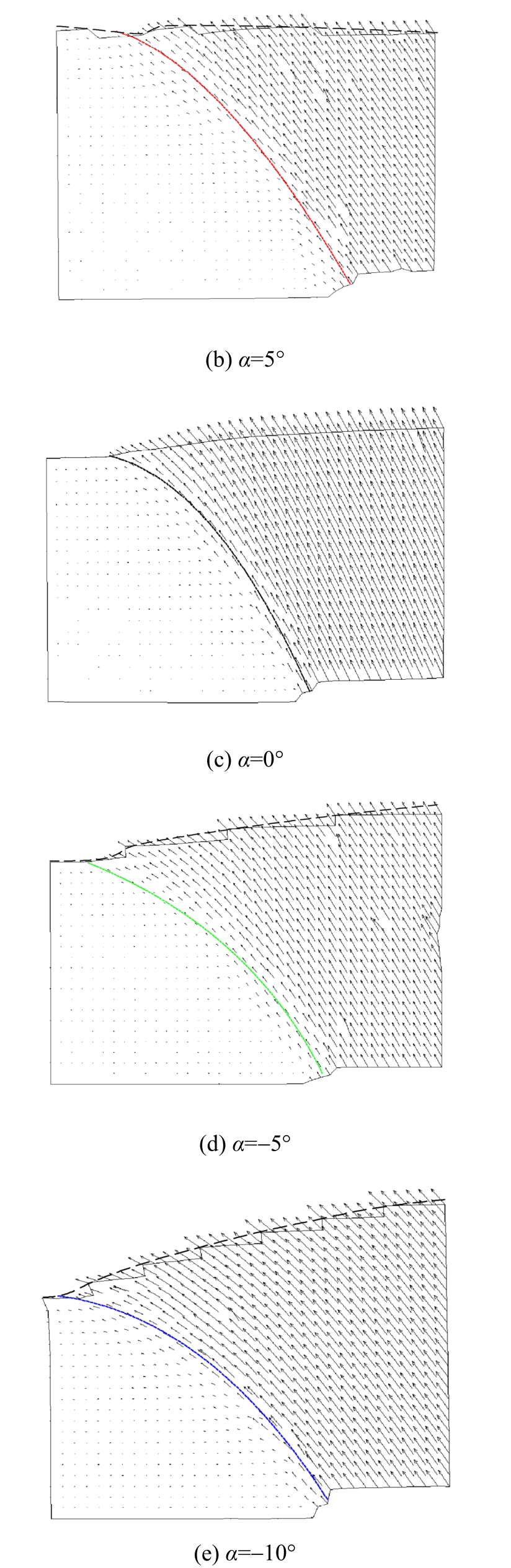
图7 露头时上覆土体位移矢量
Fig.7 Displacement field at time of rupture outcrop
图8~图10所示分别为破裂带露头时土体剪应变εxy云图、x向正应变εx云图、等效应变ε云图。土体中某点处的等效应变ε反映了该点偏应变的综合作用,与土体塑性变形关系密切,在一定程度反映土体中塑性变形的分布。ε的计算公式如式(4):



图8 倾斜场地剪应变εxy云图
Fig.8 Contour of shear strain εxyin inclined grounds
由图8可以看出,剪应变的范围由土体深处到地表逐渐扩展,最后表现为一个三角形的“剪切区”,尤其是 α=5°和水平场地时的剪应变云图中这种特征更为明显。这种剪应变的分布模式也印证了三角剪切模型中关于土体位移(速度)场呈三角形分布的设定。破裂带附近剪应变值最大,α=10°时破裂带内全部产生正剪应变,而随着地表倾角由正变为负,破裂带露头处出现负剪应变区域,α=-10°时负剪应变区范围最大。破裂带露头处土体负剪应变的出现表明此处剪切方向发生了改变,这种剪切方向的改变实际上是破裂带倾角变化规律的另一种反映。
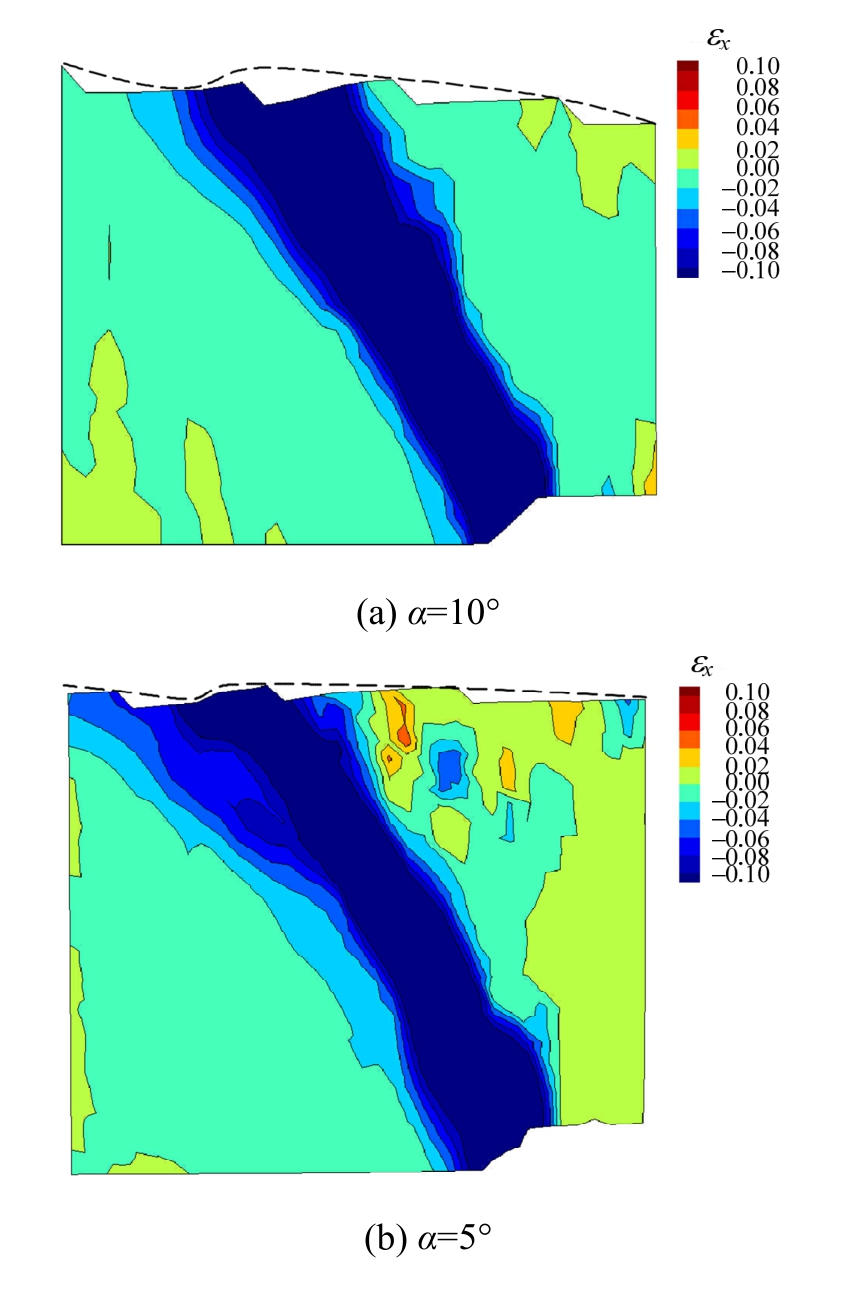
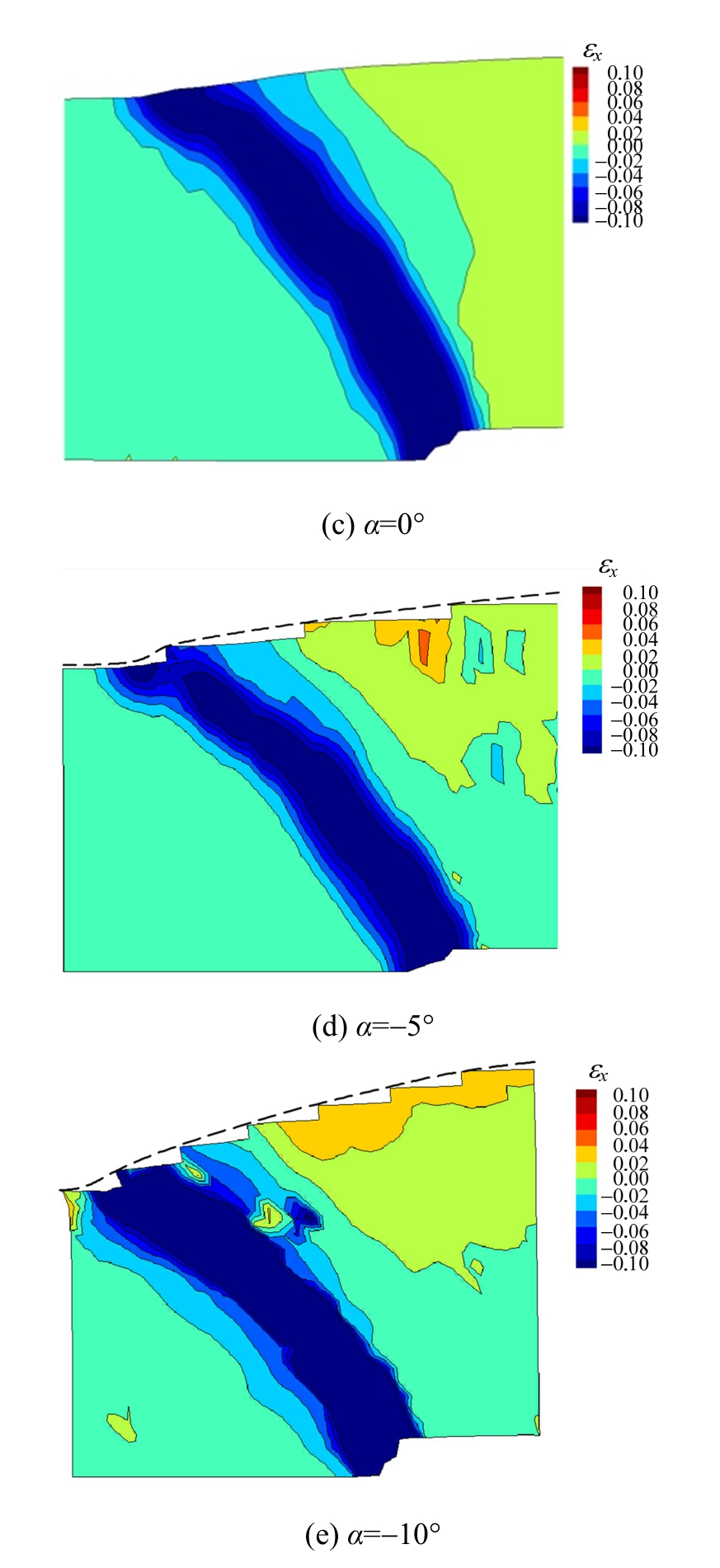
图9 倾斜场地正应变εx云图
Fig.9 Contour of normal strain εxin inclined grounds


图10 倾斜场地等效应变ε云图
Fig.10 Contour of equivalent strainε in inclined grounds
而不同于剪应变的类似三角形分布的特征,土体内正应变和塑性变形的分布更为集中(图9和图10),均呈现出明显的带状,其形状与破裂带的扩展路径均吻合。这种集中的特性可以提供一种地下建构筑物的设计思路,当建构筑的选址可以避开已有或潜在破裂带时,其抗震措施可以仅以抗剪为主,而断层错动过程中的压应力随着与破裂带距离的增加而迅速衰减,因此当地下建构筑物与破裂带有一定距离时可以不必考虑这种压应力所造成的破坏。由图8和图9还可以发现,无论是剪应变还是正应变(压缩),上盘土体均大于下盘土体。上盘土体中均有部分区域剪应变和正应变的值较大,而下盘土体中剪应变和正应变的值则均较小,接近 0。因此,建议地下建构筑物的选址应尽量选择下盘。
为进一步分析断层错动过程中的地表形态,采用Gompertz S形函数对地表竖向位移∆y拟合,水平地表下断层错动过程中地表竖向位移的拟合结果也可参考Chang等[25]的研究。拟合时取基岩断点为 x轴的坐标原点,Gompertz S形函数如式(5)所示。
式中,a、b、xc均为待定的拟合常数。各参数的物理含义如图 11所示,其中 a对应 x取无穷大时Gompertz S形函数值,xc对应Gompertz S形曲线拐点的横坐标值。对式(5)求一阶导数即为竖向位移梯度,如式(6),拐点处斜率(∆ y) ′xc= a /(eb)。
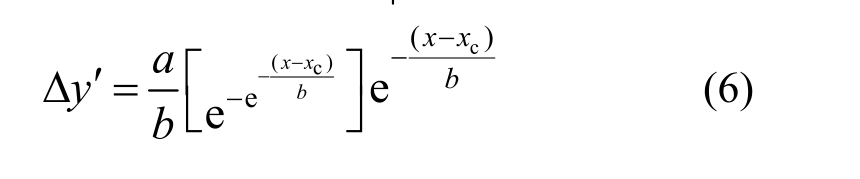
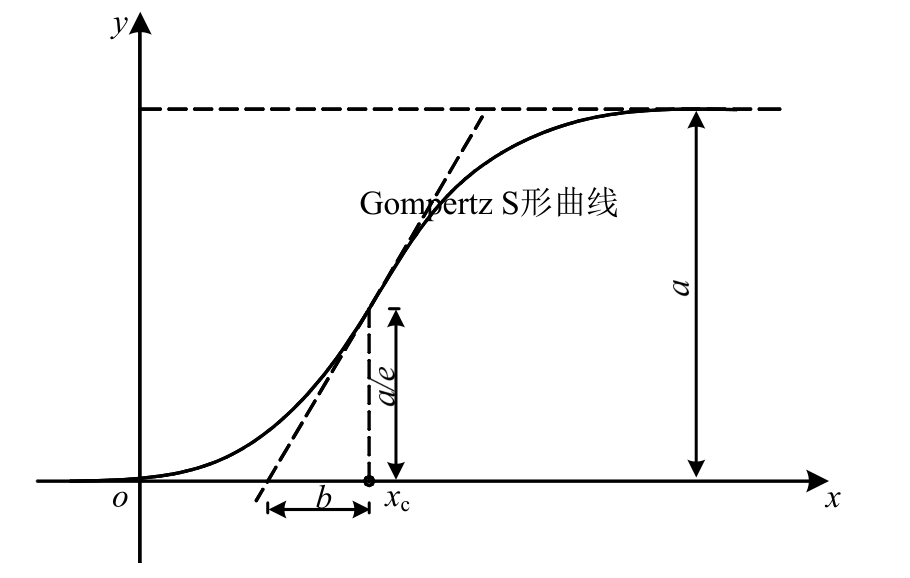
图11 Gompertz S形曲线
Fig.11 Gompertz sigmoid curve
图 12给出了场地在不同基岩竖向位移时地表竖向位移∆y的实测值和拟合曲线的对比,表 4给出了破裂带露头时刻地表竖向位移的拟合参数值。总体而言,从下盘远处逐渐到上盘远处,地表位移呈现“S”形变化,即下盘远处地表竖向位移基本为0,在接近破裂带露头处(图12中横坐标为xo处)位移迅速增加,在经过“S”形曲线拐点后位移增加速率减缓,在上盘远处地表位移逐渐趋于某个恒定值。需要指出,实际的断层错动的影响具有衰减效应,地表竖向位移会随土层厚度的增加和与破裂带距离的增加而减小。
由表4可看出,α=0°时a值最小,约为45.59 mm,随着场地倾斜程度增加,a也随之增大。对比a值和破裂带露头时基岩位移(见表2)可发现,基岩断点处(x=0)的地表竖向位移a基本与基岩竖向位移一致,表明断层错动过程中上覆土体的压缩量很小,因此在上盘距离破裂带较远处,地表的竖向位移近似等于基岩竖向位移。可见,实际上a值反映了基岩竖向位移量,因此表现出与基岩位移相同的规律。
表4 露头时刻地表竖向位移拟合常数
Table 4 Fitting parameters of vertical displacements of ground surfaces at time of outcropping



图12 地表竖向位移
Fig.12 Vertical displacement of ground surfaces
图 13为各场地的地表竖向位移梯度。位移梯度峰值点实际对应于“S”型曲线的拐点,此处斜率最大,也是地表变形最为剧烈的区域。结合图13和表4可知,破裂带露头时水平场地的地表位移梯度峰值![]() 最小,约为0.113,而随着地表倾角的增加(无论α是变为正值或者变为负值),破裂带露头时刻地表位移梯度均增大,当α=10°或α=-10°时位移梯度峰值
最小,约为0.113,而随着地表倾角的增加(无论α是变为正值或者变为负值),破裂带露头时刻地表位移梯度均增大,当α=10°或α=-10°时位移梯度峰值![]() 达到最大,均约为0.15。这个结果似乎表明水平场地在破裂带露头时刻的地表变形最弱,因此相对其他场地,水平场地上的建构筑物受到破裂带的影响较小。但需要指出,由Gompertz S形函数梯度的计算式式(6)可看出,计算得到的位移梯度值与a成正比,如果将a近似看成基岩竖向位移,则露头时刻位移梯度曲线峰值的大小实际反映了基岩竖向位移的大小,因此呈现出与基岩竖向位移相同的规律。总结而言,基岩位移对地表变形程度(无论是位移还是位移梯度)呈正相关影响。
达到最大,均约为0.15。这个结果似乎表明水平场地在破裂带露头时刻的地表变形最弱,因此相对其他场地,水平场地上的建构筑物受到破裂带的影响较小。但需要指出,由Gompertz S形函数梯度的计算式式(6)可看出,计算得到的位移梯度值与a成正比,如果将a近似看成基岩竖向位移,则露头时刻位移梯度曲线峰值的大小实际反映了基岩竖向位移的大小,因此呈现出与基岩竖向位移相同的规律。总结而言,基岩位移对地表变形程度(无论是位移还是位移梯度)呈正相关影响。
由各场地在不同基岩位移下的地表位移梯度曲线可见,随着基岩位移的增加,地表位移梯度的峰值点会逐渐趋向下盘,也即地表变形最剧烈处将逐渐靠近下盘,因此,为避免较大的地表变形带来的损伤和破坏,建议地表建构筑选址时应尽量位于上盘。
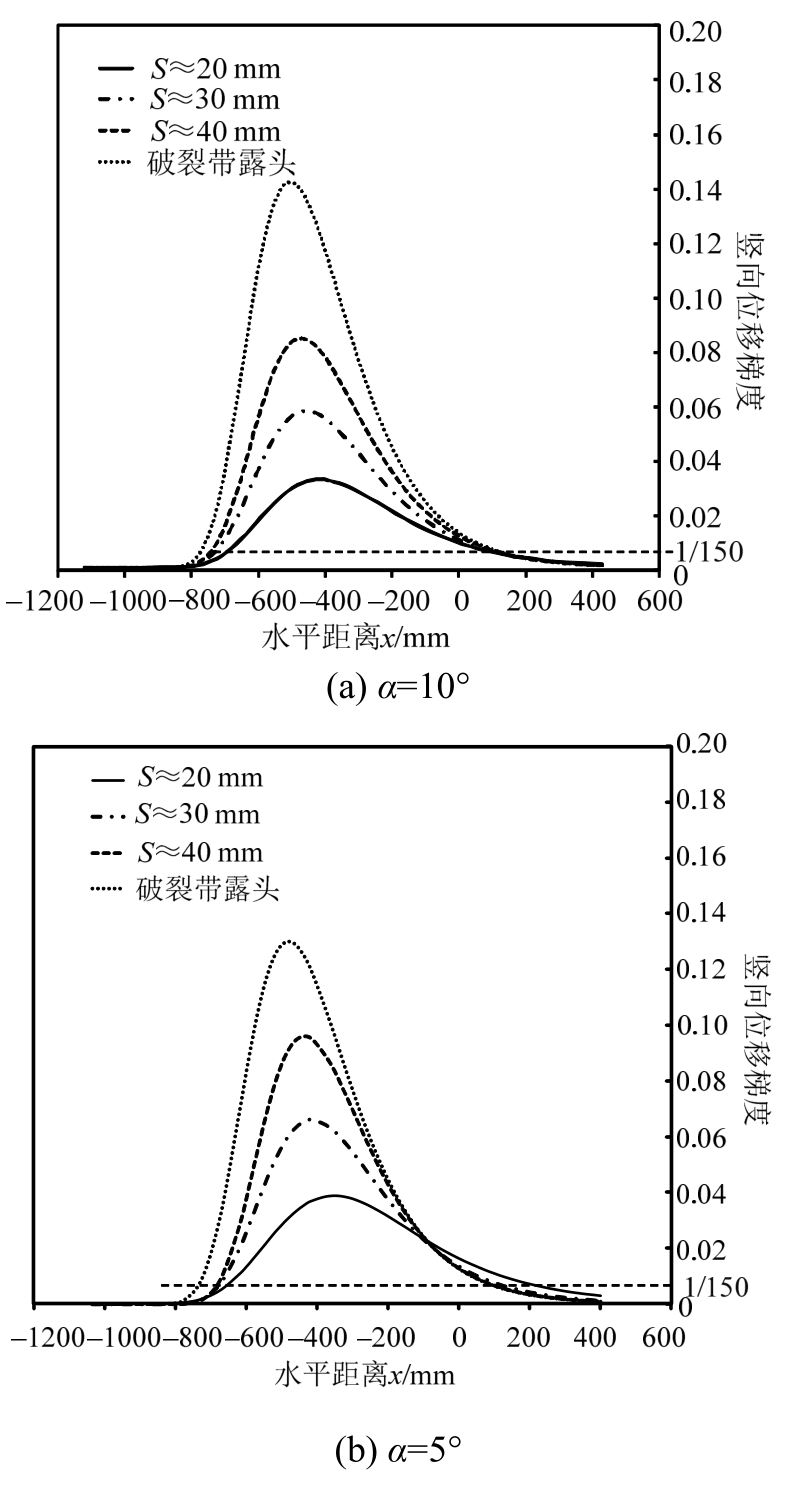
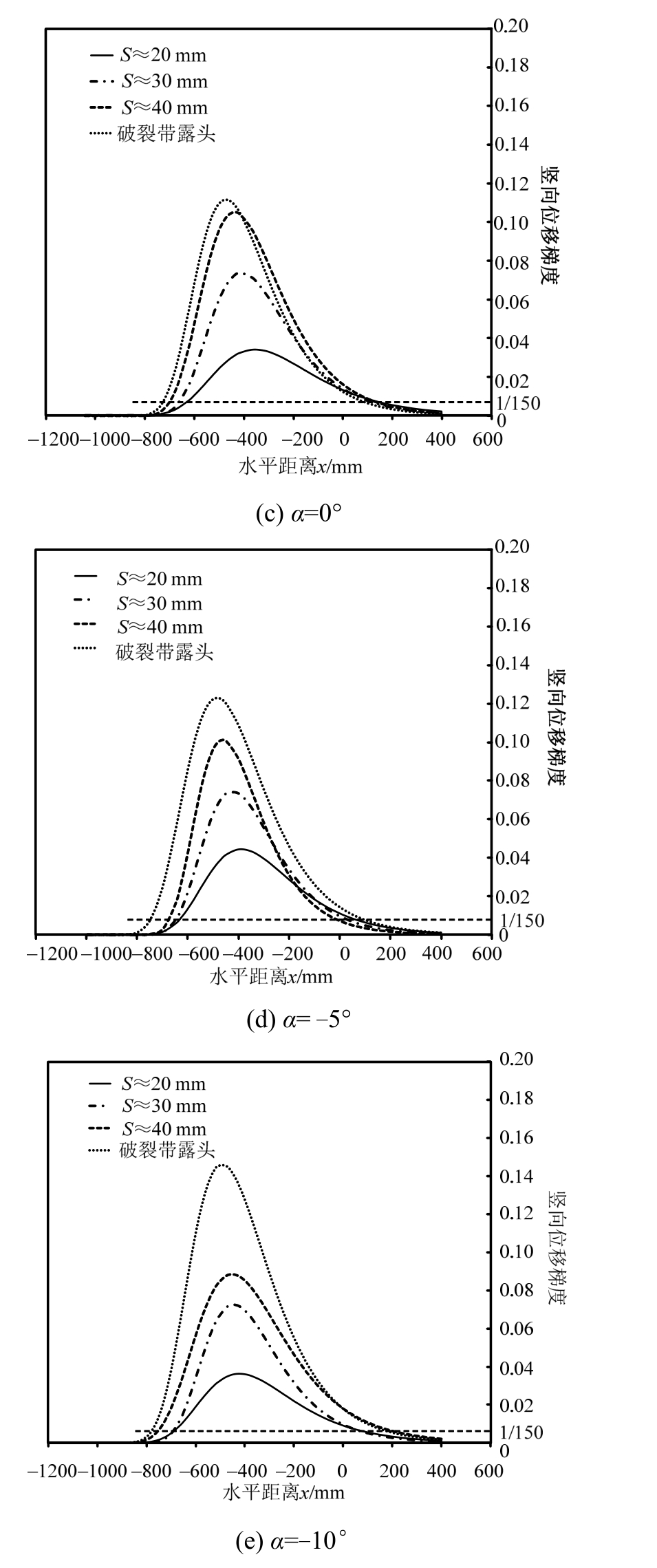
图13 地表竖向位移梯度
Fig.13 Gradient of vertical displacement of ground surfaces
一般认为,地表竖向位移梯度达到1/150时(如图13红色虚线所示),地表的建、构筑物将受到较严重的破坏[25],本文也将竖向位移梯度大于或等于1/150的区域视为破裂带的主要影响区域。表5给出了不同倾斜场地破裂带影响区域的参数值,其中,破裂带影响区域的左端点坐标为xl,右端点坐标为xr,并给出了相应露头点位置xo、破裂带影响区总宽度 L、下盘影响区宽度 lf、上盘影响区宽度lh以及lf/L的值。图14为根据计算结果绘制的破裂带影响区域分布图。
表5 破裂带影响区域参数
Table 5 Information of influence zones of rupture


图14 露头时刻破裂带影响区分布
Fig.14 Influence zones of rupture at time of rupture outcropping
由表5和图14可以看出,α=10°时破裂带影响区域总宽度L约为800.88 mm,而随着地表倾角α由正变为负,L逐渐增大,α=-10°时破裂带影响区总宽度 L达到最大值 948.19 mm°还可看出,当α=10°时破裂带露头点位置 xo约为-482.60 mm,此时下盘破裂带影响区占比lf/L约为28%,随着地表倾角α由正变为负,下盘破裂带影响区占比逐渐减小,α=-10°时lf/L降至最小值21%。可见,在逆断层作用下破裂带影响区主要位于上盘,约占70%~80%,且在地表倾角α由正变为负的过程中,上盘破裂带影响区比重逐渐增大。
Bray等[29]对加州兰德斯地震、土耳其科喀艾里地震和迪兹杰地震、台湾集集地震等的地表断层破裂的调研结果表明,逆断层作用下地表剧烈变形主要发生在上盘,而下盘建(构)筑物受损较少且地表变形主要集中在破裂带露头处附近(即地表变形梯度值较大处),现场实测结果与本文模型试验结果规律一致。
综合试验与实测结果来看,相较于下盘,上盘地表建构筑物的断层避让距离应更大,上盘的避让距离取下盘避让距离的3倍~4倍较为合适,对于地表倾角为负值的情况,上盘地表建构筑物的避让距离还应增大。
进一步采用相似理论将模型破裂带影响区宽度换算为实测值,则地震现场破裂带影响区宽度l~可近似按式(7)计算:
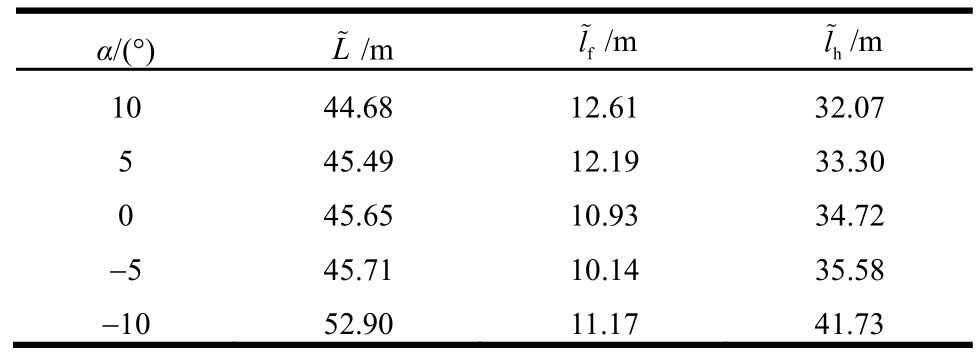
式中:l为模型试验中破裂带影响区宽度;∆~y为地震现场实测地表竖向位移最大值,通常约为2 m~4 m[29-30],此处取各实测值的平均值约 3 m;∆ y为模型试验中破裂带露头时的地表竖向位移最大值,此处同样取各场地平均值约53.77 mm。换算得到的地震现场破裂带影响区宽度如表6所示。
由表6可看出,换算得到的各场地的破裂带影响区宽度约为40 m~50 m,美国加州Alquist-Priolo法案[31]规定活断层上应有 300 m 宽的断层避让带(即距地表破裂带每侧 150 m),我国《建筑抗震设计规范》[32]规定建(构)筑物与断层的避让距离不小于 200 m (8度设防丙类建筑),本文在不同地表情况下试验得到结果均相对规范结果较小,仅为规范取值的1/4~1/3,据此可认为规范所规定的断层避让距离是合理的。
由表6还可看出,水平场地中下盘破裂带影响区宽度约为10.93 m,上盘影响区宽度约为34.72 m。Bray[29]认为上盘距离地表破裂带约 20 m的范围地表变形最为剧烈,赵纪生等[30]对汶川地震地表破裂的调查研究表明,不出现建筑物完全倒塌的避让距离为32 m。本文试验结果与Bray和赵纪生等的研究结果也较为接近。
表6 地震现场破裂带影响区宽度
Table 6 Widths of influence zones of rupture at earthquake sites
本文利用自行研制的常重力断层错动试验装置,结合PIV技术研究了更具普遍性的倾斜场地下逆断层错动引起上覆砂土层破裂的机制,重点分析了场地倾斜程度对破裂带扩展规律、土体变形和地表变形等的影响,得到的主要结论如下:
(1) 随着场地倾斜程度增大,破裂带露头时的基岩错动位移也随之增大,可能与土体中形成的破裂带长度有关。
(2) 不同倾斜场地中破裂带露头倾角均与Rankine理论预测结果更为一致,但考虑到本模型试验应力水平较低,试验时土体剪胀性的影响可能并未完全发挥,高地应力条件下破裂带扩展角度如何值得进一步研究。
(3) 断层错动过程中上盘土体应变(剪应变、正应变和等效应变)均大于下盘土体,据此本文建议地下建构筑物的选址应尽量位于下盘。
(4) 随着地表倾斜程度增加,露头时刻场地地表的变形程度(无论是位移还是位移梯度)也随之增大,这也表明基岩位移对地表变形程度呈正相关影响。随着基岩位移的增加,地表位移梯度的峰值点会逐渐趋向下盘,也即地表变形最剧烈处将逐渐靠近下盘,为避免较大的地表变形带来的损伤和破坏,建议地表建构筑选址时应尽量位于上盘。
(5) 综合试验与实测结果,相较于下盘,上盘地表建构筑物的断层避让距离应更大,上盘的避让距离取下盘避让距离的3倍~4倍较为合适,且随着地表倾角由正变为负,上盘地表建构筑物的避让距离应随之增大。
参考文献:
[1] Lin A, Ren Z, Jia D, et al. Coseismic thrusting rupture and slip distribution produced by the 2008 M w 7.9 Wenchuan earthquake, China [J]. Tectonophysics, 2009,471(Suppl 3/4): 203―215.
[2] Walker R T, Wegmann K W, Bayasgalan A, et al. The Egiin Davaa prehistoric rupture, central Mongolia: a large magnitude normal faulting earthquake on a reactivated fault with little cumulative slip located in a slowly deforming intraplate setting [J]. Geological Society London Special Publications, 2017(432): 187―213.
[3] Pucci S, De Martini P M, Civico R, et al. Coseismic ruptures of the 24 August 2016, Mw 6.0 Amatrice earthquake (central Italy) [J]. Geophysical Research Letters, 2017, 44(5): 2138―2147.
[4] 郑永来, 杨林德, 等. 地下结构抗震[M]. 上海:同济大学出版社, 2005: 10―51.Zheng Yonglai, Yang Linde, et al. Earthquake resistance of underground structures [M]. Shanghai: Tongji University Press, 2005: 10―51. (in Chinese)
[5] 吴啸龙, 杨志强, 武继峰, 等. 位错理论模型在福建省沿海交通干线地面沉降模拟中的应用[J]. 东南大学学报自然科学版, 2013(A02): 338―342.Wu Xiaolong, Yang Zhiqiang, Wu Jifeng, et al.Application of computed subsidence in fujian coastal traffic area using dislocation model [J]. Journal of Southeast University (Natural Science Edition), 2013(A02): 338―342. (in Chinese)
[6] 何登发, John Suppe. 三角剪切断层传播褶皱作用理论与应用[J]. 地学前缘, 2007, 14(4): 66―73.He Dengfa, John Suppe. Theory and application of tri-shear fault propagation folding [J]. Earth Science Frontiers , 2007 , 14(4): 66―73. (in Chinese)
[7] Cole D A, Lade P V. Influence zones in alluvium over dip-slip faults [J]. Journal of Geotechnical Engineering,1984, 110(5): 599―615.
[8] Lin M L, Chung C F, Jeng F S. Deformation of overburden soil induced by thrust fault slip [J].Engineering Geology, 2006, 88(Suppl 1/2): 70―89.
[9] 杨杰, 陈新民, 沈建. 断层错动在砂土中传播规律的模型试验研究[J]. 防灾科技学院学报, 2011, 13(02):18―23.Yang Jie, Chen Xinmin, Shen Jian. Model test research of the fault slip spreading rule in the soil [J]. Journal of Institute of Disaster Prevention, 2011, 13(02): 18―23.(in Chinese)
[10] 徐泽龙. 逆断层错动引起上覆土层破裂的模型试验研究[D]. 浙江: 浙江大学, 2015.Xu Zelong. Experimental study on the fault rupture of overlying soil induced by reverse fault slip [D]. Zhejiang:Zhejiang University, 2015. (in Chinese)
[11] Bransby M F, Davies M C R, Nahas A E, et al.Centrifuge modelling of reverse fault–foundation interaction [J]. Bulletin of Earthquake Engineering, 2008,6(4): 607―628.
[12] Bransby M F, Davies M C R, Nahas A E. Centrifuge modelling of normal fault–foundation interaction [J].Bulletin of Earthquake Engineering, 2008, 6(4): 585―605.
[13] 骆冠勇, 蔡奇鹏, 吴宏伟. 地层错动引起的上覆饱和黏土层变形特性的离心试验研究[J]. 岩土力学, 2012,33(10): 2985―2900, 3000.Luo Guanyong, CAI Qipeng, NG CWW. Centrifuge modelling of ground deformations induced by normal fault in saturated clay [J]. Rock and Soil Mechanics,2012, 33(10): 2985―2900, 3000. (in Chinese)
[14] 骆冠勇, 吴宏伟, 蔡奇鹏. 地层错动引起的上覆砂层变形特性的离心试验研究[J]. 岩石力学与工程学报,2010, 29(08): 1649―1656.Luo Guanyong, Wu Hongwei, Cai Qipeng. Centrifuge experimental study of deformation characteristics of overlying sand induced by fault rupture [J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(08): 1649―1656. (in Chinese)
[15] Wu Hongwei, Cai Q P, Hu P. Centrifuge and numerical modeling of normal fault-rupture propagation in clay with and without a preexisting fracture [J]. Journal of Geotechnical & Geoenvironmental Engineering, 2012,138(12): 1492―1502.
[16] 蔡奇鹏, 吴宏伟. 胶结黏土中正断层扩展的变形和孔压变化研究[J]. 岩石力学与工程学报, 2014(2): 390―395.Cai Qipeng, Wu Hongwei. Deformation mechanism and variation of pore pressure due to normal fault propagation in cemented clay [J]. Chinese Journal of Rock Mechanics and Engineering, 2014 (2): 390―395.(in Chinese)
[17] Anastasopoulos I, Gazetas G, Bransby MF, et al. Fault rupture propagation through sand: finite-element analysis and validation through centrifuge experiments [J].Journal of Geotechnical & Geoenvironmental Engineering, 2007, 133(8): 943―958.
[18] Shibuya S, Tamate S, Mitachi T. Interpretation of direct shear box testing of sands as quasi-simple shear [J].Geotechnique, 1997, 47(4):769―790.
[19] Adrian R J. Particle-imaging techniques for experimental fluid mechanics [J]. Annual Review of Fluid Mechanics,1991, 23 (23): 261―304.
[20] 张敏, 吴宏伟. 颗粒图像测速技术在离心试验变形分析中的应用[J]. 岩石力学与工程学报, 2010 (A02):3858―3864.Zhang Min, Wu Hongwei Application of particle image velocimetry to deformation analysis in centrifugal tests[J]. Chinese Journal of Rock Mechanics and Engineering,2010 (A02): 3858―3864. (in Chinese)
[21] White D J. An investigation into behavior of pressed-in piles [D]. Cambridge: University of Cambridge, 2003.
[22] 金浏, 李鸿晶. 逆冲断层作用下埋地管道屈曲分析[J].工程力学, 2011, 28(12): 98―104.Jin Liu, Li Hongjing. Buckling analysis of buried pipeline subject to reverse fault crossings [J].Engineering Mechanics, 2011, 28(12): 98―104. (in Chinese)
[23] 刘爱文, 胡聿贤, 李小军, 等. 大口径埋地钢管在地震断层作用下破坏模式的研究[J]. 工程力学, 2005,22(3): 82―87.Liu Aiwen, Hu Yuxian, Li Xiaojun, et al. Damage behavior of large-diameter buried steel pipelines under fault movements [J]. Engineering Mechanics, 2005,22(3): 82―87. (in Chinese)
[24] 何川, 李林, 张景, 等. 隧道穿越断层破碎带震害机理研究[J]. 岩土工程学报, 2014, 36(3): 427―434.He Chuan, Li Lin, Zhang Jing, et al. Seismic damage mechanism of tunnels through fault zones [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 427―434. (in Chinese)
[25] Chang Y Y, Lee C J, Huang W C, et al. Evolution of the surface deformation profile and subsurface distortion zone during reverse faulting through overburden sand [J].Engineering Geology, 2015, 184(2015): 52―70.
[26] Zanjani M M, Soroush A. Numerical modeling of reverse fault rupture propagation through clayey embankments[J]. International Journal of Civil Engineering, 2013, 11:122―132.
[27] Roscoe K H. The influence of strains in soil mechanics[J]. Géotechnique, 1970, 20(2): 129―170.
[28] Vermeer P. A simple shear band analysis using compliances [C]. Proceeding of IUTAM Conference on Deformation and Failure of Granular Materials, Delft,Netherland: Balkema, 1982.
[29] Bray J D. Developing mitigation measures for the hazards associated with earthquake surface fault rupture.In: Proceedings of workshop on seismic fault-induced failures-possible remedies for damage to urban facilities.Japan, University of Tokyo, 2001: 55―79.
[30] 赵纪生, 吴景发, 师黎静, 等. 汶川地震地表破裂周围建筑物重建的避让距离[J]. 地震工程与工程振动,2009, 29(6): 96―101.Zhao Jisheng, Wu Jingfa, Shi Lijing, et al. Setback distance determination in reconstruction along the trace of surface rupture caused by M_s8.0 Wenchuan earthquakee [J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(6): 96―101. (in Chinese)
[31] Hart Earl W, Bryant William A. Fault-rupture hazard zones in California: Alquist-Priolo Earthquake fault zoning act with index to earthquake fault zones maps[M]. California: Division of Mines and Geology, 1999:7―34.
[32] GB 50011―2001, 建筑抗震设计规范[M]. 北京: 中国建筑工业出版社, 2005.GB 50011―2001, Code for seismic design of building[M]. Beijing: China Architecture Industry Press, 2005.(in Chinese)
MODEL TESTING STUDY ON THE INFLUENCE OF REVERSE FAULTING ON OVERLAYING SOIL UNDER AN INCLINED GROUND
SHI Ji-sen1,2, LING Dao-sheng1,2, XU Ze-long3, HUANG Bo1,2
(1. MOE Key Laboratory of Soft soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China;2. Institute of Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;3. Institute of Industrial Science, University of Tokyo, Tokyo 1538505, Japan)
Abstract:Based on the faulting model test device designed by us and the PIV technique, the rupture process of overlaying soil due to reverse faulting under an inclined ground is studied. The emphasis of the study is put on the influence of surface inclination on the law of faulting rupture propagation, the deformation of soil and surface, etc.The study results show that the bedrock displacement increases with the inclining degree of the surfaces. The propagation angles of ruptures near the ground surfaces are more consistent with the predictions of Rankine theory for different grounds, while the predictions of Roscoe theory and Vermeer theory exhibit larger errors. The shear strain, normal strain and equivalent strain of the soil on the hanging wall are all larger than those on the foot wall during reverse faulting. The displacement of the bedrock has positive influence on the soil displacement and the displacement gradient with the inclining degree of the surfaces. Combined with field test data, the studies on the protection distance of the buildings and structures from the fault show that the protection distance of the buildings and structures on the hanging wall should be larger than those on the foot wall. When the surface inclination angle changes from positive to negative, the protection distance of the buildings and structures on the hanging wall should increase accordingly.
Key words:inclined ground; model test; reverse faulting; fault rupture; particle image velocimetry (PIV)
中图分类号:TU433
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.03.0247
文章编号:1000-4750(2018)07-0194-14
收稿日期:2017-03-27;修改日期:2017-09-28
基金项目:国家自然科学基金项目(51278451,51578502);重点基础研究发展计划(973计划)项目(2014CB047005).
通讯作者:黄 博(1973―),女,江苏人,副教授,博士,从事岩土工程的科研工作研究(E-mail: cehuangbo@zju.edu.cn).
作者简介:
石吉森(1988―),男,江苏人,博士生,从事岩土工程的科研工作研究(E-mail: 3390183284@qq.com);
凌道盛(1968―),男,安徽人,教授,博士,从事岩土工程的科研工作研究(E-mail: dsling@zju.edu.cn);
徐泽龙(1989―),男,河南人,博士生,从事岩土工程的科研工作研究(E-mail: 651136577@qq.com).