李 潇1，方 秦1，孔祥振2，吴 昊1
(1. 陆军工程大学爆炸冲击防灾减灾国家重点实验室，江苏，南京 210007；2. 白城兵器试验中心，吉林，白城 137000)
摘 要：进行了砂浆材料在不同应变率下的SHPB实验，拟合实验数据得到了动态强度放大因子DIF随应变率变化的关系曲线。基于实验测得应变率时程曲线，采用简化有限元模型，对实验进行了数值模拟。该文探讨了动态压缩实验中惯性效应产生的原因，并基于数值模拟对本实验中惯性效应对材料动态强度的影响进行了剥离，得到了砂浆材料动态强度放大因子随应变率变化的固有特性曲线，并将该固有特性曲线作为数值模拟中应变率效应的输入，计算结果与实验得到的应力-应变曲线吻合较好。进一步通过比较输入CEB推荐曲线和已有半经验公式的模拟结果，验证了所提出砂浆材料动态强度放大因子固有特性曲线的优越性。
关键词：SHPB实验；应变率效应；惯性效应；数值模拟；简化模型
混凝土类材料广泛应用于军用民用设施，在强动载(如爆炸冲击荷载)作用下的力学性能与静载时截然不同。爆炸冲击作用下混凝土类材料的力学性能研究可为防护工程设计提供有效参考，是当前学术界和工程界的关注热点[1－2]。
Abrams[3]首次发现混凝土动态抗压强度对应变速率具有敏感性；Glanville等[4]进行了大量落重试验，表明混凝土抗压强度随着应变率增加而增大；随后，许多学者通过液压试验机实验[5]、落重实验[6－7]和霍普金森杆实验[8－9]等对混凝土类材料进行了动态力学性能研究，得到了混凝土动态强度放大因子(动态强度与静态强度比，DIF)与应变率的关系。Bischoff和 Perry[10]对1910年～1990年间前人的实验数据进行了总结，给出了混凝土动态压缩DIF与应变率之间的关系曲线。欧洲混凝土委员会规范(FIP-CEB)[11]通过对实验数据的总结，给出了受压条件下的DIF与应变率关系的推荐公式。
然而，实验得到的DIF并不是材料的真实固有特性，试件尺寸、实验条件及不可避免的惯性效应等因素将直接影响实验结果。Hao和Hao[12]对SHPB实验进行数值模拟，系统地分析了试件尺寸、骨料含量及端面摩擦对实验结果的影响。上述实验的影响因素可以通过涂抹润滑剂、统一试件尺寸等方法消除，但由于惯性效应是结构响应，无法通过控制实验参数去除。SHPB实验惯性效应最早由 Brace和 Jones[13]针对岩石动态压缩强度测量结果提出。Bertholf和Karnes[14]通过数值模拟研究，说明轴向的惯性使得试件横向约束增加，试件进入多轴应力状态。Forrestal等[15]在理论上针对轴向加速度对径向围压的影响进行了探讨，在一定程度上证明了惯性效应的存在，并推导得出弹性试件的径向各点围压与轴向加速度之间的关系。Lu和 Li[16]通过数值迭代对SHPB应变率效应进行了修正，该方法可以有效地剥离惯性效应对DIF的影响。Xu和Wen[17]通过对前人混凝土动力实验的总结，得出去除惯性效应后的DIF随应变率变化的半经验公式。Hao等[18]提出了一种较为简单的利用数值模拟剥离惯性效应的方法。
上述研究主要针对混凝土，针对砂浆材料固有DIF的研究相对较少。砌体材料容易就地取材，具有良好的耐火性和较好的耐久性，具有结构自重轻、施工进度快等优点，广泛应用于我国农村城镇工业民房建设。砂浆作为砌体结构的粘结材料，对砌体结构抗压强度起到重要作用，研究砂浆材料在动载下的应变率效应在讨论砌体在地震荷载、冲击荷载等工况下的响应具有重要意义[19－20]。由于在关于砂浆材料的数值模拟中，多直接采用72号模型，该模型的材料应变率效应曲线采用的是基于大量混凝土实验所得动态强度放大因子DIFs的CEB推荐公式，由于骨料差异及接触面的影响，两者的差异不可忽视，势必会使得砂浆材料的数值模拟结果与实际存在一定差异。现有有关混凝土材料的研究方法是基于细观力学原理将混凝土看成是不同级配的骨料与砂浆以及两者界面的统一体，砂浆材料的强度参数研究可以为混凝土细观力学研究中本构模型参数的选取提供可靠的依据[21]。
本文首先对静态抗压强度为 50 MPa的砂浆材料进行了一系列应变率范围为 75 s-1～650 s-1的SHPB实验，并通过拟合实验数据得到其DIF随应变率变化曲线。进而对上述实验进行了有限元模拟，并基于数值模拟对实验中惯性效应进行了剥离，得到了砂浆材料DIF随应变率变化的固有特性曲线。最后将该特性曲线作为数值模拟中材料应变率效应的输入，与输入 CEB推荐公式[11]及半经验公式[17]作为材料应变率效应的模拟结果对比，验证了基于数值模拟剥离惯性效应后的砂浆材料动态强度放大因子固有特性曲线的优越性。
砂浆材料是应变率敏感材料，应变率效应用动态强度放大因子DIF表示，其定义为动态强度峰值与静态强度峰值的比值：
其中：fcd/Pa是材料动态强度峰值；fc0/Pa是材料静态强度峰值。
由引言讨论可知，材料DIF通常由SHPB实验得到，但实验结果包含摩擦效应、试件差异和惯性效应等的影响，且惯性效应在实验中是不可避免的。以下讨论惯性效应产生的原因[22]。
在动载作用下，由于材料径向加速度形成的围压会使得混凝土类材料强度提高[23]，这一强度的提高是由于结构响应(惯性效应)造成，与材料本身特性无关。在动力实验中，得到的是材料本身强度提高与惯性效应共同作用的结果，则如果直接采用实验得到的动态强度放大因子 DIFs作为数值模拟的材料应变率特性曲线输入，则会过高地估计材料真实的动态强度，从而使得防护结构的设计偏危险。因此需要将惯性效应引起的动态强度放大因子DIFi剥离出来，得到材料本身应变率效应引起的动态强度放大因子DIFε˙输入曲线。
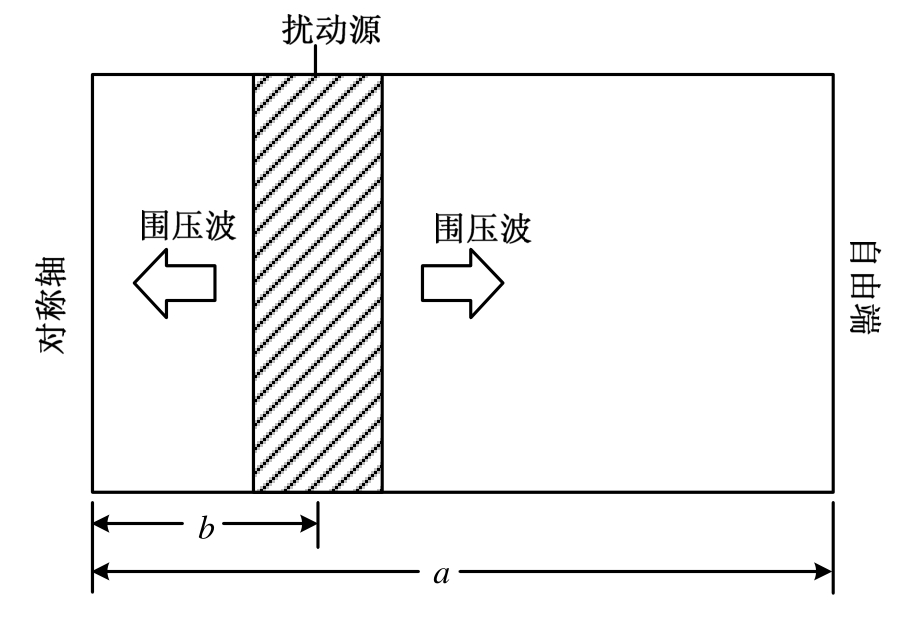
图1 围压波传播示意图[17]
Fig.1 Schematic diagram of propagation of confining pressure wave[17]
实验基于分离式霍普金森压杆(split Hopkinson pressure bar)系统，简称SHPB。SHPB是目前普遍使用的研究材料在高应变率下(102～104)力学性能的实验装置，广泛应用于材料动态力学性能研究中。SHPB杆直径为40 mm，长度为撞击杆400 mm，入射杆和透射杆1800 mm，缓冲杆1000 mm。密度为7830 kg/m3，弹性模量为 207 GPa。Li和 Meng[24]对端部摩擦进行数值模拟研究得出，当摩擦系数大于0.2时端面摩擦对动态强度有较大影响，而如果摩擦系数小于 0.1，端面摩擦的影响可以忽略。实验中试件采用自制非标准模具制备，为减少端面摩擦，经打磨后，两端面不平整度小于等于0.01 mm，且在所有试件端部均涂抹润滑油。
共进行16组砂浆圆柱体试件的SHPB实验，试件直径为 35.7 mm～36.1 mm，厚度为 20.4 mm～23.2 mm。在进行SHPB实验的同时用该批砂浆制作了三个标准立方体试件(150 mm×150 mm×150 mm)进行静态抗压实验，测得的强度分别为49 MPa、51 MPa和53 MPa，三个试件的平均强度为51 MPa，变异系数为0.032。由不同尺寸试件之间强度换算公式可知[25]，静态抗压实验试件和SHPB实验试件之间强度比值为：静态抗压试件强度/动态抗压试件强度=0.97587，故 SHPB试件的静态抗压强度为51×0.97587=49.7694 MPa，按四舍五入的原则取50 MPa。SHPB实验具体数据如表1所示。其中应变率为实验最大应力发生时刻对应的应变率。
表1 SHPB实验数据
Table 1 Experimental data of Split Hopkinson Pressure Bar
图2(a)给出了典型SHPB实验中(试件1)，粘贴于入射杆和透射杆上的应变片记录的电压信号时程图，将电压信号转为应变信号，通过式(2)～式(4)可得试件的应力、应变及应变率。
其中：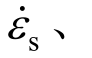
sε和σs分别为测点的平均应变率、平均应变和平均应力，均以压为正；E、C0和A分别为压杆的弹性模量、波速和横截面积；As、ls分别为试件的初始横截面积和初始长度；iε、rε和tε分别为杆上入射波、反射波和透射波应变信号。
图2 实验数据
Fig.2 Experimental data
图2(b)给出了试件1的应变率时程曲线。实验的应变率时程曲线可以作为下节数值模拟的加载依据。
图2(c)分别给出了试件4、7、10、11、13的应力应变曲线。
完整的SHPB有限元模型包括压杆和试件，计算耗时长。Hao等[18]提出一种简化模型，即忽略压杆而仅取试件部分建模，试件一端固定纵向位移，另一端采用速度加载。边界条件和有限元模型分别如图3和4所示，试件长22 mm，半径18 mm，单元类型采用3D Solid 164，材料参数采用LS-DYNA提供的自动生成算法(只需输入强度)，混凝土静态单轴抗压强度取为 50 MPa，单元尺寸为 1 mm×1 mm×1 mm。
采用简化模型进行加载时，试件上加载速度与应变率存在以下的线性关系：
其中：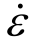
˙为加载应变率(由实验测得)；V为加载速度；L为试件长度。以试件1为例，将实验所得应变率时程曲线(图2(b))简化为图 5所示的梯形，并保证具有与实验相同的上升段、下降段时间及峰值应变率，进一步由式(5)可得到相应的加载速度时程曲线。
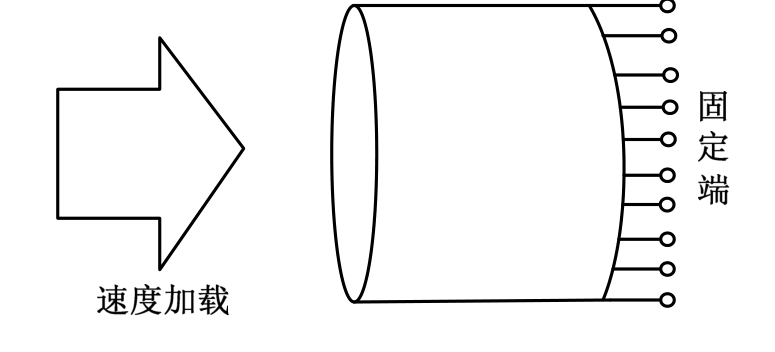
图3 试件边界条件示意图
Fig.3 Schematic diagram of boundary condition
图4 有限元模型图
Fig.4 Finite element model
图5 试件1简化加载应变率时程图
Fig.5 Simplified loading curve of specimen #1
图6给出了试件1简化模型计算所得平均应力时程曲线与完整的SHPB有限元模型计算所得平均应力时程曲线的对比。由图可知，两者的应力时程曲线重合度较高，特别是峰值应力值吻合很好，其中简化模型计算结果为 70.77 MPa，全模型计算结果为 71.05 MPa，两者误差仅为实验值的 0.4%，故本文采用简化模型，可以大量节约建模及计算时间。
为了进一步验证模拟结果与实验数据的吻合度，图7给出了试件12、14的实验与模拟应力-应变曲线，通过对比两条曲线可进一步证明该方法可以较好地还原实验结果。
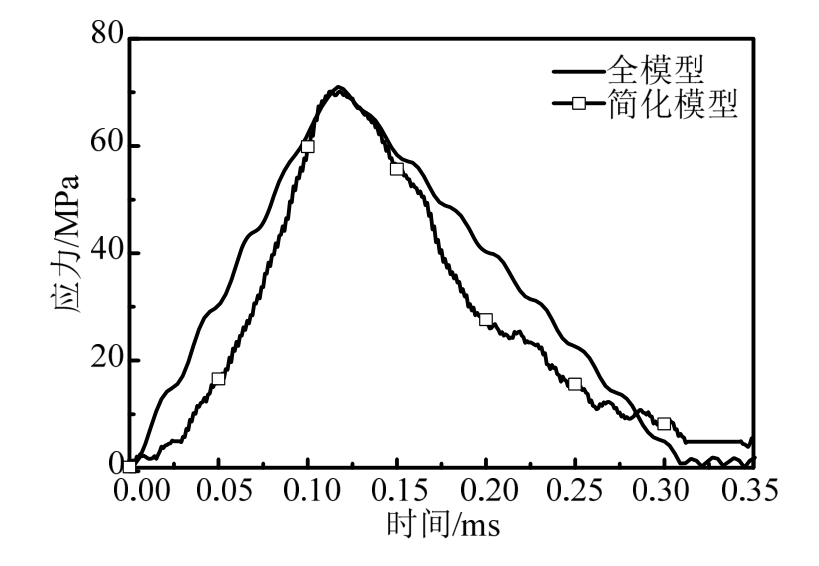
图6 简化模型与全模型计算结果对比
Fig.6 Comparison between simplified model and complete model
图7 模拟与实验应力-应变曲线对比
Fig.7 Comparison of stress-strain curves between simulation and experiment
Hao等[18]提出一种简单有效的惯性效应剥离办法，简要介绍如下。
在SHPB实验中，试件所表现出来的动态抗压强度并不是真实的材料特性。结构特性，包括惯性效应和端部摩擦都会对实验结果产生重要影响。在数值模拟中，端部摩擦可以通过设置摩擦系数来还原真实实验情况，在这里不进行讨论。
实验得到的动态强度放大因子DIFs为：
其中，Δfd是由于动载引起的强度提高，包括材料应变率效应及惯性效应，两者都是应变率的函数，可以认为两者是独立不耦合的[26]，则：
其中：∆fε˙是材料应变率效应引起的动态强度提高；Δfi是由于惯性效应引起的动态强度提高。将式(7)代入式(6)，得：
对于应变率不敏感材料，∆fε˙=0，此时的 DIF值为仅由惯性效应引起的DIFi：
其中，DIFi为试件惯性效应引起的动态强度提高因子，该值通过数值模拟得到，即在数值模拟时，不考虑材料应变率效应，将材料应变率效应输入设置为恒定值 1，此时得到的输出动态强度放大因子即为材料惯性效应引起的动态强度放大因子。真实材料应变率如下式：
将表1中实验结果绘入图8，拟合实验测得的动 态 强度 放 大 因 子 DIFs得 到 75 s-1≤ε˙c≤1000 s-1时曲线为：
材料固有的应变率效应计算步骤如下：首先，将数值模拟时材料应变率效应曲线输入设为恒值1，此时数值模拟得到(输出)的DIF即为惯性效应引起的动态强度放大因子DIFi；接着，用各试验所得动态强度放大因子 DIFs减去对应DIFi可得到每个试件的材料固有的动态强度放大因子DIFε˙；最后，将各试件DIFε˙值拟合成曲线，得到拟合公式如下：
其他范围采用CEB推荐公式[9]，
其中：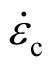
为压缩应变率；
=- 30×10-6s-1为参考应变率
将上述公式及半经验公式给出的DIFε˙汇入图8进行对比。
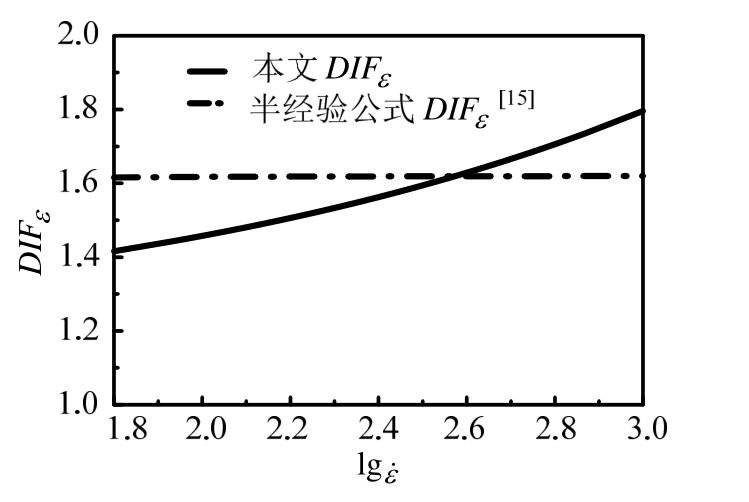
图 8 DIFε˙对比图
Fig.8 Comparison of DIFε˙
为了验证惯性效应剥离方法的有效性，在对各个试件进行模拟时，材料的应变率效应输入曲线采用式(12)，得到各试件数值模拟的输出DIF如图9所示。
图9 计算DIF与应变率关系曲线
Fig.9 Calculated relation of DIF and strain-rate
由图 8可知，在应变率小于 380 s-1(lgε˙约为2.58)时，砂浆材料的DIFε˙小于混凝土材料的DIFε˙，而当应变率大于380 s-1时，砂浆材料的 DIFε˙反而会大于混凝土材料的DIFε˙。这是因为，半经验公式[15]的DIFε˙基于混凝土实验，混凝土材料与砂浆材料的差别就在于骨料，混凝土包含骨料而砂浆没有，故可以将砂浆材料看成是骨料含量为0的混凝土。当混凝土遭受动力荷载时，材料的破坏是由裂缝的产生开始，随着应变率提高，裂缝会沿着材料薄弱面进行延伸。在低应变率应(变率小于380 s-1)下，裂缝来不及“绕过”骨料，混凝土材料中的裂缝会沿着骨料扩展，由于此时骨料强度要高于砂浆，故混凝土材料的DIFε˙会高于砂浆；随着应变率逐渐增加，当应变率高于380 s-1时，砂浆材料的强度快速增加，而骨料强度增加不明显，故砂浆材料的DIFε˙反而会高于混凝土材料的DIFε˙。
由图9可知，输入本文拟合曲线的输出结果与实验结果吻合很好。惯性效应引起的动态强度放大因子 DIFi增长趋势与实验所得动态强度放大因子DIFs拟合曲线十分接近，两者几乎是平行的，而材料应变率效应曲线增势与DIFi相比较缓。说明在中高应变率(75 s-1～1000 s-1)下，惯性效应对材料的动态强度提高起了大部分作用。
图9还分别给出了将CEB推荐公式以及Xu和Wen[15]提出的半经验公式作为模拟时材料应变率效应输入曲线得到的输出DIF。由图可知，与实验结果相比，输入CEB推荐公式及Xu和Wen[15]半经验公式的模拟结果均偏高，均会造成对材料动态强度的过高估计。说明骨料的存在会使得试件动态强度提高，也就是在动力荷载下，混凝土试件比砂浆试件有更好的抗力性能。
(1) CEB推荐的DIF公式是对混凝土实验结果的总结，由于其包含惯性效应的影响，输入该曲线作为砂浆材料 DIF有限元计算的材料应变率效应时，输出DIF值偏大，且误差较大，用于防护结构设计时偏危险。
(2) Xu和Wen[15]半经验公式是针对混凝土材料的，由于骨料的存在会使得混凝土材料的DIF值大于砂浆材料，将该公式应用于砂浆材料DIF计算时，误差虽小于 CEB推荐公式，但结果仍偏大，用于防护结构设计时偏危险。
(3) 采用Hao等[18]惯性效应剥离方法得到的砂浆材料数值模拟结果与实验吻合较好。
(4) 在75 s-1～650 s-1应变率范围内，惯性效应引起的 DIFi随应变率对数的增长趋势与实验 DIFs一致，而材料固有 DIFε˙曲线则较平缓，说明在该应变率范围内，惯性效应对材料应变率效应起到主要作用。
(5) 骨料和砂浆在动力荷载下强度都会得到提高，在不同应变率下，两者分别会对混凝土材料产生不同程度的影响。在应变率小于380 s-1时，砂浆材料的DIFε˙大于混凝土材料，在应变率小于380 s-1时，砂浆材料的DIFε˙大于混凝土材料。
参考文献：
[1] Savoikar P, Orr J. Proceedings of the international conference on advances in concrete technology materials and construction practice [M]. Excel India, 2016: 77―79.
[2] Zhou W, Tang L, Liu X, et al. Mesoscopic simulation of the dynamic tensile behavior of concrete based on a rate-dependent cohesive model [J]. International Impact Engineering, 2016, 95: 165―175.
[3] Abrams D A. Effect of rate of application of load on the compressive strength of concrete [J]. ASTM J, 1917,17(2): 70―78.
[4] Glanville W H, Grime G, Davies W W. The behavior of reinforced-concrete piles during driving. (includes photographs and appendices) [J]. Journal of the Institution of Civil Engineers, 1935, 1(2): 150―202.
[5] Cao J, Chung D D L. Effect of strain rate on cement mortar under compression, studied by electrical resistivity measurement [J]. Cement and Concrete research, 2002, 32(5): 817―819.
[6] Watstein D. Effect of straining rate on the compressive strength and elastic properties of concrete [C]. Journal Proceedings, 1953, 49(4): 729―744.
[7] Bischoff P H, Perry S H. Impact behavior of plain concrete loaded in uniaxial compression [J]. Journal of Engineering Mechanics, 1995, 121(6): 685―693.
[8] Grote D L, Park S W, Zhou M. Dynamic behavior of concrete at high strain rates and pressures: I.experimental characterization [J]. International Journal of Impact, Engineering, 2001, 25(9): 869―886.
[9] Zhang M, Wu H J, Li Q M, et al. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part I: Experiments [J]. International Journal of Impact Engineering, 2009, 36(12): 1327―1334.
[10] Bischoff P H, Perry S H. Compressive behavior of concrete at high strain rates [J]. Materials and Structures,1991, 24(6): 425―450.
[11] CEB-FIP Model Code 1990, Bulletin D’ Information No.213/214 [S]. Lausanne, Switzerland: Committee International du Beton, 1993.
[12] Hao Y, Hao H. Influence of the concrete DIF model on the numerical predictions of RC wall responses to blast loadings [J]. Engineering Structures, 2014, 73: 24―38.
[13] Brace W F, Jones A H. Comparison of uniaxial deformation in shock and static loading of three rocks[J]. Journal of Geophysical Research, 1971, 76(20):4913―4921.
[14] Bertholf L D, Karnes C H. Two-dimensional analysis of the split Hopkinson pressure bar system [J]. Journal of the Mechanics and Physics of Solids, 1975, 23(1): 1―19.
[15] Forrestal M J, Wright T W, Chen W. The effect of radial inertia on brittle samples during the split Hopkinson pressure bar test [J]. International Journal of Impact Engineering, 2007, 34(3): 405―411.
[16] Lu Y B, Li Q M. A correction methodology to determine the strain-rate effect on the compressive strength of brittle materials based on SHPB testing [J]. International Journal of Protective Structures, 2011, 2(1): 127―138.
[17] Xu H, Wen H M. Semi-empirical equations for the dynamic strength enhancement of concrete-like materials[J]. International Journal of Impact Engineering, 2013,60: 76―81.
[18] Hao H, Hao Y, Li Z X. Advances in protective structures research [M]. Boca Raton, CRC Press, 2012, 1: 107―110.
[19] Hernandez-Bautista E, Bentz D P, Sandoval-Torres S, et al. Numerical simulation of heat and mass transport during hydration of Portland cement mortar in semi-adiabatic and steam curing conditions [J]. Cement and Concrete Composites, 2016, 69: 38―48.
[20] 程选生, 张爱军, 任毅, 等. 泥石流作用下砌体结构的破坏机理和防倒塌措施[J]. 工程力学, 2015, 32(8):156―163.Cheng Xuansheng, Zhang Aijun, Ren Yi, et al. Failure mechanism and anti-collapse measures of masonry structure under debris flow [J]. Engineering Mechanics,2015, 32(8): 156―163. (in Chinese)
[21] 金浏, 杜修力. 基于细观单元等效化方法的混凝土动态破坏行为分析[J]. 工程力学, 2015, 32(4): 33―40.Jin Liu, Du Xiuli. Analysis of dynamic failure behavior of concrete based on the meso-element equivalent method [J]. Engineering Mechanics, 2015, 32(4): 33―40. (in Chinese)
[22] 方秦, 洪建, 张锦华, 等. 混凝土类材料SHPB实验若干问题探讨 [J]. 工程力学, 2014, 31(5): 1―14.Fang Qin, Hong Jian, Zhang Jinhua, et al. Issues of SHPB test on concrete-like material [J]. Engineering Mechanics, 2014, 31(5): 1―14. (in Chinese)
[23] Kong X, Fang Q, Wu H, et al. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model [J]. International Journal of Impact Engineering, 2016, 95: 61―71.
[24] Li Q M, Meng H. About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test [J]. International Journal of Solids and Structures, 2003, 40(2): 343―360.
[25] 辛雁清. 混凝土圆柱体试件和立方体试件抗压强度关系的分析[J]. 中国水能及电气化, 2015(7): 59―62.Xin Yanqing. Analysis of compressive strength relationship between concrete cylinder specimen and cube specimen [J]. China Water Power & Electrification,2015(7): 59―62. (in Chinese)
[26] 陈惠发, 萨里普 A F, 余天庆, 等. 弹性与塑性力学[M]. 北京: 中国建筑工业出版社, 2004: 109―114.Chen Huifa, Salipu A F, Yu Tianqing, et al. Mechanics of elasticity and plasticity [M]. Beijing: China Building Industry Press, 2004: 109―114. (in Chinese)
SHPB TEST AND NUMERICAL INVESTIGATION ON THE INERTIA EFFECT OF MORTAR MATERIAL
LI Xiao1, FANG Qin1, KONG Xiang-zhen2, WU Hao1
(1. State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact, Army Engineering University, Nanjing, Jiangsu 210007, China;2. Weapon Test Center of Bai-City, Bai-City, Jilin 137000, China)
Abstract:The dynamic compressive properties of mortar material at different strain-rates are experimentally investigated by split Hopkinson pressure bar (SHPB) test, in which the relationship between the dynamic increase factor (DIF) and strain-rate is obtained. Numerical simulations using a simplified model are conducted based on the strain rate curve obtained from experiments. The principle of the unavoidable inertia effect known as the“structure effect” in dynamic compressive tests is discussed. To obtain the inherent DIF of mortal material subjected to high strain-rate, numerical simulations are conducted to eliminate the inertia effect. It is found that the predicted stress-strain curves in the numerical simulation agree well with the corresponding experimental data when the above-mentioned inherent DIF is used as the numerical input. Furthermore, the superiorities of the proposed inherent DIF are validated by comparing the CEB recommended DIF and existing semi-empirical DIF as the numerical inputs.
Key words:SHPB test; strain-rate effect; inertia effect; numerical simulation; simplified model
中图分类号：O347.3
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.03.0244
文章编号：1000-4750(2018)07-0187-07
收稿日期：2017-03-24；修改日期：2017-10-24
基金项目：国家自然科学基金项目(51321064，51427807，51210012)；国家重点研发计划项目(2016YFC0305200)
通讯作者：方 秦(1962―)，男，福建福清人，教授，博士，博导，副校长，主要从事结构抗爆研究(E-mail: 13776608867@139.com).
作者简介：
李 潇(1992―)，女，湖南益阳人，硕士生，主要从事武器破坏效应和工程防护研究(E-mail: 616740632@qq.com);
孔祥振(1988―)，男，山东德州人，工程师，博士，主要从事武器破坏效应和工程防护研究(E-mail: ouckxz@163.com);
吴 昊(1981―)，男，陕西宝鸡人，副教授，博士，博导，主要从事军事工程防护研究(E-mail: abrahamhao@126.com).