
图1 结构模型及构件编号
Fig.1 Structural model and component numbers
高佳明,刘伯权,黄 华,周长泉
(长安大学建筑工程学院,陕西,西安 710061)
摘 要:采用拆除构件法对一榀两层 2×1跨带板钢筋混凝土框架结构进行拟静力倒塌试验,分析了框架结构底层边柱失效后,剩余结构竖向倒塌的变形破坏模式以及受力机制。试验结果表明:带板混凝土结构连续倒塌抗力先后由梁拱-板压膜机制、梁拱-板拉膜机制、梁悬索-板拉膜机制、板拉膜机制提供;结构变形先后经历外推、内收、倒塌三个阶段,结构最大抗力出现在框架柱内收-外推转换点(梁悬索-板拉膜机制)。框架梁破坏后,结构转化为板柱模型,现浇板仍能将抗力维持在较高水平。理论分析了结构竖向连续倒塌关键变形处的临界位移和抗力值,提出了结构极限承载力计算方法,并建议同时考虑极限承载力和梁端转角对混凝土结构进行倒塌判定。
关键词:带板钢筋混凝土框架;连续倒塌;倒塌试验;理论分析;悬索;拉膜
建筑结构在使用过程中可能会发生由于局部构件或局部区域失效引起的结构大范围的连续倒塌。这种结构连续倒塌常常发生突然、发展迅速、损害严重,对人的生命和财产造成严重威胁[1-4]。现浇板作为钢筋混凝土框架结构重要的受力构件,能够显著增强结构的整体性和安全储备,但在现有的国内外设计规范中常常忽略或简化其作用。模拟连续倒塌试验复杂且费用高,因此试验研究较少,而考虑现浇板作用的梁板柱整体空间结构的试验更少。Zineddin和 Krauthammer[5]研究了配筋率、构造措施和冲击能量对板的破坏模式的影响。张凡榛[6]的无梁楼板抗倒塌试验表明结构的破坏由板的薄膜作用控制。钱凯等[7-9]通过试验数据分析发现带板的 RC子结构对结构的极限承载能力提高了63%,在破坏初期板通过压膜作用提高抗力-位移曲线的第一个峰值点,在大变形阶段,通过拉膜作用提高结构的极限承载力。周育泷等[10]等基于钢筋混凝体框架结构楼盖系统微观受力机理分析,建立了压拱机制下梁板子结构系统的连续倒塌抗力分析模型。Pham 等[11]认为结构能否抵抗连续倒塌主要取决于板外围的压力环的强度。肖岩等[12]认为在柱突然失效时动力效应对结构整体的影响并不显著,现浇板的拉结能力在柱失效时起到巨大作用。郭义庆等[13]提出了单柱破坏后,结构连续倒塌瞬态动力响应的分析方法。
本文采用拟静力试验方法进行了带板空间框架结构的连续倒塌试验,结合结构在倒塌过程的抗力与变形的观测结果,理论分析了结构外推-内收阶段转变临界竖向位移、最大侧移量、结构的连续倒塌承载力,并给出了连续倒塌的判定标准。
依照《混凝土结构设计规范》(GB 50010―2010)和《建筑抗震设计规范》(GB50011―2010)设计了一栋八层钢筋混凝土框架结构,楼面恒载为5.5 kN/m2,活载为 2.0 kN/m2,抗震设防烈度为 7度,设计基本地震加速度值为0.1 g。取其下部两层两跨空间子结构为试验模型,缩尺比例为1∶3。结构模型及构件编号如图1所示。
模型构件尺寸如下:梁截面尺寸 100 mm×200 mm,板厚40,柱截面尺寸200 mm×200 mm,基础梁截面尺寸300 mm×500 mm,跨长1800 mm,层高1200 mm。梁、板、柱均采用C30混凝土。梁、柱纵向受力钢筋为 HRB400,箍筋选用 HPB235,梁箍筋加密区长320 mm,箍筋从距柱内表面15 mm处开始布置,底层柱根部箍筋加密区长 400 mm,其他部位加密区长 200 mm,混凝土保护层厚度15 mm;板受力钢筋选用 HPB235,每个边锚固在梁内侧 25 mm处,单层双向布置,保护层厚度10 mm。混凝土立方体28 d抗压强度为40.3 MPa;梁、柱钢筋屈服强度为 491.6 MPa,极限抗拉强度为626.8 MPa,延伸率为26%;箍筋和板钢筋屈服强度为449.2 MPa,极限抗拉强度为541.4 MPa。结构配筋及平面布置如图2所示。

图1 结构模型及构件编号
Fig.1 Structural model and component numbers

图2 结构配筋及平面布置
Fig.2 Structural reinforcement and plane arrangement
本次试验采用静力加载的试验方法进行加载。根据前期模拟分析E、F柱顶荷载对试验结果影响不大,考虑到试验的易操作性,仅在A、B、C、D柱顶施加竖向集中力,一层B柱由机械千斤顶代替。由PKPM计算出子结构部分A柱、C柱柱顶荷载为1242 kN,B柱柱顶荷载为1269 kN,D柱柱顶荷载为 1827 kN。按照相似理论荷载分析原则,模型轴向荷载与原结构荷载的比例应为1∶9,故模型A、C柱顶竖向荷载确定为1242/9=138 kN,B柱顶荷载为1269/9=141 kN,D柱顶荷载为1827/9=203 kN。试验开始前首先对A、B、C、D柱顶进行预加载,消除试件的预应力,并记录试件出现的初始裂缝,平衡测试仪器数据。试验过程中采用分段等步距方式进行位移卸载,模拟B柱失效过程。在位移加载初期,构件处于弹性阶段和弹塑性阶段,机械千斤顶每级卸载 2 mm,直至框架梁部分纵筋应变大于2400με后每级卸载4 mm,连续卸载两次,结构整体进入塑性阶段后,下挠速度加快,采用每级10 mm进行卸载,每次卸载后持荷15 min,待结构变形发展稳定后读取试件各测点的位移、钢筋以及混凝土应变等测量数据,柱端水平位移计布置如图 2(b)所示。
失效B柱卸载位移为4 mm时,一二层与失效柱相连梁的受拉区开始出现首批竖向弯曲裂缝,板和柱无明显混凝土开裂现象。当 B柱卸载位移为8mm时,结构进入非弹性阶段,1-CF、1-AE、1-DF和1-ED等梁出现扭转裂缝,表明板在此时已将荷载传递到周边框架梁。
B柱卸载位移为18 mm,与B柱直接相连梁外侧出现斜向的扭转裂缝,B柱周围板面上形成了新的弧形塌落缝,表明结构荷载在此时主要通过现浇板所提供的传力路径进行分配,此时楼板的压力薄膜作用开始转化为拉力薄膜作用。
当B柱卸载位移在80 mm~150 mm之间时,框架梁下侧受压区混凝土发生压碎破坏,混凝土梁由承受弯剪作用的构件转变为仅由钢筋承受拉力的构件。B柱卸载位移在179 mm~234 mm之间时,与B柱相连梁下部受拉区钢筋先后发生拉断破坏。此阶段结构开始由梁、板、柱结构体系逐步转变为板、柱结构体系。
在卸载位移达到380 mm过程中,混凝土板上形成明显的半圆形塌落破坏区。该区域边缘的板钢筋逐渐出现了颈缩拉断和锚固失效的情况,最终结构倒塌破坏。结构最终破坏状态如图3所示。
由试验测试得到了结构抗力与卸载位移Δ的关系曲线,如图4所示。由结构的变形破坏情况和试验测得的梁板钢筋应变可以发现结构竖向抗力先后由梁拱-板压膜机制、梁拱-板拉膜机制、梁悬索-板拉膜机制、板拉膜机制构成。

图3 结构最终破坏形态
Fig.3 Ultimate failure model of structure

图4 结构抗力与卸载位移关系
Fig.4 Relationship between structural resistance and uninstalling displacement
梁拱-板压膜机制(OA段):当0 mm<Δ<18 mm时,AB、BC、BD梁靠近B柱端上部纵筋受压,下部纵筋受拉,远离B柱端上部纵筋受拉,下部纵筋受压,形成了明显的梁拱机制;距AB、BC、BD梁150 mm处的板钢筋受压并且压应变值随着卸载位移的增加逐步增大,表明现浇板在此阶段处于压膜机制。框架梁和现浇板的受力情况非常类似,梁、板钢筋混凝土共同受压促使结构水平外推,当卸载位移Δ=18 mm时,框架梁依旧处在梁拱作用阶段,但由于梁板在平面内的刚度差异很大,现浇板钢筋由加载初期受压状态开始转化为受拉状态,表明现浇板的压膜机制已经开始转化为拉膜机制。结构在A点对应的抗力值为87 kN。
梁拱-板拉膜机制(AB段):卸载位移处于18 mm<Δ<150 mm阶段,梁的拱机制快速发展,AB、BC、BD梁受拉区钢筋先后进入屈服阶段,此阶段后期,梁端形成塑性铰,而后梁端下部混凝土开始压碎,梁拱机制产生的抗力开始退化;随着现浇板变形增大,距AB、BC、BD梁150 mm处的板钢筋拉应变逐步增大,现浇板拉膜机制产生的抗力在结构抗力中比重开始增加。B点对应的结构抗力为126 kN。
梁悬索-板拉膜机制(BC段):在Δ=150 mm时,AB、BC、BD梁远离 B柱端下部受压区混凝土全部压碎破坏,上部混凝土开裂严重,梁端部的所有纵筋几乎都进入受拉状态,此时梁通过悬索机制为结构提供竖向抗力。从Δ=179 mm时梁纵筋逐根开始发生断裂破坏,梁悬索机制逐步消失,现浇板钢筋拉应变迅速增大,小部分钢筋进入屈服阶段,现浇板逐步替代框架梁成为最主要的受力构件。结构抗力随着各梁纵筋的拉断破坏持续大幅度下降,直到Δ=234 mm,AB、BC、BD梁近B柱端下部纵筋均已拉断破坏,此时认为空间框架结构形式由梁板柱结构转变为板柱结构。C点对应的结构抗力为107 kN。
板拉膜机制(CD段):此阶段板钢筋拉应变继续增大,结构承载力几乎全部由现浇板提供,板钢筋拉断和锚固端拉脱是导致该阶段抗力逐渐下降的原因。D点卸载位移为跨度的 1/5,此时结构的各主要受力构件基本已经破坏,而后抗力持续下降,结构进入倒塌阶段。D点对应的结构抗力为98 kN。
结构的最大抗力 126 kN出现在 130 mm<Δ<179 mm 之间,此阶段结构处于从外推转入内收阶段的交界点附近,梁悬索-板拉膜机制提供了结构的极限承载力。
框架结构的水平侧移曲线与卸载位移之间的关系如图5所示,从图5(a)和图5(b)中可以发现A柱和C柱整体侧移呈现先外推而后内收的趋势,变形对称性较好。开始加载后A柱向外侧移动,说明在加载初期结构梁、板构件一直承受由变形引起的压力作用。由于现浇板的存在,框架梁为L形梁,梁上部的抗弯刚度有显著增强,致使梁承受“纯弯曲”正弯矩时,梁的中性轴明显上移,所以AB梁、BC梁与失效柱相连的近端承受正弯矩时出现竖向弯曲裂缝的时间早于梁远端上侧承受负弯矩出现的弯曲裂缝。随着梁近失效柱端截面弯曲裂缝开裂,梁中性轴向上移,而梁远端出现弯曲裂缝后梁中性轴向下移动。框架梁两端截面转动中心不在同一水平线上,由于梁轴向刚度较大,梁中性轴随着加载过程产生转动,使得框架梁内产生轴向压力,对框架柱产生了向外的推力,这种作用就是梁拱机制。从现浇板的混凝土应变和钢筋应变可以发现板在此时也产生了压膜作用,但由于现浇板在平面外刚度较小,其受力现象不是很明显。在外推阶段后期,由于板平面内刚度较大,且与梁的变形不协调,导致柱附近板面拉裂破坏,板裂缝宽度发展较快,其参与结构受力的方式由压膜作用转变为拉膜作用,板面钢筋由受压转化为受拉。
当卸载位移Δ=150 mm时结构水平位移达到最大值 7 mm,框架梁中性轴转动中心位于支座塑性铰转动中心以下时,结构进入内收阶段,框架梁内产生轴向拉力,框架柱在纵向梁轴向拉力的作用下开始向内侧移,此时梁端受压区域混凝土逐渐开始压碎退出工作,梁的拱效应转化为梁悬索效应。从图5(c)可以看到,随卸载位移的增加,D柱侧移趋势为先内收而后外推,第一层框架柱最大侧移量约为12 mm,第二层框架柱最大侧移量约为9mm。由于已经移除了B柱,结构受力不对称,致使失效柱一侧柱的抗剪变形能力小于D柱的抗剪能力,因此框架向失效柱一侧整体侧移,表现为 D柱向内侧移。当BD梁的“中性轴”逐渐转动,失效柱一侧的抗剪能力逐渐发挥到极致,B柱向外侧变形增大,可以从试验现象中观察到:2-B柱柱底出现了水平裂缝。当中柱卸载位移达到14 mm左右时,一层框架开始向外侧移;当中柱卸载位移达到150 mm左右时,二层框架开始向外侧移。一层、二层框架的侧移不同主要是由于空间横向框架不同楼层侧向刚度不同,不同层柱顶侧向约束不同和剩余结构整体向失效柱方向的弯曲(空腹作用)共同作用的结果。
框架柱的侧移量小于抗震规范规定的 1/50层高的限值,说明按照抗震规范设计的结构在某单根柱子破坏的情况下一般不会引起其相邻竖向受力构件发生次生的连续性倒塌[14]。
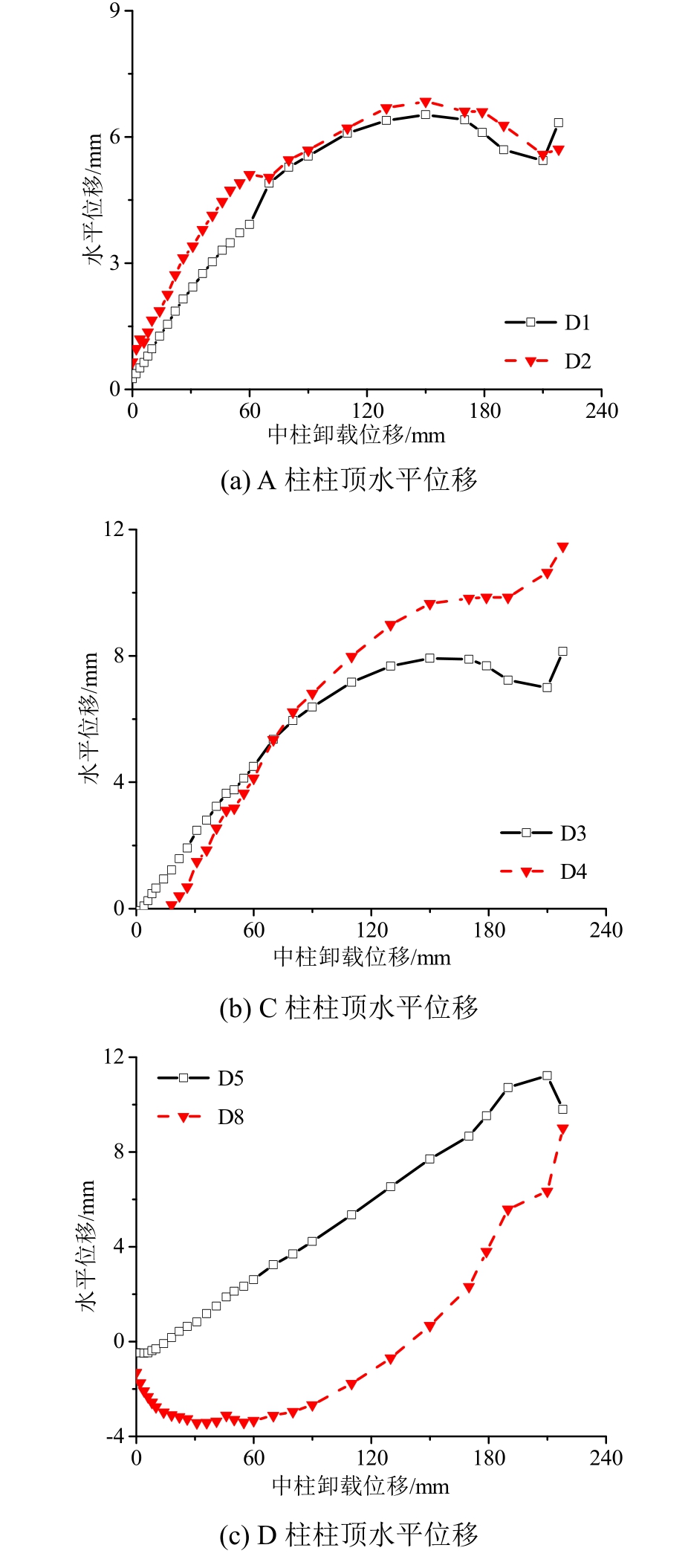
图5 柱顶水平位移与卸载位移关系
Fig.5 Relationship between horizontal displacement of column cap and uninstalling displacement
通过试验分析发现钢筋混凝土结构在竖向倒塌过程中有三个关键的临界变形:结构外推-内收转变临界竖向位移,结构承载力在该变形处达到最大;框架梁破坏后结构由梁、板、柱结构退化为板、柱结构处的临界竖向位移,结构承载力在此处发生了较大幅度的下降;框架柱最大水平位移,该位移的幅值决定了失效柱是否会引起相邻柱的连续破坏。
当卸载位移Δ=150 mm时,框架结构由外推进入到内收阶段,通过试验现象和测试得到的水平位移-卸载位移分析可知,空间 RC框架外推-内收阶段转换临界竖向位移应是AB、BC框架梁中性轴转动至水平时的卸载位移量。由于现浇板内钢筋和梁端负弯矩钢筋的存在,AB梁A端下部、BC梁C端下部的受压区高度相比AB梁B端上部、BC梁B端上部偏大,在计算框架梁两端受压区高度时应区别考虑,计算简图如图6所示。

图6 外推-内收转换竖向临界位移计算简图
Fig.6 Computing model of vertical displacement about extrapolation-adduction transition point
框架梁距失效柱近端受压区高度:
框架梁距失效柱远端受压区高度:
结构外推-内收阶段转换临界竖向位移:
式中:c为梁混凝土保护层厚度;d为梁纵向受力钢筋直径;η为受压区高度增大系数,取1.1;h为框架梁截面高度。
代入试验数据:c =20 mm,d=8 mm,h=200 mm,可得到Δ=149.6 mm,与试验值150 mm相差极小。
以框架结构一层的变形情况为准,计算简图如图7。

图7 结构最大侧移计算简图
Fig.7 Computing model of maximum lateral displacement
求解结构的最大侧移量,需先求得框架梁中性轴长度L,在不考虑梁的轴向伸缩量时,由变形几何关系可得:
中性轴长度:
最终可得框架的最大侧移量:
式中,l为梁的净跨长度。
将l=1600 mm,∆侧移=149.6 mm代入式中,可得到 Smax=7.9 mm。结构一层柱的最大侧移量平均值为7.6 mm,计算值比试验值大3.9%,证明该推论较为可信。在结构外推过程中,框架梁的拱机制起到了最关键的作用,现浇板的存在对框架梁远端受压区高度有一定影响,但对结构的整体外推变形过程影响不大。
试验表明梁板柱构件的钢筋混凝土空间框架结构随着失效点位移增大结构形式将发生转变,卸载后期结构由梁板柱受力体系退化为板柱受力体系,结构受力特征产生了较大变化,现在对结构形式变化临界位移进行分析。
试验观测试件卸载位移达到Δ=234 mm之后,结构一层、二层框架梁近B柱端底部钢筋几乎全部拉断失效,悬索效应不复存在,结构形式由梁板柱结构体系转变为板柱结构体系。
由试验中梁钢筋的应变可知,前期框架梁钢筋受拉区为失效柱近端下部和远端上部。结构受力体系的改变主要是由于梁下部钢筋的断裂引起的,在现浇板的加强作用影响下,虽然框架梁远端上部几乎没有发生拉断破坏的现象,但是也发生了较大的变形。结合试件结构体系转变时的几何变形情况和材料属性,提出结构形式转变的临界竖向位移计算方法,计算简图如图8所示。

图8 结构形式转换竖向临界位移计算简图
Fig.8 Computing model of vertical displacement about structural style transition point
钢筋变形主要在梁端受拉区产生,所以仅考虑梁端部钢筋的变形情况。梁下部受拉区长度d1根据试验结果可取为梁截面高度的 1/4;梁上部在现浇板的加强作用下延性明显增大,受拉区长度d2取为梁高的1/2,如图9所示。

图9 受拉区长度
Fig.9 Length of tensile area
则梁纵筋端部延伸长度:
式中:d为钢筋受拉区长度;δ为钢筋延伸率。框架梁上下纵筋间对角线长度:
式中:l为框架梁净跨长度;h为梁截面高度;c为框架梁混凝土保护层厚度。
变形后对角线长度:
结构由梁板柱体系转变为板柱体系时的临界竖向位移量:
代入试验数据:d=20 mm,δ=0.26,l=1600 mm,h =200 mm,c=20 mm,可得结构形式转变时的临界竖向位移为∆转变=230.57 mm。理论计算值比物理试验值234 mm偏小1.5%,精确度较高。
文献[15-16]提出了框架结构的连续倒塌抗力分析方法,但对钢筋混凝土结构现浇板的受力计算并不明确。通过试验发现梁、板、柱构件组成的结构竖向连续倒塌抗力主要由框架梁和现浇板提供,因此将整体结构抗力分为框架梁抗力和现浇板抗力分别进行分析。
对空间框架结构的连续性倒塌计算模型做出部分假定,以简化受力模型,方便计算。假定如下:① 在计算现浇板抗力时,仅考虑现浇板“拉膜”效应中板钢筋的拉力,忽略板的刚度、混凝土的拉压力及板钢筋分布不均匀等因素;② 梁截面应变始终符合平截面假定,现浇板随结构变形表现出线性变化;③ 从梁塑性铰出现到梁受力机制完全转变,假定梁塑性铰承担的弯矩保持为定值;在梁完全进入悬索机制,梁承受弯矩值变为零,梁仅由钢筋承受拉力;④ 忽略与失效柱直接相连的空间框架梁的扭转受力,仅考虑梁在梁拱机制阶段弯剪破坏和梁悬索机制阶段的梁轴向的受拉破坏。
4.1.1 结构外推阶段框架梁承载力
结构外推阶段框架梁以梁拱机制为结构提供竖向抗力,梁拱机制受力简图如图10所示。

图10 梁拱机制计算简图
Fig.10 Computing model of beam arch mechanism
梁拱作用主要依靠框架梁的混凝土抗压能力,参考混凝土设计规范考虑现浇板对梁的加强作用,将框架梁分类为两种,一种为“T”型梁,例如BD梁;另一种为“L”型梁,例如AB、BC梁。在相同的变形情况下框架梁的弯矩大小与梁的刚度相关,在不考虑翼缘的情况下,假设框架梁的抗弯刚度为I0,通过上文试验结论可知,在梁拱机制阶段,框架梁主要由弯剪变形产生的抗力提供结构的承载力,所以可以通过混凝土结构设计规范(GB50010―2010)给出的正截面抗弯计算公式等效。可以得到“T”型梁等效弯曲刚度为2I0,说明梁端在相同的转动角位移下“T”型梁承担的弯矩为矩形梁的2倍。同理,纵向框架方向与失效柱直接相连的空间框架梁为倒“L”型梁,其等效弯曲刚度1.5I0。在后续计算现浇板抗力时,板的计算宽度需要扣除翼缘宽度。
梁拱机制工作阶段失效柱上方各楼层梁端产生塑性铰时梁截面竖向承载力P梁1:
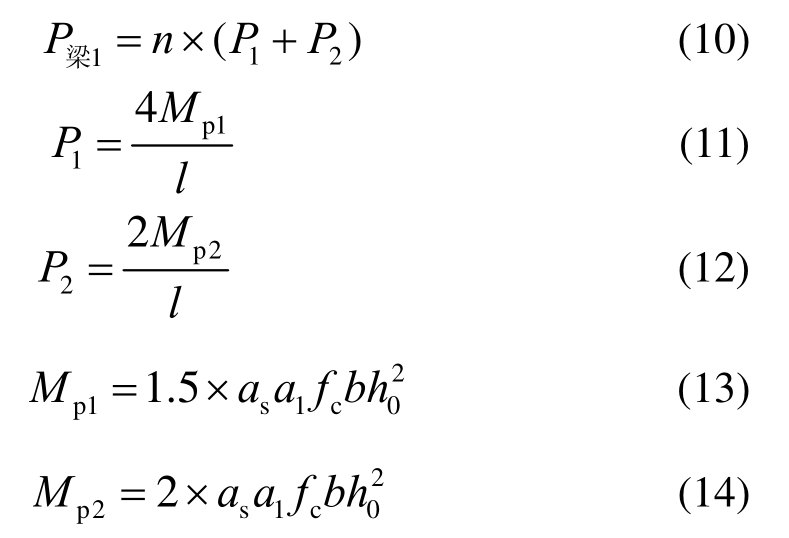
其中:

式中:P1、P2为纵、横向框架竖向抗力;Mp1、Mp2为纵、横向框架梁端弯矩;n为失效柱以上框架结构楼层数;a1为计算系数;l为梁跨长;fc为混凝土轴心抗压强度设计值;fs为梁纵筋抗拉强度;As为梁底或梁顶受力钢筋的横截面积,本试验中梁上下配筋相同;h0为梁截面有效高度,h0=h-as;b为梁截面宽度。
4.1.2 结构内收阶段框架梁承载力
本次试验模拟结构长边中柱失效情况,框架进入内收阶段后梁端混凝土虽然没有完全压碎破坏,但是框架梁已经开始进入悬索阶段。对于平面框架来说只有对称结构才能产生悬索效应,悬臂梁的悬索效应并不明显。本次试验发现由于现浇板的约束情况良好,BD梁在结构内收阶段同样发挥了很强的拉结作用,所以在计算梁的拉结作用时应把AB、BC、BD梁等同考虑。另外结构进入内收阶段后主要考虑钢筋的拉结作用,所以框架梁和现浇板可以分离计算,在计算梁提供的抗力时无需考虑板对梁的加强作用,空间框架梁抗力计算受力简图如图11所示。

图11 梁悬索机制计算简图
Fig.11 Computing model of beam catenary mechanism
可得钢筋混凝土框架梁悬索机制梁竖向承载力P梁2:

式中:θ为梁端截面的转角;T1、T2为框架梁纵筋拉力;n为失效柱以上框架结构楼层数;∆为失效点竖向位移;l为框架梁净跨长度;fst为梁纵筋极限抗拉强度;As为框架梁配筋面积。
由前文对试验的分析可知现浇板在倒塌过程中以受拉为主、受弯剪扭为辅,受力情况非常复杂,板的压膜效应仅在试件卸载位移很小的阶段出现,考虑到结构连续倒塌为大变形过程,所以本文在现浇板抗力计算时仅考虑板钢筋的受拉情况。另外,由于现浇板中钢筋的数目较多且受拉程度不尽相同,累加每根钢筋拉力计算板抗力非常繁琐也不准确,因此参考有限元软件整体式建模的方法,认为板中钢筋均匀分布在现浇板中,采用板配筋率ρ和板钢筋平均变形计算现浇板抗力。
4.2.1 结构外推阶段现浇板承载力
在整体结构的外推阶段计算框架梁时,由于在梁拱机制阶段计算梁抗力时采用的是等效抗弯刚度,现浇板一部分已经作为“T”和“L”型梁翼缘部分,所以现浇板的计算长度应扣除框架梁的翼缘长度。
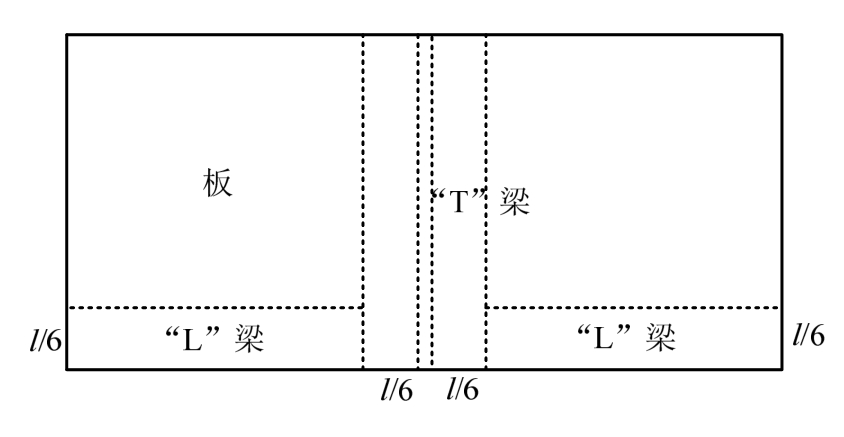
图12 现浇板钢筋从属于梁区域
Fig.12 Steel bars of slabs that belong to beam area

图13 板拉膜机制计算简图
Fig.13 Computing model of slab tensional membrane mechanism
翼缘长度根据混凝土结构设计规范(GB50010―2010)取值为 l/6,其中 l为框架梁净跨长度。现浇板钢筋从属梁区域如图 12所示。现浇板的拉膜机制计算简图如图13。
可得钢筋混凝土框架现浇板在外推阶段的竖向承载力:

式中:θ为框架梁转角;Δ为失效点竖向位移量;l为框架梁净跨长度;ρ为现浇板单向受拉钢筋配筋率;As为单块现浇板单向受拉钢筋总面积;A为现浇板横截面积;m为试验中板拉结边数量;b为现浇板厚度;fy为现浇板钢筋设计强度。
4.2.2 结构内收阶段现浇板承载力
内收阶段现浇板的计算长度为板的净尺寸,其计算方法与外推阶段相同,可得内收阶段钢筋混凝土框架现浇板竖向承载力P板2:
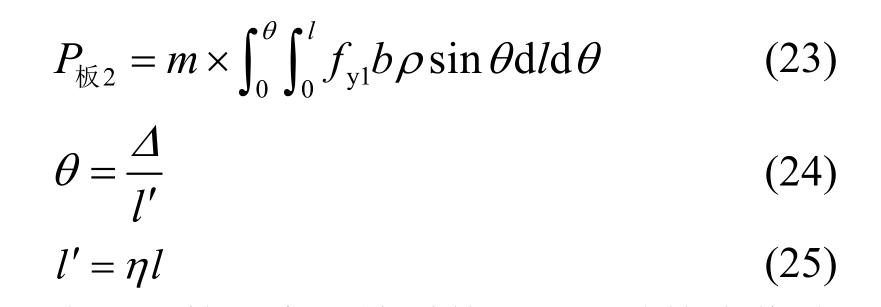
式中:η为板计算长度调整系数,由于结构内收阶段现浇板变形已经很大,板面塌落区已经基本形成,现浇板弧形变形区域长度明显小于梁的净跨长度,因此对板钢筋变形量进行积分时必须对变形量进行调整,根据塌落区的几何尺寸,取η=0.6;fy1为现浇板钢筋屈服强度测试值。
整体结构抗力为各个阶段框架梁抗力与现浇板抗力的总和,可得:
内收阶段整体结构抗力:
外推阶段整体结构抗力:
由于结构连续倒塌是一个非线性大变形的过程,受力非常复杂,想要做到全过程抗力计算值-卸载位移曲线拟合度良好比较困难,现仅对结构抗力最大值点和结构形式转变点进行验证。
对于结构外推-内收转化临界点,结构抗力最大值点的卸载位移 Δ=150 mm,此时框架梁纵筋已经全部屈服,根据式(17),可得 P梁 2=74.8kN ,根据式(20),可以得到 P板 2=39.9kN,最终可得结构抗力为114.7 kN,比试验值126 kN偏小了8.9%。
结构形式转变临界位移 Δ=234 mm,框架梁下部钢筋全部拉断,仅剩上部两根钢筋受力,可得P梁 2=48.9kN。现浇板抗力 P板 2=65.2kN ,最终可得结构形式转变时结构抗力为114.1 kN,与试验测试值107 kN相比大了6.6%,计算比较精确。
文献[17]在2010年进行了三层4×2跨不带板钢筋混凝土框架结构的连续倒塌拟静力试验,柱截面尺寸为 200 mm×200 mm,横梁截面尺寸为100 mm×200 mm,纵梁截面尺寸为 100 mm×150 mm。试验模型框架梁纵筋选用4根直径10 mm的HRB335钢筋,屈服强度为360 MPa,极限抗拉强度为450 MPa。试验测试结果表明结构在卸载位移为171.023 mm时,结构竖向抗力约为109 kN,此时结构已经进入内收阶段,且梁端钢筋已经受拉屈服,因此取钢筋强度400 MPa进行计算,将以上数据代入式(17)可得结构竖向抗力为 107.2 kN,与试验值非常接近。
由于该试验模型是无板纯框架模型,试验抗力值明显小于实际结构的竖向抗力。按照实际结构板的配筋为6@80,采用单层双向方式进行布置,当卸载位移为 171.023 mm时,板内部分钢筋进入屈服状态,此处将板钢筋平均受拉强度保守取值为屈服强度的50%,即117.5 MPa,代入式(23)进行计算可得板拉膜机制提供的竖向抗力为137.2 kN,所以结构总抗力为 244.4 kN,抗力提高 128%。可见在钢筋混凝土框架中现浇板的拉膜作用大幅度提高了结构整体抗力,现行各国规范中忽略板的作用或仅定性考虑板对整体抗力的增益作用是偏于保守的。
在混凝土结构受力计算理论中,混凝土开裂后引入了裂缝间受拉钢筋应变不均匀系数,为了简化结构连续倒塌抗力计算过程,本文根据试验数据确定板钢筋在结构极限荷载出现时钢筋平均应力比为0.6,即梁转角为0.09时板钢筋平均拉应力达到其抗拉强度的60%。对于本次边柱破坏的连续倒塌试验,带板结构在梁相对转角介于 0.03~0.13之间时抗力达到最大且较为稳定,在此期间随着结构持续变形,结构梁、板主要受力钢筋相继进入屈服阶段。随后梁端钢筋相继发生拉断破坏,结构承载力有明显的降低,但由于板钢筋的拉结作用,在梁端钢筋全部破坏以后结构仍旧保持了较高的承载力,约为极限承载力的78%。当转角超过0.21后板钢筋出现了明显的颈缩和脱锚的现象,结构承载力再次出现显著下降,结构进入倒塌极限状态。此时失效点最大竖向位移为 380 mm,板钢筋的平均应力比约为0.85。钢筋平均应力比为钢筋应力与钢筋抗拉强度比值的平均值,板钢筋该比值随着结构的变形的增大逐渐增大,最终拉断或者脱锚破坏,其物理意义为钢筋拉断准则,所以建议可将梁转角为0.21作为竖向连续倒塌的位移控制限值。
针对边柱破坏导致的钢筋混凝土结构竖向连续倒塌破坏,建议先对结构按照式(28)进行竖向抗力验算。GSA[18]和DoD[19]规范给出了针对混凝土结构连续倒塌设计的结构荷载取值标准,DoD规范主要对应于军用建筑物,荷载取值标准较高,所以Qi可以选取GSA结构静力设计荷载2(DL+0.25LL),其中2为结构动力效应放大系数,DL为结构恒荷载,LL为结构活荷载。根据4.3节的计算结果,本文按照我国现行规范设计的原八层结构不会在单根边柱破坏的情况下发生竖向连续倒塌破坏。因为试验子结构仅考虑了底部两层的承载力,对于原型结构,若单层结构的极限承载力为Pi,单层荷载为Qi,i=8 则:
如果结构极限承载力小于该荷载,梁端转角将超过0.09进而继续增大,但是考虑到结构动力作用与柱失效时间,结构自重、荷载的重力加速度效应以及材料的动力硬化均相关,短时间的冲击作用导致梁破坏后,现浇板依旧能够提供较高的承载力,所以若结构的最终梁转角没有超过0.21,则认为结构仍然不会发生连续倒塌破坏。考虑到结构跨度、梁跨高比、梁板的配筋与构造以及约束条件等对结构变形的影响,后续可对以上因素进行参数分析,对梁转角限值进行补充修正。
通过对带板钢筋混凝土框架连续倒塌试验的研究和理论分析,主要得出以下结论:
(1) 基于拆除构件法的带板钢筋混凝土框架连续倒塌试验结果表明:带板钢筋混凝土框架结构的连续倒塌变形过程(抗力构成机制)分为:外推阶段(梁拱-板压膜机制和梁拱-板拉膜机制)、内收阶段(梁悬索-板拉膜机制和板拉膜机制)和倒塌阶段。
(2) 结构承载力在外推-内收转变临界位移处位于峰值,在框架结构形式转变临界位移处出现了较大幅度的下降,通过本文的理论分析可以较精确的计算出以上两个临界位移点,建立了计算结构极限承载力的基础。
(3) 在计算钢筋混凝土结构整体抗力时,将结构分为外推和内收两个变形阶段进行考虑,并在每个阶段分别考虑框架梁和现浇板对结构竖向抗力的贡献,提出了梁、板构件的抗力计算方法,两者之和为结构的总承载力,关键位移处计算结果与试验测试抗力值吻合较好。考虑现浇板作用的混凝土框架结构竖向承载力比不带板结构提高幅度巨大。
(4) 建议通过极限承载力验算对结构进行合理设计,将梁转角为0.21作为带现浇板RC结构的竖向连续倒塌变形控制值。
参考文献:
[1] 高超, 宗周红, 伍俊. 爆炸荷载下钢筋混凝土框架结构倒塌破坏试验研究[J]. 土木工程学报, 2013, 46(7):9―20.Gao Chao, Zong Zhouhong, Wu Jun. Experimental study on progressive collapse failure of RC frame structures under blast loading [J]. China Civil Engineering Journal,2013, 46(7): 9―20. (in Chinese)
[2] Sasani M, Bazan M, Sagiroglu S. Experimental and analytical progressive collapse evaluation of an actual RC structural [J]. Structural Journal, 2007, V104(6):731―739.
[3] 徐颖, 韩庆华, 练继建. 单层球面网壳抗连续倒塌性能研究[J]. 工程力学, 2016, 33(11): 105―112.Xu Ying, Han Qinghua, Lian Jijian. Progressive collapse performance of single-layer latticed shells[J].Engineering Mechanics, 2016, 33(11): 105―112. (in Chinese)
[4] 喻莹, 谭长波, 金林, 等. 基于有限质点法的单层球面网壳强震作用下连续倒塌破坏研究[J]. 工程力学,2016, 33(5): 134―141.Yu Ying, Tan Changbo, Jin Lin, et al. Research on seismic progressive collapse of single-layer reticulated dome using the finite particle method [J]. Engineering Mechanics, 2016, 33(5): 134―141. (in Chinese)
[5] Zineddin M, Krauthammer T. Dynamic response and behavior of reinforced concrete slabs under impact loading [J]. International Journal of Impact Engineering,2007, 34(9): 1517―1534.
[6] 张凡榛, 易伟建. 无梁楼板的抗倒塌性能试验研究及分析[J]. 湖南大学学报(自然科学版), 2010, 37(4): 1―5.Zhang Fanzhen, Yi Weijian. Collapse experiment research and analysis of a RC flat plate [J]. Journal of Hunan University: Natural Sciences Edition, 2010,37(4): 1―5. (in Chinese)
[7] Kai Q, Li B. Dynamic performance of RC beam-column substructures under the scenario of the loss of a corner column-Experimental results [J]. Engineering Structures,2012, 42(12): 154―167.
[8] Qian K, Li B. Performance of Three-dimensional reinforced concrete beam-column substructures under loss of a corner column scenario [J]. Journal of Structural Engineering, 2013, 139(4): 584―594.
[9] Kai Q, Li B, Ma J X. Load-Carrying mechanism to resist progressive collapse of RC buildings [J]. Journal of Structural Engineering, 2014, 141(2): 04014107-1.
[10] 周育泷, 李易, 陆新征, 等. 钢筋混凝土抗连续倒塌的压供机制分析模型[J]. 工程力学, 2016, 33(4): 34―42.Zhou Yulong, Li Yi,Lu Xinzheng, et al. An analytical model of compressive arch action of reinforced concrete frames to resist progressive collapse [J]. Engineering Mechanics, 2016, 33(4): 34―42. (in Chinese)
[11] Pham Xuan Dat, Tan Kang Hai. Membrane actions of RC slabs in mitigating progressive collapse of building Structures [J]. Engineering Structures, 2013, 55: 107―115.
[12] Xiao Y, Kunnath S, Li F W, et al. Collapse test of three-story half-scale reinforced concrete frame building[J]. ACI Structural Journal, 201 5, 112(4): 429―438.
[13] 郭义庆, 喻君. 单柱失效下结构连续倒塌的动力响应分析[J]. 工程力学, 2017, 34(4): 72―77.Guo Yiqing, Yu Jun. Dynamic structural response of progressive collapse under a single-column-removal scenario [J]. Engineering Mechanics, 2017, 34(4): 72―77. (in Chinese)
[14] 高佳明, 刘伯权, 黄华, 等. 考虑现浇板作用的钢筋混凝土框架结构抗连续倒塌性能试验[J]. 长安大学学报(自然科学版), 2017, 37(6): 54―62.Gao Jiaming, Liu Boquan, Huang Hua, et al.Experimental Study on Anti-collapse Performance of RC Space Frame Considering the Effect of Cast-in-place Slabs [J]. Journal of Chang’an University (Natural Science Edition), 2017, 37(6): 54―62. (in Chinese)
[15] 初明进, 周育泷, 陆新征, 等. 钢筋混凝土单向梁板子结构抗连续倒塌试验研究[J]. 土木工程学报, 2016,49(2): 31―40.Chu Mingjin, Zhou Yulong, Lu Xinzheng, et al. An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse[J]. China Civil Engineering Journal, 2016, 49(2): 31―40. (in Chinese)
[16] 何庆峰, 易伟建. 考虑悬索作用钢筋混凝土梁柱子结构抗倒塌性能试验研究[J]. 土木工程学报, 2011, 44(4):52―59.He Qingfeng, Yi Weijian. Experimental study of the collapse-resistant behavior of RC beam-column substructures considering catenary action [J]. China Civil Engineering Journal, 2011, 44(4): 52―59. (in Chinese)
[17] 熊进刚, 吴赵强, 何以农, 等. 钢筋混凝土空间框架结构连续倒塌性能的试验研究[J]. 南昌大学学报(工科版), 2012, 34(3): 229―232.Xiong Jingang, Wu Zhaoqiang, He Yinong, et al.Experimental research on progressive collapse performance of RC spatial frame structures [J]. Journal of Nanchang University: Engineering & Technology,2012, 34 (3): 229―232. (in Chinese)
[18] GSA2005, Progressive collapse analysis and design guidelines for new federal office buildings and major mordernization project [S]. Washington D C: the General Services Administration, 2005.
[19] DoD2005, UFC4-023-03, Design of structures to resist progressive collapse [S]. Washington D C: Department of Defence, 2005.
THEORETICAL ANALYSIS ON THE PROGRESSIVE COLLAPSE OF RC FRAME STRUCTURES WITH SLABS
GAO Jia-ming , LIU Bo-quan , HUANG Hua , ZHOU Chang-quan
(School of Civil Engineering, Chang’an University, Xi’an, Shaanxi 710061, China)
Abstract:A quasi-static test was carried out to experimentally study the progressive collapse of a two-story 2 ×1 bay spatial frame structure with slabs. The progressive collapse mechanism and deformation failure mode of the residual structure due to a side column loss were analyzed. The results indicate that the whole collapse resistance of RC frame structure is successively provided by beam arch-slab pressure membrane mechanism, beam arch-slab tensional membrane mechanism, beam catenary-slab tensional membrane mechanism and slab tensional membrane mechanism. The structural deformation process experiences three stages including the extrapolative stage, adductive stage and collapsed stage. The maximum resistance appears at a breaking point, which lies between stringing inward section and pushing outward section of the frame column (beam catenary-slab tensional membrane mechanism). The structure changes into a slab-column model when the beam is damaged, and the slab can maintain the resistance at a high level. The resistance and critical displacement at the key points of structural collapse are theoretically analyzed. A calculation method of structural ultimate load-bearing capacity is proposed.The ultimate load-bearing capacity and beam’s rotation angle should be taken into consideration in the criteria for structural collapse.
Key words:RC frame structure with slab; progressive collapse; collapse experiment; theoretical research;catenary; tensional membrane
中图分类号:TU375.4;TU317.1
文献标识码:A
doi:10.6052/j.issn.1000-4750.2017.03.0201
文章编号:1000-4750(2018)07-0117-10
收稿日期:2017-03-15;修改日期:2017-09-29
基金项目:国家自然科学基金项目(51578077,51778060);陕西省自然科学基础研究计划项目(2016JM5050);高等学校博士点专项科研基金项目(20130205130001);中央高校基本科研业务费专项基金资助团队项目(310828173401);中央高校基本科研业务费专项资金资助项目(310828171012)
通讯作者:刘伯权(1956―),男,甘肃定西人,教授,博士,博导,主要从事结构抗震与倒塌机理研究(E-mail: bqliu@chd.edu.cn).
作者简介:
高佳明(1986―),男,河北张家口人,博士生,主要从事结构抗震与加固研究(E-mail: jiamingcareer@163.com);
黄 华(1979―),男,江苏常州人,教授,博士,硕导,主要从事结构抗震与加固研究(E-mail: huanghua23247@163.com).