何浩祥1,2，王文涛1，范少勇1
(1. 北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124；2. 首都世界城市顺畅交通北京市协同创新中心，北京 100124)
摘 要：如果结构在外部激励下产生均匀损伤或均匀变形，则可避免出现薄弱层且可提高承载能力和安全性，以此为目标进行结构优化具有重要意义。将弯剪型结构简化为连续变截面悬臂杆，假定结构截面函数具有自然指数型和幂函数型等形式，将地震和风荷载等外部激励等效为均布、倒三角和惯性相关等三种荷载分布模式。根据均匀变形准则将结构绝对位移曲线关于高度的二次导数为零作为优化目标，建立结构连续化位移方程并进行优化求解，获得了考虑荷载分布形式的弯剪型结构最优刚度和截面分布解析解。理论和数值分析结果表明：截面按幂函数变化的结构能够实现均匀损伤，不同荷载分布模式下的最优刚度或截面分布有所不同。有限元静动力分析结果进一步验证了解析解的准确性和实用性。
关键词：均匀损伤；最优截面；刚度分布；层间位移角；地震作用
建筑结构在风荷载及地震作用等外部激励下将产生水平变形，如果设计方案不合理或施工质量不佳将导致结构出现变形过大或抗力不足等问题，因此需要针对工程需求、结构形式和受力模式进行优化设计和验算。结构优化设计是指在给定约束条件下按某种优化目标获得最优的设计方案[1]。对建筑结构进行优化设计，不仅可以提高其可靠性，从而更全面地实现基于性能的设计理念，还能够显著降低工程造价，实现投资效益的最大化。
由于设计理念和需求不同，针对具体结构的优化目标虽然并不完全一致，但也存在着诸如重量最小、成本最低、刚度最大等普适性原则。在众多优化目标中，满应力设计(Fully Stressed Design, FSD)准则[2―3]的重要性十分突出。所谓满应力设计是指针对某种形式的荷载组合或分布模式，按“同步失效”的概念进行设计，力求充分发挥所有材料和构件的能力，使绝大部分杆件或楼层同时达到其承载力极限和设计容许值，从而确保结构具有最优的抗力和安全性。对应于多高层结构的满应力设计准则可以简化为均匀损伤准则，即在风荷载或多遇地震作用下，多高层结构中各楼层的水平方向位移角应当相等或相近；在飓风或罕遇地震作用下，且各层的损伤程度相等或相似[4―5]。如果能够实现结构发生均匀损伤，则可以避免结构出现薄弱层和集中损伤，使结构整体性能全面提高，因而亟需在优化设计中重视和完善。
我国多高层结构的传统设计主要考虑地震作用的影响，采用“三水准”设防目标和“两阶段”设计方法。在第一阶段设计主要是取第一水准地震动参数计算结构弹性地震作用效应，在第二阶段设计再进行弹塑性变形验算。在具体抗震设计中，通常根据设计经验初步设定截面尺寸，经过详细的构件设计之后进行整体层间角位移验算，如果不满足规范要求，则需重新设定截面尺寸并再次验算，最终通过不断调试完成设计。这种设计方法简单易行，但是不能从机理上实现对结构薄弱层和损伤分布的有效调控，更没有充分实现优化设计的理念。由于目前结构弹塑性分析技术在设计中的应用尚十分有限，且缺乏被广泛认可的损伤评估准则和方法，因此很难实现第二阶段设计水平的迅速提升。有鉴于此，提高第一阶段设计的水平和优化能力是更加切实可行的，其研究和工程意义均十分重大。
如果只针对第一阶段设计进行结构优化，则满应力设计准则和均匀损伤准则可进一步简化为均匀变形准则，即在传统设计中可将“各楼层水平方向层间位移角相等或相近”作为重要的优化目标。在水平荷载作用下，结构的变形主要包括剪切变形和弯曲变形两种。在一般的结构设计和研究中，为了分析简便通常将结构简化为纯弯曲或纯剪切结构模型，即只考虑剪切变形或弯曲变形。实际上，结构的剪切变形和弯曲变形是同时存在的，对于许多结构不能仅考虑一种变形，因此从普适性上来讲，应将结构等效为弯剪型结构并进行相应的优化设计。由于结构和构件的变形主要与其刚度分布和荷载模式相关，因此在指定荷载作用下通过优化结构的各层刚度分布或构件截面(尺寸)分布即可实现各层的剪切变形与弯曲变形之和相等或相近，从而实现“均匀变形”目标并完成最终的结构优化设计。
国内外许多学者针对结构最优性能参数分布进行过深入研究。Hisatoku等[6]针对地震作用下的大量等质量、等层高的剪切型框架响应进行统计分析，提出了各楼层之间的最优强度比经验公式。Kato等[7]采用数学规划方法认为剪切型框架各楼层刚度分布为线性函数时可以使结构接近满应力状态。王光远等[8]充分考虑了结构层数、地基性质和地震烈度等因素的影响，按满应力设计准则统计得到了适合不同情况的剪切型多层框架的最优刚度分布经验公式。秋山宏[9]基于能量平衡方法和经验损伤分布模式研究了结构楼层能量分配规律并提出了剪切型框架结构楼层最佳剪力系数分布。和田章等[10]将高层建筑等效为悬臂梁并建立了同时考虑结构剪切变形和弯曲变形的刚度分布近似解析解，并按照“变形均匀”准则提出了楼层最优刚度分布经验公式，但该理论假设较多且没有充分考虑荷载模式的影响。王星星等[11―12]提出基于最佳侧移刚度分布的多高层钢框架结构抗震设计方法，力求使结构各层的累计塑性变形率相等。但由于没有建立抗侧移刚度与构件截面尺寸的明确关系，无法根据最佳侧移刚度分布指导结构截面的优化设计。Chan等[13]基于均匀变形准则对RC框架分别在弹性阶段和弹塑性阶段进行了截面与配筋优化设计。Allahdadian等[14]以结构位移最小化为目标研究了地震作用下多层结构的拓扑优化形状。Elghazouli等[15]分析了地震动频谱特性对多层钢框架层间位移分布的影响，提出了楼层刚度优化设计准则。Losanno等[16]提出了一种能够有效控制结构最大层间位移的阻尼器和支撑性能参数优化方法。Park等[17]建立了考虑振型组合效应的水平荷载分布统一函数表达式，并建议按照基于均匀损伤理念进行规则框架结构的抗震优化设计，但缺乏明确的理论分析和优化算法。Hajirasouliha等[18]基于Park-Ang损伤指数提出了实现RC结构在地震下具有均匀损伤与结构自重最小的迭代优化方法。黄铭枫[19]提出基于风振性能的结构优化设计方法来克服目前高层建筑的风致振动设计不足。徐龙河等[20]为避免建筑结构由于薄弱层而引起整体倒塌提出基于楼层组损伤控制函数与失效概率的结构抗震性能多目标优化方法。白久林等[21]提出了基于均匀损伤的抗震设计思路和基于优化准则法的等损伤优化设计方法，在保持结构材料造价恒定的情况下，采用优化算法不断调整各楼层刚度使楼层破坏程度或损伤指数尽量均匀。Wang等[22]提出了基于均匀层间位移的梁贯通式支撑钢框架简化抗震设计方法和3个优化设计性能目标，通过合理考虑刚度比和等效阻尼比，并给出具体设计流程。
综上所述，基于均匀损伤或均匀变形的结构优化设计研究已经逐渐受到重视并不断发展。目前主要不足包括：1) 缺乏对弯剪型结构弹性变形规律和最优刚度或截面分布规律的精细化解析理论分析，无法提供准确的优化设计公式；2) 缺乏准确且能够被广泛接受的结构损伤指数和评价标准；3) 通常针对地震动和结构第一振型进行优化，对风荷载和其他荷载的分布形式考虑不够，尚无法实现考虑多种荷载的最优设计。
有鉴于此，本文将结构简化为连续变截面悬臂杆，采用不同形式的水平分布荷载全面反映地震作用和风荷载等外力激励。根据均匀变形准则提出了使结构绝对位移曲线关于高度的二次导数为零的优化目标，对连续化方程进行优化求解，获得了考虑荷载分布形式的弯剪型结构最优刚度和截面分布解析解。通过数值模拟和有限元分析验证了解析解的正确性和实用性。本文的方法和结果可为高层建筑结构的层间刚度优化和构件截面尺寸优化提供借鉴，从而有效提高结构的优化水平和可靠性。
多高层建筑结构的变形和损伤与内因和外因均密切相关。内因主要包括结构形式、约束条件、平立面不规则程度、材料性能、构件截面和配筋、楼层刚度及质量分布等。外因主要包括等效荷载分布模式、重力二阶效应及加载速率等。综合考虑以上内因，本文将较规则的多高层建筑结构其简化为连续变截面悬臂杆模型，并同时考虑剪切变形和弯曲变形。为了求解方便，假定悬臂杆的截面尺寸沿结构高度按确定性函数变化，本文考虑的函数类型主要包括常数(等截面)、自然指数函数和幂函数三种。经验证，通过调整以上三种函数的参数可以模拟绝大部分结构的截面分布形式。由于结构可能遭受风荷载和地震作用等不同形式的水平外力，需要针对荷载的各自特点建立相应的水平力分布形式，从而反映前述的外因影响。钟振宇等[23]在考虑风重耦合效应的基础上通过振型分解法推导了设计用的等效静风荷载表达式及分布形式，结果表明等效静力风荷的分布形式非常接近倒三角形，因此本文将风荷载等效为倒三角分布的水平力。当仅考虑结构第一振型时，可将地震作用简化为倒三角分布水平力；当考虑全部振型效应时，应将地震作用等效为均布水平力或与惯性力(质量)分布直接相关的水平力。为了全面反映地震作用的影响，建议对以上形式均予考虑。因此，本文最后考虑的水平荷载分布模式包括均布、倒三角和惯性力相关三种。
在全面建立不同的结构截面形式和不同的水平荷载分布模式之后，需要进一步建立结构连续化力学方程并针对不同截面形式和水平荷载形式的组合求得结构连续化位移分布的解析形式，在此基础上根据均匀变形准则探讨结构优化方法。通过优化各个函数方程的设计参数使结构各楼层的水平位移角相等。上述优化目标等价于绝对位移曲线沿结构高度为一条斜直线，也相当于使绝对位移曲线关于结构高度的一次导数为常数或二次导数为零。为了计算方便并提高优化精度，本文将绝对位移曲线的二次导数为零作为优化目标函数，由此获得结构最优的截面和刚度分布规律。
按照前述优化思想，本文建立不同截面形式的等效悬臂杆模型。为了计算简便，假定结构的横截面均为实心圆形。等截面结构示意图如图1(a)所示。在此情况下，结构在任意高度处的截面面积和刚度都相同，设结构底面半径为h，构件高度为H，则任意截面处的半径x可表示为：
横截面按自然指数函数连续变化的结构示意图如图1(b)所示。自然指数函数的底数取自然常数e，结构的高度为H，底面半径为h，顶部半径为h，则任意截面处的半径r(y)可表示为关于高度y的如下函数：
式中，α为控制函数外形的参数。
横截面按幂函数连续变化的结构示意图如图1(c)所示。高度y和截面半径r呈幂函数形式，即有：
式中：β为控制结构底部半径h的参数；n为控制函数外形的常数，当n取不同值时可以使截面半径随高度的变化呈线性或非线性，且形状可以是内凹或外凸，通用性较强。
此时，任意截面处的半径r关于高度y的函数如下：
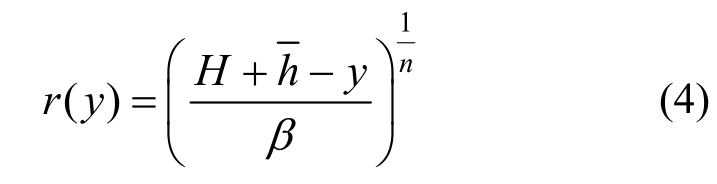
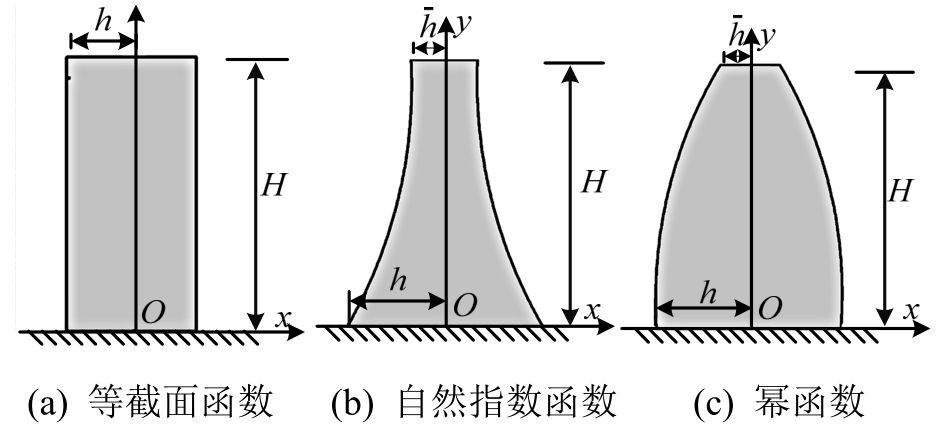
图1 三种截面函数模型悬臂杆构件示意图
Fig.1 Schematic diagram of three kinds of function models
在建立了具有不同截面形式的弯剪结构等效模型之后，可根据相关截面函数建立位移方程，并以“均匀位移”为优化目标求得结构的刚度最优分布形式。
1.3.1 等截面结构位移方程及优化
当等截面结构承受均布水平荷载时，悬臂杆构件任意高度y处由均布荷载q作用产生的剪力V(y)和弯矩M(y)分别为：
结构任意高度 y处由剪力作用引起的位移DS(y)为：
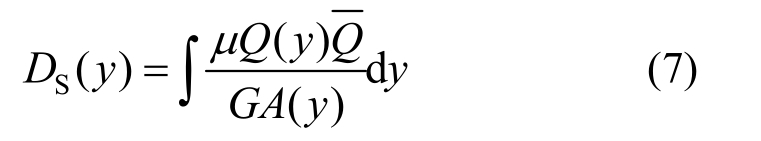
式中：μ为考虑截面剪切应变不均匀分布的系数(圆形截面μ=10/9)；G为结构的剪切模量；A(y)为高度为y处的截面面积。
结构任意高度 y处由弯矩引起的位移 DB(y)关于高度的二阶导数可表示为：
式中：E为结构的弹性模量；I(y)为任意高度y处的截面惯性矩。
按照前述观点，本文将绝对位移曲线的二次导数为零作为优化目标函数，此时应有：
式中，c表示需要优化的广义参数。将式(7)和式(8)代入上式，有：
由式(10)可以看出：除了高度外，影响等截面结构在均布荷载下位移的相关参数均为常数，并不能通过调控物理和材料参数实现优化目标，因此将结构设计成等截面是无法实现均匀变形或均匀损伤的。
当等截面结构承受倒三角水平荷载时，荷载在顶部具有最大值 qmax，在底部为 0。任意截面处的剪力可表示为：
悬臂杆构件任意高度y处由倒三角荷载q(y)作用产生的剪力Q(y)和弯矩M(y)分别为：
结构任意高度y处由剪力作用引起的位移DB(y)和由弯矩作用引起的位移 DB(y)的计算公式参见式(7)和式(8)，计算叠加后的位移二次导函数如下：
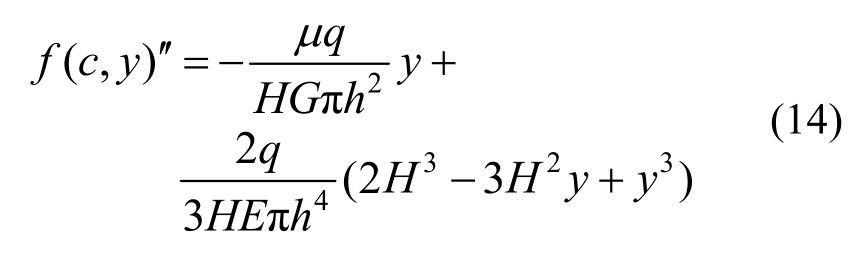
与式(10)类似，式(14)中也不存在可调控参数，即无法使倒三角荷载下的等截面结构具有产生均匀变形。
当等截面结构承受与惯性力相关的荷载时，质量分布集度
(y)可表示为：
式中，ρ为等效面密度，其余参数同前。
和惯性力相关的荷载分布集度
(y)可表示为：
式中，λ为质量相关常数，用来控制荷载幅值。
结构任意高度 y处由惯性力相关荷载
(y)作用产生的剪力Q(y)和弯矩M(y)分别为：
按照式(7)和式(8)计算相应位移，并获得位移二次导函数如下：
式(19)中也不存在可调控参数。最终的分析结果表明：在不同形式的荷载下等截面结构均不具有产生均匀变形的能力。要实现结构的均匀变形优化准则，必须使结构的横截面沿高度发生变化。下面对横截面按自然指数函数和幂函数连续变化的结构进行位移求解和优化。
1.3.2 截面为自然指数函数的结构位移方程及优化
对于横截面按自然指数函数连续变化的结构，可采用与前述计算等截面结构响应相同的计算方法分别求得在均布荷载、倒三角荷载和惯性力相关荷载作用下的绝对位移二次导函数，相应的具体公式分别如下：
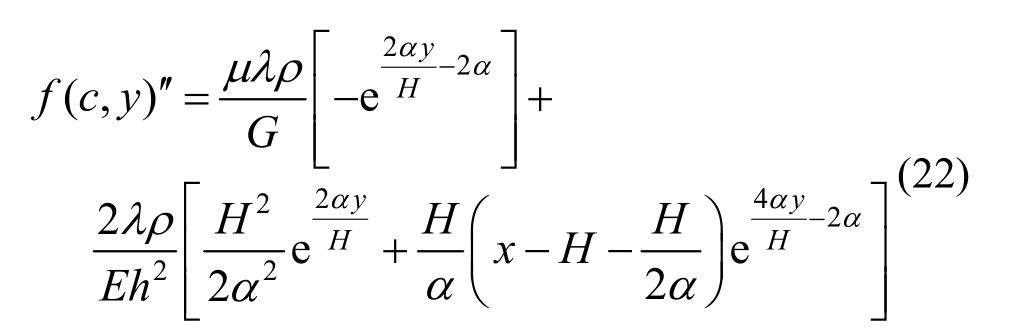
经过对以上公式分析，可以认为：通过合理地调控自然指数函数中的外形参数α及其他材料和物理参数可能使绝对位移二次导函数为零成立，从而可以实现优化目标。
1.3.3 截面为幂函数的结构位移方程及优化
对于横截面按幂函数连续变化的结构，可分别求得在均布荷载、倒三角荷载和惯性力相关荷载的作用下的位移二次导函数，相应的具体公式分别如下：
通过以上分析可以认为：通过合理地调控幂函数中的底部半径影响参数β及其控制外形常数n可使上3式为0分别成立。
从上述分析可以看出，对于横截面按自然指数函数或幂函数连续变化的结构，通过调控参数可能实现均匀变形优化目标。为了验证可行性，本文选择一典型的连续化悬臂杆结构并根据以上解析公式进行数值分析。结构的总高度 H=20 m，弹性模量E=200 GPa，剪切模量G=80 GPa，截面剪切应变不均匀分布的系数μ=1.11。均布荷载q和倒三角荷载最大值qmax均为1.0×108N。对于与惯性力相关的荷载，等效面密度 ρ=7800 kg/m3，质量相关常数 λ取为1。
为了得到结构截面函数的最优形式，对相应的绝对位移二次导函数方程进行数值分析，通过优化各个参数使不同荷载形式下各截面函数模型的绝对位移二次导函数无限趋向于零，然后将不同的优化结果进行比较并对不同截面函数和荷载对应的优化性能进行评价。具体优化时约束条件分为无约束和使结构体积保证不变两种，当将体积不变作为约束条件时需使体积值V=720 π/m3，此情况相当于保证工程材料造价不变。
首先考虑均布荷载下的结构优化效果，分别通过调整优化影响参数使式(10)、式(20)和式(23)均趋向于零，优化后的设计参数值见表1。
表1 优化结果
Table 1 Optimization results
对于横截面按自然指数函数连续变化的结构，在底部截面半径h一定的情况下，顶部截面半径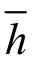
随α的减小而增大，悬臂杆位移二次导函数越趋于零，当 α≤0.1时，优化效果明显趋缓，故取α=0.1。
对于横截面按幂函数连续变化的结构，当n=2时，式(23)的前一部分等于零，后一部分为常数，通过优化β可以使方程趋于零。随着β的不断减小，结构绝对位移二次导函数趋于零，当β≤0.05时，优化效果趋缓。考虑到结构高宽比及使用功能的要求，取 β=0.05，此时底部半径和构件总高度相同。
在无约束条件下，均布荷载作用下的不同截面函数结构的绝对位移二次导函数如图2所示，通过对比可以发现截面为幂函数时优化效果最佳，而等截面和自然指数函数模型效果相对不理想。在等体积条件约束下，相应的优化效果如图3所示，可见仍然是截面为幂函数时的优化效果最佳。
图2 均布荷载下三种函数模型的对比
Fig.2 Comparison of section functions under uniform load
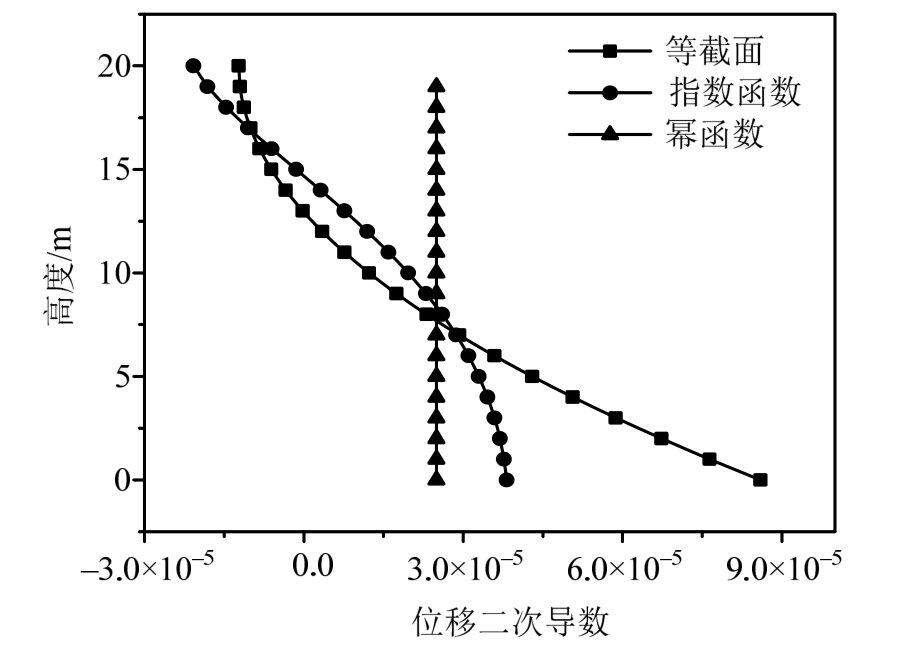
图3 均布荷载下等体积的三种函数模型的对比
Fig.3 Comparison of section functions and equal volume
下面考虑倒三角荷载下的结构优化效果，分别通过调整优化影响参数使式(14)、式(21)和式(24)进行均趋向于零，优化后的设计参数值见表 1。在无约束条件和等体积条件约束下，不同截面函数结构的优化结果对比分别如图4和图5所示，结果表明截面为幂函数时的优化效果仍然是最佳的，且整体变化规律与均布荷载的结果十分接近。
以下考虑惯性力相关荷载下的结构优化效果，分别通过调整优化影响参数使式(19)、式(22)和式(25)进行均趋向于零，优化后的设计参数值见表1。
对于横截面按自然指数函数连续变化的结构，在底部截面半径h一定的情况下，顶部截面半径
随α的减小而增大，结构绝对位移二次导函数也越趋于零，当α≤1时，优化效果趋缓，故取α=1。
对于横截面按幂函数连续变化的结构，当n=1时，式(25)后一部分为常数，通过优化 β可使方程趋于零。随着β的减小，结构底面半径增大，优化效果越明显，当β=1.6时，效果最佳。此外，因为在均布荷载下和倒三角荷载下n的最优参数为2，为了进行比较将该种情况也进行了计算分析。
图4 倒三角荷载下三种函数模型的对比
Fig.4 Comparison of section functions under triangular load
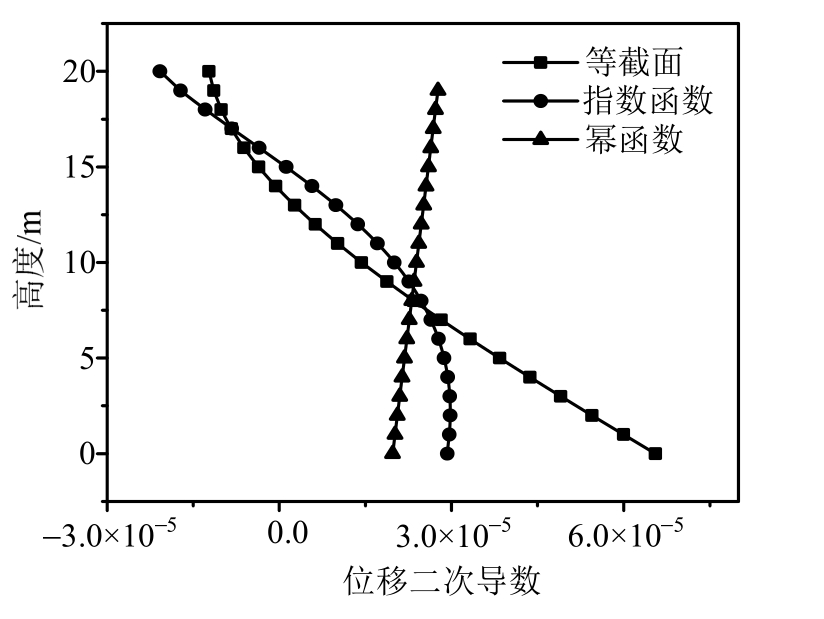
图5 倒三角荷载下等体积的三种函数模型的对比
Fig.5 Comparison of section functions and equal volume
在无约束条件和等体积条件约束下，不同截面函数结构的优化结果对比分别如图6和图7所示。结果表明当时截面函数为n=1的幂指数函数时优化效果最佳，而截面为其他函数时优化效果均不够理想。
根据上述得出的结论，在弹性状态下如果横截面按照幂函数连续变化，则结构更容易实现均匀变形的优化目标，且其最优剪切刚度和弯曲刚度分布公式分别如下：
图6 惯性力相关荷载下三种函数模型的对比
Fig.6 Comparison of section functions under inertial load
图7 惯性力相关荷载下等体积的三种函数模型的对比
Fig.7 Comparison of section functions under inertial load
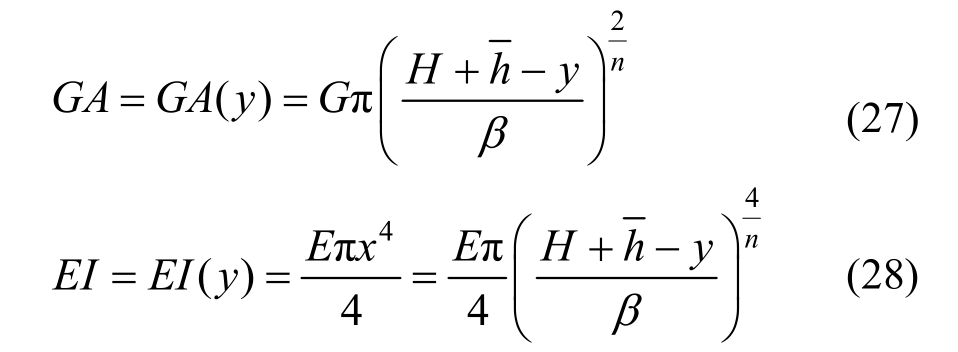
式中，各个参数值取等体积约束条件下的优化结果，详见表1。最优剪切刚度和弯曲刚度如图8和图9。
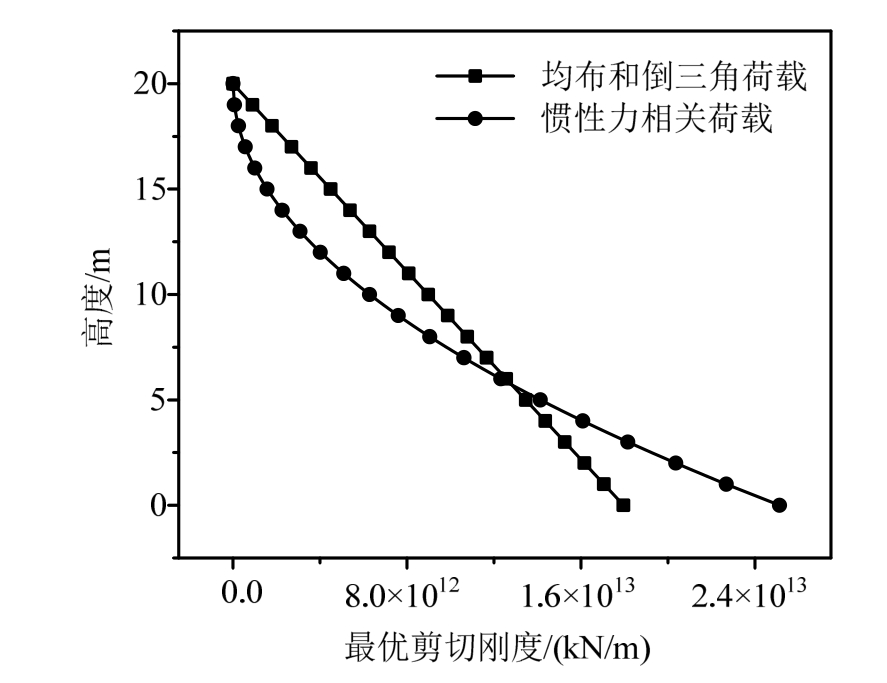
图8 最优剪切刚度分布图
Fig.8 Optimal shear stiffness distribution
图9 最优弯曲刚度分布图
Fig.9 Optimal bending stiffness distribution
可见在均布荷载和倒三角荷载下，结构的最优剪切刚度和弯曲刚度的分布形式接近向上衰减的线性分布；而在惯性力相关荷载下，结构的最优刚度分布为向上衰减的内凹型曲线。以上结果可为结构的优化设计提供基本的参考。
上文通过数值分析及优化求解验证了采用横截面按自然指数函数或幂函数连续变化的结构能够实现均匀变形，并对相关设计参数进行了优化。但在上述分析中假定结构是完全连续化的且没有充分考虑动力效应。为了更深入地探究上述优化方法和结论的准确性和精度，本文利用有限元软件ANSYS建立了由实体单元构成的悬臂结构并进行静动力分析。
结构的基本设计参数为：高度 H=20 m，弹性模量E=200 GPa，泊松比为0.3。建立了21个按高度均匀划分的节点，并采用了实体单元建模，结构底层截面与地面刚性固结，并按等体积约束条件进行优化。参考前文研究结果，建立了4种横截面连续变化的结构，相应的函数分别为：等截面型、自然指数函数、幂函数(n=2)和幂函数(n=1)，如图 10所示。具体优化参数取值详见表1。各节点绝对位移变形图，进而求得位移二次导数。在不同荷载下，不同截面形式结构的绝对位移二次导数对比参见图11。
图10 函数结构模型示意图
Fig.10 Schematic diagram of function structure model
图11 等体积条件下的不同模型优化结果对比
Fig.11 Results of different models under equal volume
可以看出：在均布荷载和倒三角荷载下，截面按幂函数(n=2)变化的结构优化效果最佳，该结果与前文图3和图5的结果相吻合。在惯性力相关荷载下，截面按幂函数(n=1)变化的结构优化效果最佳，该结果也与前文图7的结果接近。考虑到有限元分析结果在约束条件和力学性能上的模拟精度更高，本文提出的优化方法和优化结果的准确性进一步得到了验证。
在上述研究中都是通过对结构施加等效静力荷载研究结构在地震和风载下的变形和优化设计。为了验证上述优化准则、方法和结论能否与结构动力响应和效应相吻合，本文基于ANSYS对上述4种结构模型进行地震动时程分析。在结构基底输入单向El Centro地震波，时间间隔为0.02 s，持时为15 s。在弹性时程分析后获得不同模型所有节点的水平位移时程，由于所有模型的节点位移均在1.68 s时出现最大值，因此选该时刻的位移分布作为主要分析数据。对该情况下 21个节点的绝对位移分布曲线进行二次求导，结果如图 12所示。此外，为了反映动力响应的统计规律，将各节点位移时程绝对值之和的分布曲线也进行分析，二次求导后的结果如图13所示。
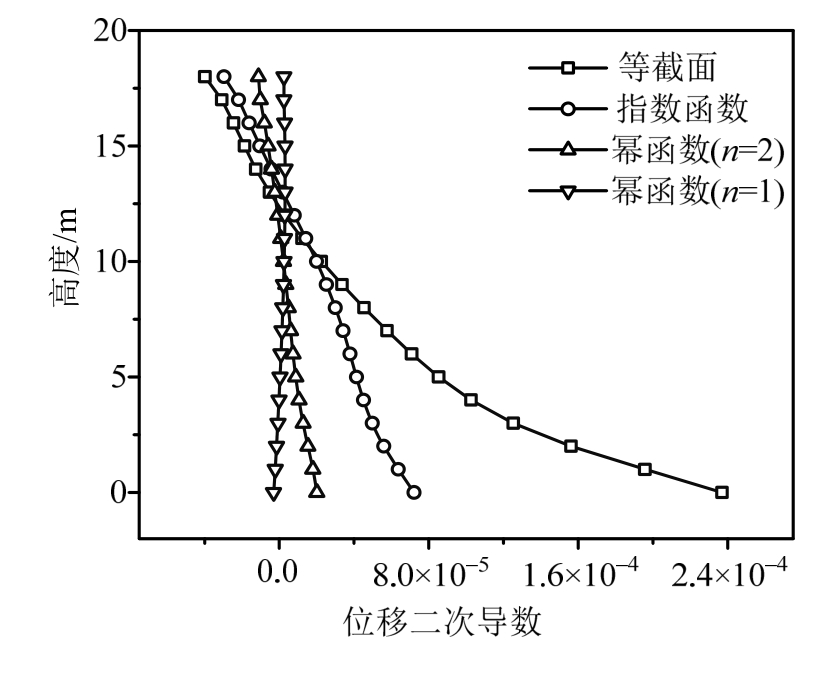
图12 结构最大位移的动力优化结果对比
Fig.12 Optimal results of structural maximum displacement
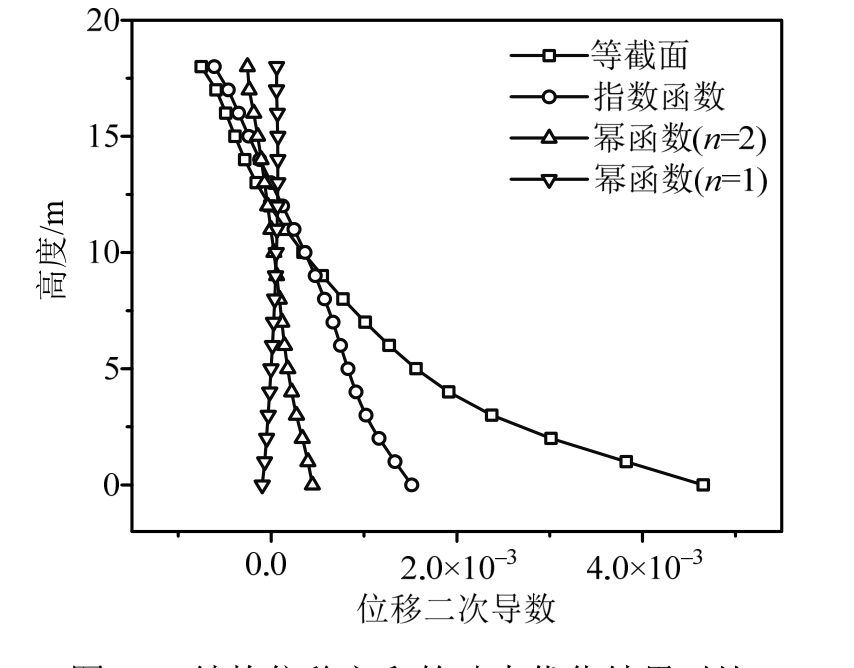
图13 结构位移之和的动力优化结果对比
Fig.13 Optimization results of structural displacement sum
可以看出：在等体积条件和地震作用下，截面按幂函数(n=1)变化的结构更充分地实现均匀变形的优化目标，幂函数(n=2)和自然指数函数也有一定的效果，而等截面结构无法实现均匀变形。此外，由于惯性力相关荷载下的结果与动力时程分析结果最接近，表明将地震作用按惯性力相关荷载进行静力等效是最精确的，而等效为均布荷载或倒三角荷载则不够准确的，不推荐采用。由于风荷载可以等效为倒三角分布荷载，因此在仅考虑风荷载的情况下将截面按幂函数(n=2)进行设计更可能实现均布变形的优化目标。综合分析以上结果可知：荷载分布形式和截面变化形式均明显影响结构优化设计的能力和结果，当截面按幂函数(n=1)和幂函数(n=2)连续变化时可分别实现地震作用和风荷载下的均布变形优化。如果想实现同时考虑地震作用和风荷载的结构综合优化，需要将幂函数中的幂次常数n在1～2之间取值。
值得指出的是，本文为了计算简便将结构横截面设置为实心圆形，当横截面为空心时，只要截面仍沿高度连续变化，其截面惯性矩的计算公式是相同的，因此相关的优化结果和规律是类似的。对于有空间需求的实际结构，可将连续化结构的最优刚度分布作为标准值，通过改变截面或调整配筋的方式将结构的实际剪切刚度和弯曲刚度进行适当匹配，确保各层的等效刚度比例一致即可实现结构优化。在此情况下，各层的空间和构件布局是可以灵活调控的，因此优化方法切实可行。
均匀损伤是建筑结构破坏和变形的理想模式，以此为目标进行结构优化具有重要的理论和工程意义。针对建筑结构弹性状态下的优化设计，将基于均匀损伤的设计理论简化为均匀变形准则。将结构简化为连续变截面悬臂杆，提出三种变截面函数形式，同时将风荷载和地震作用等激励简化为均布、倒三角和惯性力相关荷载等荷载分布模式。在此基础上建立了结构位移方程，并根据均匀变形准则提出了使结构绝对位移曲线关于高度的二次导数为零的优化目标。对连续化方程进行优化求解，获得了考虑荷载分布形式的弯剪型结构最优刚度和截面分布解析解。通过数值模拟和有限元分析验证了解析解的正确性和实用性。得出以下结论：
(1) 结构截面尺寸沿高度均匀分布或呈自然指数函数分布是不可能实现均匀损伤的，截面尺寸呈幂函数分布的结构则可能实现均匀损伤。
(2) 对于截面尺寸沿高度呈幂函数分布的结构，在均布荷载和倒三角荷载作用下，幂函数公式n取 2，即结构外形呈外凸型抗风效果最佳。在惯性力相关荷载作用下，幂函数公式n取1，即结构外形呈线性变化抗震效果最佳。
(3) 在均布荷载和倒三角荷载下，结构的最优剪切刚度和弯曲刚度的分布形式接近向上衰减的线性分布；而在惯性力相关荷载下，结构的最优刚度分布为向上衰减的内凹型曲线。
(4) 通过有限元软件建立上述三种函数类型的四种模型进行静动力优化验证，结果表明理论解析解与有限元数值解吻合，具有较高的准确性，相关结果可为结构优化设计提供指导和借鉴。
参考文献：
[1] Kirsch U. Structural optimization: fundamentals and application [M]. Berlin: Springer-Verlag, 1993.
[2] 隋允康, 乔志宏, 杜家政. 采用相似变换解决含压杆稳定约束 [J]. 工程力学, 2005, 22(6): 112―116.Sui Yunkang, Qiao Zhihong, Du Jiazheng. Full stress design of truss structures with local stability problem using similar transformation [J]. Engineering Mechanics,2005, 22(6): 112―116. (in Chinese)
[3] 郭鹏飞, 韩英仕, 魏英姿. 离散变量结构优化的拟满应力设计方法[J]. 工程力学, 2000, 17(1): 94―98.Guo Pengfei, Han Yingshi, Wei Yingzi. Quasi full stress design method for structural optimization with discrete variables [J]. Engineering Mechanics, 2000, 17(1): 94―98. (in Chinese)
[4] Zou X K, Chan C M, Li G. Multiobjective optimization for performance-based design of reinforced concrete frames [J]. Journal of Structural Engineering, 2007,133(10): 1462―1474.
[5] 孙爱伏, 侯爽, 欧进萍. 高层钢结构基于均匀损伤设计的整体抗震能力提高方法[J]. 地震工程与工程振动,2012, 32(2) : 74―81.Sun Aifu, Hou Shuang, Ou Jinping. A method for increasing the integral seismic capacity of tall steel buildings based on uniform-damage seismic design [J].Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(2): 74―81. (in Chinese)
[6] Hisatoku T, Kobori T, Minai R, Lnoue Y. On the optimum aseismic design data of tall building structures based on the elasto-plastic earthquake responses [J]. Journal of Earthquake Engineering, 1969, 10(18): 1623―1631.
[7] Kato B, Nakamura Y, Anraku H. Optimum earthquake design of shear buildings [J]. Journal of the Engineering Mechanics Division, 1972, 98(4): 891―910.
[8] 王光远, 董明耀, 郭骅. 剪切型多层框架抗震设计的最优刚度分布[J]. 地震工程与工程振动, 1980, 1(1):92―105.Wang Guangyuan, Dong Mingyao, Guo Hua. The optimal stiffness distribution of seismic design for multi story shear frame [J]. Earthquake engineering and Engineering Vibration, 1980, 1(1): 92―105. (in Chinese)
[9] 秋山宏.エネルギ－ の钓合に基づく建筑物の耐震设计[M]. 日本: 技报堂出版, 1999.Akiyama H. Seismic design of building structures based on energy balance [M]. Japan: Technology News Publishing, 1999. (in Japanese)
[10] 和田章, 岩田卫, 清水敬三. ほか·建築物の損傷制御設計 [M]. 日本: 丸善出版社, 1998.Wada A, Iwata M, Shimizu K. Damage control design of building structures [M]. Japan: Maruzen Co. Ltd., 1998.(in Japanese)
[11] 王星星, 裴星洙, 王维. 多高层钢结构最佳侧移刚度分布与最佳截面惯性矩分布研究[J]. 工程抗震与加固改造, 2011, 33(1): 19―27.Wang Xingxing, Pei Xingzhu, Wang Wei. Study on optimum lateral stiffness ratio and optimum moment of inertia ratio for multi-story steel structure [J]. Earthquake Resistant Engineering and Retrofitting, 2011, 33(1): 19―27. (in Chinese)
[12] 裴星洙, 王星星, 王维. 基于抗震的多高层钢结构层间侧移刚度优化分布的研究[J]. 江苏科技大学学报,2011, 25(4): 119―125.Pei Xingzhu, Wang Xingxing, Wang Wei. Optimal distribution of story lateral stiffness of multi-storey steel structure based on anti-seismic [J]. Journal of Jiangsu University of Science and Technology, 2011, 25(4):119―125. (in Chinese)
[13] Chan C M, Zou X K. Elastic and inelastic drift performance optimization for reinforced concrete building under earthquake loads [J]. Earthquake Engineering and Structural Dynamics, 2004, 33(8): 929―950.
[14] Allahdadian S, Boroomand B. Topology optimization of planar frames under seismic loads induced by actual and artificial earthquake records [J]. Engineering Structures,2016, 115(3): 140―154.
[15] Elghazouli A Y, Kumar M, Stafford P J. Prediction and optimization of seismic drift demands incorporating ground motion frequency content [J]. Bulletin of Earthquake Engineering, 2014, 12(1): 255―276.
[16] Losanno D, Spizzuoco M, Serino G. An optimal design procedure for a simple frame equipped with elastic deformable dissipative braces [J]. Engineering Structures, 2015, 101(5): 677―697.
[17] Park K, Medina R A. Conceptual seismic design of regular frames based on the concept of uniform damage [J]. Journal of Structural Engineering, 2007, 133(7): 945―955.
[18] Hajirasouliha I, Asadi P, Pilakoutas K. An efficient performance-based seismic design method for reinforced concrete frames [J]. Earthquake Engineering and Structural Dynamics, 2012, 41(4): 663―679.
[19] 黄铭枫. 基于风振性能的高层建筑抗风设计优化[J].工程力学, 2013, 30(2): 240―246.Huang ming feng. Wind-induced vibration performance based optimal structural design of tall buildings [J].Engineering Mechanics, 2013, 30(2): 240―246. (in Chinese)
[20] 徐龙河, 于绍静, 卢啸. 基于损伤控制函数与失效概率的结构抗震性能多目标优化与评估[J]. 工程力学,2017, 34(10): 61―67.Xu Longhe, Yu Shaojing, Lu Xiao. Damage control function and failure probability based structural seismic performance multi-objective optimization and assessment[J]. Engineering Mechanics, 2017, 34(10): 61―67. (in Chinese)
[21] 白久林, 杨乐, 欧进萍. 基于等损伤的钢框架结构抗震性能优化[J]. 工程力学, 2015, 32(6):76―83.Bai Jiulin, Yang Le, Ou Jinping. Aseismic performance optimization of steel frame structures based on uniform damage concept [J]. Engineering Mechanics, 2015,32(6): 76―83. (in Chinese)
[22] Wang W, Zou C, Chen Y, Zhang Y, Chen Y. Seismic design of multistory tension-only concentrically braced beam through frames aimed at uniform inter-story drift[J]. Journal of Constructional Steel Research, 2016,122(3): 326―338.
[23] 钟振宇, 楼文娟. 基于风重耦合效应超高层建筑顺风向等效静力风荷载[J]. 工程力学, 2016, 33(5): 74―81.Zhong Zhenyu, Lou Wenjuan. Equivalent static wind load on extra-high buildings along wind based on wind-gravity coupling effect [J]. Engineering Mechanics,2016, 33(5): 74―81. (in Chinese)
ANALYTICAL STUDY ON OPTIMAL STIFFNESS DISTRIBUTION OF BEND-SHEAR STRUCTURES CONSIDERING LOAD DISTRIBUTION
HE Hao-xiang1,2, WANG Wen-tao1, FAN Shao-yong1
(1. Beijing Key Lab of Earthquake Engineering and Structural Retrofit, Beijing University of Technology, Beijing, 100124, China;2. Beijing Collaborative Innovation Center for Metropolitan Transportation, Beijing 100124, China)
Abstract:For structures subjected to external excitation, the weak layers can be avoided and the bearing capacity and safety can be improved if all the damage degrees or the relative displacements of each story are the same, i.e., the uniform damage or uniform deformation occurs. It is significant to carry out structural optimization with uniform damage as the optimization objective. The bend-shear structure is simplified as a continuous variable cross-section cantilever. The assumed cross section functions include the forms of a natural exponential function and a power function. The external excitation such as earthquake effects and wind loads are idealized to three load modes, that is, the uniform distribution, the inverted triangle distribution and the inertia correlation distribution. According to the uniform deformation criterion, to make the second derivative of the absolute displacement curve of the structure equals zero is taken as the optimization target. The continuous displacement equation is established and the optimization results are discussed. The analytical solution of the optimal stiffness and the cross section distribution of the bend-shear structure is obtained. According to the theoretical and numerical results, the uniform damage can be realized if the cross section function is taken as power function, and the optimal distributions of stiffness and cross sections are different for different load distribution modes. The accuracy and the practicability of the analytical solution is verified by static-dynamic analysis based on the finite element method.
Key words:uniform damage; optimal section; stiffness distribution; story drift angle; earthquake action
中图分类号：TU311.1
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.03.0197
文章编号：1000-4750(2018)07-0094-10
收稿日期：2017-03-14；修改日期：2017-12-28
基金项目：国家自然科学基金项目(51478024)；工程抗震与结构诊治北京市重点实验室重点项目(USDE201403).
通讯作者：何浩祥(1978―)，男，辽宁人，教授，博士，从事结构抗震减震及健康监测研究(E-mail: hhx7856@163.com).
作者简介：
王文涛(1991―)，男，河北人，硕士生，主要从事结构抗震减震研究(E-mail: S201504183@emails.bjut.edu.cn);
范少勇(1992―)，男，河北人，硕士生，主要从事结构抗震减震研究(E-mail: fansghaoyon@emails.bjut.edu.cn).