杨庆山1,3,田玉基2,3,陈 波2,3,黄国庆1
(1.重庆大学土木工程学院,重庆 400044;2.北京交通大学土木建筑工程学院,北京 100044;3.结构风工程与城市风环境北京市重点实验室,北京 100044)
摘 要:全面介绍了新编行业规范《屋盖结构风荷载标准》的主要内容。针对多种屋盖主体结构的风振响应计算分析和抗风设计,采用平均风压与脉动风振等效静力风压之和表达主体结构的风压标准值,提出了脉动风荷载作用下结构风振响应极值的单目标、多目标等效静力荷载表达方式;采用多目标等效静力风荷载分析方法,给出了平面桁架、张弦梁、网架、球壳、柱壳、鞍形屋盖和悬挑屋盖的风振等效风压系数图表及体型系数图表。采用围护结构风压系数极值表达围护结构的风压标准值,规定了长/短时距的风压极值估计方法,给出了低矮房屋单坡/双坡类屋盖、四坡屋盖、中高层房屋屋盖、开敞屋盖、悬挑罩蓬的风压系数极值图表。《屋盖结构风荷载标准》引入屋盖主体结构风振等效风压系数和围护结构风压系数极值的概念,完善和发展了我国屋盖结构抗风设计的相关规定。
关键词:屋盖结构;抗风设计;主体结构;风振等效风压系数;围护结构;风压系数极值
在强季风、台风作用下,建筑结构的风致灾害现象表明,建筑物屋面、墙面的围护结构在风荷载作用下最容易发生破坏。在屋盖的角部、边缘、屋脊等尖锐部位,气流发生分离,在屋面上形成旋涡脱落、气流再附等现象,这些部位的围护结构承受极大的风吸力,造成围护结构的风致破坏。围护结构的尺寸较小,自振频率相对较高,其风荷载通常不考虑围护结构的振动效应,直接按照风荷载的从属面积确定围护结构的最小风荷载(吸力)、最大风荷载(压力)。因此,在基本风速、基本风压给定的情况下,合理预测估计屋盖围护结构风压系数极值的最小值、最大值成为确定围护结构风荷载标准值的关键问题。
在强风/台风作用下,屋盖主体结构发生风致破坏的情况屡见不鲜。在强风/台风作用下,屋盖表面承受较大的平均风压;屋盖主体结构不仅承受围护结构传来的较大平均风荷载,而且主体结构在脉动风荷载作用下产生振动。考虑屋盖结构多振型参与风致振动,采用合理方式表达屋盖主体结构的等效静力风荷载成为确定屋盖主体结构风荷载标准值的关键问题。
针对上述两个关键问题,新编行业标准《屋盖结构风荷载标准》总结、借鉴了美国、加拿大、欧洲、日本、澳洲、中国等国家、地区的屋盖结构风荷载规定,引入主体结构风振等效风压系数和围护结构风压系数极值的概念,规定了屋盖主体结构、围护结构风压标准值的表达形式,列出了典型屋盖的体型系数、风振等效风压系数和风压系数极值,完善、发展了我国规范、规程关于屋盖结构风荷载方面的相关规定,为屋盖结构的抗风设计提供了科学依据。
20世纪70年代之前,在结构风工程的发展历史上,建筑结构的抗风设计经历静力抗风设计阶段、拟静力抗风设计阶段。从 1980年代开始,综合考虑来流湍流和建筑湍流对屋盖、墙面围护结构风荷载的贡献,美国、加拿大、日本等国家的荷载规范采用全风向局部风压极值进行围护结构的抗风设计,而欧洲、澳洲等国家、地区的荷载规范采用风向区间的局部风压极值进行围护结构的抗风设计;在国外荷载规范中,考虑脉动风荷载作用下建筑主体结构的振动效应,先后提出了主体结构等效静力风荷载的包络值设计方法和单风向等效静力风荷载设计方法。
我国第一本自主制定的较为完整的荷载规范是《工业与民用建筑结构荷载规范》TJ 9-74,这本规范规定了建筑表面的平均风压计算公式,承重结构与围护结构的平均风压均采用相同的体型系数确定风荷载。在 1980年代,我国科技工作者经过大量的实测、调查、研究,以《建筑结构设计统一标准》GBJ 68-84为准则,基于极限状态设计方法制定了《建筑结构荷载规范》GBJ 9-87。在这本荷载规范中,考虑了结构或构件的振动效应,规定了建筑表面的风压标准值计算公式;其中,明确规定了高层、高耸结构的风振系数确定方法。同时,规范给出了气流分离区(负压区)围护结构“局部风压体型系数”的部分数值,用以确定围护结构的风压标准值。
直至 2002年,我国开始执行《建筑结构荷载规范》GB 50009―2001,明确规定了围护结构的风荷载标准值计算公式,围护结构的风压标准值等于局部风压体型系数与阵风速压的乘积,而后者等于阵风系数与10 min平均速压的乘积。其中,局部风压体型系数按照外表面的正压区和负压区分别确定,正压区的局部风压体型系数按照承重结构的体型系数取值,负压区的局部风压体型系数按照墙面、屋面的位置分别取不同数值,同时规定了封闭式房屋的内压系数。在GB 50009―2001 (2006修订版)中,增加了围护结构风荷载的面积折减系数。在《建筑结构荷载规范》GB 50009―2012中,修订了局部体型系数的取值和面积折减系数的计算公式,增加了单、双坡房屋的墙面、屋面的局部体型系数取值。
从国内外风荷载规范规定的发展演变历史可以看出,我国规范关于围护结构风荷载的规定滞后于国外规范,尚缺少多种体型建筑物围护结构局部体型系数的详细规定。作用在建筑物表面的风荷载具有时间-空间的变异性,围护结构的风荷载极值与构件受风面积、风向效应等因素存在密切关系,我国科研工作者在这些方面的研究还较少,特别是缺少系统、持续的科学研究,因此,我国荷载规范在这些方面的规定也比较模糊,甚至没有规定。
GB 50009―2001和 GB 50009―2012延续了1987年我国荷载规范的规定,采用风振系数与平均风压乘积的形式表示主体结构风压标准值;其中,风振系数反映了高层/高耸建筑主体结构等效静力风荷载与平均风荷载的比值。虽然我国规范规定的主体结构风压标准值也适用于低矮房屋屋盖主体结构,但规范未给出风振系数的确定方法。GB 50009―2012的条文说明指出,屋盖结构的等效静力风荷载不宜采用与高层建筑和高耸结构相同的风振系数表示方法。
我国工程设计人员在屋盖抗风设计方面亟需规范、标准作为设计依据,而我国国家级、行业级标准在屋盖风荷载及抗风设计方面存在条文不明确或风荷载参数取值欠合理的缺陷,住房和城乡建设部于 2015年启动了行业标准《屋盖结构风荷载标准》的制订工作。
新编行业标准《屋盖结构风荷载标准》主要解决屋盖结构的风荷载标准值表达方式及参数取值、屋盖结构的抗风计算及抗风构造、屋盖结构的风洞试验技术及数值风洞模拟技术等方面的重要问题;其中,屋盖主体结构、围护结构的风荷载标准值确定方法是需要解决的关键问题。
2017年底,《屋盖结构风荷载标准》编制组完成了报批稿。本文总结了编制组全体成员过去三年的劳动成果,重点介绍了主体结构和围护结构的风荷载确定方法。
风荷载对屋盖主体结构的效应包括平均风效应和脉动风效应,其中脉动风效应包括阵风的准静力效应和结构动力放大效应,当结构跨度较大时,结构动力放大作用将更为显著。目前,屋盖主体结构的风压标准值有两种表达形式,一种为平均风压乘以风振系数,即我国《建筑结构荷载规范》GB 50009采用的表达形式;另一种为平均风压加上由脉动风压引起结构风振的等效风压。屋盖表面有时出现平均压力幅值较小,甚至为零的区域,此时若按照风振系数概念,将导致平均压力幅值较小处风振系数很大,或出现奇异值,同时从概念上也将导致放大作用更为显著的错觉。同时,屋盖结构多阶模态及模态耦合效应比较明显,脉动风对应的等效静风荷载常与平均风荷载差别显著,若按照风振系数概念,将导致屋面区内风振系数变化剧烈。因此,屋盖结构不宜采用与高层建筑和高耸结构相同的风振系数计算方法。
在这一共识的基础上,《屋盖结构风荷载标准》采用平均风压与风振等效静力风压之和的形式表达屋盖主体结构的风压标准值;作用在屋盖主体结构表面的风压标准值按照下式计算:
式中:w0、μs、μz含义与《建筑结构荷载规范》相同,分别表示基本风压、体型系数和风压高度变化系数;μd表示脉动风作用下结构风振等效风压系数。上式的第一项是平均风荷载,第二项的风振等效风压系数μd体现了脉动风的阵风效应和结构动力放大效应,相当于《建筑结构荷载规范》中的(βz-1)μs,这一表述方式能避免体型系数μs过小所导致的问题。
计算风振等效风压系数是屋盖结构抗风研究的一个难点问题。屋盖结构的风振响应的显著特点是多阶振型参与振动,振动过程中不同部位的响应不在同一时刻达到结构的响应极值,导致等效风荷载控制目标不明确,以不同部位的不同极值响应(包括结构节点的最大位移响应、构件的最大内力响应和最大支座反力等)作为等效目标可得到不同的等效荷载分布,称为“单目标等效静力风荷载”;以不同部位的全部极值响应作为等效目标可得到单一的等效荷载分布,称为“多目标等效静力风荷载”。基于国内外针对这一问题的研究成果,《屋盖结构风荷载标准》同时规定了单目标、多目标等效静风荷载分析方法。
单目标等效静力风荷载分析方法针对每个极值响应计算结构的风振等效风压系数;多个极值响应将对应多个风荷载工况,当关心的响应等效目标数量很多时,将对应很多个风荷载工况。目前,单目标等效静风荷载分析方法较多,如阵风荷载因子法、扩展的荷载响应相关系数法、惯性力法。考虑到扩展的荷载响应相关系数法有较明确的理论基础,且计算过程较为简单,《屋盖抗风设计规范》规定采用该方法计算单目标等效静力风荷载及风振等效风压系数。
多目标等效静力风荷载分析方法同时针对多个极值响应计算结构的风振等效风压系数。该方法是近年来新发展的方法,并逐渐被认同和采纳,其具体过程可参见文献[1―7]。多目标等效静力风荷载分析方法针对多个极值响应只需给出一个或少量几个工况的风荷载空间分布,减少了风荷载与其它类型荷载的组合工况,方便工程应用。采用多目标等效静力风荷载分析方法,《屋盖抗风设计规范》给出了平面桁架、张弦梁、平面网架、球壳、柱壳、鞍形屋盖和悬挑屋盖的体型系数图表和风振等效风压系数图表。
例如,50 m跨度的平面方形网架结构,屋檐高度为20 m,B类地貌,基本风压为0.5 kN/m2,结构的第一阶振型的自振频率 0.8 Hz。《屋盖结构风荷载标准》给出了平板网架不利风向 0°的分区体型系数sμ(图1)。对于跨度小于80 m的四边铰支方形平面平板网架,按照下式确定风振等效风压系数:
式中:x、y表示距网架左下角的水平和竖向距离;L表示结构跨度;μp表示风振等效风压系数的峰值,![]() 对于该结构,折算频率
对于该结构,折算频率![]() 峰值μp= 0.48;代入上式,得到风振等效风压系数(正值)的等值线图,如图2所示。
峰值μp= 0.48;代入上式,得到风振等效风压系数(正值)的等值线图,如图2所示。
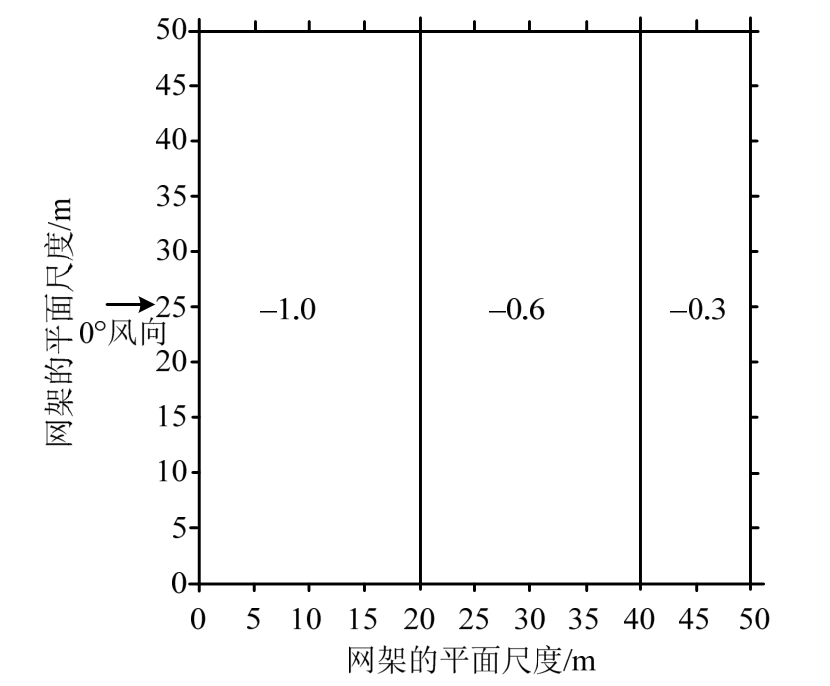
图1 方形平面网架的体型系数
Fig.1 Shape factors for square flat grid structures

图2 方形平面网架的风振等效风压系数(正值)
Fig.2 Equivalent pressure factors (positive values) of wind responses for square flat grid structures
值得注意的是,方形网架的体型系数为负值,表示向上的风吸力;方形网架的振动变形以第一振型为主,采用二维正弦函数表示第一振型,因此,网架的风振等效风压系数近似表示为二维正弦函数的乘积的形式。在脉动风荷载作用下,网架的振动包括向上振动和向下振动;网架向上振动时,风振等效风压系数取负值,表示等效静力风荷载为向上的风吸力;网架向下振动时,风振等效风压系数取正值,表示等效静力风荷载为向下的风压力。
围护结构的风荷载不仅与来流湍流特性(风速、风向,湍流强度、积分尺度等)有关,而且与来流-建筑表面的相互作用产生的建筑湍流特性(气流冲击、分离、旋涡脱落、再附等)有关。在来流湍流和建筑湍流的共同作用下,围护结构表面瞬时发生的风压极值是确定围护结构风压标准值的依据。《屋盖结构风荷载标准》采用外表面风压极值与室内风压之差的形式表达屋盖围护结构的风压标准值;垂直于屋盖围护结构表面的风压标准值按照下式计算:
式中:wk/(kN/m2)表示屋盖围护结构的风压标准值,负压标准值不应小于1.0 kN/m2,正压标准值不应小于0.5 kN/m2;w0/(kN/m2)表示基本风压,按照现行《建筑结构荷载规范》GB 50009取值;μH表示屋盖平均高度H处的风压高度系数,按照现行《建筑结构荷载规范》GB 50009取值;Cpi表示内压系数;Cpe表示风压系数极值,包括风压系数极值的最大值 Cpe,max和最小值 Cpe,min。
屋盖结构围护构件直接、间接承受的风压最大值、最小值分别除以屋盖高度处的速压,得到风压系数最大值、最小值,二者统称为风压系数极值。根据风压时程样本数目,《屋盖结构风荷载标准》推荐了三种估计风压系数极值的方法,即极值平均计算方法、最好线性无偏估计方法、修正的Hermite矩模型变换方法[8―11]。在式(3)中,外表面风压极值为全风向风压系数极值与速压之积,风压系数极值相当于《建筑结构荷载规范》GB 50009中的局部体型系数与阵风系数之积。引入全风向风压系数极值的概念,简化了围护结构风压标准值的表达形式,更加方便设计人员应用。
借鉴国内外规范[12―20]的规定,《屋盖结构风荷载标准》只考虑封闭式房屋的内压系数。内压系数Cpi的最小值取-0.3;在式(3)中,封闭式建筑物围护结构的内压系数Cpi按其外表面风压的正负情况取值;外表面风压为正时, Cpi= - 0.3;外表面风压为负时, Cpi=+0.2。
《屋盖结构风荷载标准》按照屋盖形状分为单坡屋盖、双坡屋盖、四坡屋盖、曲面屋盖,分别给出了四类体型多种屋盖形式的风压系数极值;其中,单坡屋盖包括封闭式单跨单坡屋盖、封闭式锯齿形屋盖、开敞式单坡屋盖和悬挑式罩蓬,双坡屋盖包括低矮房屋单跨双坡屋盖、多跨双坡屋盖、不等高多跨双坡屋盖、屋盖挑檐、中高层平/坡屋盖、开敞式双坡/槽形屋盖等,四坡屋盖包括单跨四坡屋盖,曲面屋盖包括球面屋盖、柱面屋盖、鞍形屋盖。
借鉴国内外规范的相关规定[12―20]以及国内外多家风洞实验室的研究结果[21―36],《屋盖结构风荷载标准》给出了低矮房屋单坡/双坡类屋盖、中高层房屋屋盖、四坡屋盖、开敞屋盖的风压系数极值图表,发展和完善了围护结构风荷载标准值的表达方式。例如,《屋盖结构风荷载标准》给出的屋盖坡度为 0°~7°的双坡屋盖的围护结构风压系数极值如图3所示(注:1) 适用范围:0°≤θ≤7°;H≤20 m且H≤D,H≤B。2) 图中a取0.1B、0.1D和0.4H中的较小值;并且a不小于0.04B和0.04D中的最小值,不小于1 m。3) 风压系数极值Cpe为负值时,外表面风荷载为垂直于表面的吸力;Cpe为正值时,外表面风荷载为垂直于表面的压力)。


图3 双坡屋盖的风压系数极值
Fig.3 Extreme wind pressure coefficients for gable roofs
在借鉴国内外风荷载规范条文及系列风洞试验结果的基础上,《屋盖结构风荷载标准》引入屋盖主体结构风振等效风压系数和围护结构风压系数极值,规定了屋盖主体结构、围护结构的风压标准值,给出了典型屋盖结构的系数图表,为我国屋盖结构抗风设计提供了科学依据。
参考文献:
[1] Chen Bo, Yan Xiaoyu, Yang Qingshan. Wind-induced response and universal equivalent static wind loads of single layer reticular dome shells [J]. International Journal of Structural Stability and Dynamics, 2014,14(4): 1450008-1―1450008-22.
[2] Chen Bo, Yang Qingshan, Wu Yue. Wind-induced response and equivalent static wind loads of long span roofs [J]. Advances in Structural Engineering, 2012,15(7): 1099―1114.
[3] 陈波, 晁建秋, 王科, 等. 平面拱形桁架的等效静风荷载研究[J]. 建筑结构学报, 2016, 37(1): 91―96.Chen Bo, Chao Jianqiu, Wang Ke, et al. Equivalent static wind loads on arched truss [J]. Journal of Building Structures, 2016, 37(1): 91―96. (in Chinese)
[4] 陈波, 李明, 杨庆山. 大跨平屋盖的多目标等效静风荷载研究[J]. 振动与冲击, 2013, 32(24): 22―27.Chen Bo, Li Ming, Yang Qingshan. Equivalent static wind loads of multi-targets for long span plane roofs [J].Journal of Vibration and Shock. 2013, 32(24): 22―27.(in Chinese)
[5] 陈波. 多风向多目标等效静风荷载分析方法及应用[J].建筑结构学报, 2013, 34(6): 54―59.Chen Bo. Method and application of equivalent static wind loads for multiple targets and wind directions [J].Journal of Building Structures. 2013, 34(6): 54―59. (in Chinese)
[6] 陈波, 李明, 杨庆山. 基于风振特性的多目标等效静风荷载分析方法[J]. 工程力学, 2012, 29(11): 152―157.Chen Bo, Li Ming, Yang Qingshan. Equivalent static wind loads for multiple targets based on wind-induced response [J]. Engineering Mechanics, 2012, 29(11):152―157. (in Chinese)
[7] 陈波, 杨庆山, 武岳. 大跨空间结构的多目标等效静风荷载分析方法[J]. 土木工程学报, 2010, 43(3): 62―67.Chen Bo, Yang Qingshan, Wu Yue. Multi-objective equivalent static wind loads for large-span structures [J].China Civil Engineering Journal, 2010, 43(3): 62―67.(in Chinese)
[8] Yang Q, Tian Y. A model of probability density function of non-Gaussian wind pressure with multiple samples [J].Journal of Wind Engineering and Industrial Aerodynamics, 2015, 140: 67―78.
[9] 田玉基, 杨庆山. 非高斯风压时程峰值因子的简化计算式[J]. 建筑结构学报, 2015, 36(3): 20―28.Tian Yuji, Yang Qingshan. Reduced formula of peak factor for non-Gaussian wind pressure history [J].Journal of Building Structures, 2015, 36(3): 20―28. (in Chinese)
[10] Huang G Q, Luo Y, Yang Q S, et al. A semi-analytical formula for estimating peak wind load effects based on Hermite polynomial model [J]. Engineering Structures,2017, 152: 856―864.
[11] 李波, 田玉基, 杨庆山. 非高斯风压时程的矩模型变换与峰值因子计算公式[J]. 振动工程学报, 2016,29(3): 395―402.Li Bo, Tian Yuji, Yang Qingshan. Moment-based transformation of non-Gaussian wind pressure histories and non-Gaussian peak factor formulae [J]. Journal of Vibration Engineering, 2016, 29(3): 395―402. (in Chinese)
[12] GB 50009―2012, 建筑结构荷载规范[S]. 北京: 中国建筑工业出版社, 2012.GB 50009―2012, Load code for the design of building structures [S]. Beijing: China Architecture Industry Press, 2012. (in Chinese)
[13] AIJ 2004, Recommendations for loads on buildings [S].Tokyo: Architectural Institute of Japan, 2004.
[14] ANSI/ASCE 7-10, Minimum design loads for buildings and other structures [S]. Reston, VA: American Society of Civil Engineers, 2013.
[15] BS 6399-2, Loading for buildings: Part 2, Code of practice for wind loads [S]. London: British Standards Institution, 2002.
[16] BSI 33685707, Code of basic data for the design of buildings: Chapter V Loading, Part 2 Wind loads, CP3. 5.2 [S]. London: British Standards Institution, 1972.
[17] CEN 2005, Eurocode 1: Actions on structures – Part 1–4:General actions – Wind actions, EN1991-1-4:2005 [S].London: Thomas Telford Ltd, 2004.
[18] AS/NZS 1170.0 2011, Australian/New Zealand standard:Structural design actions – Part 2: Wind actions, AS/NZS 1170.2:2011 [S]. Sydney: SAI Global Limited, 2011.
[19] NRCC 2005, National building code of Canada [S].Ottawa: National Research Council of Canada, 2005.
[20] NRCC 2005, User’s guide: NBC 2005 structural commentaries: part 4 of division B: NBC-2005 [M].Ottawa: National Research Council of Canada, 2005.
[21] Prevatt D O, Cui B. Wind tunnel studies on sawtooth and monosloped roofs [J]. Journal of Structural Engineering,2010, 136(9): 1161―1171.
[22] Stathopoulos T. Wind loads on eaves of low buildings[J]. Journal of the Structural Division, 1981, 107(10):1921―1934.
[23] Stathopoulos T. Wind loads on low-rise buildings: a review of the state of the art [J]. Engineering Structures,1984, 6(2): 119―135.
[24] Stathopoulos T, Mohammadian A R. Wind loads on low buildings with mono-sloped roofs [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 23:81―97.
[25] Stathopoulos T, Dumitrescu-Brulotte M. Design recommendations for wind loading on buildings of intermediate height [J]. Canadian Journal of Civil Engineering, 1989, 16(6): 910―916.
[26] Stathopoulos T, Luchian H D. Wind pressures on buildings with stepped roofs [J]. Canadian Journal of Civil Engineering, 1990, 17(4): 569―577.
[27] Stathopoulos T, Saathoff P. Wind pressure on roofs of various geometries [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1991, 38(2): 273―284.
[28] Saathoff P J, Stathopouios T. Wind loads on buildings with sawtooth roofs [J]. Journal of Structural Engineering, 1992, 118(2): 429―446.
[29] Stathopoulos T, Luchian H. Wind-induced forces on eaves of low buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 52: 249―261.
[30] Stathopoulos T, Wang K, Wu H. Proposed new Canadian wind provisions for the design of gable roofs [J].Canadian Journal of Civil Engineering, 2000, 27(5):1059―1072.
[31] Stathopoulos T, Wang K, Wu H. Wind pressure provisions for gable roofs of intermediate roof slope [J].Wind and Structures, 2001, 4(2): 119―130.
[32] Stathopoulos T. Wind loads on low buildings: in the wake of Alan Davenport’s contributions [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003,91(12): 1565―1585.
[33] Uematsu Y, Isyumov N. Peak gust pressures acting on the roof and wall edges of a low-rise building [J]. Journal Of Wind Engineering and Industrial Aerodynamics, 1998,77: 217―231.
[34] Uematsu Y, Isyumov N. Wind pressures acting on low-rise buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 82(1): 1―25.
[35] Uematsu Y, Stathopoulos T. Wind loads on free-standing canopy roofs: a review [J]. Journal of Wind Engineering,2003, 28(2): 95_245―95_256.
[36] Uematsu Y, Stathopoulos T, Iizumi E. Wind loads on free-standing canopy roofs: Part 1 local wind pressures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6): 1015―1028.
MAIN CONTENTS OF THE STANDARD FOR WIND LOADS ON ROOF STRUCTURES
YANG Qing-shan1,3, TIAN Yu-ji2,3, CHEN Bo2,3, HUANG Guo-qing1
(1. School of Civil Engineering, Chongqing University, Chongqing 400044, China;2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;3. Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, Beijing 100044, China)
Abstract:This paper comprehensively introduces the main contents of the Standard for Wind Loads on Roof Structures. Regarding the wind-induced response analyses and wind-resisting design for main load-resisting structures of roofs, the nominal values of wind loads on the main structures are expressed by the sum of mean wind pressures and equivalent static wind pressures. The equivalent static wind pressures correspond to extreme responses induced by fluctuating wind loads, which can be obtained by the proposed method for single or multiple targets. On these bases, the design figures and tables of shape factors for the mean wind pressures and equivalent pressure factors for fluctuating wind responses considering multiple targets are presented for different types of roof structures. These include plane truss structures, beam string structures, grid truss structures,spherical/cylindrical shell structures, saddle structures and overhanging structures. The extreme wind pressure coefficients are estimated based on specified methods, which are applicable to different cases of short/long wind pressure samples, to consequently determine the nominal values of wind loads on cladding and components.Furthermore, the design figures and tables of corresponding extreme wind pressure coefficients are proposed for mono-slope, gable, hip roofs of low-rise buildings; roofs of middle-/high-rise buildings; open roofs and overhanging canopies. Generally, in the current Standard for Wind Loads on Roof Structures, the Chinese wind-resisting design specifications for roof structures have been improved by introducing the concepts of equivalent pressure factors for the wind-induced fluctuating responses of main load-resisting structures and the extreme wind pressure coefficients of cladding and components.
Key words:roof structures; wind-resisting design; main load-resisting structures; equivalent pressure factors for wind-induced responses; cladding and components; extreme wind pressure coefficients
中图分类号:TU312.1
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.06.ST03
文章编号:1000-4750(2018)07-0001-06
收稿日期:2017-06-01;修改日期:2017-12-20
基金项目:国家自然科学基金项目(51378061);北京市自然科学基金项目(8152023)
通信作者:杨庆山(1968―),男,河北人,教授,博士,主要从事结构风工程研究(E-mail: qshyang@cqu.edu.cn).
作者简介:
田玉基(1967―),男,山东人,教授,博士,主要从事结构风工程研究(E-mail: yujitian@bjtu.edu.n);
陈 波(1979―),男,湖北人,教授,博士,主要从事结构风工程研究(E-mail: bochen@bjtu.edu.cn);
黄国庆(1976―),男,江苏人,教授,博士,主要从事结构风工程研究(E-mail: 824656975@qq.com).
注:该文在第26届结构工程学术会议(2017 长沙)应邀作特邀报告