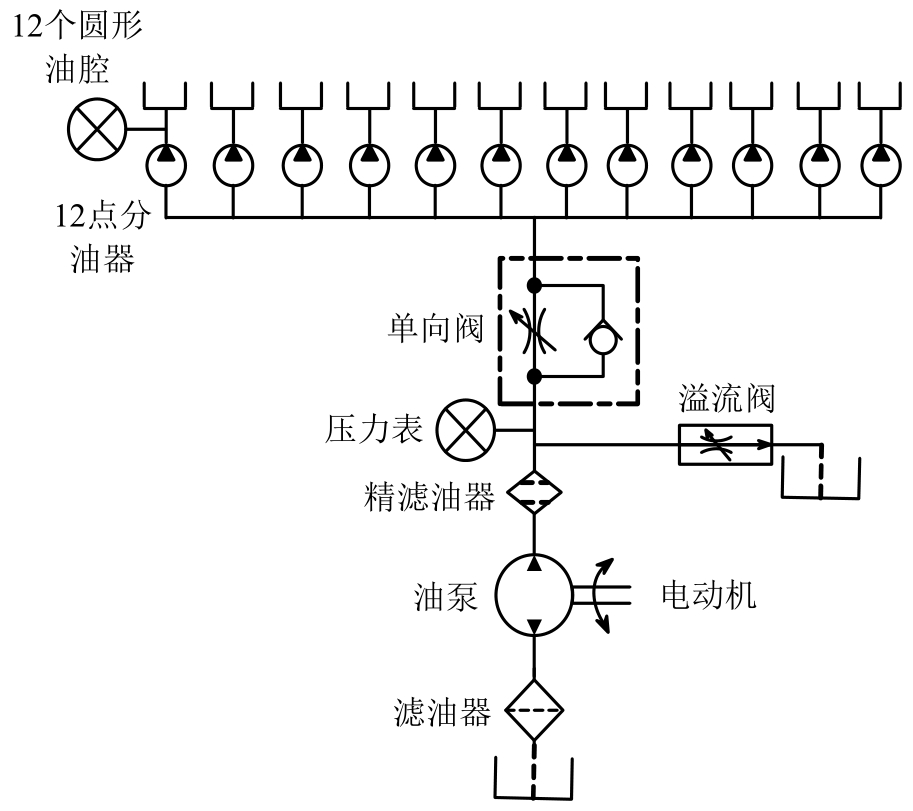
图1 静压支承工作示意图
Fig.1 Principle diagram and structure dimension of hydrostatic bearing
于晓东,刘 超,左 旭,张艳芹
(哈尔滨理工大学机械动力工程学院,哈尔滨 150080)
摘 要:摩擦副变形对静压支承摩擦学性能有显著影响,不均匀变形会引起润滑油膜破裂和干摩擦,严重时导致静压支承摩擦失效。针对环形缝隙节流静压支承,运用计算流体动力学、弹性理论和有限元法对静压支承摩擦副变形进行流热力耦合求解,得到了旋转速度和工作台自重对支承摩擦副变形的影响规律和摩擦失效机理。并进行了实验验证,数值模拟结果和实验值吻合较好,验证了数值模拟方法的正确性。研究结果表明:随着旋转工作台转速增加,间隙油膜温度升高,热变形增大。工作台自重产生摩擦副的弹性变形对热变形有均匀化作用,但其挤压效应会加大热变形,造成工作台和底座的变形为内边靠近外部开口的喇叭状。工况继续恶劣,润滑油黏度急剧下降,局部油膜迅速变薄,出现干摩擦润滑,导致静压支承摩擦失效。
关键词:静压推力轴承;摩擦副变形;高速重载特性;摩擦失效;流热力耦合方法
静压推力轴承是重型数控加工装备的关键部件,其支承摩擦副变形对间隙油膜形状及其润滑性能影响极大。尤其在高速重载等特殊或极端工况下,高速和重载加剧其间隙油膜温度升高,润滑油黏度降低,从而油膜厚度减薄,摩擦副变形加大且不均匀,进一步加剧油膜厚度不一致性,致使静压支承承载能力下降,严重时出现摩擦失效现象。
东方电机股份有限公司研究中心张帆等[1]利用FORTRAN和ANSYS计算软件联合仿真计及轴瓦变形的轴承性能,发现弹性变形对轴承静特性影响较小,而热变形对轴承静特性影响较大。广东工业大学陈凌珊等[2]建立了动压滑动轴承等温弹性流体动力润滑方程并求解,得到了动载滑动轴承弹性变形对润滑油膜的影响规律。浙江大学钟崴等[3]采用热流耦合方法求解轴瓦及油膜温度场,应用有限差分法对雷诺方程求解得到油膜压力分布,对轴瓦进行热固耦合求解,得到轴瓦的变形和应力分布,该方法有效地完成动压滑动轴承变形和应力的数值模拟。合肥工业大学孙军等[4]采用动力学法进行曲轴轴承的润滑分析,利用变形矩阵法计算油膜压力下轴瓦的变形,计入表面弹性变形,轴承最大油膜压力有不同程度的减小,表面弹性变形对端泄流量、轴颈摩擦因数以及最小油膜厚度的影响甚小。合肥工业大学蔡晓霞等[5]针对内燃机曲轴主轴承,考虑机体变形因素的影响,进行了曲轴轴承弹性流体动力润滑分析。计算中采用动力学法进行曲轴轴承的润滑分析,采用变形矩阵法计算油膜压力作用下轴承表面的变形。重庆大学彭晋民等[6]分析了水润滑塑料合金轴承在动压条件下的弹性变形,推导出支承间隙方程式,并通过傅里叶级数对压强函数进行展开,分析了弹性变形和压强的关系,得出动压条件下压强分布函数和弹性变形函数。西安交通大学王建磊等[7]基于ANSYS软件分析了动静压轴承的温度场和热变形。华南理工大学牛荣军和黄平[8]研究了粗糙表面塑性变形对静压推力轴承润滑性能的影响,考虑塑性变形后,接触的高压区油膜变小,油膜压力在接触区域也显著变小,油膜分布宽度增加。华中科技大学赵明等[9]对预载恒流静压导轨工作台静压计算时,考虑了结构变形对油膜厚度的影响,提出了静压-结构耦合的迭代求解方法。山东科技大学王智伟等[10]研究了流固耦合对油静压导轨动静特性的影响,得到了流固耦合对静压导轨压板变形量、动静刚度以及阶跃响应的影响规律,建议在静压支承实际设计和计算过程中必须考虑流固耦合的影响。北京工业大学申峰等[11]利用粒子图像测速技术和计算流体动力学方法,研究了高档数控机床液体静压支承系统中油腔内部的流场特性。北京工业大学刘志峰等[12]根据微元法建立一种引入转台倾角的雷诺方程,基于有限差分法求解出不同倾角时定量式支承油垫的油膜压力分布状态以及油垫的油腔压力和承载能力,并得到油腔工作参数及性能随倾角的变化规律。Novikov和Canbulut等[13-14]对圆形腔静压推力轴承温度场和变形特性进行了优化分析。Hemmi、Vakilian和Moldovan等[15-17]研究了温度和惯性力对静压推力轴承性能的影响,对不同的承载位置和油膜厚度比下,油膜的压力场进行了仿真。
综上所述,国内外参考文献主要针对动压轴承变形研究,仅少数采用流固耦合方式对静压推力轴承变形进行探讨,而对于高速重型静压支承摩擦副变形流热力耦合求解研究鲜见报道。采用数值模拟方法对圆形腔静压支承摩擦副变形进行流热力耦合求解,并进行实验验证,揭示其变形特征及变形规律,为探究轴承摩擦失效机理提供理论依据,避免静压支承摩擦失效发生。
定量式静压支承利用定量式供油系统将定量润滑油送到支承的静压腔内,利用静压油腔之间缝隙节流作用形成具有压力的润滑油层,产生静压支承的承载力,将支承工作台浮升并承受外载荷[18-20]。静压支承为开式多油垫恒流静压支承结构,12个油腔之间被回油槽隔开,相邻油腔间不会出现窜油现象,各油腔压力不会受到相邻油腔压力影响,形成12个彼此独立支承,静压支承工作原理和具体结构尺寸如图1所示。

图1 静压支承工作示意图
Fig.1 Principle diagram and structure dimension of hydrostatic bearing
静压支承间隙流体遵守基本物理定律的数学表述,即满足连续方程、动量方程、能量方程和状态方程[21-24]。
间隙流体满足的连续方程为:
矢量形式:
张量形式:
式中:ρ为流体密度;V为流动速度矢量;u、v、w是其在x、y、z方向上的分量;xi是空间点的坐标;ui为在时间t坐标xi点的速度分量,i=1,2,3。
间隙流体适用普遍的动量守恒方程为:

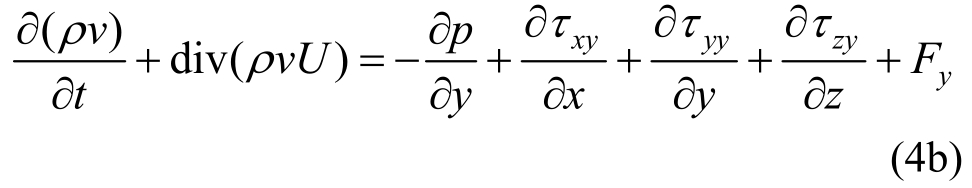

式中:p为流体压力;Fx、Fy和Fz分别为单位质量流体所受外部体力在x、y、z方向上的分量。
间隙流体符合能量守恒定律与转换定律的能量方程:

式中:cp为比热容;T为温度;k为流体的传热系数;P为流体压力;ST为黏性耗散项。二左边表示流体内能,右边第1项为热传导项,第2项为体积膨胀,第3项为黏性耗散,可见,热传导与体积膨胀将降低内能,而黏性耗散即黏性剪切发热则增加内能,对于不可压缩流体,体积膨胀项为零。
采用计算流体动力学法对静压支承间隙油膜温度场和压力场求解,具体步骤如下:
1)利用UG建立间隙油膜三维模型。
2)将模型导入ICEM CFD中,采用功能强大的网格产生器ICEM CFD对流体进行结构化网格划分。
3)将 ICEM CFD生成的网格输出到ANSYS CFX-Pre中进行物理模型、材料属性和边界条件定义。
4)控制方程是基于有限体积法求解,对流项离散格式采用High Resolution求解控制方法,收敛标准以均方根残差(RMS)达到0.0001即为良好收敛结果。
求解计算并得到间隙油膜温度场和压力场,为摩擦副热变形和弹性变形计算提供体载荷。
旋转工作台和底座作为静压支承的摩擦副,其变形计算必须满足热固耦合控制方程和弹性变形方程。
考虑离心力润滑计算的雷诺方程形式:
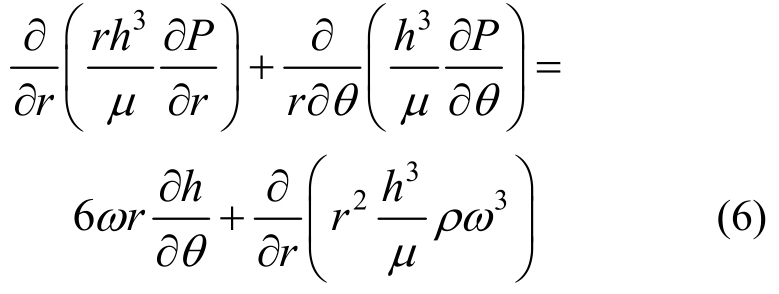
式中:P为流体压力;μ为流体黏度;h为油膜厚度;ω为角速度。
将上述求解得到的间隙油膜温度场作为体载荷加载到静压支承摩擦副的上、下表面,采用热固耦合方法求解支承摩擦副变形和应力。热固耦合控制方程如下[25]:
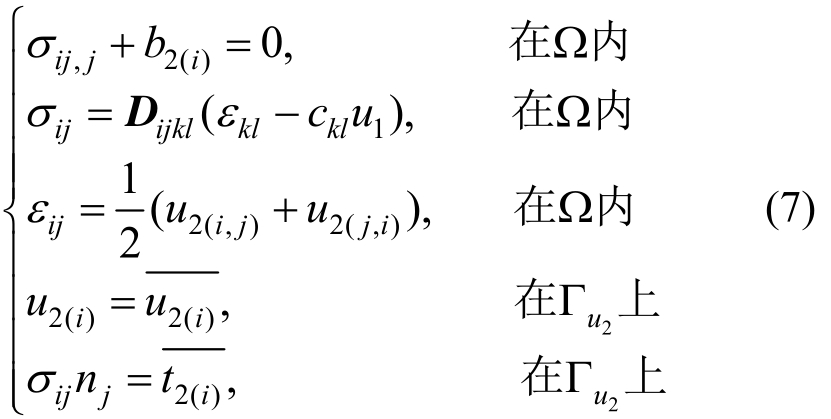
式中:Ω表示目标区域内;Γ为目标区域边界上;u2(i)为已知位移量;b2(i)为体积分量;Dijkl为结构弹性矩阵;εij、σij、ckl分别为应变、应力和热膨胀系数张量;应力σij为温度场u1下的函数,下标i和j表示对坐标的微分。
根据弹性力学理论可知,弹性表面上分布的压力p(x,y)在表面上各点产生的变形位移δ(x,y)为:
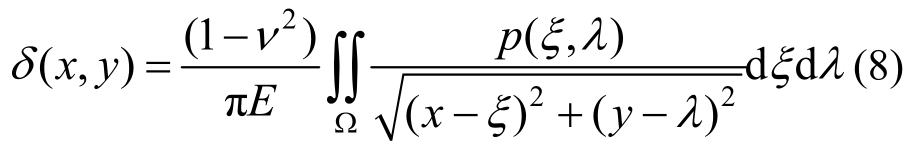
式中:ξ和λ对应于x和y的附加坐标表示节点压力;Ω指求解域为整个润滑平面;E为材料的弹性模量;ν为泊松比。
边界条件施加包括两个部分:力变形条件和热变形条件。力边界条件包括回转工作台回转中心固定约束,旋转工作台重力加速度施加以及油膜接触处导轨面油膜压力。热初始条件即所求工作台和底座温度场施加,润滑油和导轨面与底油垫热传导,另外,由于工作台高速旋转,其强制对流换热远远大于自然对流换热,故自然对流换热可忽略不计,只施加强制对流换热边界,底座静止不动,只有自然对流换热,无强制换热。具体边界条件设置如图2和图3所示。

图2 工作台变形边界条件
Fig.2 Boundary conditions of rotating workbench deformation

图3 底座变形边界条件
Fig.3 Boundary conditions of base deformation
数值模拟了入口流量60L/min、环境温度12℃、46号润滑油,旋转速度为10r/min、20r/min、30r/min、40r/min、50r/min、60r/min、70r/min和80r/min空载工况下支承摩擦副工作台和底座变形。限于篇幅,仅给出旋转速度10r/min和80r/min时工作台和底座的变形,如图4~图7所示。
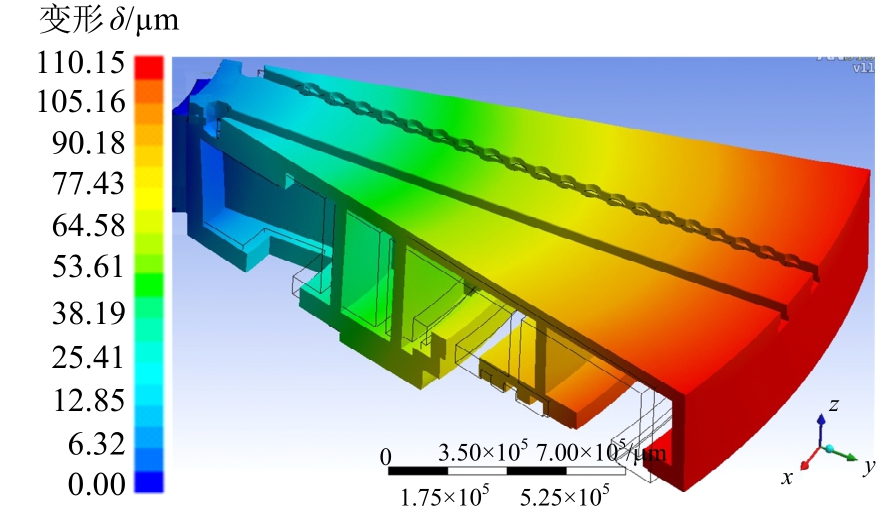
图4 10r/min旋转工作台变形场
Fig.4 Total deformation of rotating workbench at 10r/min
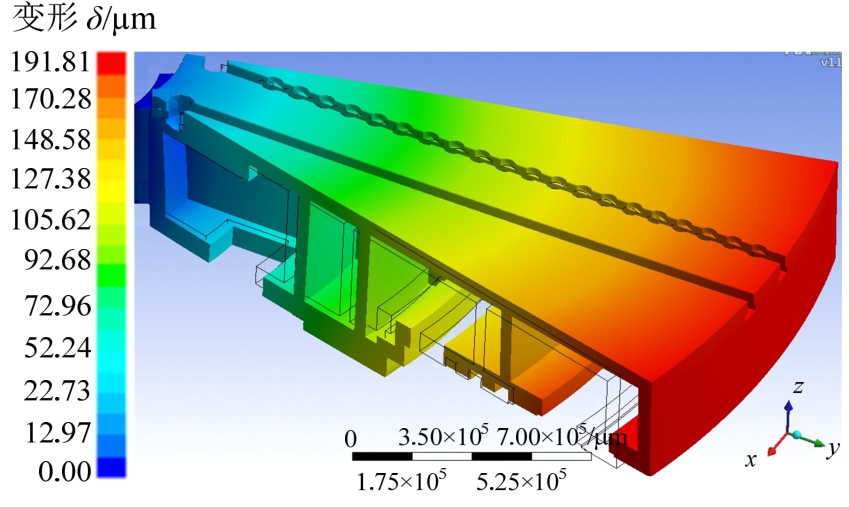
图5 80r/min 旋转工作台变形场
Fig.5 Total deformation of rotating workbench at 80r/min

图6 10r/min 底座变形场
Fig.6 Total deformation of base at 80r/min
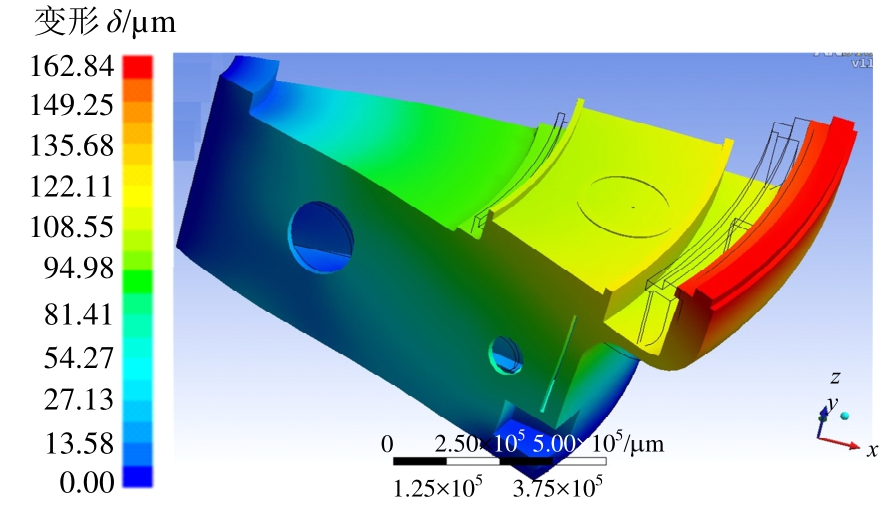
图7 80r/min底座变形场
Fig.7 Total deformation of base at 80r/min
由工作台变形图可知,温度分布不均匀产生的热变形使工作台边缘上翘,而力变形作用结果则使工作台四周下翻,工作台变为“半喇叭状”结构。从耦合效果可以发现,热变形影响大于力变形,工作台变形趋势倾向于热变形,最大变形量发生在工作台外缘下部,整体变形趋势随转速升高而增大。同时发现底座上热载荷分布并不均匀,外侧变形大于内侧,总体上为由内向外逐渐增大。底座热变形随着转速升高而增大,但转速上升到一定程度时,其变形量增加较快。最大变形出现在入油口处,究其原因此处润滑油膜较薄,油膜温升较快,导致温度分布不均,支承摩擦副变形较大。侧面由下到上变形量逐渐增大,最大变形出现在径向外缘顶部。旋转工作台和底座在流-热-力联合作用下的变形导致静压导轨和油腔接触部分靠近内圈处间隙变小,油膜变薄,靠近外圈处间隙变大,油膜变厚,径向由内向外油膜呈张口状,导致封油边外侧出油液阻急剧下降,油腔压力变小,间隙无油膜,致使工作台和底座间靠近导轨内侧部位发生边界润滑或干摩擦,导致静压轴承局部温升,油膜破裂,进而造成局部变形,发生摩擦失效。
为了验证数值模拟正确性,研制了静压支承摩擦副变形测量实验装置,实验在DVT500×50/150Q-NC双柱立式数控车床上进行,实验装置如图8所示。为了较准确地测量静压支承摩擦副变形,各安装6块千分表,每1/2圆周内外各3块,工作台变形测量装置如图9所示,图中数据单位为mm,底座测量装置如图10所示。

图8 实验装置
Fig.8 Test device

图9 工作台变形测量装置
Fig.9 Test device of rotating workbench deformation

图10 底座变形测量装置
Fig.10Test device of base deformation
为了探究旋转速度对摩擦副变形的影响,在旋转工作台自重25 t工况下进行了不同旋转速度时摩擦副变形测试实验,46号润滑油,流量为60L/min,油腔压力0.8 MPa,环境温度为12℃。实验数据与模拟数据对比见表1和表2。
从表1实验数据和模拟数据可以看出,随着工作台旋转速度的增加,旋转工作台整体变形逐渐增大,从工作台中心至边缘处变大趋势增加。由表2实验数据和模拟数据可以看出,随着工作台旋转速度的增加,底座整体变形逐渐增大,从底座中心至边缘处变大趋势增加。从实验数据和模拟数据又知,工作台变形呈上翘形式,而底座整体变形呈下翻形状,静压支承摩擦副变形为喇叭状,两者数据吻合较好,误差在3%以内。经实验验证不同流量下静压支承摩擦副变形规律一致。
表1 不同旋转速度工作台变形实验值与模拟值对比
Table1 Comparison between experimental and simulated deformations of rotating workbench under different rotational speeds /(×10-2mm)
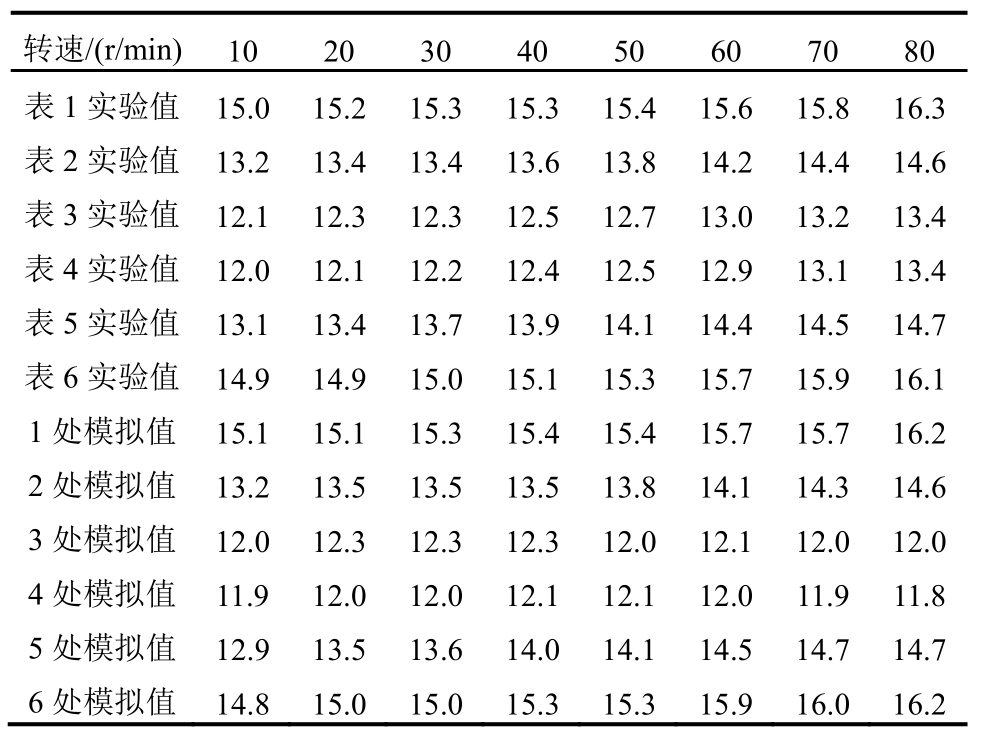
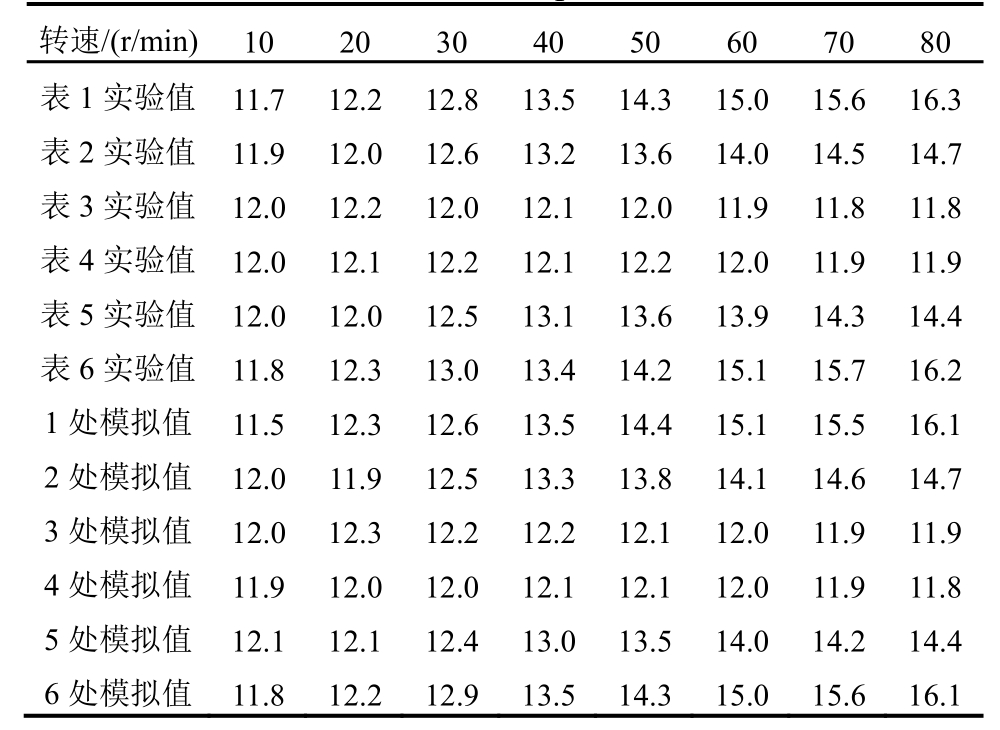
表2 不同旋转速度底座变形实验值与模拟值对比
Table2 Comparison between experimental and simulated deformations of base under different rotational speeds /(×10-2mm)
通过数值模拟和实验验证相结合的方法,进行了高速重型环形腔静压推力轴承支承摩擦副变形流热力耦合求解,得到了考虑工作台自重条件下静压支承摩擦副变形分布规律及速度载荷特性,揭示了高速重型静压支承摩擦学失效机理,实验验证理论计算和数值模拟所得结论的正确性。具体结论如下:
(1)根据计算流体动力学方法得到了静压支承间隙油膜的温度场和压力场,将其作为支承摩擦副流热力耦合体载荷。
(2)随着旋转工作台转速增加,旋转工作台和底座变形逐渐增大。
(3)在热变形和弹性变形耦合作用下靠近工作台内径边处向下变形,而沿着半径方向向外变形逐渐上翘,而底座变形正好与之相反,变形后工作台和底座形状类似于两个盘底相对。
(4)经计算发现,工作台上作用载荷产生的弹性变形对热变形有抵消作用,但其挤压效应会加大热变形,所以其综合作用仍然导致静压推力轴承工作条件恶化。
(5)高速重载工况下静压支承摩擦副产生不均匀变形,形成“喇叭”形状,液阻减小,局部形成了边界润滑或干摩擦,产生摩擦学失效,进而探明了此类支承摩擦行为和失效机理。
参考文献:
[1]张帆,钟海权,孙丽军,等.轴瓦热弹变形对大直径重载滑动轴承性能的影响研究[J].机械设计与研究,2014,30(2):59―64.Zhang Fan,Zhong Haiquan,Sun Lijun,et al.The performance study on thermo-elastic deformation of journal bearing with large diameter and heavy load[J].Machine Design and Research,2014,30(2):59―64.(in Chinese)
[2]陈凌珊,赵吉华,唐国兰.轴承弹性变形对动载滑动轴承润滑状况影响的分析[J].润滑与密封,2003(1):65―69.Chen Lingshan,Zhao Jihua,Tang Guolan.A analysis of the lubricating condition for the elastic deformation on dynamically loaded journal bearing[J].Lubrication Engineering,2003(1):65―69.(in Chinese)
[3]钟崴,崔敏,童水光.油膜润滑条件下滑动轴承变形与应力数值模拟[J].浙江大学学报(工学版),2012,46(7):1227―1232.Zhong Wei,Cui Min,Tong Shuiguang.Numerical simulation of deformation and stress in sliding bearing considering oil film lubrication[J].Journal of Zhejiang University(Engineering Science),2012,46(7):1227―1232.(in Chinese)
[4]孙军,王震华,桂长林.计入曲轴受载变形的粗糙表面曲轴轴承弹性流体动力润滑分析[J].机械工程学报,2009,45(1):135―140.Sun Jun,Wang Zhenhua,Gui Changlin.Elastohydrodynamic lubrication analysis of crankshaft bearing considering crankshaft deformation under load and roughness surface[J].Journal of Mechanical Engineering,2009,45(1):135―140.(in Chinese)
[5]蔡晓霞,孙军,刘利平,等.计及机体变形的内燃机主轴承弹性流体动力润滑分析[J].摩擦学学报,2010,30(2):118―122.Cai Xiaoxia,Sun Jun,Liu Liping,et al.Elastohydrodynamic lubrication analysis of main bearing for internal combustion engine considering block deformation[J].Tribology,2010,30(2):118―122.(in Chinese)
[6]彭晋民,王家序,余江波,等.水润滑塑料合金轴承的弹性变形及其影响[J].农业机械学报,2002,33(3):102―105.Peng Jinmin,Wang Jiaxu,Yu Jiangbo,et al.Elastic deformation of water lubricated plastic alloy bearings and its effect[J].Transactions of the Chinese Society for Agricultural Machinery,2002,33(3):102―105.(in Chinese)
[7]王建磊,李军杰,杨培基,等.动静压轴承温度场和热变形的仿真分析[C]// 第十届全国振动理论及应用学术会议论文集.南京:南京航空航天大学,2011:389―393.Wang Jianlei,Li Junjie,Yang Peiji,et al.Liquid hybrid bearing temperature field and thermal deformation simulation[C]// 10th National Vibration Technology and Application NVTA’2011.Nanjing:Nanjing University of Aeronautics and Astronautics,2011:389―393.(in Chinese)
[8]牛荣军,黄平.粗糙表面塑性变形对弹流润滑性能的影响[J].润滑与密封,2006:20―23.Niu Rongjun,Huang Ping.The influences of elasticplastic deformation of rough surfaces on elastohydrodynamic lubrication for line contacts[J].Lubrication Engineering,2006(6):20―23.(in Chinese)
[9]赵明,黄正东,陈立平.重型数控立车工作台静压计算与优化[J].中国机械工程,2008,19(22):2742―2747.Zhao Ming,Huang Zhengdong,Chen Liping.Hydrostatic pressure calculation and optimization of worktable for heavy duty CNC vertical turning mill[J].China Mechanical Engineering,2008,19(22):2742―2747.(in Chinese)
[10]王智伟,查俊,陈耀龙,等.流固耦合对油静压导轨动静特性的影响[J].机械工程学报,2015,50(9):148―152.Wang Zhiwei,Zha Jun,Chen Yaolong,et al.Influencing of fluid-structure interactions on static and dynamic characteristics of oil hydrostatic guideways[J].Journal of Mechanical Engineering,2015,50(9):148―152.(in Chinese)
[11]申峰,陈从连,刘赵淼.圆形静压油腔流场特性的PIV实验与数值模拟研究[J].工程力学,2015,32(1):226―233.Shen Feng,Chen Conglian,Liu Zhaomiao.PIV measurements and numerical simulation for flow characteristics in round hydrostatic oil cavity[J].Engineering Mechanics,2015,32(1):226―233.(in Chinese)
[12]刘志峰,湛承鹏,赵永胜,等.倾斜状态下静压油垫承载性能研究[J].工程力学,2015,32(5):208―212,220.Liu Zhifeng,Zhan Chengpeng,Zhao Yongsheng,et al.Research on the bearing performance of hydrostatic oil pad under tilting condition[J].Engineering Mechanics,2015,32(5):208―212,220.(in Chinese)
[13]Novikov E A,Shitikov I A,Maksimov V A.Calculation of the characteristics of a hydrostatic ring thrust bearing for refrigeration compressors[J].Chemical and Petroleum Engineering,2004,40(40):23―26.
[14]Canbulut F,Sinanoglu C,Yildirim S.Analysis of effects of sizes of orifice and pocket on the rigidity of hydrostatic bearing using neural network predictor system[J].KSME International Journal,2004,18(30):432―442.
[15]Hemmi M,Hagiya K,Ichisawa K,et al.Computation of thermal deformation of thrust bearing pad concerning the convection by non-uniform oil flow[C]// Proceedings of World Tribology Congress III,Washington,DC,Sept.12―16,ASME.Washington,D C,2005:61―62.
[16]Vakilian M,Abdolreza S,Nassab G,et al.CFD-based thermohydrodynamic analysis of rayleigh step bearings considering an inertia effect[J].Tribology Transactions,2004,57(1):123―133.
[17]Moldovan S I,Braun M J,Balasoiu A M.A three-dimensional parametric study and numerical/experimental flow visualization of a six-pocket hydrostatic journal bearing[J].Tribology Transactions,2013,56(1):1―26.
[18]斯坦斯菲尔德F M.静压支承在机床上的应用[M].北京:机械工业出版社,2003.Adam Stansfield F M.Application of hydrostatic bearing in machine tools[M].Beijing:China Machine Press,2003.(in Chinese)
[19]陈燕生.液体静压支承原理和设计[M].北京:国防工业出版社,1980.Cheng Yansheng.Principle and design of hydrostatic bearing[M].Beijing:National Defence Industry Press,1980.(in Chinese)
[20]丁振乾.液体静压支承设计[M].上海:上海科学技术出版社,1986.Ding Zhenqian.Design of hydrostatic bearing[M].Shanghai:Shanghai Science and Technology Press,1986.(in Chinese)
[21]章本照.流体力学数值方法[M].北京:机械工业出版社,2003.Zhang Benzhao.Numerical methods of fluid dynamics[M].Beijing:China Machine Press,2003.(in Chinese)
[22]ANSYS,Inc.ANSYS CFX-solver modeling guide[M].ANSYS,Inc.2007.
[23]王福军.计算流体动力学分析—FLUENT软件原理与应用[M].北京:清华大学出版社,2004.Wang Fujun.Calculation flow mechanics analysesfluent software principle and applies[M].Beijing:TsingHua University Press,2004.(in Chinese)
[24]韩占忠,王敬,兰小平.FLUENT流体工程仿真计算实例与应用[M].北京:北京理工大学出版社,2004.Han Zhanzhong,Wang Jing,Lan Xiaoping,The FLUENT fluid project simulates calculating an example and applies[M].Beijing:Press of Beijing Institute of Technology,2004.(in Chinese)
[25]左孔天,钱勤,赵雨东.热耦合结构的拓扑优化设计研究[J].固体力学学报,2005,26(4):447―452.Zuo Kongtian,Qian Qin,Zhao Yudong.Research on the topology optimization about thermostructural coupling field[J].Acta Mechanica Solid Sinica,2005,26(4):447―452.(in Chinese)
FLUID-THERMAL-MECHANICAL COUPLED SOLUTION AND EXPERIMENT ON DEFORMATION OF BEARING FRICTION PAIRS IN HYDROSTATIC BEARING
YU Xiao-dong,LIU Chao,ZUO Xu,ZHANG Yan-qin
(Mechanical Power & Engineering College,Harbin University of Science and Technology,Harbin 150080,China)
Abstract:The deformation of friction pairs has a significant influence on friction performance of hydrostatic bearing,and the non-uniform deformation will result in oil film rupture,dry friction,and even friction failure.The fluid-thermal-mechanical interaction model of oil hydrostatic bearing with annular slit restrictors is established.The deformation of hydrostatic bearing friction pairs has been solved through fluid-thermal-mechanical coupled method based on computational fluid dynamics,elastic theory and finite element method.The relationship among the deformation of hydrostatic thrust bearing and rotational speed and workbench weight is established,and its deformation distribution law is revealed.A test rig is established for testing deformation.The results show that the experimental data are basically identical with the simulation results,and demonstrate the validity of the proposed numerical simulation method.The results prove that the clearance oil film temperature of hydrostatic bearing rise sharply and the thermal deformation is also increasing with the increase of rotational speed.The thermal deformation are homogenized by the elastic deformation caused by the workbench weight,but the squeeze effect will increase the thermal deformation.The deformation of the rotating workbench and the base is like a trumpet.The inner edge is closing and outer edge is opening.By further increasing the rotational speed and load weight,the lubricating oil viscosity declines sharply,the oil film grows thin quickly,the bearing friction pair exhibitsuneven deformation,and the local bearing friction pairs sustain boundary lubrication or dry friction which may cause the friction failure.
Key words:hydrostatic thrust bearing;deformation of bearing friction pairs;high speed and heavy load characteristics;friction failure;fluid-thermal-mechanical coupled method
中图分类号:TU136
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.01.0049
文章编号:1000-4750(2018)05-0231-08
收稿日期:2017-01-12;修改日期:2017-09-12
基金项目:国家自然科学基金项目(51375123,51075106);黑龙江省自然科学基金项目(E2016040)
通讯作者:于晓东(1971―),男,黑龙江人,教授,博士,硕导,主要从事润滑理论及轴承研制方面的研究(E-mail:hustyuxiaodong@163.com).
作者简介:刘 超(1993―),男,黑龙江人,硕士生,主要从事润滑理论及摩擦学方面的研究(E-mail:liuchao1993@163.com);
左 旭(1994―),男,黑龙江人,硕士生,主要从事润滑理论及摩擦学方面的研究(E-mail:380430381@qq.com);
张艳芹(1981―),女,黑龙江人,教授,博士,硕导,主要从事润滑理论及轴承研制方面的研究(E-mail:yinsi1016@163.com).