
图1 桁架结构形式
Fig.1 Structure form of truss
李 天,晁进涛,樊 嘉
(郑州大学土木工程学院,郑州 450001)
摘 要:为研究腹杆对称布置的等腰三角形空间桁架的抗扭性能,以经典的自由扭转理论为基础,根据自由扭转变形的特点对桁架扭转变形关系进行了简化。给出了桁架的扭心位置、弹性抗扭刚度和屈服扭矩的计算方法,并分析了桁架破坏的机理。为验证桁架抗扭性能的计算方法,进行了桁架的扭转试验,试验构件弹性抗扭刚度和屈服扭矩的计算值和试验值的误差均小于10%。运用有限元方法对试验构件和计算方法进行了模拟和验证。结果表明:该文方法的计算值、试验值和有限元分析数值符合良好,该文的研究为等腰三角形空间桁架自由扭转提供了一种实用计算方法。
关键词:空间桁架;自由扭转;等腰三角形;抗扭刚度;扭心;屈服扭矩;理论分析;试验研究
对桁架结构分析时,桁架往往被视为杆系结构,简单明确。但将桁架作为一种构件,在结构系统中起到梁或其他类型构件的(如桁架梁、桁架柱等)作用时,就需要对桁架作为一种构件时的基本性能进行研究,抗扭性能是基本性能的重要组成部分。目前对桁架的研究主要侧重于抗弯和稳定性能[1−10],对抗扭性能的研究较少,对抗扭性能缺少深入的认知。目前对实腹式构件和组合构件抗扭性能的研究越来越多[11−18],但对桁架-混凝土组合构件的抗扭性能研究较少。对桁架构件的抗扭性能进行研究,也为研究桁架-混凝土组合构件的抗扭性能奠定基础,具有重要的理论意义和工程应用价值。
对扭心位置和抗扭刚度的研究,是研究桁架在弯扭联合作用下的受力性能和受纯弯作用时侧向失稳等问题的基础[19−22]。传统上对于桁架抗扭刚度的求解一般利用虚功原理和能量法[23],但求得的为数值解,未给出解析解,较难有效反映不同杆件对抗扭刚度影响的大小和机理。对扭心位置的确定一般仅考虑弦杆的作用,忽略腹杆的影响。
文献[24―26]对桁架的抗扭刚度进行了试验研究。文献[25―28]为简化求解过程,根据剪切刚度相等原则将杆件和复合材料等效为均质各向同性薄板。熊波[26]求得了等截面桁架的抗扭刚度,对扭心位置和屈服扭矩未进行理论分析。李国豪[27]研究了横截面为四边形的桁架抗扭性能。
综上,现有文献对桁架抗扭性能的研究主要针对横截面为四边形的桁架,而针对横截面为三角形的桁架研究较少,且对三角形桁架的抗扭性能研究仅限于等截面桁架弹性阶段的抗扭刚度,并未对其扭心位置、屈服扭矩和破坏机理进行研究,未对变截面桁架的抗扭性能进行研究。本文根据剪切刚度相等原则[27],利用桁架的内力平衡、几何变形、内力与变形间弹性关系和扭心的特点等条件,推导出桁架扭心位置、抗扭刚度和屈服扭矩的计算公式,并给出桁架破坏的机理。
本文以横截面为等腰三角形的倒立四棱锥空间桁架为研究对象,见图1,但不限于此类桁架,对于具有类似特征的桁架也适用。桁架几何尺寸为:节间长度相等均为s,宽度为a,高度为h;左、右侧面斜腹杆长度、截面均相同,截面面积为Af1,与下弦夹角均为θ1;上平面斜腹杆截面面积为Af2,与上弦夹角为θ2;左右侧面夹角为θ3;下弦、上弦和横杆截面面积分别为Ax、As和Ah;各个杆件的弹性模量均为E。

图1 桁架结构形式
Fig.1 Structure form of truss
分析基本假定:
1)横杆和斜腹杆为二力杆,仅承受轴力,不考虑失稳;
2)桁架受扭时扭矩由桁架腹杆承担,忽略弦杆自身的抗扭;
3)桁架为自由扭转,采用钢构件自由扭转截面形状不变假定;
4)符合小变形假定,且各个杆件的受力均在弹性范围内。
由假定2)~假定4),腹杆对称等腰三角形桁架自由扭转时,主要通过桁架腹杆来抵御扭转变形。因此,桁架的抗扭刚度可根据组成桁架三个面的剪切刚度得到。在桁架左右侧面内斜腹杆截面及倾角相等情况下,可以用图2所示的计算单元,来计算桁架左右侧面的剪切刚度K1和K3,对于上平面也可类似计算。
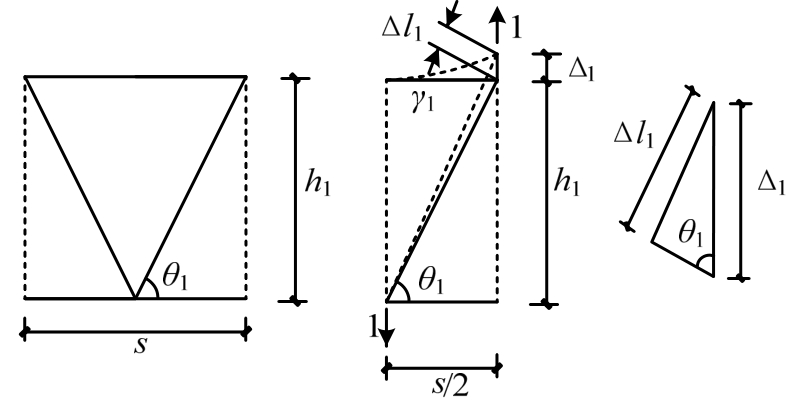
图2K1和K3计算简图
Fig.2 Calculation diagram ofK1andK3
图2中,左右侧面斜腹杆长度记为l1,轴力为:
斜腹杆轴向变形为:
由变形的几何条件可得竖向变形为:
剪切变形为:
由此得到左、右侧面剪切刚度K1、K3为:
上平面剪切刚度采用类似方法计算,K2为:
将桁架截面等价为三角形闭口截面,每个桁架面的腹杆等价为相应面的连续分布腹杆条,只有轴力(对于扭转来说就是桁架截面上的扭转剪力)[27];由假定3)可知,桁架在两端截面扭矩T作用下计算简图见图3。以扭转中心点C为零点建立直角坐标系x-y-z。图中x轴与桁架上平面平行,y轴与桁架上平面垂直,z轴为桁架纵向,对应于坐标轴x轴、y轴、z轴的位移分别表示为u、v、w。
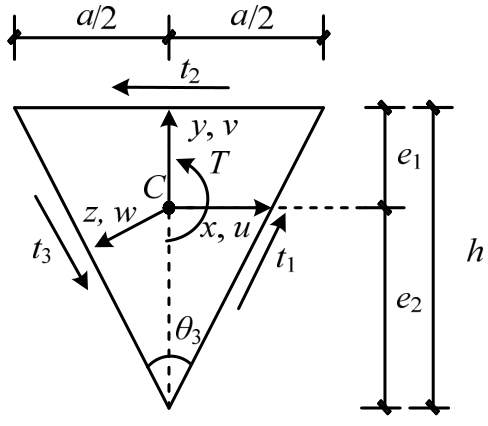
图3 计算简图(x-y-z坐标系)
Fig.3 Calculating diagram(x-y-zcoordinate system)
在扭矩T作用下,对应于桁架截面三个侧面上的剪力按均匀分布考虑,腹杆条轴力表示为t1、t2和t3,由平衡条件可得:
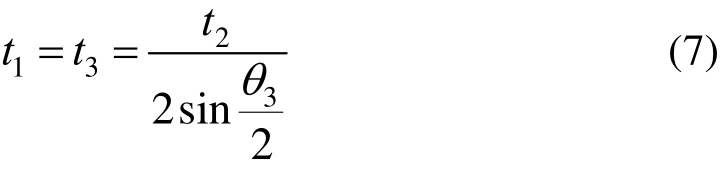
桁架三个侧面腹杆条轴力t1、t2、t3与桁架三个侧面腹杆条所对应的剪切变形γ1、γ2、γ3之间的关系可表示为:
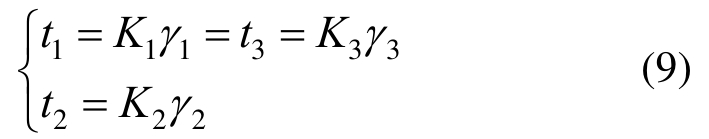
在图3直角坐标系x-y-z中,桁架截面在自由扭转时绕扭心C转动,扭转角为φ(z)时,截面任一点水平和竖向位移为:
桁架侧面剪切变形见图4。将桁架上平面沿x轴的位移表示为u2,则γ2为:
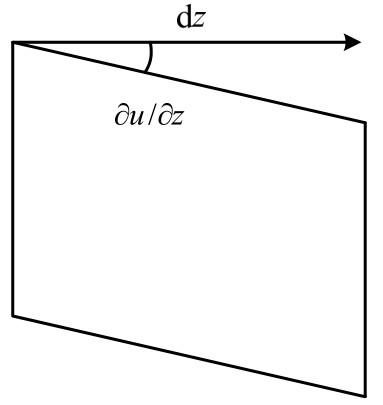
图4 侧面剪切变形
Fig.4 Shear deformation of side
为求右侧面的剪切变形,仍以扭转中心C作为零点,建立如图5所示的直角坐标系ξ-η-z,坐标轴ξ与右侧面垂直,η与右侧面平行,z轴与坐标系x-y-z中一致。桁架截面扭转角为φ(z)时,截面任一点沿ξ轴和η轴方向的位移分别为:

右侧面剪切变形γ1为:
式中,![]() 为右侧面沿η轴位移。
为右侧面沿η轴位移。
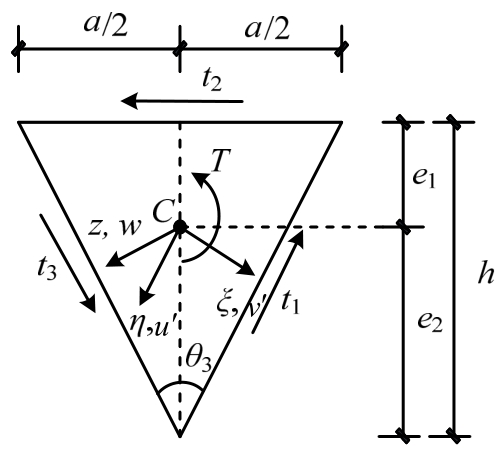
图5 计算简图(ξ-η-z坐标系)
Fig.5 Calculating diagram(ξ-η-zcoordinate system)
桁架沿y轴对称,扭心沿x轴的坐标为零,只需确定扭心沿y轴的坐标e1便可确定扭心的位置。
将式(9)、式(11)、式(13)代入式(7)得:
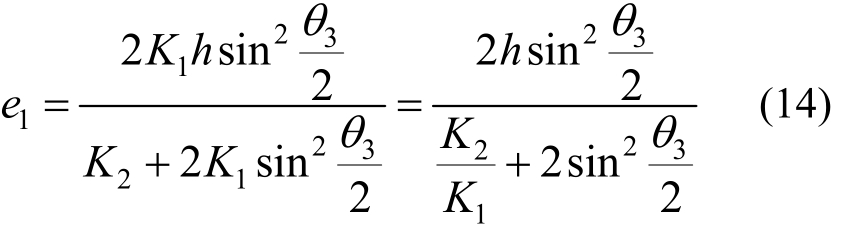
由式(14)可知:当h和θ3一定时,扭心位置主要与K2/K1有关,K2/K1无限小时,e1≈h,扭心位置接近下弦形心,K2/K1无限大时,e1≈0,扭心位置沿y轴接近上弦形心,即K2/K1越小扭心位置距上平面越远。
将式(11)代入式(9)可得:
将式(15)代入式(8)可得:
将式(14)代入式(16)得桁架抗扭刚度J为:
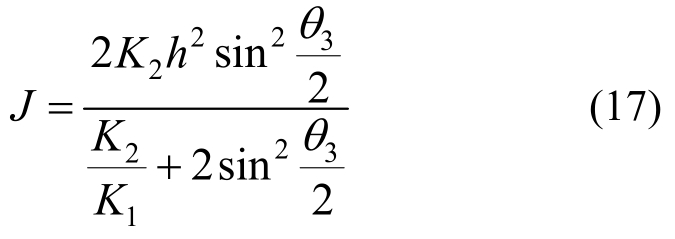
以上对横截面为等腰三角形且三个侧面中斜腹杆沿桁架纵向为等截面的桁架弹性抗扭刚度进行了分析,工程中为满足抗剪要求,沿桁架纵向斜腹杆可以采用不同的截面,本文中变截面桁架指沿桁架纵向斜腹杆截面面积不同的桁架,此类桁架的弹性抗扭刚度亦可用上述方法进行分析。
在1.1节中分析假定基础上,假定桁架不同截面具有不同的抗扭刚度且互不影响。定义整个桁架的抗扭刚度Jo为:扭矩T与桁架端部相对于整个桁架单位长度扭转角![]() 的比值。
的比值。
据此可得端部单位长度扭转角![]() 为:
为:
Jo为:

式中:l为桁架总长度;li为同一类型截面桁架的长度;Ji为li对应截面的抗扭刚度。
在工程应用中,不仅需要确定桁架的扭转刚度,往往还需要确定桁架的承载能力,这样对最不利面的判别具有重要的意义。桁架抗扭刚度分析过程可知,扭转产生的剪力由斜腹杆承担,故对于自由扭转的桁架屈服实质为斜腹杆的屈服,这里定义桁架最早屈服的斜腹杆所在的面为最不利面,屈服时的扭矩为整个桁架的屈服扭矩,记为Ty。
由于忽略上平面内横杆的抗剪刚度,由式(7)和式(8)可得:
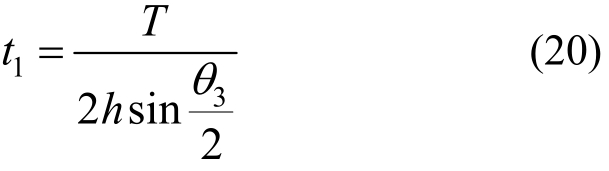
左、右侧面斜腹杆的轴力Nf1和Nf3为:
上平面斜腹杆的轴力Nf2为:
左、右侧面和上平面斜腹杆达到屈服强度时能承受的最大轴力Nf1max、Nf2max和Nf3max分别为:
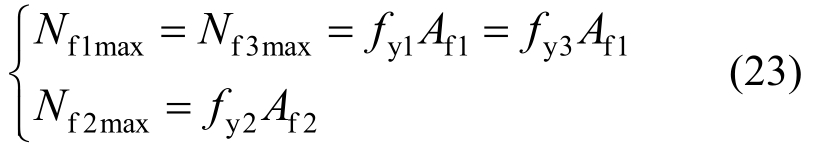
式中:fy1、fy2和fy3分别为三个面斜腹杆的屈服强度。
由式(20)~式(23)可得:
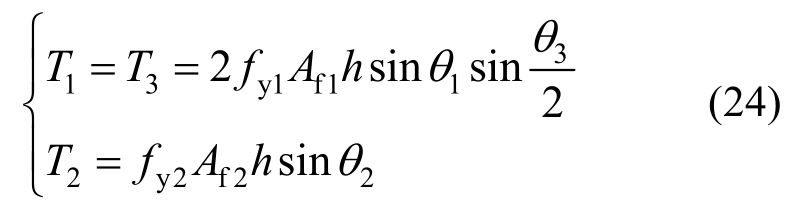
式中,T1、T2和T3分别为桁架左、右侧面和上平面斜腹杆屈服时所能承受的最大扭矩,三者当中最小者对应的面即为最先破坏的面,对应的扭矩即为桁架的屈服扭矩。Ty为:
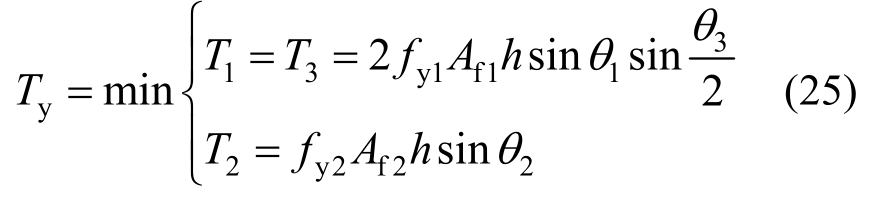
由等截面桁架屈服扭矩的分析过程可知,屈服扭矩主要和斜腹杆有关,变截面桁架的屈服扭矩可仍按式(25)计算,但需在三个面中分别找出最薄弱的截面,将对应截面的参数代入式(25)即可求得变截面桁架的屈服扭矩。
4.1.1构件设计
为对桁架抗扭性能理论分析的验证,设计了一个桁架进行试验。具体参数为:桁架杆件为圆钢管,材料为Q345B。构件总长度为2600mm,有效长度为2400mm,n=7;上弦截面为Φ50mm×5 mm,下弦截面为Φ70mm×4 mm,斜腹杆和横杆截面均为Φ42 mm×5 mm;s=a=h=400mm。杆件实测材料参数见表1。
表1 杆件材料参数
Table1 Material parameters of member

4.1.2 加载装置
为实施对三角形截面桁架的自由扭转试验,本文作者设计了一种加载装置,试验的加载方式采用在加载端一侧使用一个带有球铰的千斤顶以产生扭矩。加载端装置下部中间位置通过一个弧形的钢板和一个圆辊轴连接,可以实现钢桁架的扭转,加载试验装置见图6(a)和图6(d),固定端装置见图6(b)和图6(e)。
为了保证自由扭转,使试件在扭转加载中自由翘曲,需要释放构件纵向约束,故在固定端的上部和下部均设置辊轴。在两端部上弦和下弦位置处通过螺栓的紧固作用固定弦杆与加载端装置、固定端装置的相对位置,螺栓与弦杆接触位置垫有弧形的钢板,以减小螺栓对上弦杆的局部作用,而对弦杆纵向约束较小。整个试件加载见图6(c)和图6(f)。

图6 加载装置
Fig.6 Test set-up
4.1.3 加载制度
由式(25)计算知试验构件的屈服扭矩约为69.00kN·m。以杆件应变达到0.01或扭转角急剧增大作为构件的破坏标准,达到其中一个条件时认为构件破坏。加载过程采取荷载增量控制,荷载增量为每级4.2 kN·m,如出现应变或扭转角增加过快的情况,应减小荷载增量。
4.1.4 测点布置
在构件的5个截面布置扭率测点,如图7所示。扭率量测方法为:在同一截面两根上弦杆处布置位移计,量测两根上弦测点竖向位移差Δy,由式(26)计算测点所在横截面的扭转角φ,然后利用式(27)计算两个截面间的相对扭率φ'。
式(26)和式(27)中:Δφ为两个截面间扭转角差值;Δz为两个截面沿构件纵向长度差值;x轴、y轴和z轴具体方向见图3。

图7 扭率测点布置
Fig.7 Measuring points position of torsional curvature
通过实测,在斜腹杆屈服前,沿构件长度方向5个截面的扭转角基本按线性比例增大,不同荷载作用下沿构件纵向的扭转角见图8。即试验中,在相同扭矩作用下,构件的扭率为定值,这符合自由扭转的特征。
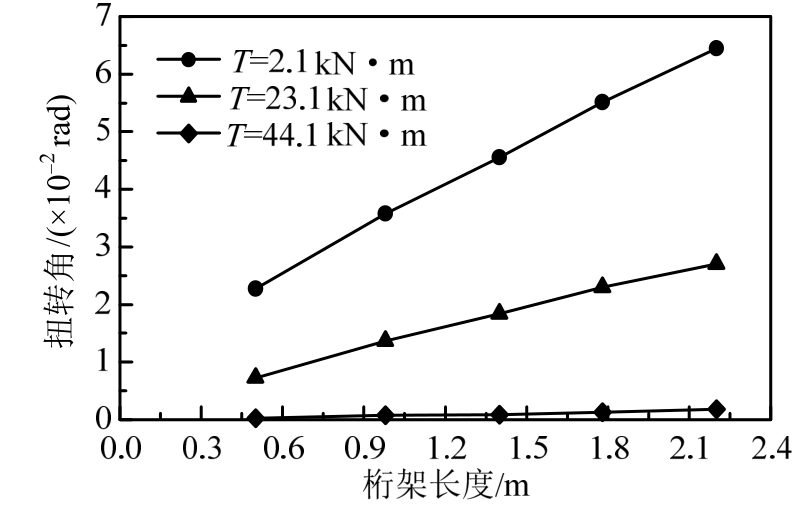
图8 扭转角沿桁架纵向变化
Fig.8 Longitudinal variation of torsional angle along the truss
构件的扭矩-扭率曲线见图9。可见,以扭矩-扭率表示的扭转变形曲线可分为两个阶段:阶段I,扭矩-扭率为直线,各个杆件均处于弹性阶段,构件抗扭刚度为定值;阶段II,三个平面相对较弱的上平面中斜腹杆首先屈服,扭矩-扭率出现明显的转折,扭率急剧增大。
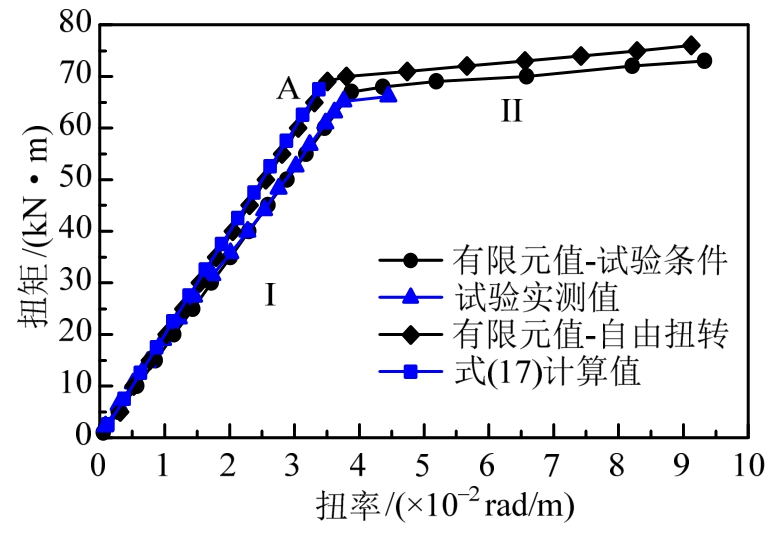
图9 扭矩-扭率曲线
Fig.9 Torque-torsional curvature curve
因试验构件受加载、约束以及连接等影响,试验条件与理论分析的基本假定并不完全相符。为此,采用有限元软件ANSYS建立了同试验条件一致的模型。在ANSYS模型中,弦杆选取beam189单元,斜腹杆和横杆选取Link8单元。材料为双线性随动强化模型,屈服强度取材料试验值。模型中固定端和加载端均与试验装置的约束相同,加载方式与试验相同,即在加载端施加扭矩。有限元模拟结果和试验实测值对比见图9(图中的有限元-试验条件曲线)。可见有限元模拟的结果与试验符合较好,两者抗扭刚度误差为4.60%。
由于受试验条件所限,试验加载装置不能保证试件扭转时绕试件的扭心转动,试件并不是纯扭。为对比试验结果与自由扭转的差异,采用有限元软件建立了构件自由扭转的模型。在有限元模型中,约束构件两端部的扭心,在构件两端施加等值反向的扭矩。将扭矩-扭率曲线绘于图9(图中有限元值-自由扭转曲线)。对比结果表明:式(17)计算值和有限元值-自由扭转间误差为2.51%。
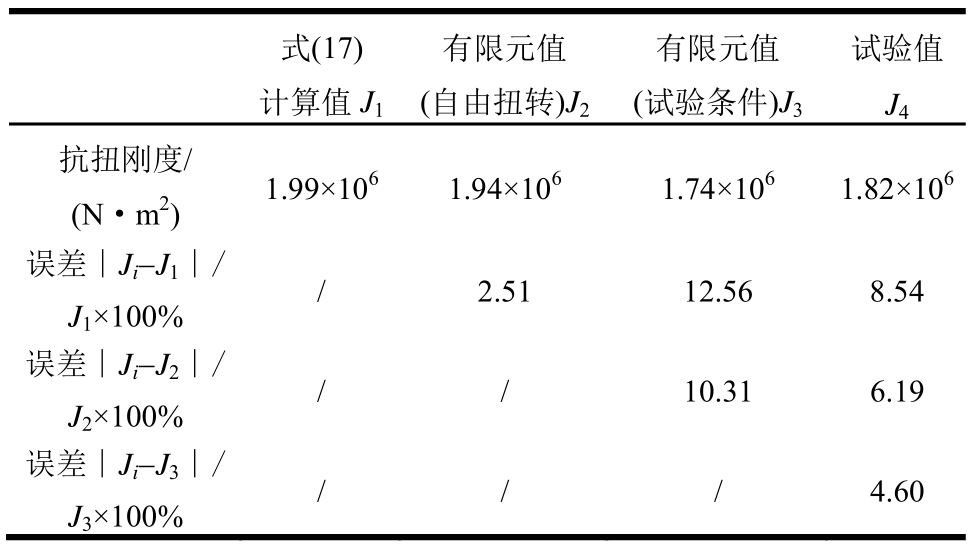
以上对比结果表明:试验实测值和有限元值-试验条件间误差较小;式(17)计算值和有限元值-自由扭转间误差较小;两种有限元模型模拟结果相比,同试验条件时的抗扭刚度小于自由扭转时的抗扭刚度;试验实测值小于式(17)计算值,详见表2。对比可见,试验值略低,而式(17)计算的结果略大,但相差均不大。
表2 试验构件弹性抗扭刚度对比
Table2 Comparison of elastic torsional stiffness of test member
为进一步验证桁架抗扭刚度计算式(17)的正确性,分别取4种桁架利用有限元对自由扭转时抗扭刚度验证,桁架的结构形式同试验构件,a和s均为500mm,h为变量,对应的宽高比范围为0.60~0.93,钢材屈服强度为345 MPa,上弦和横杆截面均为Φ42 mm×5 mm,下弦截面均为Φ70mm×5 mm。对比结果见表3。
有限元模拟结果表明:4种桁架抗扭刚度式(17)计算值和有限元值误差均小于5%,进一步验证了计算方法的可行性。
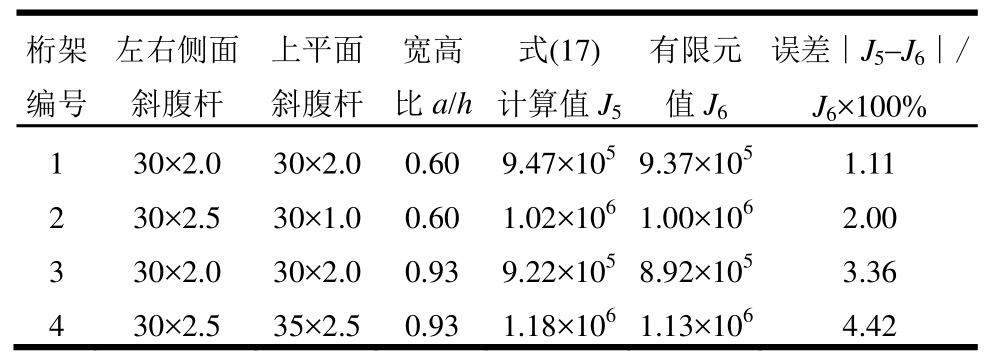
为验证变截面桁架抗扭刚度计算式(19),取4种桁架利用有限元进行验证,这4种桁架仅部分斜腹杆截面面积增大一倍,其余参数同试验构件,具体变化的斜腹杆和对比结果见表4。结果表明:式(19)计算结果和有限元值符合性较好。
表3 等截面桁架弹性抗扭刚度计算值和有限元值对比
Table3 Comparison of elastic torsional stiffness between calculated and FEM values of constant section truss
注:表中截面单位为mm;抗扭刚度单位为N·m2。
表4 变截面桁架弹性抗扭刚度理论值和有限元值对比
Table4 Comparison of elastic torsional stiffness between calculated and FEM values of variable cross-section truss
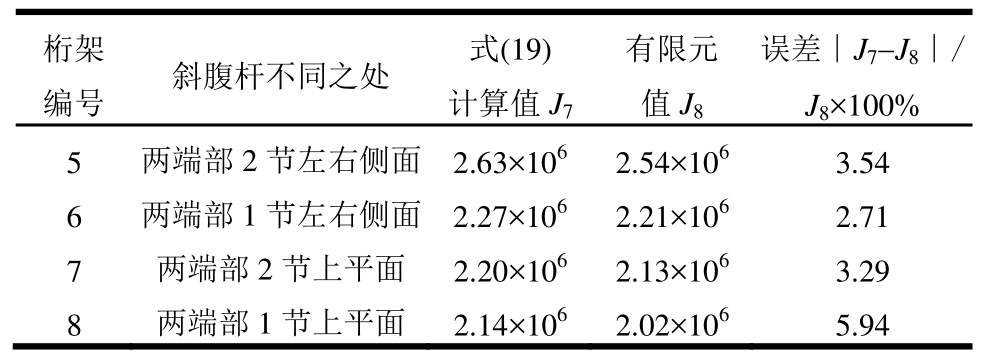
注:抗扭刚度单位为N·m2。
试验中当扭矩为63.00kN·m时上平面中临近两端部的斜腹杆达到屈服强度,对应图9中扭矩-扭率曲线中的A点,当扭矩为66.15 kN·m时,上平面全部斜腹杆达到屈服强度,扭率急剧增大。说明桁架从弹性向塑性发展很快,这是因为桁架斜腹杆的截面小,斜腹杆进入塑性时,整个桁架就进入了塑性阶段。这也验证了桁架以斜腹杆作为抗扭构件的假定。故在确定桁架的屈服扭矩时,可将桁架三个侧面中最早屈服的斜腹杆开始进入塑性作界限。同时一旦腹杆屈服,桁架的扭转变形将发展很快,故也将斜腹杆屈服时对应的扭矩作为桁架的极限扭矩。
试验构件屈服扭矩计算式(25)计算值、试验实测值和两种有限元模型模拟结果见表5。屈服扭矩间误差对比情况与抗扭刚度有类似的结果:相同条件的结果相近;自由扭转结果大于试验条件结果,按本文推导的式(25)计算值略大于试验值,但相差都不大。
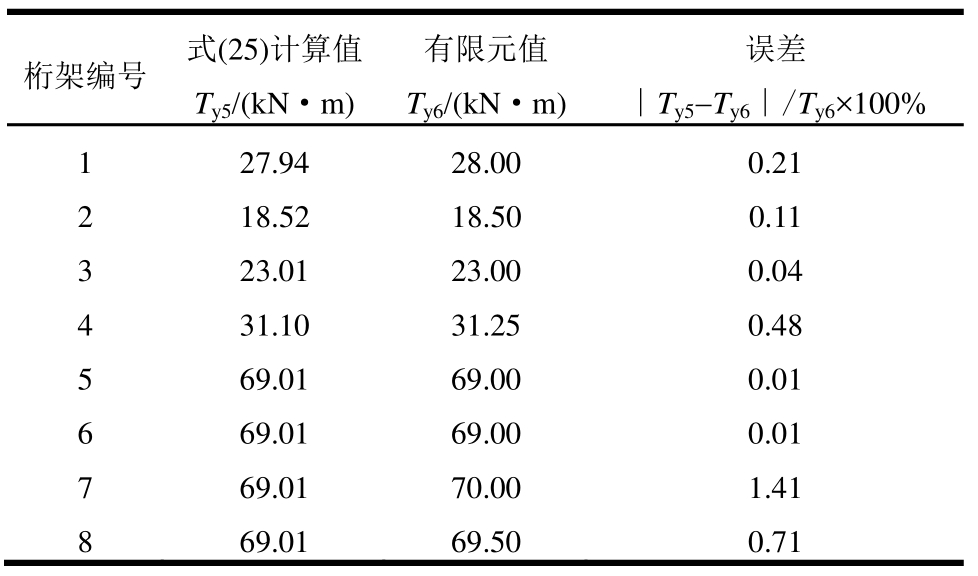
为进一步验证桁架屈服扭矩计算式(25)的正确性,同样取表3和表4中的8种桁架进行验证,对比结果见表6。
桁架1~桁架4对比结果表明:屈服扭矩的有限元值和式(25)计算值误差均较小,式(25)对等截面桁架屈服扭矩的计算是可行的。桁架5~桁架8对比结果表明:计算误差也较小,式(25)对变截面桁架同样适用。
表5 试验构件屈服扭矩对比
Table5 Comparison of yield torque of test member
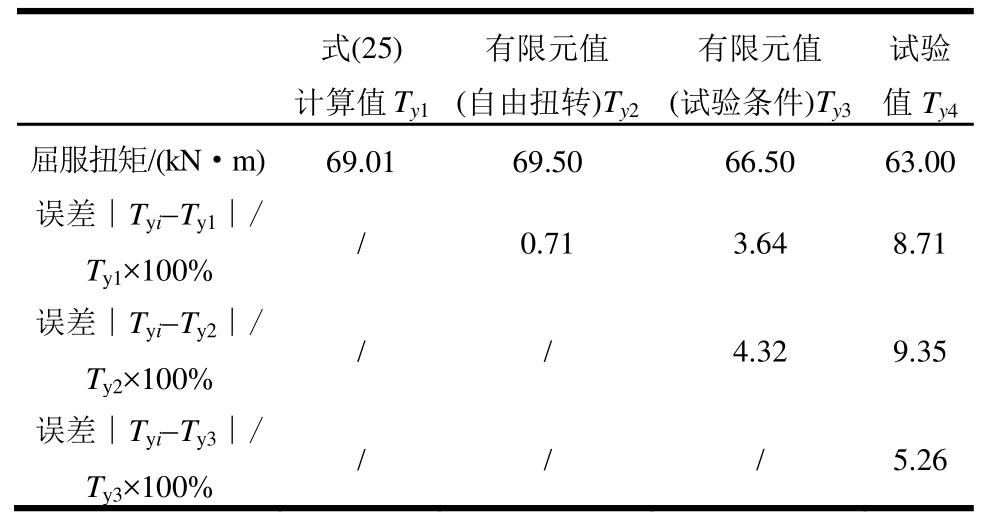
表6 屈服扭矩计算值和有限元值对比
Table6 Comparison of yield torque between calculated and FEM values
作用于桁架的扭矩,在扭心位置不产生挠曲而仅产生扭转。利用这一特性,通过对桁架端部施加扭矩,分别求出扭矩作用在端部横截面内沿y轴不同位置时扭矩作用点的偏移量,当偏移量最小时(接近于零)所对应的位置即为桁架的扭心。施加的扭矩取8 kN·m,使桁架处于弹性阶段。分析结果见图10,图中横坐标为桁架横截面内扭矩作用点距下弦形心的距离,纵坐标为加载端对应位置的偏移量。理论计算e2=288.83 mm,有限元模拟为270mm,两者误差为6.52%,验证了扭心位置计算方法可行。
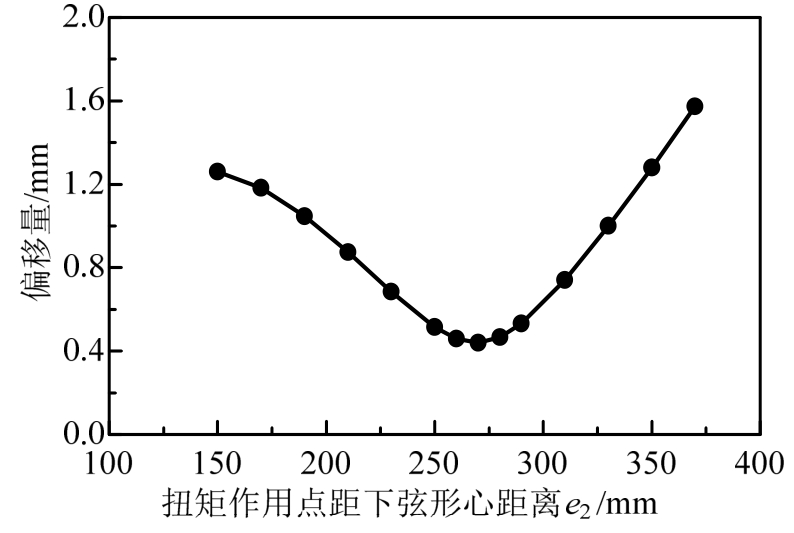
图10 扭矩施加在不同位置时扭心的偏移量
Fig.10 Displacement of torsion center when torque is applied at different positions
本文通过对工程中常见的等腰三角形空间桁架的抗扭刚度、屈服扭矩的理论分析,试验验证和有限元模拟分析,得到了如下结论:
(1)本文给出的等腰三角形的空间桁架扭心、抗扭刚度和屈服扭矩的计算方法,与试验和有限元分析结果符合性较好。
(2)本文以横截面为等腰三角形的倒立四方锥空间桁架为研究对象,得到了扭心位置、抗扭刚度和屈服扭矩的理论计算公式。从理论推导的过程,本文所提出的计算方法不限于倒立四方锥空间桁架,对于横截面为等腰三角形两侧腹杆对称布置的空间桁架均可适用。只需对组成空间桁架的三个平面桁架的抗剪刚度K1、K3和K2进行计算便可,且杆件截面不限于圆管。
(3)桁架扭转中心、扭转刚度和屈服扭矩,对于桁架构件的基本力学特性的确定具有重要意义。本文研究为桁架作为一种构件用于楼层或组合构件提供了理论基础。
参考文献:
[1]Pfeil M S,Teixeira A,Battista R C.Experimental tests on GFRP truss modules for dismountable bridges[J].Composite Structures,2009,89(1):70―76.
[2]何珊瑚.三肢钢管混凝土弦杆-钢管腹杆桁架抗弯力学性能研究[D].北京:清华大学,2012.He Shanhu.Flexural performance of three-main components concrete-filled steel tubular chord-steel tubular brace truss[D].Beijing:Tsinghua University,2012.(in Chinese)
[3]朱兰影,王志军,刘界鹏.蝶撑桁架梁跨中挠度的计算方法研究[J].工程力学,2016,33(5):184―192.Zhu Lanying,Wang Zhijun,Liu Jiepeng.Study on the deflection of butterfly-shaped clips truss girders[J].Engineering Mechanics,2016,33(5):184―192.(in Chinese)
[4]江克斌,丁勇,杨建奎,等.波形钢腹板PC组合箱梁纯扭作用下抗扭承载力试验研究[J].工程力学,2013,30(6):175―182.Jiang Kebin,Ding Yong,Yang Jiankui,et al.Experimental study on ultimate torsional strength of PC composite box-girder with corrugated steel webs under pure torsion[J].Engineering Mechanics,2013,30(6):175―182.(in Chinese)
[5]袁辉辉,吴庆雄,陈宝春,等.平缀管式等截面钢管混凝土格构柱荷载-位移骨架曲线计算方法[J].工程力学,2016,33(12):206―216.Yuan Huihui,Wu Qingxiong,Chen Baochun,et al.Calculation method of load-displacement skeleton curve for uniform sectional CFST lattice column with flat lacing tube[J].Engineering Mechanics,2016,33(12):206―216.(in Chinese)
[6]范栋浩,杜咏,盛红梅.高温下张弦梁结构力学特征解析解[J].工程力学,2016,33(4):195―204.Fan Donghao,Du Yong,Sheng Hongmei.Mathematical calculations for the characteristics of beam string structure in fire[J].Engineering Mechanics,2016,33(4):195―204.(in Chinese)
[7]文颖,孙明文,李特,等.杆系结构非线性后屈曲分析的增量割线刚度法[J].工程力学,2016,33(12):12―20.Wen Ying,Sun Mingwen,Li Te,et al.Nonlinear post-buckling analysis of truss structures using an incremental secant stiffness approach[J].Engineering Mechanics,2016,33(12):12―20.(in Chinese)
[8]Hou Chao,Han Linhai,Mu Tingmin,et al.Analytical behaviour of CFST chord to CHS brace truss under flexural loading[J].Journal of Constructional Steel Research,2017,134:66―79.
[9]Guo Yanlin,Chen Hang,Pi Yonglin.In-plane failure mechanisms and strength design of circular steel planar tubular Vierendeel truss arches[J].Engineering Structures,2017,151:488―502.
[10]Konkong N,Aramraks T,Phuvoravan K.Buckling length analysis for compression chord in cold-formed steel cantilever truss[J].International Journal of Steel Structures,2017,17(2):775―787.
[11]陈圣刚,许见超,郭全全,等.混凝土U形薄壁梁纯扭及弯扭承载力计算[J].建筑结构学报,2017,38(2):99―105.Chen Shenggang,Xu Jianchao,Guo Quanquan,et al.Ultimate bearing capacity of U-shaped thin-walled RC beams under pure torsion and bending-torsion interaction[J].Journal of Building Structures,2017,38(2):99―105.(in Chinese)
[12]王宇航,李硕,周绪红,等.弯-剪-扭耦合荷载作用下钢管混凝土短柱受力性能研究[J].建筑结构学报,2017,38(11):1―12.Wang Yuhang,Li Shuo,Zhou Xuhong,et al.Study on mechanical behavior of concrete filled steel tubular short columns under compound bending-shear-torsion load[J].Journal of Building Structures,2017,38(11):1―12.(in Chinese)
[13]Ding Y,Jiang K B.Nonlinear analysis for PC box-girder with corrugated steel webs under pure torsion[J].Thin-Walled Structures,2012,51(35):167―173.
[14]Tan E L,Uy B.Nonlinear analysis of composite beams subjected to combined flexure and torsion[J].Journal of Constructional Steel Research,2011,67(5):790―799.
[15]Lee E T,Yun B H,Shim H J,et al.Torsional behavior of concrete-filled circular steel tube columns[J].Journal of Structural Engineering,2009,135(10):1250―1258.
[16]Wang Y H,Nie J G,Fan J S.Theoretical model and investigation of concrete filled steel tube columns under axial force-torsion combined action[J].Thin-Walled Structures,2013,69(8):1―9.
[17]陈卓异,李传习,黄侨,等.波形钢腹板组合槽形梁抗扭性能试验研究[J].工程力学,2017,34(3):108―114.Chen Zhuoyi,Li Chuanxi,Huang Qiao,et al.Experimental study on torsional property of composite trough girder with corrugated steel webs[J].Engineering Mechanics,2017,34(3):108―114.(in Chinese)
[18]董桔灿,吴庆雄,陈康明,等.波形钢腹板(钢腹杆)-混凝土组合箱抗扭承载力试验与计算[J].工程力学,2016,33(11):220―230.Dong Jucan,Wu Qingxiong,Chen Kangming,et al.Experiment and calculation on torsion bearing capacity of concrete composite box section with corrugated steel webs and steel truss webs[J].Engineering Mechanics,2016,33(11):220―230.(in Chinese)
[19]赵文艳,刘文洋,张文福.正交正放类网架结构分析的分解刚度法[J].计算力学学报,2007,24(5):689―692.Zhao Wenyan,Liu Wenyang,Zhang Wenfu.Splitting rigidity method for analysis of orthogonal and ortho-laid double-layer space grids[J].Chinese Journal of Computational Mechanics,2007,24(5):689―692.(in Chinese)
[20]陈骥.钢结构稳定理论与设计[M].北京:科学出版社,2008.Chen Ji.Stability of steel structures theory and design[M].Beijing:Science Press,2008.(in Chinese)
[21]赵思远,郭彦林,窦超.倒三角截面空间桁架拱平面外弹塑性稳定设计方法研究[J].工程力学,2014,31(9):71―80.Zhao Siyuan,Guo Yanlin,Dou Chao.Out-of-plane strength and design of space truss arches with triangular sections[J].Engineering Mechanics,2014,31(9):71―80.(in Chinese)
[22]黄政华,张其林,杨宗林,等.平面钢管桁架的面外稳定分析模型研究[J].土木工程学报,2011,44(5):49―56.Huang Zhenghua,Zhang Qilin,Yang Zonglin,et al.Study of model for out-of-plane stability of planar tubular trusses[J].China Civil Engineering Journal,2011,44(5):49―56.(in Chinese)
[23]余佳亮.无站台柱张弦桁架雨棚结构性能分析与倒塌模拟研究[D].杭州:浙江大学,2012.Yu Jialiang.Performance analyze and collapse research of non-platform-column truss string shelters[D].Hangzhou:Zhejiang University,2012.(in Chinese)
[24]Zhang Dongdong,Huang Yaxin,Zhao Qilin,et al.Evaluation of the torsional mechanism by analytical solution for a hybrid fiber-reinforced polymer-aluminum triangular deck truss beam[J].Advances in Structural Engineering,2016,19(5):871―879.
[25]Weaver T J,Jensen D W.Mechanical characterization of a graphite/epoxy iso truss[J].Journal of Aerospace Engineering,2000,13(1):23―35.
[26]熊波,罗锡林,谭惠丰.全复合材料桁架扭转刚度分析[J].复合材料学报,2015,32(2):501―507.Xiong Bo,Luo Xilin,Tan Huifeng.Analysis of torsional stiffness of all-composite truss[J].Acta Materiae Compositae Sinica,2015,32(2):501―507.(in Chinese)
[27]李国豪.桁梁扭转理论:桁梁桥的扭转、稳定和振动[M].北京:人民交通出版社,1975.Li Guohao.Torsion theory of truss beam:torsion,stability and vibration of truss bridge[M].Beijing:China Communications Press,1975.(in Chinese)
[28]Li M,Wu L Z,Ma L,et al.Torsion of carbon fiber composite pyramidal core sandwich plates[J].Composite Structures,2011,93(9):2358―2367.
THEORETICAL AND EXPERIMENTAL STUDY ON FREE TORSION OF ISOSCELES TRIANGULAR SPACE TRUSS
LI Tian,CHAO Jin-tao,FAN Jia
(School of Civil Engineering,Zhengzhou University,Zhengzhou 450001,China)
Abstract:On the basis of classical theory of free torsion and the deformation characteristics of a truss,the torsional deformation is simplified to study the torsional behaviors of isosceles triangular space trusses with symmetrically-distributed web members.The methods of calculating torsional center,elastic torsional stiffness,and yield torque of a truss are proposed,and the mechanism of truss failure is analyzed.In order to verify the calculation method of the torsional behaviors of a truss,the torsional test of a truss is done,and the error between the value of calculating elastic torsional stiffness and the test value of the test member is less than 10%,the same as a yield torque.The Finite Element Method(FEM)is employed to simulate and verify the test member and calculation method.The results show that the calculation values,test values and FEM values are well consistent with each other.A practical calculation method is proposed for the free torsion of isosceles triangular space trusses.
Key words:space truss;free torsion;isosceles triangle;torsional stiffness;torsion center;yield torque;theoretical analysis;experimental study
中图分类号:TU391
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.12.0984
文章编号:1000-4750(2018)05-0223-08
收稿日期:2017-12-26;修改日期:2018-03-15
基金项目:国家自然科学基金项目(51478437);郑州市重大科技专项项目(152PZDZX033)
通讯作者:晁进涛(1986―),男,河南人,博士生,主要从事钢结构和组合结构研究(E-mail:04.tumu@163.com).
作者简介:李 天(1960―),男,浙江人,教授,博士,博导,主要从事钢结构和组合结构研究(E-mail:litian@zzu.edu.cn);
樊 嘉(1989―),男,河南人,博士生,主要从事钢结构和组合结构研究(E-mail:zzufanjia@126.com).