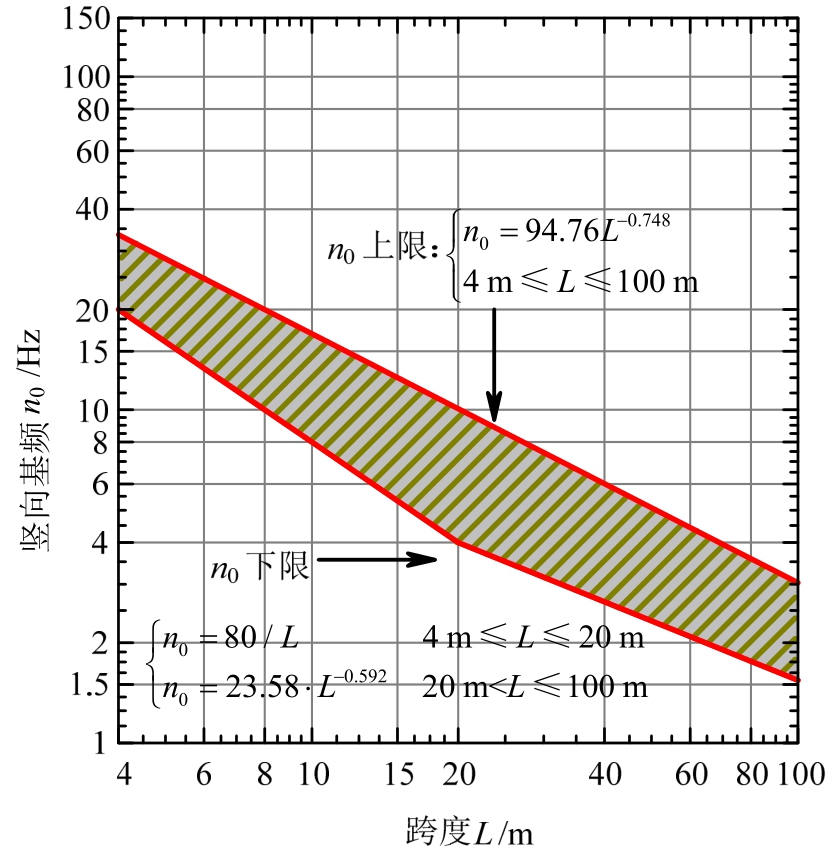
图1 欧盟及UIC 规范规定的不同跨度简支梁竖向基频限值[1]
Fig.1 The UIC code of the vertical basic frequency limit of simply supported beam with different spans[1]
李小珍1,邱晓为1,刘德军1,2,秦 羽1
(1.西南交通大学桥梁工程系,四川,成都 610031;2.嘉兴学院建筑工程学院,浙江,嘉兴 314001)
摘 要:建立有限元模型,计算常用跨度预应力混凝土简支箱梁的竖向基频,以设计荷载对桥梁的动力效应不小于运营列车对桥梁的动力效应为准则,确定梁体容许动力系数;基于移动荷载模型,得到常用跨度简支箱梁在列车作用下的动力系数;在综合分析桥梁动力响应与列车类型、运营速度、桥梁竖向基频关系的基础上,提出了时速400km/h常用跨度预应力混凝土简支箱梁的竖向基频限值。研究表明:通过调整车长与桥梁跨度之比可避开基阶振型的共振,有利于行车安全;在车长25 m左右的列车作用下,跨度24 m、32 m和40m的预应力混凝土简支箱梁竖向自振基频限值取125/L、155/L和90/L时,可以有效地降低梁体动力响应。
关键词:高速铁路;简支箱梁;竖向基频限值;移动荷载;400km/h;动力系数
列车以一定速度通过简支梁时,对桥梁的作用类似于频率固定的激振源。当列车速度改变时,相应的激振频率亦发生变化。当简支箱梁的竖向自振频率与激振频率接近时,将会导致共振现象,进而引发道床不稳定、钢轨损伤、混凝土开裂,甚至危及桥梁的安全。而高速铁路桥梁结构竖向基频是结构体系刚度和列车作用下梁体动力效应的综合反映,一方面可以保证列车的运行安全及舒适性,另一方面可以优化结构,降低结构工程的造价,因此研究高速铁路梁体竖向自振基频具有重要意义。
目前国外关于铁路桥梁设计荷载及基频限值方面的研究主要分为两类:一类以国际铁路联盟为代表,一类以日本为代表。国际铁路联盟以保证桥梁不产生共振以及实际运营荷载产生的内力不超过设计值为原则,通过控制桥梁的竖向自振频率来控制梁体实际的动力系数,保证梁体的设计安全。不同跨度简支梁竖向基频限值规定如图1所示[1]。国际铁路联盟规范的动力系数中不包含速度相关效应,仅与跨度有关,对于跨度一定的简支梁其值是一定的,简单易用;通过对梁体竖向基频的控制即可轻易地初拟桥梁结构的断面形式。

图1 欧盟及UIC 规范规定的不同跨度简支梁竖向基频限值[1]
Fig.1 The UIC code of the vertical basic frequency limit of simply supported beam with different spans[1]
相比之下,日本规范包含速度效应,梁设计标准采用近似运营列车的H荷载作为活载图式,动力系数按式(1)取值,其中ia、ic分别表示连续移动荷载的速度效应及车辆摇摆引起的冲击效应[2]。速度效应的冲击系数ia与列车类型和速度参数α有关,式(2)为速度参数α的表达式。当速度参数α>0.33时,将引起较大冲击。
式(2)中:v/(km/h)表示列车或车辆的最高速度:n/Hz表示构件的自振频率:Lb/m表示构件的跨度。
国内外学者针对铁路车桥系统的共振机理和共振条件做了大量的研究。Siringoringo和Fujino[3]采用有限元的方法来研究移动列车作用下桥梁的强迫和自由振动,与数值方法相比可以得到足够可靠的结果;Gao等[4]采用理论分析与数值模拟相结合的方法,提出了一种改进的计算桥梁基本频率的公式;松浦章夫[5]利用二系悬挂多刚体车辆模型分析了列车质量、轴距、连挂数目等因素对桥梁冲击系数的影响,给出了桥梁共振时列车的计算公式。Fryba[6]将列车简化为移动荷载模型,采用理论方法推导了列车通过匀质等截面简支梁桥时引起桥梁共振的临界车速的计算公式。夏禾等[7]通过理论推导和分析实例研究列车以一定速度通过桥梁时,车桥系统的共振机理和发生共振的条件。沈锐利[8]针对高速铁路线上简支梁桥,指出了简支梁振动响应较大的跨度及频率范围,初步提出了避免共振及减小振动的技术措施。宁晓骏等[9]应用车辆-桥梁耦合振动理论,讨论和分析了跨径布置和共振的相互关系。郭文华和路萍[10]运用列车桥梁空间振动时域分析方法,研究了TMD(Turned Mass Damper)不同参数对箱梁振动控制的效果。
速度是现代交通的命脉,我国已开通运营设计时速300km/h~350km/h的多条高速铁路,发展运营设计时速400km/h及以上的高速铁路成为下一步的趋势,但是我国现有的高速铁路设计规范最高设计时速为350km/h。该文针对设计时速400km/h常用跨度24 m、32 m、40m铁路预应力混凝土简支箱梁,基于移动荷载数值模型,通过动力仿真分析、计算运营典型列车(CRH2、CRH3、ICE2和ЭР200号列车)及HSLM(High Speed Load Mode)移动荷载以不同速度通过简支梁时,不同自振基频梁体的动力响应,以设计荷载对桥梁的动力效应不小于运营列车对桥梁的动力效应为准则,确定简支箱梁的竖向自振基频限值。
列车以一定的速度通过桥跨结构时,桥梁的竖向冲击效应主要来自两个方面:列车轴重组成的移动荷载列的速度效应及轨道不平顺与桥梁振动激发的车辆振动效应[11]。根据欧洲规范[12],仿真计算外部激励下桥梁结构的动态响应时,实际列车的动力效应可以以移动荷载列来代替,车-桥之间的相互作用可以忽略。同时,沈锐利[8]比较了移动荷载列模型与车-桥耦合模型作用下简支梁的动态性响应,两者图形形状比较一致,峰值个数与位置基本一致,说明了它们所反映的振动响应特征基本是一致的。车辆的振动效应必须借助复杂的车桥耦合程序分析,相比之下,对移动荷载速度效应的分析则简便宜行,且能很好地反映列车荷载作用下桥梁动力响应的变化规律,对桥梁的设计具有很强的指导意义。
该文采用移动荷载分析模型,该模型不考虑车辆的振动效应,可以较好地反映出列车对桥梁的周期性激励规律[6,13]。选择不同竖向基频的桥梁模型,通过计算列车以不同速度通过时桥梁的动力响应,在综合分析桥梁动力响应与列车类型(轴重、轴距和车长),运营速度,桥梁刚度(竖向基频)关系的基础上,确定梁体竖向基频合理限值。
建立任意移动荷载作用下简支梁桥竖向振动数学模型,桥梁模型考虑欧拉-伯努利梁模型,列车荷载简化为一系列具有一定间距的移动常量力。假设简支梁为等截面(EI为常数),截面细部尺寸如图2所示,梁体质量均匀分布(单位长度梁的质量m为常数),阻尼为黏滞阻尼c(即阻尼力与结构的振动速度成正比),阻尼效应和质量及刚度性质成正比,荷载列以匀速v在梁上通过,梁的运动满足弹性范围内的小变形理论。受力模型如图3所示,移动荷载作用下简支梁桥竖向振动响应分析详见文献[14],限于篇幅,该文不再赘述。运营列车参数详见表1,其中Lv表示车辆全长(钩到钩间的距离),Lc表示车辆定距,Lw表示转向架固定轴距。

图3 移动荷载列作用于简支梁
Fig.3 Moving loads acting on simply supported beam
表1 车辆参数
Table1 Vehicle parameters

该文通过调节梁体截面高度来改变其刚度,建立有限元模型,计算简支箱梁的竖向自振频率,并定义简支箱梁的竖向自振基频计算公式:
式中:m指基频系数;L为桥梁跨度。
动力系数是桥梁设计过程中一项非常重要的参数。列车对桥梁结构的动力作用,不仅和桥梁结构本身的振动特性有关,而且还取决于运行列车的车辆类型、振动特性以及行车速度,同时还和桥上线路的状态有关,动力系数是以上各种因素的综合反映。而制定桥梁基频限值的关键在于对桥梁的动力系数机理的研究,只有掌握了桥梁的动力系数变化规律,才能根据对桥梁振动控制的要求确定相应的结构竖向基频限值。
高速铁路竖向荷载设计图式是桥梁设计的基础。鉴于我国客运专线桥梁设计活载图示和动力系数是在欧盟规范基础上制定的[15],根据式(4)和式(5)以设计荷载对桥梁的动力效应不小于运营列车对桥梁的动力效应为准则,确定各列车作用下梁体的容许动力系数。
式(4)中的1+φ为对应列车活载相应的容许动力系数;式(5)为对应ZK活载相应的动力系数,Lφ/m表示加载长度,简支梁取梁的跨度。
移动荷载作用下,对各跨度简支箱梁进行有限元静力计算,得到各跨度简支箱梁的容许动力系数,如表2所示。从移动荷载作用下不同跨度梁体容许动力系数对比图(图4)可以看出:容许动力系数随着跨度的增加总体呈增大趋势。
表2 容许动力系数
Table2 The allowable impact factor


图4 移动荷载作用下不同跨度梁体容许动力系数对比
Fig.4 Comparison of allowable impact factors of different span under moving loads
基于移动荷载通过简支箱梁的数值模型,对不同竖向自振基频的梁体进行动力仿真研究,动力分析中采用Rayleigh阻尼。移动列车作用下,桥梁结构的动力响应峰值主要取决于阻尼比,为偏于安全设计,参考欧洲规范[12],针对预应力混凝土简支箱梁采用阻尼比的最低限值1%进行动力仿真分析。
理论研究表明[7]:当列车以速度v通过桥梁时,由于其轴重荷载的规则性排列,会对桥梁产生周期性的动力作用。对于常用中小跨度简支梁,列车对桥梁的竖向激振频率主要取决于列车的速度v/(km·h-1)和列车长度dv/m,激振频率为:
由式(6)可知,对于列车长度一定的荷载列,激振频率随列车速度的变化而变化,当激振频率等于桥梁竖向自振基频的1/i,(i=1,2,3,…)时,会使桥梁结构发生共振或超谐共振,此时列车速度为:
定义式(7)中的vbr,1为桥梁共振速度,vbr,2、vbr,3……为2、3……阶超谐共振速度,实际中,当i≥3时引起的桥梁谐振响应很小,在此不作讨论。
以车长25 m的CRH2型列车为例,列车作用于竖向自振基频为120/L的简支箱梁,如图5所示,通过对不同列车速度条件下简支箱梁动力系数和竖向振动加速度对比可以看出,较大的动力响应发生在24 m跨度工况,此时桥梁跨度与车长基本相当;对32 m、40m跨度工况,梁体动力响应均出现峰值,但40m跨度工况,梁体动力响应峰值较小;同一跨度下梁体的动力系数和竖向振动加速度曲线变化基本一致;对于竖向自振基频一定的简支箱梁,当列车速度接近某一确定速度时,将引起桥梁产生较大的动力响应。

图5 CRH2型列车作用下不同跨度桥梁动力响应对比
Fig.5 The dynamic response comparison of the bridges under the action of CRH2
根据式(6)和式(7)可得:车长为25 m的CRH2型列车的激振频率fv=0.011v,图5中跨度24 m、32 m、40m简支箱梁竖向自振基频分别为5.00Hz、3.75 Hz和3.00Hz,理论共振速度如表3所示。根据图5仿真动力曲线:CRH2型列车作用下,使24 m、32 m和40m跨度简支箱梁动力响应达到最大值的运行速度分别为440km/h、340km/h和270km/h,此时列车激振频率与梁体竖向自振基频的比值分别为0.98、1.01和1.00,发生共振,数值模拟与理论分析一致;梁体在2阶超谐共振速度下的动力响应远小于共振速度下的动力响应。所以高速铁路设计中,主要通过控制简支箱梁的竖向自振频率避开列车的激振频率,控制梁体竖向共振现象的发生。
表3 理论共振速度
Table3 Theoretical resonance velocities

通过调节简支箱梁的截面高度,改变梁体竖向自振基频,图6为不同跨径工况下简支箱梁竖向基频与梁体刚度的关系曲线。由图可知:简支箱梁的刚度越大,其竖向基频越大;相同竖向基频条件下,简支箱梁跨度越大,其抗弯刚度亦越大。
理论研究表明,为保证移动荷载对简支箱梁的动力效应不超过设计值,简支箱梁应满足一定自振基频(刚度)的要求,为量化分析梁体自振基频(刚度)对其动力系数的影响,图7列出了运营列车作用下不同跨度简支箱梁竖向基频由120/L提高至160/L时的梁体动力系数特征曲线。可以看出:
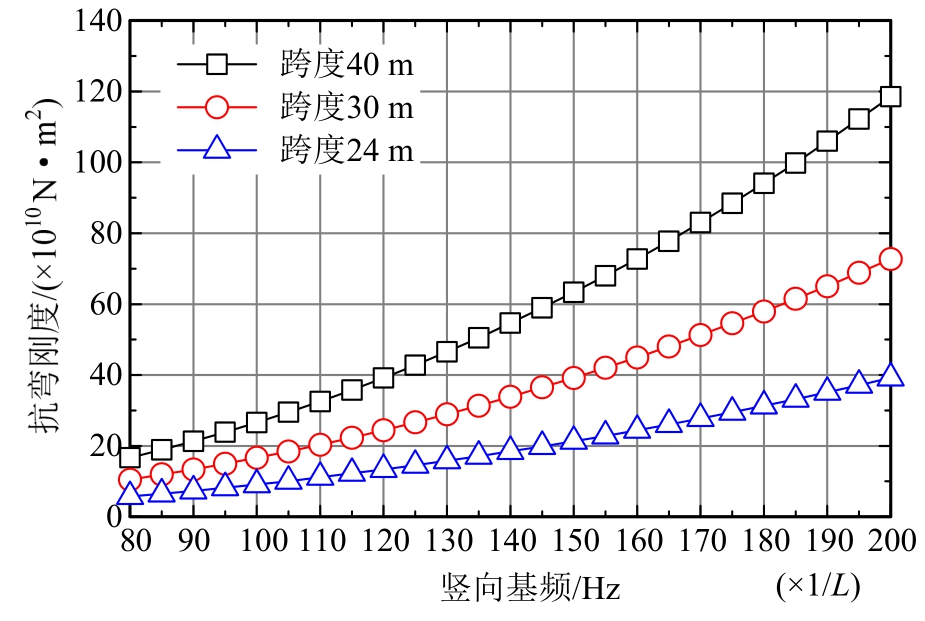
图6 竖向基频与抗弯刚度关系
Fig.6 The relationship between vertical basic frequency and flexural rigidity
1)不同刚度的简支箱梁在运营列车作用下的动力系数特征曲线相似,但桥梁共振速度随着梁体自振基频(刚度)的增大而增大。
2)对于24 m、32 m跨度简支梁,提高梁体基频可以有效地提高共振速度,降低列车在400km/h及以下速度行驶时的动力系数。
3)对于40m跨度简支梁,提高梁体竖向自振基频对共振速度影响较小,当列车以小于400km/h速度行驶时,梁体的动力系数峰值无明显改善。
按照结构动力学理论:对于单自由度有阻尼的简支梁结构体系,式(8)为其在谐振荷载作用下动力系数表达式,则频率比和阻尼比是影响动力系数的主要因素。该文动力仿真中简支箱梁阻尼比ξ取1%,现主要分析β对其动力系数的影响:当β≌1,即列车激振频率等于梁体自振频率时,动力系数达到最大值。因此共振速度(vbr=3.6fbdv)必将随简支箱梁的竖向自振基频(fb)的增大而增大。所以根据设计速度,提高中型跨度简支箱梁的自振基频可以有效地降低梁体动力响应。
式中:β=fv/fb为激振频率与简支箱梁固有频率之比;ξ为结构阻尼比。
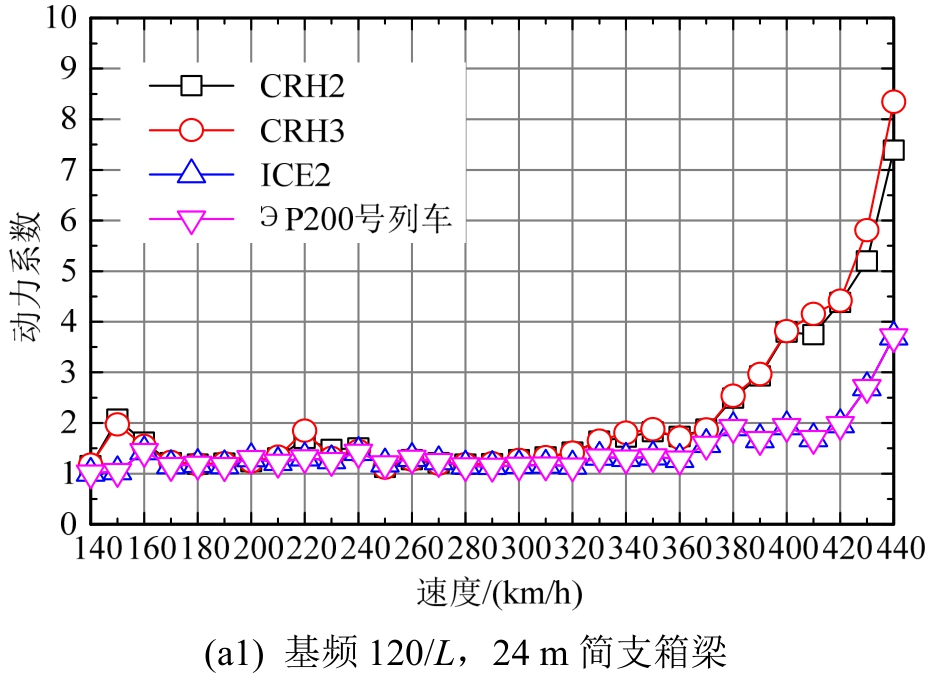


图7 不同竖向基频的简支箱梁动力系数特征
Fig.7 Impact factor characteristics of simply supported box-girder with different vertical basic frequencies
由式(8)可知,当激振频率与简支箱梁的固有频率相等时,此条件下(β=1)的动力放大系数为Dβ=1=1/(2ξ),所以不同梁体自振基频条件下,动力系数的峰值变化较小。图8表示运营列车作用下(140km/h~400km/h),不同竖向自振基频简支箱梁的最大动力响应特征,可以看出:当简支箱梁竖向自振基频位于Ⅰ区时,相应的共振速度vbr=3.6fbdv<vmax时,梁体动力响应峰值变化较小;当简支箱梁竖向自振基频位于Ⅱ区时,相应的共振速度vbr=3.6fbdv接近vmax时,梁体的动力效应与梁体的竖向基频具有直接的关系;当简支箱梁竖向自振基频位于Ⅲ区时,相应的共振速度vbr=3.6fbdv>vmax时,移动荷载作用下梁体动力响应较小,梁体自振竖向基频不再影响梁体最大动力响应,其中vmax表示线路的最大设计时速;梁体竖向最大振动加速度与最大动力系数变化规律基本一致,且随着简支箱梁的竖向自振基频的增大,梁体的动力效应总体呈下降趋势。

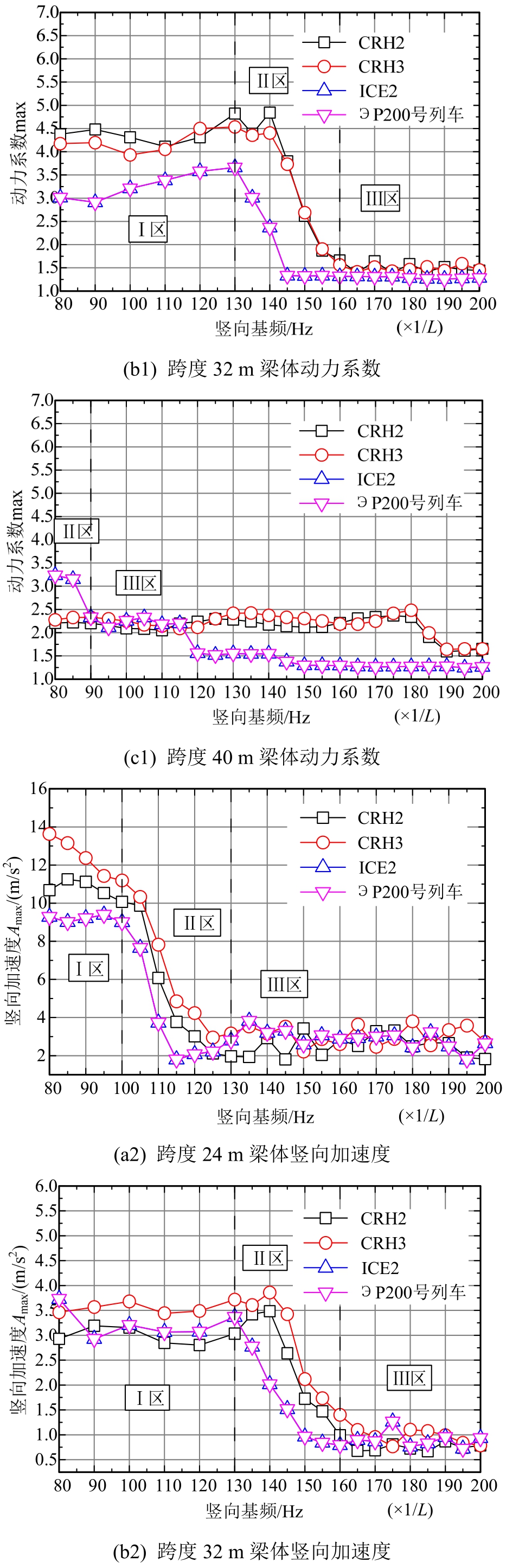

图8 不同竖向基频简支箱梁动力响应特征
Fig.8 Dynamic response characteristics of simply supported box-girder with different vertical basic frequencies
由于高速列车车长并不统一,如HSLM-A1~A10车长在18 m~27 m之间,所以相同的运营速度下,不同列车的激振频率并不相同,关于HSLM-A参数的定义如表4和图9所示。
表4 HSLM-A 参数
Table4 HSLM-A parameters

图10为HSLM A1~A10作用下(400km/h及以下)梁体最大动力响应特征,可以看出:
1)对于24 m跨度简支箱梁,相同基频的梁体,在不同类型列车作用下,梁体动力响应有所差别,提高梁体竖向自振基频限值可以有效地降低车长20m~25 m列车作用下的梁体动力响应,车长越长,通过调节简支箱梁自振基频规避共振的效果越明显。
2)对于32 m跨度简支箱梁,将梁体竖向自振基频提高至160/L及以上时,可以有效地降低车长23 m及以上列车作用下的梁体动力响应。
3)对于40m跨度简支箱梁,调整梁体竖向自振基频对动力响应影响较小。
理论研究表明[16]:梁体最大、小动力响应与车长、跨度间比值相关。当列车车速同时满足共振与消振要求时,消振起主要作用,将会出现共振消失的现象,即当vr=vc时,Lb/Lv=(2n−1)/(2αm),m,n=1,2,3,…其中α为无量纲参数,该文取1,表示单个荷载行为的第一类消振效应;m、n分别表示1阶振型下的共振与消振阶数。所以,当梁体不存在1阶共振点,铁路桥动力响应最小时,桥跨与车长比
可表示为:Lb/Lv=k+0.5,k=1,2,3,…;当梁体不存在2阶共振点时,桥跨与车长比可表示为:Lb/Lv=1/2(k+0.5),k=1,2,3,…;相反,当Lb/Lv为整数时,消振不再起主要作用,动力响应倍率增大。因此理论上通过调整车长与桥跨之比可避开基阶振型的共振,有利于行车安全。

图9 HSLM-A
Fig.9 HSLM-A
注:①动力车(前、后动力车相同);②端车(前、后端车相同);③中车

图10 不同列车作用下简支箱梁动力响应特征
Fig.10 Dynamic response characteristics of simply supported box-girder under the action of different trains

图11 不同Lb/Lv工况下的简支箱梁动力系数响应特征
Fig.11 Dynamic response characteristics of simply supported box-girder under differentLb/Lvconditions
图11分别为跨度24 m、32 m和40m,不同Lb/Lv工况下的简支箱梁动力系数响应特征曲线,由图中动力系数变化曲线可知:对跨度24 m、32 m和40m简支箱梁,当Lb/Lv接近或等于1.00、2.00,满足共振条件时,梁体动力响应倍率增大;但是对于跨度32 m简支梁,当Lb/Lv接近2.00时,梁体挠度是由长列荷载引起的,荷载产生的突变效应减弱,共振波峰的梁体动力响应倍率会减小。当Lb/Lv接近或等于1.50,满足共振条件时,梁体动力响应较小,仿真分析与理论研究一致。
现行运营列车的车长为25 m左右,当Lb/Lv=1.5,Lb=37.5 m和Lb/Lv=2.5,Lb=62.5 m时,梁体不存在1阶共振点;当Lb/Lv=0.75,Lb=18.75 m时,梁体不存在2阶共振点;根据前述简支箱梁竖向自振基频限值取值标准并结合图8、图10简支箱梁最大动力响应特征可得:时速400km/h运营列车作用下,满足设计荷载对桥梁的动力效应不小于运营列车对桥梁的动力效应时简支箱梁的竖向自振基频限值统计表(表5)。
表5 满足动力要求的竖向基频限值
Table5 Vertical basic frequency limit that meet the impact requirements

(1)根据运营荷载动力效应小于等于设计荷载效应,得到24 m、32 m和40m常用跨度简支箱梁在实际运营列车(CRH2、CRH3、ICE2和ЭР200号列车)作用下的容许动力系数。
(2)列车激振频率fv和简支箱梁竖向自振频率fb接近或相等时,梁体发生共振或较大振动,此时动力系数出现峰值;根据设计速度,控制简支箱梁的竖向自振频率,避开运营列车对桥梁产生的激振频率,可以有效地降低梁体动力响应。
(3)梁体最大动力响应与桥跨Lb和车长Lv之比有关。共振条件下,当Lb/Lv为1或2时,梁体动力响应倍率增大;当Lb/Lv接近或等于1.5时,梁体动力响应较小。通过调整车长与桥跨之比可避开基阶振型的共振,有利于行车安全。
(4)基于移动荷载数值模型,通过理论与仿真分析提出预应力混凝土简支箱梁的竖向自振基频限值。车长25 m左右的运营列车作用下,建议设计时速400km/h,跨度24 m、32 m和40m的预应力混凝土简支箱梁竖向自振基频限值取125/L、155/L和90/L。
该文的研究可为今后更高速同类铁路桥梁的初步设计工作提供技术资料。
参考文献:
[1]UIC 776-2R,Design requirements for rail-bridges based on interaction phenomena between train,track and bridge[S].UIC:2009.
[2]日本铁路结构设计标准和解释-混凝土结构[R].东京:日本铁道综合技术研究所,2004.Japanese railway structure design standard and explanation -concrete structure[R].Tokyo:Japan Railway Comprehensive Technology Research Institute,2004.(in Japanese)
[3]Siringoringo D M,Fujino Y.Estimating bridge fundamental frequency from vibration response of instrumented passing vehicle:Analytical and experimental study[J].Advances in Structural Engineering,2012,15(3):417―433.
[4]Gao Q F,Wang Z L,Liu Y,et al.Modified formula of estimating fundamental frequency of girder bridge with uniform cross-section[J].Key Engineering Meterials,2012,540:99―106.
[5]松浦章夫.高速鉄道における車両と橋桁の動的挙動に関する研究[J].土木学会論文,1976,256(12):35―47.Matsuura A.Study of dynamic behaviors of bridge girders for high-speed railway[J].Journal of JSCE,1976,256(12):35―47.(in Japanese)
[6]Fryba L.Vibration of solids and structures under moving loads[M].London:Thomas Telford,1999.
[7]夏禾,郭薇薇,张楠.车桥系统共振机理和共振条件分析[J].铁道学报,2006,28(5):52―58.Xia He,Guo Weiwei,Zhang Nan.Analysis of resonance mechanism and conditions of train-bridge system[J].Journal of the China Railway Society,2006,28(5):52―58.(in Chinese)
[8]沈锐利.高速铁路简支梁桥竖向振动响应研究[J].中国铁道科学,1996,17(3):24―34.Shen Ruili.Research of vertical vibration response of simple supported beam bridge on high speed railways[J].China Railway Science,1996,17(3):24―34.(in Chinese)
[9]宁晓骏,叶燎原,缪昇.高速铁路中桥梁跨径布置与共振关系的探讨[J].振动与冲击,2000,19(3):73―75.Ning Xiaojun,Ye Liaoyuan,Miao Sheng.Research on the relationship between the bridge span arrangement in high railway and the bridge resonance[J].Journal of Vibration and Shock,2000,19(3):73―75.(in Chinese)
[10]郭文华,路萍.TMD对高速列车通过简支箱梁桥时的振动控制研究[J].振动与冲击,2008,27(11):42―45.Guo Wenhua,Lu Ping.Vibration suppression for simply supported bridges passed by high-speed trains using tuned mass dampers(TMD)[J].Journal of Vibration and Shock,2008,27(11):42―45.(in Chinese)
[11]Sogabe M,Matsumoto N,Kanamori M,et al.Impact factors of concrete girders coping with train speed-up[J].Quarterly Report of RTRI,2005,46(1):46―52.
[12]EN 1991-2,Eurocode 1:Actions on structures -part 2:traffic loads on bridges[S].European Committee for Standardisation,2003.
[13]邓建良,吴定俊,李奇.简支梁桥动力系数的移动荷载列分析[J].工程力学,2012,29(10):177―179,181―183,204.Deng Jianliang,Wu Dingjun,Li Qi.Dynamic factor analysis of simple-supported bridges using discrete moving load model[J].Engineering Mechanics,2012,29(10):177―179,181―183,204.(in Chinese)
[14]李小珍,张志俊,刘全民.任意移动荷载列作用下简支梁桥竖向振动响应解析分析[J].振动与冲击,2012,31(20):137―142.LI Xiaozhen,Zhang Zhijun,Liu Quanmin.Vertical dynamic response analysis of a simply supported beam bridge under successive moving loads[J].Journal of Vibration and Shock,2012,31(20):137―142.(in Chinese)
[15]TB 10621―2014,高速铁路设计规范[S].北京:中国铁道出版社,2014.TB 10621―2014,Code for design of high speed railway[S].Beijing:China Railway Press,2014.(in Chinese)
[16]苏木标,李建中,梁志广.高速铁路简支梁桥的竖向共振现象[J].工程力学,2001,18(5):84―94.Su Mubiao,Li Janzhong,Liang Zhiguang.Vertical resonance phenomenon of simply-supported girder bridges on high-speed railway[J].Engineering Mechanics,2001,18(5):84―94.(in Chinese)
RESEARCH ON THE BASIC FREQUENCY LIMIT OF RAILWAY COMMON SPAN PRESTRESSED CONCRETE SIMPLY SUPPORTED BEAM WITH 400km/h
LI Xiao-zhen1,QIU Xiao-wei1,LIU De-jun1,2,QIN Yu1
(1.Department of Bridge Engineering,Southwest Jiaotong University,Chengdu,Sichuan 610031,China;2.College of Civil Engineering & Architecture,Jiaxing University,Jiaxing,Zhejiang 314001,China)
Abstract:Finite element model is established to calculate the vertical basic frequency of PC(prestressed concrete)simply supported box-girder with common span.The allowable impact factor of girder is determined according to the principle of the bridge dynamic effect under the action of running train not greater than that of design value.Based on the moving load model,the impact factor of the simply supported box-girder with common span is determined under moving train.The lower vertical basic frequency limit of PC simply supported box-girder with common span is recommended as 400km/h,through comprehensively analyzing the relationship between the dynamic response of the girder and the type of train,the operation speed and the girder vertical basic frequency.The research shows that adjusting the ratio of the vehicle length to the bridge span could avoid the resonance of the fundamental vibration mode,which is beneficial to vehicle running safety.The lower vertical basic frequency limit of PC simply supported box-girder with span of 24 m,32 m and 40m are recommended,which are 125/L,155/Land 90/L,respectively,which could effectively reduce the dynamic response of girder caused by vehicle with 25 m length.
Key words:high speed railway;simply supported box-girder;vertical basic frequency limit;moving load;400km/h;impact factor
中图分类号:U238,U441+.3
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.04.0273
文章编号:1000-4750(2018)05-0204-10
收稿日期:2017-04-09;修改日期:2017-10-26
基金项目:国家自然科学基金项目(U1434205);中国铁路总公司科研重大课题项目(2016G002-A);中央高校基本科研业务费专项资金项目(2682016CX020)
通讯作者:刘德军(1977―),男,四川人,讲师,博士,主要从事风车桥耦合振动研究(E-mail:djliu@swjtu.edu.cn).
作者简介:李小珍(1970―),男,湖南人,教授,博士,博导,桥梁系副主任,主要从事车桥耦合振动研究(E-mail:xzhli@swjtu.cn);
邱晓为(1990―),男,山东人,博士生,主要从事风车桥耦合振动研究(E-mail:qxw542106512@126.com);
秦 羽(1992―),男,重庆人,硕士生,主要从事风车桥耦合振动研究(E-mail:1145539394@qq.com).