余 波，陈 冰，唐睿楷
(广西大学土木建筑工程学院，工程防灾与结构安全教育部重点实验室，广西防灾减灾与工程安全重点实验室，广西，南宁 530004)
摘 要：传统的钢筋混凝土(RC)梁抗剪承载力模型属于确定性模型，难以有效考虑几何尺寸、材料特性、边界约束条件等因素存在的客观(物理)不确定性和在模型推导过程中存在的主观(模型)不确定性的影响，导致计算结果的离散性较大，计算精度和适用性有限。鉴于此，该文首先结合修正压力场理论和考虑剪跨比影响的临界斜裂缝倾角模型，建立了RC梁的确定性抗剪承载力模型；然后综合考虑主观不确定性和客观不确定性因素的影响，结合贝叶斯理论和马尔科夫链蒙特卡洛法(MCMC)，建立了RC梁抗剪承载力计算的概率模型；最后通过与试验数据和传统确定性计算模型的对比分析，验证了该模型的有效性和适用性。分析结果表明，所建立的概率模型不仅可以合理地描述RC梁抗剪承载力的概率分布特性，而且可以校准传统确定性计算模型的计算精度和置信水平，还可以根据预定的置信水平确定RC梁抗剪承载力的概率特征值，具有良好的计算精度和适用性。
关键词：钢筋混凝土梁；抗剪承载力；修正压力场理论；临界斜裂缝倾角；概率模型
钢筋混凝土(RC)梁的抗剪承载力分析对于RC结构的承载力设计和安全性评估具有重要意义。由于RC梁的抗剪机理比较复杂，而且影响因素较多[1]，现行的国内外设计规范[2―5]普遍基于简化的力学模型，结合工程经验和试验数据拟合分析[6]，建立RC梁的抗剪承载力分析模型，本质上属于半经验半理论模型，由于缺乏严密的理论基础，导致计算精度和适用性有限。目前，RC梁的抗剪承载力分析理论主要包括定角桁架理论[7]、变角桁架理论[8]、压力场理论[9]和修正压力场理论(MCFT)[10―11]等。由于MCFT的理论相对严密，而且可以考虑斜裂缝之间混凝土拉应力对抗剪承载力的影响，所以被加拿大[12]和美国[13]设计规范采用。然而，文献[12]中的模型需要迭代分析，计算过程较为繁琐，不便于工程应用；文献[13]中的模型需要通过查表确定混凝土抗剪承载力贡献系数β和临界斜裂缝倾角θ，只适用于斜裂缝间距为300mm的条件，计算结果往往偏于危险；针对该问题，文献[14]通过拟合分析，分别建立了β和θ与配箍率、箍筋屈服强度、纵筋应变、截面有效抗剪高度等参数之间的经验关系模型；文献[15]基于MCFT建立了RC梁的抗剪承载力计算模型，但是该模型忽略了剪跨比对临界斜裂缝倾角的影响，适应性有限[16]。此外，上述模型均属于确定性计算模型，由于难以考虑RC梁的几何尺寸、材料特性、边界约束条件等因素存在的客观不确定性和在模型推导过程中存在的主观不确定性的影响，从而无法合理描述RC梁抗剪承载力的概率特性，导致计算结果的离散性较大，计算精度和适用性有限。
鉴于此，本文首先结合修正压力场理论和考虑剪跨比影响的临界斜裂缝倾角模型，建立了RC梁抗剪承载力的确定性计算模型；然后综合考虑主观不确定性和客观不确定性因素的影响，结合贝叶斯理论和马尔科夫链蒙特卡洛法(MCMC)，建立了RC梁抗剪承载力计算的概率模型；最后通过与试验数据和传统确定性计算模型的对比分析，验证了该概率模型的有效性和适用性。
根据修正压力场理论[11，17―18]，RC梁的抗剪承载力V主要由混凝土的抗剪承载力贡献值Vc和钢筋的抗剪承载力贡献值Vs两部分承担，即：
当RC梁发生斜截面受剪破坏时，其典型的裂缝分布如图1所示，从中选取一个微元体Ω进行应力平衡分析[18]，并绘制对应的应力莫尔圆，如图2所示。根据MCFT[11，17―18]，可以建立应力平衡条件：
式中：ρs和ρv分别为纵向钢筋和横向钢筋的配筋率；θ为临界斜裂缝倾角；fx和fy分别为x和y方向上的总应力；f1为垂直于混凝土裂缝方向的平均主拉应力；f2为平行于混凝土裂缝方向的平均主压应力；v为与RC梁抗剪承载力对应的剪应力；fsx和fsy分别为纵向钢筋和横向钢筋的拉应力。对式(4)进行变换可得：
式中：b为截面宽度；dv为截面的有效抗剪高度，可以近似取为dv=max(0.9h0，0.72h)，h为RC梁的截面高度，h0为RC梁的截面有效高度。由式(5)可知，截面剪应力v由斜拉应力f1和斜压应力f2抵抗。其中，f1满足应力-应变关系[17]：
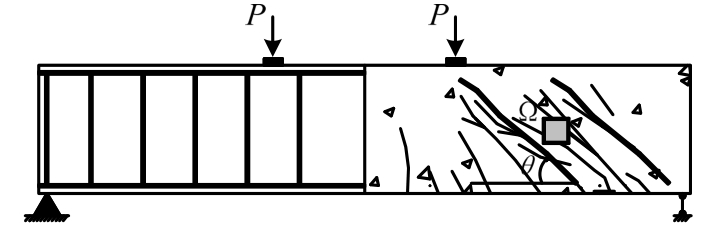
图1 带斜裂缝的钢筋混凝土梁
Fig.1 Reinforced concrete beam with diagonal crack
图2 微元体的应力平衡条件与应力莫尔圆
Fig.2 Stress balance condition and stress Mohr circle of microelement
式中：εcr为混凝土的开裂应变，通常取0.5×10-3；Ec为混凝土的弹性模量；
为混凝土的抗压强度；ε1为主拉应变。
文献[16]分析了剪跨比对临界斜裂缝倾角θ的影响规律，并建立了考虑剪跨比影响的临界斜裂缝倾角模型：
式中：kλ=α2λ+α3为剪跨比修正系数；α2和α3为剪跨比修正参数，建议值分别为-0.04和1.11；kns=1+(nρs)-1；knv=1+(nρv)-1；n=Es/Ec为钢筋和混凝土之间的弹性模量比，Es为钢筋的弹性模量；α1=vc/v=Vc/V，建议值为0.38；vc为与混凝土抗剪承载力贡献值对应的剪应力。
RC梁的受力情况如图3所示，由竖向力平衡条件可得：
式中：fvy为横向钢筋的屈服强度；s为横向钢筋间距；Av为横向钢筋的截面面积。结合式(5)和式(8)可得：
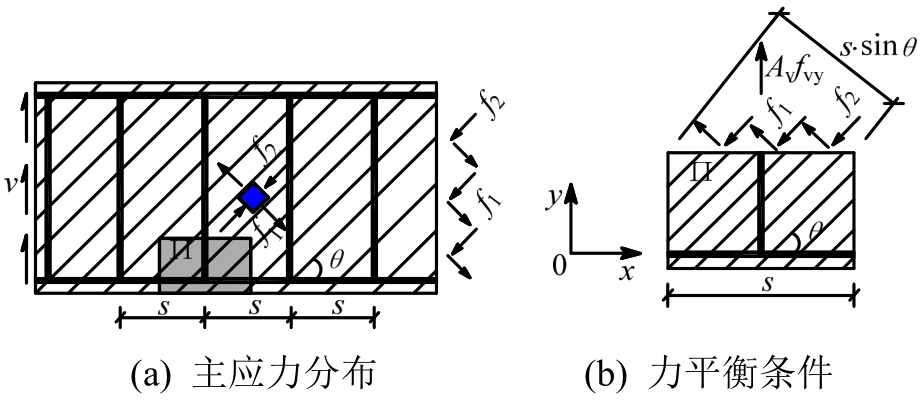
图3 RC梁的主应力和力平衡示意图
Fig.3 Principal stress and force balance of RC beam
根据式(9)可知，RC梁的抗剪承载力V与斜拉应力f1有关，而根据式(6)可知，f1与主拉应变ε1有关。对于传统的MCFT[17]，ε1与斜裂缝间距和临界斜裂缝倾角θ有关，而θ又与待求的V有关，所以需要通过迭代计算才能对式(9)进行求解，计算过程繁琐。为了克服上述缺陷，文献[19]建立了ε1与横向钢筋屈服应变εy之间的关系：
式中：α4为横向钢筋影响系数，建议值为1.2[19]；εy=fvy/Es为横向钢筋的屈服应变。
基于上述理论推导，根据RC梁的纵向钢筋配筋率ρs、横向钢筋配筋率ρv、剪跨比λ和弹性模量比n，利用式(7)可以计算临界斜裂缝倾角θ，结合混凝土抗压强度、横向钢筋屈服强度fvy和钢筋弹性模量Es，利用式(6)和式(10)可以计算f1，然后代入式(9)可以计算RC梁的抗剪承载力V。该文模型的计算值(记为Vd)与试验值(记为Vt)的对比分析如图4所示。由图4可知，虽然由式(9)定义的确定性抗剪承载力模型综合考虑了剪跨比、截面尺寸、弹性模量比、混凝土抗压强度、配筋率、配箍率、横向钢筋屈服强度等因素的影响，具有相对严密的理论基础，但是该模型无法考虑RC梁的几何尺寸、材料特性、边界约束条件等因素存在的客观不确定性和在模型推导过程中存在的主观不确定性的影响，所以存在一定的离散性。因此，有必要在确定性抗剪承载力模型的基础上建立RC梁抗剪承载力计算的概率模型，从而合理地描述RC梁抗剪承载力的概率分布特性。
图4 模型计算值与试验值的对比
Fig.4 Comparison between calculated and experimental data
结合式(6)、式(7)、式(9)和式(10)可知，由式(9)所描述的确定性抗剪承载力模型虽然通过理论分析考虑了剪跨比、截面尺寸、弹性模量比、混凝土抗压强度、配筋率、配箍率、钢筋屈服强度等因素的影响，但是无法通过理论分析确定式(7)中的模型参数α1、α2、α3以及式(10)中的模型参数α4。同时，由式(9)所定义的确定性抗剪承载力模型无法考虑RC梁的几何尺寸、材料特性、边界约束条件等因素存在的客观不确定性和在模型推导过程中存在的主观不确定性的影响。其中，主观不确定性包括模糊性、未确知性和知识的不完善性[20]。模糊性主要是指因为难以明确事物类别的界定而产生的不确定性；未确知性和知识的不完善性主要是指因为认识手段、信息资源、知识水平、自然和社会环境等条件的限制，不能准确确定事物的性质、状态、功能以及影响因素而产生的不确定性。鉴于此，该文利用概率模型参数α1、α2、α3和α4来考虑客观不确定性的影响，利用概率模型参数α5来描述由未确知性和知识的不完善性引起的主观不确定性[21]，从而建立RC梁抗剪承载力计算的概率模型：
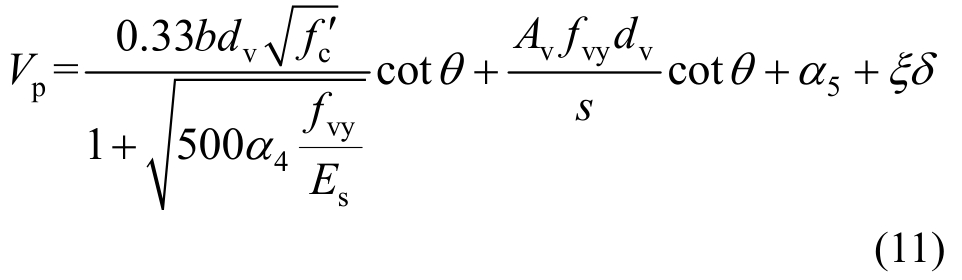
式中：Vp为RC梁抗剪承载力的概率值；ξδ为概率模型的系统误差；α=[α1，α2，α3，α4，α5]T为概率模型参数向量；ξ为标准正态分布随机变量；δ为系统误差的标准差。
根据概率模型参数α的先验分布，结合试验数据和贝叶斯理论，可以确定α的后验分布：
式中：
为α的后验分布概率密度函数；P(α)为α的先验分布概率密度函数；
的似然函数；
为归一化因子，也称为全概率密度函数。
根据现有的试验数据，可以确定概率模型参数α的先验分布。文献[16]根据80组RC梁的试验数据，利用统计分析确定了参数α1、α2和α3的均值和标准差。其中，α1、α2和α3的均值分别为0.38、-0.04和1.11，标准差分别为0.09、0.02和0.20。因此，该文假定α1的先验分布服从均值和标准差分别为0.38和0.09的正态分布；α2的先验分布服从均值和标准差分别为-0.04和0.02的正态分布；α3的先验分布服从均值和标准差分别为1.11和0.20的正态分布。对于横向钢筋影响系数α4，文献[19]建议取值为1.2，具有一定的经验性。为了描述α4的随机性，该文假定α4的先验分布服从均值和标准差分别为1.2和0.3的正态分布。
此外，
的计算通常涉及高维积分问题，求解较为困难。鉴于此，本文采用MCMC方法[22]来确定概率模型参数α的后验分布信息，进而建立RC梁抗剪承载力计算的概率模型。
从文献[23―31]中收集119组RC梁的抗剪承载力试验数据，见表1。由表1可知，梁的截面宽度b的范围为127 mm～300mm，截面高度h的范围为230mm～559 mm，有效截面高度h0的范围为198 mm～464 mm，剪跨比λ的范围为1.17～4.97，弹性模量比n的范围为4.47～11.34，配筋率ρs的范围为1.04%～4.54%，配箍率ρv的范围为0.04%～1.22%，纵筋的屈服强度实测值fy的范围为321 MPa～555 MPa，横向钢筋的屈服强度实测值fvy的范围为212 MPa～668 MPa，混凝土抗压强度实测值的范围为23.1 MPa～89.4 MPa，抗剪承载力试验测试值Vt的范围为115.00kN～321.10kN。选取文献[2，4，5，12]中的确定性计算模型(分别简记为VGB、VJTG、VACI和VCSA)来对比验证本文概率模型(其均值简记为Vm)的有效性和适用性。
选取表1中的前90组试验数据，利用本文方法可以确定各概率模型参数的后验分布信息。首先利用K-S检验来确定概率模型参数α的经验概率分布类型。当显著水平取为0.05、样本容量取为1000时，K-S检验的临界值为0.043。当概率模型参数的经验分布函数和理论分布函数的差的绝对值的最大值(通常称为D值)小于K-S检验的临界值时，表示该模型参数不拒绝服从该分布。各概率模型参数的K-S检验的D值见表2。表中，“×”表示样本序列的取值不能满足对应分布类型的物理意义要求。由表2可知，α1和α3不拒绝服从正态分布、对数正态分布和伽马分布，α4不拒绝服从正态分布和伽马分布，α2和α5不拒绝服从正态分布。
以D值最小的分布类型作为各模型参数的最优分布，α的后验分布统计信息见表3。其中，α1的均值为0.47，表明混凝土对抗剪承载力的贡献值占RC梁抗剪承载力的47%左右；α2的均值为负值，表明RC梁的临界斜裂缝倾角随着剪跨比的增大呈减小趋势，与理论分析和试验数据的变化规律一致[16]。此外，系统误差的标准差δ为17.71 kN。
表1 RC梁的基本参数和抗剪承载力试验值
Table1 Basic parameters and tested shear strength of RC beams
续表
续表
表2 概率模型参数K-S检验的D值
Table2D-value of K-S test for probabilistic model parameters
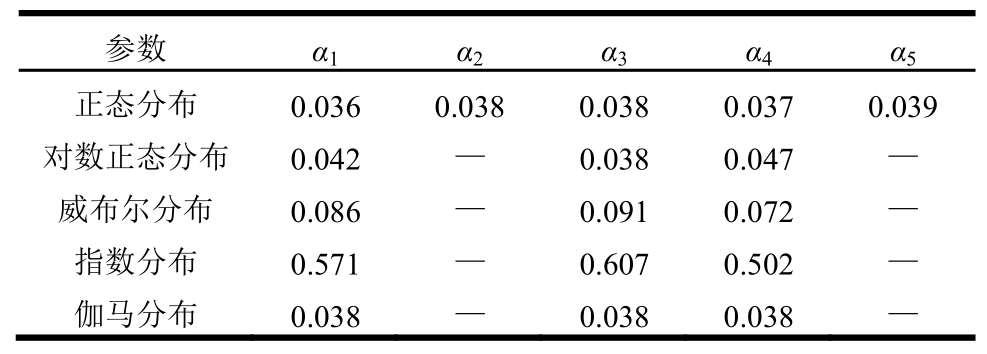
表3 概率模型参数后验分布的统计信息
Table3 Statistical information of posterior for probabilistic model parameters
在确定α的概率统计信息的基础上，结合式(11)和蒙特卡洛方法(MCS)，可以确定RC梁抗剪承载力的概率统计特征值(如均值和标准差)以及不同置信水平的置信区间。以50%和95%置信区间为例，概率模型的均值(Vm)与试验测试值(Vt)的对比分析如图5所示。由图5可知，有将近一半的实测值位于50%置信区间内，而几乎全部实测值均位于95%置信区间内，说明所建立的概率模型能够较好地描述RC梁的抗剪承载力的概率分布特性。
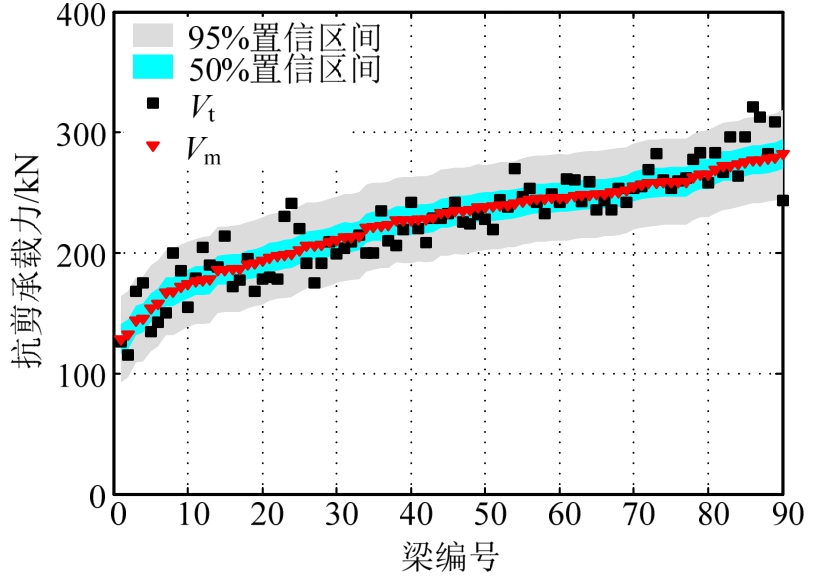
图5 试验值在概率模型置信区间中的分布(前90组)
Fig.5 Distribution of tested data in confidence interval of probabilistic model(first 90groups)
为了对比分析各模型的计算精度，分别计算各模型计算值与试验值之间的均方根误差δV：
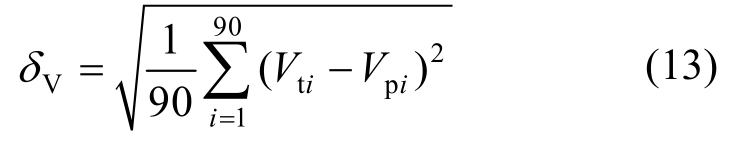
式中：Vti为第i条RC梁的抗剪承载力试验测试值；Vpi为第i条RC梁的抗剪承载力模型计算值。通过计算，Vm、VGB、VJTG、VACI和VCSA的均方根误差δV分别为16.61 kN、72.01 kN、70.40kN、85.56 kN和44.84 kN。由于该文模型的均方根误差δV最小，说明该文概率模型的计算精度更高。
为了验证概率模型的适用性，选取表1中的第91～119组数据(独立于建模使用的前90组)进行验证分析。利用概率模型所确定的RC梁抗剪承载力的均值(Vm)与试验测试值(Vt)的对比如图6所示。由图6可知，概率模型均值与试验测试值吻合较好，所以概率模型的均值具有较好的计算精度和较强的适用性。
图6 试验值在概率模型置信区间中的分布(91～119 组)
Fig.6 Distribution of tested data in confidence interval of probabilistic model(91-119 groups)
所建立的概率模型的优势之一在于能够校准传统确定性模型的计算精度。以文献[2，4，5，12]中的确定性计算模型(分别简记为VGB、VJTG、VACI和VCSA)为例，各模型的计算值和试验测试值在概率模型置信区间内的分布如图7所示。由图7可知，VGB、VJTG和VACI模型的计算结果均偏离试验值较远，且有较大部分计算值落在95%置信区间之外，说明这三种模型的计算精度较低，主要原因在于这三种模型本质上属于半经验半理论模型，由于缺乏严密的理论基础，导致计算精度和适用性有限；VCSA模型的计算值虽然大部分位于95%置信区间之内，但是总体偏离实测值较远，说明离散性较大、计算精度有限。总体而言，概率模型的均值与试验测试值吻合较好，而且概率模型能够较好地描述抗剪承载力的概率分布特性，主要原因在于概率模型不仅综合考虑了剪跨比、临界斜裂缝倾角、混凝土强度、配筋率和配箍率等重要因素的影响，而且考虑了主观不确定性和客观不确定性因素的影响。
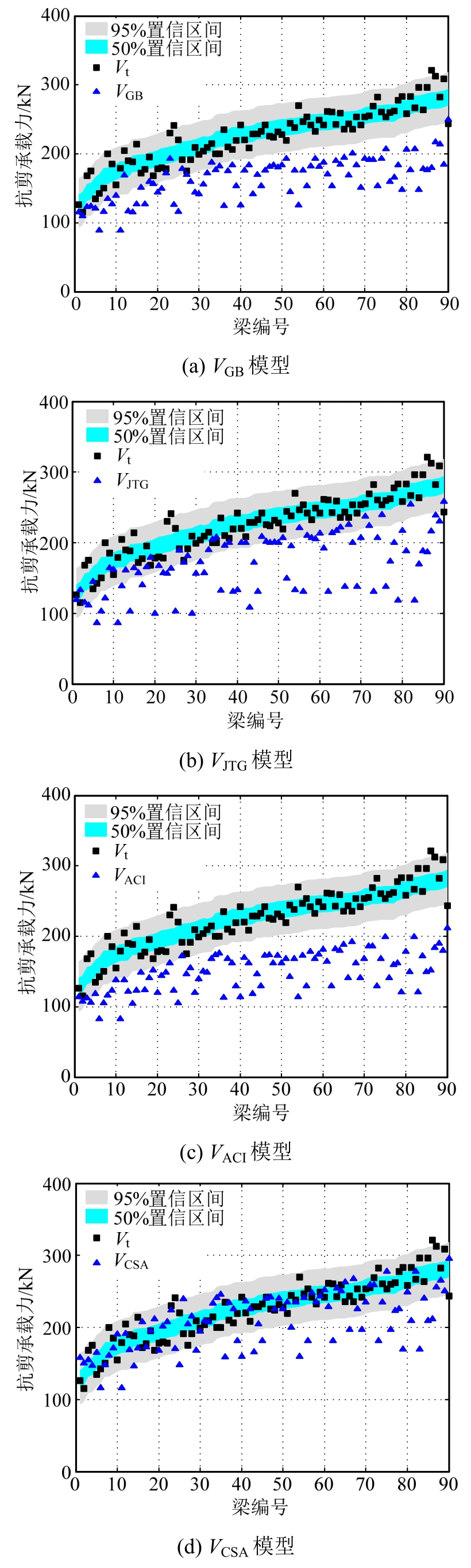
图7 确定性模型在概率模型置信区间内的分布
Fig.7 Distribution of deterministic models in confidence interval of probabilistic model
同时，利用本文概率模型可以校准传统确定性模型的置信水平(即分位数)。从表1中任选一条RC梁(如第16组)为例，由概率模型所确定的临界斜裂缝倾角的均值和标准差分别为148.96 kN和18.13 kN，经过K-S检验，抗剪承载力不拒绝服从正态分布，其概率密度分布如图8所示。VGB模型、VJTG模型、VACI模型和VCSA模型的计算值分别为151.31 kN、157.19 kN、148.96 kN和207.61 kN。由图8可得，VGB模型、VJTG模型和VACI模型的计算值均远小于均值，其分位数分别为0.03、0.05和0.02；VCSA模型的计算值略大于均值，其分位数为0.87。由此可见，利用概率模型可以校准传统确定性模型的置信水平。
图8 抗剪承载力的确定性模型的分位数
Fig.8 Quantile of deterministic model for shear strength
此外，利用概率模型可以确定对应于不同置信水平的抗剪承载力的概率特征值。同样以表1中的第16条RC梁为例，利用概率模型可以绘制出RC梁抗剪承载力的累积分布函数，如图9所示。以30%、50%、90%、95%置信水平为例，相应的RC梁抗剪承载力的概率特征值分别为177.49 kN、187.00kN、210.23 kN和216.82 kN。总的来说，基于概率模型可以根据工程需求确定具有不同置信水平的抗剪承载力特征值，进而为RC梁的概率安全性评估和概率极限状态设计提供依据。
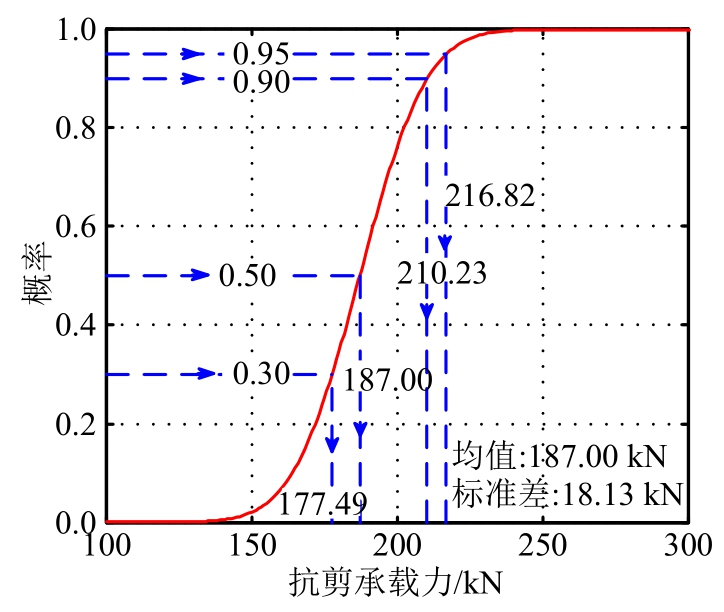
图9 不同置信水平下抗剪承载力的特征值
Fig.9 Characteristic values of shear strength with different confidence levels
基于修正压力场理论和考虑剪跨比影响的临界斜裂缝倾角模型，综合考虑主观不确定性和客观不确定性因素的影响，结合贝叶斯理论和MCMC，建立了RC梁抗剪承载力计算的概率模型。根据分析结果，可以得出以下结论：
(1)所建立的概率模型不仅具有严密的理论基础，而且综合考虑了主观不确定性和客观不确定性因素的影响，从而可以合理地描述RC梁抗剪承载力的概率分布特性。
(2)所建立的概率模型可以校准现有确定性抗剪承载力模型的计算精度和置信度水平。其中，VGB模型、VJTG模型和VACI模型的计算结果均偏离试验值较远，且有较大部分计算值落在95%置信区间之外；VCSA模型的计算值虽然大部分位于95%置信区间之内，但是总体偏离实测值较远，说明离散性较大、计算精度有限。
(3)基于所建立的概率模型可以根据预定的置信水平来确定RC梁的抗剪承载力的概率特征值，从而为RC梁的概率安全性评估和概率极限状态设计提供基础。
参考文献：
[1]曾庆响.混凝土双向受弯构件斜截面承载力设计简便方法[J].建筑结构，2005，35(1):72―75.Zeng Qingxiang.Convenient design method for oblique section strength of reinforced concrete beam subjected to biaxial bending[J].Building Structures，2005，35(1):72―75.(in Chinese)
[2]GB 50010―2010，混凝土结构设计规范[S].北京:中国建筑工业出版社，2010.GB 50010―2010，Code for design of concrete structures[S].Beijing:China Architecture & Building Press，2010.(in Chinese)
[3]SL191―2008，水工混凝土结构设计规范[S].北京:中国水利水电出版社，2008.SL191―2008，Design code for hydraulic concrete structures[S].Beijing:China Water & Power Press，2008.(in Chinese)
[4]JTG D62―2012，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社，2012.JTG D62―2012，Code for highway reinforced concrete and prestressed concrete bridges and culverts[S].Beijing:China Communication Press，2012.(in Chinese)
[5]ACI 318-11，Building code requirements of structuralconcrete[S].Farmington Hills:American Concrete Institute，2011.
[6]曾庆响，蔡健.双向受弯钢筋混凝土梁受剪承载力计算[J].土木工程学报，2009，42(4):27―32.Zeng Qingxiang，Cai Jian.Calculation of the shear capacity of reinforced concrete beams under biaxial bending[J].China Civil Engineering Journal，2009，42(4):27―32.(in Chinese)
[7]Ritter W.Die bauweise hennebique(Hennebiques construction method)[J].Schweizerische Bauzeitung，1899，33(7):59―61.
[8]Vecchio F.Disturbed stress field model for reinforced concrete:formulation[J].Journal of Structural Engineering，2000，126(9):1070―1077.
[9]Mitchell D，Collins M P.Diagonal compression field theory -a rational model for structural concrete in pure torsion[J].ACI Structural Journal，1974，71(8):396―408.
[10]Vecchio F J，Collins M P.Predicting the response of reinforced concrete beams subjected to shear using modified compression field theory[J].ACI Structural Journal，1988，85(3):258―268.
[11]Collins M P，Mitchell D.Prestressed concrete structures[M].Englewood Cliffs，NJ:Prentice Hall，1991.
[12]CSA A23.3-04，Design of concrete structures[S].Mississauga，Ontario:Canadian Standard Association，2004.
[13]AASHTO L，Bridge design specifications:SI Units[S].USA:American Association of State Highway and Transportation Officials，2007.
[14]魏巍巍，贡金鑫.钢筋混凝土构件基于修正压力场理论的受剪承载力计算[J].工程力学，2011，28(2):111―117.Wei Wewei，Gong Jinxin.Shear strength of reinforced concrete members based on modified compression field theory[J].Engineering Mechanics，2011，28(2):111―117.(in Chinese)
[15]Pan Z，Li B.Evaluation of shear strength design methodologies for slender shear-critical RC beams[J].Journal of Structural Engineering，2012，139(4):619―622.
[16]余波，陈冰，唐睿楷，等.钢筋混凝土梁临界斜裂缝倾角计算的概率模型[J].计算力学学报，2018(1):98―104.Yu Bo，Chen Bing，Tang Ruikai，et al.Probabilistic model for critical crack angle of reinforced concrete beams[J].Chinese Journal of Computational Mechanics，2018(1):98―104.(in Chinese)
[17]Bentz E C，Collins M P.Development of the 2004 Canadian Standards Association(CSA)A23.3 shear provisions for reinforced concrete[J].Canadian Journal of Civil Engineering，2006，33(5):521―534.
[18]Bentz E C，Vecchio F J，Collins M P.Simplified modified compression field theory for calculating shear strength of reinforced concrete elements[J].ACI Structural Journal，2006，103(4):614―624.
[19]De Silva S，Mutsuyoshi H，Witchukreangkrai E.Evaluation of shear crack width in I-shaped prestressed reinforced concrete beams[J].Journal of Advanced Concrete Technology，2008，6(3):443―458.
[20]刘虎堂.既有钢筋混凝土构件抗力的推断和验证[D].西安:西安建筑科技大学，2010.Liu Hutang.Resistance predicting and verifing of existing reinforce concrete member[D].Xi’an:Xi’an University of Architecture and Technology，2010.(in Chinese)
[21]吕大刚，宋鹏彦，王光远.考虑模型不确定性的结构可靠度分析方法[J].哈尔滨工业大学学报，2011，43(8):11―15.Lü Dagang，Song Pengyan，Wang Guangyuan.Reliability analysis methods of structures considering statistical uncertainty[J].Journal of Harbin Institute of Technology，2011，43(8):11―15.(in Chinese)
[22]Gilks W R，Richardson S，Spiegelhalter D J.Markov Chain Monte Carlo in practica[J].Computing Science & Statistics，1996，91(8):497―537.
[23]Cladera A，Mari A.Experimental study on high-strength concrete beams failing in shear[J].Engineering Structures，2005，27(10):1519―1527.
[24]易伟建，吕艳梅.高强箍筋高强混凝土梁受剪试验研究[J].建筑结构学报，2009，30(4):94―101.Yi Weijian，Lü Yanmei.Experimental study on shear behavior of high-strength concrete beams with high-strength stirrups[J].Journal of Building Structures，2009，30(4):94―101.(in Chinese)
[25]Ahmad S，Xie Y，Yu T.Shear ductility of reinforced lightweight concrete beams of normal strength and high strength concrete[J].Cement and Concrete Composites，1995，17(2):147―159.
[26]金琰，苏幼坡，康谷贻.集中荷载作用高强箍筋混凝土梁斜裂缝的出现与发展[J].建筑结构，2003，33(1):15―16.Jin Yan，Su Youpo，Kang Guyi.Appearance and development of diagonal crack of RC beams using high-strength stirrup under concentrated load[J].Building Structures，2003，33(1):15―16.(in Chinese)
[27]Li B，Tran C T N.Reinforced concrete beam analysis supplementing concrete contribution in truss models[J].Engineering Structures，2008，30(11):3285―3294.
[28]Bresler B，Scordelis A C.Shear strength of reinforced concrete beams[J].ACI Structural Journal，1969，111(4):809―818.
[29]Clark A P.Diagonal tension in reinforced concrete beams[J].ACI Structural Journal，1951，48(10):145―156.
[30]Krefeld W J，Thurston C W.Studies of the shear and diagonal tension strength of simply supported reinforced concrete beams[J].ACI Structural Journal，1966，63(4):451―476.
[31]Kong P Y L.Shear strength of high performance concrete beams[J].ACI Structural Journal，1998，95(6):677―688.
A PROBABILISTIC MODEL FOR SHEAR STRENGTH OF REINFORCED CONCRETE BEAMS
YU Bo，CHEN Bing，TANG Rui-kai
(Key Laboratory of Engineering Disaster Prevention and Structural Safety of China Ministry of Education，Guangxi Key Laboratory of Disaster Prevention and Engineering Safety，School of Civil Engineering and Architecture，Guangxi University，Nanning，Guangxi 530004，China)
Abstract:Traditional models for shear strength of reinforced concrete(RC)beams are generally deterministic models and exhibit low computational accuracy and large numerical fluctuation，due to the fact that they do not take into account the aleatory(physical)uncertainties of various parameters such as geometry，material properties and boundary conditions as well as epistemic(model)uncertainties of the modelling.Based on the modified compression field theory(MCFT)and the critical crack angle model considering the influence of shear span ratio，a deterministic model for shear strength of RC beams was established first.Subsequently，a probabilistic model for shear strength of RC beam was developed by using the Bayesian theory and the Markov Chain Monte Carlo(MCMC)to take into account the influences of both epistemic and aleatory uncertainties.Finally，the applicability and efficiency of the proposed probabilistic model were validated by comparing with experimental data and traditional deterministic models.Analysis results show that the proposed probabilistic model is of good accuracy and adaptability.The model not only can describe the probabilistic distribution characteristics of shear strength of RC beams，but also provide a benchmark to calibrate the confidence level of traditional deterministic models and provide an efficient way to determine the characteristic values of shear strength of RC beams with differentconfidence levels.
Key words:reinforced concrete beam;shear strength;modified compression filed theory;critical crack angle;probabilistic model
中图分类号：TU375.1
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0075
文章编号：1000-4750(2018)05-0170-10
收稿日期：2017-01-19；修改日期：2017-04-26
基金项目：国家自然科学基金项目(51668008，51368006，51478125)；广西重点实验室系统性研究项目(2013ZDX06)
通讯作者：余 波(1982―)，男，四川泸州人，副教授，工学博士，主要从事混凝土结构耐久性和抗震分析研究(E-mail:gxuyubo@gxu.edu.cn).
作者简介：陈 冰(1990―)，男，江西萍乡人，硕士生，主要从事钢筋混凝土结构抗震性能分析研究(E-mail:cblucky@foxmail.com);
唐睿楷(1993―)，男，广西梧州人，硕士生，主要从事钢筋混凝土构件承载力分析研究(E-mail:tangruikai@mail.gxu.cn).