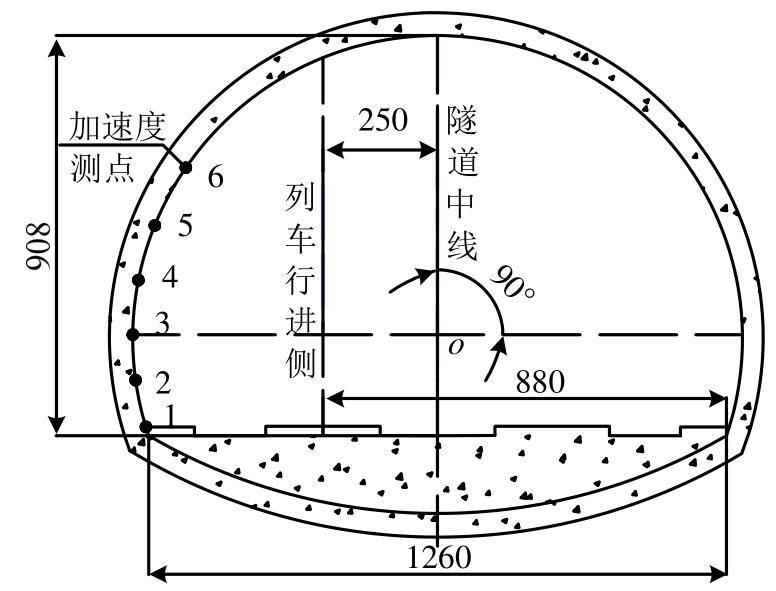
图1 隧道典型断面及测试点布置图
Fig.1 Typical tunnel section and layout of test points
田 甜1,雷 洋2,齐法琳2,黎国清2
(1.中国铁道科学研究院,北京 100081;2.中国铁道科学研究院基础设施检测研究所,北京 100081)
摘 要:通过高速铁路隧道衬砌振动响应的现场试验,发现隧道衬砌拱圈在列车荷载作用下,其振动加速度幅值随车速的增大而增大,且拱圈横向振动与竖向振动呈现不同的传递规律。文中开展理论分析与仿真计算,建立ABAQUS有限元平面模型,采用动力隐式算法对不同车速列车荷载作用下的隧道衬砌拱圈振动响应问题进行了理论分析,得出以下结果:有限元数值计算结果与实测结果基本吻合,可用作对实际测量数据的补充与预测;隧道振动响应随列车速度的增加而呈现增大趋势;不同车速引起的衬砌振动加速度响应传递规律一致;不同车速引起的衬砌竖向振动加速度幅值在拱顶位置较小,且随列车时速增大而变化不明显;衬砌拱顶横向振动明显随列车速度的增大而增大,但不同车速引起的衬砌横向振动在隧道圆心水平位置(即0°与180°)随列车时速变化不明显,且振动幅值较低;拟合了不同时速列车引起的隧道衬砌横向与竖向振动加速度的经验公式。
关键词:不同列车荷载;衬砌拱圈;振动响应;现场试验;数值模拟
当高速行驶的列车穿过运营隧道时,车辆与钢轨的作用力通过轨道传递到仰拱,再由仰拱传递给隧道衬砌与其背后围岩,从而引起隧道结构和围岩的振动,对隧道的整体稳定与服役状态存在安全威胁,这得到了广大科研工作者的广泛关注与研究[1]。
夏禾和王逢朝[2]等运用模型计算了不同位置、不同高度的邻近建筑物在列车振动荷载作用下的动力响应。张玉娥等[3]对隧道结构及围岩在时域内进行了动力响应分析,初步探讨了高速列车动荷载作用下隧道结构的动力工作状态。Degrande等[4]建立三维数值模型得到浅埋明挖隧道结构的动力响应主要受到埋深的影响,而深埋隧道结构的动力响应主要受到结构与围岩的相对刚度及围岩的岩性等因素决定的结论。
自20世纪60年代,国外学者对柏林和伦敦地铁的振动响应进行了简单的现场测试,并获得了振动荷载谱[5]。到2006年,Degrande等[6]依托欧盟CONVURT科研项目,对35辆列车以20km/h ~50km/h的速度穿越伦敦地铁时进行了测试,得到了仰拱以及隧道边墙的动力响应随车速的提高而增大的结论。
从20世纪80年代到21世纪初,潘昌实等[7-8]对北京地铁崇文门到前门区间隧道、木樨地到军事博物馆区间隧道进行了现场实测,获得了车速在70km/h下隧道衬砌部分控制点的动态响应状态。随后李德武等[9-11]根据隧道的现场实测结果,基于有限单元法,对列车竖向荷载下的隧道衬砌响应做了分析研究。在铁路隧道方面,高峰[12]在北京-通辽线扎栏营子隧道进行了列车振动现场测试的加速度试验和列车车辆体系的振动试验。王祥秋等[13-14]在京广线上朱亭隧道进行了动力响应现场测试,对隧道结构的频响特征进行了较深入的分析研究。
2005年,李亮等[15]采用激振函数模拟了高速列车竖向振动荷载,运用弹塑性有限元方法对大断面隧道结构在列车振动荷载作用下的不同断面形式、车速和阻尼比系数下的动响应进行了分析;宗刚等[16]人基于上海地铁实测加速度响应,获得了加速度在时域和频域内的能量分布特点,总结得到了地振动水平随遇振源距离增加衰减的规律及振动频率的分布范围;席兆凯和陈清军[17]在某地铁线路进行了现场振动与噪声测试,获得了地铁运行引起的地面振动加速度记录和站点噪声记录,分析得到了地铁运行引起的地面振动主频率成分在60Hz~80Hz的结论;巴振宁等[18]基于Biot流体饱和多孔介质理论,求得层状饱和地基表面移动荷载的动力格林函数,建立了2.5维间接边界元方法,研究了高速移动列车荷载作用下层状饱和地基-轨道耦合系统的动力响应,得到了列车移动速度接近饱和地基的Reileigh波速时,会引起饱和地基-轨道耦合系统的共振并产生较大动力响应的结论。
以上专家的研究,基本均基于地铁隧道,而针对高速铁路隧道的现场实测和理论研究工作较少,所以本文主要研究某高速铁路隧道在列车通过时,对列车荷载引起的隧道衬砌拱圈动力响应进行现场实测。根据实测高铁线路隧道的工程环境条件,建立了ABAQUS数值模型,对隧道衬砌拱圈在不同速度列车通过时的振动特性进行了研究。经过实测数据与数值计算结果的对比分析,验证了数值计算结果的正确性,并总结了振动的传播规律。
试验隧道现场选择位于某高速铁路干线某双线隧道,符合我国350km/h双线隧道建筑限界及轮廓要求。隧道全长11882 m,埋深约20m,隧道内轮廓净高8.78 m,净宽12.6 m,采用CRTSⅡ型板式无砟轨道。
试验中,选择远离隧道洞口浅埋区的隧道断面进行布点,在隧道内钢轨下侧轨道板上设置测点A,用于信号触发与采集轨道板处竖向振动加速度,即当列车通过隧道时,轨道板处传感器A触发,系统将进行列车通过隧道测点断面处的衬砌及轨道板加速度采集。隧道衬砌布点从拱脚处每隔近1 m布置竖向与横向加速度传感器,共设6个测点,其中测点1位于拱脚处,h1=0m,其余测点高度依次递增,均为相对轨道板处测点A的高度,隧道断面尺寸及布点如图1所示,各测点对应角度值见表1。试验测试开始前,传感器与采集仪均经过标定。采用DASP-V10工程版平台软件进行采集,采集仪及测点传感器安装布置如图2所示。

图1 隧道典型断面及测试点布置图
Fig.1 Typical tunnel section and layout of test points

图2 采集仪、电源及传感器
Fig.2 Acquisition instrument,battery and sensor
表1 衬砌实测点对应角度
Table1 Measurement points corresponding to the lining angle
本次试验共测得近50组高铁列车以250km/h~300km/h时速沿下行线方向通过隧道与42组高铁列车以250km/h~300km/h时速沿上行线方向通过隧道的实测数据,取每次实测加速度的均峰值进行分析。
高铁列车沿下行线通过隧道断面时,此时测点位于近车侧,提取列车以不同时速穿越实测隧道时,衬砌测点竖向与横向加速度数据的计算峰值平均值。将列车分别沿上行与下行方向行驶时,将隧道衬砌测点振动响应竖向与横向加速度数值大小进行对比,如图3和图4所示。
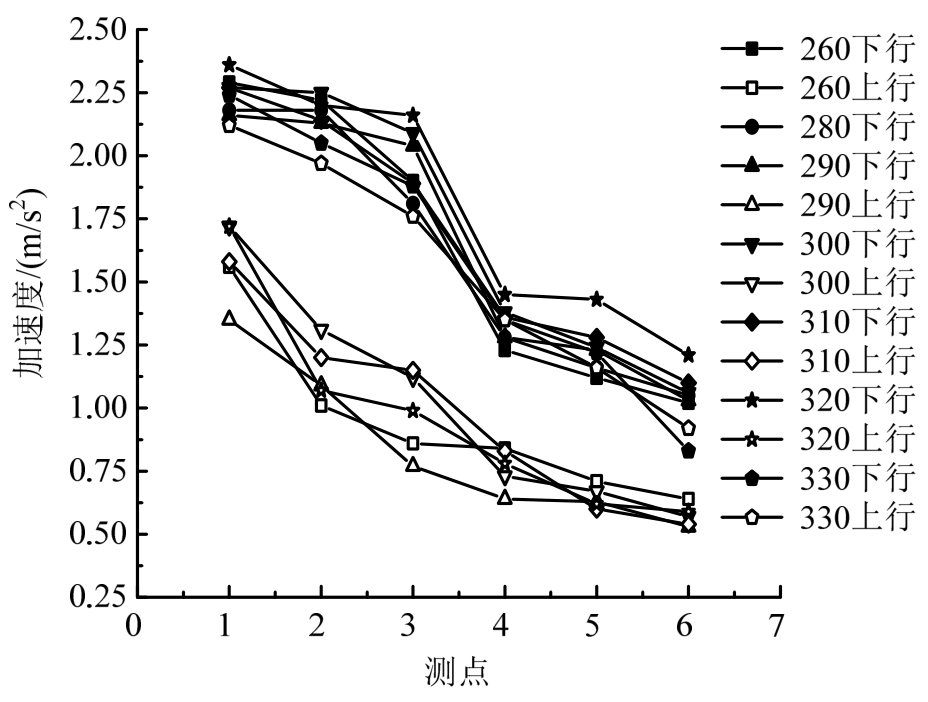
图3 不同时速下行线列车引起测点竖向加速度峰值对比图
Fig.3 Comparison of the vertical acceleration peak of the measured points caused by the different speeds of the train

图4 不同时速下行线列车引起测点横向加速度峰值对比图
Fig.4 Comparison of the transverse acceleration peak of the measured points caused by the different speeds of the train
由图3和图4可知,当列车以不同速度穿越隧道断面时,所引起的隧道衬砌竖向与横向加速度呈现随车速的增加而增大的趋势;衬砌振动加速度沿衬砌拱圈传递规律均表现为:竖向振动加速度沿衬砌拱圈有拱脚向拱顶传递时逐渐降低的趋势;横向振动加速度由衬砌拱圈拱脚向拱顶传递时,在拱脚处最大,之后出现显著下降后向拱顶呈现逐渐增大的传递趋势;衬砌拱圈振动加速度响应在拱圈中的传递规律与列车所在位置无关,但当测点位于近车一侧时。试想,若近车一侧衬砌存在缺陷,那么列车荷载此时所造成的安全隐患也越大。
提取实测过程中不同列车时速作用下衬砌墙脚加速度的频谱,分析发现衬砌振动加速度频谱受列车时速影响较小,主要受列车轮对固有频率和轨道不平顺影响,衬砌振动加速度优势频率为186.7 Hz,对应列车轮对垂向振动第二阶固有频率。
由以上数据的分析,基本了解了列车荷载引起的振动响应在隧道衬砌拱圈上的传递特性和衬砌振动加速度频率的分布规律,但由于数据有限且测试过程中未能测试隧道拱顶的振动响应,此处引用数值计算方法,选用合适的模型及边界,以实测数据为依据,模拟计算隧道在列车不同时速下的拱顶区域的振动响应规律。
隧道在列车振动荷载的作用下,其振动响应以中、低频成分为主,采用稳定性良好的Newmark隐式积分算法,根据动力学原理,隧道结构体系在t+Δt时刻的动力平衡微分方程表示为:
式中:M为体系总体质量矩阵,是由各单元的质量矩阵组合而成,体系的单元质量矩阵可表示为:
K为体系总体刚度矩阵,是由各单元的刚度矩阵组合而成,各单元刚度矩阵可表示如下:
式中:t为单元厚度;Δ为单元面积;B为应变矩阵;Dep为弹塑性矩阵。
C为总体阻尼矩阵,由Rayleigh线性组合法确定:
式中,α、β分别为与结构体系质量和刚度相关的阻尼常数,可以按照两种不同的震动频率下测得的阻尼比进行确定。
![]() 分别为体系内各质点处在t+Δt时刻的加速度向量、速度向量和位移向量。
分别为体系内各质点处在t+Δt时刻的加速度向量、速度向量和位移向量。
F为列车振动荷载向量。
根据试验测试高铁线路隧道现场水文地质状况,建立隧道有限元模型,模型尺寸如图1所示。隧道上层覆土厚度选取实际厚度20m,整体模型与网格划分如图5所示。为便于计算,在建立有限元模型时,视其为连续、均质、各向同性介质,隧道围岩、初期支护与衬砌均采用CPS4R单元进行计算。

图5 数值模型及网格
Fig.5 Numerical model and mesh
围岩材料属性采用D-P准则,由于在列车荷载作用下,隧道不出现塑性变形,将支护结构视为全弹性材料。围岩物理力学参数参照地质资料和现行《铁路隧道设计规范》[19]进行选取,选用实测隧道实际Ⅳ级围岩,围岩重度19.5 kN/m3,弹性模量2.8 GPa,泊松比0.3。初期支护重度20kN/m3,弹性模量23.7 GPa,泊松比 0.21。二次衬砌重度25 kN/m3,弹性模量31 GPa,泊松比0.23。采用黏弹性边界作为边界条件,即在截断的边界上同时施加黏性阻尼器与弹簧。
首先在静力分析步中仅施加重力荷载进行计算,进而提取结构的应力和约束反力,将应力与约束反力导入计算模型进行应力平衡,然后运用隐式动力学算法添加列车荷载对模型再次计算。实测时列车通过隧道断面所用时间为2.5 s左右,此处设置分析步时间3 s进行计算,即动力隐式分析步时长设置为3 s。
列车荷载采用考虑了轮轨力在线路上的移动与叠加效应,并且考虑钢轨的分散作用和轨道不平顺的影响等因素的激振力函数[20]:
文中选取列车轴重为16 t,列车簧下质量取为M0=800kg,其余各参数选取与计算参见文献[20],其中轮轨力频率值是根据部分实测列车以200km/h、250km/h和300km/h速度级行驶下的轮轨力频谱分析所得,考虑了轮轨力中的高、中、低频成分,中频成分取衬砌加速度优势频率186.7 Hz,而高频中增加了轨道不平顺的假设,以求式(5)能够与实测值接近,所以计算结果中的频率即为公式计算中所选取的三个ωi频率,能够近似模拟实际衬砌受力状态,得到列车不同时速行驶时所对应的激振力。
数值计算数据由列车荷载加载一侧拱脚每隔10°取至拱顶,相应的在远离荷载一侧,采取与下行线一侧对称方式由拱脚取至拱顶,计算模型数据提取点布置如图6所示,各提取点对应角度见表2所示。
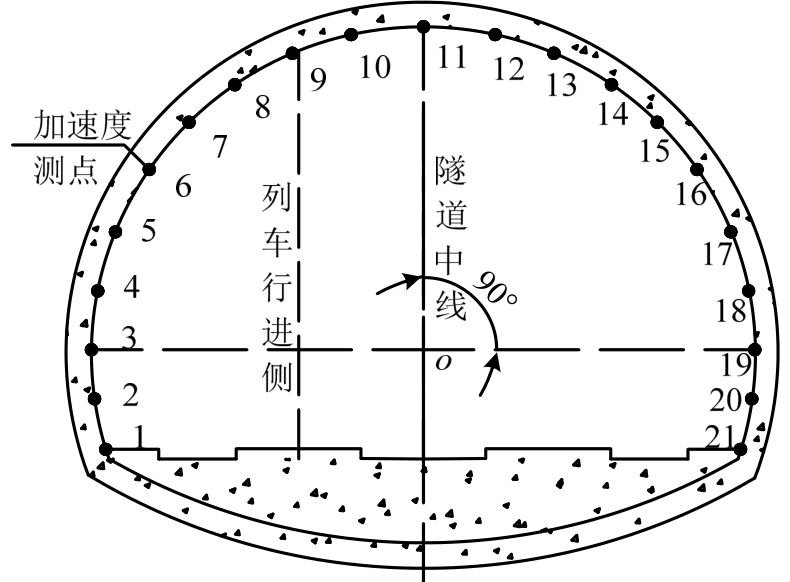
图6 模型数据提取点布置
Fig.6 Model data extraction point layout
表2 观测点在拱圈内对应角度值
Table2 Observation points in the corresponding value of the angle of arch

对提取的横向与竖向加速度数据进行统计,选取各观测点竖向与横向加速度峰值进行数据分析,并选择列车时速为260km/h、320km/h时实测数据与模型计算数据进行对比分析,如图7~图10所示。
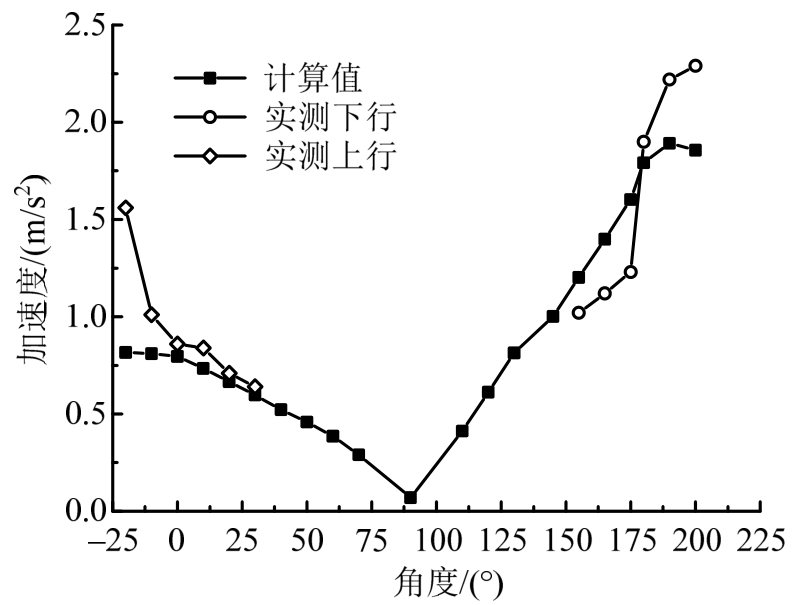
图7 260km/h 实测竖向与模型计算数据对比
Fig.7 Comparison of measured vertical acceleration of 260km/h and model calculation data
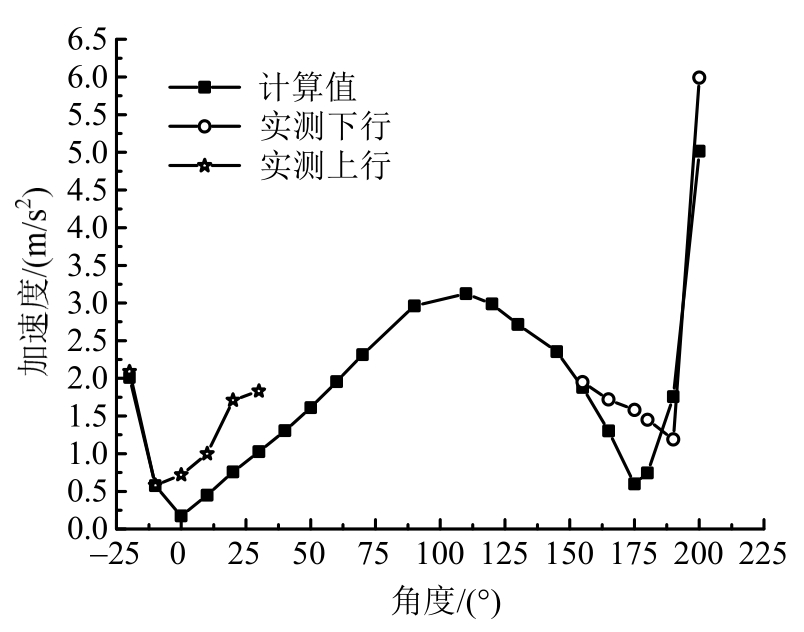
图8 260km/h实测横向与模型计算数据对比
Fig.8 Comparison of measured transverse acceleration of 260km/h and model calculation data
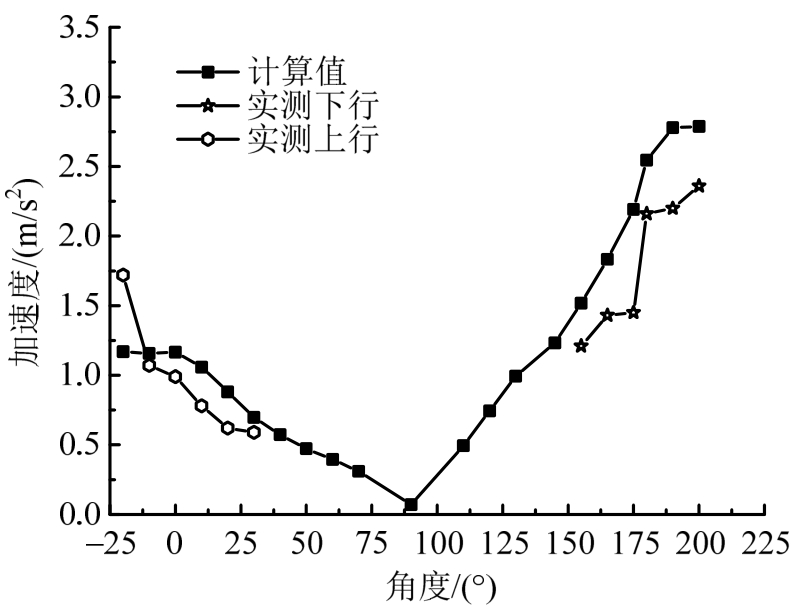
图9 320km/h 实测竖向与模型计算数据对比
Fig.9 Comparison of measured vertical acceleration of 320km/h and model calculation data
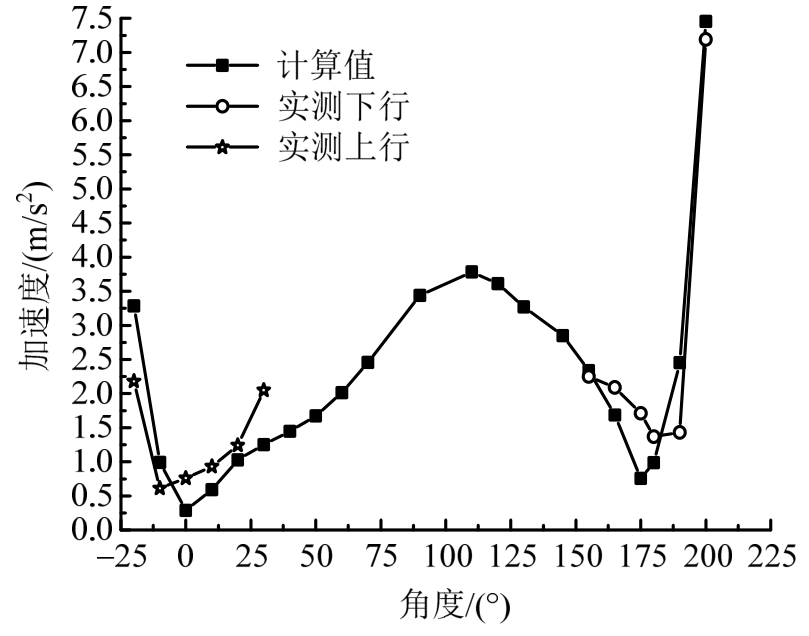
图10 320 km/h 实测横向与模型计算数据对比
Fig.10 Comparison of measured transverse acceleration of 320km/h and model calculation data
由图7~图10分析可知,列车在不同时速下通过隧道时,引起的隧道衬砌加速度响应,其数值模型计算结果与实测值基本吻合,且具有相同的传递趋势。说明有限元模型各参数的选取符合实际,可以用以计算并作为对实际测量数据的弥补与预测。
从图11与图12分析得知,隧道衬砌竖向或横向加速度响应随着列车时速的增大而增大;不同列车速度下衬砌竖向加速度响应在拱顶位置(90°)随列车时速的增加,其变化不明显,说明衬砌拱圈竖向加速度响应传递至拱顶位置时振动响应加速度幅值很低;衬砌拱圈横向加速度传递至拱顶位置时,其随着速度增加而响应增大规律明显,但横向加速度在圆心水平位置0°与180°时,其幅值较低,且速度的变化对幅值没有明显影响。
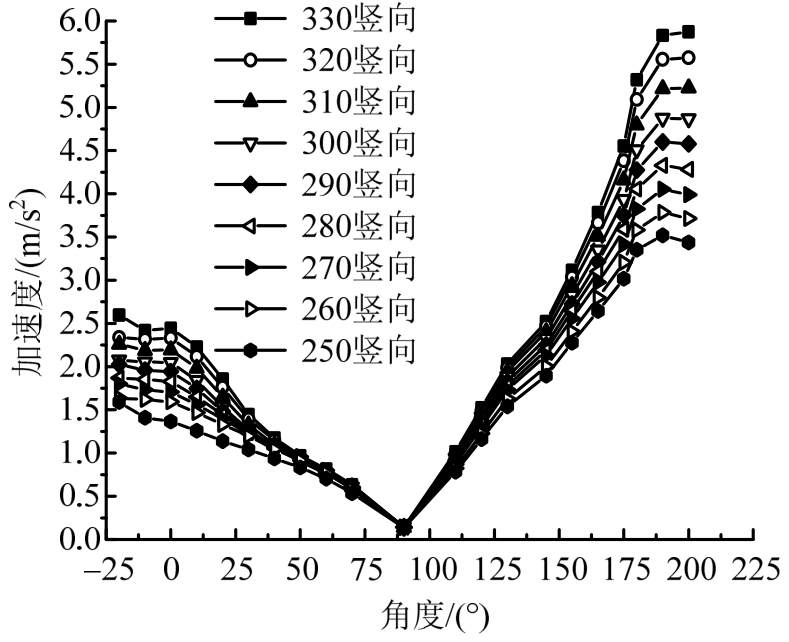
图11 不同时速下拱圈竖向振动加速度响应对比图
Fig.11 The vertical vibration acceleration of arch under different speeds response comparison chart

图12 不同时速下拱圈横向振动加速度响应对比图
Fig.12 The transverse acceleration of arch under different speeds response comparison chart
根据数值计算结果,为更好地探究隧道衬砌沿拱圈横向加速度振动传递数据曲线与竖向加速度振动数据曲线的特性,将数据振动加速度数据与观测点对于隧道拱圈圆心与水平轴角度建立函数关系,参考实测值数据,对拱圈振动响应特性进行逼近拟合。函数中涉及角度与加速度幅值之间的关系,宜采取三角函数展开式对数据进行拟合,根据计算,三项及以下的三角函数拟合度较低,而四项与五项三角函数组合拟合度较好,但五项函数较四项函数在实测值接近程度上无明显优势,故优选四项函数表达式。因此假设隧道衬砌在列车荷载作用下,衬砌竖向振动与横向振动加速度沿拱圈传递随速度变化的经验函数为:
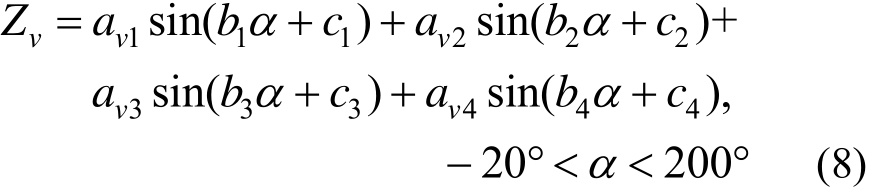
式中:Zv为拱圈观测点处竖向振动加速值;av1、av2、av3、av4为与速度相关的竖向加速度分项幅值;α为观测点在隧道衬砌拱圈对应圆心与水平轴角度;b1=0.0139,b2=0.02862,b3=0.06531,b4=0.09863,c1=0.06529,c2=2.8058,c3=1.3154,c4=-4.7562。

式中:Zt为拱圈观测点处横向振动加速值;at1、at2、at3、at4为与速度相关的横向加速度分项幅值;bt1=0.00856,ct1=0.25256,bt2=0.0708,ct2=1.3784,bt3=0.0751,ct3=4.2123,bt4=0.07768,ct4=0.90152。
因a所表示的加速度三角函数分项幅值随速度的变化产生较大变化,故考虑进一步探究a与v(v>0)的数学关系,并拟通过数学表达式建立二者既定物理单位下的数值关系。表达方式通常有多项式、三角函数表达式、指数对数表达式等形式,经过不同表达方式的拟合效果在实际值逼近度和公式繁简程度等方面对比,最终得出:
式中:m11=13.04,n11=0.07718,q11=0.268,m12=1.016,n12=6.282,q12=0.4051,m13=1.747,n13=3.244,q13=0.8784。
式中:m21=3.569,n21=0.04648,q21=0.8869,m22=1.177,n22=4.589,q22=1,m23=1.755,n23=2.059,q23=0.6522。

式中:m31=5697,n31=65.39,q31=1.295,m32=0.2833,n32=74.12,q32=2.444,m33=0.09285,n33=91.87,q33=35.3。
式中:m42=0.1761,n41=0.953,q41=1.204,m42=0.1181,n42=1.566,q42=-2.1,m43=0.01464,n43=4.68,q43=3.528。
式中:k=0.04373,p=-0.363。
式中:ξ21=31.73,ψ21=0.02429,τ21=11.6,ξ22=7.591,ψ22=0.5211,τ22=-19.75,ξ23=10.82,ψ23=0.9965,τ23=-13.33。
式中:ξ31=4382,ψ31=0.00437,τ31=0.01354,ξ32=9.897,ψ32=3.056,τ32=-2.087,ξ33=16.38,ψ33=7.15,τ33=4.506。
式中:ξ41=169.4,ψ41=1.1,τ41=1.35,ξ42=139.4,ψ42=1.319,τ42=-1.706,ξ43=6.613,ψ43=6.73,τ43=4.692。
将实际车速与拱圈角度代入拟合曲线公式进行计算,并将拟合值与实测值进行对比分析,此处以320km/h车速为例,绘制计算值、实测值与拟合值得对比图,如图13、图14所示。
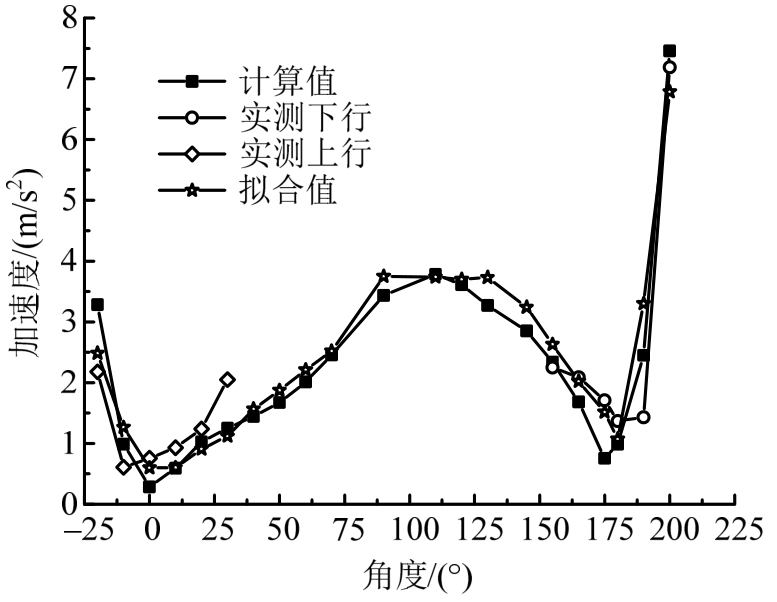
图13 320km/h 竖向加速度数据对比
Fig.13 Comparison of 320km/h vertical acceleration data
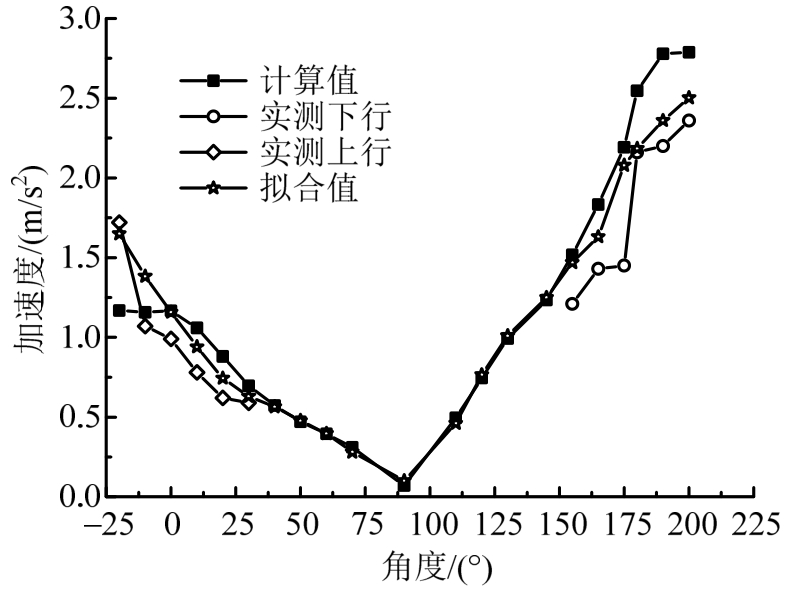
图14 320km/h 横向加速度数据对比
Fig.14 Comparison of 320km/h transverse acceleration data
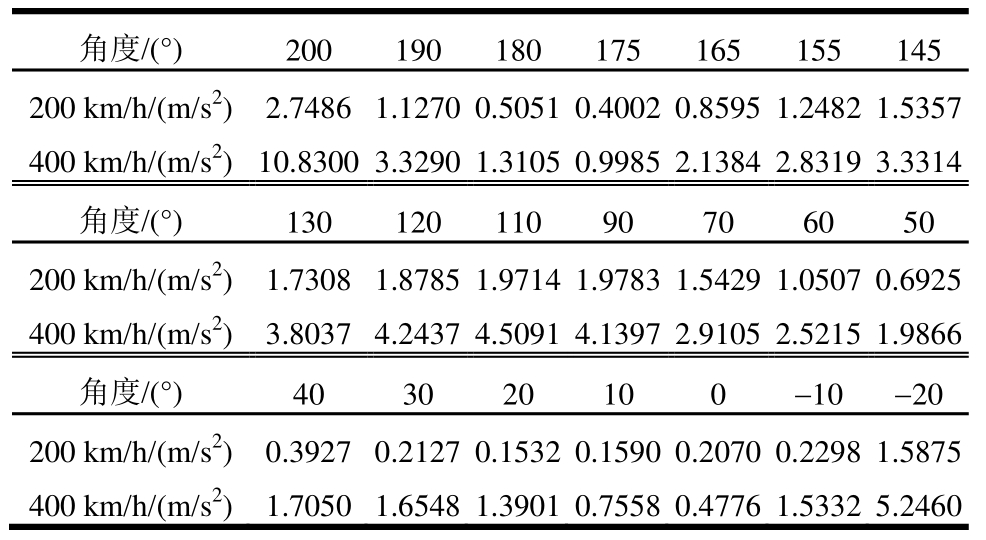
由全速度计算数据分析可知,拟合曲线计算结果与实际数据结果较为接近,且具有相近规律性,误差范围控制在10%~15%,衬砌竖向振动与横向振动加速度沿拱圈传递时,其幅值随速度变化的相应规律与特性在一定程度上,能够代替实测数据对衬砌振动响应进行指导,从而预测列车通过隧道时,隧道衬砌各断面角度位置加速度响应情况。此处,将时速200km/h与400km/h代入加速度拟合公式进行计算,并将竖向加速度与横向加速度计算结果列于表3、表4,如图15、图16所示。由表可知,当车速接近400km/h时,隧道衬砌拱脚横向加速度增大到10.83 m/s2,接近1.1g。
表3 200km/h与400km/h车速下衬砌竖向加速度预测值
Table3 Prediction value of vertical acceleration of lining under 200km/h and 400km/h

表4 200km/h与400km/h车速下衬砌横向加速度预测值
Table4 Prediction value of transverse acceleration of lining under 200km/h and 400km/h
综上所述,隧道振动响应数值模拟与实测数据趋势基本吻合,表明所建立的数值模型具有较好的适用性和可信性。研究结果揭示了高速列车振动荷载在衬砌拱圈中表现出一定的传递规律。其主要结论有以下几个方面。
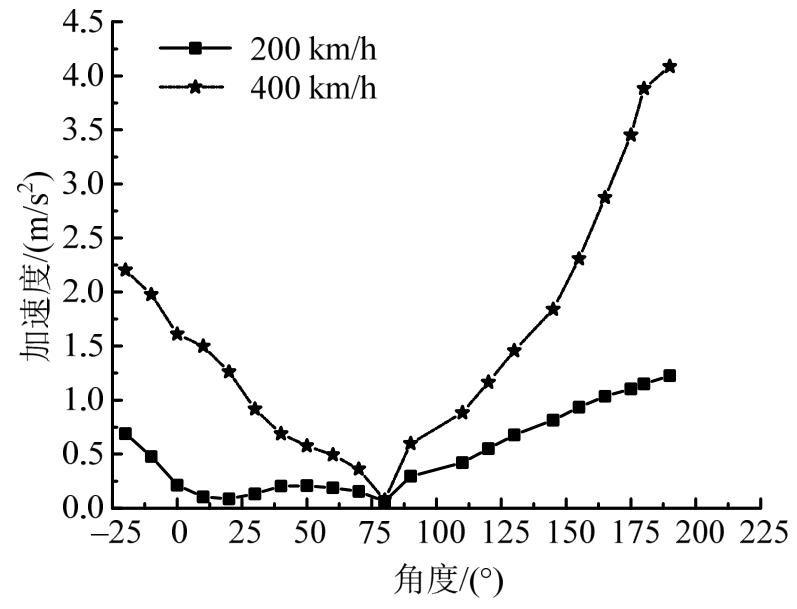
图15 200km/h与400km/h车速下衬砌竖向加速度预测值
Fig.15 Prediction value of vertical acceleration of lining at the speed of 200km/h and 400km/h
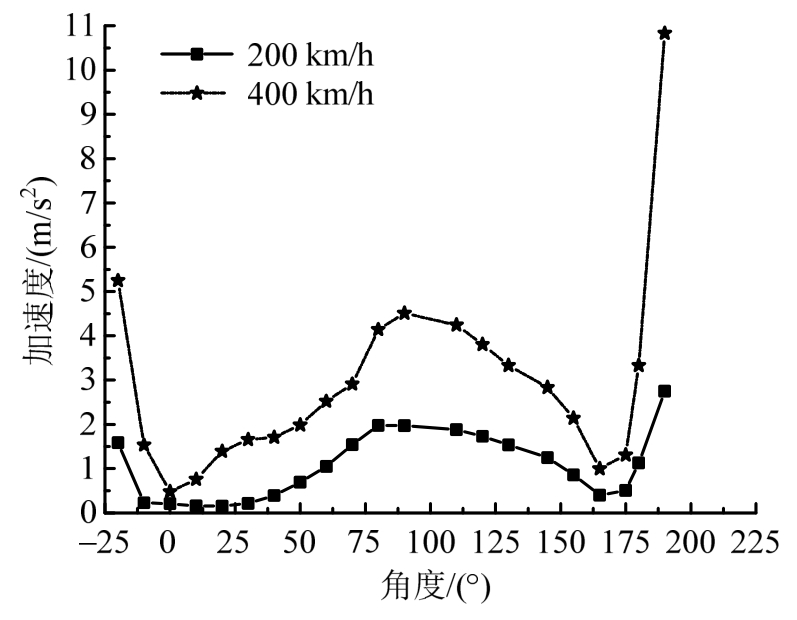
图16 200km/h与400km/h车速下衬砌横向加速度预测值
Fig.16 Prediction value of transverse acceleration of lining at the speed of 200km/h and 400km/h
(1)列车以不同的车速通过隧道时,引起的衬砌振动响应加速度幅值随列车车速的增大而增大且传递规律一致;竖向响应振动加速度由拱脚向拱顶呈现下降趋势,衬砌近车一侧振动响应较远车一侧剧烈;横向振动响应加速度幅值由拱脚向圆心水平180°位置有明显降低,并由水平位置向拱顶呈现增大趋势,也同样表现为近车一侧较远车一侧振动响应明显。
(2)有限元数值计算结果与实测值结果基本吻合,模型计算结果符合实际,可用以计算并作为对实际测量数据的补充与预测;不同列车时速下引起的隧道衬砌竖向振动加速度在拱顶位置较小,且随列车时速增大而变化趋势不明显;衬砌横向振动在拱顶位置变化规律明显随列车速度增大而增大;不同列车时速下引起的隧道衬砌横向振动在隧道圆心水平位置(即0°与180°)随列车时速变化不明显。
(3)拟合了列车在不同时速下引起的隧道衬砌振动响应横向与竖向振动加速度的经验公式,能够为后续研究提供参考。
参考文献:
[1]闫维明,聂晗,任珉,等.地铁交通引起地面振动的实测与分析[J].铁道科学与工程学报,2006,3(2):1―5.Yan Weiming,Nie Han,Ren Min,et al.In situ experiment and analysis of ground surface vibration induced by urban subway transit[J].Journal of Railway Science and Engineering Ground Vibration 2006,3(2):1―5.(in Chinese)
[2]夏禾,王逢朝.地铁列车振动对邻近建筑物的影响[J].北方交通大学学报,1999,23(2):45―48.Xia He,Wang Fengzhao.Vibration effects of subway trains on surrounding buildings[J].Journal of Northern Jiaotong University,1999,23(2):45―48.(in Chinese)
[3]张玉娥,白宝鸿,张昀青.埋深对地铁区间隧道列车振动响应的影响[J].振动与冲击,2006,25(3):58―60,65.Zhang Yu’e,Bai Baohong,Zhang Yunqing.Influence of subway burial depth on dynamic response of train[J].Journal of Vibration and Shock,2006,25(3):58―60,65.(in Chinese)
[4]Degrande G,Clouteau D,Othman R,et al.A numerical model for ground-borne vibrations from underground railway traffic based on a Periodic finite element-boundary element formulation[J].Journal of Sound and Vibration,2006,293(3/4/5):645―666.
[5]Landon transportation office of the scientific advisor:Vibration measurement at bake street[R].Jubilee Line,London,England,1982.
[6]Degrande G,Schevenelsa M,Chatterjeea P,et al.Vibrations due to a test train at variable speeds in a deep bored tunnel embedded in london clay[J].Journal of Sound and Vibration,2006,293(l):626―644.
[7]潘昌实,谢正光.地铁区间隧道列车振动测试与分析[J].土木工程学报,1990,23(2):21―28.Pan Changshi,Xie Zhengguang.Test and analysis of train vibration in subway tunnel[J].Journal of Civil Engineering,1990,23(2):21―28.(in Chinese)
[8]潘昌实,李德武,谢正光.北京地铁列车振动对环境影响的探讨[J].振动与冲击,1995(4):29―34.Pan Changshi,Li Dewu,Xie Zhengguang.Vibration Effects of Beijing Sunway Traffic on The Environment[J].Journal of Vibration and Shock,1995(4):29―34.
[9]李德武.列车振动对隧道衬砌影响的分析[J].兰州交通大学学报,1997(4):24―27.Li Dewu.Analysis of the influence of train vibration on tunnel lining[J].Journal of Lanzhou Jiaotong University,1997(4):24―27.(in Chinese)
[10]李德武,高峰.金家岩隧道列车振动现场测试与分析[J].兰州交通大学学报,1997(3):7―11.Li Dewu,Gao Feng.In-situ measurement and frequency-spectrum analysis of traffic vibrations in Jinjiayan tunnel[J].Journal of Lanzhou Jiaotong University,1997(3):7―11.(in Chinese)
[11]李德武,高峰.隧道基底结构列车振动现场测试与分析[J].甘肃科学学报,1999,11(1):52―54.Li Dewu,Gao Feng.On site test and analysis of train vibration in basement structure[J].Journal of Gansu Science,1999,11(1):52―54.(in Chinese)
[12]高峰.铁路隧道列车振动响应分析[J].兰州铁道学院学报,1998,17(2):6―12.Gao Feng.Vibration response analysis of railway tunnel[J].Journal of Lanzhou Railway Institute,1998,17(2):6―12.(in Chinese)
[13]王祥秋,杨林德,高文华.铁路隧道提速列车振动测试与荷载模拟[J].振动与冲击,2005,24(3):99―102.Wang Xiangqiu,Yang Linde,Gao Wenhua.Railway tunnel test and train vibration load simulation[J].Journal of Vibration and Shock,2005,24(3):99―102.(in Chinese)
[14]王祥秋,杨林德,周治国.列车振动荷载作用下隧道衬砌结构动力响应特性分析[J].岩石力学与工程学报,2006,25(7):1337―1342.Wang Xiangqiu,Yang Linde,Zhou Zhiguo.Dynamic response analysis of tunnel lining structure under train vibration load[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(7):1337―1342.(in Chinese)
[15]李亮,张丙强,杨小礼.高速列车振动荷载下大断面隧道结构动力响应分析[J].岩石力学与工程学报,2005,24(23):4259―4259.Li Liang,Zhang Bingqiang,Yang Xiaoli.Analysis of dynamic response of large cross-section tunnel under vibration load induced by high speed train[J].Chinese Journal Rock Mechanics and Engineering,2005,24(23):4259―4259.(in Chinese)
[16]吕鹏,宗刚,李文涛,等.地铁引发场地振动的实测信号能量分析[J].工程力学,2013,30(S1):325―328.Lü Peng,Zong Gang,Li Wentao,et al.Energy analysis of ground vibration induced by subway trains[J].Engineering Mechanics,2013,30(Suppl 1):325―328.(in Chinese)
[17]席兆凯,陈清军.地铁运行引起地面振动与噪声的实测分析[C]// 全国结构工程学术会议,2014.Xi Zhaokai,Chen Qingjun.Measurement analysis of ground vibration and noise caused by subway operation[C]// National Conference on Structural Engineering,2014.(in Chinese)
[18]巴振宁,梁建文,金威.高速移动列车荷载作用下层状饱和地基-轨道耦合系统的动力响应[J].工程力学,2015,32(11):189―200.Pakistan Zhenning,Liang Jianwen,Jin Wei.Dynamic response of coupled system of track and layered fluid-saturated ground under moving high-speed loads[J].Engineering Mechanics,2015,32(11):189―200.(in Chinese)
[19]中铁二院工程集团有限责任公司.铁路隧道设计规范(TB 10003—2016)[M].北京:中国铁道出版社,2017.China Railway Eryuan Engineering Group Co.Ltd.Code for Design of Railway Tunnel(TB 10003—2016)[M].Beijing:China Railway Culture Medie Co.Ltd,2017.(in Chinese)
[20]梁波,罗红,孙常新.高速铁路振动荷载的模拟研究[J].铁道学报,2006,28(4):89―94.Liang Bo,Luo Hong,Sun Changxin.Simulated study on vibration load of high speed railway[J].Journal of China Railway Society,2006,28(4):89―94.(in Chinese)
VIBRATION RESPONSE TRANSMISSION OF LINING ARCH DUE TO TRAIN SPEED-CHANGING VIBRATION LOAD
TIAN Tian1,LEI Yang2,QI Fa-lin2,LI Guo-qing2
(1.China Academy of Railway Science,Beijing 100081,China;2.China Academy of Railway Science,Infrastructure Inspection Research Institute,Beijing 100081,China)
Abstract:Through the field tests,the study finds that the vibration of a lining arch under train load grows up with the increasing of train speed,and that the lateral and vertical vibrations of the arch show different transfer laws.A finite element model was established based on ABAQUS,and the vibration response of a tunnel lining arch under train loads at different speeds was analyzed by an implicit method.The study results show that:the calculation results of finite element agree well with the measured values,which could be used as a supplement and forecast of the actual measurement data;and the vibration response of tunnel grow up with the increasing of train speed;the accelerations of the vibration response of lining caused by different speeds are consistent;and the vertical vibrations of the lining caused by different train speeds are smaller in the vault,whose change is not obvious with the increasing of the train speed;and the lateral vibration of the lining arch increases obviously with the increasing of the train speed,but the different speed caused by transverse vibration in the horizontal positionof the center of lining tunnel(at 0° and 180°)with the train speed did not change significantly,and the vibration amplitude is lower;the empirical formula is fitted for the lateral and vertical vibration accelerations of the tunnel lining caused by different speed trains.
Key words:train load at different speeds;arch lining;vibration response;field tests;numerical simulation
中图分类号:U25
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.01.0065
文章编号:1000-4750(2018)05-0143-09
收稿日期:2017-01-16;修改日期:2017-09-19
基金项目:国家自然科学基金委员会-中国铁路总公司高速铁路基础研究联合基金项目(U1434211);国家重点基础研究发展计划项目(973计划)(2013CB036205)
通讯作者:齐法琳(1970―),男,山东龙口人,研究员,硕士,从事隧道检测技术研究(E-mail:qifl@rails.cn).
作者简介:田 甜(1988―),男,河南鹿邑人,助理研究员,博士生,从事桥梁与隧道工程方面研究(E-mail:14171008@bjtu.edu.cn);
雷 洋(1987―),男,山西太原人,助理研究员,硕士,从事动力学及检测技术研究(E-mail:leiyang@rails.cn);
黎国清(1966―),男,江西人,研究员,硕士,博导,从事铁路基础设施检测方面研究(E-mail:lgq_iic@126.com).