图1 楼盖试件构造尺寸详图
Fig.1 Dimensional details of floor specimens
管 宇1，周绪红1，2，卫世杰1，石 宇2
(1.长安大学建筑工程学院，西安710061；2.山地城镇建设与新技术教育部重点实验室，重庆大学，重庆 400045)
摘 要：对冷弯薄壁型钢-压型钢板楼盖和冷弯薄壁型钢—石膏基自流平砂浆组合楼盖足尺模型进行了人行荷载和激励锤冲击下的振动试验以及1 kN集中荷载作用下的静载试验，研究楼面板形式以及钢丝网布置对组合楼盖自振频率、阻尼比以及跨中竖向挠度的影响。研究表明：在压型钢板上浇筑石膏基自流平砂浆会降低组合楼盖的自振频率、阻尼比以及跨中竖向挠度，而在石膏基自流平砂浆中加入钢丝网并不会显著增加楼盖的动力特性以及减小楼盖的竖向挠度。采用ABAQUS有限元软件对试验模型进行模态分析，并对验证后的有限元模型进行了变参数分析，研究表明：增大楼盖梁腹板高度、楼盖梁板厚以及楼盖面板厚度，加强楼盖端部约束会提高冷弯薄壁型钢组合楼盖的基频、减小楼盖跨中挠度。理论计算时，可将楼盖等效为具有均匀质量和刚度的简支梁模型用于预测冷弯薄壁型钢组合楼盖的基频；推荐使用加拿大木楼盖挠度计算公式用于预测冷弯薄壁型钢组合楼盖在1 kN集中荷载作用下的跨中挠度。
关键词：冷弯薄壁型钢；石膏基自流平砂浆；组合楼盖；振动性能；试验研究
多层冷弯薄壁型钢结构住宅是一种新型的“绿色”住宅结构体系，对落实中央“节能、省地”的战略要求、建设节约型社会以及改善中小城镇居民的住宅条件具有重要社会意义和广泛应用前景。
周绪红等[1]对不同边界条件的冷弯薄壁型钢梁—定向刨花板(OSB)板组合楼盖进行了静力挠度及振动性能试验，结果表明：边界条件不同时组合楼盖在1 kN集中荷载作用下跨中挠度约为0.6 mm～0.9 mm，在动力荷载作用下自振频率均高于15 Hz。贾子文和周绪红[2―3]对不同构造设置的冷弯薄壁型钢-混凝土组合楼盖模型进行了动载试验，结果表明：构造设置不同时组合楼盖在动力荷载作用下自振频率约为10Hz～14 Hz，减小压型钢板与楼盖梁连接的螺钉间距及楼盖梁间距、设置刚性支撑件等侧向支撑构件均能够提高组合楼盖的基频。由试验现象可知，当人在楼盖上行走和弹跳时，OSB板组合楼盖较混凝土组合楼盖更易发生振动现象，给人不舒适的感觉，但混凝土组合楼盖自重较大、施工效率较OSB板组合楼盖低，故选择一种轻质、防火、舒适度高的楼面板材料是提高组合楼盖振动性能的关键因素。
Davis和Parnell等[4―6]对冷弯薄壁型钢—OSB板(以及纤维增强水泥板、石膏基胶合板上浇筑混凝土和压型钢板上浇筑混凝土)组合楼盖进行了振动试验，研究了楼盖梁开洞、楼盖跨度及吊顶等对组合楼盖振动性能的影响，建议采用阻尼比4%作为冷弯薄壁型钢梁组合楼盖的设计值，并在美国应用技术委员会(ATC)设计方法的基础上进行改进，提出了适用的振动舒适度设计方法。Xu等[7―8]对冷弯薄壁型钢—OSB板组合楼盖进行了跨中1 kN静载试验、振动试验以及现场检测，试验结果对比表明：现场测试组合楼盖的自振频率和阻尼比均比试验条件下的实测结果高，而楼盖梁跨中挠度则较小。魏健[9]和赵建华[10]对冷弯薄壁型钢—意杨胶合板组合楼盖进行了振动性能试验，测取组合楼盖的基本频率和阻尼比，并从舒适度角度对钢—木组合楼盖的设计提出了建议。基于文献[1]，李颖[11]推导了组合楼盖跨中挠度的简化计算公式，并提出用挠度来控制组合楼盖振动的实用设计方法以及控制楼盖振动的措施。
国外规范如美国钢结构设计协会AISC[12]、加拿大国家建筑法规NBCC[13]等对组合楼盖振动性能的评价标准相对完善，而我国现有规范如《高层民用建筑钢结构技术规程》(JGJ 99—2015)[14]、《钢结构住宅设计规范》(CECS 261—2009)[15]等对于楼盖自振频率的限制并不统一，而且自振频率的计算方法也不相同，目前缺乏可靠、统一的振动评价标准。
基于石膏基自流平材料具有良好的稳定性和流动性、施工操作简便、成型后表面光洁平整、强度较高、绿色环保等特点，采用石膏基自流平砂浆作为楼面板材料，以期在保证楼盖轻质、防火的情况下，大幅度提高楼盖的振动性能以及居住舒适度，而且楼面板不会因热胀冷缩而产生开裂、起鼓等现象。冷弯薄壁型钢—石膏基自流平砂浆组合楼盖由楼盖梁、边梁、刚性支撑件、压型钢板以及楼面板等组成，基本构造如图1(a)所示。楼盖梁采用单根冷弯薄壁型钢C形截面梁或拼合截面梁，楼面板采用压型钢板上浇筑石膏基自流平砂浆的组合楼板形式，组合楼盖的所有构件均通过自攻螺钉进行连接。
为编制国家或行业标准提供可靠依据，推动冷弯薄壁型钢结构在我国的发展与应用，对足尺冷弯薄壁型钢组合楼盖的振动性能和静力挠度进行试验研究和理论分析，研究楼面板形式、楼盖梁规格、楼盖面板厚度以及边界条件对组合楼盖基频和跨中挠度的影响，并在试验研究基础上，提出冷弯薄壁型钢组合楼盖动力荷载作用下自振频率和1 kN静力荷载作用下跨中挠度的计算方法和设计建议。
试验共设计3个组合楼盖试件，根据楼面板形式的不同进行编号，其中，试件FL-1楼面板形式为压型钢板；试件FL-2楼面板形式为在压型钢板上浇筑40mm厚C30石膏基自流平砂浆；试件FL-3楼面板形式为在压型钢板上浇筑40mm厚C30石膏基自流平砂浆，并设置单层钢丝网，其直径为1.9 mm，网格尺为60mm×60mm。试件主要参数见表1，试件构造尺寸见图1。
图1 楼盖试件构造尺寸详图
Fig.1 Dimensional details of floor specimens
表1 试件参数
Table1 Specimen parameters
注：表中C254×40×13×1.5表示梁腹板高度为254mm，翼缘宽度为40mm，卷边宽度为13mm，厚度为1.5mm；U254×40×1.5表示梁腹板高度为254mm，翼缘宽度为40mm，厚度为1.5mm；YX-14-63-820表示压型钢板波峰高度为14mm，波距为63mm，宽度为820mm。
组合楼盖总尺寸为3.6m×3.6m，采用ST4.8自攻螺钉连接C形与U形楼盖梁，C形楼盖梁间距为400mm，并在C形楼盖梁的支座处设置C100×35×12×1.5加劲件，如图1(a)。为了防止楼盖梁发生侧向扭转，在边部和中部楼盖梁之间设置3个C200×40×14×1.5刚性支撑件，在楼盖梁跨中位置的下翼缘垂直于梁的方向设置通长的扁钢带拉条，宽度为50mm，厚度为1mm，见图1(b)。热镀锌压型钢板板肋垂直于楼盖梁跨度方向布置，厚度为0.75mm，采用ST5.5自攻螺钉连接楼盖梁与压型钢板，周边螺钉间距为125mm，中间螺钉间距为250mm，见图1(c)。
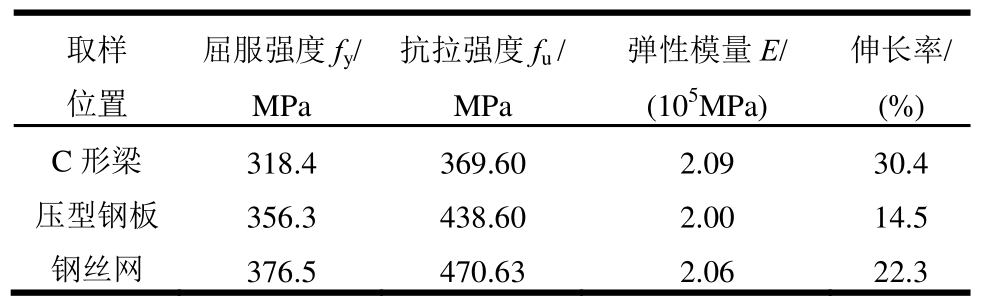
钢材材性试验根据《金属材料 拉伸试验第1部分：室温试验方法》(GB/T 228.1—2010)[16]的规定，从C形梁腹板平行于轧制方向切取3个板状试件以及从压型钢板、钢丝网上各取3个试样进行拉伸试验，钢材主要性能指标见表2。按照水∶石膏基自流平材料∶细砂=0.5∶1∶1.5的配合比拌制石膏基自流平砂浆时，留置边长为100mm的立方体和棱柱体试块进行同条件养护，测得28 d后石膏基自流平砂浆立方体抗压强度标准值为27.08 MPa，弹性模量为2.34×104MPa。
表2 钢材力学性能
Table2 Mechanical properties of steel and bars
因足尺试件自重较大及吊装不便，试验仅考虑两边支撑，梁端固结这种边界条件。采用钢框架台座和工字形梁作为试验支撑装置，钢框架台座的柱脚与地面导槽固定，工字形梁与台座顶面通过高强螺栓进行连接。试验时将组合楼盖沿U形边梁方向的两个端部分别搁置在钢梁翼缘上，采用连接件将U形边梁与钢梁翼缘进行固定，楼盖梁腹板与连接件通过自攻螺钉进行连接，钢梁翼缘与连接件进行焊接，以模拟梁端固结的边界条件，见图2。
图2 试验装置
Fig.2 Test device
冷弯薄壁型钢组合楼盖振动性能试验包括：1)为了测试组合楼盖的振动频率、阻尼比以及前3阶振型，对3个组合楼盖试件进行了两种方式的振动性能试验：①采用激励锤沿着楼盖跨度及宽度方向，在楼盖1/4跨位置处用力竖向锤击组合楼盖翼板进行激振，每次锤击位置间隔300mm，共锤击50次，每次采样持续试件为5 s，见图3(a)；②75 kg体重的男人以2 Hz步率依次沿着平行于C形楼盖梁方向、垂直于C形楼盖梁方向和对角线的方向行走，对组合楼盖施加冲击荷载，行走时间持续1 min，如图3(b)～图3(d)。试验中，动力响应由ICP(R)压电加速度传感器记录，动力特性通过LMS动态数据采集分析系统采用时域法进行测定采集。
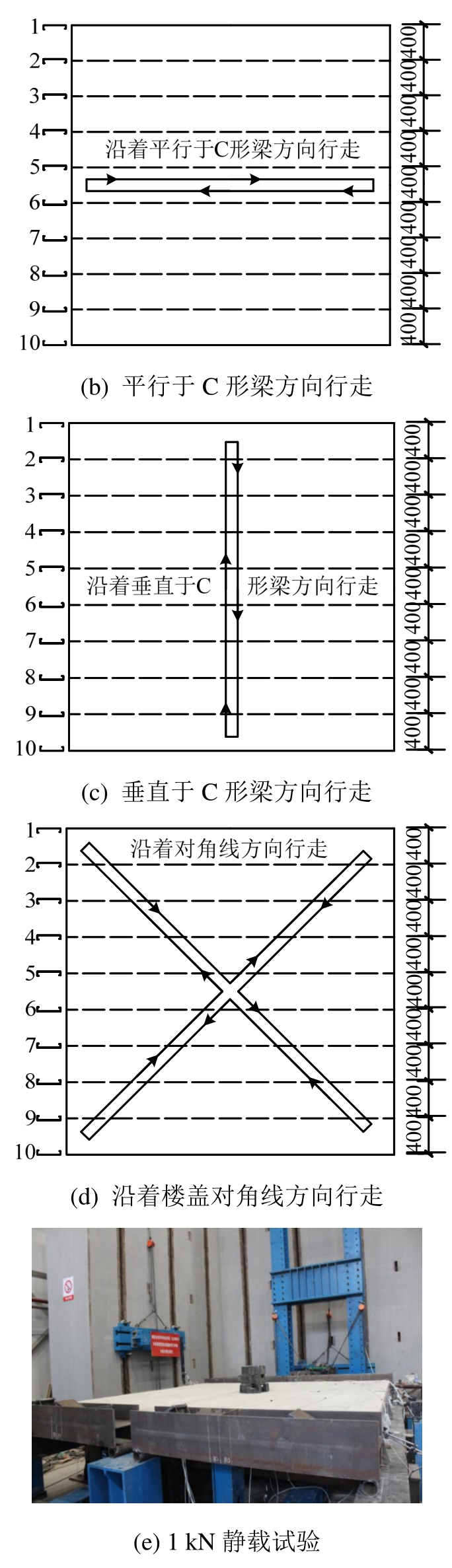
图3 试验加载方案
Fig.3 Test loading program
2)为了测试组合楼盖的竖向挠度，对3个组合楼盖试件进行了跨中1 kN静载试验。试验中，采用总质量为100kg的砝码作为1 kN集中荷载施加在组合楼盖中心位置处，以测得中间C形楼盖梁跨中下翼缘和压型钢板跨中底部在单位荷载作用下的挠度，试验持荷10min，试验加载工况见图3(e)。
测试组合楼盖在激励锤和正常行走激励下的动力特性时，采用压电加速度传感器测量楼盖的振动频率和阻尼比，压电加速度传感器测点布置见图4(a)，图中D1～D20表示压电加速度传感器的编号，共20个，分别粘贴在C形楼盖梁的下翼缘位置处，另一端通过ICP转换头连接到LMS动态数据采集分析系统，并通过计算机软件获得各测点的加速度信息。
测试在1 kN集中荷载作用下组合楼盖跨中挠度的位移计测点布置见图4(b)，图中将组合楼盖的中心位置设为坐标原点，楼盖梁跨度方向设为x轴，垂直于跨度方向设为y轴，位移计Y1和Y2布置在5号和6号楼盖梁下翼缘跨中位置处，以测量中间楼盖梁跨中位置的竖向挠度，位移计Y3布置在楼盖的压型钢板下方(坐标原点正下方)，以测量楼盖翼板中心位置的竖向挠度。
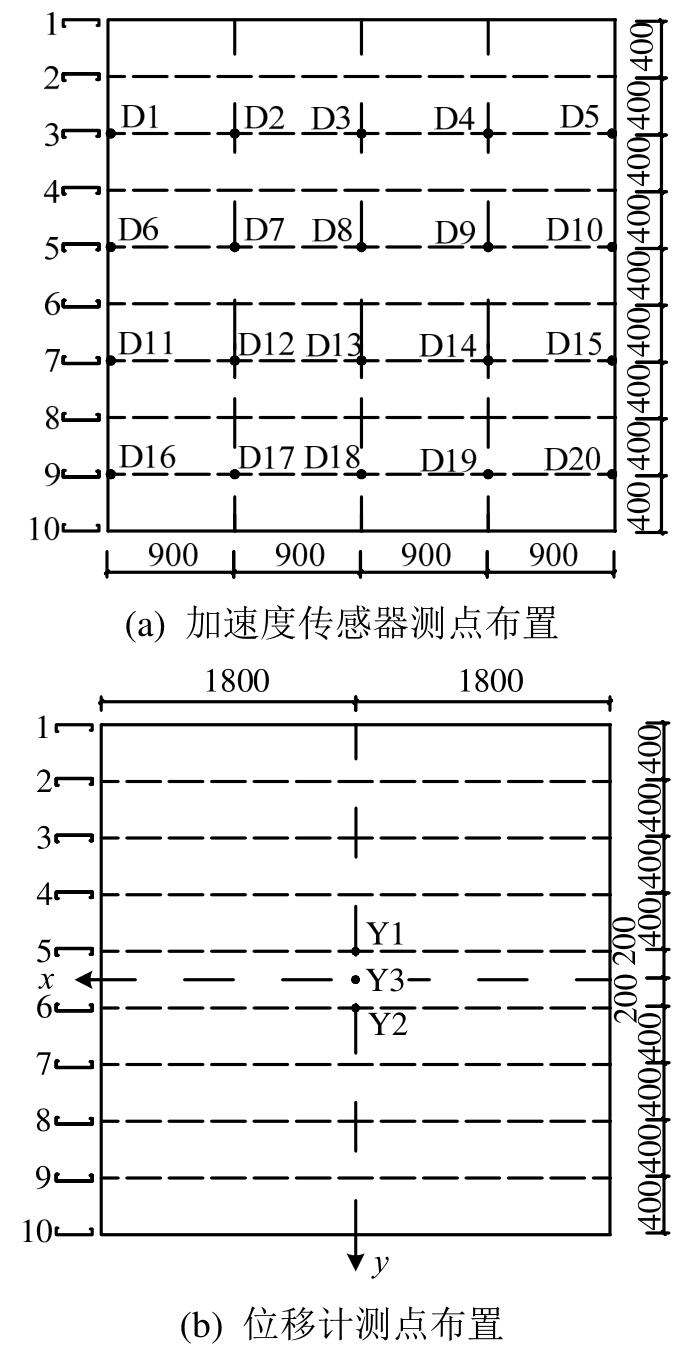
图4 测点布置
Fig.4 Layout of measuring points
冷弯薄壁型钢组合楼盖振动试验结果表明：
1)通过数据处理，可得到组合楼盖在两种工况下的前三阶自振频率和阻尼比，见表3。由表可知：①3个组合楼盖前三阶频率在激励锤和正常行走两种激励作用下测试结果相近，而阻尼比结果略有不同，表明自振频率和阻尼比是结构本身固有的动力性能，这些动力特性参数是由结构形式、质量分布、结构刚度、材料特性以及构造连接方法等因素决定的，并不会随着外部激励的改变而发生较大变化；②试件FL-2和试件FL-3的自振频率相近，且均小于试件FL-1的自振频率，表明石膏基自流平砂浆面板增大了组合楼盖的自重，降低了自振频率，组合楼盖的自振频率与自身质量成反比，同时在组合楼盖面板中增设钢丝网并不会显著增加楼盖的动力特性，在楼盖自重相同时，组合楼盖的自振频率与抗弯刚度成正比。组合楼盖FL-2前两阶振型见图5，可知冷弯薄壁型钢组合楼盖的振型符合其振动规律，前两阶振型图与楼盖前两阶自振频率相对应，表明试验各测点测量数据较准确，分析结果精度较高。
表3 楼盖在冲击荷载作用下的自振频率和阻尼比
Table3 Vibration frequencies and damping ratios of floors under impact load
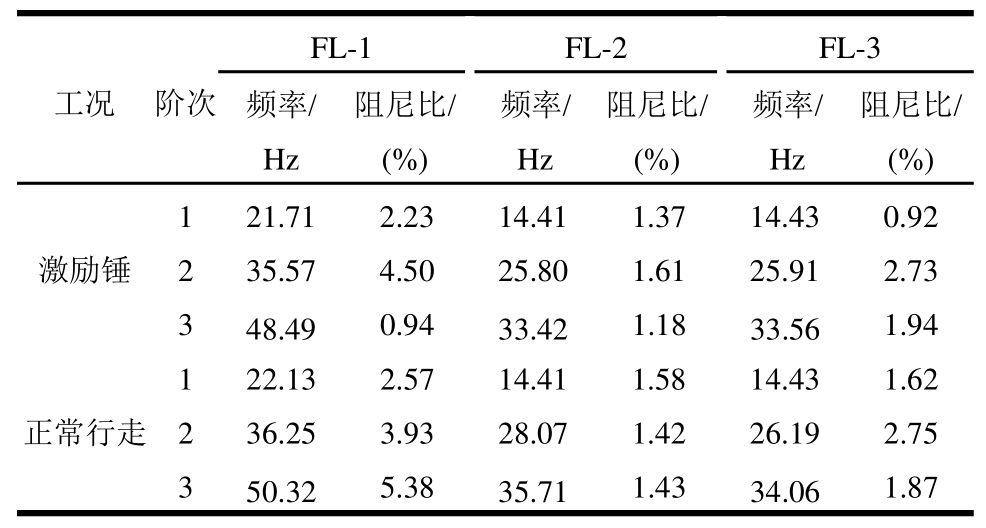
图5 组合楼盖FL-2振型图(试验)
Fig.5 Vibration mode of floor FL-2(test result)
组合楼盖的加速度响应与外部冲击荷载作用下的能量密切相关。图6为人行荷载作用下FL-2试件沿x轴和y轴方向各测点的功率谱密度分布图，曲线峰值点对应的频率即为楼盖的自振频率，表明楼盖在发生振动时，大部分能量集中在自振频率范围内。由图可知：①沿x轴方向和沿y轴方向不同测点的功率谱密度分布形状以及峰值点发生的位置相近，表明各测点测得组合楼盖的自振频率相近，组合楼盖的自振频率和频域分布与测点布置的位置无关；②功率谱密度曲线的峰值点大小随测点位置的不同而发生改变，当行走路径接近于测点位置时，该测点能量分布最大，而远离该测点的位置能量逐渐减小，而且支撑边测点测得的功率谱密度曲线峰值较自由边测点测得的功率谱密度曲线峰值小；③各测点功率谱密度曲线峰值发生的位置存在差异，原因为在人行荷载等外部冲击荷载作用下各楼盖梁的变形不能完全协调统一。
图6 人行荷载下FL-2试件各测点的功率谱密度分布图
Fig.6 Power spectral density distribution of FL-2 specimen measuring points under walking load
2)在1 kN集中荷载作用下，组合楼盖5号、6号楼盖梁及压型钢板底部x方向跨中竖向变形见图7，竖向位移计测取结果见表4。由图表可知：①在1 kN集中荷载作用下，5号和6号楼盖梁跨中挠度相近，且均小于压型钢板底部跨中挠度，表明楼面板与楼盖梁在受力时不能保证完全同步变形，压型钢板不平整，存在初始缺陷，且各构件之间存在施工间隙；②试件FL-2和试件FL-3楼盖梁和压型钢板底部跨中挠度相近，且均小于试件FL-1的跨中挠度，表明在压型钢板上浇筑石膏基自流平砂浆可以增加楼盖的抗弯刚度，减小楼盖的竖向挠度，而在石膏基自流平砂浆中加入钢丝网对降低楼盖的竖向挠度影响较小，主要原因与砂浆面板厚度较薄，以及试件在吊装过程中产生较多裂缝有关。
图7 组合楼盖在1 kN作用下沿x向竖向变形图
Fig.7 Vertical deformation alongxdirection of floors under 1 kN load
表4 楼盖跨中挠度有限元结果与试验结果对比
Table4 Comparison of floor mid-span deflection of finite element results and test results
采用ABAQUS有限元软件对试验试件进行有限元分析。冷弯薄壁型钢构件均采用壳单元S4R进行模拟，石膏基自流平砂浆楼板采用实体单元C3D8R进行模拟，钢筋网采用桁架单元T3D2进行模拟，自攻螺钉连接采用耦合螺钉连接位置处两个结点x、y、z三个方向平动自由度的方法进行模拟。冷弯薄壁型钢构件的单元网格密度取为300mm，石膏基自流平砂浆面板的单元网格密度取为450mm，钢丝网的单元网格密度取为20mm。为了保证组成组合楼盖的基本构件之间不出现相互穿透的现象，要求在相互接触的构件间建立摩擦接触，对于法向作用采用硬接触，对于切向作用采用库仑摩擦模型，抗滑移系数根据《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[17]中规定选为0.3。由于石膏基自流平砂浆黏结性较好，故在压型钢板与石膏基自流平砂浆面板之间建立tie约束，FL-3试件中的钢丝网采用Embedded region命令嵌入砂浆面板中，忽略了砂浆与钢丝网之间的黏结滑移问题。
钢材的本构关系采用双折线，按照材性试验结果进行选取，泊松比为0.3，钢材采用各向同性弹塑性材料模型及von Mises屈服准则。石膏基自流平砂浆的本构关系采用塑性损伤模型进行模拟，弹性模量为2.34×104MPa，泊松比为0.2。在全局坐标系的y方向定义重力加速度g=9.8 m/s2来考虑结构自重。有限元模型按照楼盖试件两边支撑，梁端固结的边界条件，约束U形边梁x、y、z三个方向的全部自由度，即Ux=Uy=Uz=0，θx=θy=θz=0。在模拟1 kN静载试验时，耦合放置砝码范围内的所有结点，施加y方向1 kN集中荷载来模拟试验荷载的施加。组合楼盖有限元模型见图8。
图8 组合楼盖有限元模型
Fig.8 Finite element model of composite floors
分别对3个有限元模型进行振动模态分析和1 kN集中荷载作用下的受力分析。楼盖前两阶自振频率有限元分析结果和试验结果对比见表5，楼盖跨中竖向挠度有限元分析结果和试验结果对比见表4，组合楼盖FL-2前两阶振型图见图9。由图表可知，有限元模型能够较好地模拟组合楼盖在激励作用下的自振频率以及1 kN集中荷载作用下楼盖的跨中挠度，有限元分析结果与试验结果误差小于10%，楼盖前2阶振型图与试验采集得到的前2阶振型图(图5)相吻合，表明有限元模型正确，建模方法可靠。
为研究楼盖梁腹板高度对组合楼盖基频和1 kN集中荷载作用下竖向挠度的影响，建立楼盖类型为冷弯薄壁型钢—压型钢板楼盖FL-1和冷弯薄壁型钢—石膏基自流平砂浆组合楼盖FL-2，楼盖梁规格分别为C205×40×14×1.5/U205×40×1.5、C255×40×14×1.5/U255×40×1.5和C305×40×14×1.5/U305×40×1.5，共6个有限元模型；模型中压型钢板规格为YX-14-63-820，厚度为0.75 mm，石膏基自流平砂浆采用C30级，厚度为40mm，自攻螺钉间距为125/250mm；在楼盖模型下翼缘跨中位置处设置通长扁钢带，宽50mm，厚1 mm，并在扁钢带中间及两端设置刚性支撑件，规格为C200×40×14×1.5；楼盖模型的边界条件为两边支撑、梁端简支。有限元分析结果见表6。
表5 楼盖自振频率有限元结果与试验结果对比
Table5 Comparison of floor natural frequency of finite element results and test results
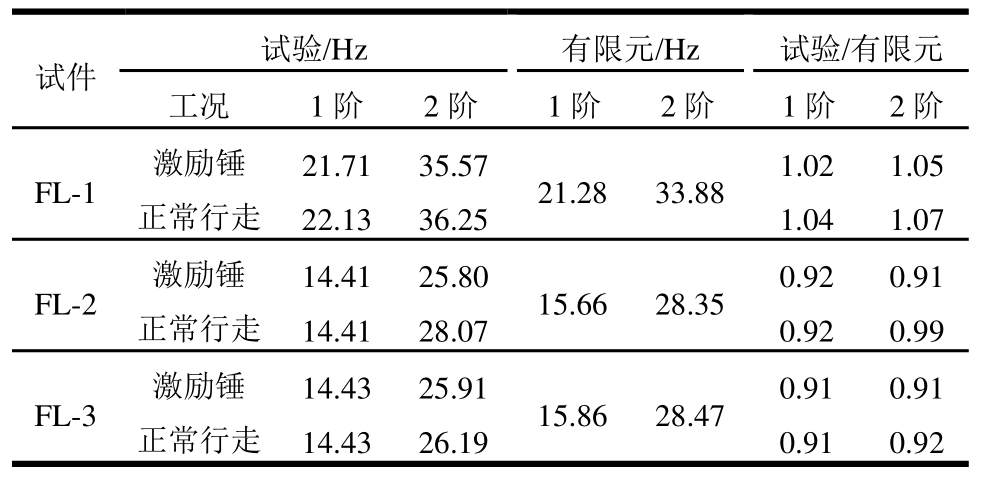
图9 楼盖FL-2振型图(有限元)
Fig.9 Vibration modes of floor FL-2(FEM results)
由表6可知，改变楼盖梁的腹板高度对组合楼盖的振动性能和静力挠度影响较大。当楼盖梁腹板高度由205 mm增大至305 mm时，冷弯薄壁型钢-压型钢板楼盖的基频依次增加15.1%和4.1%，中间楼盖梁跨中挠度依次降低29.4%和52.8%；而冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频依次增加0.7%和0.6%，中间楼盖梁跨中挠度依次降低18.2%和22.2%。原因为随着梁高的增加，楼盖抗弯刚度增大，使得楼盖跨中挠度降低、频率增大。表明楼盖的自振频率与刚度成正比。
表6 楼盖梁腹板高度的影响
Table6 Influence of web height of floor joists
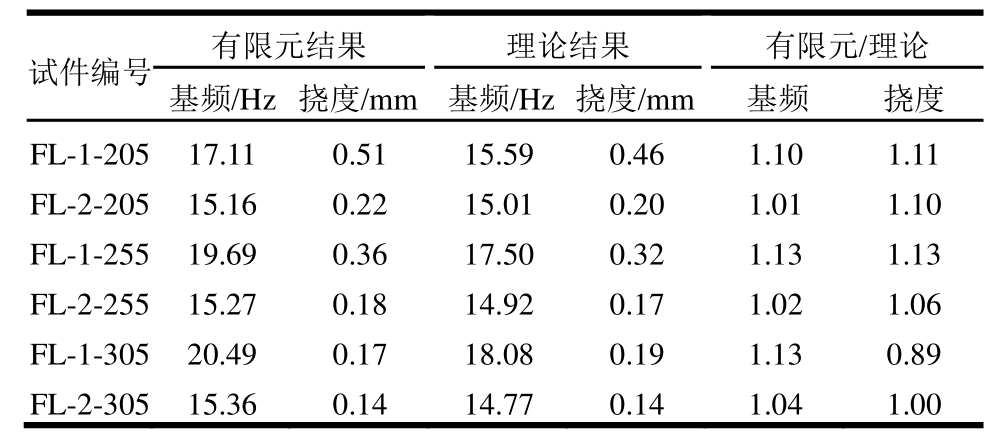
注：试件编号FL-1-205表示冷弯薄壁型钢-压型钢板楼盖模型中，楼盖梁的规格为C205×40×14×1.5和U205×40×1.5。
为研究楼盖梁板厚对组合楼盖基频和1 kN集中荷载作用下竖向挠度的影响，建立楼盖类型为冷弯薄壁型钢-压型钢板楼盖FL-1和冷弯薄壁型钢-石膏基自流平砂浆组合楼盖FL-2，楼盖梁规格为C255×40×14×t/U255×40×t，板厚t分别为1.09 mm、1.54 mm和1.73 mm，共6个有限元模型，其余楼盖模型参数同2.2节有限元模型，模型边界条件为两边支撑、梁端简支。有限元分析结果见表7。
表7 楼盖梁板厚的影响
Table7 Influence of slab thickness of floor joists
注：试件编号FL-1-1.09表示冷弯薄壁型钢-压型钢板楼盖模型中，C形和U形楼盖梁的板厚均为1.09 mm。
由表7可知，改变楼盖梁的板厚对组合楼盖的振动性能和静力挠度存在影响。当楼盖梁板厚由1.09 mm增大至1.73 mm时，冷弯薄壁型钢-压型钢板楼盖的基频依次增加2.8%和0.1%，中间楼盖梁跨中挠度依次降低23.9%和11.4%；而冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的基频依次增加1.9%和0.7%，中间楼盖梁跨中挠度依次降低5.3%和5.6%，原因为随着梁厚的增加，楼盖抗弯刚度增大，使得楼盖跨中挠度降低、频率增大。
为研究石膏基自流平砂浆面板厚度对组合楼盖基频和1 kN集中荷载作用下竖向挠度的影响，建立楼盖类型为冷弯薄壁型钢-石膏基自流平砂浆组合楼盖FL-2，楼盖梁规格为C255×40×14×1.5/U255×40×1.5，楼盖面板厚度分别为30mm、40mm、50mm和60mm，共4个有限元模型，其余楼盖模型参数同2.2节有限元模型，模型边界条件为两边支撑、梁端简支。有限元分析结果见表8。
表8 石膏基自流平砂浆面板厚度的影响
Table8 Influence of slab thickness of gypsum based self-leveling mortar
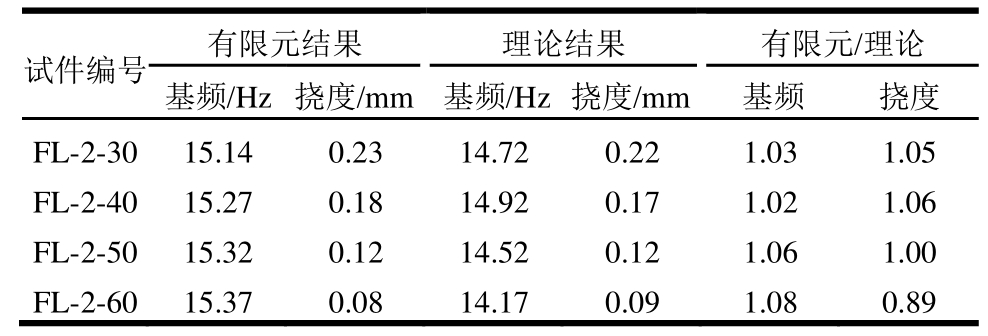
注：试件编号FL-2-30表示冷弯薄壁型钢-石膏基自流平砂浆组合楼盖模型中，石膏基自流平砂浆面板厚度为30mm。
由表8可知，改变石膏基自流平砂浆面板的厚度对组合楼盖的振动性能和静力挠度存在影响。当楼盖面板厚度由30mm增大至60mm时，组合楼盖的基频依次增加0.9%、0.3%和0.3%，中间楼盖梁跨中挠度依次降低21.7%、33.3%和33.3%，原因为随着楼盖面板厚度的增加，楼盖抗弯刚度增大，使得楼盖跨中挠度降低、频率增大，同时楼盖面板厚度的增加，增大了组合楼盖的自重，反而降低了楼盖的自振频率，故楼盖的基频增加并不显著。因此，楼盖的自振频率与刚度成正比，与质量成反比。
为研究楼盖端部约束条件对组合楼盖基频和1 kN集中荷载作用下竖向挠度的影响，建立楼盖类型为冷弯薄壁型钢-压型钢板楼盖FL-1和冷弯薄壁型钢-石膏基自流平砂浆组合楼盖FL-2，楼盖梁规格为C255×40×14×1.5/U255×40×1.5，模型边界条件分别为两边支撑和梁端简支A、两边支撑和梁端固结B、四边支撑和梁端简支C以及四边支撑和梁端固结D，共8个有限元模型，其余楼盖模型参数同2.2节有限元模型。有限元分析结果见表9。
由表9可知，加强楼盖端部约束能够提高组合楼盖的基频、减小楼盖跨中挠度。①对于相同的端部支撑条件，梁端固结下楼盖的基频大于梁端简支情况，其中冷弯薄壁型钢-压型钢板楼盖平均高出8.1%，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖平均高出5.0%；梁端固结下楼盖的跨中挠度小于梁端简支情况，其中冷弯薄壁型钢-压型钢板楼盖平均降低38.0%，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖平均降低25.8%。②对于相同的梁端约束条件，四边支撑情况下楼盖的基频均大于两边支撑的情况，其中冷弯薄壁型钢-压型钢板楼盖增加较小，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖平均高出3.0%；四边支撑情况下楼盖的跨中挠度小于两边支撑的情况，其中冷弯薄壁型钢-压型钢板楼盖平均降低1.4%，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖平均降低9.9%。
表9 楼盖端部约束条件的影响
Table9 Influence of floor end constraint conditions
注：试件编号FL-1-A表示冷弯薄壁型钢-压型钢板楼盖模型中，边界条件为两边支撑、梁端简支。
国内外对于楼盖振动性能的研究仍采用自振频率作为主要的评价指标。美国钢结构设计指南[12]规定轻质楼盖自振频率不得小于8 Hz，欧洲抗震规范[18]规定楼板自振频率不得小于9 Hz，加拿大国家建筑法规[13]规定楼板的自振频率要大于5 Hz。《钢结构住宅设计规范》(CECS 261—2009)[15]中规定住宅楼板的自振频率不宜小于8 Hz；《高层民用建筑钢结构技术规程》(JGJ 99—2015)[14]和《钢-混凝土组合楼盖结构设计与施工规程》(YB 9238—92)[19]要求组合楼板在永久荷载作用下的自振频率不得小于15 Hz。试验中楼盖FL-1、FL-2和FL-3在冲击荷载激励下的自振频率基本能满足国内外规定要求，表明该组合楼盖有较好的振动性能。
文献[1]建议对振动性能要求较高的冷弯薄壁型钢—OSB板组合楼盖的自振频率限值设为15 Hz。文献[2―3]建议冷弯薄壁型钢-混凝土组合楼盖在正常使用阶段的自振频率不应小于10Hz。由本文试验结果和影响因素分析结果可知，对于不同楼盖梁腹板高度、不同楼盖梁板厚、不同楼盖面板厚度以及不同边界条件下的组合楼盖，其中冷弯薄壁型钢-压型钢板楼盖的基频均大于17 Hz，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖的自振频率均大于14 Hz。由文献[1―3]和本文试验结果可知，在正常使用阶段永久荷载作用下，冷弯薄壁型钢—OSB板组合楼盖和冷弯薄壁型钢-压型钢板楼盖的基频相近，均大于15 Hz；而冷弯薄壁型钢-石膏基自流平砂浆组合楼盖和冷弯薄壁型钢-混凝土组合楼盖的基频较为接近，均大于10Hz。故对冷弯薄壁型钢组合楼盖在冲击荷载激励下的基频限值进行规定，见表10。
表10 组合楼盖振动性能及静力挠度评价指标
Table10 Vibration performance and static deflection evaluation index of composite floors
国外规范对楼盖在1 kN集中荷载作用下的挠度限值进行了规定，其中瑞典准则[20](Ohlsson’s准则)规定楼面承受1 kN集中荷载作用时，跨中挠度不得大于1.5 mm；澳大利亚钢结构规范[21]规定1 kN集中荷载作用在楼板任何位置时，楼板挠度均应小于2 mm；加拿大准则[22](Onysko’s准则)规定楼盖的跨度在3.0m～5.5 m时，在1 kN集中荷载作用下楼板体系跨中挠度应小于1.5 mm。试验中楼盖FL-1、FL-2和FL-3在1 kN集中荷载作用下的跨中挠度均能满足国外规定要求，表明该组合楼盖有较好的抗弯刚度。
文献[1]建议冷弯薄壁型钢—OSB板组合楼盖在1 kN集中荷载作用下跨中挠度限值取为2 mm。由本文试验结果和影响因素分析结果可知，对于不同楼盖梁腹板高度、不同楼盖梁板厚、不同楼盖面板厚度以及不同边界条件下的组合楼盖，其中冷弯薄壁型钢—压型钢板楼盖在1 kN集中荷载作用下梁跨中挠度均小于0.6 mm，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖在1 kN集中荷载作用下梁跨中挠度均小于0.3 mm。为保证挠度指标与基频指标相统一，建议冷弯薄壁型钢—OSB板组合楼盖和冷弯薄壁型钢-压型钢板楼盖的跨中挠度限值取为2 mm，冷弯薄壁型钢-石膏基自流平砂浆组合楼盖和冷弯薄壁型钢-混凝土组合楼盖的跨中挠度限值取为1 mm，见表10。
国外规范给出了楼盖基频的计算公式，而我国规范并未对组合楼盖的基频计算方法进行规定。文献[23]指出冷弯薄壁型钢组合楼盖可通过等效为具有均匀质量和刚度的简支梁模型来计算其自振频率，计算模型不考虑剪切变形、转动惯性和轴向力的影响，并假定支撑楼盖端部的墙体不产生竖向压缩变形，组合楼盖两边支撑，梁端铰接的基频计算公式如下：
式中：f为楼盖的自振频率；ξ为考虑楼盖梁跨高比、腹板高厚比等因素影响的修正系数；v为与ξ对应的楼盖在均布荷载作用下跨中的最大挠度；q为单位长度的重量，包括楼面自重和楼面活荷载；l为组合梁的跨度；Es为钢材的弹性模量；I0为组合梁的换算截面惯性矩；ψ为考虑楼盖梁跨高比、腹板高厚比等因素影响的挠度修正系数。
对于楼盖梁规格为C255×40×14×1.5，梁腹板高厚比β为100～300的组合楼盖，当梁跨高比α<24时，ξ=0.6391+0.0027β-5×10-6β2；当梁跨高比α≥24时，ξ=1。当梁跨高比α处于8～28时：ψ=4.268-0.2208α+4.0×10-3α2。考虑四种边界条件A、B、C和D(同2.5节模型边界条件)对楼盖基频的影响时，参考文献[24]引入楼板在不同边界条件下的分配系数k，其中
，
及
，则楼盖基频可采用式(3)进行计算：
采用式(1)和式(3)计算楼盖FL-1和FL-2的基频结果与有限元结果对比见表6～表9。由表可知：文献[23]中基频计算方法考虑了楼盖梁的跨高比、腹板高厚比以及楼盖梁规格等因素影响的修正系数，文献[24]考虑了各种边界条件的分配系数，理论计算结果与有限元结果误差小于15%，有较好的参考价值，可用于预测冷弯薄壁型钢组合楼盖的基频。
我国规范并未规定组合楼盖在1 kN集中荷载作用下的跨中挠度公式，而国外规范计算楼盖跨中挠度公式的计算模型均是基于单根简支梁在跨中1 kN集中荷载作用下的结果。加拿大学者Onysko[22]提出了轻质木楼盖在1 kN集中荷载作用下挠度的计算方法，方法中引入了荷载分配系数DF以修正集中荷载作用，计算公式如下：
式中：P为1 kN集中荷载；L为梁的跨度；EIeff为组合楼盖的有效抗弯刚度，计算如式(5)；DF为荷载分配系数，计算公式如式(6)。
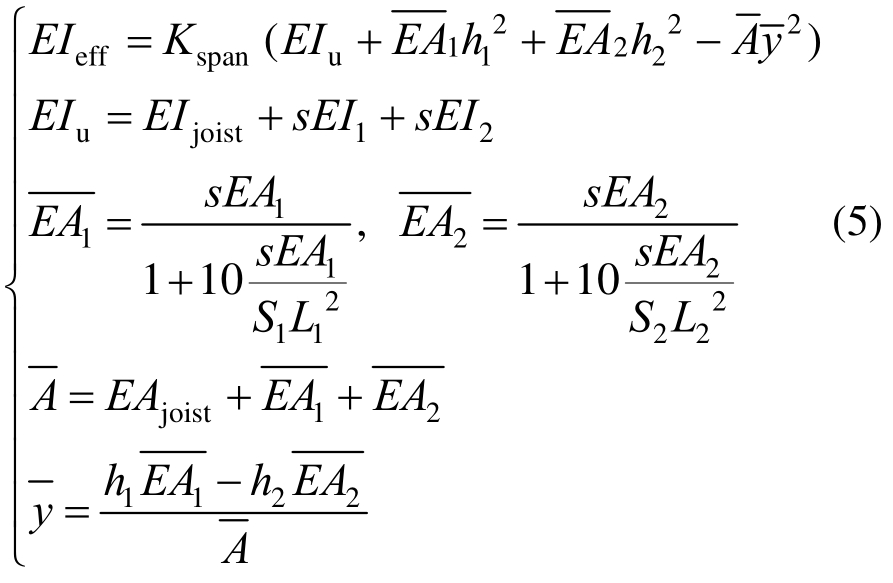
式中：Kspan为集中荷载作用下楼盖梁连续性系数；EIjoist和EAjoist分别为楼盖梁的抗弯刚度和抗拉压刚度；EI1和EA1分别为楼面板单位宽度的抗弯刚度和抗拉压刚度；EI2和EA2分别为石膏吊顶单位宽度的抗弯刚度和抗拉压刚度；
和
分别为楼面板和石膏吊顶的有效抗拉压刚度；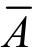
为截面的换算面积；
为从楼盖梁形心到截面中性轴之间的距离；s为楼盖梁间距；S1和S2分别为楼盖梁与楼面板之间连接和楼盖梁与石膏吊顶之间连接的滑移模量；L1和L2分别为楼面板和石膏吊顶沿楼盖梁方向上的跨度；h1和h2分别为楼面板形心和石膏吊顶形心至楼盖梁形心之间的距离。
式中：K1、K2分别为横向弯曲构件和剪切构件的刚度参数；Kj为楼盖梁竖向刚度；Kbi为横向受弯构件刚度；Kvi为剪切构件刚度；L为楼盖梁跨度；G为剪切构件的剪切模量；A为剪切构件截面积；a为剪切件距楼盖梁近端的距离；EIbi为楼面板单位宽度的抗弯刚度；EIwperp和EAwperp分别为木质楼板单位宽度的抗弯刚度和抗拉压刚度；EIc和EAc分别为混凝土面层的抗弯刚度和抗拉压刚度；hcw为楼面板总厚度的1/2。
考虑四种边界条件A、B、C和D对楼盖静力挠度的影响时，参考文献[24]引入楼板在不同边界条件下的分配系数k'，其中
，
及
，则楼盖在1 kN荷载作用下的跨中挠度可采用式(7)进行计算：
采用式(4)和式(7)计算楼盖FL-1和FL-2在1 kN集中荷载作用下跨中挠度结果与有限元结果对比见表6～表9，由表可知：加拿大木结构计算公式中考虑了组合楼盖不同构造方式对跨中位移的影响，如吊顶情况、刚性支撑件的设置情况、楼面板与楼盖梁的连接方式、楼板面层的构造方式等，文献[24]考虑了各种边界条件的分配系数，理论计算结果与有限元分析结果误差小于15%，有较好的参考价值，可用于预测冷弯薄壁型钢组合楼盖在1 kN集中荷载作用下的跨中位移。
通过对冷弯薄壁型钢—压型钢板楼盖和冷弯薄壁型钢—石膏基自流平砂浆组合楼盖的振动性能和静力挠度进行试验研究和理论分析，得出以下结论：
(1)在压型钢板上浇筑石膏基自流平砂浆会增大楼盖的自重和抗弯刚度，减小楼盖的自振频率和跨中竖向挠度，楼盖的自振频率与刚度成正比，与质量成反比。而在石膏基自流平砂浆中加入钢丝网并不会显著增加楼盖的动力特性，减小楼盖的竖向挠度。
(2)增大楼盖梁腹板高度和板厚，增加楼盖面板厚度以及加强楼盖端部约束能够提高冷弯薄壁型钢组合楼盖的基频、减小楼盖跨中挠度。
(3)建议冷弯薄壁型钢—压型钢板楼盖的基频限值取为15 Hz，1 kN集中荷载作用下梁跨中挠度限值取为2 mm；建议冷弯薄壁型钢—石膏基自流平砂浆组合楼盖的基频限值取为10Hz，1 kN集中荷载作用下梁跨中挠度限值取为1 mm。
(4)文献[23]中组合楼盖基频公式可用于预测冷弯薄壁型钢组合楼盖的基频；加拿大木楼盖挠度计算公式可用于预测冷弯薄壁型钢组合楼盖在1 kN集中荷载作用下的跨中挠度。
参考文献：
[1]周绪红，高婷婷，石宇.冷弯薄壁型钢梁—OSB板组合楼盖静力挠度及振动性能试验研究[J].工程力学，2014，31(5):211―217.Zhou Xuhong，Gao Tingting，Shi Yu.Experimental study on static deflection and vibration behavior of cold-formed steel OSB composite floor[J].Engineering Mechanics，2014，31(5):211―217.(in Chinese)
[2]贾子文，周绪红.冷弯薄壁型钢—混凝土组合楼盖振动性能试验研究[J].土木工程学报，2011，44(4):42―51.Jia Ziwen，Zhou Xuhong.Experimental study of vibration behavior of cold-formed steel concrete composite floor[J].China Civil Engineering Journal，2011，44(4):42―51.(in Chinese)
[3]贾子文，周绪红.冷弯薄壁型钢—混凝土组合楼盖基频研究[J].工程力学，2010，27(11):144―153.Jia Ziwen，Zhou Xuhong.Study on fundamental frequency of cold-formed steel concrete floor[J].Engineering Mechanics，2010，27(11):144―153.(in Chinese)
[4]Davis B W.Influence of construction details on vibration characteristics of cold-formed steel floor systems[D].Waterloo，Ontario，Canada:Department of Civil Engineering，2008.
[5]Parnell R A.Vibration serviceability and dynamic modeling of cold-formed steel floor systems[D].Waterloo，Ontario，Canada:Department of Civil Engineering，2008.
[6]Parnell R A，Davis B W，Xu L.Vibration performance of lightweight cold-formed steel floors[J].Journal of Structural Engineering，2010，136(6):645―653.
[7]Xu L，Tangorra F M.Experimental investigation of lightweight residential floors supported by cold-formed steel C-shape joists[J].Journal of Constructional Steel Research，2007，63:422―435.
[8]Xu L.Floor vibration in lightweight cold-formed steel framing[J].Advances in Structural Engineering，2011，14(4):659―672.
[9]魏健.冷弯薄壁型钢—意杨胶合板组合楼盖振动性能研究[D].南京:南京林业大学，2014.Wei Jian.Vibration performance of cold-formed steel-Italian poplar structure plywood composite floorsystem[D].Nanjing:Nanjing Forestry University，2014.(in Chinese)
[10]赵建华.钢—木组合楼板舒适度研究[D].南京:南京林业大学，2014.Zhao Jianhua.Study on comfortableness of composite slab of thin-walled steel-Italian poplar plywood[D].Nanjing:Nanjing Forestry University，2014.(in Chinese)
[11]李颖.冷弯薄壁型钢组合楼盖的刚度研究[D].西安:长安大学，2009.Li Ying.Study on the stiffness of cold-formed steel floor systems[D].Xi’an:Chang’an University，2009.(in Chinese)
[12]AISC/CISC.Steel design guide series 11— floor vibrations due to human activity[M].Chicago:American Institute of Steel Construction，1997.
[13]NBCC 2005，National building code of Canada[S].Ottawa:National Research Council of Canada，，2005.
[14]JGJ 99―2015，高层民用建筑钢结构技术规程[S].北京:中国建筑工业出版社，2015.JGJ 99―2015，Technical specification for steel structure of tall building[S].Beijing:China Architecture and Building Press，2015.(in Chinese)
[15]CECS 261―2009，钢结构住宅设计规范[S].北京:中国建筑工业出版社，2009.CECS 261-2009，Code for design of steel structure residential buildings[S].Beijing:China Architecture and Building Press，2009.(in Chinese)
[16]GB/T 228.1―2010，金属材料 拉伸试验第1部分：室温试验方法[S].北京:中国标准出版社，2010.GB/T 228.1―2010，Metallic materials-tensile testing-Part I:Method of at room temperature[S].Beijing:China Standard Press，2010.(in Chinese)
[17]GB 50018―2002，冷弯薄壁型钢结构技术规范[S].北京:中国计划出版社，2002.GB 50018―2002，Technical code of cold-formed thin-wall steel structures[S].Beijing:China Planning Press，2002.(in Chinese)
[18]BS EN 1998―1:2004，Design of structures for earthquake resistance[S].United Kingdom:European Committee for Standardization，Management Centre，rue de Stassart，2005.
[19]YB 9238―92，钢-混凝土组合楼盖结构设计与施工规程[S].北京:冶金工业出版社，1992.YB 9238-92，Code for steel-concrete composite floor design and construction[S].Beijing:Metallurgical Industry Press，1992.(in Chinese)
[20]Ohlsson S V.Springiness and human-induced floor vibrations—a design guide[S].Stockholm，Sweden:Swedish Council for Building Research，1988.
[21]AS3623，Domestic metal framing code[S].Homebush，NSW:Standards Association of Australia，1993.
[22]CCMC.Development of design procedures for vibration controlled spans using engineering wood members[R].Ottawa:Final Report Prepared for Canadian Construction Materials Centre and the Industry Partnership Consortium，National Research Council of Canada，1997.
[23]贾子文.冷弯薄壁型钢-混凝土组合楼盖受力性能研究[D].西安:长安大学，2010.Jia Ziwen.Study on the behavior of cold-formed steel concrete composite floor[D].Xi’an:Chang’an University，2010.(in Chinese)
[24]燕妮.冷弯薄壁型钢住宅组合楼板的振动及设计准则[D].西安:长安大学，2008.Yan Ni.Composite floor vibration and design criterion for cold-formed steel framing residential[D].Xi’an:Chang’an University，2008.(in Chinese)
STUDY ON VIBRATION PERFORMANCE AND STATIC DEFLECTION OF COLD-FORMED THIN-WALLED STEEL COMPOSITE FLOORS
GUAN Yu1，ZHOU Xu-hong1，2，WEI Shi-jie1，SHI Yu2
(1.School of Civil Engineering，Chang’an University，Xi’an 710061，China;2.Key Laboratory of New Technology for Construction of Cities in Mountain Area，Ministry of Education，Chongqing University，Chongqing 400045，China)
Abstract:Full scale models of cold-formed thin-walled steel-profiled steel sheet floors and cold-formed thin-walled steel-gypsum based self-leveling mortar composite floors were subjected to vibration test under dynamic loading including walking and hammer impact，and to static test under 1 kN concentrated load.The effects on the fundamental frequency，damping ratio and mid-span vertical deflection of the composite floors were studied when floor panels were different and steel meshes were installed.The study shows that casting gypsum based self-leveling mortar on the profiled steel sheet could reduce the fundamental frequency，damping ratio and mid-span vertical deflection of composite floors.Nevertheless，it did not significantly increase the dynamic characteristics and decrease the vertical deflection of composite floor via installing steel mesh into gypsum based self-leveling mortar.ABAQUS finite element software was used to conduct modal analysis of the test models as well as variable parametric analysis based on the calibrated model.The research shows that the floor fundamentalfrequency could be improved and floor mid-span deflection could be reduced by increasing the web height，slab thickness of the floor joist and slab thickness of gypsum based self-leveling mortar，along with strengthening the floor end constraints.In theoretical calculation，the floor could be equivalent to a simply supported beam with uniform mass density and stiffness for predicting the fundamental frequency of cold-formed thin-walled steel composite floors.Additionally，the timber floor deflection calculation formula of Canada was recommended to predict the mid-span deflection of cold-formed thin-walled steel composite floors under 1 kN concentrated load.
Key words:cold-formed steel;gypsum based self-leveling mortar;composite floor;vibration performance;experimental study
中图分类号：TU392.5;TU398
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0060
文章编号：1000-4750(2018)05-0131-12
收稿日期：2017-01-14；修改日期：2017-07-21
基金项目：国家自然科学基金面上项目(51678060)；国家重点研发计划“绿色建筑及建筑工业化”专项(2016YFC0701201)；中央高校基本科研业务费专项资金项目(310828171011)
通讯作者：管 宇(1988―)，男，天津人，讲师，工学博士，主要从事轻型钢结构和钢-混凝土组合结构研究(E-mail:guanyu88927@163.com).
作者简介：周绪红(1956―)，男，湖南南县人，教授，工学博士，中国工程院院士，重庆大学校长，主要从事钢结构和钢筋-混凝土组合结构基本理论及应用研究(E-mail:zhouxuhong@126.com)；
卫世杰(1990―)，男，山西人，硕士生，主要从事轻型钢结构研究(E-mail:weishijiexa@163.com)；
石 宇(1978―)，女(苗族)，湖北宣恩人，副教授，工学博士，主要从事轻型钢结构理论与应用研究(E-mail:shiyu7811@163.com).