朱立华1，李 钢1，李宏男1，2
(1.大连理工大学海岸和近海工程国家重点实验室，辽宁，大连 116024；2.沈阳建筑大学土木工程学院，辽宁，沈阳 110168)
摘 要：与基于承载力和基于位移方法相比，基于能量的抗震设计方法能够更为全面的评估结构抗震性能。该文从能量的角度提出了一种考虑主结构损伤耗能的简化抗震设计方法，将结构滞回耗能设计由阻尼器和主结构共同承担，并据此用等效阻尼比将损伤引入到主结构，通过延性系数建立了结构损伤指数与等效阻尼比之间的关系，给出了阻尼器耗能求解公式及设计流程。该方法无迭代过程，且能在设计之初实现主结构的损伤控制。算例表明，该方法简单、实用，为消能减震结构设计提供了一个新方法。
关键词：基于能量抗震设计；消能减震结构；结构损伤；等效阻尼比；钢框架
消能减震技术作为结构被动控制的一种方法，以其特有的经济性、实用性在实际工程中得到了广泛的应用，其在工程中的设计方法也成为抗震领域的热点问题。基于性能的抗震设计方法兴于美国，国内外学者开展了一系列研究工作[1-18]，基础研究趋于完善并逐渐被各国规范所采纳[19-21]。目前，基于性能的结构抗震设计方法主要有两种：基于位移的抗震设计方法[1-5]和基于能量的抗震设计方法[6-18]。位移指标为广大工程技术人员所熟悉，利于推广，但未考虑地震作用下结构的累积时间效应；而能量指标考虑了时间效应，概念清晰。自1956年Housner[6]首次提出将能量的概念应用到建筑结构中以来，许多学者对一般结构的基于能量设计方法进行了研究。其中，Akiyama[7]从理论研究层面给出了基于能量的抗震设计思路和方法；Fajfar等[8]利用综合考虑两种数学模型的非线性分析方法(简称N2)进行了钢筋混凝土结构设计；Shen等[9]基于概率分析和能量分布线性假定建立了钢结构的能量设计方法，得到了能量输入和分配的一般规律；Chou等[10]在此基础上结合MPA(Modal Pushover Analysis)方法[11]，针对钢框架结构提出了用前两阶振型等效单自由度体系吸收能之和代替原结构吸收能的方法；白久林等[12]考虑混凝土结构的承载力、刚度退化和捏缩效应等因素，对结构的非弹性应变能进行了修正，并提出了框架结构的塑性设计方法。针对消能减震结构的能量设计方法，各国学者也开展了大量研究。叶列平等[13]建议先进行损伤耗能机制设计，设计中使损伤耗能集中在次要构件，并引入能力系数和能力比，通过调整两参数实现了结构损伤控制；Choi等[14]提出了装有约束屈曲支撑结构的能量设计方法，该方法假定梁柱节点铰接，即全部水平地震作用由约束屈曲支撑承担，主结构仅承受竖向重力荷载；Benavent[15－16]基于优化设计理论提出了一种用滞回型阻尼器加固结构的能量设计流程，通过对既有结构加固，验证了该方法的有效性；Habibi等[17]在Chou基础上提出了一种适用于不同阻尼器的能量设计方法，该方法假定主结构始终保持弹性，对于阻尼器耗能计算则需要进行大量的迭代；Abdi等[18]对地震反应系数进行修正给出了不同阻尼体系的系数修正公式，并采用静力分析法分析了带有粘滞阻尼的钢结构。
事实上，消能减震结构在罕遇地震下主体结构往往进入了非线性，绝对的弹性很难在设计中得到保证，同时也不经济。当结构塑性损伤累积到一定程度时，允许部分主结构构件进入弹塑性范围则更为合理。针对损伤状态的定量描述，许多学者提出了不同的损伤模型，大致可分为单参数损伤模型和双参数损伤模型。单参数损伤模型一般包含最大延性、滞回耗能等指标，如Powell等[22]提出基于极限延性的损伤指标；Fajfar等[23]提出基于滞回耗能的损伤指标。因双参数损伤模型可以同时考虑结构变形和能量，Park等[24]在大量钢筋混凝土构件损伤试验中发现构件损伤与其最大变形和累积滞变耗能密切相关，提出了Park-Ang双参数地震损伤模型。
本文将主结构损伤引入到基于能量的抗震设计方法中，以阻尼器耗散大部分能量、主结构部分构件辅助耗能的能量分配准则为前提，建立了损伤指数与等效阻尼比之间的关系，给出了考虑主结构损伤的阻尼器耗能求解公式及设计流程。同时该方法无迭代过程，求解过程简单，损伤耗能机制明确，实现了多道防线的设计理念。
本节结合既有损伤模型，通过延性系数将损伤模型转化为可用于能量设计的等效阻尼比，进而建立结构损伤指数与等效阻尼比之间的关系。
地震损伤模型用来描述地震作用下结构损伤程度与损伤指标的关系。罕遇地震下结构往往进入弹塑性状态，并产生低周疲劳效应，相对于单参数损伤模型，双参数损伤模型可较为真实的反映结构地震损伤状态。欧进萍等[25]给出了钢结构改进的双参数损伤模型为：
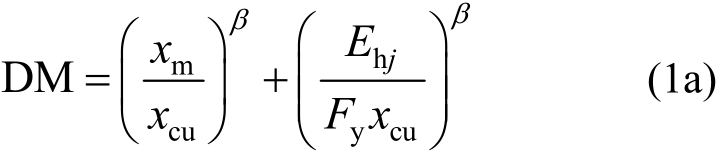
利用正规化累计耗能系数γh，式(1a)可改成：
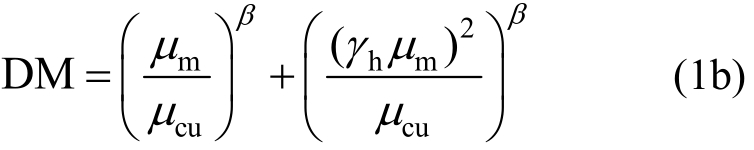
式中：DM为地震损伤指数，根据不同性能目标可选取不同的损伤指数；xm为实际地震下最大层间位移；xcu为单调荷载下极限层间位移；Fy为单调荷载下层屈服剪力；μm为地震作用下结构的最大延性系数；μcu为单调荷载下结构极限破坏延性系数；β为非线性组合系数，一般建筑取β=2.0[26]；γh为正规化累计耗能系数，一般取[0.8，1.0][23]；Ehj为实际地震下结构第j层滞回耗能[27]，如下式：
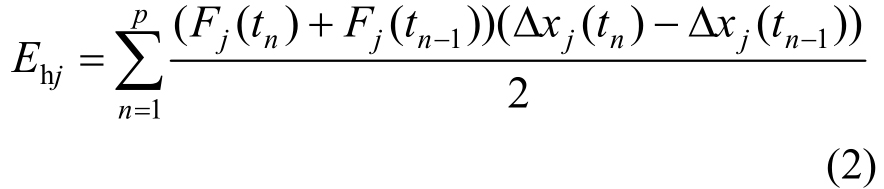
式中：Fj(tn)、Fj(tn-1)为实际地震下第tn、tn-1时刻的结构第j层层间剪力；Δxj(tn)、Δxj(tn-1)为实际地震下第tn、tn-1时刻结构第j层的层间位移；p为地震记录数据采集点总数。
损伤指数是实现结构性能目标的量化指标，一般情况下，当DM=0时，表示震后结构或构件处于完好状态；当DM≥1时，表示结构或构件处于完全破坏状态。由于以往研究采用的模型不同，所依据的震害和试验资料也存在差异，得到结构损伤程度对应的损伤指数范围也不一致[28]。
等效阻尼比是损伤指数与损伤耗能之间的纽带，其取值对损伤设计产生直接影响。为此，许多学者开展了深入研究。Rosenblueth等[29]给出了原结构与等效单自由度体系周期之间的关系，并据几何关系得到了等效阻尼比；Iwan[30]利用滑移单元和弹性单元建议了一种组合滞回模型，基于统计学提出等效阻尼比关系式；Gulkan等[31]根据试验结果给出了一种用等效替代思想进行弹塑性反应分析的简化方法，该方法认为在地震作用下原结构与等效单自由度体系耗能相等，并以此来确定等效阻尼比；Kowalsky等[32]据结构割线刚度确定等效周期，将Jacobsen法推广到Takeda模型提出了适用于单自由度体系的等效阻尼比模型；Priestley等[33]采用Takeda和理想弹塑性滞回模型，针对多种结构给出了其等效阻尼比的经验公式；Dwairi等[34]经过大量研究发现等效阻尼比与结构自振周期相关，并提出了与周期有关的等效阻尼比公式。本文采用Kowalsky等[32]给出的计算模型，假定结构力与位移关系为双线性，认为双线性模型在一个循环内耗散的能量与弹簧-阻尼-质量体系正弦激励下的产生共振现象时一个循环内耗散的能量相等。其公式如下：
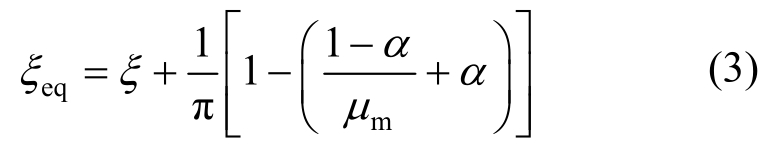
式中：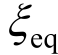
为等效阻尼比；ξ为初始阻尼比；α为第二刚度系数。
地震作用下结构发生损伤破坏包括首次超越破坏和双重累积破坏。不同的破坏形式对应不同的破坏准则，破坏准则能够评价结构或构件的损伤机理，是对震后结构性能的唯象描述。而考虑主结构损伤的能量设计方法需要解决的首要问题是建立结构损伤程度与损伤指标、损伤指标与等效阻尼比之间的关系。本文以欧进萍等[25]和Kowalsky等[32]理论为基础将式(3)代入式(1b)得：
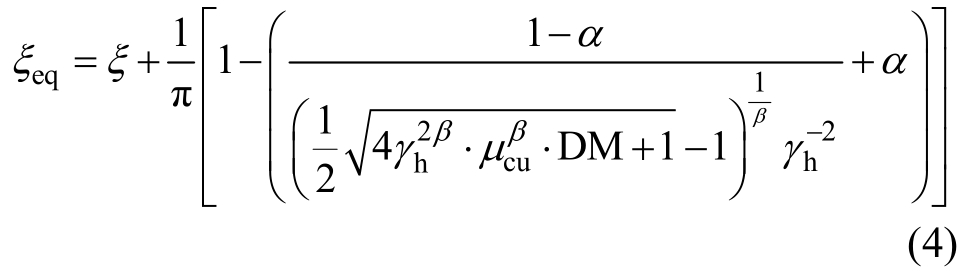
式(4)建立了损伤指数DM与单自由度体系等效阻尼比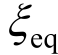的关系，依据GB 50011―2010《建筑抗震设计规范》[21](后简称《抗震规范》)中结构性能设计方法选择相应的性能目标，确定损伤指数代入式(4)，即可求得结构的等效阻尼比。
消能减震结构设计通常包括结构性能设计和阻尼器设计，本文建议方法的思路是将结构的部分滞回耗能用阻尼器耗散，具体过程是通过对结构进行模态分析取前i阶振型及周期，依据各振型分别对结构进行模态推覆分析，将推覆曲线等效线性化。结合初始阻尼比对应的弹塑性反应谱，进而可求初始阻尼比下前i阶振型对应的吸收能。根据确定的性能设计目标和式(4)可求考虑损伤的等效阻尼比及其对应的吸收能。第i阶振型下初始阻尼比和等效阻尼比的吸收能相减并将各个振型对应的吸收能之差求和，得到阻尼器总耗能。在此基础上，结合变形需求设计阻尼器相关参数。
对于高阶振型影响较大的结构，采用本文方法进行阻尼器设计时，仅考虑一阶振型的结构吸收能比考虑多阶振型的结构吸收能要小，会低估结构的吸收能，则由此得到的阻尼器耗能减小，主结构构件将产生不可预料的损伤，结构更不安全。
结构性能设计核心思想是使设计的结构在未来地震作用下能够满足所要求的性能水平，本节依据弹塑性反应谱及结构自身特性参数，得到结构吸收能，为后续阻尼器设计提供基础理论。
1)结构吸收能
基于能量的抗震设计本质上是从结构自身耗能能力出发，在获得地震总输入能量的基础上确定其在结构各耗能机制中的分配，据此对结构的整体性能进行评估，并给出合理有效的结构设计方案。地震作用下结构能量的输入、转化和耗散不仅与结构自身特性相关，同时也与地震动强度、频谱特性以及持续时间等有关。一般单自由度体系在地震作用下能量方程为：
即动能为：
固有阻尼耗能为
吸收能为：
总输入能为：
式中：Eh为滞回耗能；Es为弹性应变能；m为结构质量；c为阻尼系数；u˙为结构速度；f为结构恢复力；u˙g为地震加速度；t为地震持续时间。
结构的动能和弹性应变能不耗能，属于能量的转化，结构固有阻尼耗能约为5%，因此结构进入非线性以后其耗能主要集中在滞回耗能。对于消能减震结构，其滞回耗能包括主结构滞回耗能和阻尼器耗能，而主结构滞回耗能又是结构发生损伤破坏的主要原因。
为建立结构吸收能与弹塑性反应谱之间的关系，Housner[6]定义了等效速度，并将其作为结构吸收能的量化指标。因此，若已知结构动力特性，通过构建的弹塑性反应谱，即可得到单自由度体系的吸收能。其中，等效速度Va的计算式为：
2)弹塑性反应谱
为获得用于计算结构吸收能的等效速度以及确定用于结构变形需求分析的最大位移，需构建与结构特征参数相关的弹塑性反应谱，包括屈服强度系数谱、等效速度谱和最大位移谱。弹塑性反应谱是指在某一地震作用下对多个单自由度体系进行弹塑性时程分析得到的屈服强度、等效速度、位移等弹塑性反应最大值的图形化表示，不同的地震作用有不同的弹塑性反应谱。由结构动力特性参数和标准屈服强度系数谱即可确定结构延性系数。结合等效速度谱可求得等效速度和结构吸收能。其中，屈服强度系数和最大位移通过下式确定：
式中：Cy为单自由度体系屈服强度系数；Ds为单自由度体系最大位移；fy为结构屈服强度；Dy为结构屈服位移；μ为延性系数。
阻尼器设计主要包含两方面内容：能量需求和变形需求。其中，能量需求需先确定阻尼器总耗能大小，根据能量分布曲线确定结构各层阻尼器耗能；变形需求则是据能量需求中模态推覆分析的结果，利用2.1节最大位移谱计算结构各阶振型下层间位移，从而得到阻尼器各层变形需求。在此基础上，选择合适的阻尼器，即可确定其设计参数。
1)阻尼器耗能
在罕遇地震下，结构滞回耗能由外加阻尼器和主结构累积损伤两部分共同耗散，即：
式中：EDh为阻尼器耗能；Efh为主结构损伤耗能。
滞回耗能是结构吸收能的一部分，因此阻尼器耗能可以转化为初始阻尼比对应的结构吸收能和等效阻尼比对应的结构吸收能之差。设计过程中，若已知结构的损伤指数，由式(4)可求等效阻尼比，采用2.1节方法可知等效阻尼比的吸收能，与初始阻尼比的吸收能做差，则可得到阻尼器耗能为：
式中：Ea为初始阻尼比ξ的吸收能；
为等效阻尼比qξe的吸收能。
对于高阶振型影响较大的结构，若采用仅考虑第一阶振型的静力弹塑性分析方法计算结构吸收能比本文方法考虑多阶阶振型的结构吸收能小，由此求得的阻尼器耗能减小。因此，对于该类结构建议采用本文方法计算结构的吸收能。
2)阻尼器耗能分布
按上述方法获得阻尼器耗能以后，为实现基于能量设计，将阻尼器耗能落实到构件层次，需要进行阻尼器耗能分布计算。本文假定阻尼器耗能分布与结构滞回耗能分布形式相等。一般情况下，可用模态推覆分析方法确定能量分布曲线，将原结构推覆到目标位置后据此时本层各构件弯矩-转角关系可得该层能量，各层能量标准化即为该振型下能量分布曲线。模态推覆分析中采用的振型数与结构高度相关，一般结构取前两阶即可。
结构耗能机制不同，则能量分布形式略有区别，此外不同的加载阶段也将影响其分布形式。在结构抗震设计过程中，先要明确结构的耗能机制。一般情况下，框架结构耗能机制为强柱弱梁，而框剪结构则为强墙肢弱连梁等。依据耗能机制出现的先后次序将加载过程分为三个阶段，如图1示，分别为：第1阶段为弹性阶段，取OA中点位置；第2阶段为塑性阶段，取AB中点位置；第3阶段也为塑性阶段，与B点重合。其中，A点表示进入屈服耗能机制第一阶段；B点表示进入屈服耗能机制第二阶段。以A、B点对应位置的层间位移角为界限，各阶振型能量分布曲线可按下式选用：
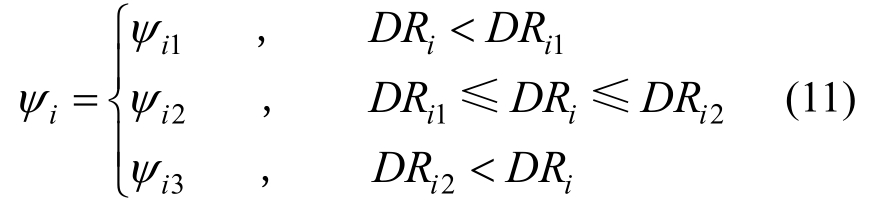
式中：ψi为标准化能量分布列向量；DRi1为第i阶振型下屈服耗能机制第一阶段对应的层间位移角；DRi2为第i阶振型下屈服耗能机制第二阶段对应的层间位移角；DRi为第i阶振型目标位移下的层间位移角，对第1阶振型为首层层间位移角，第2阶振型为转换层层间位移角。
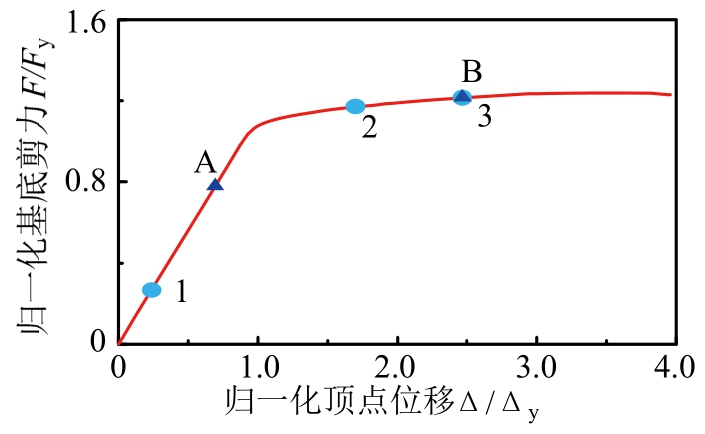
图1 标准化基底剪力-顶点位移曲线
Fig.1 Normalized push-over curves
3)阻尼器变形
用模态推覆分析方法得到各阶振型下结构的各层位移，各振型下位移组合为阻尼器变形需求。具体过程为将原结构等效为各阶振型下单自由度体系，利用最大位移谱和等效单自由度体系特征参数，确定各阶振型下单自由度体系最大位移，并通过振型参与系数将其转化为原结构顶点位移；对原结构进行推覆分析至目标位置，求得此时各层位移，并进行平方和开方组合，即可得各层阻尼器变形需求。在设计中，一般依据结构层数选择组合振型数。
4)阻尼器参数设计
《抗震规范》将阻尼器分为速度相关型、位移相关型或其他类型阻尼器。常用的阻尼器有：摩擦阻尼器、金属屈服型阻尼器、黏滞阻尼器、黏弹性阻尼器等，其设计参数[2]见表1，表中给出了不同阻尼器附加阻尼比和等效刚度计算公式。
在已知阻尼器耗能和变形需求基础上，确定各层阻尼器数量，对两种常用耗能装置进行设计如下：
①位移型阻尼器
由各阻尼器变形需求及其空间位置、布置形式等，确定各阻尼器轴向相对位移u0，j。由各阻尼器耗能和其他设计参数(对金属阻尼器为应变硬化系数αj和延性系数μj等)，参照表1附加阻尼比ξED计算式，即可求得各阻尼器的屈服力Fy，j(或起滑力F0，j)。在此基础上，即可确定其等效刚度KED，j。
表1 常用被动耗能装置设计参数(表中变量均为国际单位)
Table1 Characteristics of various energy dissipation devices
②速度型阻尼器
与位移型阻尼器类似，先确定阻尼器轴向相对位移u0，j。由阻尼器耗能、附加阻尼比公式和其他参数(对黏滞阻尼器为结构固有频率
，黏弹性阻尼器为等损伤因子η等)，确定黏滞阻尼器的阻尼系数cj和黏弹性阻尼器的刚度系数k′等控制参数。
本文提出设计方法具体流程如下：
1)结构承载力设计
根据结构高度和结构类型，结合我国现行规范，初选截面尺寸对结构进行承载力设计。设计过程中以选定的耗能机制为控制条件，合理的耗能机制是基于能量抗震设计方法能够顺利实现的前提。
2)初始阻尼比吸收能
由模态分析确定前i阶振型的周期Ti、振型参与系数Γi和振型φi等；利用弹塑性时程分析法，建立在给定场地下某一地震波的标准屈服强度系数谱和等效速度谱；由模态推覆分析可得基底剪力-顶点位移曲线，并将其等效线性化得到主结构的屈服力Fyi、等效单自由度的屈服力fyi和屈服强度系数Cyi为：
选定结构初始阻尼比ξ，结合Ti、Cyi利用屈服强度系数谱确定μi；利用上述参数，由等效速度谱确定等效速度Vai，则初始阻尼比吸收能Eai为：
3)等效阻尼比吸收能
选定性能目标后，确定损伤指数，将其代入式(4)求得等效阻尼比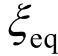
；更新阻尼比，重复步骤1)即可求得等效阻尼比吸收能
。
4)阻尼器耗能
将已求的吸收能
、
代入式(10)，可得第i阶振型下阻尼器耗能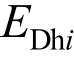
。
5)耗能分布及各层总耗能
利用2.2节的能量分布曲线ψi，得到第i阶振型下第j层阻尼器耗能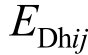
，各振型耗能叠加得到第j层阻尼器耗能
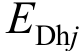，即：
式中：ψij为第i阶振型第j层能量分布系数；q为选取的振型总数。
6)阻尼器变形
利用弹塑性时程分析法，建立在给定场地下某一地震波的最大位移谱；利用2.2节阻尼器变形求解方法，结合步骤2)已有模态推覆分析结果，得到第j层阻尼器各层位移xj和层间位移Δxj。
7)阻尼器设计
据结构实际条件及其使用要求等，选择合适的阻尼器类型。利用2.2节阻尼器参数设计方法，由各层耗能需求EDj、层间位移jδ以及阻尼器参数，进行设计。
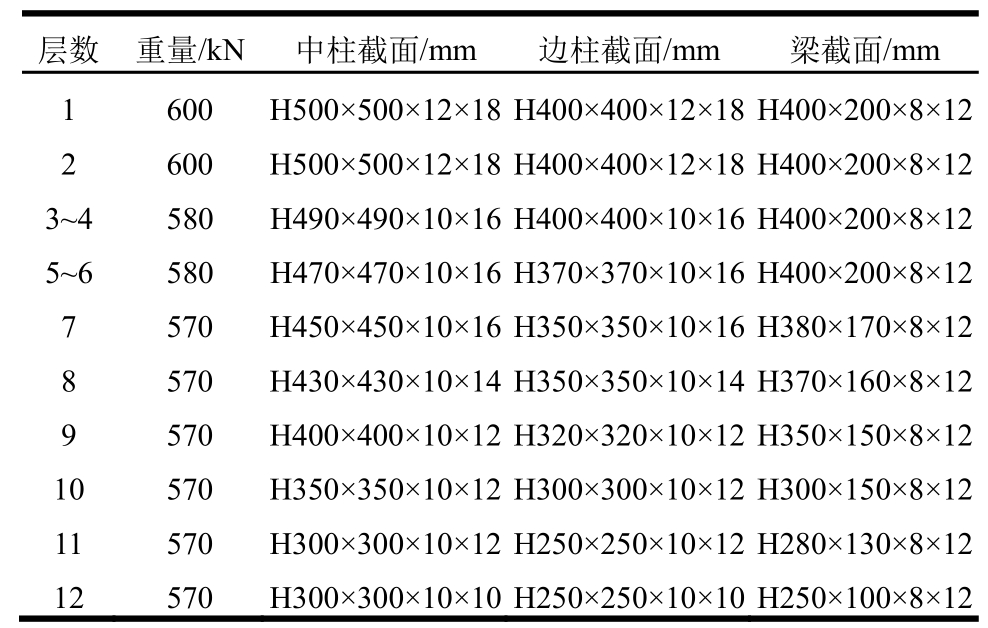
某12层钢框架结构按照强柱弱梁耗能机制进行承载力设计，模型平面图和立面图，如图3所示，抗震设防烈度为8度(0.2g)，II类场地，设计地震分组为第二组(Tg=0.4 s)。梁和柱均采用焊接H型截面，Q235钢，构件具体尺寸见表2。楼屋面恒荷载为4.6 kN/m2，楼屋面活荷载为2.0kN/m2。在多遇地震下其层间位移角均满足《抗震规范》限值要求，罕遇地震下第10层、第11层层间位移角分别为1/49.8和1/49.3大于规范限值1/50，采用增设阻尼器的措施提高结构抗震性能。选择性能目标为罕遇地震下结构发生轻微损伤破坏，损伤指数取DM=0.21[25]。
选一榀框架，如图2示，用SAP2000建模。模型采用如下假定：结构质量集中在楼板梁柱节点处，该榀框架各层重量取阴影部分楼面荷载、填充墙荷载及其梁柱自重之和的近似值，见表2；塑性铰采用FEMA356默认值，梁单元塑性铰长度应为柱截面尺寸的一半；模型与地面固端约束；刚性楼板假定；梁单元无剪切变形；考虑重力二阶效应。地震波选用El Centro(NS)波，峰值加速度为341.7 gal。
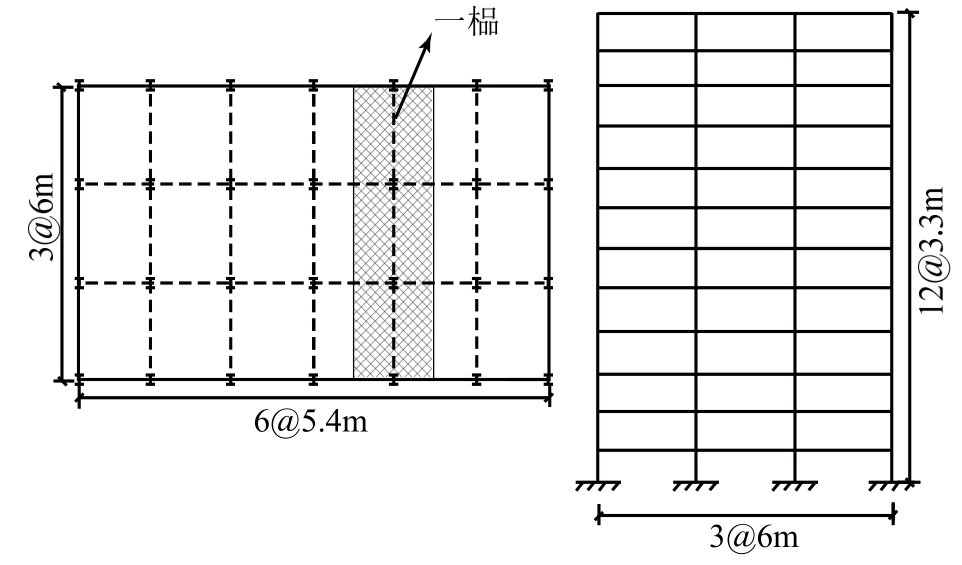
图2 12层抗弯钢框架
Fig.2 12-Story MRF
表2 结构基本参数及截面尺寸
Table2 Summary of design parameters and member sections for the 12-story frame
1)初始阻尼比吸收能。对已完成承载力设计的结构进行模态推覆分析，取前两阶计算，由弹性模态分析确定结构动力特性参数；建立结构在El Centro(NS)波下的标准屈服强度系数谱和等效速度谱，如图3、图4所示。
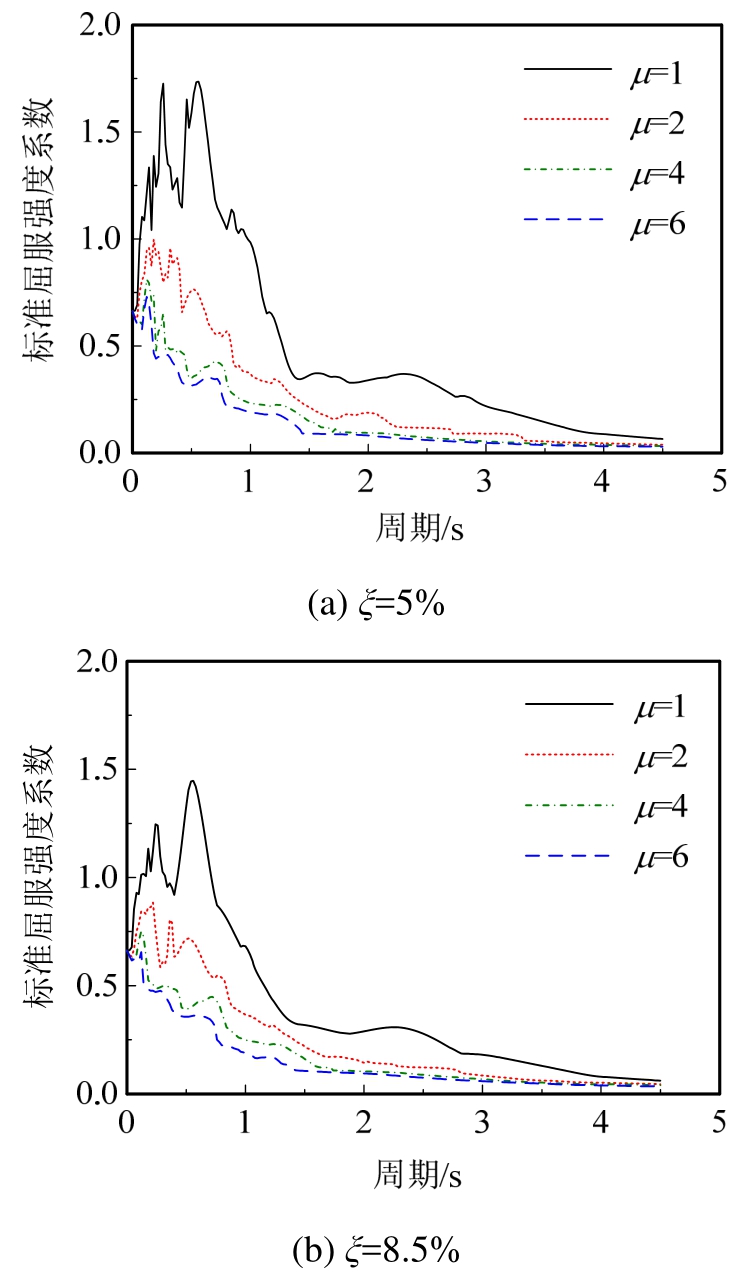
图3 标准屈服强度系数谱
Fig.3 Normalized yield strength coefficient spectra
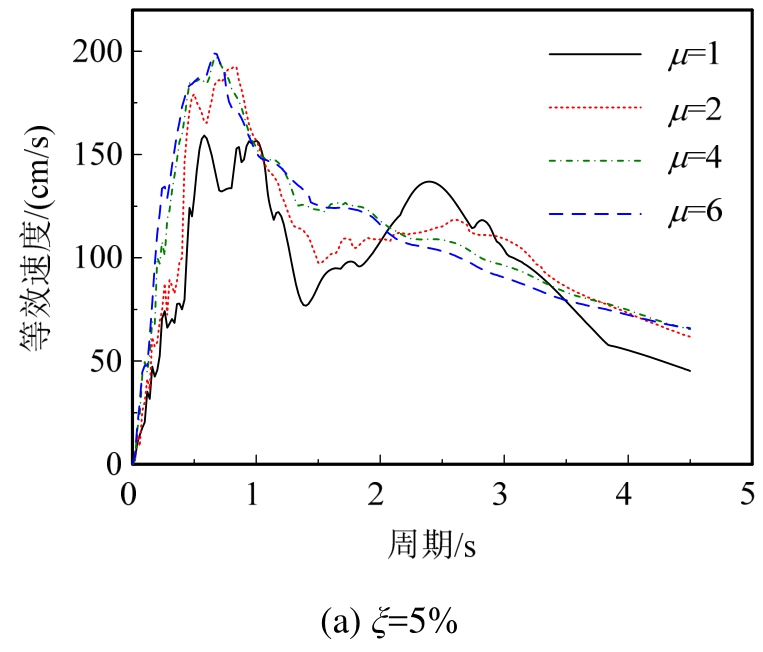
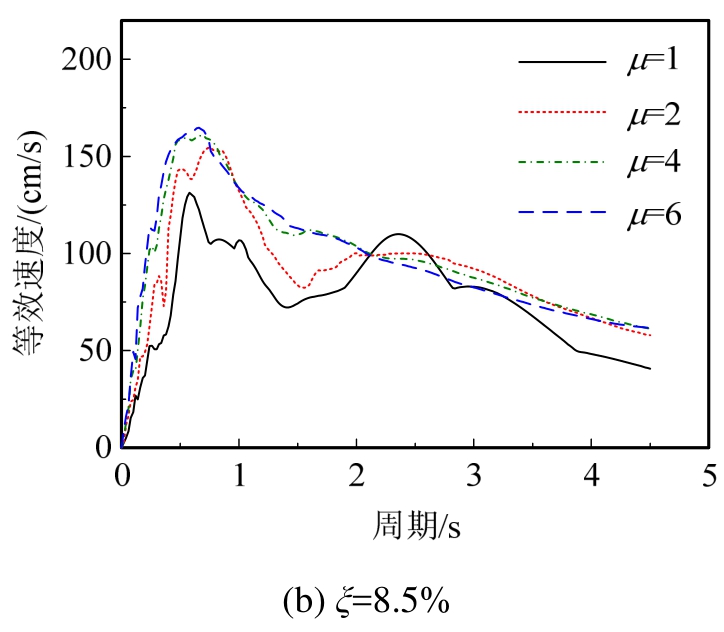
图4 等效速度谱
Fig.4 Equivalent velocity spectra
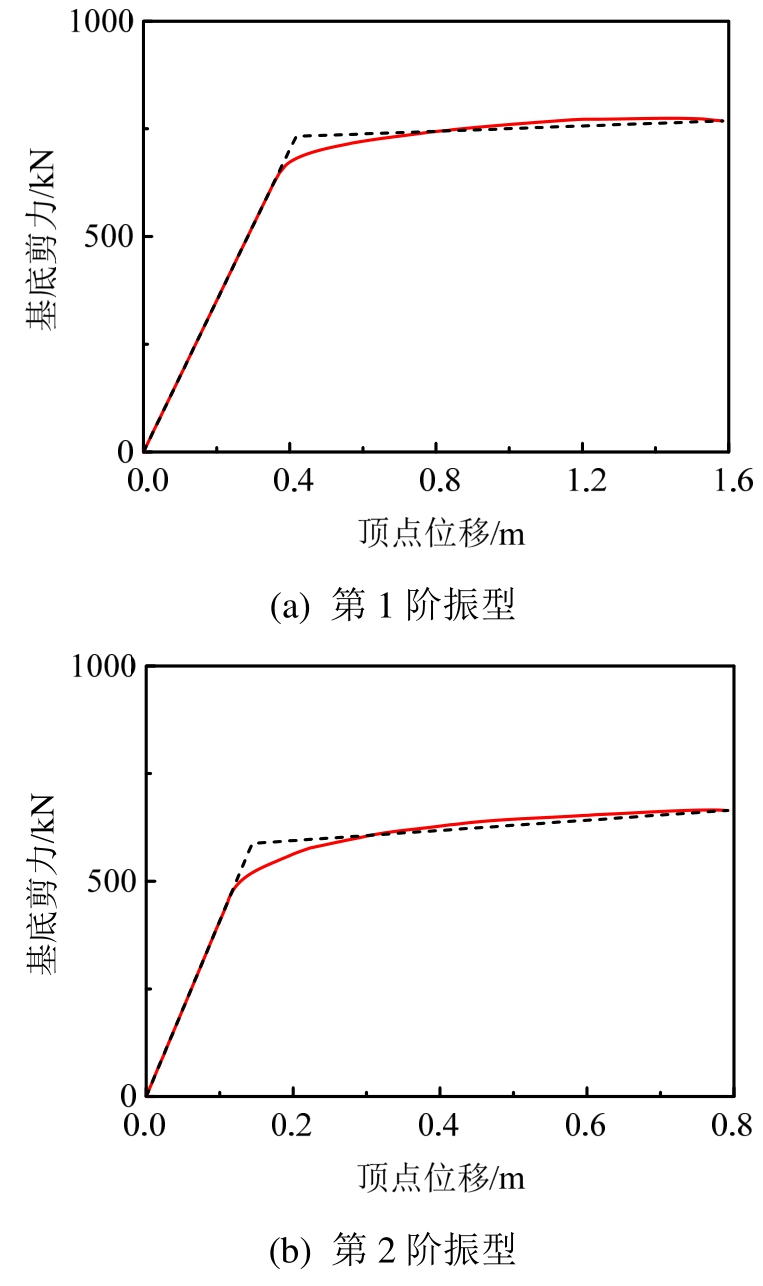
图5 MPA基底剪力-顶点位移等效线性化曲线
Fig.5 Properties of the inelastic SDOF system from MPA curve
模态推覆分析可得基底剪力-顶点位移曲线并将其等效线性化，可得到等效单自由度性能参数，如图5所示。
确定结构初始阻尼比ξ，本文取5%，由2.1节方法可求Vai、Eai，计算结果如下。
2)等效阻尼比吸收能。将已知的损伤指数DM代入式(4)可求等效阻尼比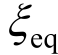，重复步骤1)可知其吸收能Eai，计算结果见表3。
表3 初始阻尼比吸收能计算结果
Table3 The results of absorb energy for initial damping ratio
3)阻尼器耗能。将已求的吸收能Eai、
代入式(10)，可得各振型阻尼器耗能需求EDhi，计算结果见表4。
表4 等效阻尼比吸收能计算结果
Table4 The results of absorb energy for equivalent damping ratio
4)耗能分布及各层耗能。本例模型为框架结构，其耗能机制为强柱弱梁，图1中A点表示梁端出现第一个塑性铰；B点表示柱端出现第一个塑性铰，采用FEMA356默认塑性铰机制。利用2.2节方法得到能量需求分布曲线ψi，如图6所示。
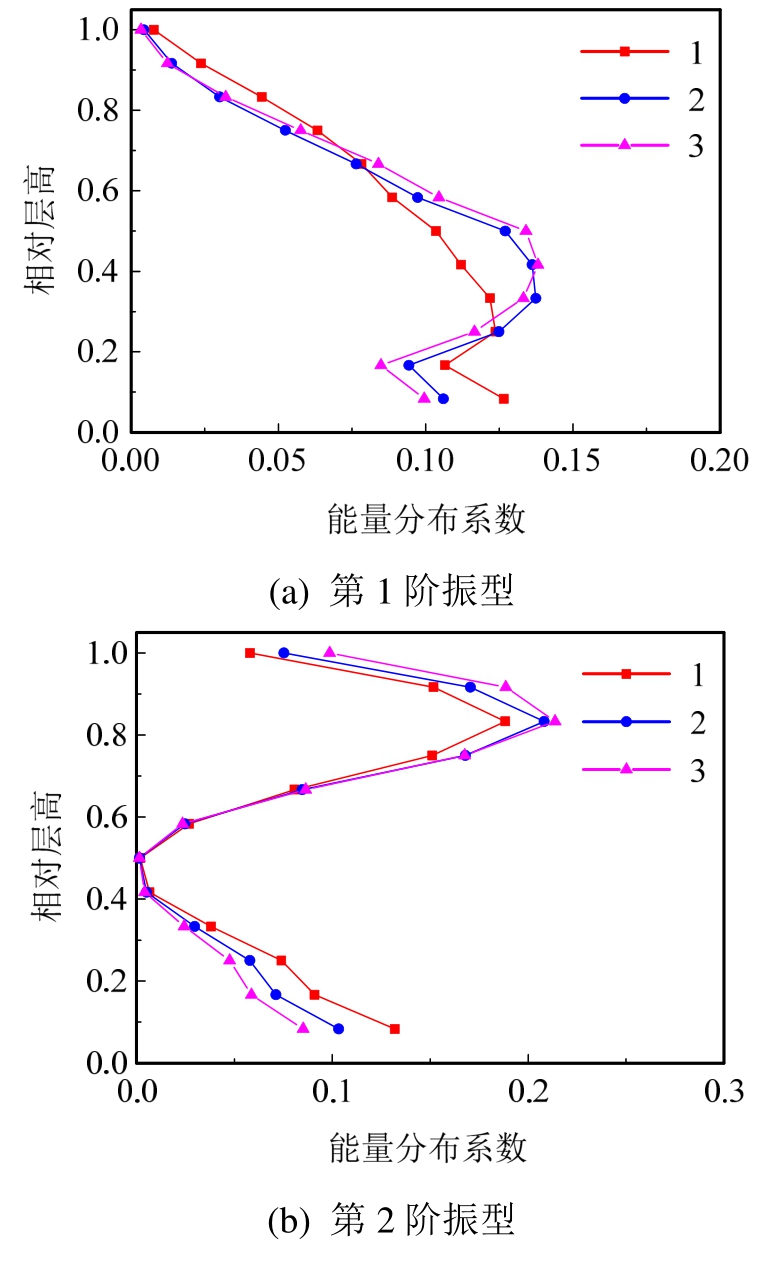
图6 能量分布曲线
Fig.6 Energy profiles
由式(15)得到各层阻尼器耗能EDhj，具体计算结果见表5。能量分布曲线选择过程中，第1阶振型采用首层层间位移角，第2阶振型用第10层层间位移角，过程如下：
由推覆分析结果知，DR11=0.418%，DR12=0.800%；DR21=0.130%，DR12=2.494%；Ds1=4 0.6 cm，DR1=0.72%，DR11≤DR1≤DR12，选择ψ12；Ds2=1 8.28 cm，DR2=0.89%，DR21＜DR2＜DR22，选择ψ22。
表5 各层阻尼器耗能和变形需求
Table5 Demand of dissipated energy and deformation
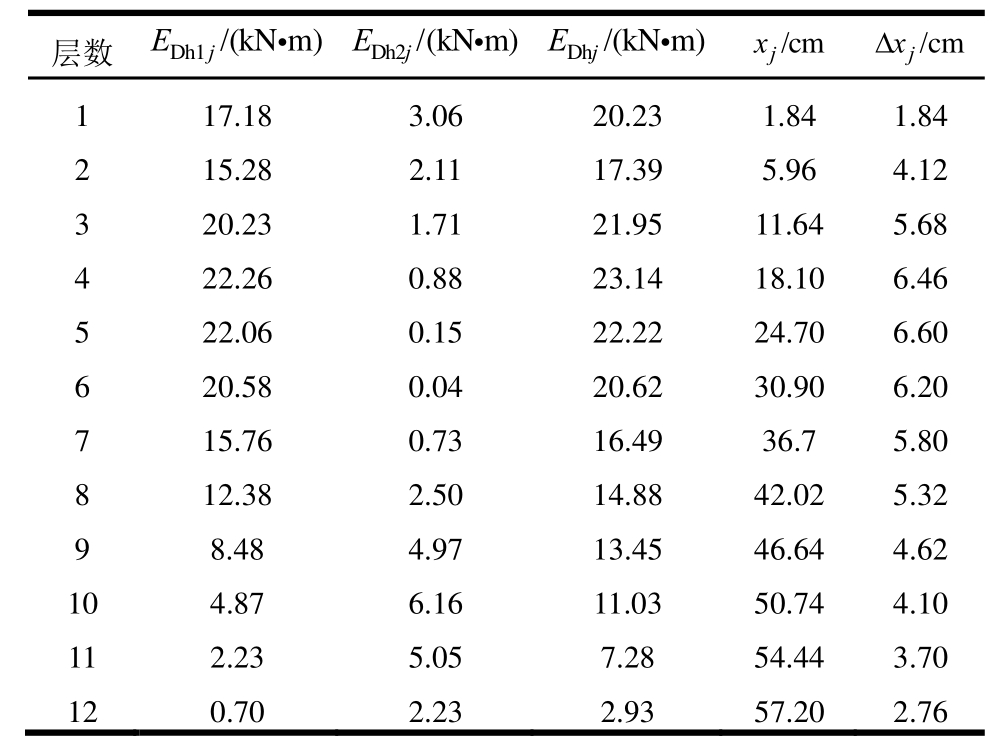
5)阻尼器变形计算。建立结构在El Centro(NS)波下最大位移谱，如图7示。利用2.2节阻尼器变形求解方法，依据本文层数选择第一阶振型下结构的位移作为变形需求，第j层阻尼器各层位移xj和层间位移Δxj的计算结果见表5。
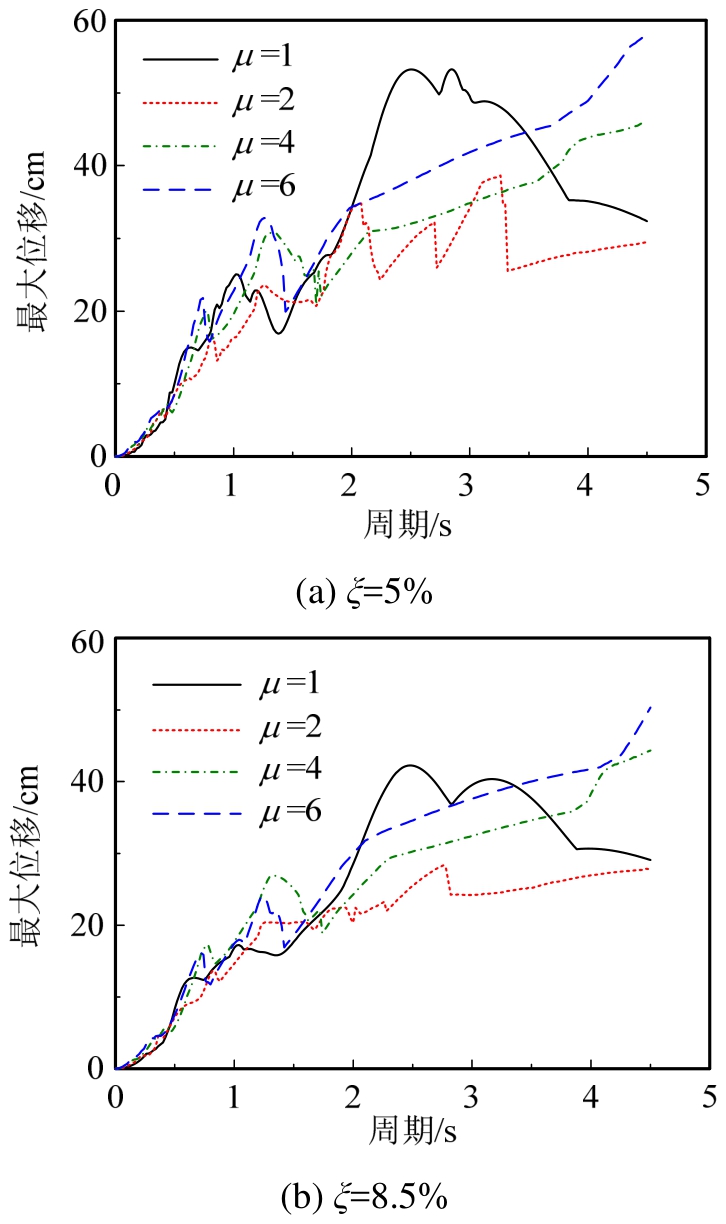
图7 最大位移谱
Fig.7 Maximum displacement spectra
6)阻尼器设计。选用摩擦阻尼器，利用2.2节阻尼器参数设计方法，Plastic(Wen)连接单元模拟摩擦阻尼器，主要力学参数包括屈服位移、初始刚度、屈服力(或起滑力)、屈服后刚度比和屈服指数。屈服后刚度比为阻尼器屈服后与屈服前的刚度之比，对于摩擦阻尼器取0。屈服指数是力-位移曲线中在屈服点附近的光滑过渡段范围，该值越大则过渡范围越小，通常取5～10之间，本文取10，结构各层摩擦阻尼器的力学参数见表6。阻尼器在中跨全高布置，每层两个，呈倒V型，如图8所示。
表6 各层摩擦阻尼器的设计参数
Table6 Design of friction dampers per story
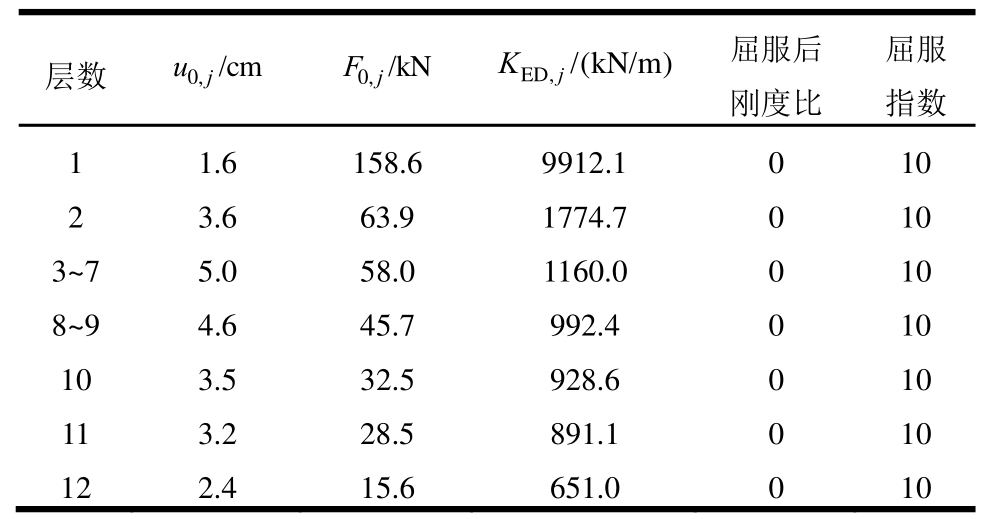
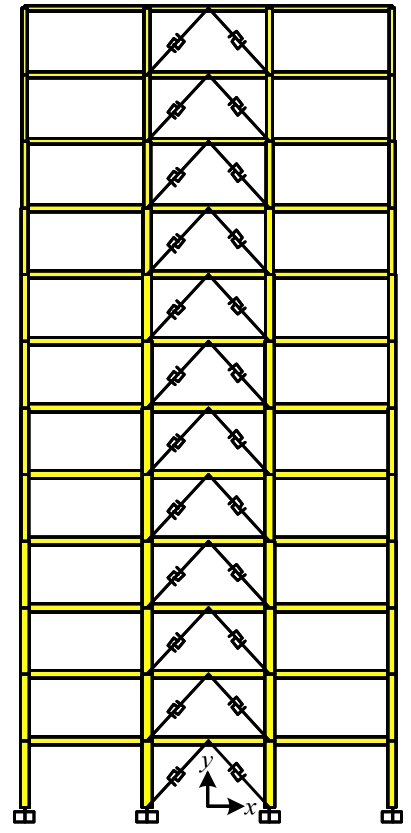
图8 摩擦阻尼器布置图
Fig.8 Configuration of friction dampers
为验证本文方法的准确性，分别对上述方法建立的模型(简称本文方法)和采用主结构为弹性能量方法设计的模型(简称主体弹性方法)进行罕遇地震和设防地震下时程分析。地震波峰值加速度按照《抗震规范》8度(0.2g)罕遇地震和设防地震的规定分别调整为400cm/s2、200cm/s2。分析如下：
1)损伤性能评估
本文方法在罕遇地震下第11层为薄弱层，层间位移最大值xm=3.4 cm，由式(2)，知层滞回耗能值Ehj=7.11 kN·m；单调荷载下，其极限层间位移值xcu=8.2 cm ，层屈服剪力值Fy=6 45.67 kN，由式(1a)，可求出该层的损伤指数为DM=0.19。薄弱层的损伤指数比等效单自由度体系略小，设计值趋于保守，满足性能目标要求。
2)层间位移时程曲线
结构顶层层间位移时程曲线如图9所示，在罕遇地震下，本文方法与主体弹性方法的层间位移最大值基本同时出现在地震记录的5.76 s，二者相差24.51%。在设防地震下，本文方法层间位移最大值出现在5.8 s左右，而主体弹性方法最大值出现在2.6 s，最大值相差10.84%。值得注意的是，罕遇地震下，两模型均在经历地震作用初期的最大振幅后保持较小幅度振动且二者在地震作用前10s差别较明显，10s后相差不大。造成上述现象的原因是本文方法比主体弹性方法阻尼器起滑力降低35%，罕遇地震初期地震动强度较大，主体弹性方法耗能较多，层间位移相对较小，随着地震动强度的减弱，地震作用中后期二者减震效果差别不大。
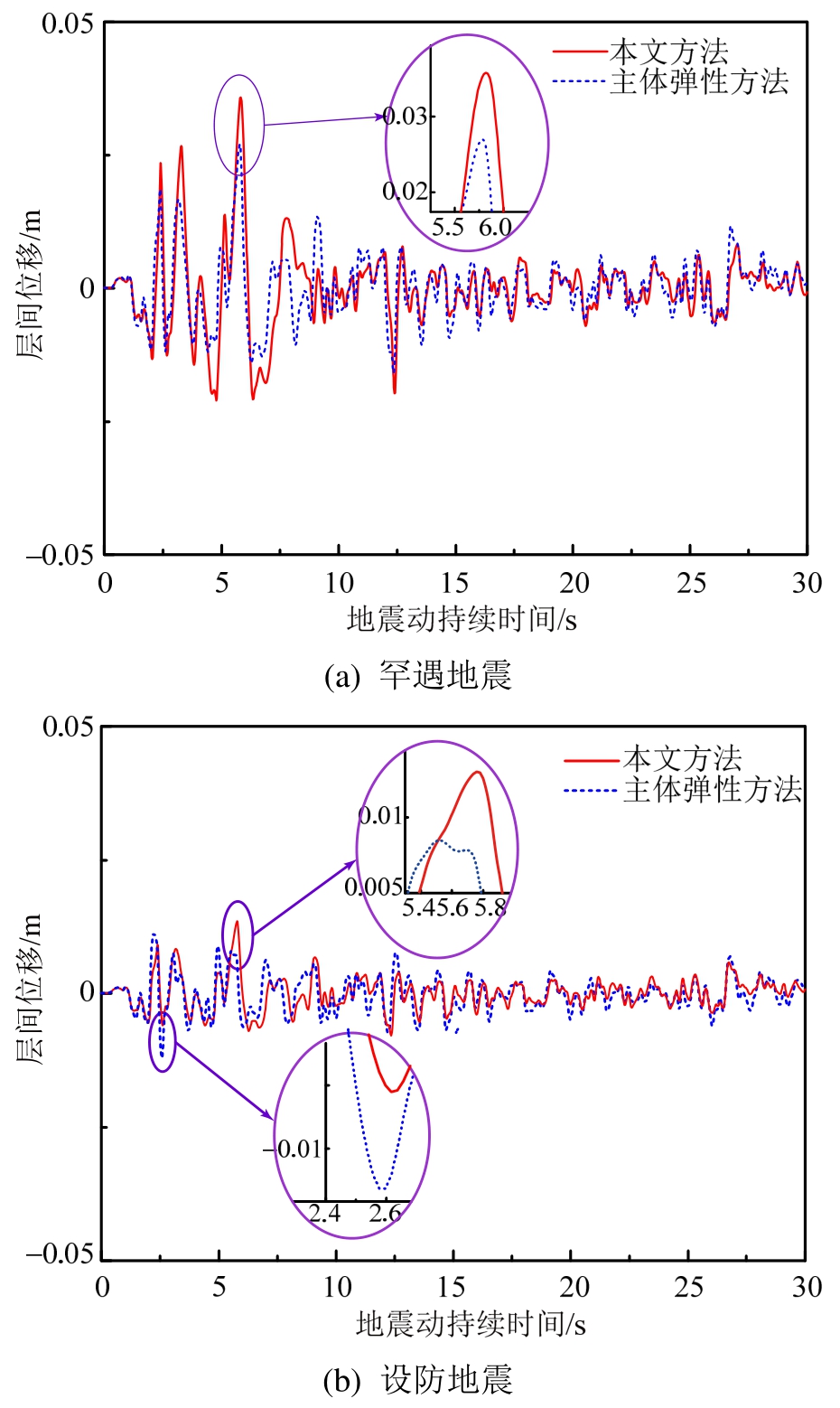
图9 顶层层间位移时程曲线
Fig.9 Drift time history at the top of structure
3)塑性铰分布
图10给出了罕遇地震结束时两种模型塑性铰分布情况，分析过程中采用FEMA356默认塑性铰机制，图例B代表塑性铰屈服，C代表结构失去承载力，IO、LS、CP分别代表直接使用、生命安全和防止倒塌抗震性能目标。本文方法塑性铰相对较多，共形成塑性铰24个，均处于屈服状态且集中在结构的中部；主体弹性方法无塑性铰。需要说明的是，虽然本文方法塑性铰比主体弹性方法多，但均处在屈服状态且均在梁中出现，对结构完成预定功能影响不大，此现象恰好验证了本文方法的准确性，达到了允许主结构部分构件进入塑性状态的设计目标。
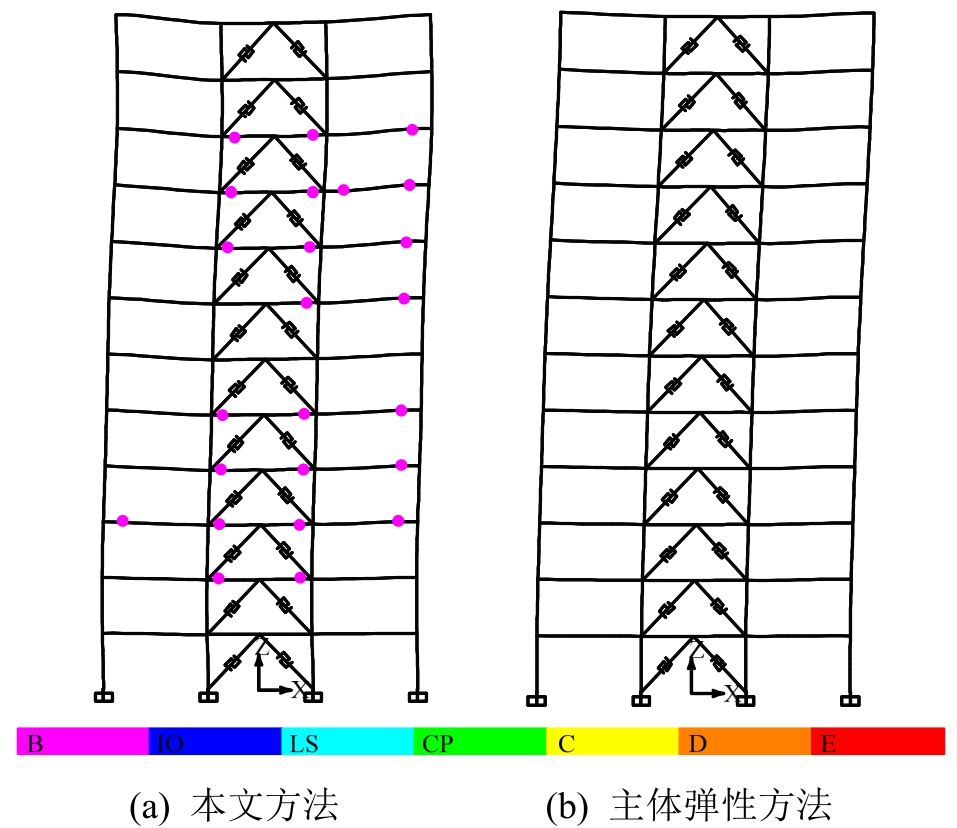
图10 罕遇地震下塑性铰分布情况
Fig.10 Evolution of plastic hinges under rare earthquake
本文提出了一种基于能量抗震设计的新思路，并给出了设计流程和算例，对采用本文方法建立的模型和采用主结构弹性方法建立的模型进行了时程对比分析，验证了本文方法的实用性和准确性，得出以下结论：
(1)在设计之初通过延性系数将主结构的损伤指数转化为等效阻尼比，以此来考虑主结构的损伤耗能的方法是可行的，可以实现结构抗震多道防线的设计理念。
(2)对于高阶振型影响较大的结构，建议采用通过结构损伤前后阻尼比吸收能来计算阻尼器耗能的方法，并根据实际选择更多振型计算阻尼器耗能，同时该方法适用于装有不同被动耗能装置的结构体系。
(3)本文提出的利用结构损伤前后阻尼比吸收能来计算阻尼器耗能的方法，无迭代过程，求解过程简单，较好的实现了由主结构损伤耗能分担部分阻尼器耗能的性能化设计目标。
参考文献：
[1]Kowalsky M J.RC structural walls designed according to UBC and displacement-based methods[J].Journal of Structural Engineering，2001，127(5):506―516.
[2]Lin Y Y，Tsai M H，Hwang J S，et al.Direct displacement-based design for building with passive energy dissipation systems[J].Engineering Structures，2003，25(1):25―37.
[3]李钢，李宏男.基于位移的消能减震结构抗震设计方法[J].工程力学，2007，24(9):88―94.Li Gang，Li Hongnan.Direct displacement-based design for buildings with passive energy dissipation devices[J].Engineering Mechanics，2007，24(9):88―94.(in Chinese)
[4]黄小宁，杜永峰，李慧.平面不规则RC框剪结构基于性能的减震设计方法[J].工程力学，2017，34(3):68―75.Huang Xiaoning，Du Yongfeng，Li Hui.Performancebased design method for irregular plane RC frame-shear-wall structure with dissipation devices[J].Engineering Mechanics，2017，34(3):68―75.(in Chinese)
[5]白久林，金双双，欧进萍.钢筋混凝土框架结构强柱弱梁整体失效模式可控设计[J].工程力学，2017，34(8):51―59.Bai Jiulin，Jin Shuangshuang，Ou Jinping.Strong-column weak-beam global seismic failure mode control-based design of reinforced concrete frame structures[J]Engineering Mechanics，2017，34(8):51―59.(in Chinese)
[6]Housner G W.Limit design of structures to resist earthquakes[C]// Proceedings of the First World Conference on Earthquake Engineering.Berkeley，California:Earthquake Engineering Research Institute，1956:1―12.
[7]Akiyama H.Earthquake resistant limit state design for buildings[M].Tokyo:University of Tokyo Press，1985:23―30.
[8]Fajfar P，Gaspersic P.The N2 method for the seismic damage analysis of RC buildings[J].Earthquake Engineering and Structural Dynamics，1996，25(1):31―46.
[9]Shen J，Akbaş B.Seismic energy demand in steel moment frames[J].Journal of Earthquake Engineering，1999，3(04):519―559.
[10]Chou C C，Uang C M.A procedure for evaluating seismic energy demand of framed structures[J].Earthquake Engineering & Structural Dynamics，2003，32(2):229―244.
[11]Chopra A K，Goel R K.A modal pushover analysis procedure for estimating seismic demands for buildings[J].Earthquake Engineering & Structural Dynamics，2002，31(3):561―582.
[12]白久林，欧进萍.基于能量平衡的钢筋混凝土框架结构抗震塑性设计方法[J].建筑结构学报，2012，33(10):22―31.Bai Jiulin，Ou Jinping.Seismic plastic design of RC frame structure based on energy balance[J].Journal of Building Structures，2012，33(10):22―31.(in Chinese)
[13]叶列平，缪志伟，程光煜，等.建筑结构基于能量抗震设计方法研究[J].工程力学，2014，31(6):1―12.Ye Lieping，Miao Zhiwei，Cheng Guangyu，et al.Study on the energy-based seismic design method of building structures[J].Engineering Mechanics，2014，31(6):1―12.(in Chinese)
[14]Choi H，Kim J.Energy-based seismic design of buckling-restrained braced frames using hysteretic energy spectrum[J].Engineering Structures，2006，28(2):304―311.
[15]Benavent-Climent A.An energy-based method for seismic retrofit of existing frames using hysteretic dampers[J].Soil Dynamics and Earthquake Engineering，2011，31(10):1385―1396.
[16]Benavent-Climent A，Mota-Páez S.Earthquake retrofitting of R/C frames with soft first story using hysteretic dampers:Energy-based design method and evaluation[J].Engineering Structures，2017，137:19―32.
[17]Habibi A，Chan R W K，Albermani F.Energy-based design method for seismic retrofitting with passive energy dissipation systems[J].Engineering Structures，2013，46(1):77―86.
[18]Abdi H，Hejazi F，Saifulnaz R，et al.Response modification factor for steel structure equipped with viscous damper device[J].International Journal of Steel Structures，2015，15(3):605―622.
[19]ATC40，seismic evaluation and retrofit of concrete buildings[R].Applied Technology Council，1996.
[20]FEMA 356 Prestandard and commentary for the seismic rehabilitation of buildings[R].Federal Emergency Management Agency，Washington，D.C.，2000.
[21]GB 50011―2010，建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.GB 50011―2010，Code for seismic design of buildings[S].Beijing:China Architecture & Building Press，2010.(in Chinese)
[22]Powell G H，Allahabadi R.Seismic damage prediction by deterministic methods:concepts and procedures[J].Earthquake Engineering & Structural Dynamics，1988，16(5):719―734.
[23]Fajfar P，Vidic T.Consistent inelastic design spectra:Hysteretic and input energy[J].Earthquake Engineering & Structural Dynamics，1994，23(5):523―537.
[24]Park Y J，Ang H S.Mechanistic Seismic Damage Model for Reinforced Concrete[J].Journal of Structural Engineering，1985，111(4):722―739.
[25]欧进萍，牛荻涛，王光远.多层非线性抗震钢结构的模糊动力可靠性分析与设计[J].地震工程与工程振动，1990，10(4):27―37.Ou Jinping，Niu Ditao，Wang Guangyuan.Fuzzy dynamical reliability analysis and design of muti-storey nonlinear aseismic steel structures[J].Earthquake Engineering and Engineering Vibration，1990，10(4):27―37.(in Chinese)
[26]欧进萍，何政，吴斌，等.钢筋混凝土结构基于地震损伤性能的设计[J].地震工程与工程振动，1999，19(1):21―30.Ou Jinping，He Zheng，Wu Bin，et al.Seismic damage performance-based design of reinforced concrete structures[J].Earthquake Engineering and Engineering Vibration，1999，19(1):21―30.(in Chinese)
[27]邱法维，钱稼茹，陈志鹏.结构抗震实验方法[M].北京:科学出版社，2000:14―16.Qiu Fawei，Qian Jiaru，Chen Zhipeng.Seismic test methodology for structures[M].Beijing:Science Press，2000:14―16.(in Chinese)
[28]胡聿贤.地震工程学[M].第二版.北京:地震出版杜，2006:44―53.Hu Yuxian.Earthquake engineering[M].2nd ed.Beijing:Seismological Press，2006:44―53.(in Chinese)
[29]Rosenblueth E，Herrera I.On a kind of hysteretic damping[J].Journal of Engineering Mechanics Division，ASCE，1964，90(1):37―48.
[30]Iwan W D.Estimating inelastic spectra from elasitc spectra[J].Earthquake Engineering and Structural Dynamics，1980，8(4):375―388.
[31]Gulkan P，Sozen M.Inelastic response of reinforced concrete structures to earthquake motions[J].ACI Structural Journal，1974，71(12):604―610.
[32]Kowalsky M J.Displacement-based design:A methodology for seismic design applied to RC bridge columns[D].La Jolla:University of California at San Diego，1994.
[33]Priestley M J，Calvi G M，Kowalsky M J，et al.Displacement-based seismic design of structures[J].Earthquake Spectra，2008，24(2):555―557.
[34]Dwairi H M，Kowalsky M J，Nau J M.Equivalent damping in support of direct displacement-based design[J].Journal of Earthquake Engineering，2007，11(4):512―530.
ENERGY-BASED ASEISMIC DESIGN FOR BUILDINGS WITH PASSIVE ENERGY DISSIPATION SYSTEMS CONSIDERING DAMAGE
ZHU Li-hua1，LI Gang1，LI Hong-nan1，2
(1.State Key Laboratory of Costal and Offshore Engineering，Dalian University of Technology，Dalian 116023，China;2.College of Civil Engineering，Shenyang Jianzhu University，Shenyang 110168，China)
Abstract:Energy-based design method is a more comprehensive evaluation tool compared with strength and displacement-based methods for structural aseismic performance.In this paper a simplified energy-based design method is proposed，considering main structure damage for aseismic structures with passive energy dissipation systems.The hysteretic energy of structures is being dissipated by dampers and structural members together during severe earthquakes.Thusly，this method utilizes an equivalent damping ratio to determine the damage of the main structure and establishes the relationship between the equivalent damping ratio and main structural damage index through the ductility coefficient of the structure.At the same time，the formula is developed to solve dissipative energy of dampers and a step-by-step process is proposed.This is in stark contrast to the previous energy-based method that the proposed method has no iterative process and realizes damage control of the main structure at the beginning of design.At last，the simplicity and practicability of the proposed design method for buildings with passive energy dissipation systems is verified through a numerical case of 12-story frame.
Key words:energy-based design;passive energy dissipation systems;structural damage;equivalent damping ratio;steel moment resisting frames
中图分类号：TU352.1+1
文献标志码：A
doi:10.6052/j.issn.1000-4750.2016.12.0997
文章编号：1000-4750(2018)05-0075-11
收稿日期：2016-12-26；修改日期：2017-10-17
基金项目：国家自然科学基金优秀青年科学基金项目(51422802)；大连市高层次人才创新支持计划项目(2015R044)
通讯作者：李 钢(1979―)，男，辽宁葫芦岛人，教授，博士，博导，主要从事结构工程抗震等研究(E-mail:gli@dlut.edu.cn).
作者简介：朱立华(1986―)，男，河北唐山人，博士生，主要从事消能减震结构的研究(E-mail:zhulihuahd@163.com);
李宏男(1957―)，男，辽宁沈阳人，教授，博士，博导，主要从事结构工程抗震和结构健康检测等研究(E-mail:hnli@dlut.edu.cn).