颜王吉，王朋朋，孙 倩，任伟新
(合肥工业大学土木与水利工程学院，安徽，合肥 230009)
摘 要：与频响函数反映动力系统输入-输出的关系不同，振动响应传递比函数反映的是系统输出-输出之间的关系。振动响应传递比函数可以有效地避免对系统输入的测量，近年来成为系统识别领域重要的分析手段。该文对振动响应传递比函数进行了分类，揭示了传递比函数的特性，并着重阐明了传递比函数与频响函数之间的内在联系。以此为基础，综述了局部传递比(local transmissibility)和传递比矩阵(transmissibility matrix)在结构模态参数识别、损伤识别和模型修正应用中的研究进展。最后，该文指出了基于传递比函数的系统识别存在的问题，并对将来的研究思路作出了展望。
关键词：传递比；参数识别；损伤识别；模型修正；健康监测
结构安全监测是国内外研究的热点，其过程一般包括在一段较长时间内通过布设一系列传感器收集结构的响应信号，从这些响应信号中提取对结构损伤比较敏感的特征，对这些特征进行统计分析，确定结构当前健康状况。其中需要重点解决的一个关键问题就是准确识别结构的固有特性，主要包括三个方面：一是正确地识别或监测结构工作时的动力特性或模态参数，即结构的参数识别问题；二是抽取对结构损伤比较敏感的动力特征，确定结构当前健康状况，即结构的损伤识别问题；三是通过修正结构有限元分析模型(参数)，使有限元分析值与实际结构的测试值之间的误差尽可能减小[1]，即结构模型修正问题。
上述三个问题的研究在结构安全评估领域占据重要的地位，同时也为基于监测数据的结构安全评估提供了基础和依据。一般来说，目前用于解决以上问题的方法通常可以分为两类。一类是基于已知的系统输入和输出数据的方法。这类方法依据结构的激励(输入)和动力响应(输出)的测量值，求出系统在频域内的频率响应函数或时域内的脉冲响应函数，以完成结构特征参数的识别，进一步识别损伤，修正结构模型[2]。另一类是仅基于输出数据的方法。这类方法只根据结构的响应数据实现参数识别、损伤识别和模型修正。
与基于输入-输出数据的方法相比，仅基于输出数据的方法无需借助于昂贵的激励设备对结构施加人工激励，不需要测定激励数据，费用低廉，大大缩短了测试时间，同时还避免了结构的正常运营的中断，具有很大的工程实用价值和广阔的应用前景。为了便于数学处理，仅基于输出数据的参数识别方法通常对输入模型作了理想化假定。然而，这些理想化条件在实际工程中很难得到严格满足，在阵风、车辆等环境荷载激励下，很多时候工程结构难以避免地受到复杂激励的作用，如有色噪声激励甚至是谐波激励，实践与理论的差异无疑会影响系统识别结果的鲁棒性与准确性，甚至会导致识别出错误的结果[3]。
基于以上考虑，有必要在系统识别阶段引入新的方法来充分考虑输入的影响，这可以为土木工程结构动力灾变和安全监测分析提供更稳健可靠的基础和依据。近年来，振动响应传递比函数在系统识别领域受到越来越多学者的关注。应用振动响应传递比函数时，系统输入只作为动力源而不需要参与运算，因此避免了对系统荷载测量的依赖，从而有效地避免了输入数据的测量。本文系统阐述了传递比函数的分类、特性及其内涵，综述了传递比函数在模态参数识别、损伤识别和结构模型修正三个方面的应用，并指出了相关研究存在的一些问题，对将来的研究思路作了进一步的讨论。
与频响函数不同，振动响应传递比函数反映的是动力系统输出与输出之间的关系。振动响应传递比函数一般可分为两类[4]：一类是局部传递比(local transmissibility)，也有文献称其为标量传递比函数(scalar transmissibility)[5―6]，另一类是传递比矩阵(transmissibility matrix)[7―8]，也有文献称其为全局传递比(global transmissibility)。这两类响应传递比函数的具体定义为：
1)局部传递比：假定xi(t)和xo(t)分别为结构动力系统测点i、o的响应记录，局部传递比定义为两测点快速傅里叶变换(FFT)系数之比，即：
式中，Xi(ω)和Xo(ω)分别表示xi(t)和xo(t)的FFT系数。局部传递比与频响函数之间存在以下关系：
式中：Hi，m(ω)为反映i和m自由度输入-输出关系的频响函数(FRF)；Fm(ω)为作用于m自由度外部激励的FFT系数；NF为作用系统的激励点数。
2)传递比矩阵：假定XA(ω)和XB(ω)为系统两组振动响应的FFT向量，传递比矩阵Γ(ω)可以用于表征XA(ω)和XB(ω)的关联，即：
更进一步，Γ(ω)的表达式为：
式中：HA(ω)和HB(ω)为频率响应函数矩阵，分别表示输入f(t)与响应xA(t)和xB(t)之间的输入-输出传递关系。
当仅在系统m点作用激励时，局部传递比和传递比矩阵均可以化简为以下公式：
由式(5)可知，单点激励作用下，振动响应传递比与输入性质及其强度无关。
对于土木工程结构而言，工作模态参数分析是指结构处于正常运营状态下进行的模态分析，其分析过程仅建立在结构动力输出的基础上，无需中断工程结构的正常使用，具有费用低、测试时间短的优点。近年来振动传递比被广泛应用于结构工作模态参数识别中。由于对谐波激励拥有良好的鲁棒性，因而，振动传递比具有广阔的应用空间[9―10]。比利时布鲁塞尔自由大学Devriendt与Guillaume[5―6]较早地将传递比函数引入模态参数识别中，提出了基于传递比测试的工作模态参数识别(Transmissibility Based Operational Modal Analysis，TOMA)方法。他们证明了局部传递比函数Tio(ω)在系统极点(即固有频率处)与对应测点模态振型之比等价的性质，即：
式中：ωr为第r个系统极点；Φir和Φor分别为测点i和o的第r阶阵型值；i2=-1。任意两个荷载工况k和l
下传递比函数的差值满足：
换言之，
的倒数满足：
由式(7)和式(8)可知，系统的极点刚好是传递比差值函数的零点，也就是传递比差值函数
的倒数
的极点。因此，联合不同工况下的传递比函数可以有效地识别出系统的模态参数。Devriendt等[3]还将其用于识别作用有谐波干扰的系统模态参数，并与传统功率谱模态识别方法对比分析，发现TOMA方法具有不依赖输入的特性。基于TOMA方法的基本思想[5―6]，最近一些学者在TOMA方法的工程应用方面进行了改进，文献[11]结合PolyMax方法估算极点，利用绘制的稳定图剔除虚假模态，并将其应用于机翼的模态分析[12]。在国内，韩杰[13]将该方法应用于悬臂结构模态分析，研究发现该方法与稳态图结合能够在谐波干扰下准确地提取系统的模态参数，弥补了基于功率谱工作模态参数识别方法在这方面的不足。
为降低选择虚假极点的风险，Devriendt课题组还将多个激励工况下传递比函数构建为特殊的矩阵形式，并采用奇异值分解技术进一步改善方法的实际应用效果[14]：
式中：上标(j)表示各载荷工况(j=1，2，…，Nl，Nl为系统激励工况数)；下标i表示系统i测点；u表示固定测点；No表示测点数。对式(9)进行奇异值分解，可以识别出系统的模态参数。对弱阻尼系统而言，当振动频率达到共振频率(系统极点)时，[
(ω)]的秩为1。因此，引入矩阵奇异值分解理论，选择第i个奇异值(i≠1)，并取其倒数即可识别出系统的模态频率，操作方法类似于传统的频域分解法。
需要指出的是，Devriendt与Guillaume等学者完成的以上工作都至少需要记录两个不同荷载工况下的结构振动响应，才能完成模态参数的识别。然而，对于大型土木工程结构(如大跨桥梁、大坝等)而言，改变荷载工况对结构进行多次环境激励振动测试，不但增加了工程应用难度，而且还提高了应用成本。针对这一问题，Yan和Ren[15]受Devriendt等学者工作的启发，提出了功率谱传递比(Power Spectrum Density Transmissibility，PSDT)的概念。引入参考点的思路，PSDT可以定义为任意两测点关于同一参考点的功率谱之比，即：
式中，Sip(ω)和Sop(ω)分别为系统测点i、o响应记录与参考点p处响应记录的互谱。根据证明得到的函数极限的一个引理，阐明了在系统极点处功率谱传递比不依赖于系统的输入及参考点选择，与两测点的模态振型比值等价，即：
由于系统的极点刚好是同一个工况下任意两个不同参考点对应的“功率谱传递比差值函数”的零点，同一荷载工况下不同参考点对应的功率谱传递比可以用来识别结构的固有频率和振型。从式(10)和式(11)不难得到，在同一测试条件下两个具有不同参考输出的PSDT相减满足：
换言之，系统的极点即为
的零点。因此，依据
的倒数可以获得系统极点，即
需要指出，
可能包含与系统无关的极点，仅有部分极点等同于系统的极点。为了降低错误识别系统极点的风险，可以将不同测点和参考点构成的PSDT函数加以融合，以达到提高识别精度的目的。一系列实践表明，由以下函数组成的PSDT函数具有非常好的鲁棒性：
式中：
基于同样的思路，作者将PSDT与连续小波变换结合起来，提出了连续小波变换传递比(CWTR)的概念[16]。结合不同参考点对应的CWTRs可以提取出结构的频率和模态振型。
PSDT方法具有计算速度快，操作简单，能够提取结构固有频率，也能够较好地识别结构模态振型等特点。PSDT峰值的拾取依赖于人为的主观判断，结构模态参数识别的结果尚有改善的空间。为了进一步探索基于功率谱传递比方法提取真实峰值的鲁棒性，国内外一些学者做出了努力。如Araújo和Laier[17]基于功率谱传递比的概念及其在系统极点处的特性，联合一系列不同参考点对应的功率谱传递比构成PSDT矩阵：
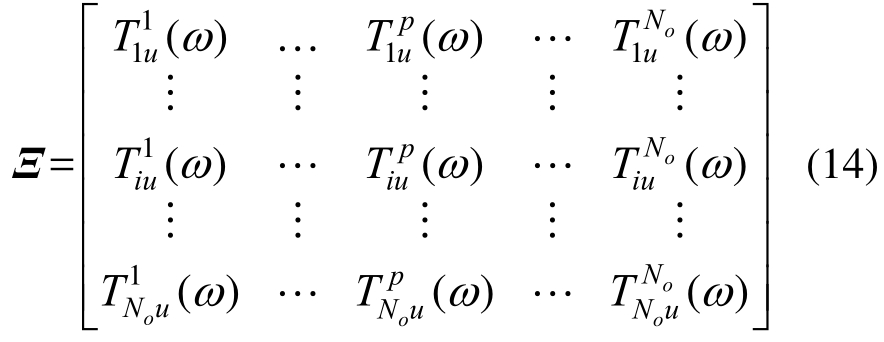
对PSDT矩阵进行奇异值分解可以求出结构固有频率与振型。该文还指出了该方法能够识别出频域分解法(FDD)无法识别出的某些频率峰值。Yan和Ren[18]还引入了最小二乘复频域算法(LSCF)估计，通过绘制稳定图来分离稳定的系统极点，利用参数化拟合的思路识别结构动力参数。基于功率谱传递比的方法是根据模态信息寻找系统极点，因而理论上可以避免识别色噪声引起的错误结果。PSDT的参数识别方法还被拓展到相干函数[19]，理论上可以证明相干函数在系统极点处趋于1，因此可以用相干函数判别系统的极点。
结构发生损伤后，其物理参数(如质量、刚度等)将会发生改变，从而引起结构固有特性的变化。与频响函数等动力特征函数类似，局部传递比函数较为完整地包含了某一频带内系统动力特性的信息[20]。过去几十年，响应传递比函数被不同课题组广泛地应用于结构损伤识别中。例如，英国谢菲尔大学Worden教授课题组结合神经网络算法、异常值检验方法等模式识别或机器学习技术，提出了一系列基于传递比函数的结构损伤识别方法[21―23]，并通过对机翼的损伤识别试验研究表明，传递比函数对刚度变化十分敏感，取得了良好的应用效果[24―27]。同时，Worden的方法也被用于定位实际结构上的附加质量模拟的故障[28]。
美国航空航天局的Schulz研究组将结构无损状态以及损伤状态对应的传递比函数的差值在固定频带[ω1，ω2]内进行积分，对该积分归一化后得到了新的损伤指标[20，29―31]：
式中：上标h、d分别代表无损状态和损伤状态；ω为频率。随后这一指标被众多学者采用。例如，Caccese等[32]利用螺栓松动模拟损伤，并用该损伤指标成功识别出单个螺栓松动，同时发现该指标对螺栓松动程度变化十分敏感。文献[33―34]将Schulze提出的损伤指标嵌入到无线传感器中，利用框架结构动态测试数据来验证，这些研究工作通过质量块加载、螺栓松动等方式来模拟损伤。最近，该方法又被用于隧道结构的损伤识别[35]。
Maia教授课题组[36]采用与文献[30]类似的方法，研究了振动传递比在量化结构损伤程度、确定损伤位置中的可行性。受模态置信准则的启发，他们构建了传递比函数向量置信准则(RVAC)：
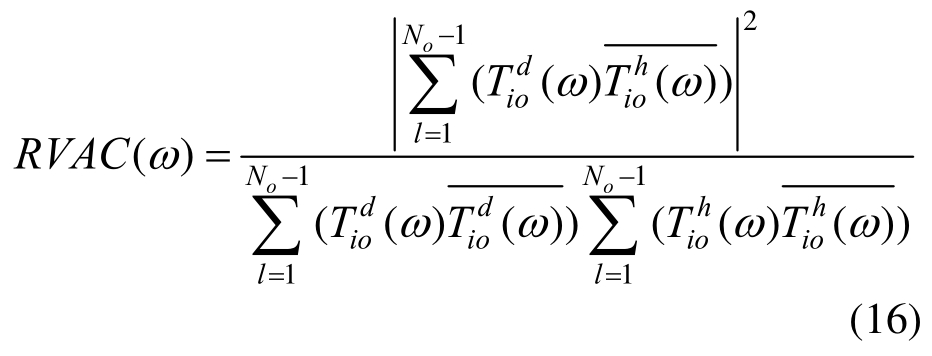
式中：上标“—”表示复共轭；考虑系统受到不同工况的激励，根据RVAC可以融合不同激励工况下的传递比函数，构建如下损伤指标：
式中：Nω为某一频带的频率点数。该损伤指标只需要测量系统响应数据，避免了训练数据的过程。另一方面，研究表明RVAC指标对结构损伤具有较高的灵敏度。最近，RAVC指标也被拓展到车桥耦合系统，用来识别车辆激励下桥梁结构的损伤状况[37]。
除了上述介绍的损伤识别方法外，近几年学者们还提出了其他一些基于局部传递比函数的损伤识别方法。例如，为了研究非离散系统的损伤识别问题，Chesné和Deraemaeker[38]详细分析了四类子系统的响应传递比函数，讨论了采用式(15)所示的损伤指标确定损伤位置的适用条件。此外，文献[38]还对比了各种基于传递比函数的损伤识别方法的优缺点，阐明了这类方法的局限性和需要重点注意的方面。
最近，Mao和Todd[39―40]提出了局部传递比函数估计不确定性量化的解析概率密度函数。根据该传递比函数的概率函数，可以分析结构损伤状态和无损状态下传递比函数的统计特征。在特定置信水平下，通过对两种状态下振动响应传递比之间的显著性进行分析，可以确定结构是否存在损伤[41―42]。Lang等[43]将局部传递比概念拓展到非线性系统，探讨了非线性系统损伤识别和损伤定位问题[44―45]。此外，还有学者提出将传递比函数和Mahalanobis距离结合起来进行系统损伤定位[46]。在国内，曹茂森[47]较早地研究了利用传递比函数进行损伤识别的能力，概括了振动传递比用于结构损伤识别的若干优势，通过框架的数值模拟对方法的适用性和优越性进行了验证。
传递比函数仅仅依赖于结构响应数据，能够避免测量外部激励，为有限元模型修正问题提供有效的解决途径[48―49]。Steenackers等[48]提出用传递比函数代替频响函数进行有限元模型修正，证明了当系统激励输入点的位置固定时，以输入点为参考点构建的传递比函数极点与结构的共振频率之间存在对应关系，基于这一特性可以对结构有限元模型进行修正。为了说明方法的有效性，他们还通过某移动变电站的支柱有限元动力模型数值算例进行了验证，同时发现运用传递比修正的有限元模型与频响函数修正的模型等效。
由于模态振型一般是无法精确识别的，因此依据模态振型信息修正模型将不可避免地降低修正结果的精度。针对这一问题，同样包含模态振型及固有频率信息的反共振频率可以被应用于结构模型修正研究中，Meruane[49]提出将反共振频率(anti-resonance frequency)概念和TOMA方法联合对结构有限元模型进行修正。通过对一个弹簧-质量体系有限元模型和一汽车尾气系统有限元模型进行模型修正和结构损伤评估。数值算例证明，反共振频率和TOMA方法结合可以有效应用于结构动力有限元模型修正中，同时发现反共振频率相较于模态振型更易于识别，具有更高的测量精度。因此，在外部输入未知时，局部传递比函数也可以作为一种选择引入结构有限元模型修正研究中。
除了上述提到的应用以外，局部传递比函数概念在其他领域也有着广泛的应用，如结构设计等领域。为了确定合适的候选节点以实现结构设计调整的最小化，Kim等[50]提出一种新的基于传递比函数的灵敏度分析技术。Steenackers等[51]将传递比函数引入结构优化设计中，以提高有限元分析阶段计算效率。除此以外，局部传递比函数还被用于运行工况下传递路径分析[52]。
Devriendt等[53]基于传递比的工作模态参数识别技术，成功地将局部传递比函数拓展到传递比矩阵。文章通过“虚拟局部传递比函数”巧妙地将多点激励下传递比矩阵和局部传递比函数联系在一起。研究发现“虚拟局部传递比函数”具有在系统极点处与外部激励无关的性质：
式中：
和
代表{K&L}及其{K&M}两个不同荷载工况组合下的“虚拟局部传递比函数”。基于这一特性，构建两个不同激励工况下“虚拟局部传递比函数”的差值函数，即可实现系统的参数识别。
正如上面所提到的，采用基于“虚拟局部传递比函数”的模态参数识别方法至少需要两种不同荷载工况，才能完成模态参数识别任务。事实上需要的荷载工况个数总比不相关的输入源个数多，并随着不相关输入源数目的增多而增多，最终导致测试时间的增加。为了解决这一问题，Weijtjens等[54]提出了多参考点传递比函数的工作模态参数识别(pTOMA)方法。该方法可以准确、可靠地识别系统参数，能够有效剔除谐波激励或强有色激励引起的虚假结果。最近，Weijtjens等[55]基于传递比矩阵提出了一种能够提取模态振型归一化参数的方法。与传统方法不同，该方法不需要对原有结构进行调整(如在结构上增加质量)，仅需要测定响应数据和获取系统激振力的位置。
与局部传递比函数一样，传递比矩阵被提出以来，也引起了广泛关注[7―8，56―57]。Mottershead[58]针对频响函数零点的损伤灵敏度进行了研究，证明了其零点的损伤灵敏度可由模态振型的和固有频率相应灵敏度的线性组合表示。由于传递比函数共振处和反共振处对应的频率点，与构成传递比的两测点相应的频响函数零点存在对应关系。基于这一对应关系，在传递比矩阵概念[7]和频响函数零点灵敏度[58]相关研究的基础上，美国普渡大学的Johnson和Adams课题组[59]结合Schulz课题组早期的方法[20，29―31]，采用传递比函数作为新损伤指标，实现对结构损伤的识别、定位和量化。Adams方法随后又用于检测不同类型结构的损伤，如钢框架结构、旋翼机机身[60]。此外，他们还解决了频带选择问题[61]，有效避免了运行状况和环境状况变化引起的识别结果变异。
传递比矩阵还被用于结构的响应重建研究中。Law团队[62]提出将相邻子结构作用的界面内力作为子结构的激励，采用传递比矩阵用测量的响应预测其他指定位置的响应，从而重建得到指定子结构的响应信号。在上述动力响应重建方法的基础上，他们[63]又提出了子结构的损伤识别方法，并通过数值算例和实验对该损伤识别方法进行了验证。除此以外，传递比矩阵也从频域推广到了小波域[47]。最近，Law团队[64―65]将小波域的传递比用于子结构的响应重建，他们采用类似文献[62―63]中方法实现单位脉冲响应函数，利用获得的响应函数进行子结构的响应重建。Zhu等[66]采用状态空间域传递比矩阵识别局部结构损伤。利用系统Markov参数表示两组加速度响应测试之间的关系，推导出传递比矩阵状态空间表达式，应用状态空间域传递比概念对结构进行测点响应重建，最后，利用新的基于灵敏度模型修正方法将响应测量值与重建值之间的差异最小化，以此实现结构局部损伤的识别。
由于传递比矩阵反映的是两组响应向量之间的频域关系，一旦系统激励位置已知，传递比矩阵可以将实测的动力响应向量与动力学模型参数联系起来，实现结构模型参数的修正。文献[67―68]直接利用测定的结构响应，应用贝叶斯模型修正方法对结构模型进行修正。这类方法充分利用了快速傅里叶变换系数服从多元复高斯分布的统计特性。受上述工作的启发，Yan和Katafygiotis[69]近期基于传递比矩阵概念和服从Wishart矩阵分布的功率谱密度矩阵迹的统计特性，提出了一种改进的随机模型修正方法。文献[67―69]中的这些方法的主要优点是能够修正作用非平稳激励的子结构的参数，从而降低模型修正参数维度过高引起的收敛问题。
振动响应传递比函数因为其独特的性质近年来引起了较为广泛的关注，它在单点激励下与输入的性质和大小无关，在构建损伤指标和模型修正的目标函数时，可以充分避免算法对系统输入的依赖。在系统固有频率处，传递比函数不依赖于激励的性质和作用位置，等于两测量点的模态振型之比，利用“传递比差值函数的倒数”可以快速识别结构的模态参数。需要指出，基于响应传递比的系统识别仍然面临许多难题，需要继续深入探索，主要包括：
(1)基于传递比的损伤指标对结构刚度变化较为敏感，是结构损伤识别的理想选择。然而，正如文献[38]指出，利用传递比函数进行损伤程度判断仍然是很困难的。将传递比函数用于结构损伤识别另一个主要问题是频带选取对结果有较大影响[38]。因此，如何选取最优频带范围内的响应传递比函数进行损伤识别仍然是一个没有得到很好解决的问题。
(2)基于响应传递比函数的模态参数识别方法本质上属于频域方法，能够较好地识别频率和振型，但是对于阻尼的识别，尤其是阻尼较大工况的识别，其精度仍然有待进一步提高。此外，与其他频域方法一样，PSDT识别精度会受到功率谱估计精度的影响。因此，如何提高谱估计的精度来进一步提高PSDT方法仍然是一个值得研究的内容[70]。
(3)结构系统识别存在着不同形式的不确定性，如测试不确定性、数值不确定性和模型不确定性等[71―73]。为了提高系统识别结果的鲁棒性和准确性，在结构动力安全性分析中引入统计方法来充分考虑这些误差或不确定性的影响不失为一种很好的手段。文献[74―76]在相关方面进行了探索，证明了复数域比例随机向量的统计推断定理，解析推导出了高维相关传递比随机向量的复数域解析概率模型，并将其应用于统计模态分析，实现了模态参数识别的不确定性量化。但是，如何将这一概率模型用于损伤识别和模型修正等领域达到充分考虑多源不确定性的目的，仍是一个需要深入探索的问题。
(4)复杂环境和运营条件的作用下，结构参数和测试信号会发生变化，导致基于传递比函数的系统识别得到的结果产生变化。显然，环境因素如温度引起的参数变化或者波动并非结构本身的健康状态导致的，而是结构正常运营状态下允许出现的差异[77]。所以，如何利用长期传递比函数和环境数据的统计，分离环境变异与结构损伤导致的参数变异，目前仍是远没有得到很好解决的问题。
(5)基于响应传递比函数的模态参数识别已经成功应用于大型工程结构[70]。然而，基于振动响应传递比的损伤识别和模型修正方法更多地局限于实验模型或数值模拟。对于土木工程结构，其尺寸庞大且模型复杂，有限元模型的自由度往往成千上万。因而，如何将振动响应传递比应用到复杂的实际工程结构中，仍是一个值得努力的方向。
参考文献：
[1]王浩，王付全，李爱群，等.大跨度缆索支撑桥梁分阶段有限元模型修正[J].工程力学，2009，26(10):111―116.Wang Hao，Wang Fuquan，Li Aiqun，et al.Multi-phase FE model updating on long-span cable-supported bridges[J].Engineering Mechanics，2009，26(10):111―116.(in Chinese)
[2]任伟新.环境振动系统识别方法的比较分析[J].福州大学学报:自然科学版，2001，29(6):80―86.Ren Weixin.Comparison of system identification methods using ambient vibration measurements[J].Journal of Fuzhou University，Natural Science Edition，2001，29(6):80―86.(in Chinese)
[3]Devriendt C，De Sitter G，Vanlanduit S，et al.Operational modal analysis in the presence of harmonic excitations by the use of transmissibility measurements[J].Mechanical Systems and Signal Processing，2009，23(3):621―635.
[4]Urgueira A P V，Almeida R A B，Maia N M M.On the use of the transmissibility concept for the evaluation of frequency response functions[J].Mechanical System and Signal Processing，2009，25(3):940―951.
[5]Devriendt C，Guillaume P.The use of transmissibility measurements in output-only modal analysis[J].Mechanical Systems and Signal Processing，2007，21(7):2689―2696.
[6]Devriendt C，Guillaume P.Identification of modal parameters from transmissibility measurements[J].Journal of Sound and Vibration，2008，314(1-2):343―356.
[7]Ribeiro A M R，Silva J M M，Maia N M M.On the generalization of the transmissibility concept[J].Mechanical Systems and Signal Processing，2000，14(1):29―35.
[8]Maia N M M，Silva J M M，Ribeiro A M R.The transmissibility concept in multi-degree-of-freedom systems[J].Mechanical Systems and Signal Processing，2001，15(1):129―137.
[9]Tcherniak D，Chauhan S，Hansen M H.Applicability limits of operational modal analysis to operational wind turbines[M].New York:Structural Dynamics and Renewable Energy.Springer，2011，1:317―327.
[10]Devriendt C，Steenackers G，De Sitter G，et al.From operating deflection shapes towards mode shapes using transmissibility measurements[J].Mechanical Systems and Signal Processing，2010，24(3):665―677.
[11]De Sitter G，Devriendt C，Guillaume P.Transmissibilitybased operational modal analysis:Enhanced stabilisation diagrams[J].Shock and Vibration，2012，19(5):1085―1097.
[12]Devriendt C，De Troyer T，De Sitter G，et al.Transmissibility-based operational modal analysis for flight flutter testing using exogenous inputs[J].Shock and Vibration，2012，19(5):1071―1083.
[13]韩杰.基于传递率的工作模态参数识别方法的研究[D].太原:太原理工大学，2012.Han Jie.Study of operational modality parameter identification based on transmissibility[D].Taiyuan:Taiyuan University of Technology，2012.(in Chinese)
[14]Devriendt C，Weijtjens W，De Sitter G，et al.Combining multiple single-reference transmissibility functions in a unique matrix formulation for operational modal analysis[J].Mechanical Systems and Signal Processing，2013，40(1):278―287.
[15]Yan W J，Ren W X.Operational modal parameter identification from power spectrum density transmissibility[J].Computer-Aided Civil andInfrastructure Engineering，2012，27(3):202―217.
[16]Yan W J，Ren W X.Use of continuous-wavelet transmissibility for structural operational modal analysis[J].Journal of Structural Engineering，ASCE，2012，139(9):1444―1456.
[17]Araújo I G，Laier J E.Operational modal analysis using SVD of power spectral density transmissibility matrices[J].Mechanical System and Signal Processing，2014，46(1):129―145.
[18]Yan W J，Ren W X.An enhanced power spectral density transmissibility(EPSDT)approach for operational modal analysis:Theoretical and experimental investigation[J].Engineering Structures，2015，102:108―119.
[19]Yan W J，Feng Z，Ren W X.New insights into coherence analysis with a view towards extracting structural natural frequencies under operational conditions[J].Measurement，2016，77:187―202.
[20]Schulz M J，Pai P F，Inman D J.Health monitoring and active control of composite structures using piezoceramic patches[J].Composites Part B:Engineering，1999，30(7):713―725.
[21]Chen Q，Chan Y W，Worden K，et al.Structural fault detection using neural networks trained on transmissibility functions[C]// Proceedings of the International Conference on Vibration Engineering，1994:446―456.
[22]Worden K.Structural fault detection using a novelty measure[J].Journal of Sound and Vibration，1997，201(1):85―101.
[23]Worden K，Manson G，Fieller N R J.Damage detection using outlier analysis[J].Journal of Sound and Vibration，2000，229(3):647―667.
[24]Chen Q，Chan Y W，Worden K.Structural fault diagnosis and isolation using neural networks based on response-only data[J].Computers and Structures，2003，81(22):2165―2172.
[25]Worden K，Manson G，Allman D.Experimental validation of a structural health monitoring methodology:Part I.Novelty detection on a laboratory structure[J].Journal of Sound and Vibration，2003，259(2):323―343.
[26]Manson G，Worden K，Allman D.Experimental validation of a structural health monitoring methodology:part II.Novelty detection on a gnat aircraft[J].Journal of Sound and Vibration，2003，259(2):345―363.
[27]Manson G，Worden K，Allman D.Experimental validation of a structural health monitoring methodology:Part III.Damage location on an aircraft wing[J].Journal of Sound and Vibration，2003，259(2):365―385.
[28]Papatheou E，Manson G，Barthorpe R J，et al.The use of pseudo-faults for novelty detection in SHM[J].Journal of Sound and Vibration，2010，329(12):2349―2366.
[29]Schulz M J，Abdelnaser A S，Pai P F，et al.Detecting structural damage using transmittance functions[C]//Proceedings of the 15th International Modal Analysis Conference，Florida，United States，1997，3089:639―644.
[30]Zhang H，Schulz M J，Naser A，et al.Structural health monitoring using transmittance functions[J].Mechanical Systems and Signal Processing，1999，13(5):765―787.
[31]Ghoshal A，Sundaresan M J，Schulz M J，et al.Structural health monitoring techniques for wind turbine blades[J].Journal of Wind Engineering and Industrial Aerodynamics，2000，85(3):309―324.
[32]Caccese V，Mewer R，Vel S S.Detection of bolt load loss in hybrid composite/metal bolted connections[J].Engineering Structures，2004，26(7):895―906.
[33]Zhu D，Yi X，Wang Y.Sensitivity analysis of transmissibility functions for structural damage detection[C]// Proceedings of SPIE.International Society for Optics and Photonics，San Diego，United States，2011，7983:79832M-1―79832M-12.
[34]Zhu D，Yi X，Wang Y，et al.A mobile sensing system for structural health monitoring:design and validation[J].Smart Materials and Structures，2010，19(5):055011.
[35]Feng L，Yi X，Zhu D，et al.Damage detection of metro tunnel structure through transmissibility function and cross correlation analysis using local excitation and measurement[J].Mechanical Systems and Signal Processing，2015，60:59―74.
[36]Maia N M M，Almeida R A B，Urgueira A P V，et al.Damage detection and quantification using transmissibility[J].Mechanical Systems and Signal Processing，2011，25(7):2475―2483.
[37]Kong X，Cai C S，Kong B.Damage detection based on transmissibility of a vehicle and bridge coupled system[J].Journal of Engineering Mechanics，ASCE，2014，141(1):04014102.
[38]Chesné S，Deraemaeker A.Damage localization using transmissibility functions:a critical review[J].Mechanical Systems and Signal Processing，2013，38(2):569―584.
[39]Mao Z.Uncertainty quantification in vibration-based structural health monitoring for enhanced decision-making capability[D].San Diego，USA:University of California，2012.
[40]Mao Z，Todd M.A model for quantifying uncertainty in the estimation of noise-contaminated measurements of transmissibility[J].Mechanical Systems and Signal Processing，2012，28:470―481.
[41]Mao Z，Todd M.Rapid structural condition assessment using transmissibility with quantified confidence for decision making[M].New York:Topics in Model Validation and Uncertainty Quantification，Springer，2012，4:133―140.
[42]Mao Z，Todd M.Uncertainty propagation of transmissibility-based structural health monitoringfeatures[C]// SPIE Smart Structures and Materials Nondestructive Evaluation and Health Monitoring.International Society for Optics and Photonics，2012:834811-1―834811-8.
[43]Lang Z Q，Park G，Farrar C R，et al.Transmissibility of non-linear output frequency response functions with application in detection and location of damage in MDOF structural systems[J].International Journal of Non-Linear Mechanics，2011，46(6):841―853.
[44]Zhao X Y，Lang Z Q，Park G，et al.A new transmissibility analysis method for detection and location of damage via nonlinear features in MDOF structural systems[J].IEEE/ASME Transaction on Mechatronics，2015，20(4):1933―1947.
[45]Liu W，Ewins D J.Transmissibility properties of MDOF systems[C]// Proceedings of the International Modal Analysis Conference No16.Santa Barbara CA，USA.1998，2:847―854.
[46]Zhou Y L，Figueiredo E，Maia N，et al.Damage detection in structures using a transmissibility-based Mahalanobis distance[J].Structural Control and Health Monitoring，2015，22(10):1209―1222.
[47]曹茂森.基于动力指纹小波分析的结构损伤特征提取与辨识基本问题研究[D].南京:河海大学，2005.Cao Maosen.Study on fundamental issues in extraction and identification of structural damage feature based on wavelet analysis of dynamic fingerprint[D].Nanjing:Hohai University，2005.(in Chinese)
[48]Steenackers G，Devriendt C，Guillaume P.On the use of transmissibility measurements for finite element model updating[J].Journal of Sound and Vibration，2007，303(3):707―722.
[49]Meruane V.Model updating using antiresonant frequencies identified from transmissibility functions[J].Journal of Sound and Vibration，2013，332(4):807―820.
[50]Kim C J，Kang Y J，Lee B H，et al.Design sensitivity analysis of a system under intact conditions using measured response data[J].Journal of Sound and Vibration，2012，331(13):3213―3226.
[51]Steenackers G，Guillaume P，Vanlanduit S.Development of a regressive finite element model optimization technique making use of transmissibilities[J].Structural and Multidisciplinary Optimization，2009，39(1):47―62.
[52]Gajdatsy P，Janssens K，Desmet W，et al.Application of the transmissibility concept in transfer path analysis[J].Mechanical Systems and Signal Processing，2010，24(7):1963―1976.
[53]Devriendt C，De Sitter G，Guillaume P.An operational modal analysis approach based on parametrically identified multivariable transmissibilities[J].Mechanical Systems and Signal Processing，2010，24(5):1250―1259.
[54]Weijtjens W，De Sitter G，Devriendt C，et al.Operational modal parameter estimation of MIMO systems using transmissibility functions[J].Automatica，2014，50(2):559―564.
[55]Weijtjens W，De Sitter G，Devriendt C，et al Relative scaling of mode shapes using transmissibility functions[J].Mechanical Systems and Signal Processing，2013，40(1):269―277.
[56]Fontul M，Ribeiro A M R，Silva J M M，et al.Transmissibility matrix in harmonic and random processes[J].Shock and Vibration，2004，11(5/6):563―571.
[57]Sampaio R，Maia N M M，Ribeiro A，et al.Transmissibility techniques for damage detection[C]//Proceedings of the International Modal Analysis Conference.2001，2:1524―1527.
[58]Mottershead J E.On the zeros of structural frequency response functions and their sensitivities[J].Mechanical Systems and Signal Processing，1998，12(5):591―597.
[59]Johnson T J，Adams D E.Transmissibility as a differential indicator of structural damage[J].Journal of Vibration and Acoustics，2002，124(4):634―641.
[60]Johnson T J，Brown R L，Adams D E，et al.Distributed structural health monitoring with a smart sensor array[J].Mechanical Systems and Signal Processing，2004，18(3):555―572.
[61]Kess H R，Adams D E.Investigation of operational and environmental variability effects on damage detection algorithms in a woven composite plate[J].Mechanical Systems and Signal Processing，2007，21(6):2394―2405.
[62]Law S S，Li J，Ding Y.Structural response reconstruction with transmissibility concept in frequency domain[J].Mechanical Systems and Signal Processing，2011，25(3):952―968.
[63]Li J，Law S S，Ding Y.Substructure damage identification based on response reconstruction in frequency domain and model updating[J].Engineering Structures，2012，41:270―284.
[64]Li J，Law S S.Substructural response reconstruction in wavelet domain[J].Journal of Applied Mechanics，2011，78(4):041010.
[65]Li J，Law S S.Substructural damage detection with incomplete information of the structure[J].Journal of Applied Mechanics，ASME，2012，79(4):041003.
[66]Zhu H P，Mao L，Weng S.A sensitivity-based structural damage identification method with unknown input excitation using transmissibility concept[J].Journal of Sound and Vibration，2014，333(26):7135―7150.
[67]Yuen K V，Katafygiotis L S.Model updating using noisy response measurements without knowledge of the input spectrum[J].Earthquake Engineering & Structural Dynamics，2005，34(2):167―187.
[68]Yuen K V，Katafygiotis L S.Substructure identification and health monitoring using noisy response measurements only[J].Computer-Aided Civil and Infrastructure Engineering，2006，21(4):280―291.
[69]Yan W J，Katafygiotis L S.Application of transmissibility matrix and random matrix to Bayesian system identification with response measurements only[J].Smart Materials and Structures，2016，25(10):105017.
[70]孙倩，颜王吉，任伟新.基于响应传递比的桥梁结构工作模态参数识别[J].工程力学，2017，34(11):194―201.Sun Qian，Yan Wangji，Ren Weixin.Operational modal analysis for bridge engineering based on the dynamic transmissibility measurements[J].Engineering Mechanics，2017，34(11):194―201.(in Chinese)
[71]韩建平，郑沛娟.环境激励下基于快速贝叶斯 FFT的实桥模态参数识别[J].工程力学，2014，31(4):119―125.Han Jianping，Zheng Peijuan.Modal parameter identification of an actual bridge by fast Bayesian FFT method under ambient excitation[J].Engineering Mechanics，2014，31(4):119―125.(in Chinese)
[72]翁梦秀，雷鹰.考虑不确定性的结构损伤概率分析[J].工程力学，2016，33(增刊):29―32.Weng Mengxiu，Lei Ying.Probability analysis of structure damage identification including system uncertainty[J].Engineering Mechanics，2016，33(Suppl):29―32.(in Chinese)
[73]Yan W J，Katafygiotis L S.A two-stage fast Bayesian spectral density approach for ambient modal analysis.Part I:posterior most probable value and uncertainty[J].Mechanical Systems and Signal Processing，2015，54:139―155.
[74]Yan W J，Ren W X.Circularly-symmetric complex normal ratio distribution for scalar transmissibility functions.Part I:Fundamentals[J].Mechanical Systems and Signal Processing，2016，80(1):58―77.
[75]Yan W J，Ren W X.Circularly-symmetric complex normal ratio distribution for scalar transmissibility functions.Part II:Probabilistic model and validation[J].Mechanical Systems and Signal Processing，2016，80(1):78―98.
[76]Yan W J，Ren W X.Circularly-symmetric complex normal ratio distribution for scalar transmissibility functions.Part III:Application to statistical modal analysis[J].Mechanical Systems and Signal Processing，2018，98:1000―1019.
[77]伊廷华，郭庆，李宏男.基于控制图的GPS异常监测数据检验方法研究[J].工程力学，2013，30(8):133―141.Yi Tinghua，Guo Qing，Li Hongnan.The research on detection methods of GPS abnormal monitoring data based on control chart[J].Engineering Mechanics，2013，30(8):133―141.(in Chinese)
RECENT ADVANCES IN SYSTEM IDENTIFICATION USING THE TRANSMISSIBILITY FUNCTION
YAN Wang-ji，WANG Peng-peng，SUN Qian，REN Wei-xin
(Department of Civil Engineering，Hefei University of Technology，Hefei，Anhui 230009，China)
Abstract:Different from a frequency response function which reflects the input-output relationship of a dynamic system，the transmissibility function represents the output-output relationship of a dynamic system.Not needing the measurement of the system input，the transmissibility function has been viewed as a good candidate for system identification.In this study，the classification of transmissibility function and the relationship between transmissibility function and frequency response function were elucidated.Based on the classification，the applications of the local transmissibility and the transmissibility matrix in modal parameter identification，damage identification and model updating，were systematically summarized.Finally，the underlying issues and research prospects of transmissibility analysis were highlighted.
Key words:transmissibility function;parameter identification;damage identification;model updating;health monitoring
中图分类号：TU311
文献标志码：A
doi:10.6052/j.issn.1000-4750.2017.01.0073
文章编号：1000-4750(2018)05-0001-09
收稿日期：2017-01-18；修改日期：2017-06-24
基金项目：国家重点研发计划项目(2016YFE0113400)；国家自然科学基金项目(51408176，51478159)
通讯作者：任伟新(1960―)，男，湖南长沙人，长江学者特聘教授，博士，博导，主要从事桥梁结构稳定与振动研究(E-mail:renwx@hfut.edu.cn).
作者简介：颜王吉(1985―)，男，浙江金华人，研究员，博士，博导，主要从事振动信号处理、系统识别和安全监测研究(E-mail:civilyanwj@gmail.com，yanwj0202@163.com)；
王朋朋(1990―)，男，河南商丘人，硕士生，主要从事桥梁健康监测与检测研究(E-mail:wangppfreedom@163.com)；
孙 倩(1990―)，女，安徽六安人，博士生，主要从事振动信号处理研究(E-mail:sqhorse90@126.com).