近年来微型飞行器的研究已成为热点。大多数微型飞行器因其体积小、速度低,因而其飞行雷诺数较低。一般地,低雷诺数(104≤Re≤106)条件下翼型表面边界层流动处于层流状态,抗逆压梯度能力较弱,容易产生流动分离,对翼型升阻比和飞行稳定产生严重影响[1-3]。因此,寻求有效的流动控制方法以延迟甚至消除其表面流体分离已成为近年的研究热点。
目前具有应用前景的流体分离主动控制方法主要有合成和抽吸射流。前者通过放大分离边界层中的扰动来促进流体流动状态的转变和分离再附[4],这类方法使大部分翼型表面为湍流边界层,同时摩阻增大。抽吸射流通过在分离区附近分布抽吸小孔,吸除部分低能流体,延迟逆压梯度,可以有效抑制边界层分离,并且在不增大摩阻的情况下减小压阻。前人研究表明[5-7],翼型表面抽吸控制能有效抑制其流体分离,但对具有最佳控制效果的抽吸作用区域及其对升阻比的影响等仍没有完全一致结论。
Huang等[8-9]从喷口位置、射流速度比和射流角度三个方面,数值研究了吸气和吹气方式对Re=5.0×105和攻角为18°的NACA0012翼型分离流动的控制效果。研究发现抽吸气与吹气的控制机理不同,吸气控制可以在上表面产生大范围的低压区以增加升力,而吹气经常恶化流动,不过下游吹气控制效果要好于上游吹气。垂直吸气时,射流在翼型前缘的升力效果最好。而对于吹气,分离点下游(0.371~0.8)切向吹气的增升效果较佳。Genc等[10]针对雷诺数Re=2×105条件下NACA2415翼型表面流体分离现象,在翼型上表面开宽为2.5%倍弦长的单喷口,进行吹/吸气式控制研究,分析了喷口位置、射流速度比和射流角度的影响,结论与 Huang[8-9]类似。Goodarzi等[11]数值研究了抽吸控制对低雷诺数下 NACA0012翼型在不同攻角下气动性能的影响。在翼型上表面10%、50%和80%倍弦长位置开槽,其宽为2.5%倍弦长,抽吸系数有0.173、0.337和0.5。发现当槽位于 10%倍弦长处和抽吸系数为0.5时,抽吸控制效果最好,此时升力系数增加了45%,阻力系数减少了 29%,并且失速角从 14°增加到 20°。
李锋等[12-14]数值研究了圆柱和大攻角下翼型表面吸气对分离流动的控制及其增升机制。在一定吸气压强范围内,绕圆柱流动的卡门涡街基本消失,吸气孔位置在圆柱表面逆时针方向 60°时,圆柱升阻比最高。对于大攻角翼型流动,吸气可以将翼型头部非稳态涡稳定在翼面上,起到驻涡作用而提供涡升力,结合吸气孔附近较低的负压,使得翼型升力获得提高。吸气孔位置在翼型中部附近时增升效果较好。张华良等[15]数值研究了边界层抽吸对具有不同分离特征的两个叶栅流场的影响。通过比较抽吸前后极流线谱和叶栅损失的变化,发现对于以闭式分离为主要特征的叶栅流场,其最佳抽吸位置在主分离区的起始位置,对以开式分离为主要特征的叶栅流场,其最佳抽吸位置位于主分离区的上游。
由上可知,前人对抽吸控制中最佳控制起始位置以及抽吸区域大小对控制效益的影响仍不足,故本课题组张旺龙等[16]对雷诺数Re=104,攻角α=6°,马赫数Ma=0.2下的NACA0012翼型进行了系统研究,详尽解释了低雷诺数下,抽吸区域相对分离点的作用位置、孔间距和孔径,以及抽吸方向对分离流动的影响。但文献[16]没有对控制初始位置位于分离点以后的位置进行讨论,且针对控制域为Ls=0.2c的情况,无法完全说明抽吸开始位置的最优点以及抽吸域大小对抽吸控制的影响等。
基于此,本文采取与文献[16]相同的初始条件与翼型,进一步数值模拟与分析低雷诺数下,不同抽吸域位置对流动气动性能的影响,以及不同控制区域与抽吸系数对翼型控制收益与升阻比的影响。本文先对抽吸域大小Ls=0.3c,起始抽吸点位置位于分离点(0.26c)及其后面不同点(0.46c、0.66c)时的抽吸流场控制情况进行研究,确定最佳起始抽吸位置后,再研究不同抽吸域大小对翼型分离控制时的阻力、升阻比及品质因数等的影响。本文可为翼型抽吸控制以得到最大收益与升阻比提供重要参考。
1 数值方法
在笛卡尔坐标系下,基于Favre过滤的大涡模拟方程可表示为[17]:
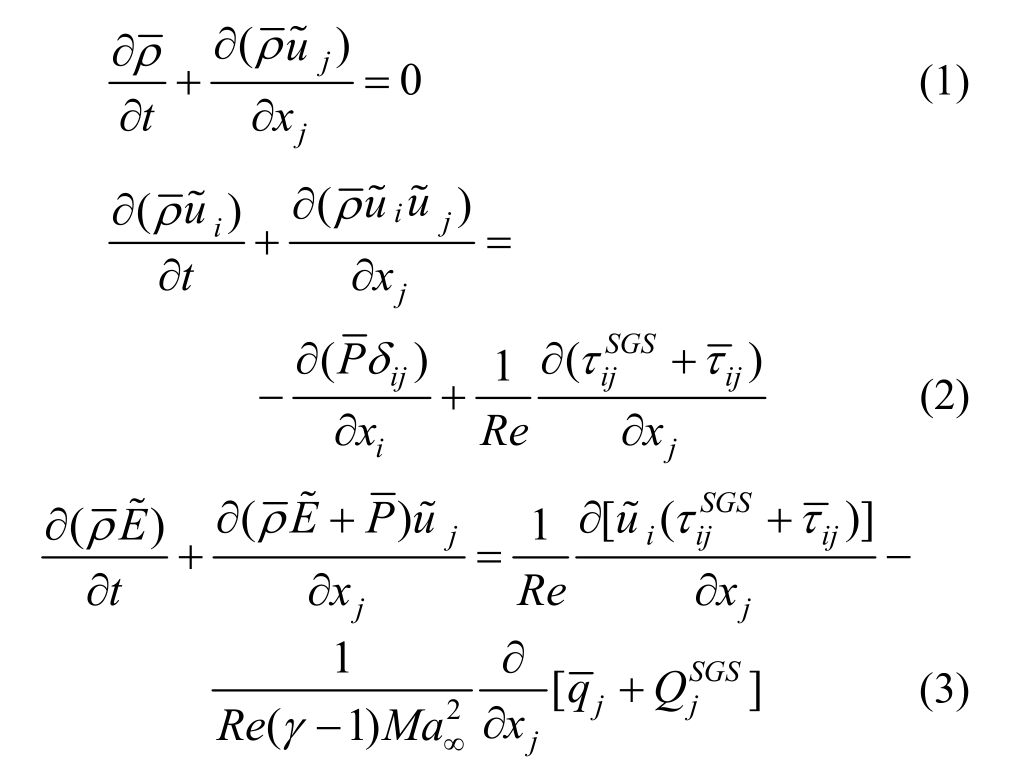
式(1)~式(3)中各个变量的说明参见文献[18]。
亚格子应力张量和亚格子热通量分别为:
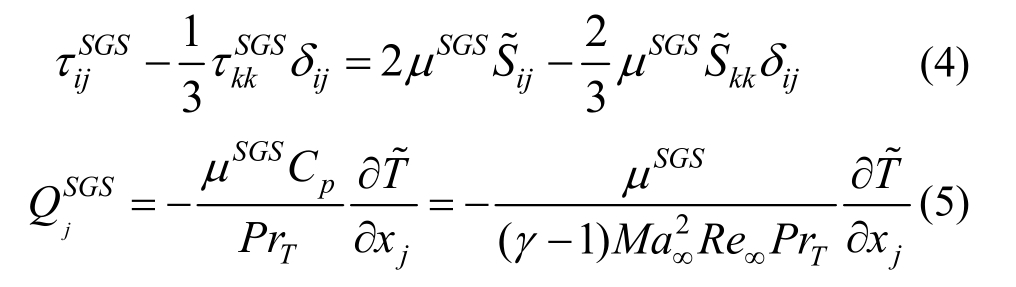
式中:PrL和PrT分别为层流普朗特数和湍流普朗特数;γ为流体的比热比:
PrL=0.72,PrT=0.90,γ=1.4
亚格子模型采用WALE模型,即:
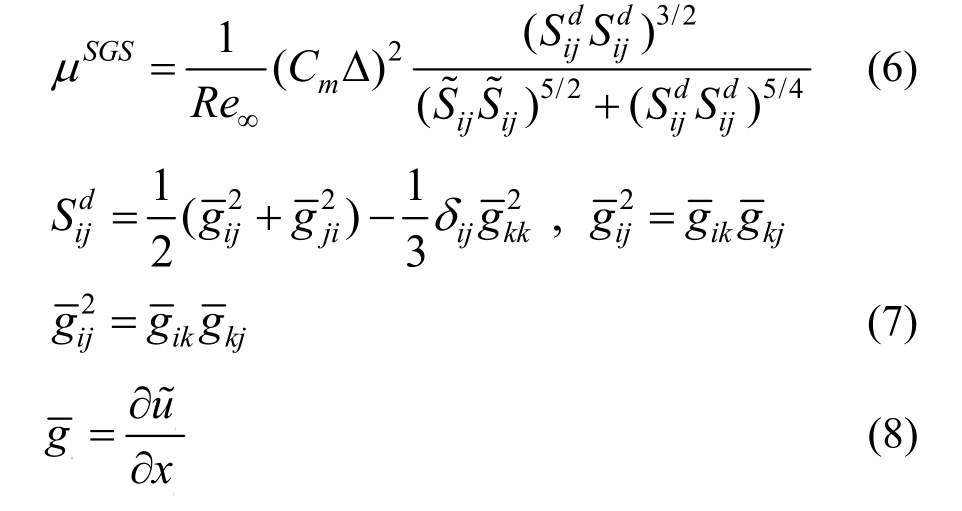
WALE模型的常数Cm取可以通过![]() 关系式[19]得到,Cs为Smagorinsky模型常数。Nicoud发现在各向同性湍流中,Cm=0.45;在壁湍流中,Cm=0.5。
关系式[19]得到,Cs为Smagorinsky模型常数。Nicoud发现在各向同性湍流中,Cm=0.45;在壁湍流中,Cm=0.5。
另外,控制方程采用有限体积法进行离散。对流项采用AUSM+-up格式进行离散。黏性通量采用二阶中心差分格式离散。时间项则采用具有二阶精度的双时间步长(LU-SGS)全隐式算法。详细说明可参见文献[20]。
2 算法验证
本文选取Re=104,α≤6°,Ma=0.2的低雷诺数流动下的NACA0012翼型为计算模型,在该工况下,流动具有准二维性,故为减小计算量,本文采用二维层流进行计算[20]。另采用椭圆方法生成C型网格,以翼型弦长c=1为参考长度,计算域左边界距离翼型前缘6.5c,上下边界距翼型弦线为7.5c,右边界距翼型尾缘 9c,壁面第一层网格间距为10-4c,且满足y+<1.0。为了精确模拟抽吸控制对流场的影响,对抽吸孔周围网格进行了加密,且每个抽吸孔内有3个网格点,如图1所示。
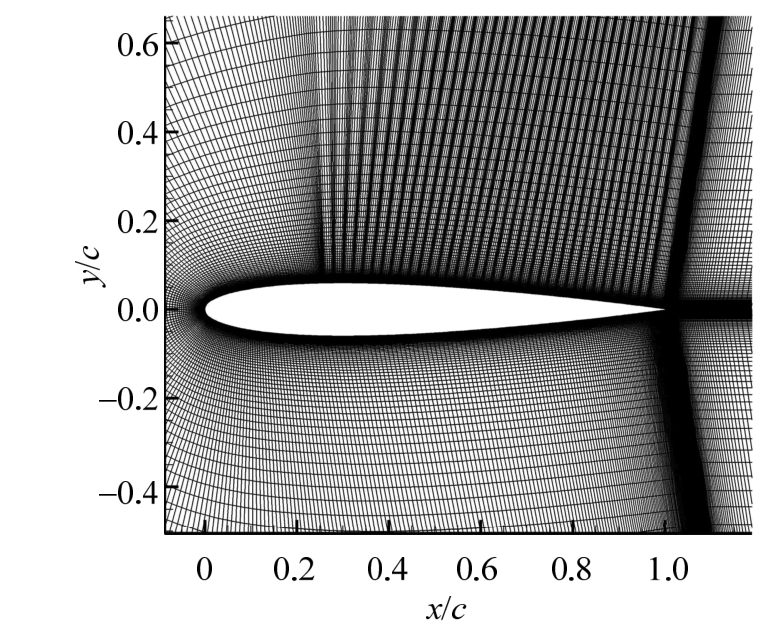
图1 NACA0012翼型周围网格示意图
Fig.1 Schematic diagram of grid around NACA0012 airfoil
通过网格无关性检验,最终选取网格节点数为871×100,图2为数值模拟结果与实验结果[21]对比,在较小攻角下,计算值与实验值吻合较好,而随着攻角的增大,流动分离现象加重,并出现展向流动使得二维层流计算失效,误差较大。故对于α≤6°情况下的NACA0012翼型绕流,本文的数值算法具有良好的可靠性和准确性。
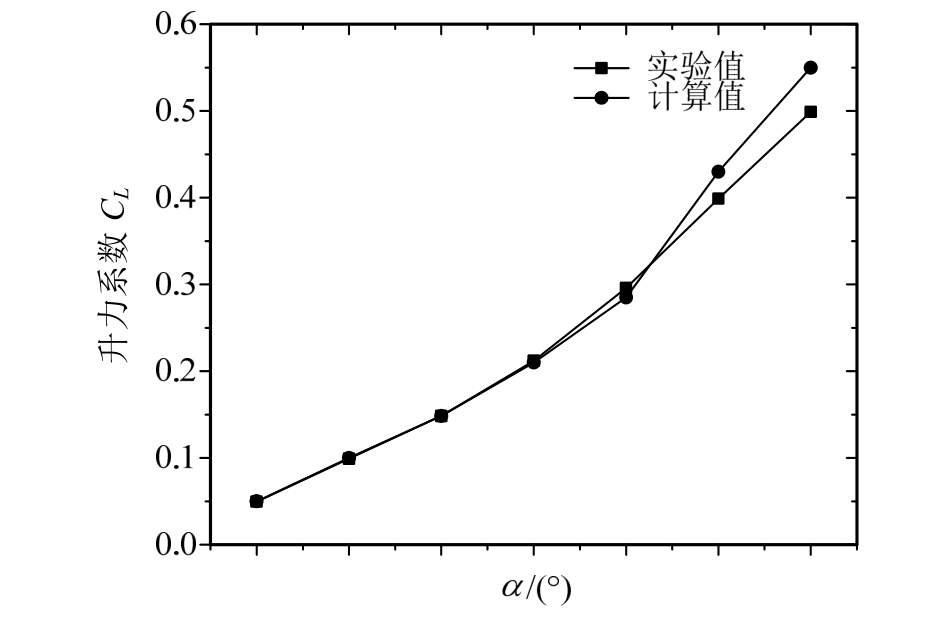
图2 NACA0012翼型时均升力系数与实验值对比
Fig.2 Comparison between mean lift coefficients and experimental results of NACA0012 airfoil
3 结果与分析
本文引入无量纲抽吸系数的定义如下[13]:
式中:![]() 表示单位时间内通过抽吸孔的空气质量,ρs、Vs分别表示抽吸孔相关的密度和速度;而dS表示抽吸孔微元面积;c为弦长;ρ∞为来流气体密度;U∞为来流速度。
表示单位时间内通过抽吸孔的空气质量,ρs、Vs分别表示抽吸孔相关的密度和速度;而dS表示抽吸孔微元面积;c为弦长;ρ∞为来流气体密度;U∞为来流速度。
压力系数Cp定义如下:
为了保证抽吸控制能耗小于抽吸控制效益,引入一种评价抽吸收益的方法[22],即认为抽吸所需的能量必须能够使抽吸室内的气体排到环境中,定义抽吸控制的品质因数(Figure of Merit, FOM)如下:
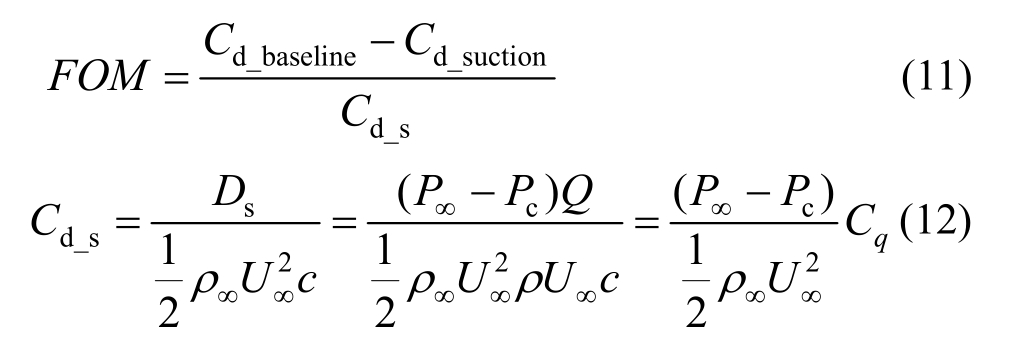
式中:Pc为抽吸腔内的压强;Cd_baseline为基准状态的阻力系数;Cd_suction为抽吸控制后的阻力系数,Cd_s为当量吸气阻力系数。FOM>1时,表示能量消耗小于抽吸控制收益,且FOM值越大,则表明控制收益越好。
关于抽吸起始位置的选取,张旺龙等针对NACA0012 翼型绕流在Re=104,Ma=0.2,α=6°条件下3种抽吸区域(前端抽吸:0.04c~0.24c,中部抽吸:0.15c~0.35c,后端抽吸:0.26c~0.46c),从升阻比和抽吸品质因数进行比较,证明了后端抽吸明显优于前端和中部抽吸,且抽吸始端处于分离点的控制效果最好[16]。但文献[16]没有对控制初始位置位于分离点以后的位置进行讨论,且针对控制域为Ls=0.2c的情况,无法完全说明抽吸开始位置的最优点以及抽吸域大小对抽吸控制的影响等。
基于此,以下先对抽吸域大小Ls=0.3c,起始抽吸点位置位于分离点(0.26c)及其后面不同点(0.46c、0.66c)时的抽吸流场控制情况进行研究,确定最佳起始抽吸位置后,再研究不同抽吸域大小对翼型分离控制时的阻力、升阻比及品质因数等的影响。
对于固定抽吸域,其中取孔径d=2×10-3c,孔间距Ld=10d。考虑到品质因数FOM≥1,取抽吸系数Cq=0.0015。
图 3为翼型不同控制位置的升力系数变化曲线。图4为某时刻翼型周围涡量等值分布。可知,抽吸控制之前,翼型前缘涡与后缘涡周期性脱落,导致翼型升力周期性振荡,反映了流动分离翼型气动参数的影响。施加抽吸控制后,控制区域在0.26c~0.56c时,流体分离得到完全控制,无涡街产生,且升力系数明显增加,控制区域为0.46c~0.76c和0.66c~0.96c时,翼型表面流体分离没有完全消失,仍有涡脱落,且升力系数仍产生振动。
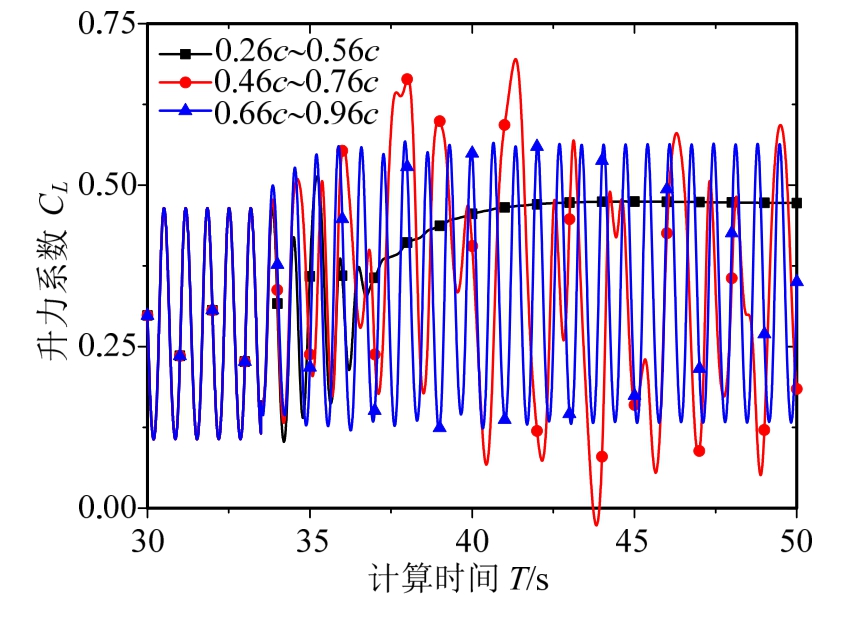
图3Cq=0.0015下的翼型升力系数的变化
Fig.3 Variation of airfoil’s lift coefficient whenCq=0.0015
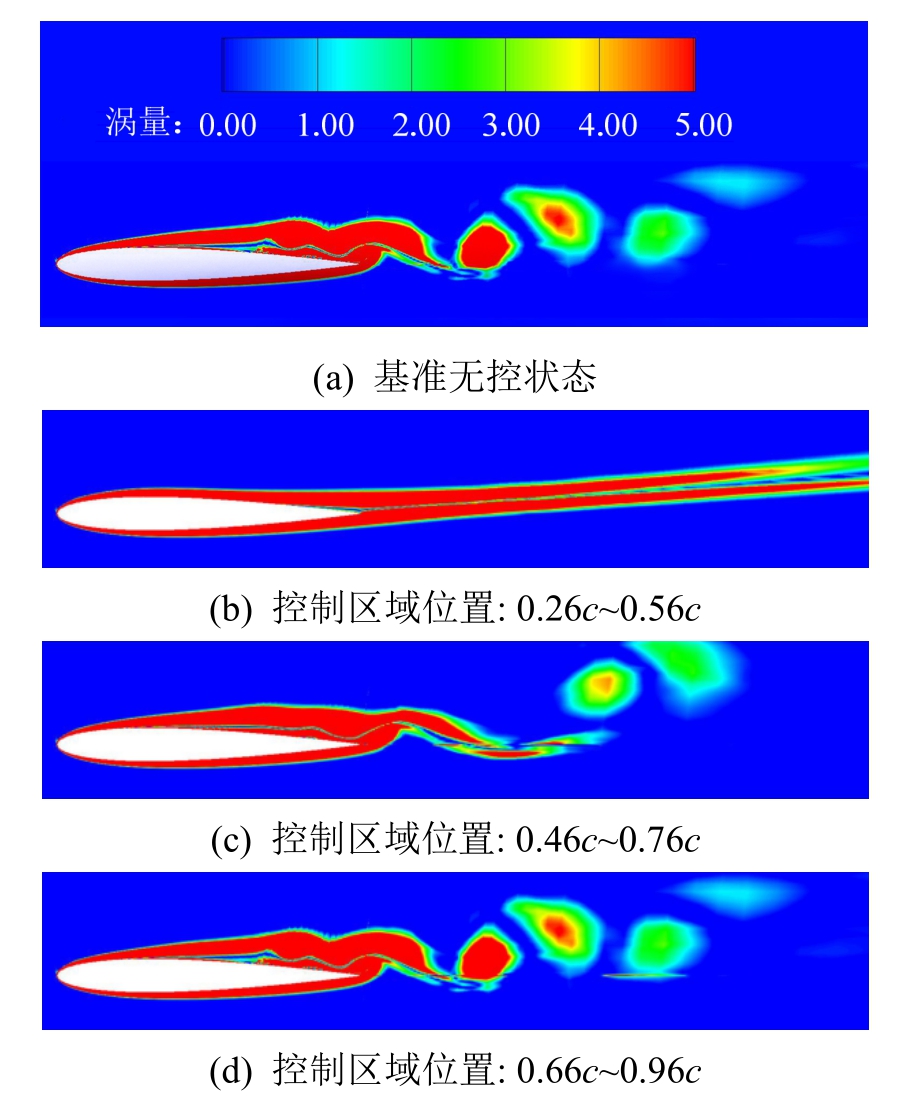
图4Cq=0.0015时,不同抽吸位置下的涡量图
Fig.4 Vorticity at different suction positions whenCq=0.0015
图5为与图4对应的4种不同工况条件下,翼型表面平均压力系数分布。在抽吸孔处,在吸气作用下,压力P明显减小。而在两孔之间,压力P得到回升。抽吸越强,抽吸孔处的压力与孔间的压力差就越大,进而导致抽吸区域呈现较大波动。对比三种抽吸域作用下的压力系数,可知,控制域在0.26c~0.56c时,翼型背风面前半部处的压力系数降低,后半部的压力系数增大,极大的提高了翼型抗逆压能力。而迎风面翼型压力系数均增大,使得翼型上下压差增大,升力系数大幅提升。
而对于控制域在0.46c~0.76c与0.66c~0.96c时,翼型背风面前半部分与翼型迎风面的压力系数与无控时基本相同,没有产生影响。在抽吸孔处,流动速度加快,压力系数开始减小并在抽吸控制区后逐渐增大,因而翼型升力系数仍有小幅提升,但其抗逆压能力减弱。
综上所述,对Re=104,Ma=0.2,α=6°下的翼型绕流,在紧靠流体分离点后(本例为0.26c)进行阵列抽吸会获得较大的升力系数和抗逆压能力,可以有效地抑制涡脱落的现象。因此改变控制域仍可得到与文献[16]相同的研究结果。
在确定最佳控制域起始位置(本例为0.26c)后,可进一步研究抽吸系数Cq与控制域大小Ls变化对控制收益的影响。图6为抽吸域Ls=0.1c时,3种不同抽吸系数下的绕NACA0012翼型流动的涡量图。与图4(a)无控制情况相比,流动分离与周期性脱落涡都得到了不同程度的抑制,且流场随Cq增大逐渐趋于稳定。当Cq=0.0002时,翼型尾部涡街振荡幅度明显减弱;当Cq=0.0007时,尾涡基本得到控制,仅在尾部有较小振荡;而当Cq=0.001时,涡脱落现象完全消失,且随着抽吸系数的增大,流场结构基本不变。为了研究Cq与Ls对翼型气动性能以及能耗的影响,本文仅讨论翼型涡脱落完全控制的情况。
图7显示了不同Ls下,翼型阻力、升力及升阻比系数随抽吸系数的变化曲线。其中:
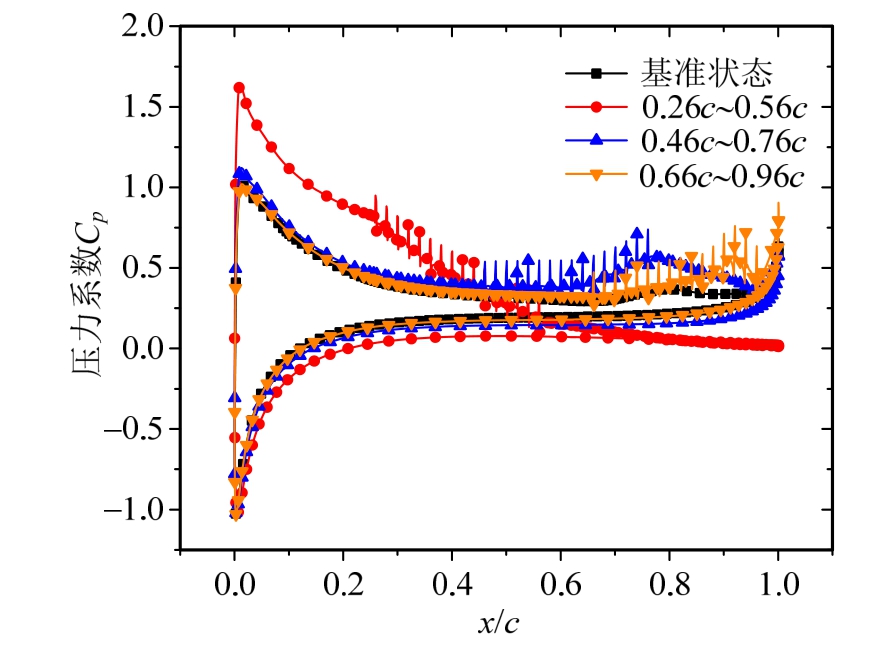
图5 不同抽吸位置下压力系数曲线对比图
Fig.5 Comparison diagram of pressure coefficient curves at different suction positions
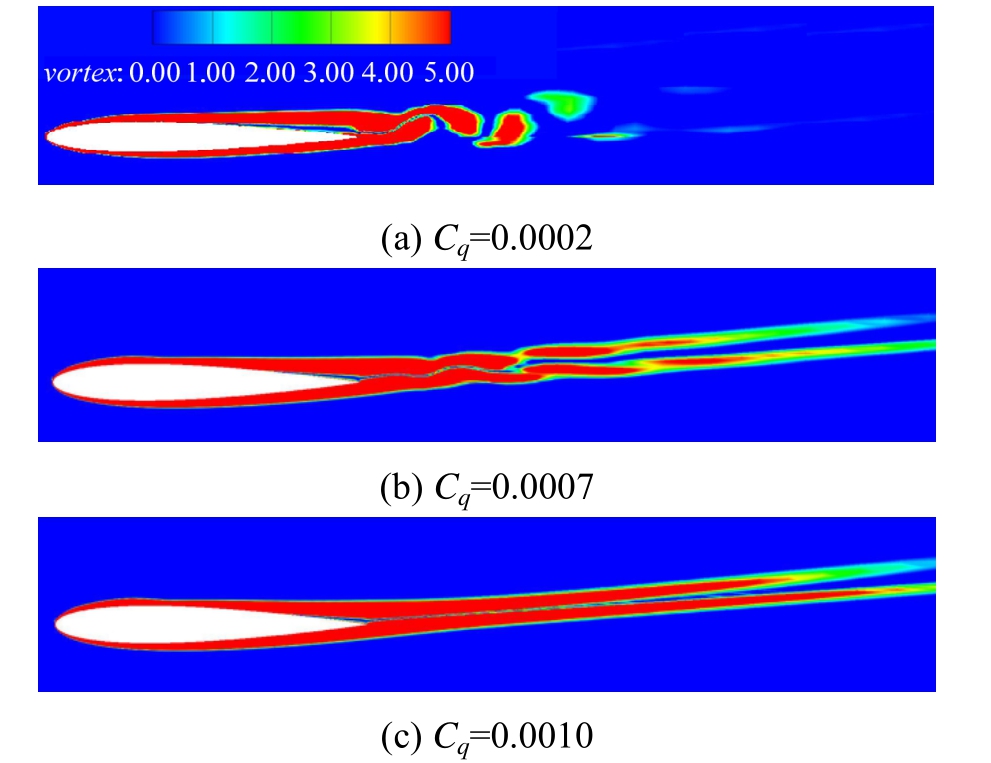
图6 抽吸区域为0.26c~0.36c时的翼型绕流涡量图
Fig.6 Vorticity of flow around airfoil when control is 0.26c~0.36c
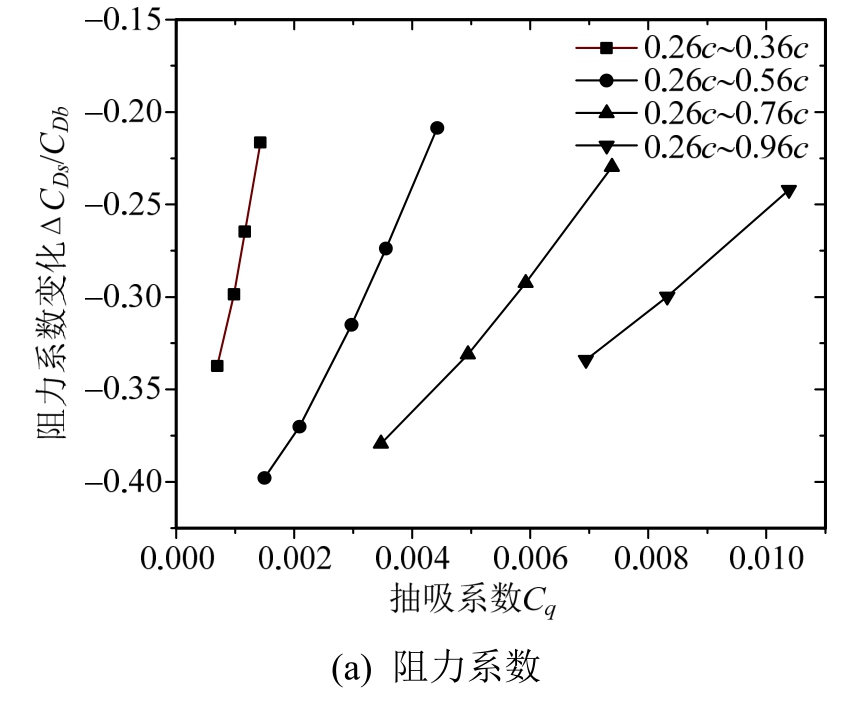

图7 不同Ls下,翼型气动力系数与抽吸系数的关系
Fig.7 Relationship between aerodynamic coefficients and
suction coefficient with differentLs
图 7中各不同控制区域中最小抽吸系数Cq为此控制域内刚好控制绕流分离时所对应的值,若其再减小,翼型尾部会出现周期性的涡脱落。由图7(a)可知,在绕流分离刚好完全控制时,相应的控制域阻力系数均为此抽吸域的极小值,且其大小均不相同,并随抽吸区域Ls的增大,其值先减小再增加。如Ls=0.1c、0.3c、0.5c与0.7c时,所对应的阻力极小值分别为-0.34、-0.40、-0.38与-0.34。可知,在抽吸域Ls=0.3c时,存在阻力最小值-0.40,所对应的抽吸系数Cq=0.00158。另外,对于不同抽吸域,在相同抽吸系数条件下,抽吸域大的阻力较抽吸域小的阻力值小。升力与升阻比随抽区域的增加而显著增加。因此,在涡脱落控制条件下,若以减阻为主要目的,存在一个最佳控制区域,即最佳抽吸区域对应位置为0.26c~0.56c。
相同控制区域(Ls=0.3c)条件下,随着抽吸系数Cq的增加,翼型上下表面压差增大(图 8),使翼型阻力系数和升力系数都增大,但其升阻比先随着抽吸系数增大随后减小,存在对应的极大值。如图7(c)所示。其中不同抽吸区域Ls=0.1c、0.3c、0.5c与0.7c条件下,所对应的升阻比均有一个对应的极大值,分别为1.58、2.10、2.50与2.95,所对应的抽吸系数分别为Cq≈0.01、0.03、0.05与0.07,即控制区域变化时的翼型最大升阻比与对应的抽吸系数Cq成近似正比关系。
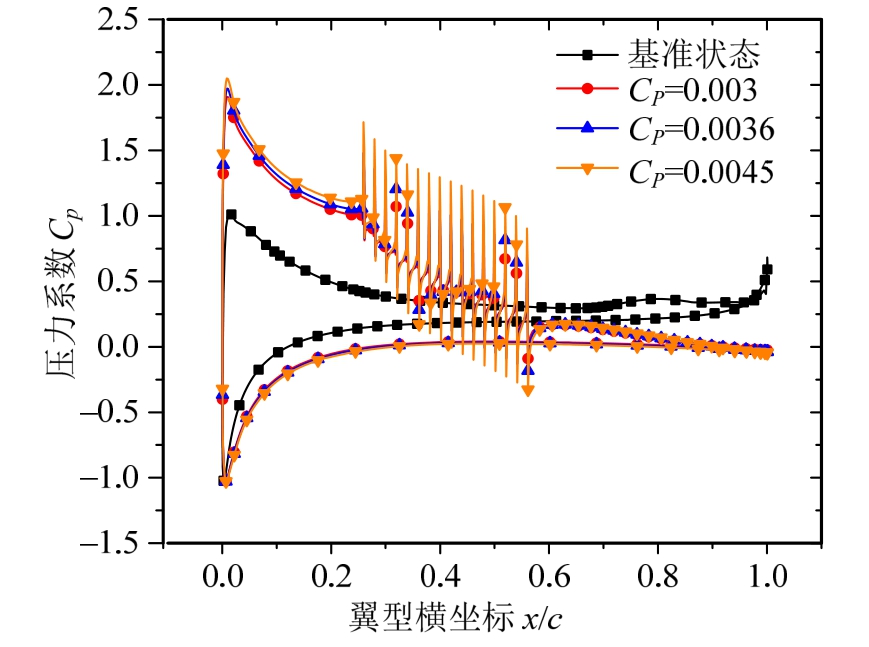
图8Ls=0.3c时,不同Cq下的压力系数曲线对比
Fig.8 Comparison diagram of drag coefficient curves with differentCq, whenLs=0.3c
FOM随不同抽吸区域大小Ls变化的曲线如图9所示。可知,相同Ls条件下,抽吸系数Cq增大时,FOM减小甚至小于1,使抽吸控制能耗大于抽吸控制效益,故每个抽吸域都有相对应的抽吸系数最大值。这是因为随着Cq增大,抽吸腔内的吸气压力变低,从而导致当量吸气阻力系数Cd_s明显增大,而阻力系数的减小量则相对较小(图 7(a)),根据式(12),FOM随着抽吸系数增大而减小。因此,对于相同抽吸控制域而言,其抽吸系数应尽量小,才能获得最多能耗控制收益。
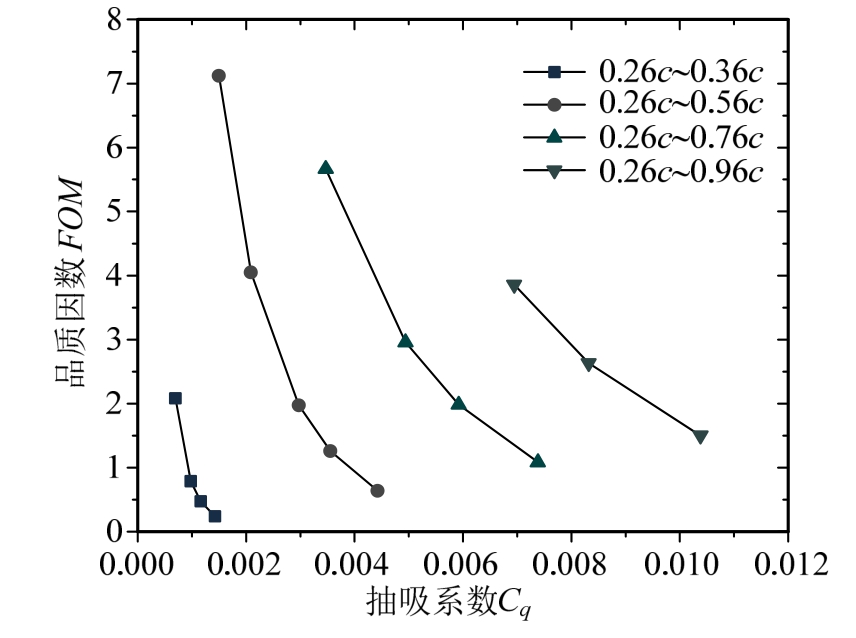
图9 不同Ls下,品质因数与抽吸系数的关系
Fig.9 Relationship between figure of meritFOMandCqwith differentLs
对于不同控制区域,Ls=0.1c、0.3c、0.5c与 0.7c,所对应的FOM极大值分别为2.2、7.2、5.7与3.8,而此时最小抽吸系数分别为Cq≈0.00065、0.00158、0.0035与0.0069。可知品质因数FOM同样随控制域增加而先增加,然后再变小,因而同样存在具有最佳控制效益(FOM最大)的控制区域,即Ls=0.3c。此时Cq=0.00158时,FOM最大值为7.2。
4 结论
本文以低雷诺数下 NACA0012翼型绕流分离流动为研究对象,以分离点后布置多孔抽吸区域对翼型绕流分离进行控制研究。通过数值模拟发现了抽吸区域、抽吸系数对翼型流场气动性能及控制能耗收益的影响规律。主要结论如下:
(1) 在紧靠流体分离点后进行阵列抽吸会获得较大的升力系数和抗逆压能力,可以更有效地抑制涡脱落现象与获得较多控制效益。
(2) 对于绕流分离刚好完全控制时,翼型升力与升阻比系数随抽吸控制域增加而明显增加,但其最小阻力系数则先减小再增加,存在一个最佳控制域尺度使翼型阻力最小,本例为Ls=0.3c,Cq=0.00158。
(3) 相同控制区域时,翼型最大升阻比同样对应有一个最佳抽吸系数。且对于不同控制区域尺度之间的翼型最大升阻比与对应的抽吸系数Cq成近似正比关系。
(4) 对于相同抽吸控制域而言,其抽吸系数应尽量小,才能获得最大控制收益。而对于抽吸区域尺度变化时,存在一个最佳控制收益(FOM最大)的控制区域,即Ls=0.3c,Cq=0.00158,此时FOM≈7.2。
参考文献:
[1]张旺龙, 谭俊杰, 陈志华, 等.低雷诺数下翼型分离流动抽吸控制特性研究[J].空气动力学报.2015, 33(1):113―119.Zhang Wanglong, Tan Junjie, Chen Zhihua, et al.Investigation on characteristics of suction control on separation flow around an airfoil at low Reynolds number [J].Acta Aerodynamica Sinica, 2015, 33(1):113―119.(in Chinese)
[2]关键, 郭正.绕翼型低雷诺数流动的数值仿真[J].科学技术与工程, 2013, 13(24): 7275―7281.Guan Jian, Guo Zheng.Numerical simulation of low-Reynolds-number flows over airfoil [J].Science Technology and Engineering, 2013, 13(24): 7275―7281.(in Chinese)
[3]周超英, 朱建阳, 汪超, 等.柔性扑翼气动性能的数值研究[J].工程力学, 2013, 30(5): 13―18.Zhou Chaoying, Zhu Jianyang, Wang Chao, et al.Numerical study on the effect of flexiblity of a flapping wing on its aerodynamic performance [J].Engineering Mechanics, 2013, 30(5): 13―18.(in Chinese)
[4]邵纯, 曹燕飞, 邹龙, 等.零质量射流及其在进气道流动控制中的应用研究[J].工程力学, 2015, 32(4): 206―211.Shao Chun, Cao Yanfei, Zou Long, et al.Active flow control applications with zero net mass flux actuator in flow field of supersonic inlet [J].Engineering Mechanics,2015, 32(4): 206―211.(in Chinese)
[5]Wright M C M, Nelson P A.Wind tunnel experiments on the optimization of distributed suction for laminar flow control [J].Proceedings of the Institution of Mechanical Engineers – Part G, 2001, 215(6): 343―354.
[6]Wahidi R, Bridges D.Control of laminar separation bubbles with distributed suction – preliminary studies[C]// Aiaa Aerospace Sciences Meeting and Exhibit,Reno USA, American Institute of Aeronautics and Astronautics, 2008: 560―569.
[7]Wahidi R, Bridges D H.Effects of distributed Suction on an airfoil at low reynolds number [J].Aiaa Journal, 1971,50(3): 523―539.
[8]Huang L, Huang P G, LeBeau R P.Numerical study of blowing and suction control mechanism on NACA0012 airfoil [J].Journal of Aircraft, 2004, 41(5): 1005―1013.
[9]Huang L, Huang P G, LeBeau R P.Optimization of blowing and suction control on NACA0012 airfoil using genetic algorithm [C]// Aiaa Aerospace Sciences Meeting and Exhibit, Reno USA, American Institute of Aeronautics and Astronautics, 2013: 485―489.
[10]Genc M S, Kaynak ü.Control of laminar separation bubble over a NACA2415 aerofoil at low Re transitional flow using blowing/suction [C].13th International Conference on Aerospace Sciences & Aviation Technology,Cairo, Egypt, 2009.
[11]Goodarzi M, Fereidouni R, Rahimi M.Investigation of flow control over a NACA0012 airfoil by suction effect on aerodynamic characteristics [J].Canadian Journal on Mechanical Sciences & Engineering, 2012, 3(3): 102―109.
[12]李锋, 汪翼云.翼型大攻角绕流的数值模拟[J].航空学报, 1992, 13(1): 19―24.Li Feng, Wang Yiyun.The numerical simulation of compressible flow around an airfoil at high angle of attack [J].Acta Aeronautica et Astronautica Sinica, 1992,13(1): 19―24.(in Chinese)
[13]李锋, 汪翼云, 崔尔杰.表面吸气方法控制分离的数值模拟[J].空气动力学学报, 1994, 12(1): 36―42.Li Feng, Wang Yiyun, Cui Erjie.Numerical simulation of separation control by suction [J].Acta Aerodynamica Sinica, 1994, 12(1): 36―42.(in Chinese)
[14]李锋, 汪翼云, 崔尔杰.提高飞行器升力的若干方法研究[J].空气动力学学报, 1994, 12(3): 237―242.Li Feng, Wang Yiyun, Cui Erjie.The investigation on some methods a force mothod for lift [J].Acta Aerodynamica Sinica, 1994, 12(3): 237―242.(in Chinese)
[15]张华良, 谭春青, 张新敬, 等.采用附面层抽吸(BLS)控制流动分离的数值模拟[J].推进技术, 2009, 30(2):192―196.Zhang Hualiang, Tan Qingchun, Zhang Xinjing, et al.Numerical investigation on application of boundary layer suction to control the flow separations [J].Journal of Propulsion Technology, 2009, 30(2): 192―196.(in Chinese)
[16]张旺龙, 谭俊杰, 陈志华, 等.抽吸控制对低雷诺数下翼型分离流动的影响[J].航空学报, 2014, 35(1): 141―150.Zhang Wanglong, Tan Junjie, Chen Zhihua, et al.Effect of suction control on separation flow around an airfoil at low Reynolds numbers [J].Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 141―150.(in Chinese)
[17]梁霆浩, 余锡平.非均匀拟形冠层内大气流动特征的大涡模拟研究[J].工程力学, 2017, 34(1): 248―256.Liang Tinghao, Yu Xiping.Large-eddy simulation of atmospheric flow over heterogenous cubes [J].Engineering Mechanics, 2017, 34(1): 248―256.(in Chinese)
[18]张兆顺.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社, 2008: 54―57.Zhang Zhaoshun.Theory and application of Large Eddy Simulation of the turbulent flow [M].Beijing: Tsinghua University Press, 2008: 54―57.(in Chinese)
[19]Nicoud F, Ducros F.Subgrid-scale stress modeling based on the square of the velocity gradient tensor [J].Flow Turbulence and Combustion, 1999, 62(3): 183―200.
[20]张旺龙.低雷诺数下附面层分离的抽吸控制及优化[D].南京: 南京理工大学, 2014: 11―26.Zhang Wanglong.Suction control and its optimization of boundary layer separation at low Reynolds number [D].Nanjing: Nanjing University of Science & Technology,2014: 11―26.(in Chinese)
[21]Ohtake T, Nakae Y, Motohashi Y.Nonlinearity of the aerodynamic characteristics of NACA0012 aerofoil at low Reynolds numbers [J].Journal of the Japan Society for Aeronautical and Space Sciences, 2007, 55(644):439―445.
[22]Bridges D H.Early flight test and other boundary layer research at Mississippi State 1949-1960 [J].Journal of Aircraft, 2007, 44(5): 1635―1652.