近二十年来,随着基坑开挖深度的增加和周边环境保护要求的提高,单纯依靠挡土墙悬臂来抵抗土压力已不能满足要求,通常需要在两侧挡土墙之间设置水平支撑。支撑梁最初使用钢材,后由于基坑规模的提高而转向钢筋混凝土。近来绿色建筑理论不断深入人心,钢支撑重被提起和应用,并且结构形式得到发展。除609圆管支撑外,组合型钢支撑因节点全部采用高强螺栓连接而在国内外建筑深基坑工程中迅速扩大应用[1-3]。
如图1和图2所示,每榀组合型钢支撑梁(简称支撑梁)由多根 H型钢组合而成,型钢间以盖板和缀条组合成整体,支撑梁通过横梁与立柱连接,构件之间的连接件均为高强螺栓[3]。由于自重仅为钢筋混凝土支撑的1/10,组合型钢支撑的立柱一般为H型钢直接插入地基,地基土质较差时可设置钻孔灌注桩作为立柱桩。所有构件均在工厂制作,工程现场不进行构件加工,可达到90%以上的循环使用率,相比钢筋混凝土支撑,在工期和造价上有一定优势。

图1 组合型钢支撑照片
Fig.1 Picture of assembly steel struts

图2 组合型钢支撑示意
Fig.2 Schematic diagram of assembly steel struts
在经济、快速、环保等优点被逐渐接受的同时,组合型钢支撑的缺点也慢慢暴露,且基本指向支撑梁承载力被高估。根据钢结构理论[4-5],支撑梁承载力实际上是稳定性问题,包括水平面内和竖直平面内,且立柱对稳定性起关键作用。而组合型钢支撑的立柱通过托座和横梁与支撑梁连接,是一种弹性支座,能否使得一榀支撑梁在竖直平面内稳定性计算长度等于相邻横梁之间的距离需要加以研究。支撑梁在水平面内也存在失稳的可能。如果假定横梁与立柱为铰接,那么支撑梁在水平面内失稳时,两根立柱作为悬臂柱对支撑梁提供约束,该约束刚度也需要加以研究。
组合型钢支撑梁可类比于钢结构中设置水平支撑的柱,对于后者的既有研究较多[6-10],可作为前者的研究基础。相较而言,前者承受的荷载更大,截面为组合形式,现有研究较少。陈绍蕃[11]采用平衡法及能量法得出设有2~4道弹性杆撑轴压钢柱的稳定临界荷载统一近似公式,可作为组合型钢支撑梁稳定性计算参考,但是其研究对象为实腹式支撑杆件。刘发前[12]依据现有规范对组合型钢支撑的稳定性进行了初步分析,但是没有考虑横梁刚度。
本文根据组合型钢支撑梁实际受力情况提出假设将问题简化,将横梁和立柱组成的门架用弹簧模拟,主要分析横梁刚度对支撑梁稳定性计算长度的影响,并提出横梁刚度要求。
1 问题简化
组合型钢支撑适合用于平面形状较规则的基坑工程。图3为某基坑支撑平面布置图,无论是设计还是施工,每榀支撑梁均独自承受土压力。
根据JGJ 120-2012《建筑基坑支护技术规程》:①水平支撑在竖向平面内的受压计算长度,不设置立柱时,应取支撑的实际长度,设置立柱时,应取相邻立柱的中心间距;②水平支撑在水平面内的受压计算长度,对无水平支撑杆件交汇的支撑,应取支撑的实际长度。对于设置钻孔灌注桩作为立柱桩的水平支撑体系来说,该规定与实际受力情况吻合。但是组合型钢支撑体系不一定能达到规范要求,关键在于立柱能否当作位移为0的固定支座,当采用如图2(a)所示型钢门架作为竖向支承时,横梁长度和立柱作法决定着型钢门架在受力时更接近弹性支座。

图3 某应用组合型钢支撑项目平面
Fig.3 Plan of a project using assembly steel struts
组合型钢支撑是装配式结构,且标准构件重复使用,尽管施工有较高要求,仍然不可避免存在初始弯曲且荷载有偏心。相比完善体系,以非完善体系分析支撑梁更加符合实际情况,但有可能无法得到理论解答。故本文先将支撑梁作为完善体系进行分析,其后考虑支撑梁缺陷和挠度的影响对解答进行修正。
按GB 50017—2017《钢结构设计规范》,压弯构件应验算强度、平面内稳定性和平面外稳定性。图4所示为组合型钢支撑梁最常用截面形式,由于立柱所起侧向约束较小,弯矩作用在绕y轴平面内的稳定性是控制性的。按不利工况将规范计算公式中系数取为1.0,则公式左边可简化为:
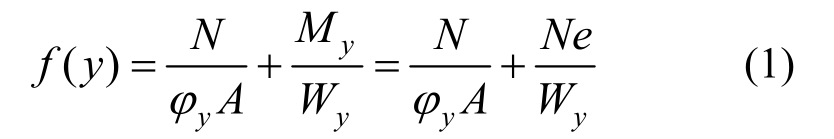
式中:N为支撑梁轴心压力;A为支撑梁截面积;φy为弯矩作用平面内轴心受压构件稳定系数;My为支撑梁在绕y轴平面内的最大弯矩,等于轴心压力N和偏心距e的乘积,偏心距按规范取为支撑梁长度的千分之一;Wy为支撑梁截面抵抗矩。若支撑梁截面为图 4,且选用 H350×350×12×19型钢,支撑梁长度为100 m时,式(1)右边第2项约为第1项的7.0%,即偏心距满足规范要求时对支撑梁稳定性影响较小。如不考虑偏心距影响,支撑梁稳定承载力与材料承载力比值即为φy。支撑梁长度为100 m时,φy约为0.50;支撑梁长度为130 m时,φy约为0.33。实际大部分支撑梁的长度范围为50 m~90 m,一般不超过120 m。
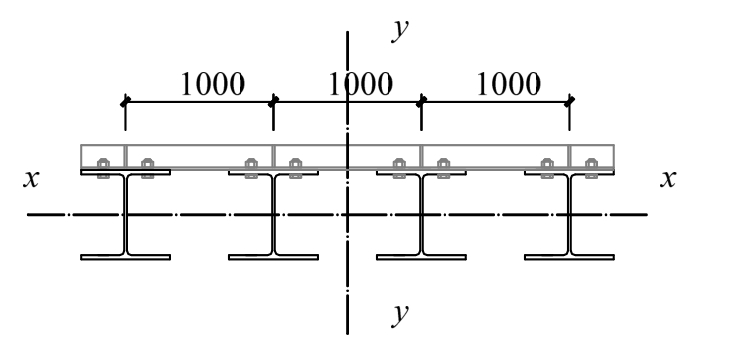
图4 常用支撑梁截面
Fig.4 Typical cross-section of assembly steel strut
组合型钢支撑梁有可能发生局部失稳。如图2(b)所示,支撑梁由数根型钢组合而成,局部稳定性主要由盖板和缀条的强度和间距控制,可通过钢结构要求验算确定最低要求。支撑梁满足该要求可认为不会发生局部失稳,实际支撑梁施工亦要求满足该要求。
2 单根横梁
支撑梁在水平面内和竖直平面内的失稳均可简化为离散弹性支座上的压杆屈曲问题。对于极端情况,支撑梁只有一根横梁支承时,可用图5(a)所示的模型进行分析。支撑梁承受轴力为P,截面抗弯刚度为EI,长度L=2l。横梁简化为弹簧,弹簧线刚度为KB。

图5 单根横梁时支撑梁稳定性计算模型
Fig.5 Stability analysis model for one support beam
假设支撑梁在两端与挡土墙的连接为铰接,支撑梁自身的接头均为等强连接。不考虑横梁支承作用时,图5(a)的支撑梁承载力为:
考虑横梁支承作用,支撑梁承载力取决于横梁的竖向抗弯刚度。如果刚度很大,则失稳模式中横梁处无侧移(图5(b)),承载力与长度为l的两端铰接柱完全相同,即:
如果横梁为弹性支座且发生一定的变形,如图5(c)所示,设弹簧因为支撑屈曲而产生的力为F,则可以建立如下的微分方程:
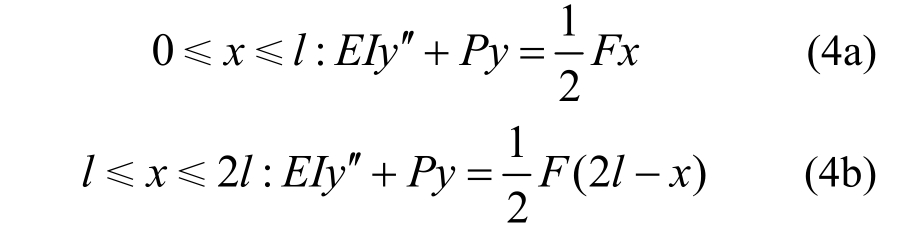
式(4a)、式(4b)的解为:

式中:![]() BF=K d,d是支撑梁跨中屈曲位移。然后,利用支撑梁两端支座处位移为0以及中点位移和斜率连续的条件[13],可以得到如下:
BF=K d,d是支撑梁跨中屈曲位移。然后,利用支撑梁两端支座处位移为0以及中点位移和斜率连续的条件[13],可以得到如下:
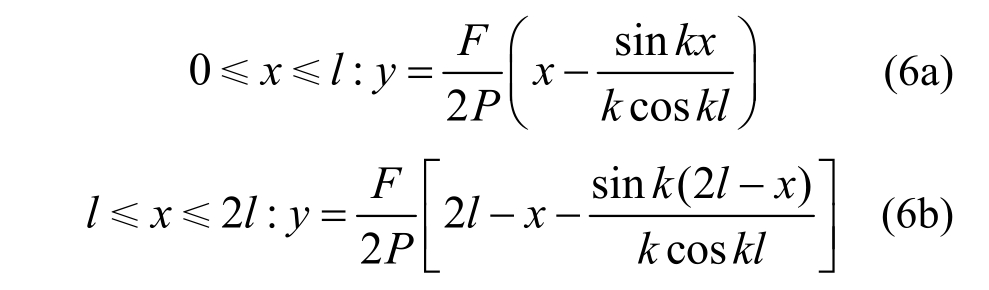
中点挠度是:
将![]() 代入式(7),并经适当变换,得到:
代入式(7),并经适当变换,得到:
可以得到如下临界方程:

前一个方程代表计算长度为l的屈曲模式(弹簧处位移为0),而第二个方程是弹簧处发生位移的屈曲模式,式(9b)改写为:

式中p=P/PEl。图6显示了弹簧线刚度和支撑承载力之间的关系,承载力增加量与弹簧线刚度之间近似成正比例关系。
支撑梁临界承载力可表示为:

图6 支撑梁承载力和弹簧刚度之间的关系
Fig.6 Relationship between strut capacity and spring stiffness
KB,th为失稳模式发生转化时的弹簧线刚度(门槛刚度)。为了使支撑梁计算长度减小到l,弹簧线刚度必须达到:
可直接写成横梁惯性矩的公式:
式中:B为横梁长度,即与横梁相连的两根立柱的间距;IB为横梁在竖直平面的截面惯性矩。如果要求支撑梁在竖向平面内的计算长度取相邻横梁之间的距离,相当于要求按照弹簧处位移为0进行支撑梁承载力计算,那么横梁刚度必须大于式(13)所表示的要求,其后进一步增加弹簧线刚度并不能提高支撑梁承载力。反之,当横梁刚度不能达到要求时,支撑梁承载力由横梁刚度决定。
然而,由于制作和安装误差,支撑梁总是存在缺陷,如初始弯曲,荷载并不完全作用在截面形心,截面残余应力等。由于是重复使用构件,组合型钢支撑梁的缺陷更加需要注意。此外,支撑梁在自重作用下有竖向挠度。假设所有缺陷和挠度都可等效为支撑梁初始弯曲,且弹簧(横梁)处的初始位移为d0。轴力作用后弹簧处的附加竖向位移为d,附加位移会在横梁中产生内力,因此对横梁以及支承横梁的两根立柱还有承载力要求。
对图5(a)的支撑,经过简单二阶分析,可得到在P=PEl时,有:
横梁承受的力为:
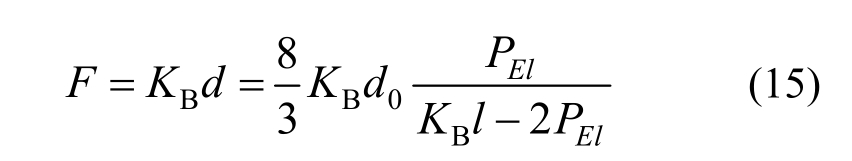
如果要求支撑梁承载力达到PEl,横梁刚度按式(13)确定,那么按式(15)横梁承受的力为无穷大,因为此时分母为0。因此从非完善体系出发,对横梁刚度要求必须在式(10)的基础上放大。
若放大到2倍,即KBl=4PEl,且d0=L/250,则:
即要按照支撑梁承载力的4.267%作用在横梁跨中进行设计。
如果放大到3倍,即KBl=6PEl,则:
上面的分析表明,弹簧线刚度越大,对横梁的承载力要求越小;反之,弹簧线刚度越小,对横梁的承载力要求越大。理想的设计是在刚度要求和强度要求之间取得某种平衡,故建议横梁刚度按照式(17)考虑。
3 多根横梁
如图7所示,假设支撑梁被(n-1)根横梁分割成相等的n段,且初始缺陷为:
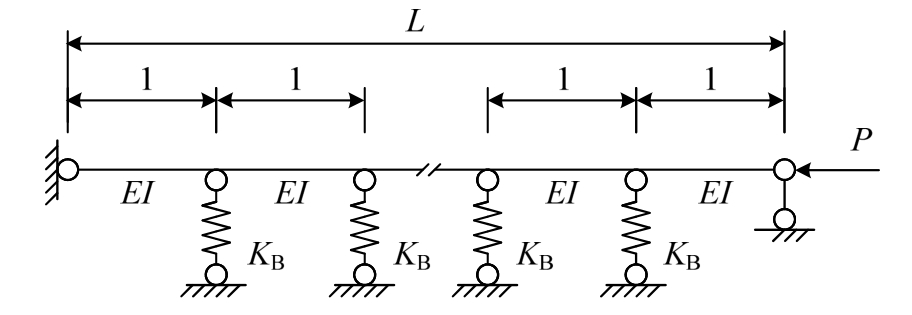
图7 多根横梁时稳定分析模型
Fig.7 Stability analysis model for multiple-support beams
对每一段均可以建立平衡微分方程:

式中:![]() 是第一个支座的反力;Fi是第i道横梁的反力,i=1,2,3…,n-1。
是第一个支座的反力;Fi是第i道横梁的反力,i=1,2,3…,n-1。
利用边界条件和连续性条件,可得到式(19)的解答,为:


另一方面:
采用矩阵表示,记:
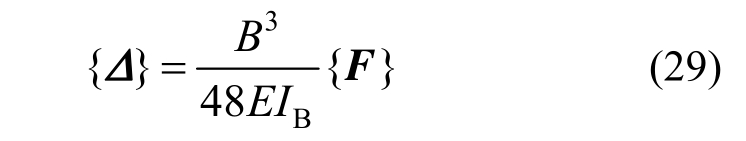

式(30)是非线性平衡方程,如果初始弯曲等于0,则得到的是屈曲方程,令系数行列式等于0,得到:
给定刚度比χ,对式(32)求解可得到临界荷载,或者给定临界荷载,从式(32)可得到刚度要求。式(32)的解为:

如果要求支撑梁计算长度为相邻横梁距离,在n-1个值中选择最大值,则i=n-1,即:
对括号中系数,n=2时为1,n=3时为1.5,n=4时为1.707,n=5时为1.866,n=∞时为2,说明弹簧线刚度要求随支撑梁跨数增加仅有限增加。
式(34)也给出弹簧线刚度未达到门槛刚度时支撑梁承载力与弹簧线刚度之间的关系,以3道横梁(n=4)为例,二者之间关系曲线如图8所示。
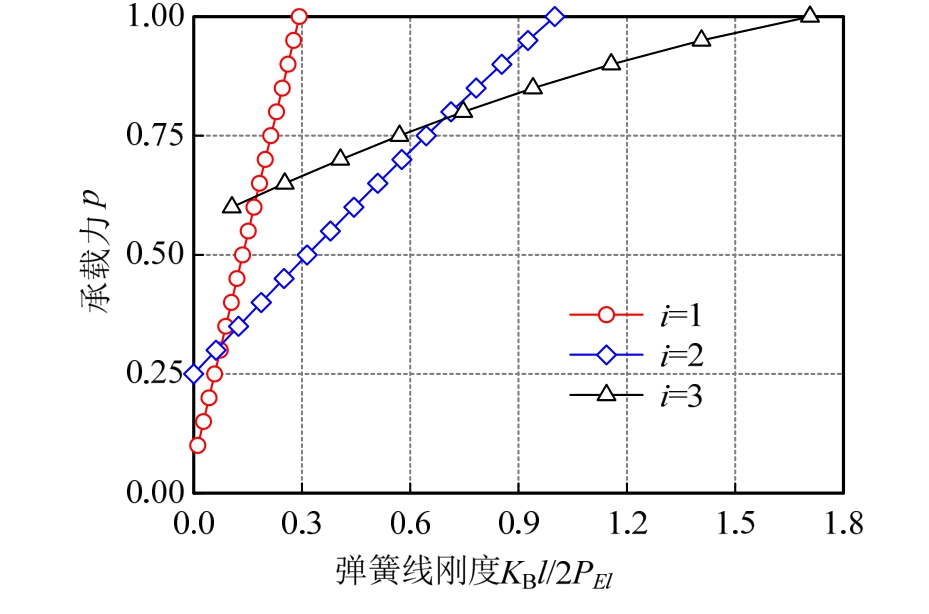
图8 支撑梁承载力与弹簧线刚度关系
Fig.8 Relationship between strut capacity and spring stiffness for three support beams
如果支撑梁有初始弯曲,应采用式(30)描述承载力与弹簧线刚度之间的关系。设P=PEl,即支撑梁的计算长度为相邻横梁之间的距离。此时kl=π,则[D1]=0,式(30)变化为:
假定初始缺陷按照总的最大挠度为L/250确定,同时考虑每个分量,并且初始挠度值与分量波长取相同百分比。设:
则用下式来决定Z的数值:
n=2时,Z=250;n=3时,Z=333;n=4时,Z=360;n=5时,Z=380。上文已对n=2的情况进行了分析,下面对其他三种情况分别进行分析。
n=3时,取KB为式(34)的3倍,可以求得横梁最大反力为:
与n=2时相比,对横梁的要求提高很多。
同理,n=4时,可以求得横梁最大反力为:
横梁内力进一步增加。
同理,n=5时,可以求得横梁最大反力为:
式(38)~式(40)说明:考虑初始缺陷后,横梁的内力非常大。作为设计建议,取较小的值为:
4 型钢分布对支撑梁影响分析
上述分析将横梁上组成支撑梁的多根型钢简化成一根作用在横梁跨中。当型钢在横梁均布,型钢与横梁简支。图9所示为横梁上有3根型钢均布情况,间距为b,由于结构对称性,中间节点力为F1,两侧节点力均为F2。
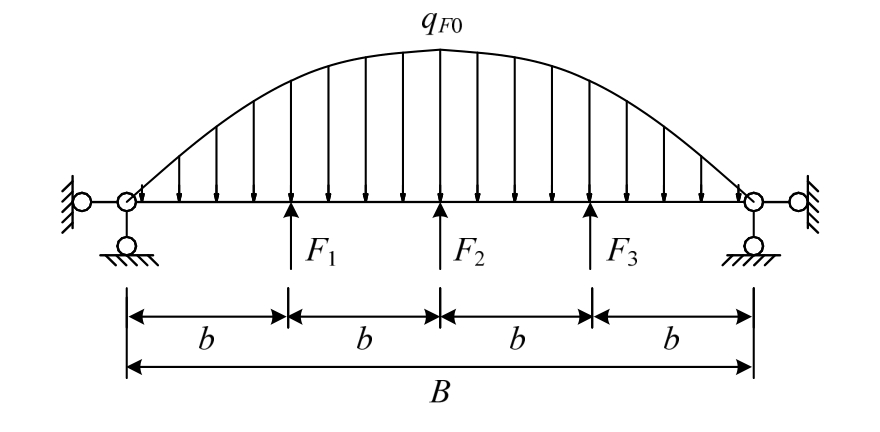
图9 横梁上均布三根型钢
Fig.9 Support beam affected by three steels
中间节点和两侧节点处的挠度分别是:
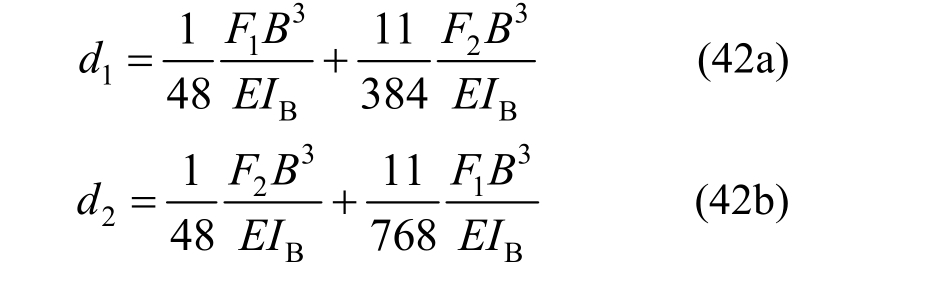
根据弹性支座的概念,弹簧线刚度系数KB为横梁节点力与相应节点挠度的比值,即:

将式(42)分别代入式(43),并利用各根型钢满足相同的刚度条件才可同时失稳即KB1=KB2=KB的条件,则屈曲时F1和F2之间应满足一定关系,设F1=αF2,则:

从式(44a)和式(44b)消去α得到求算KB的方程,为:
根据弹性理论,若作用在横梁的分布荷载为:
则横梁的挠度是:
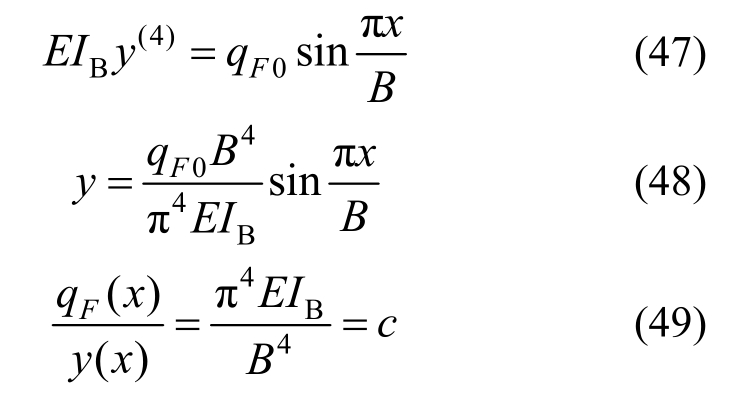
即荷载分布符合正弦规律时,挠度变化符合正弦规律,两个变量比值为常数,各根型钢支承刚度相同。
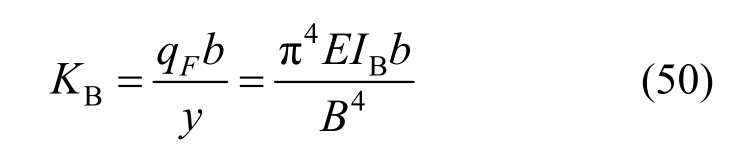
式(50)与式(45)相同,即使横梁跨中只有一根型钢,式(50)误差也仅为1.47%。
令m+1 =B/b,将式(45)代入式(34),得到:
而将支撑梁上所有型钢简化为作用在跨中的单根型钢时,根据式(34),门槛刚度要求为:
比较式(51)和式(52),后者大于前者,即将均布多根型钢简化为作用在横梁跨单根型钢后的横梁刚度要求偏于安全。
假设各根型钢的初始弯曲沿着横梁宽度方向分布满足正弦规律,则上述刚度方程可直接应用于多根型钢同时屈曲的分析,上文对有缺陷体系的相互作用力分析结果也可以直接应用。但是上述分析结果是总的相互作用力。假设分布荷载作用下的挠度和集中荷载作用下的挠度相同,则可得到将总的相互作用力分配到横梁的各个作用点的计算方法。令:
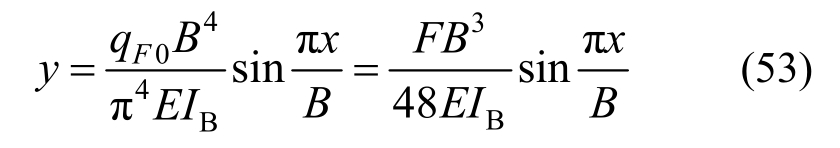
从而得到:
横梁最大弯矩为:
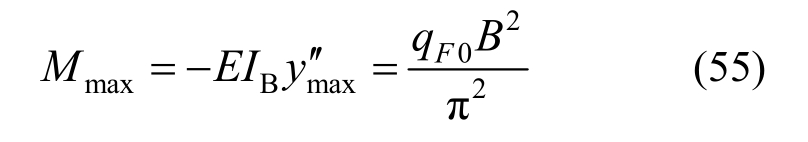
5 弹塑性修正
上文公式均由弹性体系导出,对弹塑性支撑梁,如仍假设体系无几何缺陷,将前面的公式中的E用切线模量Et代替后仍然适用[14]。如要求支撑梁计算长度为l,且处于弹塑性状态时,对横梁刚度要求仍可由式(34)和式(51)给出。但是实际工程中的支撑梁有初始弯曲。如果考虑初始弯曲影响,并认为材料是理想弹塑性的,确定横梁刚度要求只能用极限承载力分析法。陈绍蕃[11]对压杆有1~3个弹性支座情形进行弹塑性分析,发现要使压杆达到所要求的承载力,弹性支座刚度应达到按理想弹性体系决定刚度的3倍。他还认为将弹性体系所确定刚度要求放大3倍即可用于设计。这说明非完善体系分析可直接采用完善体系分析结果。但是支撑梁承载力应采用弹塑性承载力或实际承受轴力。
6 工程实例
某基坑工程处于杭州钱塘江南岸,地基土以粉砂土为主,基坑开挖深度约9 m,平面如图3所示,采用型钢水泥土搅拌墙(SMW)工法桩结合一道组合型钢水平内支撑的支护方式。支撑梁截面如图2和图 4所示。支撑梁、横梁和立柱均采用H350×350×12×19型钢,钢牌号为Q345B。1号支撑梁长65 m(不含端部八字撑),2号支撑梁长64 m,均设有6根横梁,横梁均等间距设置,横梁长度B和间距均为10 m。
根据剖面计算,作用在支撑体系上的土压力约为400 kN/m。1号支撑梁覆盖范围为20 m,2号支撑梁覆盖范围为10 m,则支撑梁设计承受压力分别为8000 kN和4000 kN。而支撑梁轴力监测结果分别为4100 kN和3800 kN。即1号支撑梁未达到设计要求,深层土体位移曲线也能对此说明,1号监测点最大水平位移约为5 cm,2号监测点最大水平位移约为3 cm。
单根 H型钢技术参数为:截面惯性矩Ix=IB=4.02×108mm4,Iy=1.36×108mm4,回转半径ix=152 mm,λx=79.7,φy为0.688,截面积A为1.74×104mm2。对 1号支撑梁进行分析,由式(34)并放大到3倍,横梁惯性矩应大于6.06×108mm4。即横梁刚度不能满足承载力要求。
若支撑梁轴力为8000 kN,则按式(41)横梁承受的力为672 kN,进而得到横梁应力为584.3 MPa,大于规范要求屈服强度295 MPa。反过来,根据横梁屈服强度可反算出支撑梁轴力约为4040 kN,与实测数值相符。如果考虑其他荷载对横梁的作用,支撑梁可承受的最大轴力更小,说明支撑梁承载力受横梁强度影响。此外,若按GB 50017―2017计算,φy=0.751,支撑梁极限承载力约为12000 kN,高于本文计算结果。说明本工程所用横梁达不到门槛刚度的要求,支撑梁承载力由横梁刚度控制。
立柱采用机械手静压插入坑底土层,支撑与坑底之间距离为7 m。由于未设立柱桩,且土层对立柱固定约束有限,故立柱的计算悬臂高度要额外增加立柱边长的4倍,即增加1.6 m。而立柱在水平面内两个方向抗侧刚度分别为435 N/mm和1300 N/mm。横梁代表的弹簧线刚度约为19285 N/mm。立柱抗侧刚度远小于横梁刚度,说明立柱对支撑梁在侧向稳定性几乎没有作用。支撑梁在水平面内稳定性由截面刚度决定,稳定计算长度应取支撑全长。并且根据图 2,立柱弱轴刚好与支撑梁可能失稳方向相同。如果通过加大立柱截面来提高稳定性,则立柱截面惯性矩需要提高 10倍才能使其刚度与横梁刚度在同一数量级,解决方法之一是采用方钢管并灌入混凝土作为立柱,立柱桩采用钻孔灌注桩。
7 结论
深基坑组合型钢对撑梁被立柱-横梁组成的门架近似等间距支承,本文分析了横梁对支撑梁在竖向平面和水平面稳定性的影响,并提出对横梁刚度要求和强度要求,主要结论如下:
(1) 横梁对支撑梁的作用可用弹簧模拟,只有横梁达到一定刚度后,支撑梁在竖向平面内稳定性计算长度才可取相邻横梁间距,其后增加横梁刚度不能提高支撑梁在竖向平面承载力。当横梁刚度不能达到要求时,支撑梁承载力由横梁刚度控制。
(2) 横梁刚度越大,承受的内力越大,兼顾刚度要求和强度要求,建议横梁承受的外力按支撑梁轴力的0.014n倍计算,n为支撑梁被横梁分隔成的跨数。
(3) 支撑梁承载力和横梁刚度受结构初始缺陷和挠度影响,设计时可近似取完善体系分析结果的3倍。
(4) 按照现有工程做法,立柱抗侧刚度不及横梁刚度十分之一,立柱对支撑梁在水平面内稳定性影响很小,支撑梁稳定计算长度应取全部长度。
(5) 现有分析假设支撑梁局部稳定性满足要求,且将立柱和横梁组成的门架简化为弹性支座,与实际有一定差距。进一步研究将结合实测数据对本文结果进行修正和完善。
参考文献:
[1]Park J S, Joo Y S, Kim N K.New earth retention system with prestressed wales in an urban excavation [J].Journal of Geotechnical and Geoenvironmental Engineering,2009, 11(1): 1596―1604.
[2]Lin D G, Woo S M.Three dimensional analysis of deep excavation in Taipei 101 construction project [J].Journal of Geo Engineering, 2007, 2(1): 29―41.
[3]李瑛, 唐登, 朱浩源.H型钢构建的绿色深基坑支护体系初探[J].科技通报,2017, 33(2): 177―180, 230.Li Ying, Tang Deng, Zhu Haoyuan.Preliminary study of steel retaining system in green deep foundation pit [J].Bulletin of Science and Technology, 2017, 33(2): 177―180, 230.(in Chinese)
[4]GB 50017―2017, 钢结构设计规范[S].北京: 中国建筑工业出版社, 2017.GB 50017―2017, Code for design of steel structures [S].Beijing: China Architecture&Building Press, 2017.(in Chinese)
[5]童根树.钢结构平面内稳定[M].北京: 中国建筑工业出版社, 2005.Tong Genshu.In-plane stability of steel structure [M].Beijing: China Architeture & Building Press, 2005.(in Chinese)
[6]刘永海, 郭彦林.十字型刚架中轴压柱面外稳定性设计方法研究[J].工程力学,2011, 28(5): 54―63.Liu Yonghai, Guo Yanlin.Out-plane buckling behavior and design method of axial loaded column in the cross-frame [J].Engineering Mechanics, 2011, 28(5):54―63.(in Chinese)
[7]Plaut R H.Requirements for lateral braing of columns with two spans [J].Journal of Struct.Engrg., ASCE,1993, 119(10): 2913―2931
[8]陈明, 黄骥辉, 赵根田.组合截面冷弯截面薄壁型钢结构研究进展[J].工程力学,2016, 33(12): 1―11.Chen Ming, Huang Jihui, Zhao Gentian.Research progress of compound section cold-formed thin-wall steel structures [J].Engineering Mechanics, 2016,33(12): 1―11.(in Chinese)
[9]张文元, 麦浩, 于海丰.板式连接中心支撑钢框架结构推覆试验研究[J].工程力学,2017, 34(10): 128―138.Zhang Wenyuan, Mai Hao, Yu Haifeng.Pushover tests of steel concentrically braced frames with gusset plate connections [J].Engineering Mechanics, 2017, 34(10):128―138.(in Chinese)
[10]张爱林, 叶全喜, 郭志鹏, 等.装配式零初始索力摩擦耗能复位支撑力学性能试验研究[J].工程力学,2017,34(11): 41―49.Zhang Ailin, Ye Quanxi, Guo Zhipeng, et al.Experimental analysis of mechanical properties of fabricated friction dissipation re-centering brace with zero initial cable force [J].Engineering Mechanics, 2017,34(11): 41―49.(in Chinese)
[11]陈绍蕃.具有多道弹性支撑杆的钢柱稳定计算[J].西安建筑科技大学学报(自然科学版), 2011, 43(2): 153―159, 276.Chen Shaofan.Stability calculation of steel columns with multiple elastic braces [J].Journal of Xi’an University of Architecture & Technology (Natural Science Edition),2011, 43(2): 153―159, 276.(in Chinese)
[12]刘发前.装配式型钢内支撑稳定性设计[J].城市道桥与防洪,2016(5): 81―83.Liu Faqian.Stability design of assembled steel inner support [J].Urban Roads Bridges & Flood Control,2016(5): 81―83.(in Chinese)
[13]童根树.平行压杆体系的侧向稳定性支撑[J].西安冶金建筑学院学报,1991, 23(4): 425―431.Tong Genshu.Stability bracing in the parallel compression member system [J].Journal of Xi’an Institute of Metallurgy & Construction Engineering,1991, 23(4): 425―431.(in Chinese)
[14]周承倜.弹性稳定理论[M].成都: 四川人民出版社,1981.Zhou Chengti.Elastic stability theory [M].Chengdu:Sichuan People’s Publishing House, 1981.(in Chinese)