风雨激振是斜拉索在风雨条件下发生的大幅、低频振动，自Hikami等[1]首次发现了风雨激振现象以来，多个国家的斜拉桥上发生过风雨激振现象。风雨激振发生时，斜拉索的大幅振动会引起斜拉索端部接头部分出现疲劳现象，严重时甚至导致斜拉索的失效，造成重大的经济损失和安全隐患[2－5]。
目前，为了抑制风雨激振现象，研究人员提出了各种控制措施，包括空气动力学措施、结构措施[6－8]和机械措施等[9—11]。其中，空气动力学措施由于其具有造价低、易于维护的优点，而在国内外很多斜拉桥上得到应用。空气动力学措施主要是指通过改变斜拉索的表面粗糙程度及横断面形状破坏水线在斜拉索表面的形成和振荡，以达到减振的效果，如在斜拉索表面缠绕螺旋线、增加凹坑或纵向肋条等，研究人员对各种气动减振措施进行了一系列的研究。Olivier[12]研究了肋条和螺旋线对斜拉索的减振效果，认为螺旋线的作用是破坏水线及气流的相关性。Gu Ming[13]在风洞试验中发现在选用一定的直径、高度、缠绕方向的螺旋线后能有效抑制风雨激振的产生。李文勃等[14]通过引入等效阻尼比指标对气动措施减振效果进行定量分析，并在人工降雨试验中发现螺旋线、纵向肋条的减振效果好于椭圆环。Kleissl等[15]对带网罩、波浪形和多变体外表的斜拉索节段模型进行了风洞试验，研究表明：带网罩的斜拉索比光滑表面斜拉索的气动稳定性好，波浪形表面和多面体外形的斜拉索容易发生驰振。李寿英等[16—17]通过试验研究和数值模拟分析了螺旋线对斜拉索平均阻力系数、脉动升力系数、旋涡脱落频率等的影响。
从以上结果可以看出，已有的研究主要从风洞试验方面对斜拉索气动力措施的减振机理进行研究，而理论方面研究很少，这并不能很好的反映改变斜拉索外形后，斜拉索的振动响应及水膜的形态分布，因此目前对于斜拉索空气动力学措施的减振机理并不十分清楚。而一些斜拉桥上已尝试采用空气动力学措施来抑制风雨激振，设计人员在空气动力学措施的选用上，有一定的盲目性和不确定性，因此很有必要从理论方面对空气动力学措施的减振机理进行深入研究。
本文基于滑移理论[18－20]，建立一种水膜和斜拉索耦合的风雨激振理论模型，可用于分析任意外形的斜拉索在风雨共同作用下斜拉索表面水膜形态的变化、气动力及斜拉索的振动响应，探究改变斜拉索外形对风雨激振现象的影响；以带有两个纵向凸起的斜拉索为研究对象，建立耦合的运动方程，利用COMSOL软件求解风压力系数Cp和风摩擦力系数Cf，采用有限差分法求解水膜和斜拉索的偏微分方程，从水膜形态、斜拉索升力、振幅方面分析斜拉索的振动情况，为斜拉索空气动力学措施的理论研究提供一定的参考依据。
1 理论部分
1.1 水膜运动方程
如图 1所示，带有不规则表面的斜拉索水平倾角为
，风偏角为
受来流风速U0和重力的共同作用。取图 1中斜拉索A-A截面为研究对象，如图2所示，将坐标原点到斜拉索表面的距离设为s(θ)，忽略重力沿斜拉索轴向的分量、气流沿拉索的方向的分量和轴向流的影响。
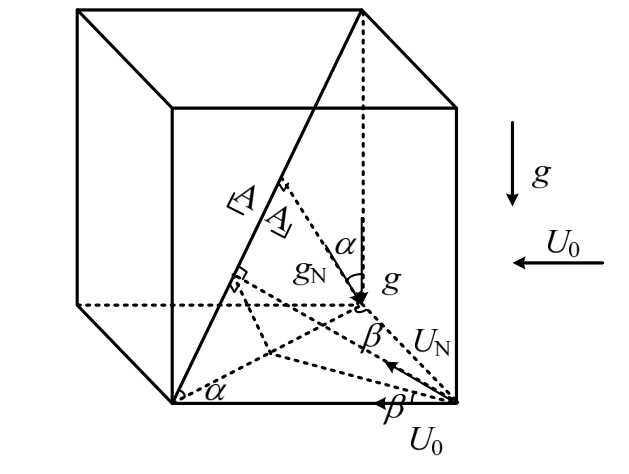
图1 斜拉索空间位置
Fig.1 Spatial position of stay cable
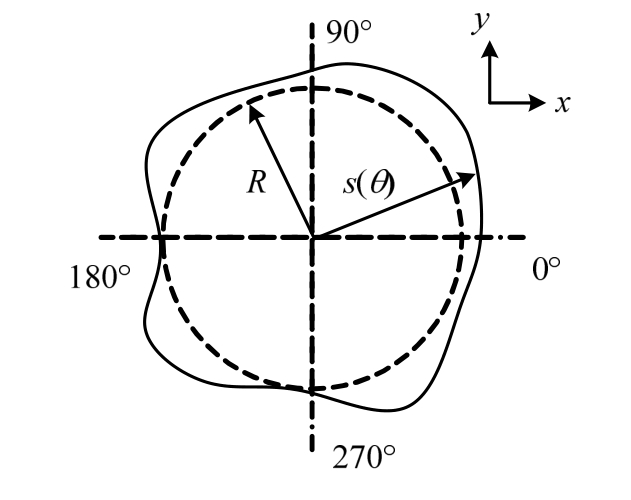
图2 斜拉索A-A横截面示意图
Fig.2 Schematic diagram of A-A cross section
根据滑移理论，假设斜拉索表面存在一层连续的水膜，则水膜的运动方程由二维Navier-Stokes公式推导：
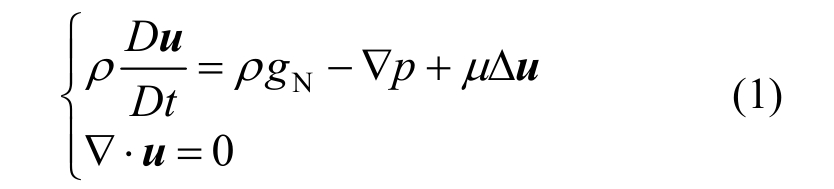
其中：u为水膜内的流场速度；ρ为水的密度；gN为作用在斜拉索断面内的重力分量；p为水膜内的压强；μ为水的动力粘度系数；?是哈密顿算子；Δ是拉普拉斯算子。
方程的边界条件包括以下3个：
1) 水膜底面r=s(θ)相对于斜拉索表面静止，即：
2) 水膜与空气交界处
的ur和uθ满足以下关系式：
3) 水膜在与空气交界处
所受的应力与表面张力相平衡，即：
其中：σ和σg分别为水膜与空气交界处水膜和空气的应力张量；γ为水在空气中的表面张力系数(γ与θ无关)；I为单位向量；pg为水膜表面所受的空气压力；τg为空气的粘滞力张量；h为斜拉索表面水膜的厚度；κ为水膜表面的曲率：
水膜与空气交界处的法向向量和切向向量分别为：
采用极坐标系
水膜内任一点的坐标为
速度u表示为分量形式
水膜底面表达式为r=s(θ)，水膜与空气交界处的表达式为
则无量纲化后的Navier-Stokes公式可写为(考虑h0＜＜R，即ε≈0)：
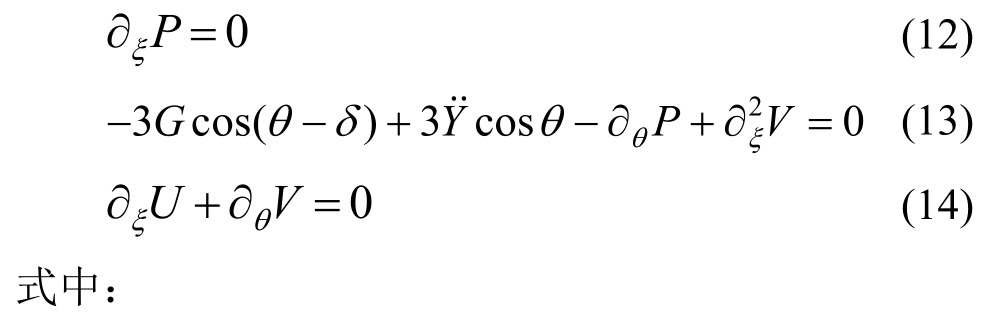
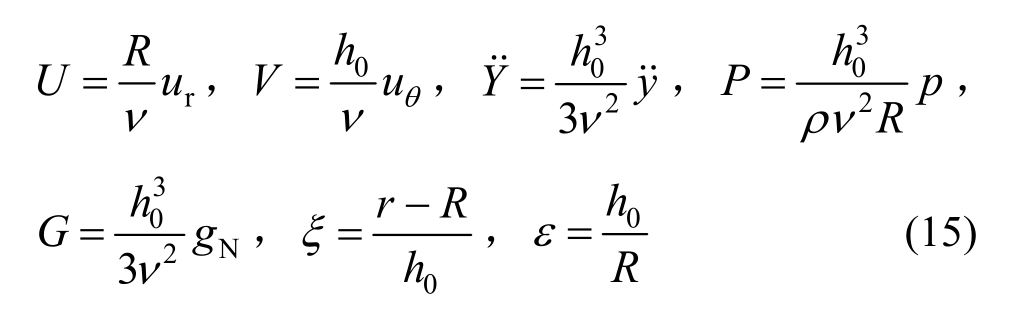
其中：h0为斜拉索表面水膜的初始厚度；R为坐标原点到斜拉索表面的最小距离；ν为水的运动粘性系数，ν=μ/ρ；y˙为斜拉索在横风向振动的加速度。
将式(6)～式(11)代入式(4)、式(5)中，并对式(2)～式(5)三个边界条件进行无量纲化处理分别得到式(16)～式(19) (设
(20)其中：ρg为空气的密度；UN为斜拉索横断面内的风速。
将三个边界条件式(16)～式(19)代入方程组式(12)～式(14)化简得到无量纲的水膜运动方程：
式(21)即为在风雨共同作用下，任意二维横断面斜拉索表面水膜的运动方程。当斜拉索表面形状为标准圆，即s(θ)=R，S=1时，式(21)与Lemaitre等[21]和Reisfeld等[22]推导出的方程相同。
1.2 斜拉索运动方程
在重力、风压力和风摩擦力、阻尼力和惯性力的作用下，斜拉索沿横风向(y轴方向)的运动方程可表示为：
式中：ω0、ξ0、M、Fy分别为斜拉索的自振频率、阻尼比、质量和横风向的升力。
和
分别为水膜底面
处的法向力和切向力。
水膜底面(斜拉索表面处)水膜的应力张量为：
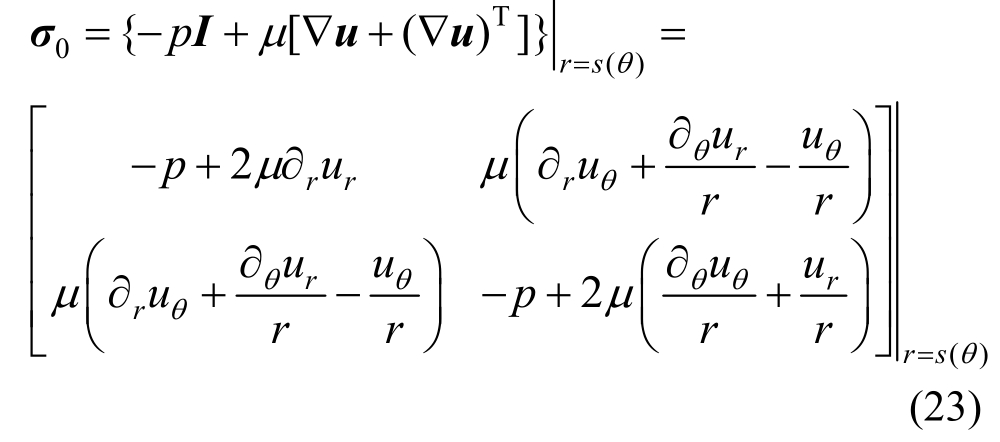
水膜底面(斜拉索表面处)的法向向量和切向向量分别为：
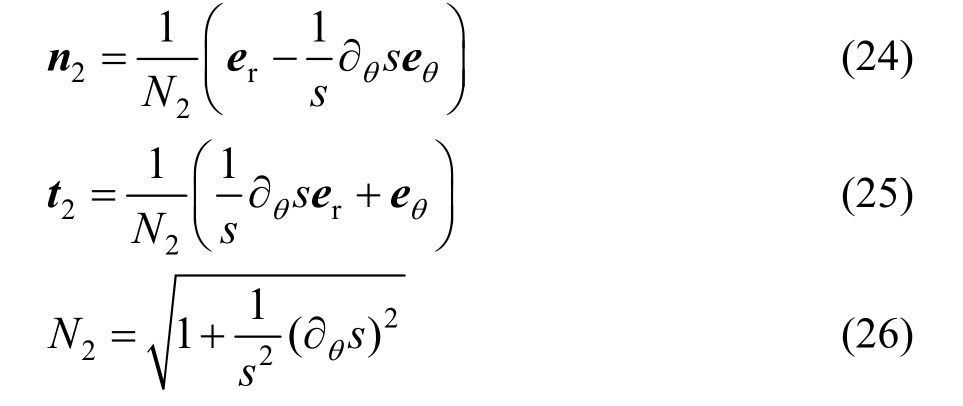
由式(23)～式(26)及式(5)和式(20)定义的无量纲参数可得无量纲的法向力和切向力：
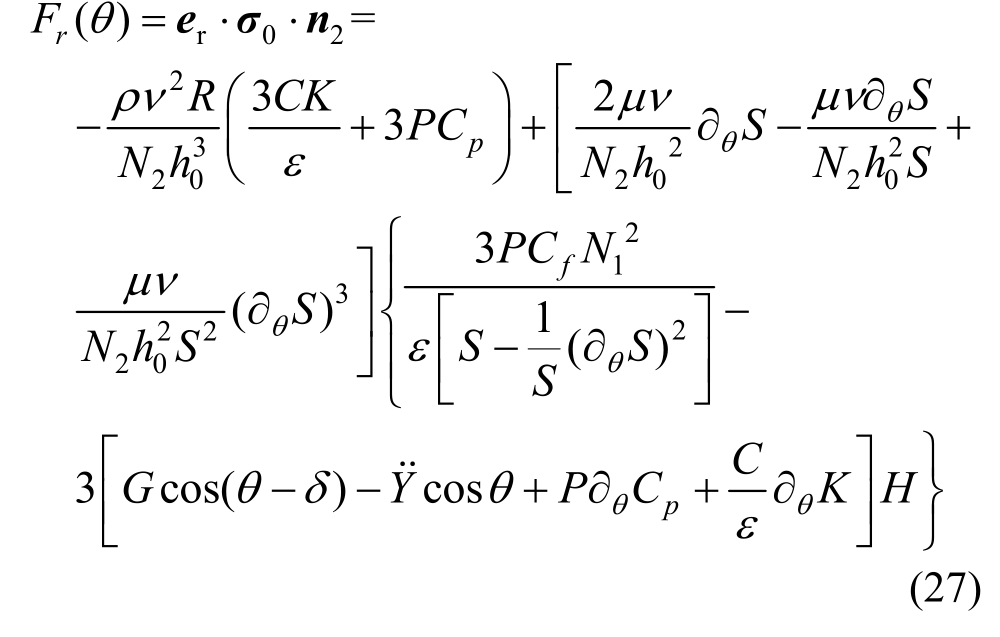
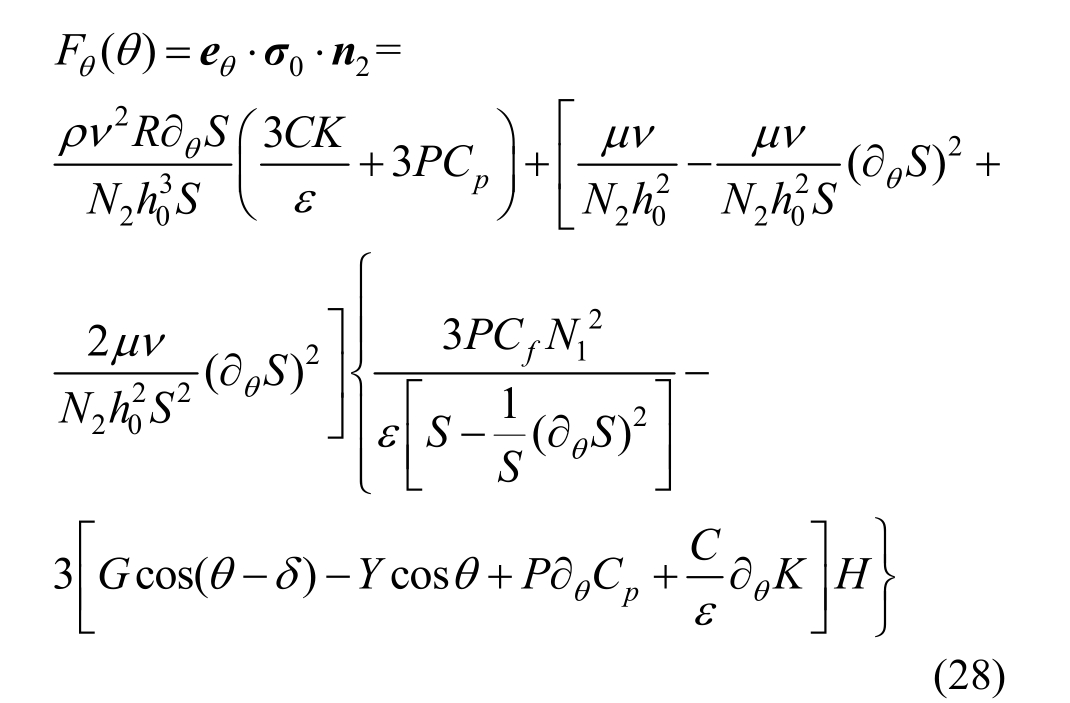
2 数值求解
2.1 数值求解过程
考虑水膜形态变化对斜拉索周围风场的影响，利用有限元软件COMSOL求解各个时间步的不同水膜形态下的风压力系数Cp和风摩擦力系数Cf，进而模拟水膜形态随时间的变化情况，采用MATLAB软件对水膜和斜拉索运动方程进行数值求解。水膜方程和斜拉索运动方程均采用有限差分法进行数值求解，计算流程如图3。
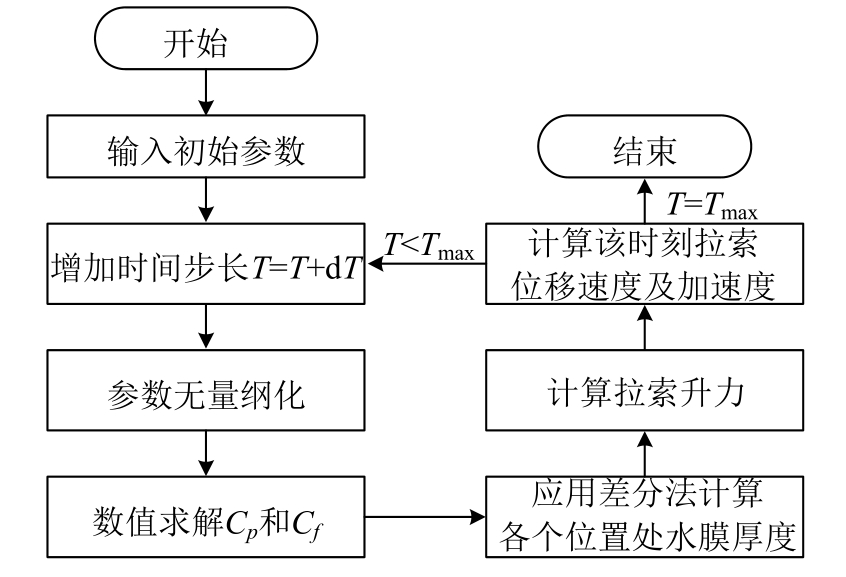
图3 数值计算流程图
Fig.3 Flowchart of numerical calculation
2.2 计算参数
将水膜在圆周空间上离散为N=128个点，并选取时间步长dt=10-4s。参照Li等[23]的试验设定水膜初始厚度h0=0.25 mm，最大厚度hmax=1.25 mm，为保证水膜的连续性，设定水膜的最小厚度hmin=0.02 mm。
图4显示了斜拉索的横截面示意图，在迎风向的斜拉索表面有两个梯形肋条，由于上水线的形成和沿斜拉索发生周期性振荡可能是斜拉索出现风雨激振现象的重要原因，已有试验数据[23]表明上水线的振荡范围θ≈30°～75°，两个纵向肋条分别放置在
处，均布置在上水线的振荡范围以内，从而可能达到减振的目的。肋条高2 mm，宽7.4 mm，可以得到各离散点上斜拉索中心到斜拉索表面的距离s()θ，其他基本参数见表1。
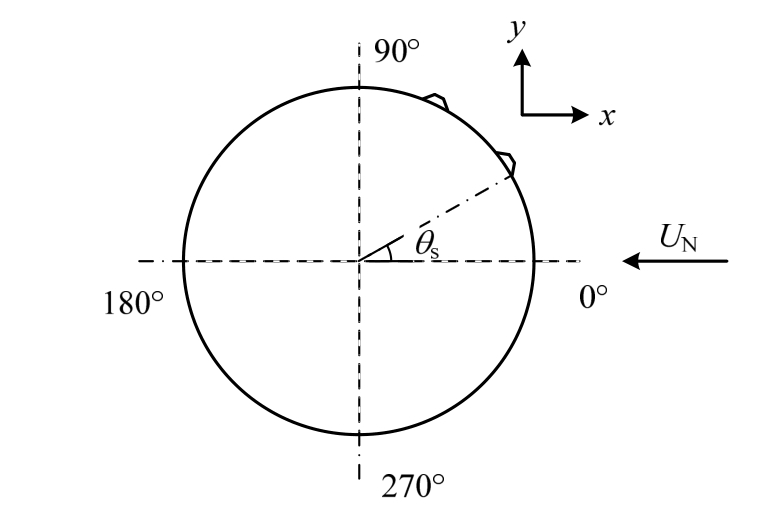
图4 斜拉索横断面示意图
Fig.4 Schematic diagram of cable cross section
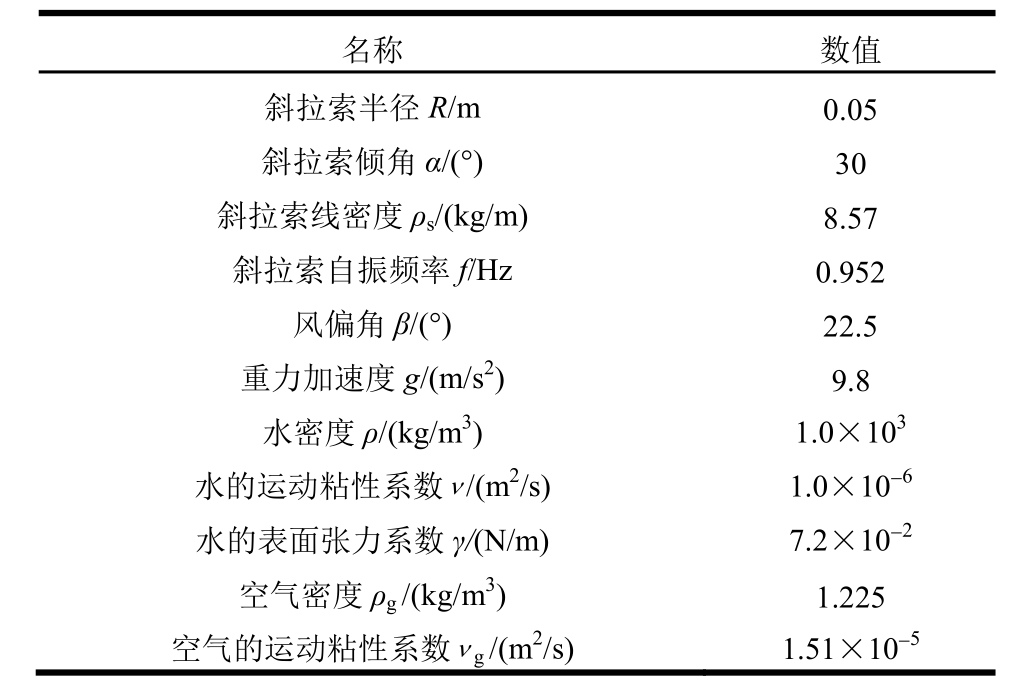
表1 基本参数
Table 1 Basic parameters
3 模型验证
为了验证理论推导和数值求解方法的可靠性和准确性，参照文献[23]中圆形斜拉索的试验工况，令s(θ)=R，S=1，计算圆形斜拉索的振动响应、升力及水膜形态变化，并与已有试验数据[23]进行比对。试验中当风速U0=7.72 m/s时风雨激振现象最为明显。对此，本文选取U0=7.72 m/s作为对比风速。采用COMSOL软件对水膜周围的流场进行数值模拟，求解随时间变化的风压力系数Cp和风摩擦力系数Cf，计算区域选取边长为27.5D×20D的矩形，将斜拉索中心置于坐标原点，斜拉索中心距离左侧入口10D，距离右侧出口17.5D，流场网格划分如图5所示。
图6显示在0～40 s内斜拉索振动响应及频谱分析。从图5所示的斜拉索振动时程曲线可以看出，斜拉索的初始时刻振幅为0.02 m，之后不断增大，在27 s以后逐渐保持稳定，振幅达到0.10 m，与试验观测结果0.09 m非常接近。斜拉索的振动主频率是1 Hz，近似等于文献[23]中得到的0.952 Hz。
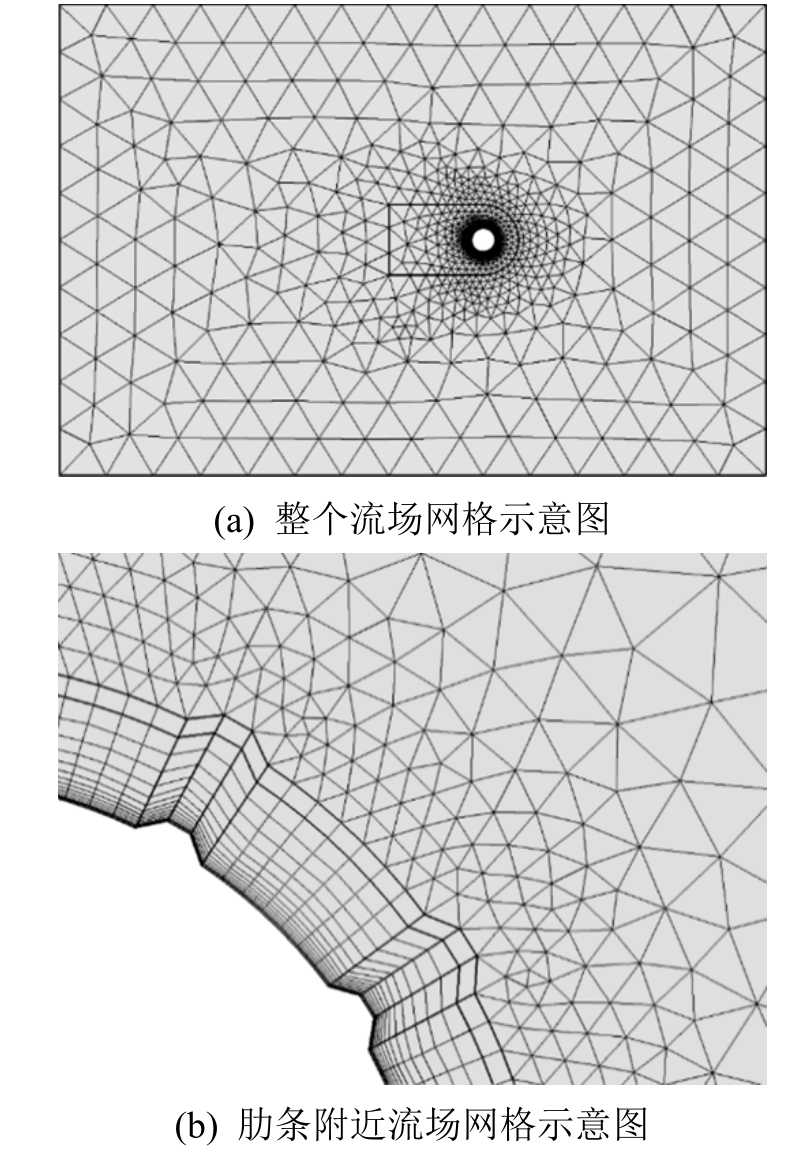
图5 流场网格示意图
Fig.5 Numerical grids of flow field
图6 斜拉索振动时程曲线及频谱分析
Fig.6 Vibration response and frequency analysis of cable
图7显示了0～40 s内斜拉索表面水膜形态的变化情况。可以看出，上水线发生明显的周期性变化，而下水线基本不发生振荡。而上水线在θ=30°～75°之间振荡，与试验观测数据一致。为了研究斜拉索表面上水线的变化规律，现选取上水线附近的某位置θ=56.25°处水膜厚度作为研究对象，如图8所示。在前 25 s内上水线厚度不断增大，之后保持在0.49 mm左右，近似等于试验观测数据 0.51 mm。经频谱分析得到上水线的振荡频率是1 Hz，与试验中频谱分析结果0.952 Hz非常接近。为便于与带有纵向肋条斜拉索的升力变化情况进行对比分析，现列出斜拉索气动升力的时程曲线及频谱分析如图 9所示，稳定以后升力的变化范围为0～1.3 N，振动的主频率为1 Hz。
图7 水膜形态变化
Fig.7 Evolution of water film around cable
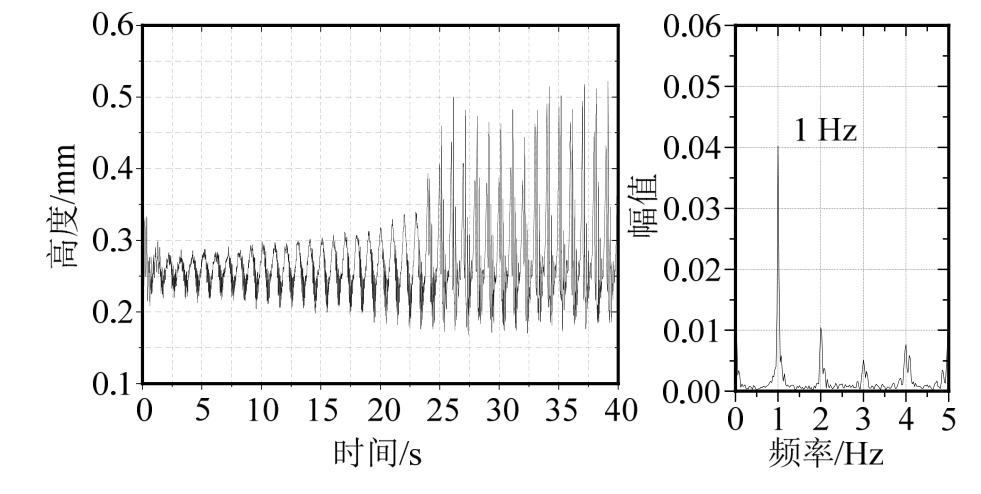
图8 56.25°处水膜厚度变化及频谱分析
Fig.8 Thickness and frequency analysis of water film atθ=56.25°
图9 斜拉索升力变化及频谱分析
Fig.9 Aerodynamic lift and frequency analysis of cable
4 计算结果与讨论
参照文献[23]中的试验参数，仍选取U0=7.72 m/s作为计算风速，对比圆形斜拉索发生风雨激振的研究成果，分析表面带有两个纵向肋条的斜拉索的振动响应、气动升力及水膜形态变化规律，探究改变斜拉索外形对风雨激振现象的影响。
图10显示了0～40 s内斜拉索的振动响应及频谱分析，斜拉索的平衡位置由初始位置沿重力方向下移，在y=-0.03 m附近斜拉索发生周期性振动，初始时刻斜拉索振幅达到0.05 m，之后开始逐渐减小，至19 s左右斜拉索振幅衰减为0.03 m，在20 s以后斜拉索振幅略有增大，稳定之后振幅保持在0.03 m左右。通过对比图6中圆形斜拉索的振动时程曲线可以看出，带两个纵向肋条的斜拉索可以大幅度减小斜拉索振幅，能够有效抑制风雨激振现象。经过频谱分析可知，斜拉索的振动主频率为0.98 Hz，近似等于其自振频率0.952 Hz。
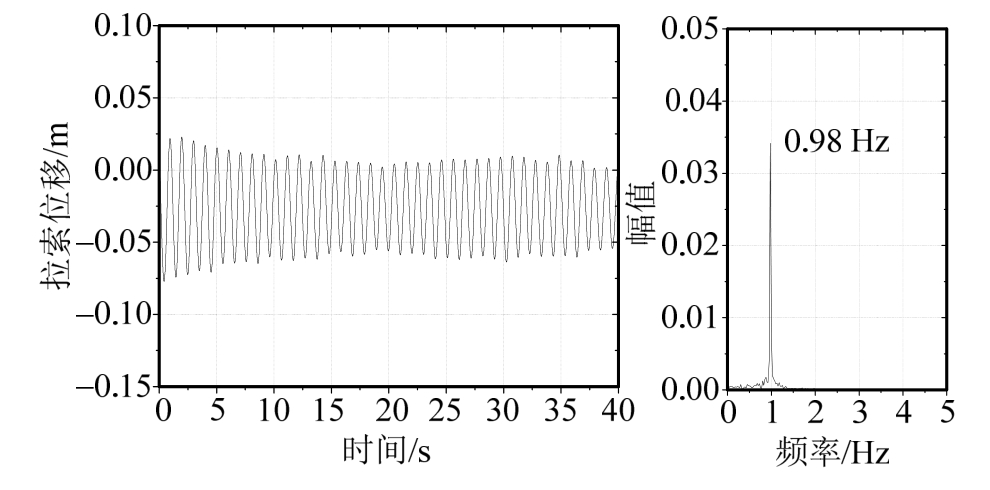
图10 斜拉索振动时程曲线及频谱分析
Fig.10 Vibration response and frequency analysis of cable with two ribs
图11是0～40 s内斜拉索气动升力的时程曲线及频谱分析，在t≈1 s以后升力基本在-1.4 N～-0.6 N之间保持周期性稳定变化，升力的变化主频为0.98 Hz，但能量很小，基本可以忽略。对比图9的升力变化时程曲线及频谱分析可以发现，斜拉索升力变化范围减小，周期性特性明显减弱。
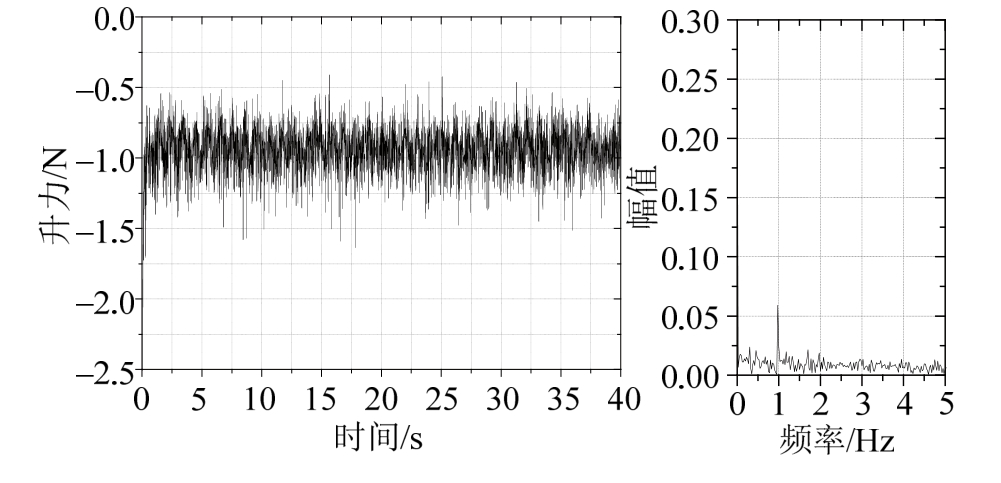
图11 斜拉索升力变化及频谱分析
Fig.11 Aerodynamic lift and frequency analysis of cable with two ribs
图12显示的是0～40 s内斜拉索表面水膜厚度变化时程图，可以看出，在t≈0.5s时下水线形成于θ=278.4°附近，随后在θ=275.6°～286.9°范围内振荡，其高度和宽度分别为hl=1.25 mm和bl=2.62 mm。由于两个纵向肋条均处于上水线的周期性变化范围内，影响了上水线的形成及周期性滑落，可以看到有三条较为明显的水线形成，水线变化的周期性并不明显，最大厚度为0.43 mm，并且由于肋条的存在阻碍了水沿斜拉索表面的流动，在两个肋条的上边缘均积聚了一部分水，形成两条固定的水线，水线厚度约为1.2 mm，在两个肋条的下边缘也积聚少量的水，厚度约为0.26 mm，说明斜拉索表面上水线附近的水主要从迎风面流向下水线。为了进一步的分析斜拉索表面上水线运动的周期性特性，现选取θ=56.25°处斜拉索表面水膜为研究对象，作0～40 s内水膜厚度变化的时程曲线及如图13所示。通过频谱分析可知，水线振荡的主频为0.98 Hz和14.45 Hz。通过与圆形斜拉索算例的研究成果进行对比可以发现：在重力、表面张力和风荷载的作用下，上水线附近其余位置处的水膜本应向上水线汇聚，而斜拉索表面的纵向肋条抑制了上水线的形成，一部分水积聚在纵向肋条的上下边缘，另一部分水在两个纵向肋条之间形成了多条上水线，而与圆形斜拉索模型中的上水线相比，厚度却明显变薄。两个纵向肋条虽不能抑制上水线的产生，却可以减小上水线的厚度，并且由于两个纵向肋条均位于上水线的周期性滑落范围内，使得上水线振荡范围减小，多条水线在运动过程中相互影响，导致水线的变化频率与斜拉索的自振频率并不十分一致，水线在14.45 Hz处也有较大的能量，斜拉索升力变化的周期性特性减弱，从而使得斜拉索振幅大幅度减小，抑制了风雨激振现象的产生。
图12 水膜形态变化
Fig.12 Evolution of water film around cable with two ribs
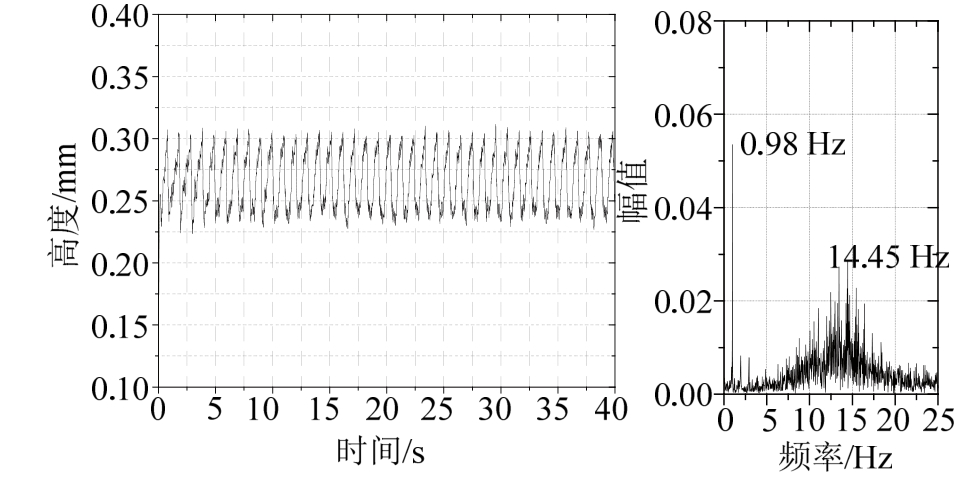
图13 56.25°处水膜厚度变化及频谱分析
Fig.13 Thickness and frequency analysis of water film around cable with two ribs atθ=56.25°
5 结论
本文基于滑移理论建立了可用于分析任意横断面外形斜拉索的耦合的水膜和斜拉索运动方程，并对其进行数值求解，探究带有纵向肋条的斜拉索的风雨激振的减振机理，得到了以下结论：
(1) 基于滑移理论和单自由度振动理论，建立可用于分析改变斜拉索的横截面外形对风雨激振现象影响的耦合理论模型，并分析了圆形截面斜拉索在风雨共同作用下的斜拉索振动响应及水膜形态发展规律，与已有的试验观测数据一致，验证了理论模型和数值求解方法的准确性。
(2) 斜拉索上水线附近的纵向肋条虽不能阻止上水线的产生，但可以减小上水线厚度，阻碍上水线的周期性滑落，避免上水线振动能量的集中分布。
(3) 纵向肋条通过阻碍上水线的周期性变化，使得斜拉索升力变化的周期性减弱，从而抑制风雨激振现象的产生，达到减振的目的。
参考文献：
[1]Hikami Y, Shiraishi N.Rain-wind induced vibrations of cables stayed bridges [J].Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(1): 409―418.
[2]李国芬, 陈研, 朱华平.南京长江第三大桥斜拉索的防腐系统研究[J].南京林业大学学报(自然科学版),2006, 30(6): 102―104.Li Guofen, Chen Yan, Zhu Huaping.Research on the cable antiseptic system of the Nanjing No.3 Yangtze River Bridge [J].Journal of Nanjing Forestry University(Natural Sciences Edition), 2006, 30(6): 102―104.(in Chinese)
[3]顾明, 杜晓庆, 李寿英.斜拉桥斜拉索风雨激振的实验和理论研究[J].振动工程学报, 2007, 20(5): 473―479.Gu Ming, Du Xiaoqing, Li Shouying.Experimental and theoretical study on rain wind induced vibration of cables of cable-stayed bridges [J].Journal of Vibration Engineering, 2007, 20(5): 473―479.(in Chinese)
[4]刘习军, 李强, 刘振宇, 等.MR阻尼器在风雨激振的斜拉索中的减振应用[J].工程力学, 2007, 24(9): 100―104.Liu Xijun, Li Qiang, Liu Zhenyu, et al.The application of MR damper in rain-wind-induced vibration reduction of stay cable [J].Engineering Mechanics, 2007, 24(9):100―104.(in Chinese)
[5]唐善然, 陈文礼, 李惠.斜拉索风雨激振的数值模拟研究[J].工程力学, 2012, 29(3): 124―132.Tang Shanran, Chen Wenli, Li Hui.Investigation on rain-wind-induced vibration of stay cables based on numerical simulations [J].Engineering Mechanics, 2012,29(3): 124―132.(in Chinese)
[6]Yamaguchi H.Modal Damping of Cable Structures and Its Theory [J].Kou Kouzou Rombunshuu, 2010, 1(3):129―138.
[7]Papadopoulos P G, Diamantopoulos A, Xenidis H, et al.Simple Program to Investigate Hysteresis Damping Effect of Cross-Ties on Cables Vibration of Cable-Stayed Bridges [J].Advanced Materials Research, 2012,452/453(1): 149―163.
[8]Ahmad J, Cheng S, Ghrib F.Impact of Cross-Tie Properties on the Modal Behavior of Cable Networks on Cable-Stayed Bridges [J].Scientific world journal, 2015,2015(2): 1―14.
[9]王修勇, 陈政清, 高赞铭, 等.磁流变阻尼器对斜拉索振动控制研究[J].工程力学, 2002, 19(6): 22―28.Wang Xiuyong, Chen Zhengqing, Gao Zanming, et el.An analysis of sinusoidal buckling of long tubulars subject to radial constraint [J].Engineering Mechanics,2002, 19(6): 22―28.(in Chinese)
[10]李寿英, 顾明, 陈政清.阻尼器对拉索风雨激振的控制效果研究[J].工程力学, 2007, 24(8): 1―8.Li Shouying, Gu Ming, Chen Zhengqing.The effectiveness of dampers to rain-wind induced vibration of stay cables [J].Engineering Mechanics, 2007, 24(8):1―8.(in Chinese)
[11]白雨润, 赵善博, 刘庆宽, 等.螺旋线参数对斜拉索风雨振抑制效果的影响[J].工程力学, 2015, 32(s1):310―321.Bai Yurun, Zhao Shanbo, Liu Qingkuan, et el.Effect of helical line parameters on rain-wind induced vibration control of cables [J].Engineering Mechanics, 2015,32(s1): 310―321.(in Chinese)
[12]Olivier F.Rain-wind induced vibration of cables [J].Journal of Wind Engineering and Industrial Aerodynamics,1995, 57(2―3): 353―362.
[13]Gu Ming, Du Xiaoqing.Experimental investigation of rain wind induced vibration of cables in cable-stayed bridges and its mitigation [J].Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(1):79―95.
[14]李文勃, 林志兴.抑制斜拉桥斜拉索风雨激振的气动措施研究[J].土木工程学报, 2005, 38(5): 48―53.Li Wenbo, Lin Zhixing.A study on aerodynamic control countermeasures to rain-wind induced vibration of cables in cable-stayed bridge [J].China Civil Engineering Journal, 2005, 38(5): 48―53.(in Chinese)
[15]Kleissl K, Georgakis C T.Aerodynamic control of bridge cables through shape modification: A preliminary study[J].Journal of Fluids and Structures, 2011, 27(7): 1006―1020.
[16]李寿英, 钟卫.缠绕螺旋线斜拉索气动性能的试验研究[J].土木工程学报, 2013, 46(7): 108―115.Li Shouying, ZhongWei.Experimental study on the aerodynamic characteristics of stay cables with helical lines [J].China Civil Engineering Journal, 2013, 46(7):108―115.(in Chinese)
[17]李寿英, 钟卫.缠绕螺旋线斜拉索气动性能的数值模拟[J].振动工程学报, 2014, 27(4): 488―496.Li Shouying, Zhong Wei.Numerical simulation on the aerodynamic characteristics of stay cables with helical lines [J].China Civil Engineering Journal, 2014, 27(4):488―496.(in Chinese)
[18]Bi J H, Wang J, Shao Q, et el.2D numerical analysis on evolution of water film and cable vibration response subject to wind and rain [J].Journal of Wind Engineering and Industrial Aerodynamics, 2013, 121: 49―59.
[19]毕继红, 王剑, 邵倩, 等.风雨激振时水膜形态与斜拉索振动间的双向耦合[J].工程力学, 2014, 31(7): 54―60.Bi Jihong, Wang Jian, Shao Qian, et al.Two-way coupling between water film morphology and rain-wind induced vibration of cable [J].Engineering Mechanics, 2014,31(7): 54―60.(in Chinese)
[20]毕继红, 关健, 王剑, 等.风雨激振时斜拉索响应、升力及水膜形态的研究[J].天津大学学报(自然科学与工程技术版), 2017, 50(4): 351―357.Bi Jihong, Guan Jian, Wang Jian, et al.Analysis on vibration of cable, lift and water film morphology during rain wind induced vibration [J].Journal of Tianjin University (Science and Technology), 2017, 50(4): 351―357.(in Chinese)
[21]Lemaitre C, Hémon P, Langre E.Thin water film around a cable subject to Wind [J].Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9): 1259―1271.
[22]Reisfeld B, Bankoff S G.Non-isothermal flow of a liquid film on a horizontal cylinder [J].Journal of Fluid Mechanics, 1992, 236: 167―196.
[23]Li F C, Chen W L, Li H, et el.An ultrasonic transmission thickness measurement system for study of water rivulets characteristics of stay cables suffering from wind-rain-induced vibration [J].Sensors and Actuators A: Physical, 2010, 159(1): 12―23.