车辆行驶通过桥梁时,桥梁结构产生振动,并辐射低频噪声,这种噪声已成为当前环境污染的一部分,不仅影响桥梁周边居民的生活与工作,严重时危害身体健康[1-2],还对野生动物的生存与繁衍产生影响[3]。因此,有必要对桥梁结构振动与噪声的机理进行分析,并设法降低这种噪声。
国内外学者已经对桥梁结构的振动与噪声进行了比较多的研究。Goromaru等[4]采用简单车辆模型从杆系结构交通振动响应研究了低频噪声辐射问题。Bewes[5]用统计能量法(SEA)计算了铁路桥梁噪声,在 200 Hz以上的噪声预测结果与实测较符合,200 Hz以下偏差较大。Au等[6]采用理论解法分析了移动荷载作用下板桥结构的声辐射。张鹤等[7]采用有限元法(FEM)分析了车桥耦合振动,然后用边界元法(BEM)计算了公路钢箱梁桥的结构噪声。上述工作表明,结构噪声的理论解法不适合复杂结构,统计能量法不适合以低频为主的桥梁结构噪声,而用有限元法适合求解结构振动,用边界元法求解结构周边无限域内的噪声,正成为桥梁结构噪声分析的常用方法。韩江龙等[8]、宋晓东等[9]在轨道交通桥梁的结构噪声,Li[10]、Zhang等[11]在高速铁路桥梁的结构噪声分析中,均采用有限元振动计算结合边界元噪声分析,取得了较好效果。上述研究均未涉及桥梁工程中广泛采用的铰接板桥。铰接板桥由预制梁板之间通过纵向铰缝连接而成,一般用于中小跨径桥梁,在我国桥梁中占比高,分布广[12-13]。因为纵向铰缝提供的横向联系弱,所以近年来,铰接板桥损坏比较严重[14],进一步加大了振动与噪声,因此对其进行研究更具现实意义。
本文在前期研究的基础上,针对铰接板桥(包括一般铰接板桥和连续桥面铰接板桥)提出了对应的车桥耦合振动分析方法;然后进一步分析了该类桥梁的结构声辐射;通过实际桥梁振动与噪声的实验,验证了上述方法的有效性。最后,利用本文提出的方法,探讨了降低铰接板桥交通振动和结构噪声的途径。
1 铰接板桥的车桥耦合振动分析
1.1 桥梁与车辆模型
采用有限元法分析铰接板桥在车辆作用下的振动,为此建立有限元模型如图1所示。
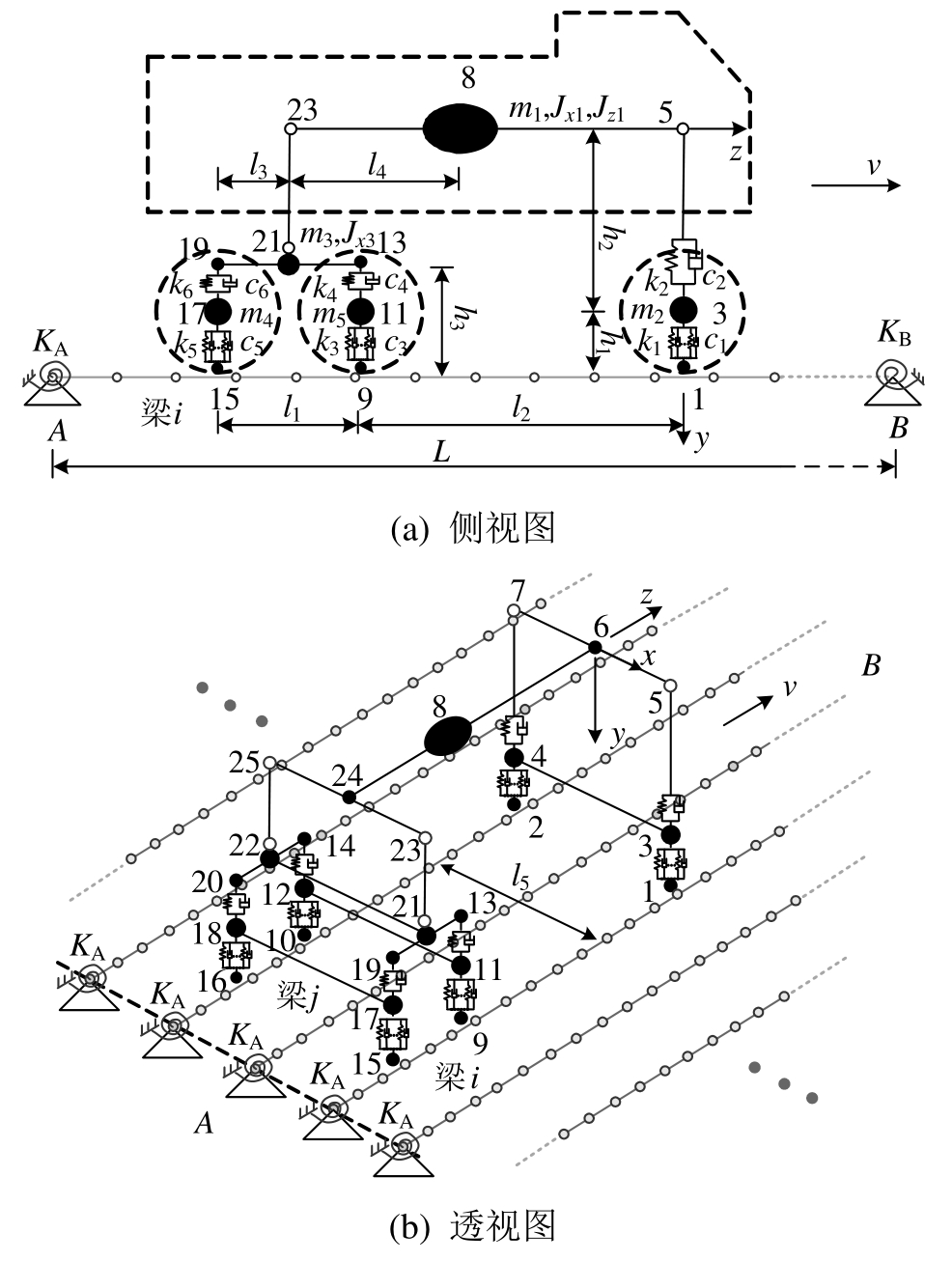
图1 车辆作用于桥梁的有限元模型
Fig.1 FEM model of bridge under vehicle
车辆模型为典型的三轴载重汽车[15],该模型由37个单元组成,其中与桥面接触的6个单元代表轮胎,采用分布式弹簧—阻尼(DSD)单元,可以模拟车辆通过伸缩缝时的跳车情况,其余分别为普通弹簧-阻尼单元(6个)、集中质量单元(9个)、刚性梁单元(16个),计算参数见表1。
桥梁模型需能反映铰缝的横向连接作用,以前往往对梁板建立实体、板壳或梁格有限元模型,用横向连接单元模拟梁板间的铰缝连接,该方法必须划分非常密集的网格,否则会导致振动位移计算结果的锯齿状失真。本文则提出了另一种建模方法,将荷载横向分布影响线[13]引入到车桥耦合振动的有限元分析中,对各梁板建立独立的单梁有限元模型,单元类型为欧拉弯曲梁单元[16],如图1所示。动态的车轮荷载按照横向分布影响线分布到各块梁板,然后分析各梁板的振动响应。如图2所示,作用在r号梁板上的力rP造成的j号梁板荷载为:
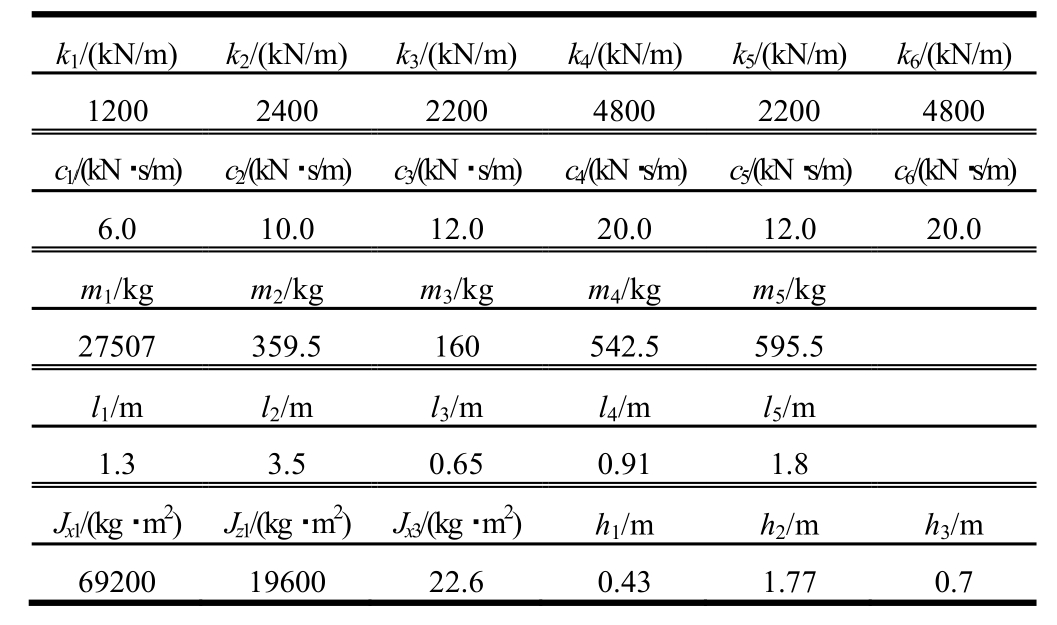
表1 车辆的计算参数[15]
Table 1 Parameters of vehicle[15]
其中,μrj为荷载的横向分布影响线竖标,即单位力作用在r号梁板上时由j号梁板承担的部分。这种车轮荷载分配方法概念清晰,描述荷载横向分布时不受有限元网格密度的影响,适用于铰接板桥的车桥耦合振动分析,特别是以纵向振动为主的低阶车桥耦合振动情形。
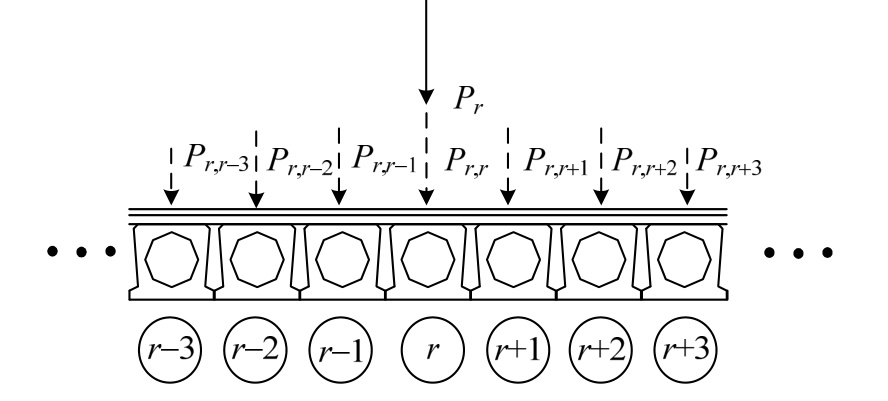
图2 车辆轮胎荷载在各梁板的分配
Fig.2 Distribution of tire load on beams
对于连续桥面的铰接板桥,除了没有伸缩缝跳车以外,连续桥面将对分析跨提供弯曲约束,因此梁端施加抗弯弹簧约束KA和KB[17],当其数值为零时,即退化为普通的带伸缩缝的铰接板桥。
1.2 车桥耦合振动分析方法
图1中车辆在单元组集后,得到动力学方程:
其中:Mv、Cv、Kv分别为质量矩阵、阻尼矩阵和刚度矩阵;uv是车辆节点位移,其中节点1、2、9、10、15、16的位移等于轮桥接触点处桥梁的振动位移与桥面粗糙度之和;![]() 是车辆受到的荷载。
是车辆受到的荷载。
铰接板桥的梁单元组集后得到动力学方程:
其中:u为桥梁节点位移;M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵。结构阻尼采用瑞雷阻尼[18];P(t)为所有车轮荷载组成的矢量,单个车轮荷载即为式(1)中的Pr,由下式计算[15]:
其中:k、c分别为车轮单元的刚度和阻尼;uA、![]() 分别为轮轴和轮底节点的位移;u˙A、u˙B分别为轮轴和轮底节点的振动速度。考虑到车辆与桥梁振动的耦合,上述车轮荷载由程序迭代得到[19]。
分别为轮轴和轮底节点的位移;u˙A、u˙B分别为轮轴和轮底节点的振动速度。考虑到车辆与桥梁振动的耦合,上述车轮荷载由程序迭代得到[19]。
1.3 桥面粗糙度度模拟
桥面粗糙度对桥梁振动响应有较大的影响,其值r(x)可用均值为零的平稳随机高斯过程生成[20]:
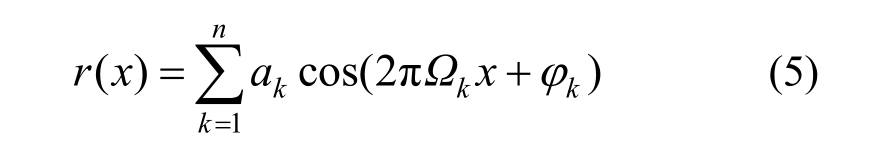
其中:φk是在[0,2π]区间内随机分布的相位角,可由蒙特卡罗方法生成;x是顺桥向的坐标;n是相位角数目;其他参数定义为:
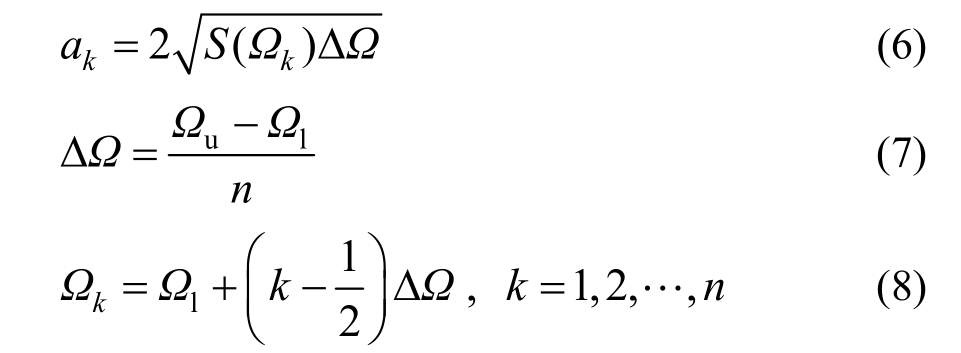
其中:![]() 是功率谱密度(PSD)函数;?l和?u分别为最低和最高切断频率。
是功率谱密度(PSD)函数;?l和?u分别为最低和最高切断频率。
实际功率谱需要基于实测数据,ISO国际标准定义了典型的功率谱[21],本文采用了图3所示A、B、C三种功率谱函数,其中B、C功率谱函数分别是A功率谱函数的30倍和100倍。由功率谱函数生成的路面粗糙度曲线样本曲线如图4所示,其中用到的参数为?l=0,?u=6,n=2500。
2 桥梁结构声辐射分析
在上述桥梁振动分析基础上,利用边界元法求解结构振动导致的声辐射。不含域内声源的瞬态声辐射波动方程为[22]:
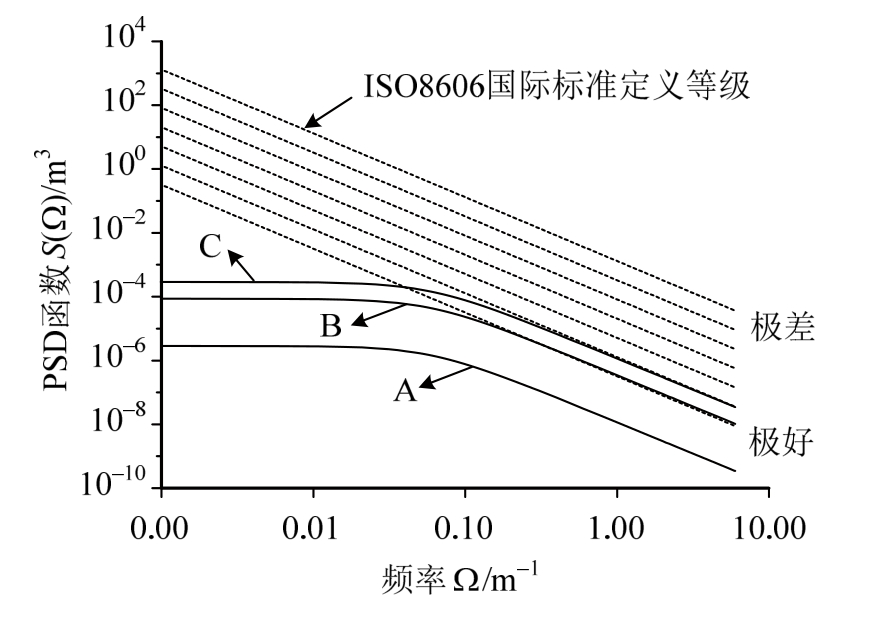
图3 桥面粗糙度功率谱
Fig.3 PSD curve of bridge surface

图4 桥面粗糙度样本曲线
Fig.4 Bridge surface profile
其中:p为声压;x为场点坐标矢量;c为空气中声波的速度。声场分析时的初始条件为:
边界条件为:
其中:n为桥梁外表面的外法线向量;vn为桥梁外表面的法向振动速度,来自本文第1节的振动分析;ρ为空气密度。
引入单位点声源的基本解,将式(9)~式(11)改写为等效积分形式,然后在时间域和空间域进行离散,即可推导得到边界元法对应的边界积分方程[22]。对于铰接板桥,计算声辐射时建立的边界元模型网格不封闭,因此需采用间接边界元法求解,求解后获得桥梁周边声场中任意一点的声压p。
本文先采用第1节计算方法得到铰接板桥各梁板节点的振动位移,然后将节点坐标和对应的位移时程映射到声学边界元网格上,最后用边界元法得到桥梁周边的瞬态声场。边界元声场计算采用声学软件Virtual Lab Acoustics实现。
为保证计算精度,每个声波波长最少包含6个线性边界单元,因此要反映100 Hz的声辐射(对应波长为3.4 m),有限元振动网格和边界元声辐射网格的边长均应小于0.55 m。
3 铰接板桥振动与声辐射实例分析
如图5所示,三轴载重汽车以24 km/h (6.6 m/s)的速度通过某连续桥面铰接板桥,汽车的左、右轮分别作用在12号、14号梁上,利用本文方法对该桥的振动与噪声进行数值计算与现场实验。实验测点布置在图5(a)中的第四跨,包括跨中动挠度和声压测点,如图5(b)、图5(c)所示,动挠度测试采用机电百分表,声压测试采用BK4190传感器和瞬态声压测试系统,频响范围3.3 Hz~3 kHz。该桥位于城郊,周边较为安静,但是为了尽量减少环境噪声与风压的影响,实验选择在晚上 10点后无风情况下进行。
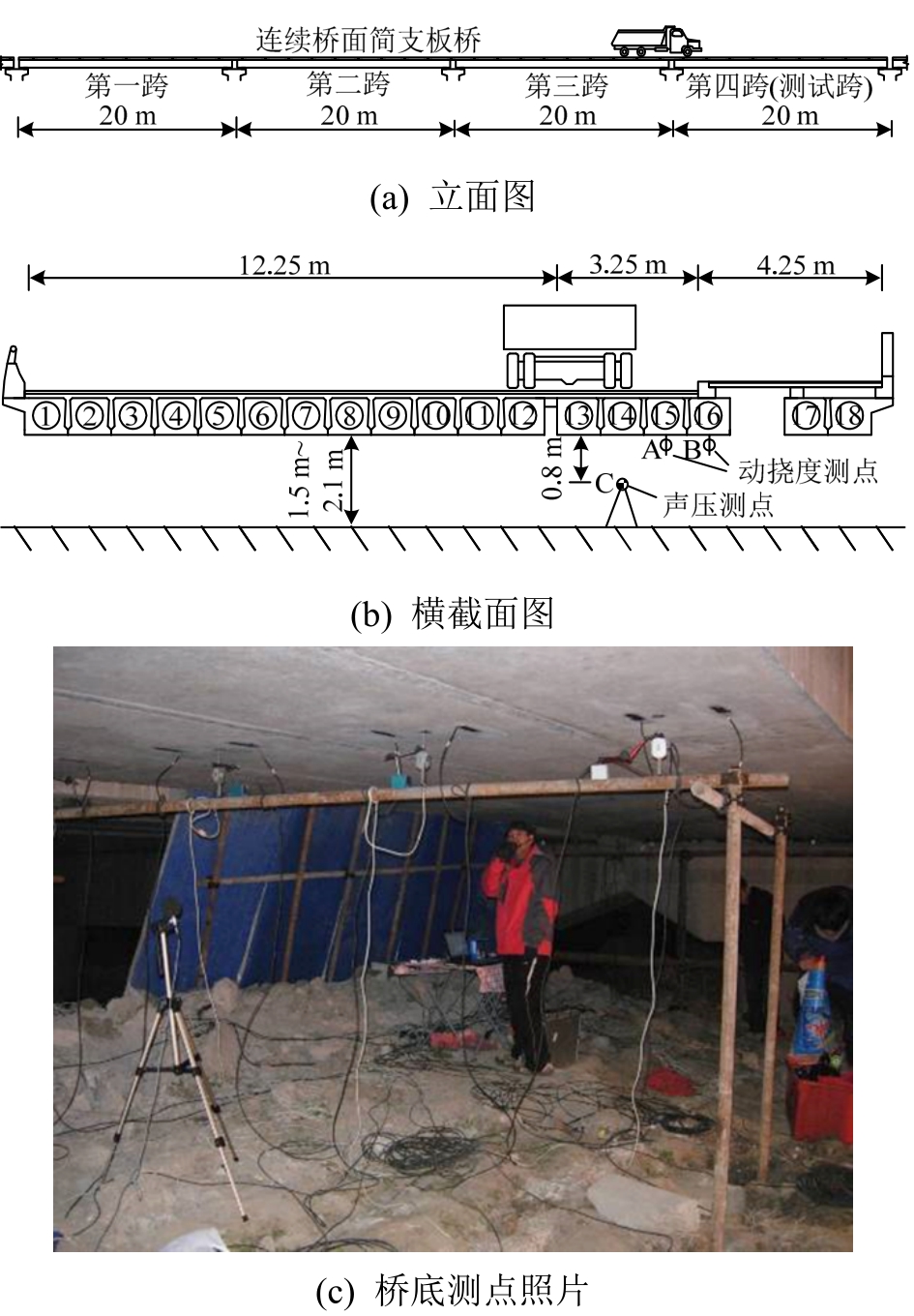
图5 铰接板桥交通振动与噪声实验
Fig.5 Experiment of vibration and sound radiation of hinged-jointed slab bridge
实验车辆的参数见表1。桥梁由18块1 m宽的预制空心梁板组成,每块梁板的参数如表2所示。在该连续桥面简支梁中,桥面板与主梁端部之间设置了20 cm的脱粘段,桥面连续段长度为44 cm,从而降低了简支梁之间的连接刚度[17],由此算得第四跨端部的边界弹簧刚度KA、KB(图1(b))见表2,其中B端有伸缩缝,所以KB为零。桥的阻尼采用瑞雷阻尼,第1阶、2阶振型对应的阻尼比取0.02[18]。
3.1 振动分析
按照本文第1节提出的算法,对上述载重车辆通过桥梁的全过程进行车桥耦合振动分析。首先建立铰接板桥的有限元模型,因为17号、18号梁与其他梁之间的横向联系弱,所以有限元模型只考虑1号~16号梁。每根梁纵向分成40个梁单元,每个单元长 0.5 m,根据第2节的讨论,由此获得的振动位移可以反映100 Hz以下的声辐射。车轮力在各梁的分布则用1.1节方法,引入荷载的横向分布影响线计算,图6为1号~8号梁板的横向分布影响线,由铰接板梁法得到,9号~16号梁板则由对称性得到。
表2 桥梁板的计算参数
Table 2 Parameters of single bridge girder


图6 荷载的横向分布影响线
Fig.6 Influence line of transverse load distribution
考虑车轮轮底与12号、14号梁板对应位置的位移协调条件,并取图4中的B类桥面粗糙度,通过迭代求得车轮动荷载,进一步确定各梁板分担的荷载,以及由此产生的动挠度。图7为汽车中轮运动到第四跨跨中时的动挠度分布。图8为跨中动挠度的计算时程,图9为实测动挠度,两者形态相似,最大计算挠度比实测挠度大15%,表明本文算法可以比较准确的反映铰接板桥的动挠度。产生误差的原因在于:① 计算模型的刚度略小于实际结构的刚度;② 机电百分表跟随桥梁变形的性能不佳,在峰值挠度测试时存在滑脱现象。
因为声辐射与桥面板的振动直接相关,所以绘制本桥 6、10、14号梁板的跨中振动速度如图 10所示,其卓越频率为4.8 Hz,反映了桥梁的一阶自振频率计算值。
3.2 噪声分析
噪声分析采用第2节方法,铰接板桥的声学边界元网格如图 11所示,采用三角形单元,相比振动分析,增加了人行道板和17号、18号板,以及实际桥底存在的挡板,以考虑它们的遮挡与反射作用。单元最长边为0.493 m,可以反映的声辐射频率上限为115 Hz。
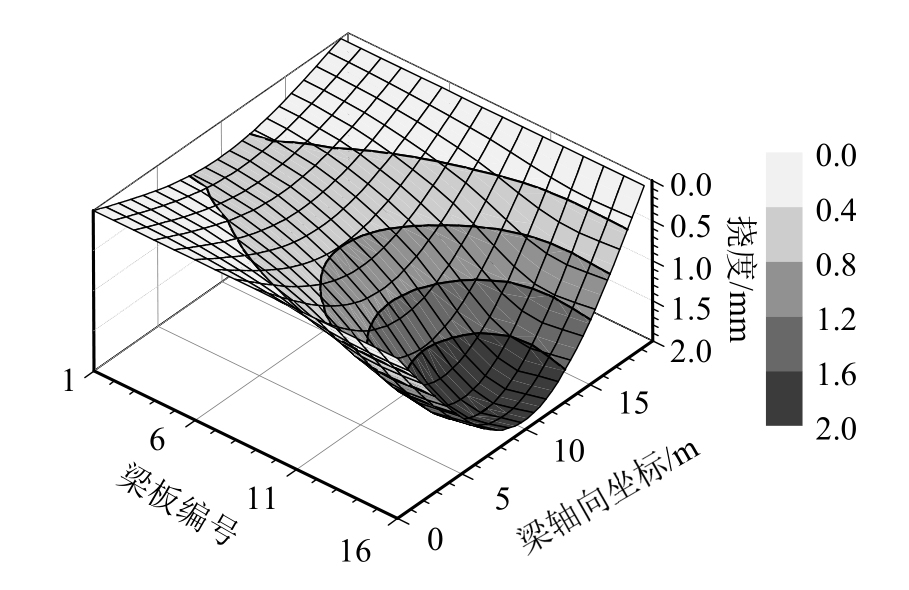
图7 第四跨动挠度
Fig.7 Dynamic deflection of fourth span of bridge

图8 第四跨跨中挠度计算值
Fig.8 Calculated middle-span deflection of fourth span
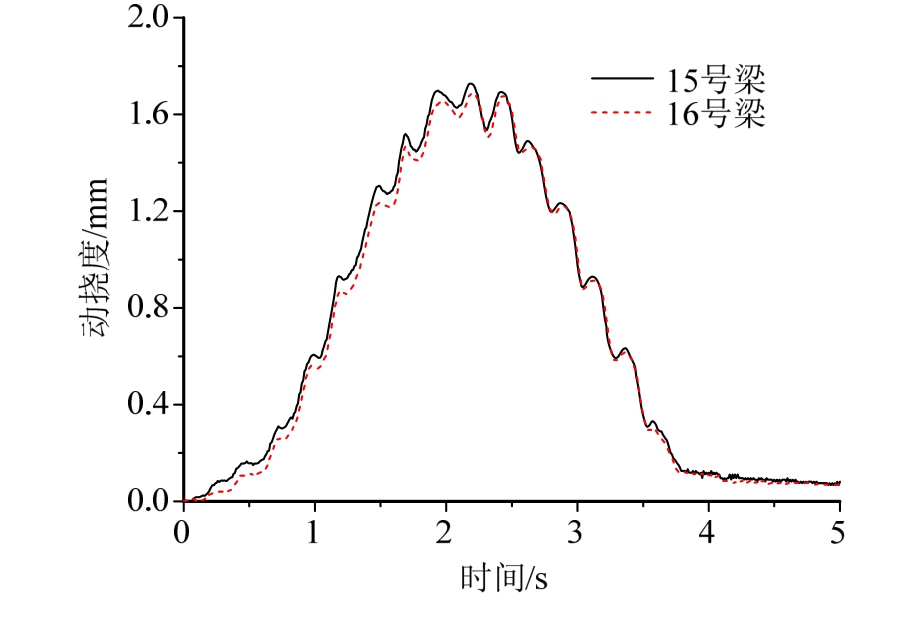
图9 跨中动挠度实测值
Fig.9 Measured middle-span deflection of fourth span
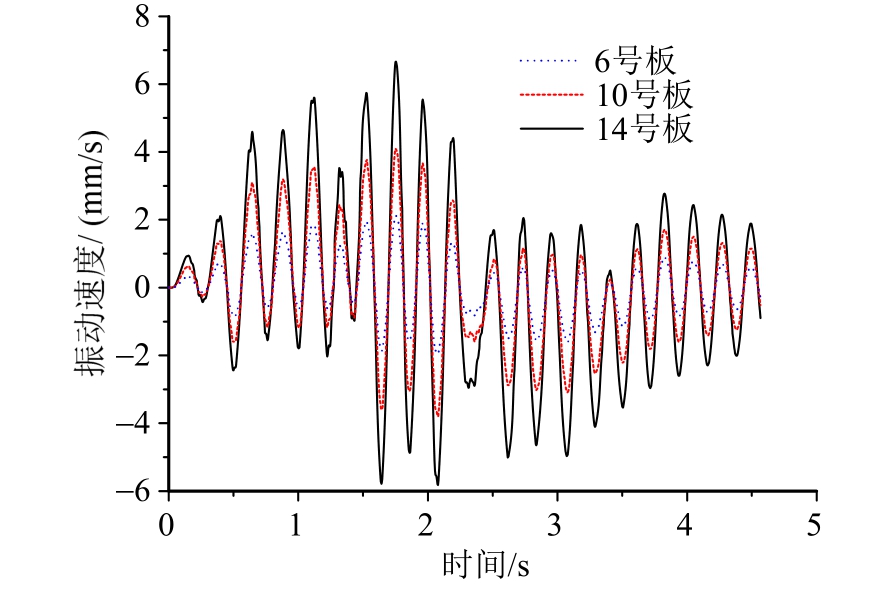
图10 跨中速度计算值
Fig.10 Calculated middle-span velocity of fourth span

图11 桥梁声辐射计算的边界元网格图
Fig.11 BEM grid for calculation of bridge sound radiation
将3.1节振动分析得到的动挠度作为输入量代入声学边界元计算中,可以获得桥梁周边任一点的声压,以图5中的声压测点C为例,载重车经过铰接板桥时的声压时程如图 12所示,边界元计算结果与实测基本一致。
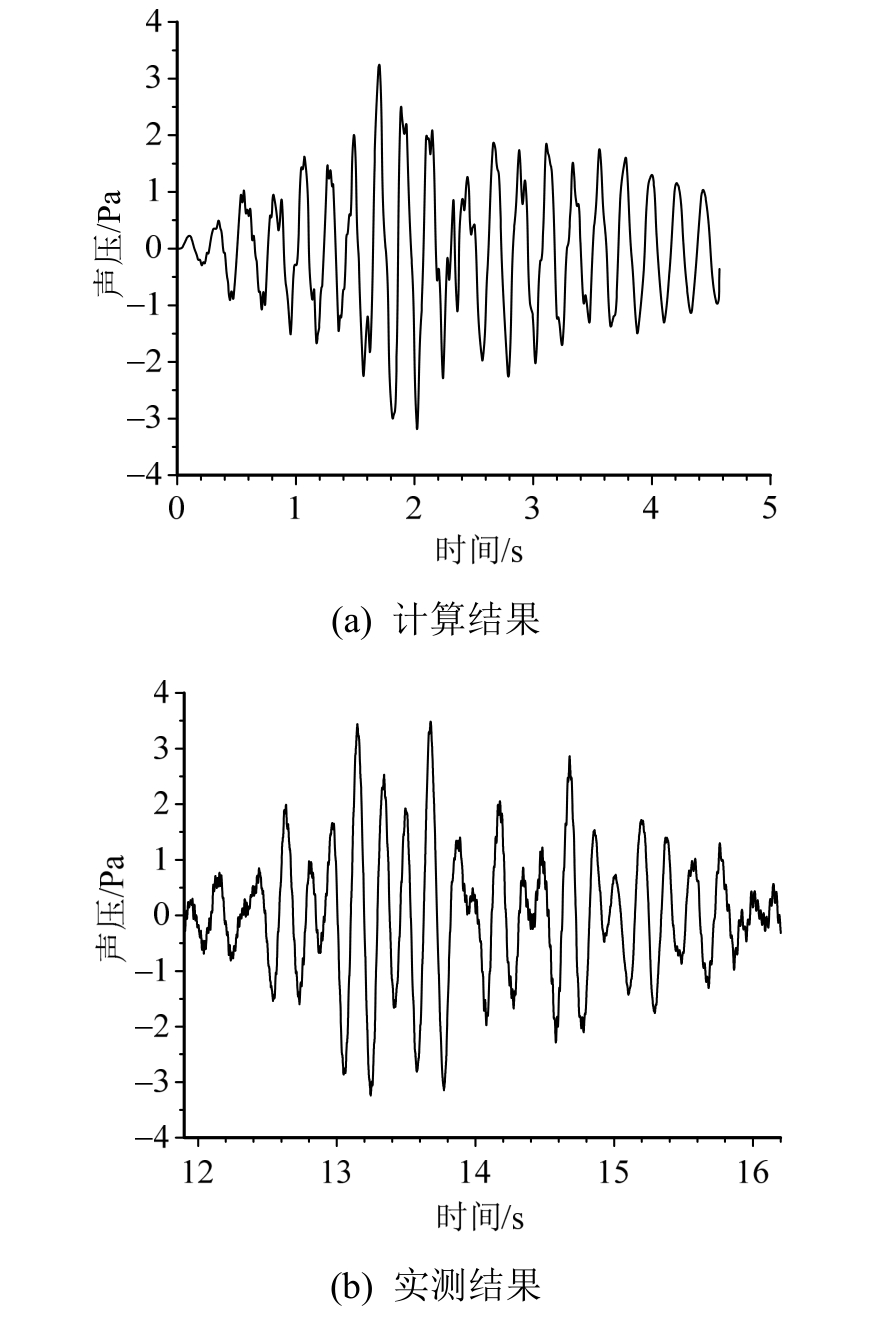
图12 桥下C点的声压时程
Fig.12 History of sound pressure of point C under bridge
对测点C的声压进行频谱分析,因为该声压时程并不是一个稳态过程,所以需要采用非稳态的信号处理方法,比如小波变换等。这里用Morlet小波变换[23]对图 12所示的声压时程进行了频谱分析,结果如图 13所示。计算声压小波变换后的峰值频率为4.8 Hz,与3.1节振动分析得到的桥梁一阶频率相同,这说明通过声压测试也可以获得桥梁的自振频率。实测声压小波变换后的卓越频率为5.5 Hz,略大于计算值,原因在于实际结构比计算模型的刚度大,因此卓越频率也偏大,这一点也在前述振动分析得到了印证。图 13中因为计算与实测采用的小波变换时域长度不同(都包含车辆通过时段),所以小波变换系数不同。
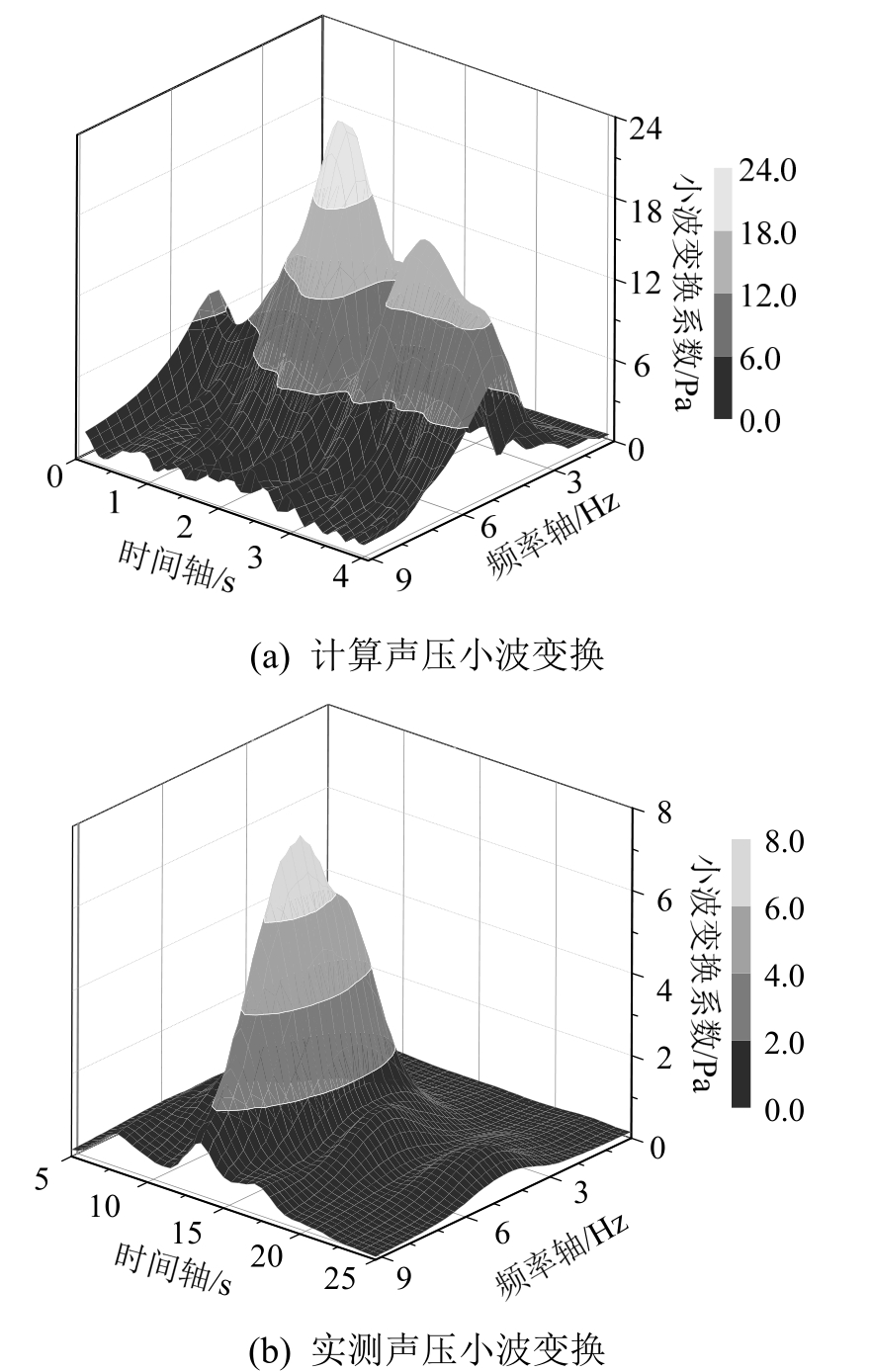
图13 桥下C点声压小波变换后的频谱
Fig.13 Spectrum of sound pressure of point C under bridge after wavelet transformation
图 14是桥梁周边的计算声场分布,选取图 5中第四跨跨中截面,时间点是载重车行驶到第四跨跨中时,此时也是该截面声压最大的时刻。结果表明:① 桥下声压比桥上大,原因在于桥下地面的反射较强;② 最大声压(3.6 Pa)在12号梁板下,该梁板为车轮作用的两块梁板(12号、14号梁板)之一,其振动最显著;③ 靠近桥梁纵向中心线位置的结构噪声较大。需要说明的是,上述声压仅来自桥梁结构的声辐射,不考虑汽车和路面噪声。
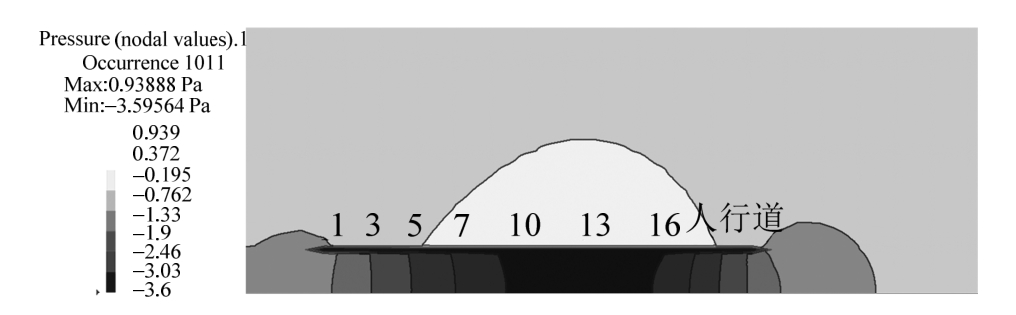
图14 实桥结构声辐射的声场分布
Fig.14 Structure-borne sound field of practical bridge
3.3 结构噪声的影响因素分析
下面以桥面粗糙度、梁板间横向联系、桥面连续结构为例,探讨铰接板桥结构噪声的影响因素。
1) 粗糙度的影响。
分别采用图3、图4中的A、B、C类桥面粗糙度,对应ISO标准的光滑、极好和次好路面,计算载重车辆经过时桥梁结构的声辐射,结果如图 15所示。

图15 桥面粗糙度对振动与噪声的影响
Fig.15 Effect of bridge roughness on vibration and sound
图 15表明,桥面粗糙度越大,车辆经过时桥梁挠度和速度波动越大,声压也越高。因此,减小桥面粗糙度是降低铰接板桥结构噪声的有效途径。
2) 横向联系的影响。
横向联系是铰接板桥的薄弱部位,也是衡量铰接板桥性能的重要指标。横向联系越强,车轮荷载由各块梁板分担得越均匀,反之,车轮荷载仅由车轮附近的梁板承担。以下考虑两种横向联系情况,第一种是图6所示的实际荷载横向分布影响线,第二种是极好的横向联系情况,即假设荷载均匀分布在各块梁板上,此时荷载的横向分布影响线竖标相同。计算得到这两种情况下各梁板的挠度、速度和2号、14号梁板下(测点C)的声压,如图16所示。

图16 桥梁横向联系对振动与噪声的影响
Fig.16 Effect of bridge lateral joint on vibration and sound
图 16表明,桥梁横向联系越好,横向各梁板间振动的差别越小,桥下各处的声压差别也越小。图17为横向联系极好时的桥梁周边声场,与图14中实桥声场比较,图17中的最大声压较小(3.02 Pa),桥下各处的声压差别也较小。这说明增强各梁板之间的横向联系,可以减小桥梁结构的声辐射。反之,当桥梁横向联系比较弱时,或者横向联系受损时,桥下的最大声压会增大,桥下横向的声压差异也会增大。
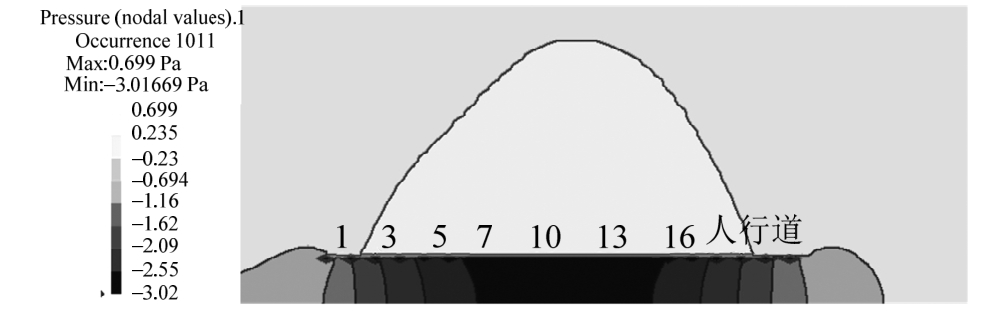
图17 横向联系极好时铰接板声辐射的声压分布
Fig.17 Structure-borne sound pressure of hinged-jointed slab bridge with perfect lateral joint
3) 桥梁伸缩缝的影响。
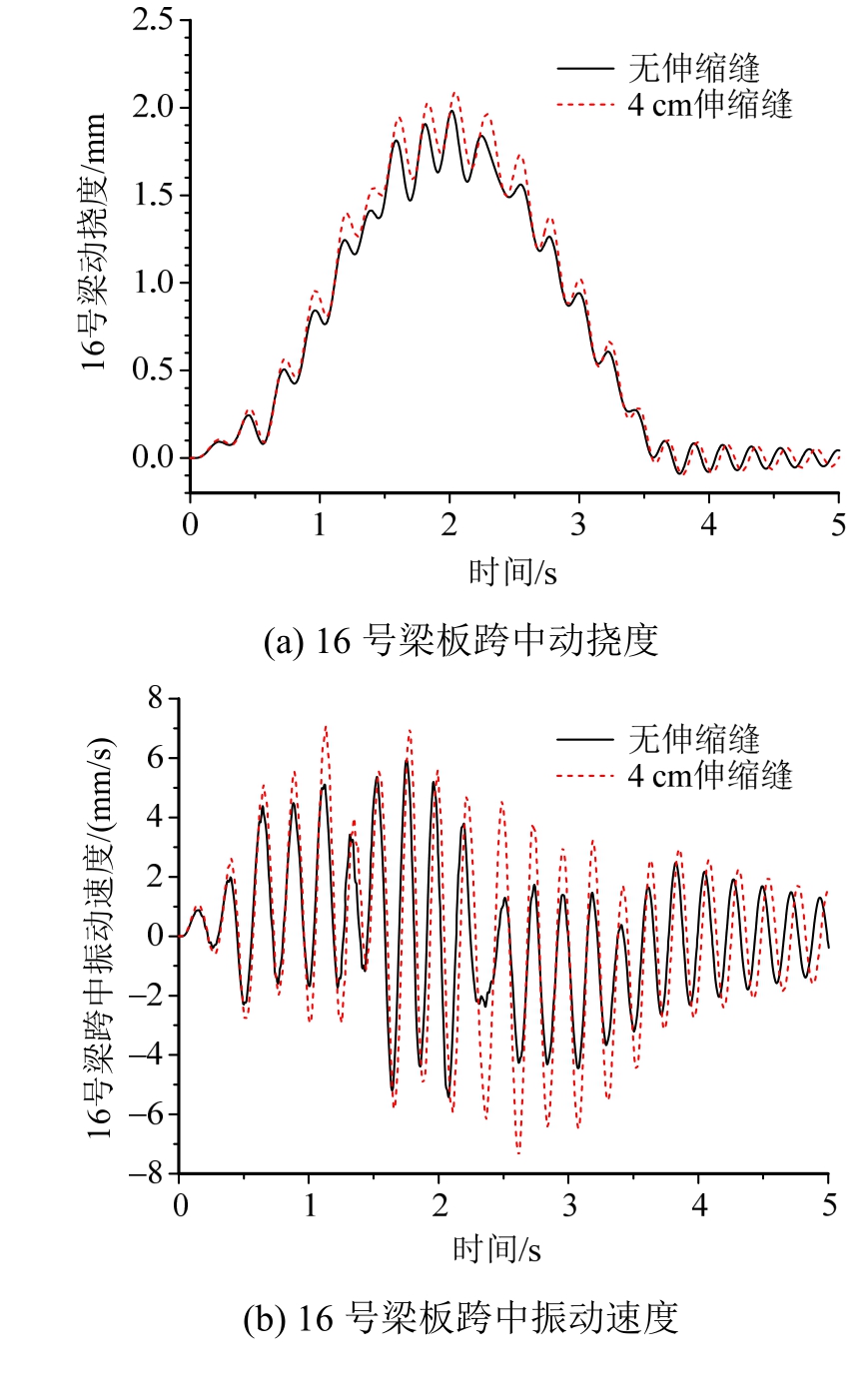
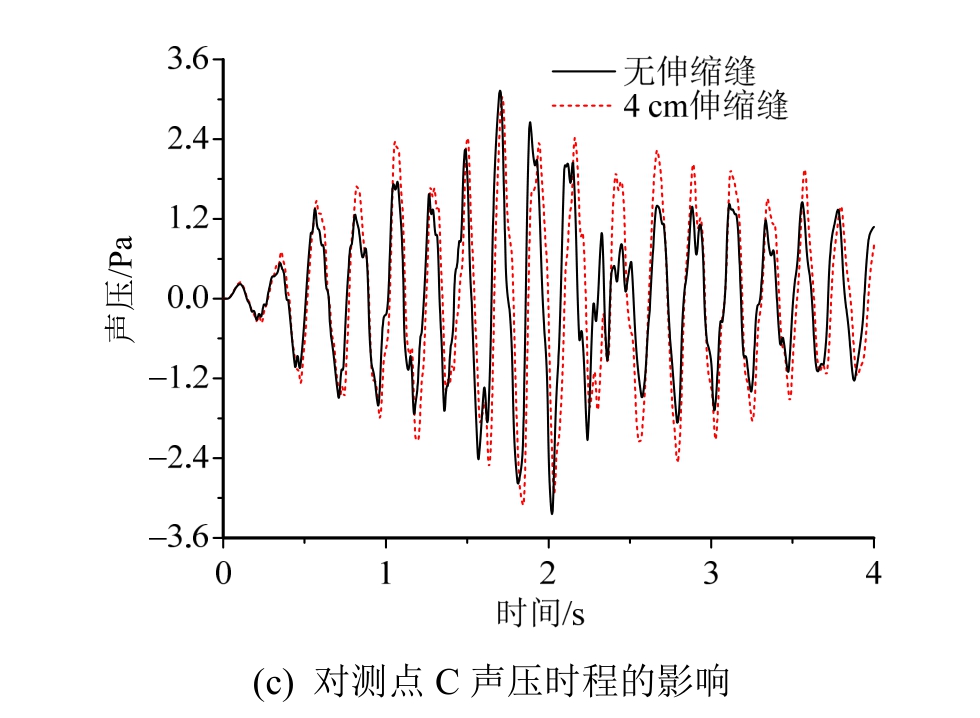
图18 伸缩缝跳车对振动与噪声的影响
Fig.18 Effect of bump in joint on vibration and sound
铰接板桥的两端可以采用伸缩缝,也可以取消伸缩缝,采用连续桥面。下面以端部有 4 cm宽度伸缩缝的铰接板桥与连续桥面的铰接板桥为例,比较两者在载重车经过时的结构噪声,结果如图 18所示。结果表明,取消伸缩缝,采用连续桥面后,桥梁的结构振动减小了;结构噪声整体上也减小了,但是声压的峰值差别不大,原因在于车辆的伸缩缝跳车主要在上、下桥时刻,采用连续桥面可以降低此时的桥梁结构噪声,而当车辆位于桥梁跨中时,伸缩缝跳车的影响已经减弱[24],因此对声压峰值影响不大。
4 结论
针对铰接板桥,提出了引入荷载横向分布的有限元车桥耦合振动算法,结合边界元结构声辐射计算,获得了该类桥梁交通振动与噪声的分析方法,并通过了实验验证。实桥计算和参数分析结果如下:
(1) 铰接板桥结构噪声的频谱分析需采用小波变换等非稳态信号处理方法,由此可得桥梁声辐射的卓越频率,且反映了桥梁的自振频率。因此,本文获得了一种确定桥梁自振频率的声学方法。
(2) 桥下空间由于声波的反射,结构噪声比桥上空间大,最大声压往往位于靠近桥梁中心线的轮胎作用梁板下方。桥梁结构噪声的控制应重视桥下空间。
(3) 增强各梁板之间的横向联系,可以减小桥梁结构的声辐射;当桥梁的横向联系受损时,桥下的最大声压会增大,横向的声压差异也会增大。
(4) 用连续桥面代替伸缩缝、减小桥面粗糙度,都可以有效降低铰接板桥在车辆作用下的结构噪声。
参考文献:
[1]Naoko Nagai, Matsumoto Matsumoto.Process and emergence on the effects of infrasonic and low frequency noise on inhabitants [J].Journal of Low Frequency and Vibration, 1989, 8(3): 87―98.
[2]Persson K, Rylande R, Benton S, et al.Effects on performance and work quality due to low frequency ventilation noise [J].Journal of Low Frequency and Vibration, 1997, 205(4): 467―474.
[3]Marek Foglar, Jakub G?ringer.Influence of the structural arrangement of bridges on the noise induced by traffic[J].Engineering Structures, 2013, 56(20): 642―655.
[4]Goromaru H, Shiraishi K, Hara H, et al.Analysis of low frequency sound radiating from simple girder highway bridge by a moving vehicle [J].Journal of Construction Management and Engineering, 1991, 427(VI-14): 133―142.
[5]Bewes O G, Thompson D J, Jones C J C, et al.Calculation of noise from railway bridges and viaducts:Experimental validation of a rapid calculation model [J].Journal of Sound and Vibration, 2006, 293(3/4/5): 933―943.
[6]Au F T K, Wang M F.Sound radiation from forced vibration of rectangular orthotropic plates under moving loads [J].Journal of Sound and Vibration, 2005,281(3/4/5): 1057―1075.
[7]Zhang He, Xie Xu, Jiang Jiqing, et al.Assessment on transient sound radiation of a vibrating steel bridge due to traffic loading [J].Journal of Sound and Vibration,2015, 336: 132―149.
[8]韩江龙, 吴定俊, 李奇.城市轨道交通槽型梁结构噪声计算与分析[J].工程力学, 2013, 30(2): 190―195,202.Han Jianglong, Wu Dingjun, Li Qi.Calculation and analysis of structure-borne noise from urban rail transit trough girders [J].Engineering Mechanics, 2013, 30(2):190―195, 202.(in Chinese)
[9]宋晓东, 李奇, 吴定俊.多跨简支梁桥低频噪声预测及空间分布研究[J].工程力学, 2017, 34(3): 22―28..Song Xiaodong, Li Qi, Wu Dingjun.Prediction and spatial distribution of low-frequency noise radiated from the multi-span bridge [J].Engineering Mechanics, 2017,34(3): 22―28.(in Chinese)
[10]Li Xiaozhen, Liu Quanmin, Pei Shiling, et al.Structure-borne noise of railway composite bridge:Numerical simulation and experimental validation [J].Journal of Sound and Vibration, 2015, 353: 378―394.
[11]Zhang X, Li X Z, Hao H, et al.A case study of interior low-frequency noise from box-shaped bridge girders induced by running trains: Its mechanism, prediction and countermeasures [J].Journal of Sound and Vibration,2016, 367(8): 129―144.
[12]桂水荣,刘律, 万水, 等.简化建模方法对空心板桥力学性能的影响[J].公路交通科技, 2014, 31(12): 50―66.Gui Shuirong, Liu Lü, Wan Shui, et al.Effect of simplified modeling method on mechanical performance of hollow slab bridge [J].Journal of Highway and Transportation Research and Denelopment, 2014, 31(12):50―57, 66.(in Chinese)
[13]陈记豪, 赵顺波, 姚继涛.既有预应力空心板桥加宽设计的荷载横向分布计算方法[J].工程力学, 2012,29(9): 265―271.Chen Jihao, Zhao Shunbo, Yao Jitao.Method for calculating vehicle load transverse distribution in widening design of existing PPCHS bridge [J].Engineering Mechanics, 2012, 29(9): 265―271.(in Chinese)
[14]王渠, 吴庆雄, 陈宝春.装配式空心板桥铰缝破坏模式试验研究[J].工程力学, 2014, 31(增刊): 115―120.Wang Qu, Wu Qingxiong, Chen Baochun.Experimental study on failure mode of hinged joint in assembly voided slab bridge [J].Engineering Mechanics, 2014, 31(Suppl):115―120.(in Chinese)
[15]丁勇, 黄奇, 谢旭, 等.载重汽车桥梁伸缩缝跳车动力荷载计算方法与影响因素分析[J].土木工程学报,2013, 46(7): 98―107.Ding Yong, Huang Qi, Xie Xu, et al.A computational method for the dynamic load in heavy-vehicle bumping at the bridge expansion joint and the analysis of influencing factors [J].China Civil Engineering Journal,2013, 46(7): 98―107.(in Chinese)
[16]Zienkiewicz O C, Taylor R L.The finite element method,ed 6th [M].London: McGraw-Hill, 2005.
[17]丁勇, 黄奇, 黄剑源.连续桥面简支梁桥静动力特性的理论分析方法研究[J].工程力学, 2015, 32(9): 100―110.Ding Yong, Huang Qi, Huang Jianyuan.Theoretical analysis for static and dynamic characteristics of multi-simple-span bridge with continuous deck [J].Engineering Mechanics, 2015, 32(9): 100―110.(in Chinese)
[18]Anil K Chopra.Dynamics of structures: theory and applications to earthquake engineering [M].2nd ed.Prentice Hall, 2004.
[19]丁勇, 布占宇, 谢旭.等.考虑桥面板振动的桥梁结构低频噪声分析[J].土木建筑与环境工程, 2011, 33(2):57―64, 69.Ding Yong, Bu Zhanyu, Xie Xu, et al.Analysis of low-frequency noise considering the vibration of bridge deck [J].Journal of Civil, Architectural and Environmental Engineering, 2011, 33(2): 57―64, 69.(in Chinese)
[20]Au F T K, Cheng Y S, Cheung Y K.Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles [J].Computers and Structures, 2001, 79(8): 853―872.
[21]ISO 8608, Mechanical vibration-road surface profilesreporting of measured data [M].Geneve Switzerland:International Organization for Standardization, 1995.
[22]TW Wu.Boundary element acoustics: fundamentals and computer codes [M].Southampton: WIT Press, 2000:161―193.
[23]Torrence C, Compo G P.A practical guide to wavelet analysis [J].Bulletin of the American Meteorological Society, 1998, 79(1): 61―78.
[24]Ding Y, Zhang W, Au F T K.Effect of dynamic impact at modular bridge expansion joints on bridge design [J].Engineering Structures, 2016, 127(22): 645―662.