接触非线性作为一种主要的非线性现象，广泛存在于各个工程学科领域，比如水利工程中拱坝橫缝两侧的坝体、机械工程中金属成形时的金属与模具之间的挤压、岩土工程中地下结构与围岩相互作用、生物力学工程中不同组件之间的连接等等[1―2]。接触问题的研究历史已有百余年，至今仍然是力学界、数学界和工程界的研究热点[3-6]，这既说明了接触问题的重要性，也反映了接触问题的求解难度之大。
接触问题的非线性主要来自两方面：一方面是接触区域在求解之前是未知的，需要根据外荷载和结构接触面特性共同确定；另一方面是接触约束条件的非线性，主要包括法向的不嵌入条件以及切向有摩擦时的摩擦准则[7]。根据约束条件施加方式的不同，接触问题的求解有多种方法，主要的方法有罚函数法和Lagrange乘子法两大类[8-10]。
罚函数方法的基本原理是通过引入罚因子来满足接触边界上的约束条件[1]。比如在工程界常采用的接触单元法属于罚函数方法的一种具体应用形式[11-14]。罚函数方法的优点是不改变原问题的求解规模，实现简便。但是由于罚因子的存在，使得罚函数方法无法避免求解过程中精度和难度的矛盾：当罚因子取值较大时，接触约束条件满足的更为精确，解的精度高，但是方程的病态性更为严重，求解难度增大，效率降低；反之，罚因子取值较小时，求解效率较高，但会发生较大的嵌入量，即接触条件并不能精确满足，从而降低了结果的精度。对于大型复杂结构的接触求解，如何选择罚因子一直是一个让人困扰的问题[15]。
Lagrange乘子法通过引入Lagrange乘子将带约束条件的优化问题转化成无约束的优化问题[16]。Lagrange乘子法同样有着广泛应用，比如 Bathe等[17-18]早在20世纪80年代就将Lagrange乘子法植入到专业有限元软件Adina中用于求解平面及三维接触问题，Wriggers、Laursen等提出的直接约束法、非匹配网格法以及国内的陈万吉、李同春等[1,19-21]应用的有限元混合法本质上也属于Lagrange乘子法类的接触求解算法。Lagrange乘子类方法的优点是能够精确反映接触条件，从而保证计算结果的精度。但传统的Lagrange乘子类方法，不仅增加了求解未知量的总数，且系数阵中零对角元素的存在使得用其求解大型结构的接触问题困难重重[1,7]；直接约束法虽然省去了 Lagrange乘子的求解，但是在每个迭代步中均需对接触状态进行更新，即需要更新整体系统的系数阵，同样不适于求解大型接触问题[22]；而有限元混合法虽然利用了接触区域局部化的优势，但是在计算过程中可能需要大量的求逆运算来生成柔度阵，这对计算机的存储能力提出了较高的要求，并且可能出现计算不收敛的问题[21]。
因此，为了求解实际工程中的大规模结构的接触问题，急需发展一种对存储量要求小、求解精度高的算法。本文从传统的Lagrange乘子法理论出发，通过降维解耦处理，推导得出了一种存储量需求小、易于实现并行的迭代求解算法，非常适合求解大规模结构的接触问题。
本文首先介绍了接触问题的基本概念，然后阐述了分步接触算法的基本原理，并通过经典 Hertz接触算例和简单的双缝坝算例验证了分步算法的正确性，最后对考虑接触非线性的穿黄隧洞整体模型进行了动力分析求解，进一步说明了本文的算法对于求解大规模结构接触问题的有效性。
1 接触问题的基本概念
一般情况下，物体间的接触关系可由图1表示。
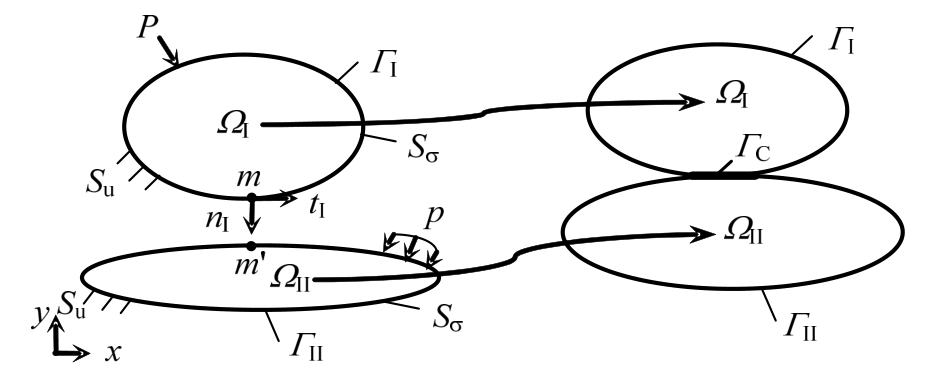
图1 弹性体接触示意图
Fig.1 Sketch of elastic contact bodies
物体I和II的内部区域为?I和?II，外部边界为IΓ和ΓII，在给定力边界Sσ和给定位移边界Su作用下，两个物体发生变形，具有共同的接触边界
。所谓不嵌入条件(也称为非穿透条件)是指一个物体内的点不能同时属于另外一个物体，该条件由数学语言表达如式(1)所示。不嵌入条件的物理意义清晰明确，但在数学上却难以处理。
接触问题的非线性除由于接触区域事先未知引起的以外，更主要的是接触约束条件所导致的，具体包括法向非嵌入条件、考虑摩擦时的切向滑动摩擦以及静摩擦状态改变所带来的相关物理量突变。根据接触体受力和位移约束条件的不同，接触状态可分为静接触和动接触两大类，不同接触状态对应的约束条件如表1所示[23]。
表1 接触约束条件
Table 1 Conditions of contact constraint
表中变量τ和R代表切向、法向接触力，其中下标I、II分别表示主、从接触体；sμ和dμ分别为静、动摩擦系数；nI和tI表示主接触体的外法向和接触面的切向方向；D0代表两个接触体之间的初始间隙。
2 分步接触算法的基本原理
2.1 基本原理
传统 Lagrange乘子法得到的接触问题的控制方程为[1]：
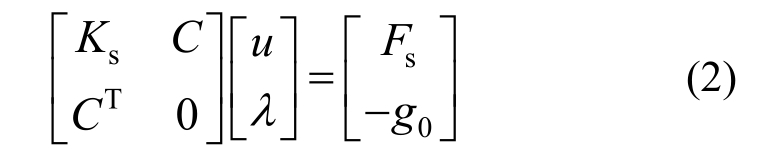
式中：Ks为结构的刚度阵；
为接触约束矩阵，若采用节点对节点的接触面离散形式则有
其中ni为主接触体上的外法向向量，对于三维接触问题
当接触体中有一个为刚体时，Ci退化成
为整个系统的外荷载，包括主、从接触体上的体力和面力。
为简化推导，假定两个接触体之间为光滑接触。对于如式(2)所述的问题，通常采用迭代法进行求解，当忽略材料和几何非线性时，式(2)可改写成如式(3)所示的增量形式：
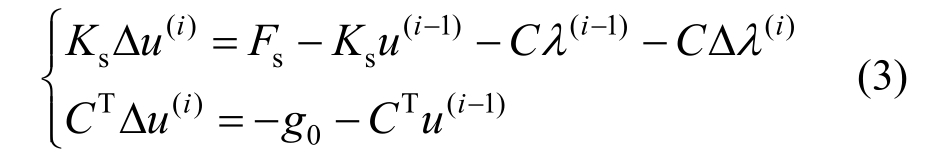
进一步将式(3)中的未知量
写成
的形式，则式(3)可以改写成式(4a)和式(4b)联立的等效形式：
式(4a)中的未知量
表征的是结构中所有节点不考虑接触的影响所产生的位移增量，故称为分步接触算法的控制方程；式(4b)中的未知量
是与接触单元相关的节点因接触力的影响而产生的位移增量，
为上一个迭代步结束时在系统不平衡力作用下接触体之间的间隙值
故式(4b)称为分步接触算法的约束方程。
式(4a)所示的分步接触算法控制方程，其物理含义是力系平衡，其求解规模同主、从接触体上所有节点的位移自由度大小，并且其系数矩阵具有对称正定的特性，故可利用预处理共轭梯度(PCG)方法等成熟高效的解法进行方程组的求解，因而不必形成并存储结构的整体刚度阵，可直接通过装配各单元的节点力向量形成整体结构的节点力向量进行求解，易于实现并行化。式(4b)所示的约束方程的物理意义是由接触条件构成的约束方程，其计算规模等同于传统Lagrange乘子法，利用2.2节的方法降低其求解规模后，将使得分步接触算法非常适合用于求解大规模结构的接触问题。
2.2 算法的优化
在实际工程中，接触通常发生在较小的局部范围内，比如拱坝的横缝与庞大坝体相比仅为其中的一小部分，利用这一特点，可以对分步接触算法的约束方程式(4b)进行降维优化处理。
约束方程式(4b)中的矩阵C可以按照是否可能发生接触写成分块的形式：
式中，首尾两个“0”块阵分别与主、从接触体上与接触区域无关的自由度相对应，中间的CC是与接触区域节点自由度相对应的接触约束阵。
同理，将结构的刚度阵也写成对应的分块形式：
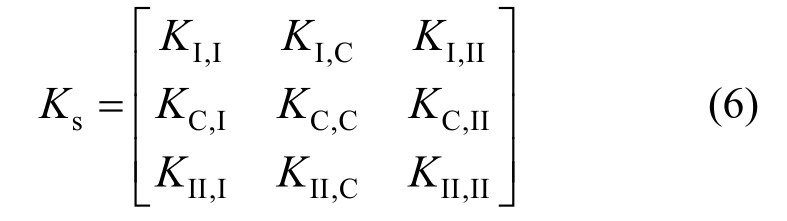
结合考虑式(5)零元素的分布特点，约束方程式(4b)可以写成式(7)的形式：
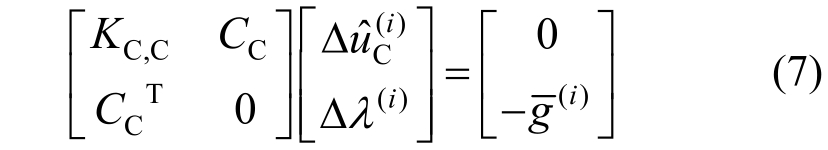
式中，KC,C和CC的规模仅与接触区域的大小有关，因此式(7)的求解规模与式(4b)相比已大为降低。
表示的是整体结构在接触节点自由度上的凝聚刚度。为进一步降低计算量，本文直接利用与接触节点相关联的接触单元所集成的局部刚度阵KCL代替KC,C，同时在控制方程式(4a)的接触力项
引入缩放因子ω，用以加快收敛速度。至此，可得优化后的分步接触算法如下：
上式中的KCL由接触单元直接集成，其维度大小由发生接触的节点数决定，并且可以进一步简化为仅保留KCL中对角线上的元素，对不同接触对进行解耦，从而将式(8b)解耦成关于每一个接触对的约束方程，便于运用并行技术高效快速求解。
至此可以得到分步接触算法迭代求解接触问题的一般步骤为：
1) 利用控制方程式(8a)求出
并更新位移量
2) 计算接触对的当前间隙值
据此判断接触状态，并对式(8b)中的系数阵进行相应的修改，求出
3) 利用
更新接触力，如果出现拉应力，则令接触力为零并修改接触状态为分离；
4) 判断是否收敛，如果式(8a)和式(8b)的解均满足收敛准则，则进入下一个时步，否则重新进入步骤1) 进行下一个迭代步。
2.3 缩放因子的确定
通过对比分步接触算法的原始式(4a)、式(4b)和优化后的式(8a)、式(8b)，可以得出缩放因子的理论最优值为：
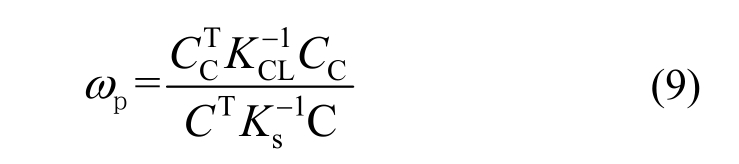
因KCL是Ks中的一部分，故可推知最优缩放因子的取值为0～1之间。下面以图2所示的一维杆静力接触问题为例来研究与说明缩放因子对接触迭代过程收敛性的影响。
图2 1D杆接触示意图
Fig.2 1D bar contact sketch
易知图2的解析解为：u1=u4=0.05，u2=u3=0.1，fc=-0.05。由式(9)计算的ωp=0.5，因此令ω=0.5，利用式(8a)、式(8b)和2.2节所述的迭代步骤进行求解，迭代收敛过程如表2所示。表2中方程的2范数是指方程未知量结果的2范数。采用不同的缩放因子，接触迭代达到给定的收敛标准所需要的迭代次数如表3所示。可以看出：缩放因子取为理论最优值时，收敛速度最快；当缩放因子的取值介于 0到理论最优值时，结果是收敛的，且缩放因子与理论最优值相差越小，收敛越快；当缩放因子大于理论最优值时，结果发散。
表2 缩放因子0.5时的迭代求解过程
Table 2 Iteration solving process for scaling factor 0.5
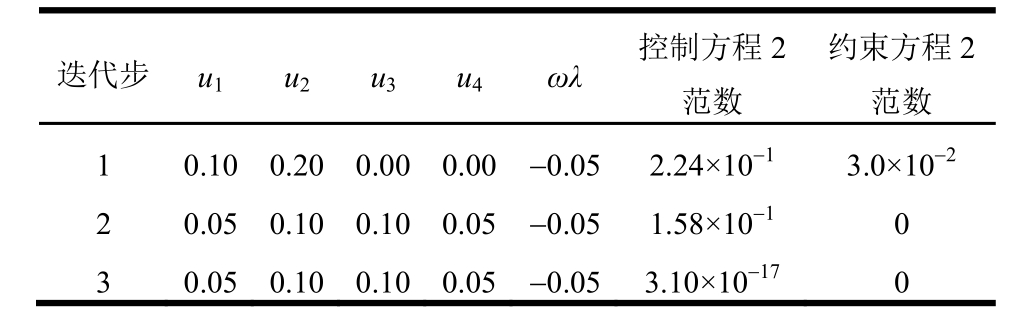
表3 不同缩放因子的收敛情况
Table 3 Convergence procedure for different scaling factors
对于实际工程接触问题，最优缩放因子不易解析求解，可以首先预估一个介于0和1之间的值，然后在迭代过程中，根据约束方程的收敛情况对缩放因子进行自动调整。比如当求得的接触力增量有放大发散的趋势时，减小缩放因子取值；当接触力增量保持持续减小，但减小的速度较慢时，可适当增大缩放因子取值，这样既保证了求解的收敛性，也可以得到较快的收敛速度。对于分步接触算法求解复杂情形接触问题的正确性，将在下一节通过更多的数值算例予以证明。
3 算例验证
3.1 Hertz接触算例
Hertz接触是最经典的接触问题之一，利用弹性力学法可求得理论解析解。在此考虑弹性圆柱和刚性平面的Hertz静力接触问题，计算模型与计算条件如图3(a)所示，利用分步接触算法对该问题进行数值求解，有限元网格模型如图3(b)所示。
图3 Hertz静力接触问题示意图
Fig.3 Sketch of Hertz static contact problem
不同外荷载P所对应的接触应力分布结果如图4所示，可以看出：本文的数值结果与解析解吻合较好。
图4 不同外荷载对应的接触应力分布图
Fig.4 Contact stress distribution under different pressure
3.2 平面双缝坝静力接触算例
混凝土坝工程中通常需要设置变形缝，以避免大体积混凝土结构产生收缩裂缝。本小节采用分步接触算法所求解的双缝静力接触问题的模型及相关参数如图5所示，模型中存在两条接触缝，分别为1号变形缝与2号变形缝。图中集中荷载F的变化规律如式(10)所示。需要说明的是，此处采用静力分级加载反映F的变化，不考虑动力效应，时间步仅对应计算加载步。
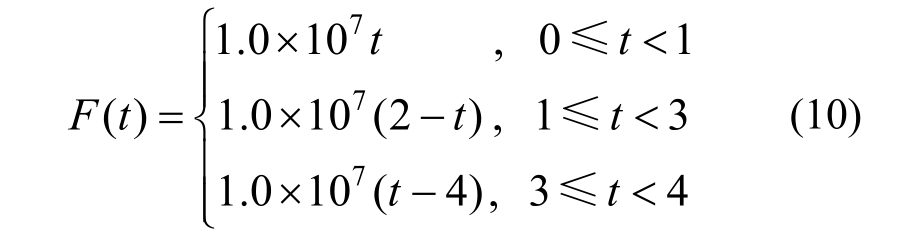
图5 双缝坝有限元模型及材料参数
Fig.5 FE model of two-joints dam and material parameters
有限元计算采用 4节点平面应变单元进行模拟。接触点对的水平位移计算结果见图 6，接触应力结果见图7。从图中结果可以看出，2.0 s时刻之前1点的接触对处于接触状态，这之后为分离状态；2点处的接触对在 2.0 s之前一直处于接触状态，2.0 s时刻发生分离，此后重新保持接触状态，但接触应力比前半段时程要小的多。计算结果与文献[20]的结果吻合较好，表明本文分步接触算法可有效求解工程中的横缝接触问题。
图6 两缝顶端处不同接触体的水平位移结果
Fig.6 Horizontal displacements of different contact points on the top of the two joints
图7 两缝顶端处接触应力结果
Fig.7 Contact stress on the top of the two joints
4 工程应用
4.1 工程概况
南水北调中线工程的穿黄隧洞采用双层衬砌，外衬为装配式钢筋混凝土管片结构(C50)，内衬为现浇预应力钢筋混凝土结构(C40)。横断面内车道平台以下内外衬粘结良好、共同受力；而其他部分的内外衬间因设防排水垫层(弹性模量非常小)，而使得内外衬独立受力。为模拟内外衬之间的独立受力特性，故采用本文提出的分步接触算法进行求解，各部分之间的接触关系见图8。
图8 双层衬砌有限元模型
Fig.8 Finite element model of double-layer lining
穿黄隧洞整体三维有限元模型包括引水隧洞、竖井及其围岩、围土等，几何尺寸约为4274 m×110 m×100 m(见图9)；节点总数约为5万，单元总数约为4万，共有2470对接触对。
图9 穿黄隧洞有限元模型
Fig.9 Finite element model of Yellow-River-Crossing tunnels
4.2 计算条件
计算采用刘晶波等学者提出的粘弹性人工边界来模拟无限地基，并通过在人工边界上施加等效力荷载来实现地震波的输入[24]。输入地震波为顺河向的剪切波，如图10所示，其加速度峰值为0.237g，同时考虑沿隧洞轴向地震波的行波效应，行波的行进速度为2000 m/s。
图10 地震波加速度时程
Fig.10 Time history of the earthquake acceleration
在进行动力分析之前，首先采用邓肯―张模型计算整体结构由自重产生的初始地应力，将此作为动力计算的初始状态。土体动力本构采用 Masing经验模型[25]，混凝土内外衬及竖井壁采用线弹性模型，具体材料参数详见相关文献[25]。
将分步接触算法与后差分时间积分算法[26]相结合，对考虑接触非线性的穿黄隧洞进行动力分析。为进一步提高计算效率，利用共享内存的OpenMP标准对计算程序实现了并行化。
4.3 计算结果
经计算分析可知，穿黄隧洞北岸竖井进水口部位的应力最为集中。表4为此处内衬内壁应力及内外衬接触应力的峰值列表。由表中结果可知：在同一断面上，内衬的拱底和两拱脚处(图8中4点、5点、6点)应力较大，这是由于隧洞内部车道平台的施作，使得车道平台下方的内外衬由独立受力变为共同受力，该处受力型式的改变导致明显的应力集中。而对于接触应力，两侧拱腰处接触应力较大，拱顶和拱脚处接触应力较小。进一步分析拱腰处的接触应力时程结果(见图11)可知，对于同一位置点，在整个地震过程中，其接触状态也会不断发生接触与分离的转变。
表4 内衬应力及接触应力峰值 /kPa
Table 4 Peak stress of the internal lining and the contact area
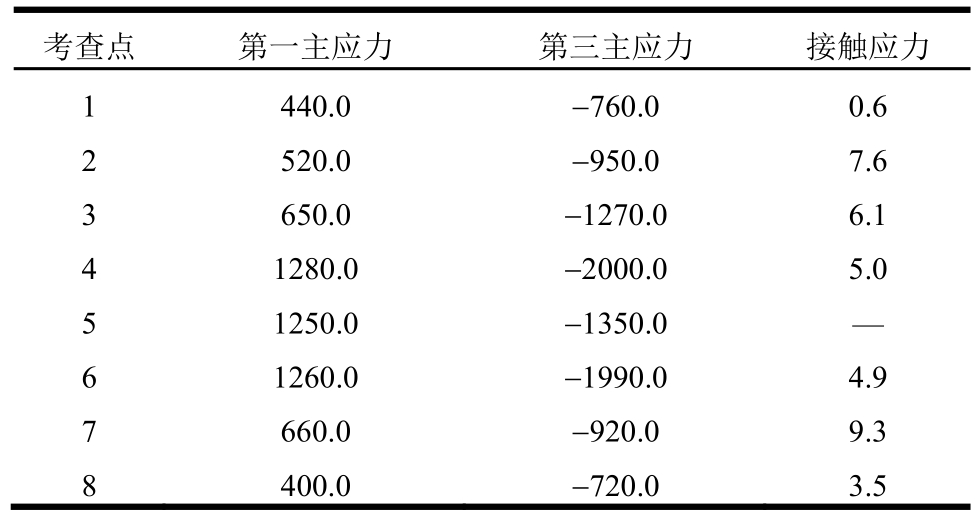
图11 考查点接触应力时程图
Fig.11 Contact stresses at the inspection points
5 结论
为了能够精确并高效求解大规模结构的接触非线性问题，本文基于Lagrange乘子法施加精确的接触约束条件，并利用接触区域局部化的特点进行降维解耦，提出了一种可充分利用并行技术求解大规模结构接触问题的分步接触算法。该算法的基本原理是将接触问题分两步求解，第一步求解由整体系统平衡方程构成的控制方程，第二步求解接触局部区域的约束方程。其中控制方程的系数阵具有对称正定特性，便于使用预处理共轭梯度等方法进行求解，从而避免整体刚度阵的形成与存储；约束方程的规模仅与接触区域的大小有关，通常远远小于整体结构的规模，且约束方程可实现解耦。因此该解法具有如下特点：
(1) 分步接触算法的求解规模远远小于传统的Lagrange乘子法，因为在整个接触求解过程中不必存储与形成整体刚度阵，易于使用并行技术处理。这为大规模结构接触问题的高效求解提供了有力的技术保证。
(2) 引入可自动调整的缩放因子对分步接触算法的迭代过程进行优化，使得该算法既能够保证求解的收敛性，也可以获得尽可能高的收敛速度，可进一步提高大规模结构接触问题的求解效率。
(3) 经典的Hertz接触算例和工程双缝坝接触算例的结果均验证了分步接触算法的正确性。
(4) 穿黄隧洞工程算例结果表明，隧洞衬砌的拱脚和拱底部分为拉应力集中区域，需在工程建设和后期运行维护中给予足够的重视，同时也表明本文的接触算法适用于求解大规模结构的接触问题。
参考文献：
[1]Wriggers P.Computational Contact Mechanics [M].Hoboken: NJ Wiley & Sons, 2002.
[2]王福军.冲击接触问题有限元法并行计算及其工程应用[D].北京: 清华大学, 2000.Wang Fujun.Parallel computation of contact-impact problems with FEM and its engineering application [D].Beijing: Tsinghua University, 2000.(in Chinese)
[3]常亮明.弹塑性接触问题的数值方法及应用[D].北京: 清华大学, 1989.Chang Liangming.Numerical methods and application for elasto-plastic contact problems [D].Beijing: Tsinghua University, 1989.(in Chinese)
[4]毛坚强.接触问题的一种有限元计算方法及其在岩土工程中的应用[D].成都: 西南交通大学, 2002.Mao Jianqiang.A finite element approach for contact problems and its application in geotechnical engineering[D].Chengdu: Southwest Jiaotong University , 2002.(in Chinese)
[5]Blum H, Frohne H, Frohne J, et al..Semi-smooth Newton methods for mixed FEM discretizations of higher-order for frictional, elasto-plastic two-body contact problems.[J].Computer Methods in Applied Mechanics and Engineering, 2016, 309: 131―151.
[6]Dabaghi F, Petrov A, Pousin J, et al.A robust finite element redistribution approach for elastodynamic contact problems[J].Applied Numerical Mathematics,2016, 103: 48―71.
[7]彼得·艾伯哈特, 胡斌.现代接触动力学 [M].胡斌,译.南京: 东南大学出版社, 2003.Eberhard P, Hu Bin.Advanced contact dynamics [M].Translated by Hu Bin.Nan Jing: Southeast University Press, 2003.(in Chinese)
[8]Bourago N, Kukudzhanov V.A review of contact algorithms [J].Mechanics of solids, 2005, 40(1):35―71.
[9]Zmitrowicz A.Contact stresses: a short survey of models and methods of computations [J].Archive of Applied Mechanics, 2010, 80(12):1407―1428.
[10]薛冰寒, 林皋, 胡志强, 等.求解摩擦接触问题的IGA-B可微方程组方法[J].工程力学, 2016, 33(10):35―43.Xue Binghan, Lin Gao, Hu Zhiqiang, et al.Analysis of frictional contact mechanics problems by IGA-B differential equation method [J].Engineering Mechanics,2016, 33 (10): 35―43.(in Chinese)
[11]Goodman R E, Taylor R L, Brekke T L.A model for the mechanics of jointed rock[J].Journal of Soil Mechanics& Foundations Division, ASCE, 1968.94(3): 637―660.
[12]Desai C S.Thin-layer element for interfaces and joints[J].International Journal for Numerical and Analytical Methods in Geomechanics, 1984.8(1): 19―43.
[13]雷晓燕.三维接触问题新模型研究[J].土木工程学报,1996, 29(3): 24―33.Lei Xiaoyan.Research on new model for analyzing three dimensional contact problems [J].China Civil Engineering Journal, 1996, 29(3): 24―33.(in Chinese)
[14]张燎军.水工结构接触问题的力学模型及其在三峡工程中的应用[D].南京: 河海大学, 2005.Zhang Liaojun.Mechanical model for hydraulic structure contact problem and its applications in the Three Gorges project [D].Nanjing: HoHai University, 2005.(in Chinese)
[15]Bednarek T, Kowalczyk P.Improvement of stability conditions, accuracy and uniqueness of penalty approach in contact modeling [J].Computational Mechanics, 2013,51(6): 949―959.
[16]Carpenter N J, Taylor R L, Katona M G.Lagrange constraints for transient finite-element surface-contact[J].International Journal for Numerical Methods in Engineering, 1991, 32(1): 103―128.
[17]Chaudhary A B, Bathe K J.A solution method for static and dynamic analysis of 3-dimensional contact problems with friction [J].Computers & Structures, 1986, 24(6):855―873.
[18]Bathe K J, Chaudhary A.A solution method for planar and axisymmetric contact problems [J].International Journal for Numerical Methods in Engineering, 1985.21(1): 65―88.
[19]Kindo T M, Laursen T A, Dolbow J E.Toward robust and accurate contact solvers for large deformation applications: a remapping/adaptivity framework for mortar-based methods [J].Computational Mechanics,2014, 54(1): 53―70.
[20]赵兰浩, 李同春, 牛志伟.有初始间隙摩擦接触问题的有限元混合法[J].岩土工程学报, 2006, 28(11):2015―2018.Zhao Lanhao, Li Tongchun, Niu Zhiwei.Mixed finite element method for contact problems with friction and initial gaps [J].Chinese Journal of Geotechnical Engineering, 2006, 28 (11): 2015―2018.(in Chinese)
[21]陈万吉.用有限元混合法分析弹性接触问题[J].大连工学院学报, 1979(2): 16―28.Chen Wanji.Analysis of elastic contact problems by mixed approach using finite element method [J].Journal of Dalian University of Technology, 1979(2): 16―28.(in Chinese)
[22]赵兰浩.考虑坝体-库水-地基相互作用的有横缝拱坝地震响应分析[D].南京: 河海大学, 2006.Zhao Lanhao.Seismic analysis of arch dam with contraction joints and dam-water-foundation interaction[D].Nanjing: HoHai University , 2006.(in Chinese)
[23]张立红, 刘天云, 李庆斌, 等.往复荷载作用下的改进动接触力方法[J].工程力学, 2014, 31(7):8―14.Zhang Lihong, Liu Tianyun, Li Qingbin, et al.Modified dynamic contact force method under reciprocating load[J].Engineering Mechanics, 2014, 31 (7): 8―14.(in Chinese)
[24]刘晶波, 吕彦东.结构—地基动力相互作用问题分析的一种直接方法[J].土木工程学报, 1998, 31(3): 55―64.Liu Jingbo, Lu Yandong.A direct method for analysis of dynamic soil-structure interaction [J].China Civil Engineering Journal, 1998, 31(3): 55―64.(in Chinese)
[25]张立红, 刘天云, 李芃, 等.三维整体模型对大型隧洞工程抗震性能的影响分析[J].水力发电学报, 2013,32(2): 240―245.Zhang Lihong, Liu Tianyun, Li Peng, et al.Effects of overall 3D model on seismic performance analysis of large-span tunnels [J].Journal of Hydroelectric Engineering, 2013, 32(2): 240―245.(in Chinese)
[26]Zhang L H, Liu T Y, Li Q B.A robust and efficient composite time integration algorithm for nonlinear structural dynamic analysis [J].Mathematical Problems in Engineering, 2015(2015): 1―11.