盘绕式伸展臂作为支承构件广泛应用于太阳翼、太阳帆、空间站等宇航结构[1－3]，具有构造简洁、刚度质量比大、收纳率高、成本低等优点。对其收展过程的力学研究是工程应用的重难点。盘绕臂收纳时杆件发生大变形并储存弹性应变能，展开时弹性应变能释放。收纳的顺利进行对材料性质、结构参数有较高要求，是展开的基础，有必要推导保证结构顺利收纳的参数要求并提出形式简单的便于工程应用的参考公式。
国外 Eiden[4]基于非线性有限元法首次分析了盘绕臂展开过程中过渡段(尚未展开段与完全展开段之间的半展开部分)的力学性能，Thomas[5]、McEachen[6]、Murphy[7]基于非线性有限元法进行10 m、20 m、40 m长的过渡段力学性能分析，并采集试验数据对模型参数进行修正。国内刘涛[8]对盘绕臂非线性屈曲进行理论和试验研究；张金龙[9]对盘绕臂杆材进行了大转角实验测量；戈东明[10]计算了盘绕臂临界荷载并研究了展开状态的动力性能；刘延柱[11]将纵杆简化为螺旋线，基于 Kirchhoff动力学比拟进行大变形分析；韩建斌[12]研究了纵杆变形，得到了伸展臂构型参数和展开模式间的关系。杨俊[13]基于 Timoshenko梁单元的多体动力学对螺母展开的伸展臂进行了收展分析。
以往研究未推导出便于工程应用的确定纵横杆直径的参考公式，本文就此进行研究。首先采用势能驻值原理和几何精确理论针对整体结构建立大变形后屈曲平衡列式，导出保证结构顺利收纳的扭矩、压力及最小三角框支承刚度，得到了易于工程应用、形式简单的参考公式。
为验证所推导公式的正确性并对收纳过程进行精确、详细的模拟，基于非线性有限元分析理论，将结构离散成有限单元，以收纳过程的大位移、大转角的几何非线性问题为切入点，进行全过程数值分析，得出收纳中结构的应力-应变及能量变化。
1 收纳过程理论分析
合理设计的盘绕臂在收纳中能保持稳定的几何形态，以此为依据确定合理的设计参数。和展开不同，盘绕臂收纳速度较缓慢(1 m/mim～2 m/min)，故计算中不考虑惯性力是能被工程接受的[5,6,12,14]。
1.1 纵杆与三角框相互作用分析
盘绕式伸展臂体系典型方案包括前期的无铰伸展臂及现今主流的有铰伸展臂。有铰伸展臂纵杆通长，杆端通过单向转动铰与端板连接，单向转动铰的转轴沿端板径向，故纵杆可以沿端板切向转动。三根横杆相互固接形成三角形弹性框架，三角框在顶点处通过单向转动铰与纵杆连接，该单向转动铰转动方向垂直于纵杆。图1为美国Orbital ATK公司制作的盘绕式伸展臂样机[15]。
为说明纵杆与三角框的相互作用，绘制两节伸展臂作为演示，如图2(以盘绕臂固定端的中心点为原点，以盘绕臂长度方向为Z轴，每个面采用X型布置拉索，为使图面清晰未画出拉索，图中粗实线是结构原始构型，虚线为转动后构型)。固定底板，转动顶板时纵杆带动三角框一起转动，三角框对纵杆形成支撑，纵杆发生图1所示的螺旋现象。
图1 盘绕臂扭转形成空间螺旋线
Fig.1 Helix of coilable mast
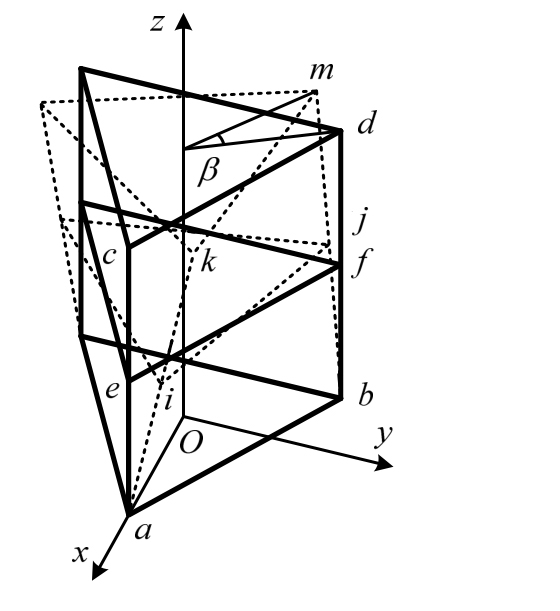
图2 两节伸展臂示意
Fig.2 Schematic of two-bay coilable mast
收纳过程中纵杆与三角框的相互作用力可分解为P和F，作用点是纵杆与三角框的结点。分力F处于三角框平面内，指向三角框形心(见图3，粗实线是原始构型，粗虚线为变形后构型)，分力P处于三角框外接圆的切平面内并倾斜向下(该切平面过纵杆与三角框的结点并垂直于三角框)。P又可分解为三角框平面内的1P(沿三角框外接圆切线)和垂直于三角框平面的2P(沿z轴向下)，1P使三角框发生刚体转动，2P使三角框向下移动。P作用下三角框不发生变形。
图3 三角框受力示意图
Fig.3 Analytical force model of triangular spacer
式中：J为三角框绕形心的转动惯量；
为三角框转动角加速度(转动中心是形心)；m为三角框质量；
为三角框整体向下运动的加速度。
收纳过程是缓慢进行的，加速度及三角框质量m均是小量，故P1、P2也是小量。同时P1、P2作用下发生的是刚体位移，故下文分析力作用下结构的变形时忽略P的影响。
1.2 三角框大挠度后屈曲分析
三角框在F作用下发生变形，F增大，变形也增大(图 3中粗虚线表示变形后三角框)。采用几何精确理论和势能驻值原理，将平衡方程建立在变形后的构型上[16－17]。三角框变形后曲率
与弧长s几何精确的微分关系为[18]：
式中：s为横杆的弧长；y为弯曲挠度；
为杆切线方向与初始轴线夹角(图3)。
以切线角
为自变函数，弧长s为坐标，设每根杆件原始长度为lt，在力F作用下发生位移h。则三角框变形能和外力势分别为：
总势能的变分：
由于δφ具有任意性，于是得到平衡方程：
式(8)与文献[19]中基于分析力学模型建立的弹性压杆大挠度屈曲的 Kirchhoff动力学比拟方程在本质上是相同的。式(8)是三角框的大挠度屈曲计算公式，以
近似sin
可以得到三角框受压发生屈曲的欧拉临界力。三角框的横杆间固接，在端点处
故上述非线性常微分方程属边值问题。基于MATLAB平台的边值问题求解器(BVP)，编制程序先求解
然后计算h，公式为：
1.3 纵杆平衡方程及稳定平衡条件
以盘绕臂整体为考察对象，收纳过程可这样进行：固定底端圆盘，在外力扭矩T作用下，结构发生大转动，在外部压力N辅助下进行收纳[6,20]。
图4 纵杆螺旋线
Fig.4 Helical line of longeron
假定纵杆轴线长度l和纵杆直径dl均为常数，以三根通长纵杆为研究对象，将三角框简化为对纵杆的支承，通过力F实现。假定收纳中纵杆在端部边界条件及三角框的支承力作用下形成空间圆柱螺旋线[6,11,20]。该螺旋线的半径r和螺距p取决于T、N和F。随收纳进行，伸展臂自由端总转角
(含义与图 2中
同)增大，纵杆螺旋线螺距p减小。可写出圆柱螺旋线参数方程为：
式中，
p为螺距。
采用势能变分原理导出纵杆在T、N和F作用下的平衡方程，根据稳定平衡的能量准则建立纵杆稳定平衡条件。设圆截面纵杆抗弯刚度为EIl，抗扭刚度为GIp，材料处于弹性状态。收纳过程中不同时刻纵杆处于不同的螺旋线状态，但在某一时刻下，纵杆形成确定的圆柱螺旋线状态。由圆柱螺旋线的特殊性(式(10))，该时刻曲率半径沿杆弧长为常数。故三根纵杆的弯曲应变能为：
式中，
是空间螺旋线曲率半径，
为螺旋升角。
纵杆与端板通过单向柱铰连接，可限制纵杆杆端的扭转自由度。当盘绕臂自由端转动角度为
时，每根纵杆沿纵杆轴线方向的扭转角也等于
。故纵杆扭转应变能为：
三角框通过力F对纵杆做功，沿力F的方向上发生位移h(图3)，力F做功等于F-h曲线与h轴围成的面积。工程要求h保持在微小量，后文分析发现与T相比，F也是一个小量(数量级相差102)。为便于数学处理，求F做功时采用线性近似的
关系，令图6中曲线转折后
其中Fz为开始转折点，
是曲线的割线刚度[21]。设三角框个数为n，求出力F做功为：
盘绕臂自由端中心点的z坐标为
(图 2及式(10))，沿力N方向上发生的位移为盘绕臂初始长度减收纳后长度为
的势能减小量：
外力矩T的势能减小量：
在收纳中沿纵杆转动方向的拉索会受拉，另一个方向的拉索不受力。根据勾股定理及两点距离公式，拉索两个端点间距离的初始值d0及收纳过程中的值d1分别为：
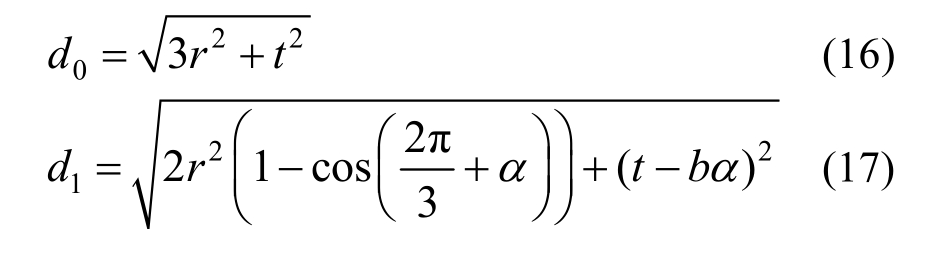
式中，
式(16)及式(17)表明拉索只在收纳开始较短时间内受拉，后文将要推导的式(22)是建立在收纳结束的状态上，此时拉索已退出工作。同时，采用表1中参数，根据式(11)、式(12)、式(13)、式(16)、式(17)计算，盘绕臂纵横杆的应变能为104mJ数量级，拉索的应变能是102mJ数量级。故推导理论公式的过程中忽略拉索的影响。
得到纵杆及各力系的总势能为：
以旋转角
为自变函数，令总势能一阶变分为零可建立扭矩T与转角
的平衡方程：
以r为自变函数，令总势能一阶变分为零导出含有K的平衡方程式(20)，总势能二阶变分大于零导出稳定平衡条件式(21)：
要保证结构顺利收纳Kd必须大于式(21)右边的最大值。cosg最大可取 1，因为：螺旋升角
当完全收纳或接近完全收纳时，螺距p很小，故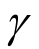
接近零度，可取cos
=1。于是式(21)简化为：
2 收纳全过程数值模拟
2.1 结构建模
从整体结构推导得到形式简单、具有通用价值的参考式(19)、式(20)及式(21)，推导时假定收纳过程中纵杆形成理想的圆柱型螺旋线[6,11,20]，但力学模型决定其并非完全理想的圆柱螺旋线[22－23]。故本文基于 ABAQUS非线性有限元软件，采用弧长迭代法求解，模拟盘绕臂从开始受扭到纵杆形成螺旋线直至完全收纳的全过程，对理论公式合理性进行验证。有限元模型中，纵杆和横杆采用 Timoshenko梁单元，纵杆通长，三根横杆固接形成三角框，三角框与纵杆间的连接释放垂直于纵杆方向的转动自由度。纵杆与端板间释放沿切向的转动自由度。拉索的截面积非常小，只能承受拉伸荷载，抗弯刚度可忽略，采用多段铰接杆单元模拟拉索[24]。
选取盘绕臂参数[20]为：半径 150 mm，总长1884 mm，共9节，节距209.33 mm，纵杆直径2 mm，拉索直径 0.2 mm，合理的横杆直径需通过计算确定。材料参数列于表1[5]。
图5 盘绕式伸展臂整体模型
Fig.5 Numerical model of coilable mast
表1 材料参数
Table 1 Material parameters
2.2 计算确定横杆直径
利用前文推导的式(8)、式(9)和式(22)，通过试算法确定保证收纳过程稳定平衡的最小横杆直径：
首先取工程允许的三角框位移h=3 mm，将2.1部分预确的参数代入式(22)求出Kd＞0.0392。
然后计算横杆直径
是否满足要求：在式(8)中以
近似sin
求出欧拉临界力Fcr=3.277 N。故计算时从2.9 N～4.5 N，以0.001 N为间距对F取值，依次代入式(8)及式(9)，求解不同F下的变形h。计算得F=3.045 N时h=0.00012 mm，认定该点为F-h曲线转折点(该点
)。即
当
(位移与3 mm的偏差在
数量级内)。求出割线刚度
所以2 mm横杆满足刚度要求。
接下来令横杆直径以 0.1 mm为单位递减，重复上述计算，确定横杆最小直径为 1.7 mm，对应刚度0.0394 N/mm。不同杆径下Kd计算结果见表2第3列。
表2 不同横杆直径与收纳顺利的关系
Table 2 Coiling process in various diameters of battern
注：表中Kr为式(22)计算出的最小刚度要求。
图6 收纳过程中作用力F与三角框顶点位移h曲线
Fig.6 Curve of applied forceFand triangle spacer tip point displacementhin folding process
上述确定横杆直径的过程可见图7。
图7 确定横杆直径计算流程
Fig.7 Flow diagram of batten diameter calculation
2.3 数值计算
针对收纳中纵横杆的大转动、大位移问题，采用自适应弧长法进行迭代求解，它采用可变的荷载增量步，可准确的捕获结构屈曲过程中的荷载顶点(刚度阵奇异)和荷载下降段(负刚度)，有效解决后屈曲结构力学问题[8]。以总转角
为计算中停止迭代的判据，
大小根据收纳过程中的几何约束条件确定。收纳中纵杆长度不变：
联立式(10)和式(23)：
完全收纳时纵杆紧密相贴，螺距
前 文 取
有
将r代入式(24)求出
数值计算中设置判据：
时停止迭代。
数值计算中取压力
仅施加扭矩T使结构发生纯扭转进行收纳，根据式(19)初步判断完全收纳时
根据弧长迭代的特点，计算中扭矩荷载应该适当偏大，取T=450 N·mm，求解出收纳过程见图8。
图8 收纳全过程
Fig.8 Whole folding process
3 结果讨论
文章采用的解析方法是从结构整体出发，采用势能驻值原理建立整体结构的平衡方程。采用的数值方法从离散结构出发，基于增量有限元法，从大变形、大转角的几何非线性问题入手求解，两种方法差异显著。对两种方法的计算结果进行对比，来验证计算的正确性。
1) 扭矩-转角平衡曲线对比
数值计算中采用纯扭工况，式(19)中，令N=0同样采用纯扭工况与数值计算进行对比。针对不同横杆直径进行数值模拟结果见图 9，曲线中斜率相当于扭转刚度，其中数值解曲线的斜率是各个点斜率的平均数。2.0 mm、1.9 mm和1.8 mm横杆直径下，理论公式(19)与数值解分别相差4.1%、2.8%、1.3%。这也表明横杆对结构整体抗扭刚度贡献较小，以至于横杆直经的变化对抗扭刚度影响不大。
图9 收纳过程中外力扭矩与总转角曲线
Fig.9 Curve of torque and rotation angle in coiling process
2) 自由端高度变化曲线对比
式(25)给出收纳过程中约束条件，以总转角
为自变量，zT为因变量，绘制式(25)以及数值计算结果的对比曲线见图10，在1范数诱导的度量空间下二者平均距离为 0.064 mm。当
=12.8 rad时，最大偏差为21.09 mm。解析解与数值解有较高的一致性，证明数值模拟较好的符合几何约束关系。
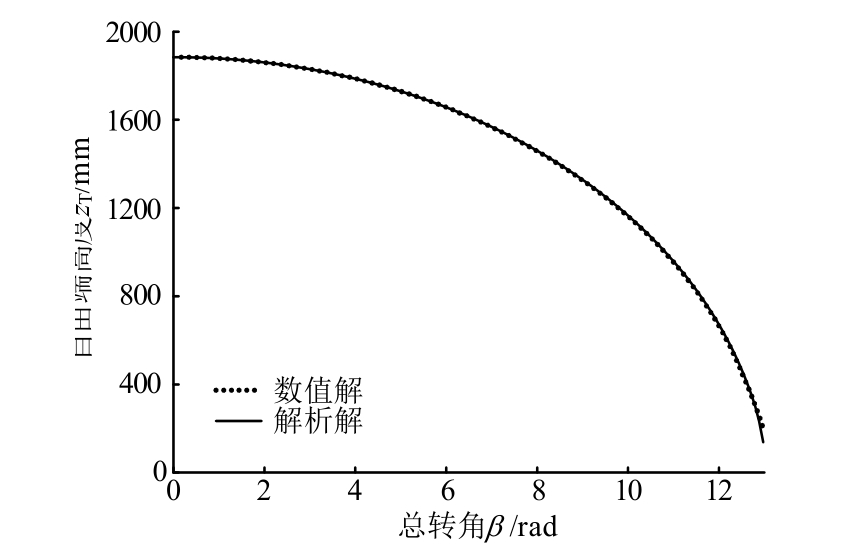
图10 伸展臂自由端高度与转角关系
Fig.10 Curve of tip height and rotation
3) 横杆直径计算结果对比
2.2部分针对不同横杆直径利用式(22)进行理论计算来判定伸展臂能否顺利收纳，现采用数值方法进行验算，计算结果列于表 2。理论公式和数值计算的判定结果基本一致。图 11展示了横杆直径为1 mm时收纳失败的情况。
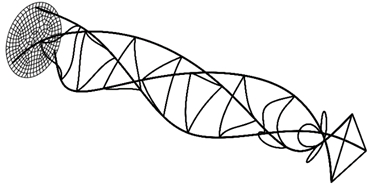
图11 横杆直径1 mm的三角框被压溃
Fig.11 Coiling failure of 1 mm batten
4) 收纳过程能量守恒验证
收纳过程中纵杆和横杆储存变形能，根据能量守恒定律，系统所存储的总应变能G应当等于外力做功ΔU。结构处于弹性工作阶段，总应变能G应等于系统的内能W，据此判断数值模拟结果的正确性[25－26]。图12展示了系统总应变能、内能以及外力做功的关系，总应变能与系统内能基本相等，与外力做功在1范数度量空间下平均偏差为0.02 J，结构收纳结束时有
表明分析过程较好的满足能量守恒定律。
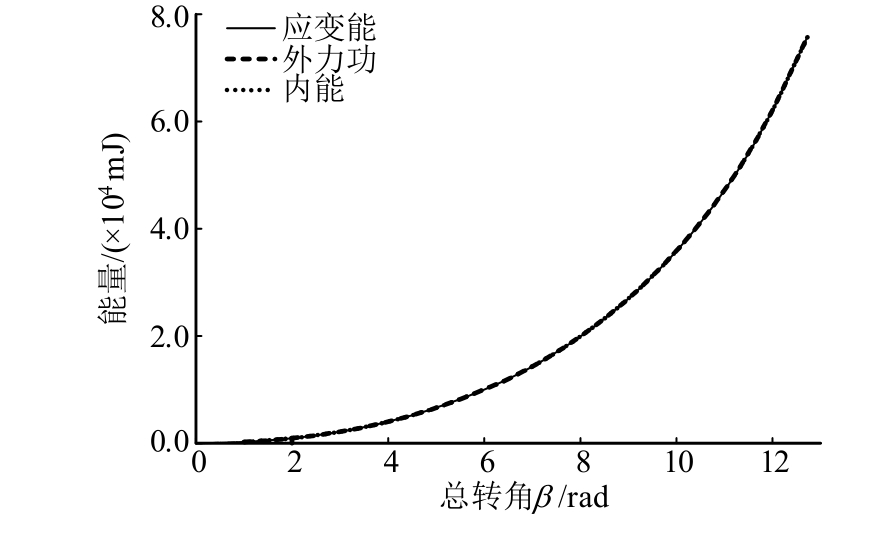
图12 收纳过程中能量随转角变化
Fig.12 Energy variation in folding process
5) 应力-应变
收纳过程中结构最大应力、应变出现在纵杆和横向框架的节点附近，这些区域是结构的危险区域，易发生破坏。图 13是应力最大的三个节点的应力变化图，三点的应力-应变曲线基本重合。收纳过程中结构的最大应力为317.25 MPa，最大应变为0.018(对数应变)，均小于材料的容许值，证明收纳过程是安全的。整个分析过程在普通双核PC上计算耗时约20 min，计算效率高。
图13 最大应力点应力变化曲线
Fig.13 Stress curve of control points
4 结论
文章从两方面对盘绕臂的收纳过程进行分析，首先利用解析算法，从整体结构出发，以收纳过程中稳定平衡状态为依据，采用几何精确理论和势能驻值原理推导了收纳过程中的平衡方程和三角框的最小刚度要求。在目前已发表的伸展臂相关文献中尚缺乏便于工程应用、形式简单的通用参考公式，文章推导出的式(19)、式(20)及式(22)可填补相关空白，用作盘绕臂初步设计、结构选型时的基本参考公式。
然后采用自适应弧长迭代和增量有限元法，将结构离散化，从收纳过程中的大变形、大转角的几何非线性问题入手进行数值模拟，对所推导理论公式的合理性进行验证。收纳中假定纵杆形成圆柱螺旋线，数值模拟表明，当三角框屈曲后刚度大于所推导的式(22)的要求时，纵杆构型较接近圆柱型螺旋线，且能顺利收纳；三角框屈曲后刚度小于式(22)的要求时，纵杆无法形成圆柱型螺旋线，同时收纳失败。与理论推导结果基本一致。
此外，数值模拟还得到收纳过程中的能量、应力-应变变化。解析方法用于推导形式简单、具有通用价值的参考公式，而数值模拟用于获取收纳过程中各物理量更精确、详细的解答。两种方法搭配应用可以提高工程设计的效率。
参考文献：
[1]Zhou K, Huang H, Wang X, et al. Magnetic attitude control for Earth-pointing satellites in the presence of gravity gradient [J]. Aerospace Science and Technology,2017(60): 115―123.
[2]Chen W, Fang G, Hu Y. An experimental and numerical study of flattening and wrapping process of deployable composite thin-walled lenticular tubes [J]. Thin-Walled Structures, 2017(111): 38―47.
[3]Li H, Liu X, Guo S, et al. Deployment dynamics and control of large-scale flexible solar array system with deployable mast [J]. Advances in Space Research, 2016,58(7): 1288―1302.
[4]Eiden M, Brunner O, Stavrinidis C. Deployment Analysis of the Olympus Astromast and Comparison with Test Measurements [J]. Journal of Spacecraft &Amp; Rockets, 1987, 1(24): 63―68.
[5]Thomas A T, Michael E M. Confirmation of non-dimensionalized (scalable) closed- form analytics for modeling slender truss behavior under combined loading[C]. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.USA, Florida, Orlando, 2010, 1492: 1―19.
[6]McEachen M. Validation of SAILMAST technology and modeling by ground testing of a full-scale flight article[C]. 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.USA, Florida, Orlando. 2010, 1491: 1―14.
[7]Murphy D M. Deployment Demonstration and validation of SABUR:A stable articulating backbone for ultra-long radar [C]. AIAA SPACE 2007 Conference & Exposition,USA California Long Beach, September 2007, 9918: 1―26.
[8]刘涛, 韩涵, 冀宾, 等. 盘绕式伸展机构非线性屈曲模式的试验研究与数值仿真[J]. 南京航空航天大学学报,2015, 47(06): 897―903.Liu Tao, Han Han, Ji Bin, et al. Experimental investigation and numerical simulation on nonlinear buckling mode of coil-able mast [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(06):897―903. (in Chinese)
[9]张金龙, 陈务军, 张大旭, 等. 盘绕式空间伸展臂连续纵杆大转角纯弯曲试验[J]. 哈尔滨工程大学学报,2015, 36(6): 750―753.Zhang Jinlong, Chen Wujun, Zhang Daxu, et al. Large rotation pure bending test for the continuous longeron of a coilable space mast [J]. Journal of Harbin Engineering University, 2015, 36(6): 750―753. (in Chinese)
[10]戈冬明, 陈务军, 付功义, 等. 铰接盘绕式空间伸展臂屈曲分析理论研究[J]. 工程力学, 2008, 25(6): 176―180.Ge Dongming, Chen Wujun, Fu Gongyi, et al. Buckling theoretic analysis of coilable hinged space mast [J].Engineering Mechanics, 2008, 25(6): 176―180. (in Chinese)
[11]刘延柱, 薛纭. 受圆柱面约束螺旋线伸展为直杆的动力学分析[J]. 力学学报, 2011, 43(6): 1151―1156.Liu Yanzhu, Xue Yun. Dynamical analysis of stretching process of helical rod to stretch rod under constraint of cylinder [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(6): 1151―1156. (in Chinese)
[12]韩建斌, 王新升, 马海波. 盘绕式伸展臂展开模式的力学原理[J]. 北京航空航天大学学报, 2013, 39(9):1169―1173.Han Jianbin, Wang Xinsheng, Ma Haibo. Mechanical principle of the deploying mode for coilable mast [J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1169―1173. (in Chinese)
[13]杨俊. 大型太阳翼盘绕式展开机构多体动力学研究[D]. 北京: 清华大学, 2013.Yang Jun. Multibody dynamics of the large-scale coilable mast and solar array [D]. Beijing: Tsinghua University,2013. (in Chinese)
[14]张鹏飞, 罗尧治, 杨超. 薄壳屈曲问题的有限质点法求解[J]. 工程力学, 2017, 34(2): 12―20.Zhang Pengfei, Luo Yaozhi, Yang Chao. Buckling analysis of thin shell using the finite particle method [J].Engineering Mechanics, 2017, 34(2): 12―20. (in Chinese)
[15]Orbital A T K. Coilable Boom Systems: Benchmark Performance with Extensive Success Heritage [Z].http://www.orbitalatk.com/space-systems, 2015.
[16]王培军, 王旭东, 张露露. 常温及火灾下蜂窝梁腹板屈曲承载力计算方法[J]. 工程力学, 2017, 34(2): 171―178.Wang Peijun, Wang Xudong, Zhang Lulu. Design method for web-post shear buckling strength of castellated beams at room temperature & in fire [J].Engineering Mechanics, 2017, 34(2): 171―178. (in Chinese)
[17]Madeo A, Groh R M J, Zucco G, et al. Post-buckling analysis of variable-angle tow composite plates using Koiter's approach and the finite element method [J].Thin-Walled Structures, 2010, 110: 1―13.
[18]Saravia C M, Gatti C D, Ramirez J M. On the determination of the mechanical properties of wind turbine blades: Geometrical aspects of line based algorithms [J]. Renewable Energy, 2017(105): 55―65.
[19]Timoshenko Stephen P, James M. Gere. Theory of elastic stability [M]. New York: Courier Corporation, 2012:76―81.
[20]陈务军, 张淑杰. 空间可展结构体系与分析导论[M].北京: 中国宇航出版社, 2006: 1―50.Chen Wujun, Zhang Shujie. Deployable space structures and analysis theory [M]. Beijing: National Defence Industry Press, 2006: 1―50. (in Chinese)
[21]文颖, 孙明文, 李特, 等. 杆系结构非线性后屈曲分析的增量割线刚度法[J]. 工程力学, 2016, 33(12): 12―20.Wen Ying, Sun Mingwen, Li Te, et al. Nonlinear post-buckling analysis of truss structures using an incremental scant secant stiffness approach [J].Engineering Mechanics, 2016, 33(12): 12―20. (in Chinese)
[22]刘延柱, 薛纭. 弹性细杆螺旋线平衡的动态稳定性[J].力学季刊, 2005, 26(1): 1―7.Liu Yanzhu, Xue Yun. Dynamical stability of helical equilibrium of a thin elastic rod [J]. Chinese Quarterly of Mechanics, 2005, 26(1): 1―7. (in Chinese)
[23]苏俊省, 王君杰, 宋彦臣, 等. 钢筋混凝土柱纵筋屈曲长度简化计算模型[J]. 工程力学, 2017, 34(2): 162―170.Su Junsheng, Wang Junjie, Song Yanchen, et al.Simplified calculation model of longitudinal reinforcement buckling length in RC columns [J].Engineering Mechanics, 2017, 34(2): 162―170. (in Chinese)
[24]庄茁, 由小川, 廖剑晖, 等. 基于 ABAQUS的有限元分析和应用[M]. 北京: 清华大学出版社, 2009: 531―542.Zhuang Zhuo, You Xiaochuan, Liao Jianhui, et al.Analysis and application of FEM based on ABAQUS[M]. Beijing: Tsinghua University Press, 2009: 531―542. (in Chinese)
[25]徐颖, 韩庆华, 练继建. 单层球面网壳抗连续倒塌性能研究[J]. 工程力学, 2016, 33(11): 105―112.Xu Ying, Han Qinghua, Lian Jijian. Progress collapse performance of single-layer latticed shells [J].Engineering Mechanics, 2016, 33(11): 105―112. (in Chinese)
[26]Le-Manh T, Huynh-Van Q, Phan T D, et al. Isogeometric nonlinear bending and buckling analysis of variable-thickness composite plate structures [J].Composite Structures, 2017(159): 818―826.