振动模态分析是获取机械结构动态特性不可或缺的技术手段[1]，是振动控制、结构状态监测、减震降噪、机械结构故障诊断[2]、有限元模型修正及确认的基础[3]。一般可将基于测试的振动模态分析归纳为两大类[4]：一是对结构加载人工激励，通过测得系统的输入和输出信号，建立系统的时域[5]或频域[6]输入-输出模型来识别出系统模态参数的试验模态分析(Experimental Modal Analysis, EMA)技术[7－8]；二是在结构工作状态下，只采集结构响应信号就可进行结构模态参数识别的运行模态分析(Operational Modal Analysis, OMA)技术[9－10]。传统的EMA技术对试验环境的要求较高，试验过程需要停止机械结构的工作状态并保持高信噪比的环境。OMA作为EMA的延伸[11]，以机械结构自身运行或周围环境产生的振动、噪声作为激励源，可仅通过系统响应估计模态参数[12]。但是，若机械结构的工作激励噪声频带宽度不够，很难保证激起系统关心频带内的全部模态，存在遗漏主要模态的风险。因此，一种工作状态下的试验模态分析技术被提了出来，其中“含额外激励的运行模态分析”(Operational Modal Analysis in presence of eXogenous inputs, OMAX)[13]是实现该技术的一种常用方法。该方法利用环境激励的响应，同时将人工激励作为补充，计算出较完备的系统函数[14]，主要用于处理随机噪声参与激励的情况[15]。然而，很多情况下机械结构工作环境中含有周期噪声[16－17]，该噪声将在测得的频率响应函数(Frequency Response Function, FRF)中产生虚假的共振峰。当谐波频率靠近某阶模态频率时，将严重影响该阶结构参数识别的精度，因此，在参数识别之前需检测并去除这些谐波成分。一种称为“脉冲-同步模态分析”(Impact-Synchronous Modal Analysis, ISMA)[18]的方法，被用来处理此类问题。此方法根据相位随机假设，通过脉冲-同步时域平均(Impact-Synchronous Time Averaging, ISTA)法来避免系统响应中因噪声激励引起的偏度干扰。为获得较理想的结果，该方法对每次脉冲激励的幅值和激励时间有较高的要求[19]，同时需要较多测试样本以得到较大的时域平均次数。
本文提出一种基于增强概率统计的谐波响应检测方法和基于谐波分解分析的谐波响应去除方法。首先，通过模态空间变换，将响应信号中的谐波噪声分离出来并估计其统计特性，根据概率密度函数和峭度的差异判定谐波成分[21]。然后，根据检测出的谐波频率，采用谐波分解计算重构出独立的谐波响应并在结构响应中将其去除。通过平面刚架的仿真算例和 GARTEUR(Group of Aeronautical Research and Technology in EURope)飞机模型实验算例来介绍提出方法的实现过程，并与传统方法对比，验证了该方法的可靠性。
1 理论背景
1.1 谐波检测
假设X和Y两变量的概率密度函数(Probability Density Function, PDF)分别为
若
根据联合概率密度函数理论可得：
其中，
的一阶导数。设正弦函数为：
考虑到变量时间t属于均匀分布，其概率密度函数是常数fT。求式(2)的反函数并代入式(1)，得到周期函数的概率密度为：
由式(3)可知，当
时，周期函数的概率密度值趋于无穷大，即分别在概率密度曲线的两端出现陡峭的峰值，使其成马鞍面[10]。一般定量的描述该曲线峰值形态(峰态)的数学量称之为峭度，其定义如下：
式中：
是期望算子；
分别为信号y的均值与标准方差。峭度反映了概率密度曲线的陡峭程度[22]，通常满足正态分布的概率密度曲线的峭度K=0；而周期函数的峭度
注意到，对于统计量的估算，一般观察的数据量越大，统计可靠性越高。然而，EMA中含有谐波噪声的脉冲响应信号，由于采样数据量远小于OMA，直接应用采样数据，可能带来统计不可靠。另一方面，对于多通道输出试验，经典的检测方法仅限处理单通道的数据。
为此，采用计及多通道响应数据的统计量估算对经典方法进行优化，以提高谐波检测的可靠性。首先对测得频响函数矩阵做奇异值分解，得：
设
则式(5)中左奇异向量矩阵
奇异值矩阵
右奇异向量矩阵
上标H为共轭转置。得到奇异值曲线上的第r个峰值频率对应的增强响应信号为：
其中：qr为第r个峰值频率对应的增强响应信号；
为第r个峰值频率所对应的左奇异向量；上标T为转置；y为测得所有通道的响应信号。将qr代入式(3)和式(4)，即得到增强信号的统计特征。
1.2 谐波去除
一般含有阻尼的系统，经历足够的时间，由脉冲激励引起的响应会衰减殆尽，可认为剩下的响应仅由未知谐波激励引起。设根据上节理论检测出的n阶谐波频率分别为
则由此表示的多正弦响应信号为：
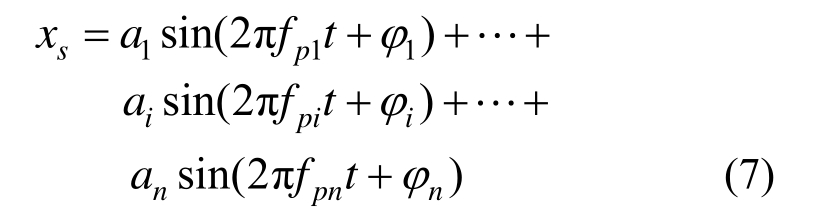
可将式(7)按相位展开成正弦-余弦的形式：
其中，系数
当时间to处的响应信号仅由谐波激励引起时，
则：
由式(9)可解出谐波叠加系数向量并代入式(8)，重构出整个时间段内的仅谐波响应并将其从脉冲响应中去除。
2 仿真算例
如图1所示为一高为4 m、宽为3 m平面刚架结构，其组成梁的宽度为 0.05 m、高度为 0.1 m、弹性模量为 210 GPa、密度为 7800 kg/m3。在结构中添加比例阻尼，其中第一阶阻尼比为 1%，其余均为1.5%。在基础上(1号节点附近)安装有直流电机，设该电机始终以 312 r/min运转，产生基频5.2 Hz及其两倍频10.4 Hz组成的谐波噪声。
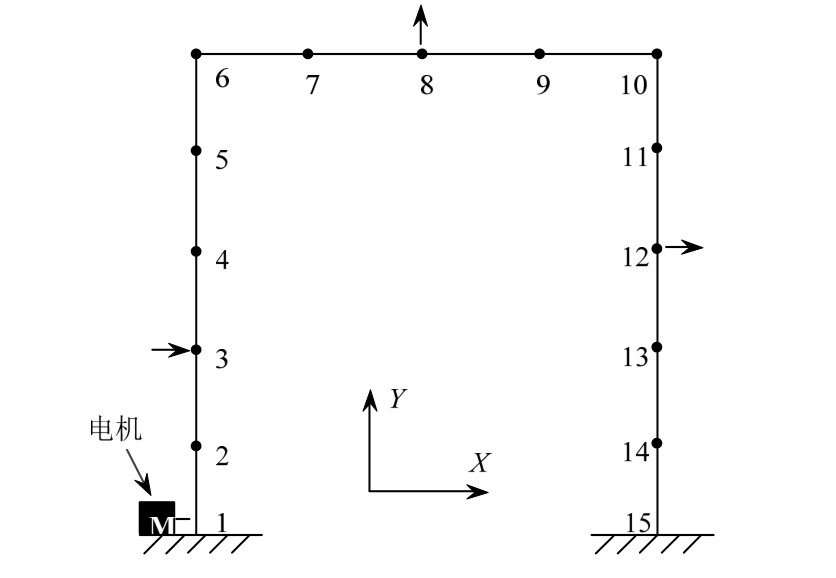
图1 平面刚架结构
Fig.1 The plane frame structure
采用移力锤法，以3X+、8Y-及12X+为参考自由度，设置采样率为 256 Hz，采样时间为 8 s，每个自由度测试 5次，仿真得到系统的加速度响应，如图2所示。
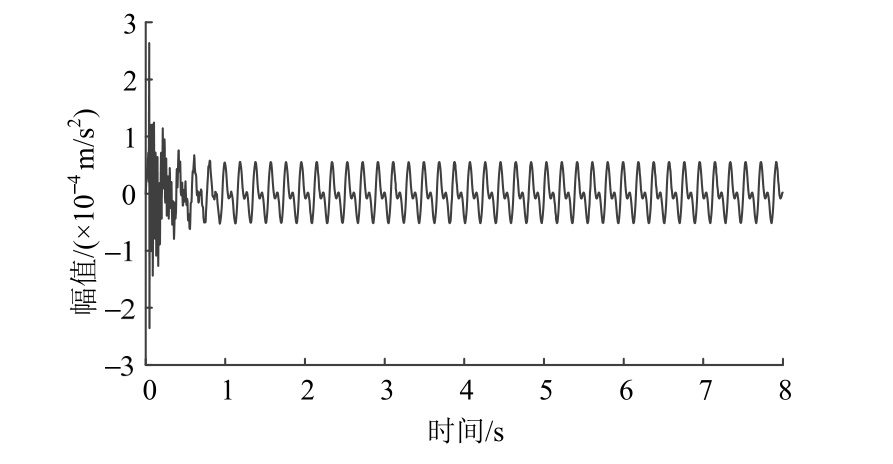
图2 含有谐波噪声的脉冲响应
Fig.2 Impulse response with harmonic noise
图2可看出因结构阻尼的存在，脉冲激励引起的响应最终会衰减殆尽，余下的为电机引起的谐波响应。由脉冲激励及其响应估计出系统的频响函数并由式(5)得到复模态指示函数(Complex Mode Indicator Function, CMIF)曲线，如图3所示。
图3 复模态指示函数
Fig.3 Complex Mode Indicator Function
图 3中的 CMIF曲线清晰指示出了 0 Hz～100 Hz内的八阶“共振”峰。根据仿真设定，其中两阶为谐波成分，并且第1阶谐波频率与第1阶模态频率很接近。采用本文提出的谐波检测方法，得到各峰值频率对应的增强概率密度函数和峭度，如图4所示。
图4中，第2阶及第3阶共振峰对应的增强概率密度曲线呈典型的马鞍状，增强峭度接近-1.5，符合谐波信号的判定，因此可认为它们是由谐波激励引起的“虚假模态”。这与仿真设定结果一致，说明本文提出的基于增强概率统计的谐波检测方法是有效的。同时注意到，与理论值相比，估计得到的概率密度函数形状不太光滑，峭度也存有一定的误差，这是由于部分结构响应信号的干扰引起。
将检测出的谐波频率代入式(9)，解出谐波叠加系数，重构出整个时间域内的谐波响应并将之去除，得到谐波去除前后的频响函数并与理论值对比，如图5所示。
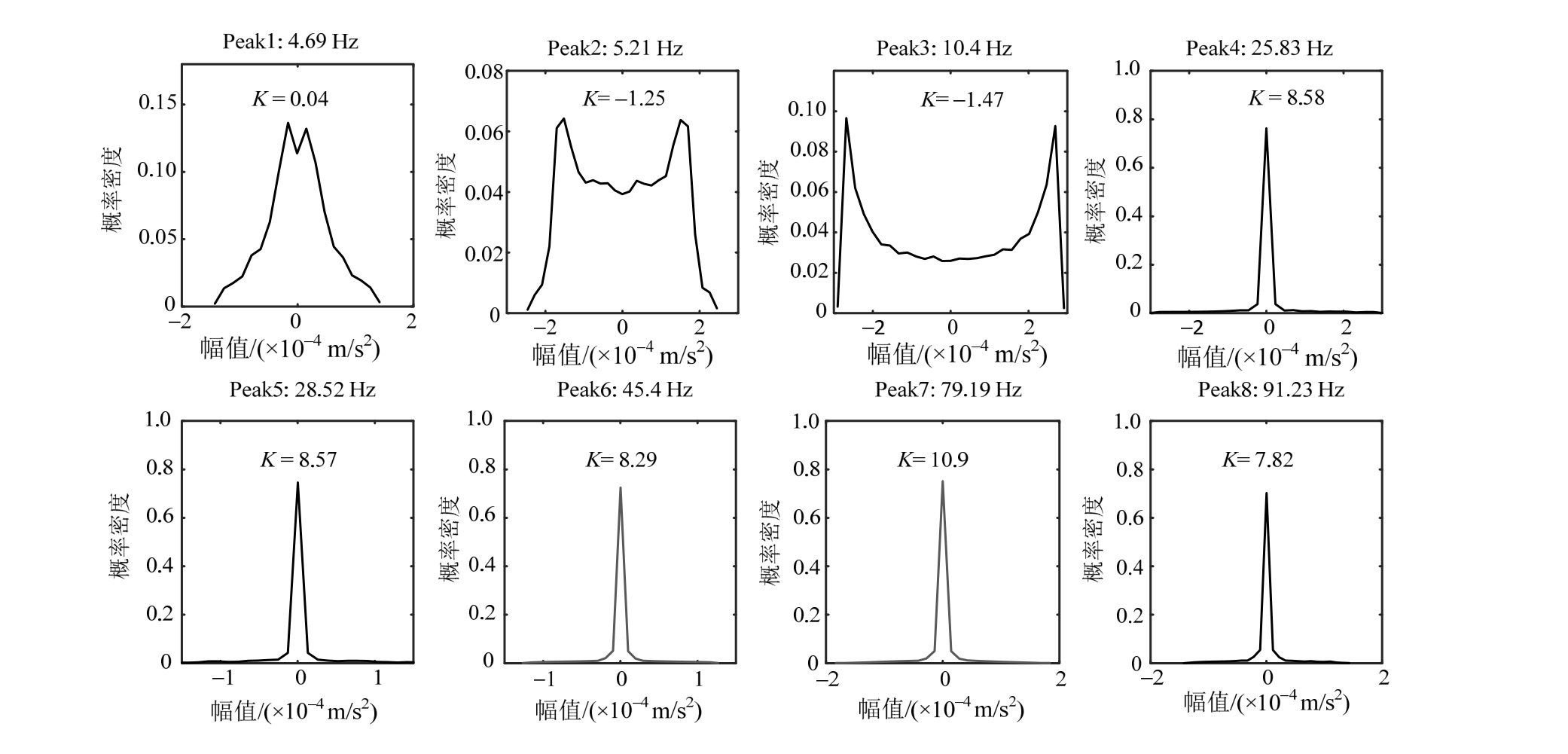
图4 各峰值对应的增强概率密度和峭度
Fig.4 The enhanced PDFs and kurtoses at each peaks
图5 谐波去除
Fig.5 The removal of harmonics
由图5显示结果可知，含谐波响应的频响函数曲线中，第1阶结构模态被谐波噪声淹没，而谐波去除后恢复到理论状态。谐波去除前后识别出的模态参数对比，如表1和表2所示。
表1 谐波去除前后识别出的固有频率及相对误差
Table 1 Modal frequencies before/after harmonics removal
表1结果表明，谐波噪声带来的误差主要对第1阶结构模态参数尤其是模态阻尼的识别影响较大。这是由于基频谐波与第1阶结构模态频率靠的太近，且模态阻尼对外界噪声的影响较敏感。除谐波后，模态参数的识别结果得到有效修正。
表2 谐波去除前后识别出的阻尼比及相对误差
Table 2 Damping ratios before/after harmonics removal
3 实验算例
GARTEUR飞机模型是欧洲航空科技研究集团于20世纪90年代中期设计制造的。该模型具有真实飞机的主要振动模态特征，因此，在航空界得到广泛应用。设定信号采样频率为128 Hz，每次采样时间为16 s，并将测试实验分为两组：第一组，在无噪声激励的情况下，利用脉冲激励测得结构频率响应函数，作为参考标准；第二组，如图 6所示，在脉冲激励的同时，用激振器模拟频率为16 Hz的正弦噪声激励，测得含谐波响应的频响函数。两组实验得到的模态指示函数及各峰值对应的增强概率统计特性分别如图7、图8所示。
图6 实验现场
Fig.6 Experimental scene
图7(b)与图7(a)相比，在16 Hz处多出一阶共振峰，而图8中指示该峰对应的增强概率密度曲线为典型的马鞍状，其增强峭度为-1.46，接近谐波峭度的理论值-1.5，因此，可以认为该峰是由谐波激励引起。这与实验设定一致，验证了本文提出谐波检测方法的有效性。采用本文提出的方法，重构出谐波响应并将之去除，得到谐波去除前后的频响函数对比，如图9所示。
图9结果显示，未知谐波激励的干扰不仅在频响函数中多出一阶伪共振峰，而且在较宽的频带内产生较大幅度的波纹，这种波纹也将会影响结构模态参数识别的精度。采用本文的方法，有效地去除了谐波成分，并修复了谐波引起的波动误差。谐波去除前后识别出结构的固有频率和阻尼比分别如表3和表4所示。
图7 复模态指示函数
Fig.7 Complex Mode Indicator Function
图8 各阶峰值对应的增强概率密度和峭度
Fig.8 The enhanced PDFs and kurtoses at each peaks
图9 谐波去除
Fig.9 The removal of harmonic
表3 谐波去除前后识别出的模态频率及相对误差
Table 3 Modal frequencies before/after harmonics removal
由表3和表4结果可知，谐波响应去除明显改善了模态阻尼的识别精度，说明了本文提出方法的必要性和可靠性。需要说明的是，由于第1阶峰值对应的是刚体模态，且其频率(0.51 Hz)已超出了加速度传感器有效频率测量范围的下限，因此，上述结构模态参数的识别是从第2阶峰值开始的。
表4 谐波去除前后识别出的阻尼比及相对误差
Table 4 Damping ratios before/after harmonic removal
4 结论
本文提出了一种含有谐波噪声的试验模态分析方法，通过增强概率密度和峭度的方法检测出谐波响应频率，利用谐波展开方法重构出时域谐波响应并将其去除。设计仿真和实验算例阐明了提出方法的实现过程，验证了该方法的可靠性，得到如下结论：
(1) 与传统方法相比，本文方法无需对单个测点进行大量的脉冲激励，减少了试验的时间成本，并能取得良好结果。事实上，仿真与实验算例中，含谐波的频响函数已使用脉冲-同步时域平均的方法处理，但受限于平均次数，效果不明显。
(2) 提出的谐波检测方法，无需事先知道谐波频率，提高了谐波判断的可靠性。提出的谐波去除方法，使谐波响应去除更彻底，并可有效的修正谐波噪声带来的误差。
(3) 通过设计仿真与实验算例，检验了本文方法对结构模态密集和谐波频率靠近某阶模态频率时的处理能力。
参考文献：
[1]Reynders E. System Identification Methods for(Operational) Modal Analysis: Review and Comparison[J]. Archives of Computational Methods in Engineering,2012, 19(1): 51―124.
[2]Wang T, Celik O, Catbas F N. Damage Detection of a Bridge Model Based on Operational Dynamic Strain Measurements [J]. Advances in Structural Engineering,2016, 19(9): 1379―1389.
[3]Pintelon R, Schoukens J. Vandersteen G. Frequency domain system identification using arbitrary signals [J].IEEE Trans Autom Control, 1997, 42(12): 1717―1720.
[4]Wang T, Zhang L M, Tamura Y. An Operational Modal Analysis Method in Frequency and Spatial Domain [J].Earthquake Engineering and Engineering Vibration,2005, 4(2): 295―300.
[5]李宇飞, 辛克贵, 樊健生, 等. 环境激励下结构模态参数识别方法综述[J]. 工程力学, 2014, 31(4): 46―52.Liu Yufei, Xin Kegui, Fan Jiansheng, et al. A Review of Structure Modal Identification Methods through Ambient Excitation [J]. Engineering Mechanics, 2014, 31(4): 46―52. (in Chinese)
[6]王彤, 张令弥. 有理分式正交多项式频响函数模态参数识别[J]. 航空学报, 2003, 24(3): 140―143.Wang Tong, Zhang Lingmi. Modal Identification with Frequency Response Function Based on Rational Fraction Orthogonal Polynomials [J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(3): 140―143. (in Chinese)
[7]孙鑫晖, 郝木明, 李振涛. 基于极大似然估计的多参考点模态参数识别方法[J]. 工程力学, 2013, 30(10):65―70.Sun Xinhui, Hao Muming, Li Zhentao. Poly-Reference Modal Identification Based on Maximum Likelihood Estimator [J]. Engineering Mechanics, 2013, 30(10):65―70. (in Chinese)
[8]Ahmed F, Kandagal S B. Modal identification of aircraft wing coupled heave-pitch modes using wavelet packet decomposition and logarithmic decrement [J]. Procedia Engineering, 2016, 144: 435―443.
[9]韩建平, 郑沛娟. 环境激励下基于快速贝叶斯 FFT的实桥模态参数识别[J]. 工程力学, 2014, 31(4): 119―125.Han Jianping, Zheng Peijuan. Modal Parameter identification of an actual bridge by fast bayesian FFT method under ambient excitation [J]. Engineering Mechanics, 2014, 31(4): 119―125. (in Chinese)
[10]Reynders E, Maes K, Lombaert G, et al. Uncertainty quantification in operational modal analysis with stochastic subspace identification: validation and applications [J]. Mechanical Systems and Signal Processing, 2016, 66/67(1): 13―30.
[11]Brinker R, Ventura C E. Introduction to operational modal analysis [M]. West Sussex: John Wiley & Sons Ltd, 2015: 6―13.
[12]Wang T, Celik O, Catbas N, et al. A frequency and spatial domain decomposition method for operational strain modal analysis and its application [J]. Engineering Structures, 2016, 27(1): 62―66.
[13]Pintelon R, Schoukens J, Vandersteen G. Nonparametric Noise Modeling in Presence of Exogenous Inputs [C]//I2MTC 2009—International Instrumentation and Measurement Technology Conference Singapore, May 5,2009: 745―748.
[14]Troyer T D, Runacres M. Frequency-domain modal analysis in the OMAX framework [C]// Proceedings of the IMAC-XXVIII, Jacksonville, Florida USA, February 1, 2010: 465―476.
[15]Devriendt C, Troyer T D, Sitter G D, et al.Transmissibilty-based operational modal analysis for flight flutter testing using exogenous inputs [J]. Shock and Vibration, 2012, 19(5): 1071―1083.
[16]Randall R B, Coats M D, Smith W A. Repressing the effects of variable speed harmonic orders in operational modal analysis [J]. Mechanical Systems and Signal Processing, 2016, 79(1): 3―15.
[17]Bednarz J, Barszcz T, Uhl T, et al. Modal analysis in identification and diagnostics of rotating machinery [C]//13th World Congress in Mechanism and Machine Science, Guanajuato, México, June 19, 2011: 151―162.
[18]Rahman A G A, Ismail Z, Noroozi S, et al. Enhancement of impact-synchronous modal analysis with number of averages [J]. Journal of Vibration and Control, 2014,20(11): 1645―1655.
[19]Rahman A G A, Ong Z C, Ismail Z. Effectiveness of impact-synchronous time averaging in determination of dynamic characteristics of a rotor dynamic system [J].Measurement, 2011, 44(1): 34―45.
[20]夏遵平, 王彤. 基于谱峭度的谐波模态检测方法[J].工程力学, 2013, 30(12): 255―258.Xia Zunping, Wang Tong. Detection of harmonic mode with spectral kurtosis [J]. Engineering Mechanics, 2013,30(12): 255―258. (in Chinese)
[21]Brincker R, Andersen P. An indicator for separation of structural and harmonic modes in output-only modal testing [C]// Proceedings of the European COST F3 Conference on System Identification & Structural Health Monitoring, Universidad Politécnica de Madrid, Spain.,2002: 265―272.
[22]Agneni A, Coppotelli G, Grappasonni G. A method for the harmonic removal in operational modal analysis of rotating blades [J]. Mechanical Systems and Signal Processing, 2012, 27(1): 604―618.