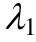 与
与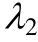 取值范围对蠕变方程的影响,从理论上确定了非定常模型能够描述蠕变的3个阶段。在此基础上,将非定常Burgers模型的蠕变方程推广至三维应力状态下,并基于Levenberg-Marquardt算法对向家坝岩石的三轴压缩蠕变试验曲线进行拟合及参数识别。通过对比定常与非定常 Burgers模型的拟合曲线与相关系数,可以发现非定常Burgers模型拟合效果更好,且能够准确描述包括加速蠕变在内的岩石三阶段蠕变特性,验证了所构建非线性模型的适用性与合理性。
取值范围对蠕变方程的影响,从理论上确定了非定常模型能够描述蠕变的3个阶段。在此基础上,将非定常Burgers模型的蠕变方程推广至三维应力状态下,并基于Levenberg-Marquardt算法对向家坝岩石的三轴压缩蠕变试验曲线进行拟合及参数识别。通过对比定常与非定常 Burgers模型的拟合曲线与相关系数,可以发现非定常Burgers模型拟合效果更好,且能够准确描述包括加速蠕变在内的岩石三阶段蠕变特性,验证了所构建非线性模型的适用性与合理性。韩 阳1,2,谭跃虎1,李二兵1,段建立1,濮仕坤1
(1. 解放军陆军工程大学国防工程学院,江苏,南京 210007;2. 南京城建项目建设管理有限公司,江苏,南京 210006)
摘 要:针对岩石蠕变的非线性特征,提出了一种非线性黏壶元件,并分别替换Burgers模型中的两个线性黏壶元件,从而建立了一种非定常参数 Burgers模型。推导了非定常 Burgers模型的一维蠕变方程,分析模型参数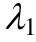 与
与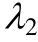 取值范围对蠕变方程的影响,从理论上确定了非定常模型能够描述蠕变的3个阶段。在此基础上,将非定常Burgers模型的蠕变方程推广至三维应力状态下,并基于Levenberg-Marquardt算法对向家坝岩石的三轴压缩蠕变试验曲线进行拟合及参数识别。通过对比定常与非定常 Burgers模型的拟合曲线与相关系数,可以发现非定常Burgers模型拟合效果更好,且能够准确描述包括加速蠕变在内的岩石三阶段蠕变特性,验证了所构建非线性模型的适用性与合理性。
取值范围对蠕变方程的影响,从理论上确定了非定常模型能够描述蠕变的3个阶段。在此基础上,将非定常Burgers模型的蠕变方程推广至三维应力状态下,并基于Levenberg-Marquardt算法对向家坝岩石的三轴压缩蠕变试验曲线进行拟合及参数识别。通过对比定常与非定常 Burgers模型的拟合曲线与相关系数,可以发现非定常Burgers模型拟合效果更好,且能够准确描述包括加速蠕变在内的岩石三阶段蠕变特性,验证了所构建非线性模型的适用性与合理性。
关键词:岩石力学;非定常Burgers模型;三维蠕变方程;加速蠕变;参数识别
岩石流变性态与岩石工程长期稳定性密切相关,因而对其进行准确描述与预测尤为重要。元件组合模型因能较好地反映岩石流变力学特性,且概念清晰明确,而得到了广泛的研究与应用。但传统模型由线性元件组合而成,仅能反映衰减蠕变与稳态蠕变特性,而对于非线性蠕变特征明显的加速蠕变则无法描述。因此,为了完整描述岩石蠕变的三个阶段,特别是加速蠕变阶段,许多研究者构建了不同的非线性蠕变模型。其方法主要有两种。一是新建立一种非线性元件与传统模型相结合,如Sterpi等[1]在Kelvin-Voigt模型基础上串联了一个黏塑性元件,构成了非线性弹黏塑性蠕变模型。而Fahimifar等[2]针对Sterpi模型在预测低应力条件下发生稳态蠕变的不足,又在其基础上串联了同样满足Mohr-Coulomb准则的塑性元件。国内外许多研究者[3-8]针对不同岩石的特性,提出了相应的非线性黏塑性元件,并与传统的线性黏弹性模型串联,形成了非线性黏弹塑性模型,均能较好地模拟岩石的三阶段蠕变特征。肖世武等[9]利用可以统一表征弹性与黏壶元件的 Koeller弹壶元件构建了分数阶导数固体流变模型。二是对线性模型的蠕变参数进行非定常化,得到改进的非线性蠕变模型,如康永刚等[10-11]考虑了黏滞系数的时间效应及应力的影响,建立了改进的非定常蠕变模型;熊良宵等[12]将Burgers模型中串联的Maxwell黏滞体替换为与时间、应力相关的非线性黏滞体,得到了修正的变参数蠕变模型;丁志坤等[13]基于定常H-K体参数拟合结果,将其中弹性模量设为非定常函数,并推导出非定常 H-K体的蠕变方程;罗润林等[14]分别将Burgers模型中Maxwell黏滞系数与Kelvin弹性模量假定为时间的函数,构建了非定常Burgers模型。另外,孙钧[15]归纳了对非线性流变问题的三种求解方法,并认为将黏滞系数η作为非定常参数的方法较为理想。但由于修正后的黏弹性系数为时间、应力状态的函数,计算较为困难,因此多数研究者仅仅将原线性方程中的参数替换为非定常参数,形成隐函数形式的蠕变方程。但隐式的蠕变方程较难从理论上分析各参数变化的影响,同时也不便于模型在数值模拟中的应用。因此,选择简化的非定常参数,并推导非线性蠕变方程是非常有必要的。
基于此,本文同时考虑 Burgers模型中两个黏滞系数的时间效应,以构建非定常Burgers蠕变模型,推导其一维蠕变方程,并分析蠕变参数的影响,进而将方程推广至三维应力状态,分别得到了基于非定常Burgers模型的等围压条件下轴向与径向蠕变显式方程。同时,基于向家坝挤压破碎带岩石的蠕变试验结果,采用Levenberg-Marquardt算法分别辨识各应力水平下 Burgers模型与非定常 Burgers模型参数,分析比较两种模型的拟合效果,验证非线性模型的适用性与合理性。
蒲成志[16]、张强勇[17]、蒋昱州[18]等从岩石蠕变损伤角度,假定损伤演化呈时间的负指数函数形式,构建了蠕变损伤本构模型。许宏发[19]、高文华[20]等由岩石蠕变试验曲线拟合得到弹性模量E与时间t的负指数关系方程,并由弹性模量变化定义损伤变量,进而得出损伤变量D与时间t的负指数关系。
蠕变参数的非定常化,其实质是对蠕变过程中岩石损伤劣化的描述。因而可借用上述损伤变量的时间函数关系对黏壶元件的黏滞系数进行修正,构成非线性黏壶元件,如图1所示。其满足:
式中: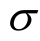 为应力;
为应力;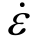 为蠕变速率;
为蠕变速率;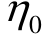 为初始黏滞系数;
为初始黏滞系数;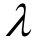 为待定常数。
为待定常数。
对黏滞系数h(t)求导可得:
由于![]()
即黏滞系数随时间衰减,可描述蠕变的损伤软化;则当![]() 即黏滞系数不随时间变化,为常规线性黏壶元件;则当
即黏滞系数不随时间变化,为常规线性黏壶元件;则当![]() 即黏滞系数随时间增大,可描述蠕变硬化。因此可以通过参数
即黏滞系数随时间增大,可描述蠕变硬化。因此可以通过参数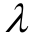 改变非线性黏壶的性质,以满足不同阶段的蠕变特性。亦能表现出范庆忠等[21]指出的岩石蠕变过程中损伤与硬化并存的机制。
改变非线性黏壶的性质,以满足不同阶段的蠕变特性。亦能表现出范庆忠等[21]指出的岩石蠕变过程中损伤与硬化并存的机制。
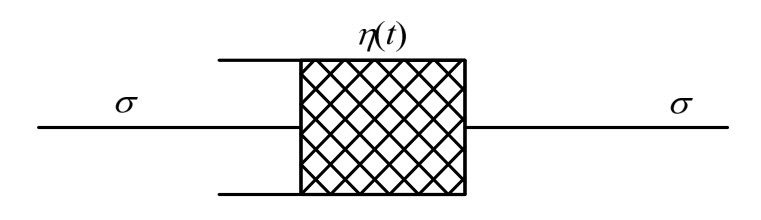
图1 非线性黏壶元件
Fig.1 Nonlinear viscous element
传统的线性 Burgers模型由 Maxwell体与Kelvin体串联构成,如图2所示。
其一维蠕变本构方程为[22]:
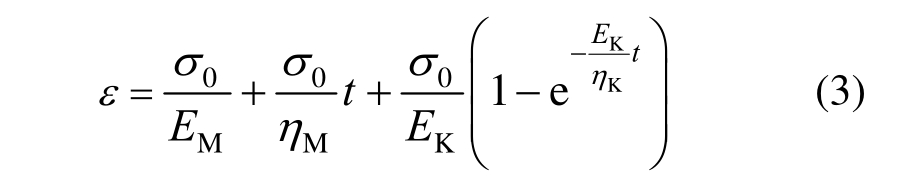
式中:EM为瞬时弹性模量;EK为黏弹性模量;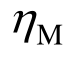 与
与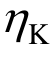 为黏滞系数。
为黏滞系数。
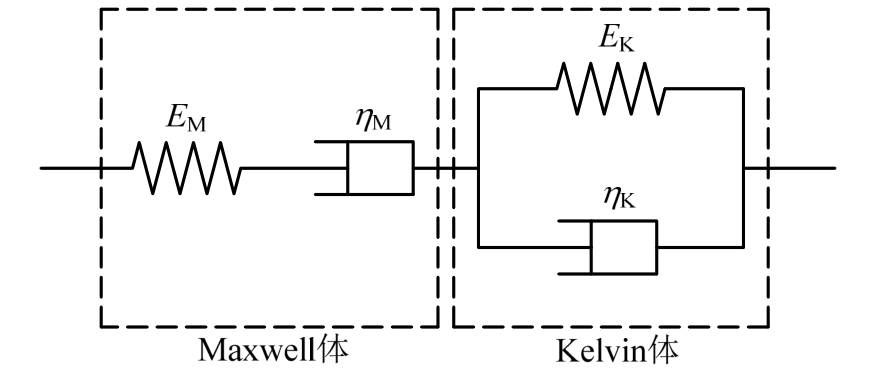
图2 Burgers蠕变模型
Fig.2 Burgers creep model
分别将M体与K体中的黏壶替换为上述非线性黏壶元件,构成图3所示非定常Burgers蠕变模型。
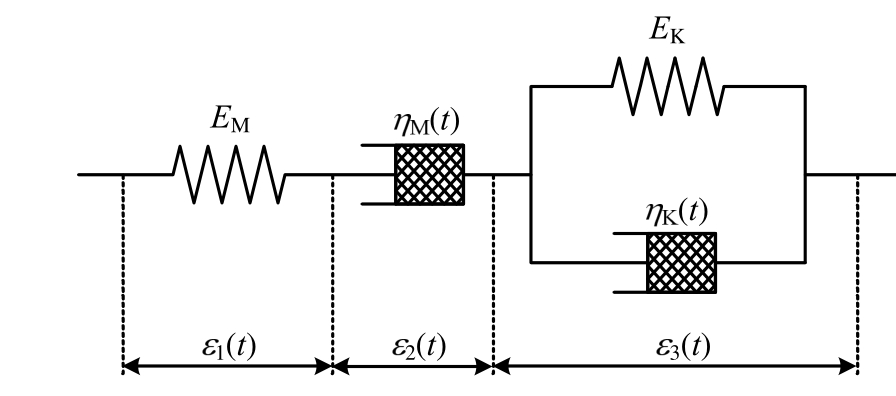
图3 非定常Burgers蠕变模型
Fig.3 Non-stationary Burgers creep model
其中,由![]() 得修正的M体弹性元件蠕变柔量为:
得修正的M体弹性元件蠕变柔量为:

修正的M体黏滞系数为:
式中:![]() 为初始黏滞系数;
为初始黏滞系数;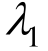 为常数。
为常数。
黏壶状态方程为:
分离变量求定积分:
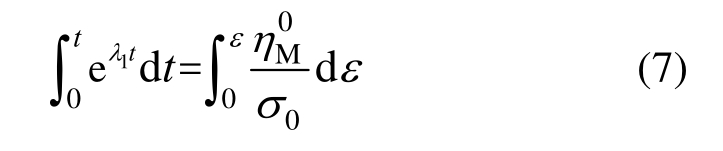
并得蠕变柔量:
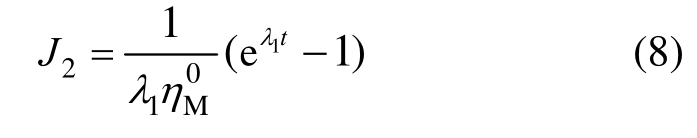
修正的K体黏滞系数为:
式中:![]() 为初始黏滞系数;
为初始黏滞系数;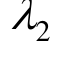 为常数。
为常数。
修正的K体状态方程为:
分离变量求定积分:
并得蠕变柔量:
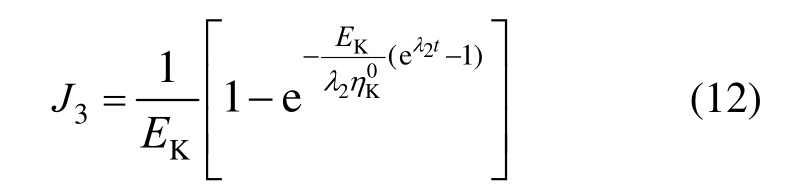
根据元件串联时应变叠加原理有:
则非定常Burgers模型蠕变柔量为弹簧、非线性黏壶以及修正后K体的蠕变柔量之和,即:
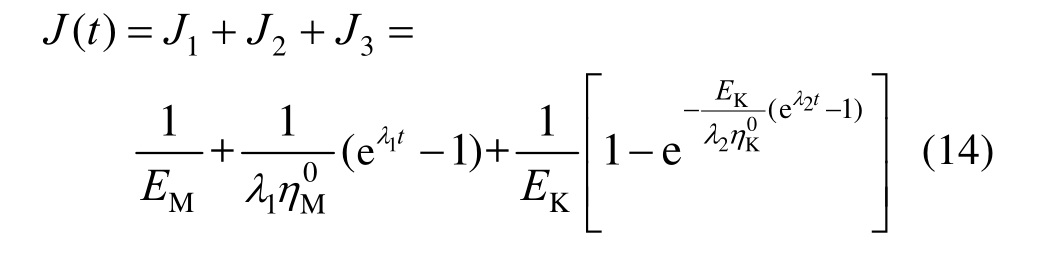
因而,非定常Burgers模型一维蠕变方程为:
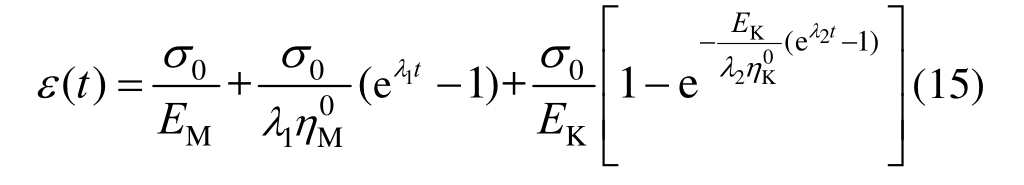
由式(15)分别讨论参数![]() 对蠕变方程的影响:
对蠕变方程的影响:
1) 当![]() 时,有:
时,有:
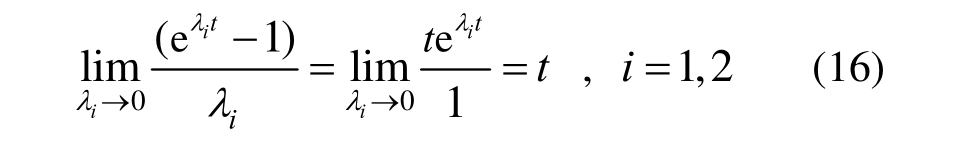
则蠕变方程为:
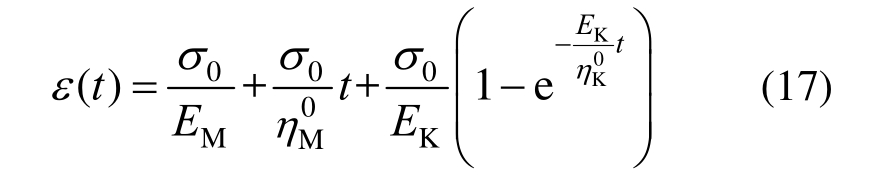
即非定常蠕变模型退化为传统Burgers模型,这与直接将![]() 分别代入式(5)、式(9)相一致。
分别代入式(5)、式(9)相一致。
2) 当![]() 时,有:
时,有:
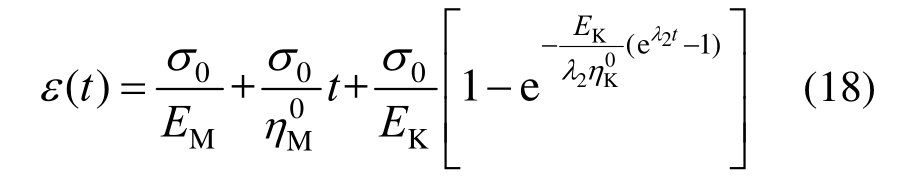
则与Burgers模型类似,可以描述衰减蠕变与稳态蠕变。![]() 时,
时,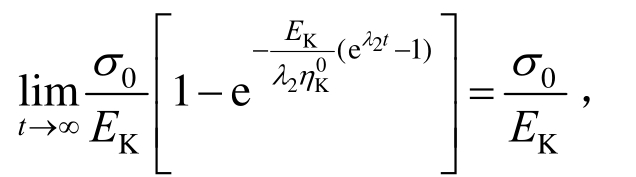 这与传统Burgers模型中的K体性质相同,而
这与传统Burgers模型中的K体性质相同,而![]() 时,
时,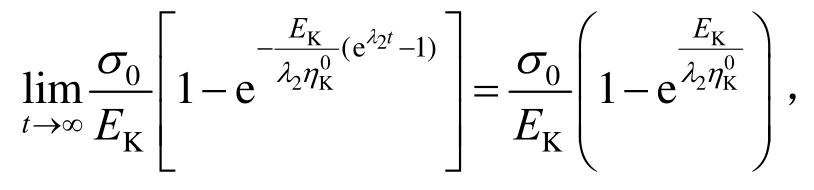 表明
表明![]() 时,修正后的K体有硬化特征,并通过
时,修正后的K体有硬化特征,并通过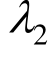 反映其硬化程度,即随着
反映其硬化程度,即随着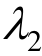 减小,硬化程度越高。
减小,硬化程度越高。
3) 当![]() 时,无论
时,无论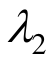 取何值,修正后K体的蠕变应变均收敛于某一定值,而
取何值,修正后K体的蠕变应变均收敛于某一定值,而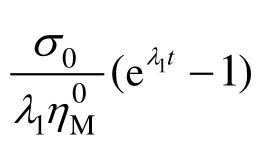 随时间t加速增大,因而可用于描述加速蠕变阶段。
随时间t加速增大,因而可用于描述加速蠕变阶段。
4) 当![]() 时,有
时,有![]() 此时模型总蠕变应变趋于定值,因而可以描述岩石在低应力状态下的衰减蠕变。特别,当
此时模型总蠕变应变趋于定值,因而可以描述岩石在低应力状态下的衰减蠕变。特别,当![]()
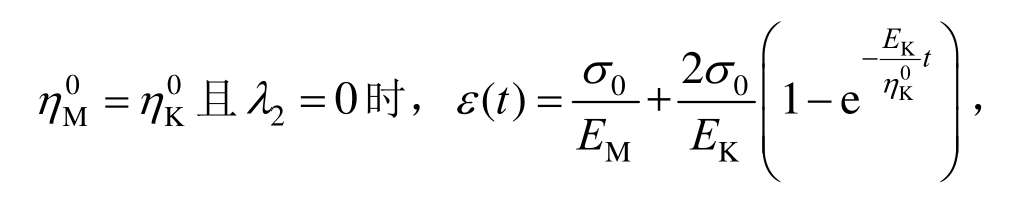
此时蠕变方程类似于广义Kelvin模型。
在三维应力状态下,岩石的应力张量σij可分解为偏应力张量Sij与球应力张量σm,相应的应变张量εij亦可分解为偏应变张量eij与球应变张量![]() 即:
即:
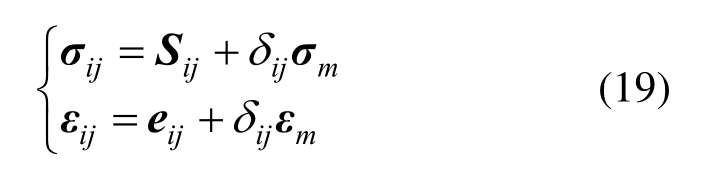
式中:ijd为Kronecker函数;球应力张量与应变张量为:
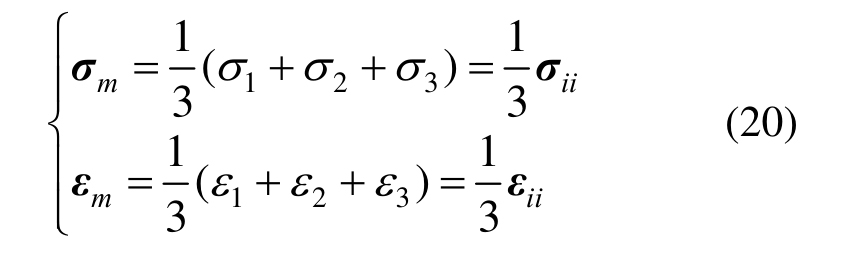
三维应力条件下,弹性元件满足广义虎克定律:

式中:G为剪切模量;K为体积模量。
通常考虑应力偏量仅引起蠕变变形,球应力引起弹性变形,同时假定岩石为各向同性体,则Bugers模型三维蠕变方程为:
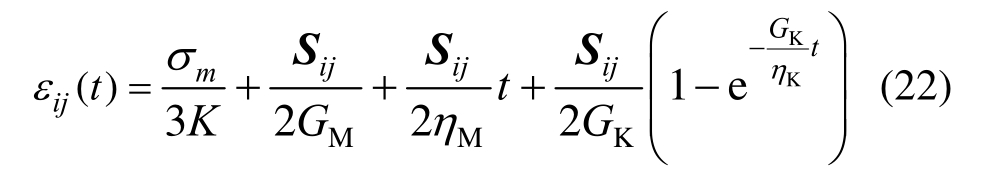
非定常Burgers模型三维蠕变方程为:
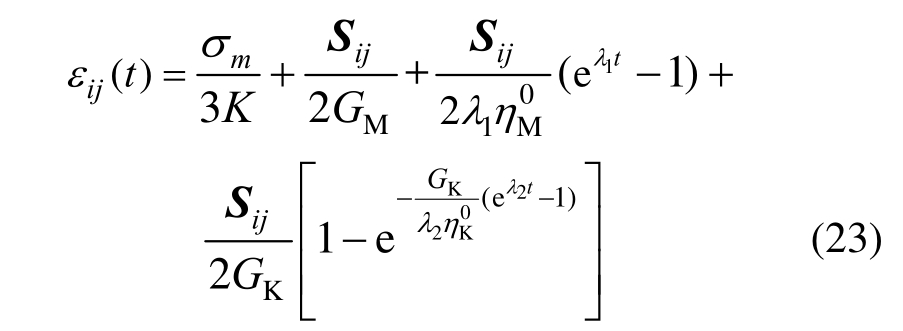
常规三轴压缩蠕变试验时,满足![]() 将其代入式(22)得 Burgers模型在等围压条件下轴向与径向蠕变方程:
将其代入式(22)得 Burgers模型在等围压条件下轴向与径向蠕变方程:
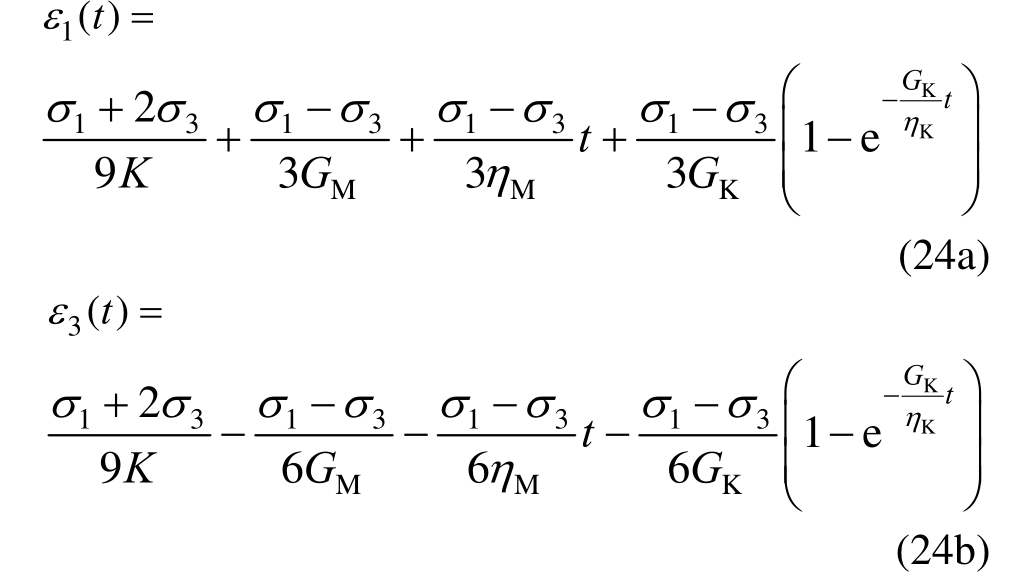
将式(24a)、式(24b)分别代入式(23)得非定常Burgers模型在等围压条件下轴向与径向蠕变方程:

为验证非定常模型的适用性与合理性,基于Zhang等[24]对向家坝挤压破碎带岩石的三轴压缩蠕变试验结果,分别采用传统 Burgers模型与非定常Burgers模型进行拟合对比与参数辨识。文献[24]中试验采用陈氏加载法,轴压分为9级,加速破坏前各级均保持48 h,围压恒为2 MPa。试验获得了岩石试件的轴向与径向蠕变阶梯曲线,但并未进行处理。因此根据玻尔兹曼叠加原理可得到岩石分别在各级应力水平下轴向与径向的蠕变曲线,如图4所示。
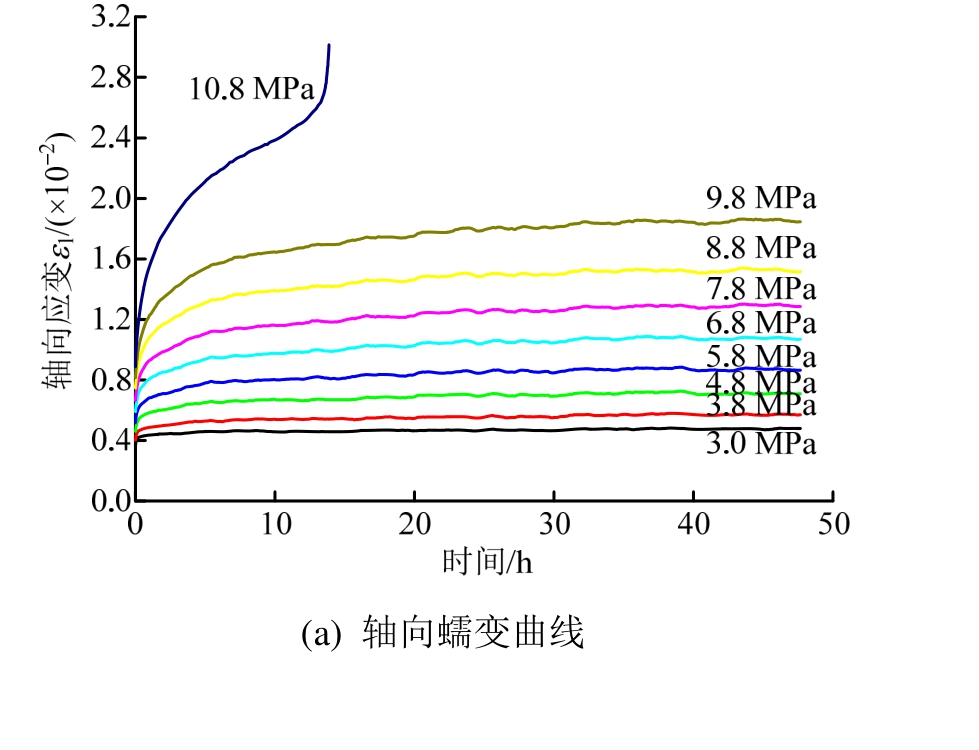

图4 各应力水平下岩石蠕变曲线
Fig.4 Creep curves of rock under different stress levels
从图4可以看出,在前8级应力条件下径向蠕变量随应力增大而缓慢增加,但小于同等应力条件下的轴向蠕变,而在破坏应力下径向蠕变迅速增大,在加速蠕变阶段其蠕变量已大于轴向蠕变。
目前最为常用的曲线拟合方法是最小二乘法,但对于非线性问题的求解,其存在初值选取困难、收敛速度较慢以及易收敛于局部极小点等问题[25]。因此,为克服以上缺陷,采用Levenberg-Marquardt算法对蠕变试验曲线进行拟合与参数辨识。
为了便于参数识别,将式(24)与式(25)中常数项进行合并,即:
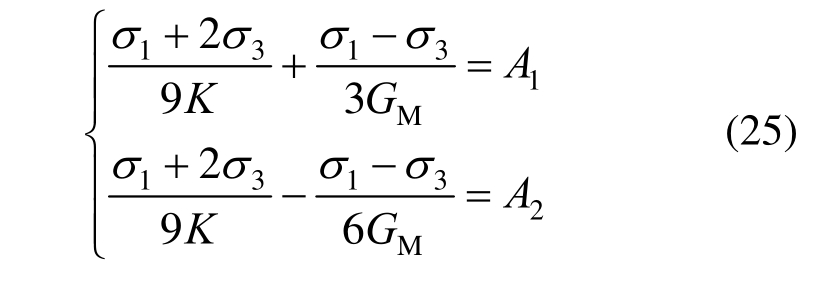
式中,A1与A2为待定常数。
通过拟合蠕变曲线,可辨识得到A1、A2,再根据关系式:
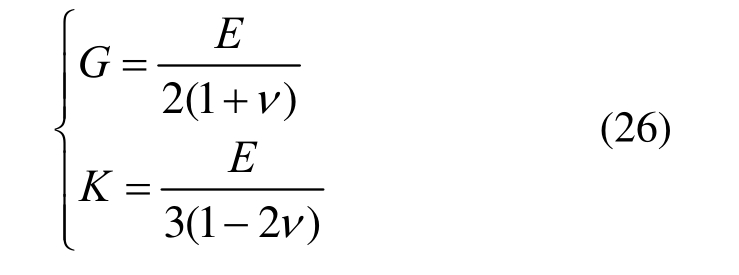
分别求出体积模量K与剪切模量G,其中泊松比假定为0.4[24]。
根据轴向与径向各级蠕变曲线反演得到的模型参数分别如表1和表2所示。
表1 基于轴向应变辨识得到的模型参数
Table 1 Parameter values of model identified by axial strain

由表1和表2可知,非定常Burgers模型拟合曲线的相关系数R均大于Burgers模型,表明采用非定常Burgers模型可以获得较高的拟合精度。
两种模型所辨识的体积模量K与剪切模量GM、GK随应力变化的趋势相一致。其中轴向辨识参数K与GM随应力增大而增加,径向辨识参数K与GM随应力增大而减小。剪切模量GK在轴向与径向均随应力增大而先增加后减小。
模型参数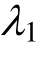 在前8级应力下均为负值,且变化很小,而在第9级应力下为正值,反映了达到破坏应力时岩石损伤劣化突增,而在低于阀值应力水平下则并不显著。模型参数
在前8级应力下均为负值,且变化很小,而在第9级应力下为正值,反映了达到破坏应力时岩石损伤劣化突增,而在低于阀值应力水平下则并不显著。模型参数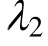 均为负值,但有随应力水平增加而增大的趋势,表明模型中K体有硬化特征,且随应力增大而减弱。
均为负值,但有随应力水平增加而增大的趋势,表明模型中K体有硬化特征,且随应力增大而减弱。
相比而言,由非定常Burgers模型辨识得到的轴向与径向蠕变参数有一定偏差,但较为接近,而由 Burgers模型辨识得到的轴向与径向蠕变参数相差很大。参数的差异主要是因为两个模型的蠕变方程均假定岩石为各相同性材料,而实际试件内部组成复杂,并非完全各向同性体。非定常 Burgers模型反演所得的参数相差较小,是因其方程中考虑了蠕变参数的时间效应,能够较好地反映岩石蠕变参数的变化。这在一定程度上也体现了所建立非线性模型的合理性。另外,为了简化推导,非定常参数并没有考虑应力-应变状态的影响,所以轴向与径向辨识的结果仍存在一定差异。
表2 基于径向应变辨识得到的模型参数
Table 2 Parameter values of model identified by axial strain

图5和图6分别是轴压为5.8 MPa、9.8 MPa和10.8 MPa时非定常Burgers模型与Burgers模型对轴向和径向应变的拟合曲线图。

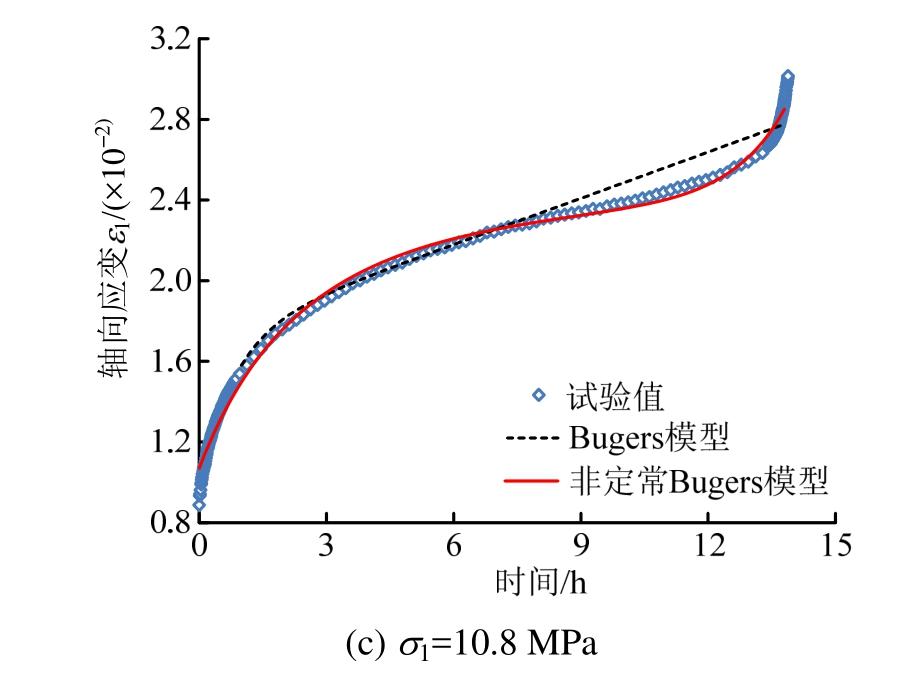
图5 轴向蠕变试验拟合曲线
Fig.5 Fitting curves of axial creep


图6 径向蠕变试验拟合曲线
Fig.6 Fitting curves of radial creep
从图5和图6可以看出Burgers模型与非定常Burgers模型对蠕变前 2个阶段拟合的曲线较为接近,但从径向蠕变拟合曲线能明显发现非定常Burgers模型在衰减蠕变阶段与试验数据更为吻合。
另外,破坏应力下的拟合曲线表明非定常Burgers模型能够描述加速蠕变阶段,而Burgers模型不能反映。总体而言,非定常Burgers模型对蠕变曲线拟合的效果更好,既能准确反映衰减蠕变与稳态蠕变特性,也能较好地描述岩石的加速蠕变。因此,所建立非线性模型较传统线性模型具有更优的拟合效果,且能够由统一的方程对蠕变全过程进行完整描述。
(1) 考虑岩石蠕变参数呈时间的负指数函数形式,对 Burgers模型中两个线性黏壶元件进行非线性化,建立了非定常Burgers模型,并推导了一维蠕变方程。
(2) 讨论了模型参数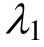 和
和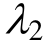 对蠕变方程的影响,通过其取值的不同可以描述蠕变的各个阶段。特别在
对蠕变方程的影响,通过其取值的不同可以描述蠕变的各个阶段。特别在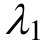 与
与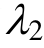 均为零时,非定常Burgers模型退化为传统Burgers模型。
均为零时,非定常Burgers模型退化为传统Burgers模型。
(3) 进行了非定常 Burgers模型的三维蠕变方程推广,并基于Lenvenberg-Marquardt算法对向家坝挤压破碎带岩石三轴压缩蠕变曲线进行拟合及参数识别。辨识得到的参数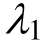 与
与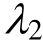 可以反映出岩石损伤与硬化情况。向家坝岩石在前8级应力水平下损伤增加不明显,而在破坏应力下损伤急剧增大。
可以反映出岩石损伤与硬化情况。向家坝岩石在前8级应力水平下损伤增加不明显,而在破坏应力下损伤急剧增大。
(4) 拟合结果表明非定常 Burgers模型拟合效果优于Burgers模型,能更准确地描述包括加速蠕变在内的蠕变三阶段。
参考文献:
[1]Sterpi D, Gioda G. Visco-plastic behaviour around advancing tunnels in squeezing rock [J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 319―339.
[2]Fahimifar A, Karami M, Fahimifar A. Modifications to an elasto-visco-plastic constitutive model for prediction of creep deformation of rock samples [J]. Soils and Foundations, 2015, 55(6): 1364―1371.
[3]李亚丽, 于怀昌, 刘汉东. 三轴压缩下粉砂质泥岩蠕变本构模型研究[J]. 岩土力学, 2012, 33(7): 2035―2040.Li Yali, Yu Huaichang, Liu Handong. Study of creep constitutive model of silty mudstone under triaxial compression [J]. Rock and Soil Mechanics, 2012, 33(7):2035―2040. (in Chinese)
[4]Zhao B Y, Liu D Y, Dong Q. Experimental research on creep behaviors of sandstone under uniaxial compressive and tensile stresses [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2011, 3(Suppl): 438―444.
[5]刘东燕, 赵宝云, 朱可善, 等. 砂岩直接拉伸蠕变特性及Burgers模型的改进与应用[J]. 岩土工程学报, 2011,33(11): 1740―1744.Liu Dongyan, Zhao Baoyun, Zhu Keshan, et al. Direct tension creep behaviors of sandstone and improvement and application of Burgers model [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1740―1744.(in Chinese)
[6]薛凯喜, 赵宝云, 刘东燕, 等. 岩石非线性拉、压蠕变模型及其参数识别[J]. 煤炭学报, 2011, 36(9): 1440―1445.Xue Kaixi, Zhao Baoyun, Liu Dongyan, et al. Nonlinear creep model of rock in tensile or compressive stress and its parameter identification [J]. Journal of China Coal Society, 2011, 36(9): 1440―1445. (in Chinese)
[7]Guan Z C, Jiang Y J, Tanabashi Y, et al. A new rheological model and its application in mountain tunneling [J]. Tunnelling and Underground Space Technology, 2008, 23(3): 292―299.
[8]蒋昱州, 张明鸣, 李良权. 岩石非线性黏弹塑性蠕变模型研究及其参数识别[J]. 岩石力学与工程学报,2008, 27(4): 832―839.Jiang Yuzhou, Zhang Mingming, Li Liangquan. Study on nonlinear viscoelasto-plastic creep model of rock and its parameter identification [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 832―839. (in Chinese)
[9]肖世武, 周雄, 胡小玲, 等. 分数阶导数线性流变固体模型及其应用[J]. 工程力学, 2012, 29(10): 354―358.Xiao Shiwu, Zhou Xiong, Hu Xiaoling, et al. Linear rheological solid model with fractional derivative and its application [J]. Engineering Mechanic, 2012, 29(10):354―358. (in Chinese)
[10]康永刚, 张秀娥. 基于Burgers模型的岩石非定常蠕变模型[J]. 岩土力学, 2011, 32(增刊1): 424―427.Kang Yonggang, Zhang Xiu’e. A non-stationary model for rock creep based on Burgers model [J]. Rock and Soil Mechanics, 2011, 32(Suppl 1): 424―427. (in Chinese)
[11]康永刚, 张秀娥. 一种改进的岩石蠕变本构模型[J].岩土力学, 2014, 35(4): 1049―1055.Kang Yonggang, Zhang Xiu’e. An improved constitutive model for rock creep [J]. Rock and Soil Mechanics,2014, 35(4): 1049―1055. (in Chinese)
[12]熊良宵, 杨林德, 张尧. 岩石的非定常Burgers模型[J].中南大学学报(自然科学版), 2010, 41(2): 679―684.Xiong Liangxiao, Yang Linde, Zhang Yao. Nonstationary Burgers model for rock [J]. Journal of Central South University (Science and Technology), 2010, 41(2):679―684. (in Chinese)
[13]丁志坤, 吕爱钟. 岩石黏弹性非定常蠕变方程的参数辨识[J]. 岩土力学, 2004, 25(增刊): 37―40.Ding Zhikun, Lü Aizhong. Parameter identification of non-stationary creep equation of rock [J]. Rock and Soil Mechanics, 2004, 25(Suppl): 37―40. (in Chinese)
[14]罗润林, 阮怀宁, 孙运强, 等. 一种非定常参数的岩石蠕变本构模型[J]. 桂林工学院学报, 2007, 27(2): 200―203.Luo Runlin, Ruan Huaining, Sun Yunqiang, et al. Nonstationary parameter creep constitutive model of rocks[J]. Journal of Guilin University of Technology, 2007,27(2): 200―203. (in Chinese)
[15]孙钧. 岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报, 2007, 26(6): 1081―1106.Sun Jun. Rock rheological mechanics and its advance in engineering applications [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081―1106.(in Chinese)
[16]蒲志成, 曹平, 张春阳, 等. 考虑时效损伤劣化的变参数非线性蠕变损伤模型[J]. 工程力学, 2017, 34(6):17―27.Pu Zhicheng, Cao Ping, Zhang Chunyang, et al. Variable parameters nonlinear creep damage model of rock with consideration of aging, damage and deterioration [J].Engineering Mechanic, 2017, 34(6): 17―27. (in Chinese)
[17]张强勇, 杨文东, 张建国, 等. 变参数蠕变损伤本构模型及其工程应用[J]. 岩石力学与工程学报, 2009,28(4): 732―739.Zhang Qiangyong, Yang Wendong, Zhang Jianguo, et al.Variable parameters-based creep damage constitutive model and its engineering application [J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(4): 732―739. (in Chinese)
[18]蒋昱州, 徐卫亚, 王瑞红, 等. 岩石非线性损伤蠕变模型研究[J]. 中国矿业大学学报, 2009, 38(3): 331―335.Jiang Yuzhou, Xu Weiya, Wang Ruihong, et al. The nonlinear creep rock damage model research [J]. Journal of China University of Mining & Technology, 2009,38(3): 331―335. (in Chinese)
[19]许宏发. 软岩强度和弹性模量的时间效应研究[J]. 岩石力学与工程学报, 1997, 16(3): 246―251.Xu Hongfa. Time-dependent behaviors of strength and elasticity modulus of weak rock [J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(3): 246―251. (in Chinese)
[20]高文华, 陈秋南, 黄自永, 等. 考虑流变参数弱化综合影响的软岩蠕变损伤本构模型及其参数智能辨识[J].土木工程学报, 2012, 45(2): 104―110.Gao Wenhua, Chen Qiunan, Huang Ziyong, et al. Study on the creep damage constitutive model of soft rocks considering rheological softening and intelligent identification of the parameters [J]. China Civil Engineering Journal, 2012, 45(2): 104―110. (in Chinese)
[21]范庆忠, 高延法. 软岩蠕变特性及非线性模型研究[J].岩石力学与工程学报, 2007, 26(2): 391―396.Fan Qingzhong, Gao Yanfa. Study on creep properties and nonlinear creep model of soft rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(2): 391―396. (in Chinese)
[22]周德培. 流变力学原理及其在岩土工程中的应用[M].成都: 西南交通大学出版社, 1995: 30―32.Zhou Depei. Rheology mechanical principles and application to geotechnical engineering [M]. Chengdu:Southwest Jiaotong University Press, 1995: 30―32. (in Chinese)
[23]张治亮, 徐卫亚, 王伟. 向家坝水电站坝基挤压带岩石三轴蠕变试验及非线性黏弹塑性蠕变模型研究[J].岩石力学与工程学报, 2011, 30(1): 132―140.Zhang Zhiliang, Xu Weiya, Wang Wei. Study of triaxial creep tests and its nonlinear visco-elastoplastic creep model of rock from compressive zone of dam foundation in Xiangjiaba hydropower station [J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 132―140. (in Chinese)
[24]Zhang Z L, Xu W Y, Wang W, et al. Triaxial creep tests of rock from the compressive zone of dam foundation in Xiangjiaba Hydropower Station [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 50(35):133―139.
[25]朱杰兵, 汪斌, 邬爱清. 锦屏水电站绿砂岩三轴卸荷流变试验及非线性损伤蠕变本构模型研究[J]. 岩石力学与工程学报, 2010, 29(3): 528―534.Zhu Jiebing, Wang Bin, Wu Aiqing. Study of unloading triaxial rheological tests and its nonlinear damage constitutive model of Jinping hydropower station green sandstone [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 528―534. (in Chinese)
NON-STATIONARY BURGERS CREEP MODEL OF ROCK AND ITS PARAMETER IDENTIFICATION
HAN Yang1,2, TAN Yue-hu1, LI Er-bing1, DUAN Jian-li1, PU Shi-kun1
(1. College of National Defense Engineering, PLA Army Engineering University, Nanjing, Jiangsu 210007, China;2. Nanjing Urban Construction Project Construction Management Co., Ltd., Nanjing, Jiangsu 210006, China)
Abstract:In view of the nonlinear characteristics of rock creep, a nonlinear viscous component is proposed to replace the two linear viscous components in the Burgers model. Accordingly, a non-stationary Burgers model is established. The one-dimensional creep equation of the non-stationary Burgers model is deduced and the concomitant influence of the range of parameters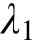 and
and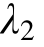 in the model is analyzed. Then, the non-stationary model is theoretically determined to describe the three stages of creep. On this basis, the creep equation of non-stationary Burgers model is extended to three-dimensional stress state. Triaxial compression creep test curve of rock in Xiangjiaba is fitted and its parameters are identified based on the Levenberg-Marquardt algorithm. By comparing the fitted curve and correlation coefficient between stationary and non-stationary Burgers models, it can be found that the fitted results of the non-stationary Burgers model are much better and can accurately describe the creep features in three stages including the accelerated creep status. The applicability and rationality of the established nonlinear model are verified.
in the model is analyzed. Then, the non-stationary model is theoretically determined to describe the three stages of creep. On this basis, the creep equation of non-stationary Burgers model is extended to three-dimensional stress state. Triaxial compression creep test curve of rock in Xiangjiaba is fitted and its parameters are identified based on the Levenberg-Marquardt algorithm. By comparing the fitted curve and correlation coefficient between stationary and non-stationary Burgers models, it can be found that the fitted results of the non-stationary Burgers model are much better and can accurately describe the creep features in three stages including the accelerated creep status. The applicability and rationality of the established nonlinear model are verified.
Key words:rock mechanics; non-stationary Burgers model; three-dimensional creep equation; accelerated creep; parameters identification
中图分类号:TU45
文献标志码:A
doi:10.6052/j.issn.1000-4750.2017.01.0025
文章编号:1000-4750(2018)03-0210-08
收稿日期:2017-01-07;修改日期:2017-09-17
基金项目:国家自然科学基金青年科学基金项目(51408605);国家核设施退役及放射性废物治理科研项目(FZ1402)
通讯作者:谭跃虎(1962―),男,江苏人,教授,博士,博导,主要从事岩石力学与地下工程研究(E-mail: tan_yuehu@126.com).
作者简介:韩 阳(1991―),男,江苏人,硕士生,主要从事岩石力学研究(E-mail: hanyang_ge@126.com);李二兵(1979―),男,湖南人,副教授,博士,主要从事岩石力学与地下工程研究(E-mail: lebingest@126.com);段建立(1971―),男,河北人,副教授,博士,主要从事岩石力学与地下工程研究(E-mail: duan_jianli@163.com);濮仕坤(1982―),男,江苏人,讲师,博士,主要从事岩石力学与地下工程研究(E-mail: kurtbush@gmail.com).