随着悬索桥跨径的增大，吊索的长度也不断增长。由于吊索的质量轻、频率低、阻尼小，极易在风、车辆等荷载作用下发生大幅振动。目前世界上最大跨径的几座悬索桥(如日本明石海峡大桥、我国西堠门大桥、丹麦大海带东桥)的吊索均出现过大幅振动现象[1－3]。悬索桥吊索振动的机理复杂，索股之间的气动干扰、桥塔尾流气动干扰、主缆和主梁的参数激励等都被认为是吊索振动的可能机理[4－5]。理论和工程应用研究结果表明，在斜拉桥拉索上安装阻尼器，可有效地提高斜拉索的结构阻尼，减小斜拉索振动[6－9]。但是，在悬索桥吊索上安装阻尼器，特别是在吊索的索股之间安装阻尼器，减振效果不佳[3]。需要说明的是，由于悬索桥吊索一般由多根(例如2根、4根、6根)索股组成，人们在悬索桥吊索上安装阻尼器时，常在索股之间安装，这样可以减少阻尼器数量，而且不需要设置阻尼器支架。事实上，早在20世纪80年代，人们就发现在两根输电线之间安装阻尼器不能起到减振效果[10]。另外，Ahmad和 Cheng等[11]则对斜拉索之间安装辅助索和阻尼器的控制效果进行了研究。梁栋和陈顺伟等[12]进一步研究了索梁动力耦合对非线性拉索阻尼器减振效果的影响。
为此，本文采用理论分析手段，研究阻尼器对悬索桥吊索的减振效果。考虑双索股吊索的面内振动，阻尼器安装在索股之间，忽略吊索的弯曲刚度，推导了吊索-阻尼器结构体系的运动微分方程；采用有限差分法，对吊索-阻尼器结构体系的运动微分方程进行数值求解，得到了结构频率、振型和阻尼比。以西堠门大桥的典型吊索为工程背景，研究了单个和多个阻尼器工况下的减振效果。
1 计算模型的建立
索股吊索-阻尼器的结构体系示意图如图 1所示。为便于绘图，将竖向布置的吊索水平绘制，左端为吊索的主梁锚固点。吊索长度为L，单根索股张力为T、单位长度质量为M、单位长度上内阻尼系数为cl。考虑了安装单个、多个阻尼器两种工况。其中，对于安装单个阻尼器工况，阻尼器安装在主梁锚固点附近，离主梁锚固点距离为xc；对于安装多个阻尼器工况，阻尼器安装在等分点位置，间距为dc。建立坐标系xoy，x轴和y轴分别为平行和垂直吊索轴向，原点位于吊索的主梁锚固点处。
图1 双索股吊索-阻尼器结构系统示意图
Fig.1 Sketch map of the hanger-damper system
系数股1和索股2在y轴方向位移分别v1(x,t)和v2(x,t)表示，仅考虑索股的面内运动，忽略吊索弯曲刚度的影响，则双索股吊索-阻尼器结构体系的运动微分方程为：
其中：J为阻尼器的个数；xi为第i个阻尼器的x坐标；
为狄拉克函数；f1i(t)和f2i(t)分别为第i个阻尼器产生的对索股1和2的阻尼力，其大小与阻尼器阻尼系数c、阻尼器安装位置处索股的运动速度有关：
2 方程的数值求解
采用分离变量法将方程组式(1)中的空间和时间自变量分离，设v1(x,t)和v2(x,t)可表示为：
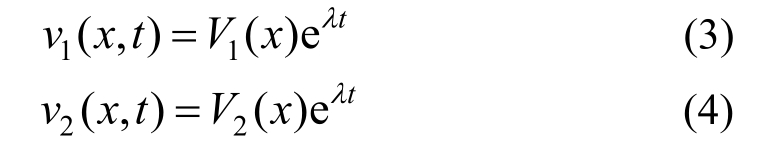
将式(2)～式(4)代入方程组式(1)中，可消去方程组式(1)中的时间变量 eλt：
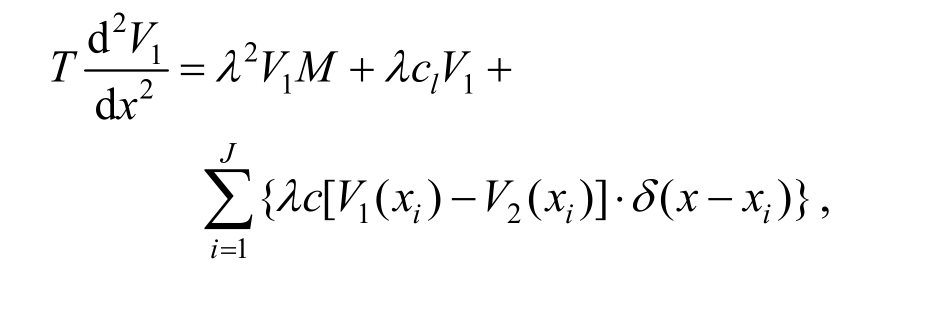
采用有限差分方法对方程组式(5)进行数值求解。方程组式(5)中的狄拉克函数
会在阻尼器安装位置处产生一个无穷大的分布阻尼，采用文献[8]提出的一种近似方法进行处理。将索股等分为N段，节点间距h=L/N。节点编号从左至右分别为0～N，其中左端点为0，右端点为N，如图2所示。需要说明的是，需确保阻尼器位于某个节点处。
图2 吊索空间离散示意图
Fig.2 Discretization of the hanger
考虑吊索两端均为固定的情形，边界条件为：
采用有限差分方法对方程组式(5)进行离散[8]，可得如下特征方程：
其中：K、M和C分别称为刚度矩阵、质量矩阵和阻尼矩阵，其计算方法可参照文献[8]得到；V为位移列向量：
引入状态向量：
可得到广义特征方程：
对式(10)进行复特征值求解，即可得到结构的频率、模态和阻尼比。
3 结果与讨论
以西堠门大桥的一根典型吊索为例进行研究。该吊索长度L=166.9 m，设计索力T=922.3 kN，索股单位长度质量M=25.2 kg/m，第 1阶自振频率f01=0.573 Hz。取单位长度拉索内阻尼系数cl=0。
3.1 单个阻尼器工况
图3给出了在主梁锚固点附近的双索股之间安装单个阻尼器的情况下，双索股-阻尼器结构体系的前9阶结构频率随阻尼器阻尼系数的变化规律，其中xc/L=0.05、0.10。图3中纵坐标中f为结构频率、f01/Hz为单根索股的第1阶频率；横坐标中的
为单根索股的第1阶圆频率，
从图3可以看出，在主梁锚固点附近的索股之间安装阻尼器之后，双索股-阻尼器结构体系的第1阶、3阶、5阶、7阶和9阶频率分别等于单根索股的第1～5阶频率；而双索股-阻尼器结构体系的第2阶、4阶、6阶和8阶频率则比单索股的第1阶～第4阶频率稍大。第2阶、4阶、6阶、8阶频率随着阻尼器阻尼系数的增大而增加，当无量纲阻尼比达到0.05～0.10时，趋于稳定值。比较图3(a)和图3(b)可以看出，随着阻尼器安装高度的增加，双索股-阻尼器结构体系的第2阶、4阶、6阶和8阶稳定频率与单索股第1阶频率f01的比值增大。当
时，第2阶、4阶、6阶、8阶稳定频率与f01的比值分别为1.05、2.10、3.16、4.21；当xc/L=0.10时，比值分别为1.11、2.22、3.33、4.44。
图3 单个阻尼器时吊索振动频率随阻尼器阻尼系数的变化规律(xc/L=0.05和0.10)
Fig.3 Relationship between the frequency of the hanger-damper system and the damping coefficient for single damper (xc/L=0.05 and 0.10)
图4给出了xc/L=0.05、无量纲阻尼器阻尼系数
时双索股-阻尼器结构体系的前 9阶模态的振型。图 3(a)的结果显示，
时前9阶模态的频率趋于稳定值。从图4可以看出，双索股-阻尼器结构体系的第1阶、3阶、5阶、7阶、9阶模态的振型与单索股的振型相同，且两根索股的振动相位完全相同，阻尼器的两端没有相对位移。因此，双索股-阻尼器结构体系的第1阶、3阶、5阶、7阶、9阶模态的频率与单根索股的第1阶～第5阶频率完全相同。但是，双索股-阻尼器结构体系的第2阶、4阶、6阶、8阶模态的振型中，两根索股的振动相位相反，这将导致阻尼器两端产生相对位移，从而对吊索-阻尼器体系的结构频率、阻尼比产生影响。需要说明的是，阻尼器安装位置为
时的双索股-阻尼器结构体系前9阶模态的振型与图4基本相同。
随着阻尼器安装位置的进一步增高，如xc/L=0.20时，吊索-阻尼器结构体系的振动频率随阻尼器阻尼系数的变化规律如图5所示。从图5可以看出，仍然存在对应的模态频率与单索股振动频率相等，但是吊索-阻尼器结构体系的各阶模态之间的存在跳跃现象。例如，当阻尼器阻尼系数较小时
第4阶频率随着阻尼器阻尼系数的增大而增大；第5阶频率随着阻尼器阻尼系数的增大而减小。但是，当
时，第4阶频率随着阻尼器阻尼系数的增大而基本保持不变；第5阶频率随着阻尼器阻尼系数的增大而迅速增大，甚至到
左右大于第9阶频率。这主要是因为随着阻尼器安装高度的增加，吊索-阻尼器结构更趋向为一个索网体系，其结构动力特性比单根索股更为复杂。
人们在索股之间安装阻尼器，是为了提高吊索的结构阻尼比，从而减小吊索振动。图6给出了单个阻尼器高度xc/L=0.05时双索股-阻尼器结构体系的前8阶模态阻尼比随阻尼器阻尼系数的变化规律。从图6可以看出，阻尼器对于奇数阶(第1阶、3阶、5阶、7阶)模态的阻尼比没有贡献，也就是说，由于第1阶、3阶、5阶、7阶模态的振型中两根单索股的振动完全同向，阻尼器两端的相对位移为零，阻尼器对这些模态不产生模态阻尼比。相比之下，阻尼器对于偶数阶(2阶、4阶、6阶、8阶)模态可实现一定的模态阻尼比，模态阻尼比的大小与阻尼器阻尼系数的大小有关，最优无量纲阻尼比
/
可达到 0.55左右，对应的最优无量纲阻尼器阻尼系数
为0.10左右，这与斜拉索中阻尼器的无量纲阻尼比曲线特征类似[6]。因此，在悬索桥吊索靠近梁端的索股之间安装阻尼器，不能对所有模态提供有效的模态阻尼比，效果不佳。当阻尼器安装高度增大到xc/L=0.10时，双索股-阻尼器结构体系的奇数阶模态的阻尼比也为零，但偶数阶模态的无量纲阻尼比曲线与xc/L=0.05时略有不同，低阶模态的最优模态阻尼比似乎更高，如图7所示。
图4 单个阻尼器时吊索前9阶模态的振型(xc/L=0.05)
Fig.4 The first top 9 mode shapes for single damper (xc/L=0.05)
图5 单个阻尼器时吊索振动频率随阻尼器阻尼系数的变化规律(xc/L=0.20)
Fig.5 Relationship between the frequency of the hanger-damper system and the damping coefficient for single damper (xc/L=0.20)
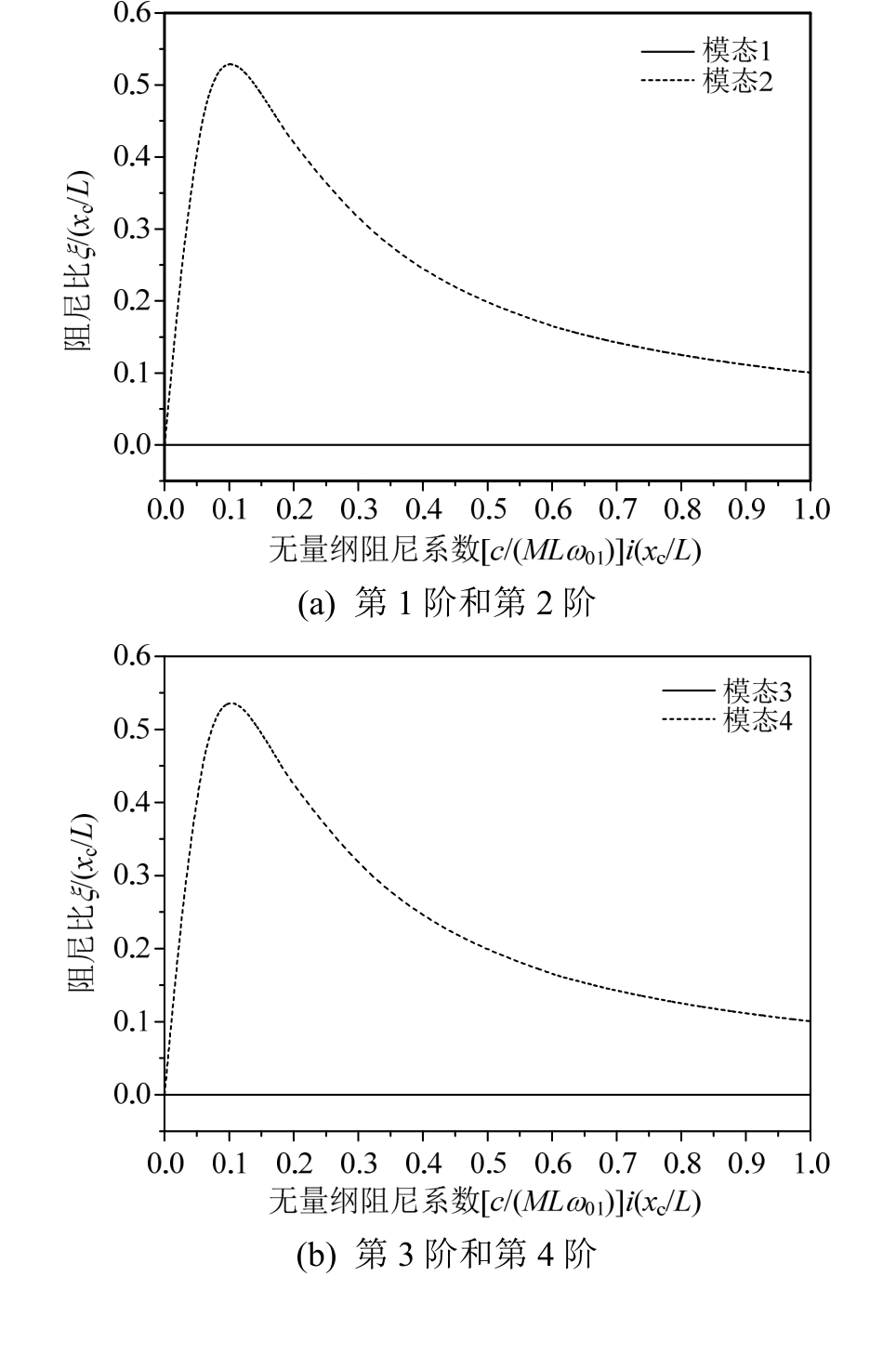
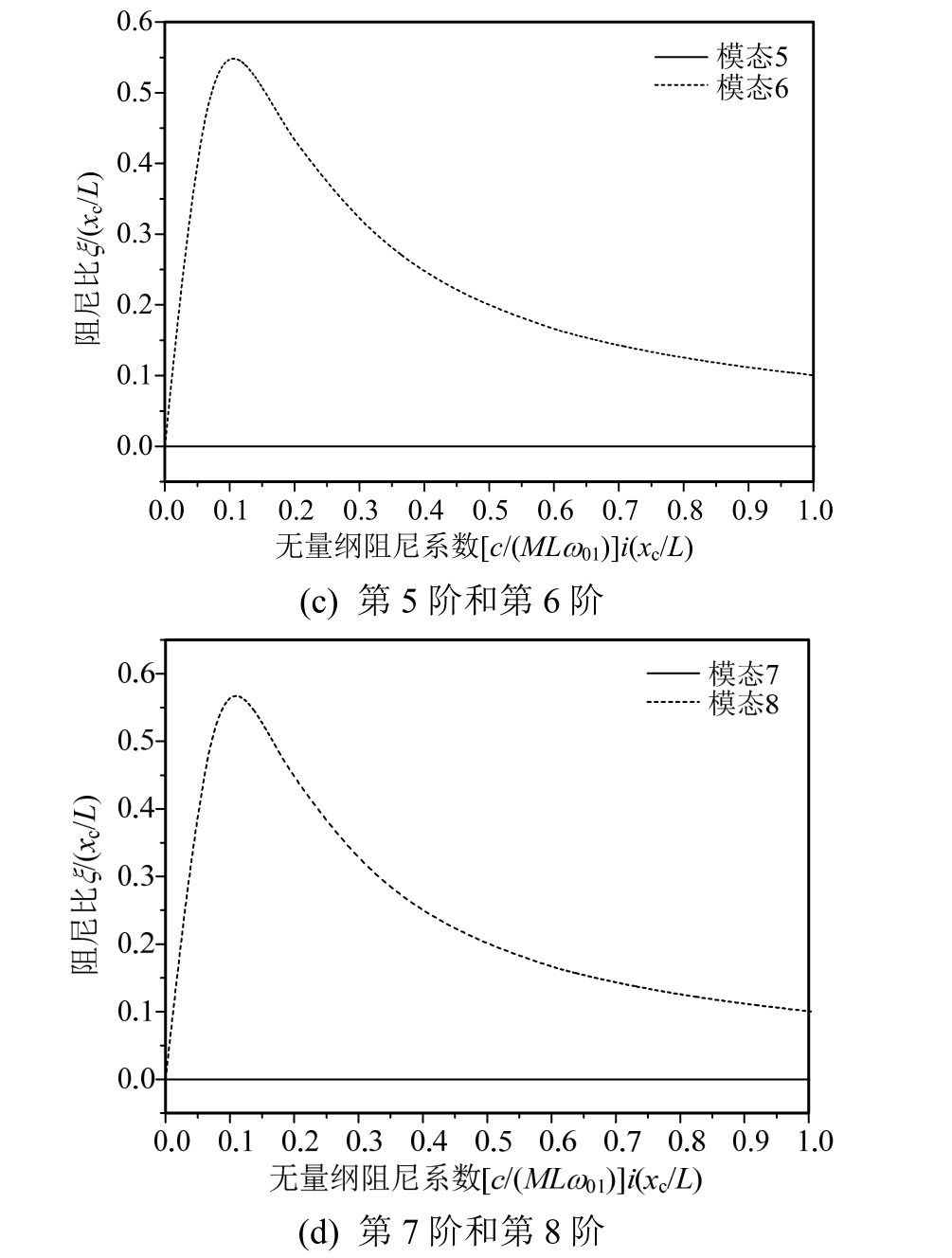
图6 单个阻尼器时吊索各阶模态阻尼比(xc/L=0.05)
Fig.6 Damping ratio of the hanger-damper system for single damper (xc/L=0.05)
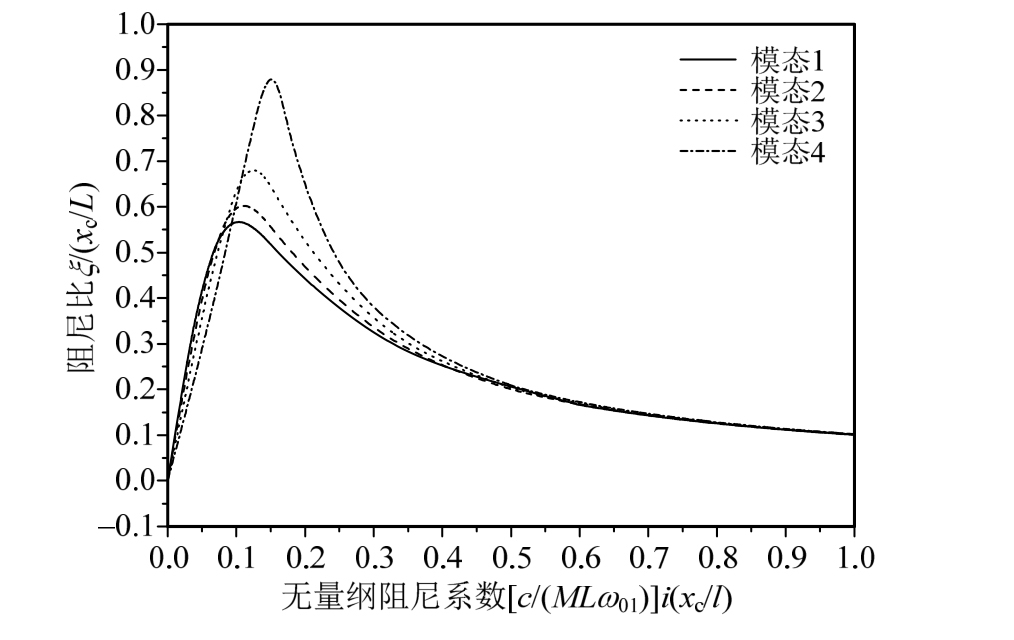
图7 单个阻尼器时吊索偶数阶模态的阻尼比(xc/L=0.10)
Fig.7 Damping ratios of even-order modes for single damper(xc/L=0.10)
3.2 多个阻尼器工况
对多个阻尼器安装在三分点和四分点位置(也就是等间距安装2个和3个阻尼器)时的吊索动力特性进行了研究。图8(a)和图8(b)分别给出了在索股之间等间距安装2个和3个阻尼器时吊索-阻尼器结构体系的前 12阶模态的振动频率随阻尼器阻尼系数的变化规律。从图8可以看出，安装多个阻尼器，吊索-阻尼器结构体系的模态频率在无量纲阻尼系数
范围内出现跳跃现象。当无量纲阻尼器阻尼系数大于0.15时，模态频率趋于稳定，阻尼器相当于一个刚性分隔架。另外，需要注意的是，尽管吊索-阻尼器结构体系的频率会随阻尼器阻尼系数不断变化，但总是有对应模态的振动频率与单索股的频率相等，这些模态均为两根索股的同向振动，阻尼器对这些模态所产生的模态阻尼比为零，这与在主梁锚固点附近安装单阻尼器情况类似。
图9给出了安装3个阻尼器时吊索-阻尼器结构体系前12阶模态的振型，其中无量纲阻尼器阻尼系数为0.15。从图9可以看出，等间距安装3个阻尼器且阻尼系数较大时，前3阶模态均为双索股同向振动，对应于单索股的前3阶模态，此时阻尼器对模态阻尼比的贡献为零。双索股反向振动的模态
图8 多个阻尼器时吊索振动频率随阻尼器阻尼系数的变化规律
Fig.8 Relationship between the frequency of the hanger-damper system and the damping coefficient for multiple dampers
出现在第6阶～第8阶，此时的振动频率为2.301 Hz～2.694 Hz，对风荷载不很敏感。第9阶～第11阶模态是双索股同向振动，对应于单索股的5阶～7阶模态。从以上分析可知，在索股之间等间距安装阻尼器，并没有提高低阶模态的阻尼比，但使得两根索股成为整体，缩短了单根索股的有效长度，提高了单根索股刚度。事实上，在索股之间安装简单的刚性分隔架，即可达到类似的效果，这一振动控制措施在西堠门大桥的吊索减振中取得了较好的效果[3]。
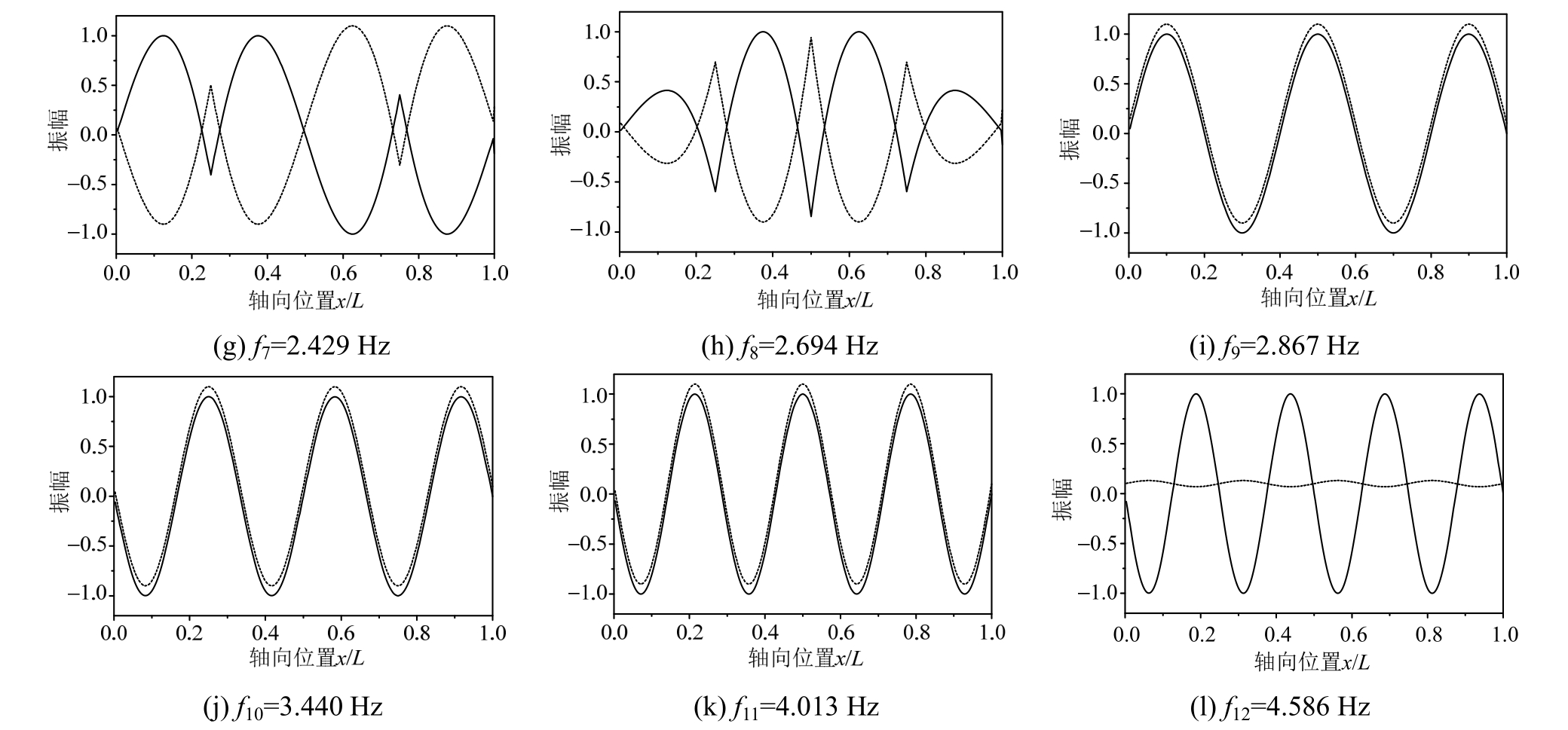
图9 四分点安装3个阻尼器时吊索-阻尼器结构体系前12阶模态的振型([c/(ML
)](xc/L)=0.15)
Fig.9 The first top 12 mode shapes for 3 uniform dampers ([c/(ML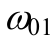
)](xc/L)=0.15)
4 主要结论
采用有限差分方法，研究了索股之间安装阻尼器对双索股吊索模态频率、振型和阻尼比的影响规律，得到了如下主要结论：
(1) 在主梁锚固点附近的索股之间安装单个阻尼器时，吊索-阻尼器结构体系会出现同向和反向模态振型。阻尼器对同向模态振型不提供模态阻尼比，对反向模态振型可实现模态阻尼比，其规律与斜拉索中阻尼器无量纲阻尼比曲线特征类似。
(2) 在索股之间安装多个阻尼器，当阻尼器阻尼系数大于模态频率跳跃区间时，相当于刚性分隔架，吊索-阻尼器结构体系的前3阶模态均为索股同向振动，阻尼器不对低阶模态提供阻尼比。但阻尼器使两根索股成为整体，缩短了单根索股的有效长度，提高了单根索股刚度，对抗风有利。
(3) 总体而言，在吊索的索股之间安装阻尼器，对提高低阶模态阻尼比效果不佳，不建议采取该方法进行吊索振动控制。从西堠门大桥的振动控制经验来看，在索股之间安装刚性分隔架能起到更好的控制效果。
参考文献：
[1]Fujino Y, Kimura K, Tanaka H. Wind resistant design of bridges in Japan: developments and practices [M]. Japan:Springer, 2012: 222―224.
[2]Laursen E, Bitsch N, Andersen JE. Analysis and Mitigation of Large Amplitude Cable Vibrations at the Great Belt East Bridge [J]. Iabse Symposium Report,2006: 64―71.
[3]陈政清, 雷旭, 华旭刚, 等. 大跨度悬索桥吊索减振技术研究与应用[J]. 湖南大学学报(自然科学版), 2016,43(1): 1―10.Chen Zhengqing, Lei Xu, Hua Xugang, et al. Research and application of vibration control method for hanger cables in long-span suspension bridge [J]. Journal of Hunan University(Natural Sciences), 2016, 43(1): 1―10.(in Chinese)
[4]肖春云, 李寿英, 陈政清. 悬索桥双吊索尾流弛振的失稳区间研究[J]. 中国公路学报, 2016, 29(9): 53―58.Xiao Chunyun,, Li Shouying, Chen Zhengqing.Investigation on Instable Region of Wake galloping for Twin Hangers of Suspension Bridges[J]. China Journal of Highway and Transport, 2016, 29(9): 53―58. (in Chinese)
[5]张志田, 吴肖波, 葛耀君, 等. 悬索桥吊索风致内共振及减振措施初探[J]. 湖南大学学报:自然科学版, 2016,43(1): 11―19.Zhang Zhitian, Wu xiaobo, Ge Yaojun, et al. Wind induced internal resonance and the control method of suspension bridge hangers [J]. Journal of Hunan University: Natural Sciences, 2016, 43(1): 11―19. (in Chinese)
[6]Pacheco B M, Fujino Y, Sulekh A. Estimation curve for modal damping in stay cables with viscous damper [J].Journal of Structural Engineering, 1993, 119(6): 1061―1079.
[7]Chen Zhengqing, Hua Xugang, Ko J M, et al. MR damping system for mitigating wind-rain induced vibration on Dongting Lake cable-stayed bridge [J].Wind and Structures, 2004, 7(5): 293―304.
[8]Li S Y, Wu T, Li S K, et al. Numerical study on the mitigation of rain-wind induced vibrations of stay cables with dampers [J]. Wind and Structures, 2016, 23(6):615―639.
[9]Yu Z, Xu Y L. Non-linear vibration of cable-damper systems part I: formulation [J]. Journal of Sound and Vibration, 1999, 225(3): 447―463.
[10]Pa?doussis M P, Price S J, de Langre E. Fluid-Structure Interactions cross-flow-induced instabilities [M]. New York: Cambridge University Press, 2011: 153.
[11]Zhou Haijun, Yang Xia, Sun Limin, et al. Free vibrations of a two-cable network with near-support dampers and a cross-link [J]. Structural Control and Health Monitoring,2015, 22(9): 1173―1192.
[12]梁栋, 陈顺伟, 孔丹丹, 等. 索梁动力耦合对非线性拉索阻尼器减振效果的影响分析[J]. 工程力学, 2012,29(9): 237―244.Liang Dong, Chen Shunwei, Kong Dandan, et al. Effects of coupling vibration between girder and cable on performance of nonlinear cable dampers for cable-stayed bridges [J]. Engineering Mechanics, 2012, 29(9): 237―244. (in Chinese)